下载文档原格式
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解：(1) 取整体(2) 2-4 在简支梁，力的大小等于20KN ，如图所示。
若解：(1)(2)求出约束反力：2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计，图中的长度单位为cm 。
已知F =200 N ，试求支座A 和E 的约束力。
解：(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解：（1）取铰链B (2) 取铰链C 由前二式可得：F FF ADF2-9 三根不计重量的杆AB，AC，AD在A点用铰链连接，各杆与水平面的夹角分别为450，，450和600，如图所示。
试求在与O D平行的力F作用下，各杆所受的力。
已知F=0.6 kN。
解：(1)间汇交力系；(2)解得：AB、AC3-1 已知梁AB 上作用一力偶，力偶矩为M ，梁长为l ，梁重不计。
求在图a ，b ，c 三种情况下，支座A 和B 的约束力解：(a) (b) (c) 3-2 M ，试求A 和C解：(1) 取 (2) 取 3-3 Nm ，M 2解：(1)(2) 3-5 大小为AB 。
各杆 解：(1)(2)可知：(3) 研究OA 杆，受力分析，画受力图：列平衡方程：AB A3-7 O1和O2圆盘与水平轴AB固连，O1盘垂直z轴，O2盘垂直x轴，盘面上分别作用力偶（F1，F’1），（F2，F’2）如题图所示。
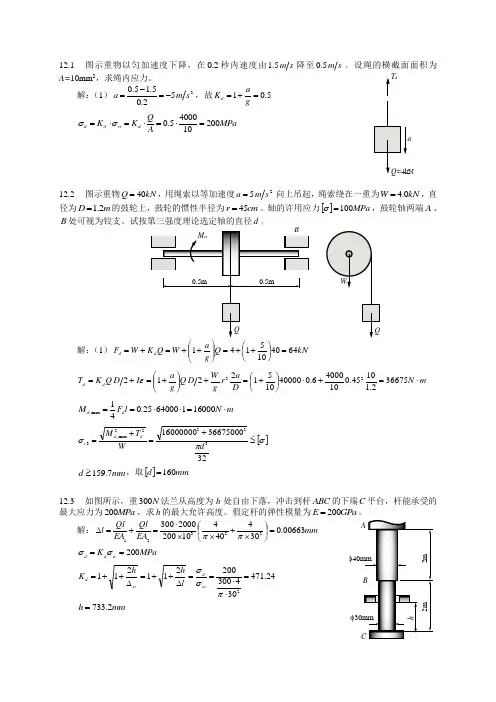
12.1 图示重物以匀加速度下降，在2.0秒内速度由s m 5.1降至s m 5.0。
设绳的横截面面积为A=10mm 2，求绳内应力。
解：（1）252.05.15.0s m a -=-=，故5.01=+=g a K dMPa A Q K K d st d d 2001040005.0=⋅=⋅=⋅=σσ12.2 图示重物kN Q 40=，用绳索以等加速度25s m a =向上吊起，绳索绕在一重为kN W 0.4=，直径为m D 2.1=的鼓轮上，鼓轮的惯性半径为cm r 45=。
轴的许用应力[]MPa 100=σ，鼓轮轴两端A 、B解：（1）kN Q g a W Q K W F d d 6440105141=⎪⎭⎫ ⎝⎛++=⎪⎪⎭⎫ ⎝⎛++=+= m N D a r g W D Q g a I D Q K T d d ⋅=+⋅⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫ ⎝⎛+=+=366752.11045.01040006.0400001051221222ε m N l F M d d ⋅=⋅⋅==1600016400025.041max , []σπσ≤+=+=32366750001600000032222max ,3d WT M d d rmm d 7.159≥，取[]mm d 160=12.3 如图所示，重N 300法兰从高度为h 处自由下落，冲击到杆ABC 的下端C 平台，杆能承受的最大应力为MPa 200，求h 的最大允许高度。
假定杆的弹性模量为E 200=解：mm EA Ql EA Ql l 00663.030440410200200030022321=⎪⎭⎫ ⎝⎛⨯+⨯⨯⋅=+=∆ππ MPa K st d d 200==σσ24.4713043002002112112=⋅⋅==∆++=∆++=πσσst d st d l h h K mm h 2.733=12.4 如图所示，重N 100物体从mm h 500=位置自由下落到铝制梁AB 上的C 点，求截面C 的位移和梁上的最大应力。
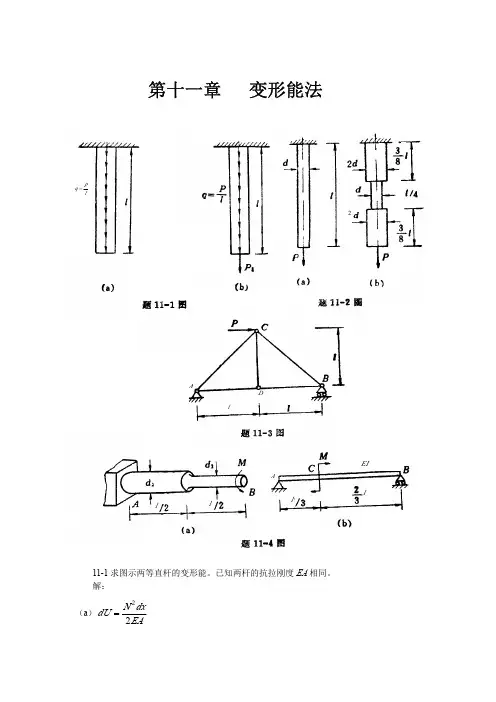
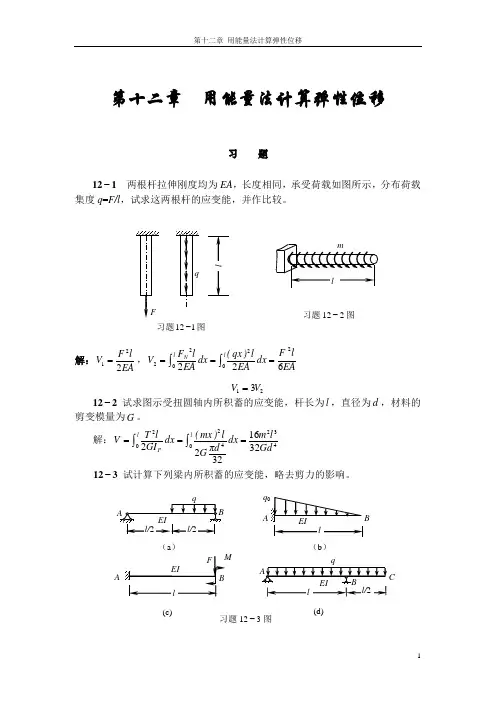
第十二章 用能量法计算弹性位移习 题12−1 两根杆拉伸刚度均为EA ，长度相同，承受荷载如图所示，分布荷载集度q =F/l ，试求这两根杆的应变能，并作比较。
解：EAl F V 221=，EA l F dx EA l )qx (dx EA l F V l l N622202022===⎰⎰ 213V V =12−2 试求图示受扭圆轴内所积蓄的应变能，杆长为l ，直径为d ，材料的剪变模量为G 。
解：4320420232163222Gdl m dx d πGl )mx (dx GI l T V l lP ===⎰⎰ 12−3 试计算下列梁内所积蓄的应变能，略去剪力的影响。
习题12−2图解：（a ）先求支座反力： ql F ,ql F RB RA 8381==以A 为坐标原点，x 1以向右为正，AC 段的弯矩方程为：118x qlM = 以B 为坐标原点，x 2以向左为正，BC 段的弯矩方程为：22222183qx x ql M -= 梁的变形能为：EIl q dx EI )qx qlx (dx EI )qlx (dx EIMdx EI M V l l l l 153601722183282252202222202120222021=-+=+=⎰⎰⎰⎰(b) 以B 为坐标原点，x 以向左为正，AB 段的弯矩方程为：306x lq M =梁的变形能为：EIl q dx EI )l x q (dx EI M V l l 504262520023002===⎰⎰ (c) 以B 为坐标原点，x 以向左为正，AB 段的弯矩方程为：Fx M )x (M +=梁的变形能为：EIl F EI MFl EI l M dx EI )Fx M (dx EI M V l l6222232220202++=+==⎰⎰ (d) 先求支座反力： ,ql F RA 8３=以A 为坐标原点，x 1以向右为正，AB 段的弯矩方程为：21112183qx x ql M -= （0≤x 1≤l ）以C 为坐标原点，x 2以向左为正，BC 段的弯矩方程为：22221qx M -=（0≤x 2≤l /2） 梁的变形能为：EIl q dx EI )qx (dx EI )qx qlx (dx EIMdx EI M V l ll l12803221221832252220222102211202221=-+-=+=⎰⎰⎰⎰12−4 试求图示结构中的弹性变形能。
材料力学习题第12章12-1一桅杆起重机，起重杆AB的横截面积如图所示。
钢丝绳的横截面面积为10mm2。
起重杆与钢丝的许用σ，试校核二者的强度。
力均为MPa[=]12012-2重物F=130kN悬挂在由两根圆杆组成的吊架上。
AC是钢杆，直径d1=30mm，许用应力[σ]st=160MPa。
BC是铝杆，直径d2= 40mm, 许用应力[σ]al= 60MPa。
已知ABC为正三角形，试校核吊架的强度。
12-3图示结构中，钢索BC由一组直径d =2mm的钢丝组成。
若钢丝的许用应力[σ]=160MPa,横梁AC单位长度上受均匀分布载荷q =30kN/m作用，试求所需钢丝的根数n。
若将AC改用由两根等边角钢形成的组合杆，角钢的许用应力为[σ] =160MPa，试选定所需角钢的型号。
12-4图示结构中AC为钢杆，横截面面积A1=2cm2；BC杆为铜杆，横截面面积A2=3cm2。
[σ]st = 160MPa，[σ]cop [F。
= 100MPa，试求许用载荷]12-5图示结构，杆AB为5号槽钢，许用应力[σ] = 160MPa，杆BC为bh= 2的矩形截面木杆，其截面尺寸为b = 5cm, h = 10cm,许用应力[σ] = 8MPa，承受载荷F = 128kN，试求：（1）校核结构强度；（2）若要求两杆的应力同时达到各自的许用应力，两杆的截面应取多大？12-6图示螺栓，拧紧时产生∆l = 0.10mm的轴向变形，试求预紧力F，并校核螺栓强度。
已知d1=8mm, d2=6.8mm, d3=7mm, l1=6mm, l2=29mm, l3=8mm; E=210GPa, [σ]=500MPa。
12-7图示传动轴的转速为n=500r/min，主动轮1输入功率P1=368kW，从动轮2和3分别输出功率P2=147kW 和P3=221kW。
已知[σ]=212MPa，[ ϕ]=1︒/m, G =80GPa。
（1）试按第四强度理论和刚度条件确定AB段的直径d1和BC段的直径d2。
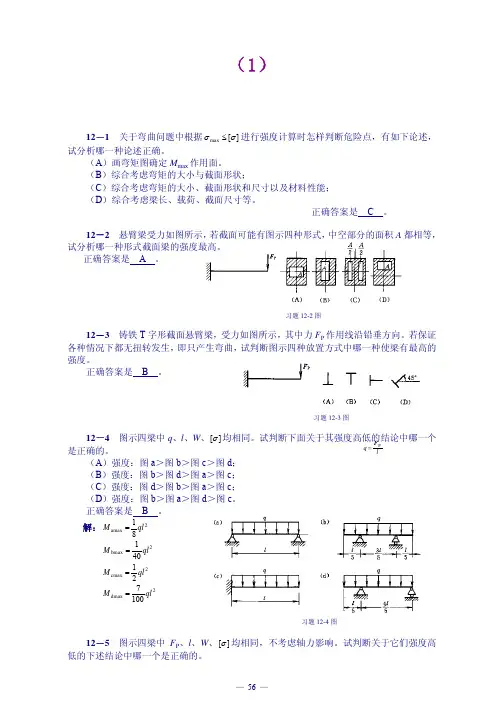
工程力学（工程静力学与材料力学）习题与解答第12章 强度理论12－1 对于建立材料在一般应力状态下的失效判据与设计准则，试选择如下合适的论述。
（A ）逐一进行试验，确定极限应力；（B ）无需进行试验，只需关于失效原因的假说；（C ）需要进行某些试验，无需关于失效原因的假说； （D ）假设失效的共同原因，根据简单试验结果。
知识点：建立强度理论的主要思路 难度：一般 解答：正确答案是 D 。
12－2 对于图示的应力状态（y x σσ>）若为脆性材料，试分析失效可能发生在： （A ）平行于x 轴的平面； （B ）平行于z 轴的平面；（C ）平行于Oyz 坐标面的平面； （D ）平行于Oxy 坐标面的平面。
知识点：脆性材料、脆性断裂、断裂原因 难度：难 解答：正确答案是 C 。
12－3 对于图示的应力状态，若x y σσ=，且为韧性材料，试根据最大切应力准则，失效可能发生在： （A ）平行于y 轴、其法线与x 轴的夹角为45°的平面，或平行于x 轴、其法线与y 轴的夹角为45°的平面内；（B ）仅为平行于y 轴、法线与z 轴的夹角为45°的平面； （C ）仅为平行于z 轴、其法线与x 轴的夹角为45°的平面； （D ）仅为平行于x 轴、其法线与y 轴的夹角为45°的平面。
知识点：韧性材料、塑性屈服、屈服原因 难度：难 解答：正确答案是 A 。
12－4 铸铁处于图示应力状态下，试分析最容易失效的是： （A ）仅图c ； （B ）图a 和图b ； （C ）图a 、b 和图c ； （D ）图a 、b 、c 和图d 。
知识点：脆性材料、脆性断裂、断裂准则 难度：一般 解答：正确答案是 C 。
12－5低碳钢处于图示应力状态下，若根据最大切应力准则， 试分析最容易失效的是： （A ）仅图d ； （B ）仅图c ； （C ）图c 和图d ； （D ）图a 、b 和图d 。
知识点：韧性材料、塑性屈服、屈服准则 难度：一般习题12-2、12-3图习题12-4、12-5图mt 2σ=σC BAmσ45D壁厚纵向(a)解答：正确答案是 B 。
220231d 3r b 3r a 3r σσσσσσσ=-=-===σσσσσσ=--=-=2)(231c 3r所以图c 最危险。
12－6 韧性材料所处应力状态如图所示，根据最大切应力准则，试分析二者同时失效的条件是： （A ）τσ>，3/2στ=； （B ）τσ<，3/4στ=； （C ）τσ=；（D ）τσ>，3/2τσ=。
知识点：韧性材料、塑性屈服、屈服准则 难度：一般 解答：正确答案是 A 。
左图：ττσσ24223r >+= （1） 右图：σσ='，τσ=''，τσ-=''' ∴τσσ+=3r （2）或τττσ2)(3r =--=（3）（由（1），此式舍去）由（1）、（2），224τστσ+=+∴τσ23=，显然τσ>∴选：A 。
12－7 承受内压的两端封闭的圆柱状薄壁容器由韧性材料制成。
试分析因压力过大表面出现裂纹时，裂纹的可能方向是： （A ）沿圆柱纵向；（B ）沿与圆柱纵向成45°角的方向； （C ）沿与圆柱纵向成30°角的方向； （D ）沿环向。
知识点：压力容器的应力分析、韧性材料、塑性屈服、屈服原因 难度：难 解答：正确答案是 B 。
设圆柱壁纵向应力为σ，则环向应力为2σ，径向应力近似为零。
t 1σσ=，m 2σσ=，03=σ σσσστ=-=-=22231max裂纹的可能方向为沿ABDC 面，平行于轴线与圆周切线方向成45°。
12－8 承受内压的两端封闭的圆柱状薄壁容器，由脆性材料制成。
试分析因压力过大表面出现裂纹时，习题12-6图裂纹的可能方向是： （A ）沿圆柱纵向；（B ）沿与圆柱纵向成45°角的方向； （C ）沿圆柱环向；（D ）沿与圆柱纵向成30°角的方向。
知识点：压力容器的应力分析、脆性材料、脆性断裂、断裂原因 难度：一般 解答：正确答案是 A 。
12－9 当韧性材料和脆性材料制成的两个两端封闭的圆柱形薄壁容器因内压发生失效时，试分析断口特征是：（A ）二者断口均沿着纵截面； （B ）二者断口均沿着横截面； （C ）韧性材料容器断口平面平行于轴线并与圆周切线方向成45°角；脆性材料容器断口平面沿纵截面； （D ）脆性材料容器断口平面平行于轴线并与圆周切线方向成45°角；韧性材料容器断口沿纵截面。
知识点：压力容器的应力分析、韧性材料、脆性材料、屈服断口、断裂断口 难度：一般 解答：正确答案是 C 。
参见12-7解理由。
12－10 有人说，杆件受拉伸时有][1σσ≤的设计准则，现在又讲“对于韧性材料，应用最大切应力准则或形状改变比能准则”。
试问二者是否矛盾？从这里可以得到什么结论？知识点：最大切应力准则、形状改变比能准则 难度：一般 解答：二者不矛盾，对于韧性材料，在平面拉伸时，01>σ，032==σσ，][14r r3σσσσ<==。
12－11 对于纯切应力状态，若将设计准则写成][ττ≤，试确定两种情形下许用切应力][τ与许用拉应力][σ之间的关系： 1．脆性材料； 2．韧性材料。
知识点：强度理论 难度：一般 解答：纯剪应力状态时b 1τσ=，02=σ，b 3τσ-=1．对于脆性材料，用最大拉应力理论的失效判据：b b στ= 则选][][στ=][11r σσσ≤=，即][1στσ≤=由 ][ττ≤，即][][τσ=用最大伸长线应变理论b b b )0(σττ=--，b b 5.0στ=，则选][5.0][στ=，与最大剪应力理论相同。
2．对于韧性材料，用最大剪应力理论： s 1τσ=，02=σ，s 3τσ-= ][2313r στσσσ≤=-=，即][21στ≤ 由 ][ττ≤，即][21][στ=由失效判据：s s s )(σττ=--，∴s s 5.0στ=，则选：][5.0][στ=用歪形能理论失效判据 s s 2132322214r 3])()()[(21στσσσσσσσ≤=-+-+-=，s s 31στ≤则选][31][στ=由][ττ=，则][577.0][31][σστ==12－12 构件中危险点的应力状态如图所示。
试选择合适的准则对以下两种情形作强度校核： 1．构件为钢制x σ= 45MPa ，y σ= 135MPa ，z σ= 0，xy τ= 0，拉伸许用应力][σ= 160MPa 。
2．构件材料为铸铁x σ= 20MPa ，y σ= -25MPa ，z σ= 30MPa ，xy τ= 0，][σ= 30MPa 。
知识点：屈服准则、断裂准则 难度：一般 解答：1．][MPa 135313r σσσσ<=-=强度满足。
2．][MPa 3011r σσσ===强度满足。
12－13 对于图示平面应力状态，各应力分量的可能组合有以下几种情形，试按最大切应力准则和形状改变比能准则分别计算此几种情形下的计算应力。
1．x σ= 40MPa ，y σ= 40 MPa ，xy τ= 60 MPa ； 2．x σ= 60MPa ，80-=y σMPa ，40-=xy τMPa ； 3．40-=x σMPa ，y σ= 50 MPa ，xy τ= 0； 4．x σ= 0，y σ= 0，xy τ= 45 MPa 。
知识点：最大切应力准则、形状改变比能准则 难度：一般 解答：1． 6040)2(222±=+-±+=xyyx y x τσσσσσ 1σ= 100 MPa ，2σ= 0，203-=σMPa 120313r =-=σσσMPa 4.111)12020100(212224r =++=σMPa 2． 2222407010)2(2+±-=++±+=xy yx y x τσσσσσ1σ= 70.6 MPa ，2σ= 0，6.903-=σMPa 2.161313r =-=σσσMPa140)2.1616.906.70(212224r =++=σMPa 3． 1σ= 50 MPa ，2σ= 0，403-=σMPa 903r =σMPa1.78)904050(212224r =++=σMPa 4． 45±=σMPa ，∴ 1σ= 45 MPa ，2σ= 0，453-=σMPa 903r =σMPa 9.77)904545(212224r =++=σMPa （9.7734r ==xy τσMPa ）12－14 钢制零件上危险点的平面应力状态如图所示。
已知材料的屈服应力s σ= 330MPa 。
试按最大切应力准则，确定下列情形下是否发生屈服，并对于不屈服的情形确定它们的安全因数。
习题12-12图习题12-13图1．0σ= 207 MPa ； 2．0σ= 248 MPa ； 3．0σ= 290 MPa 。
知识点：最大切应力准则、形状改变比能准则 难度：一般 解答：1．0σ= 207 MPa 103207)2(222±-=++±+=xy yx yx τσσσσσ∴ 1σ= 0，1042-=σMPa ，3103-=σMPa 3103r =σMPa s σ<065.1310330s ==n 2． 0σ= 248 MPa ；103248±-=σ∴ 1σ= 0，1452-=σMPa ，3513-=σMPa 3513r =σMPa s σ> 3． 0σ= 290 MPa 。
103290±-=σ∴ 1σ= 0，1872-=σMPa ，3933-=σMPa 3933r =σMPa s σ>12－15 试根据形状改变比能准则，重解习题12－14。
知识点：形状改变比能准则 难度：一般 解答：1．273)310206104(21])()()[(212222132322214r =++=-+-+-=σσσσσσσMPa s σ< 21.1273330s ==n 2． 306)351206145(212224r =++=σMPa s σ< 08.1306330s ==n 3． 341)393206187(212224r =++=σMPa s σ>12－16 钢制构件上危险点的平面应力状态如图所示。
已知材料的屈服应力为s σ= 300 MPa 。
试按形状改变比能准则，确定下列情形下是否发生屈服，并对于不发生屈服的情形确定它们的安全因数。
1．0τ= 60 MPa ； 2．0τ= 120 MPa ； 3．0τ= 130 MPa 。
