下载文档原格式
分子动力学和蒙特卡罗模拟分子动力学和蒙特卡罗模拟是两种常用的计算物理方法，用于研究原子和分子在宏观条件下的行为。
这两种方法有着各自的特点和适用范围，下面我们将分别对分子动力学和蒙特卡罗模拟进行介绍和比较。
分子动力学是一种模拟系统中原子和分子运动的方法。
通过求解牛顿运动方程，可以得到系统中每个原子或分子的位置和速度随时间的演变。
通过这种方法，我们可以研究系统的动力学性质，如扩散、振动等。
分子动力学模拟通常适用于固体和液体系统，以及温度比较高的气体系统。
在模拟过程中，需要考虑原子之间的相互作用力，通常采用势能函数来描述这种相互作用。
分子动力学模拟的精度较高，能够提供丰富的信息，但计算成本也较高。
蒙特卡罗模拟是一种通过统计抽样的方法来模拟系统行为的方法。
在蒙特卡罗模拟中，系统状态的演化是通过随机抽样进行的，而不是通过求解微分方程来得到。
蒙特卡罗模拟中的每一步都是根据一定的概率规则进行的，因此可以得到系统的平衡态性质。
蒙特卡罗模拟通常适用于温度较低的系统，例如凝聚态物质的相变过程。
蒙特卡罗模拟的优点在于计算成本低，适用于大规模系统的研究，但是通常无法提供系统的动力学信息。
总的来说，分子动力学和蒙特卡罗模拟是两种互补的计算物理方法，各有优点和局限性。
在具体研究问题时，可以根据系统的性质和研究的目的选择合适的方法进行模拟。
同时，两种方法在实际研究中也可以相互结合，以得到更全面的信息和更深入的理解。
希望本文的介绍能够帮助读者更好地理解分子动力学和蒙特卡罗模拟这两种重要的计算方法。
1、蒙特卡罗算法（该算法又称随机性模拟算法，是通过计算机仿真来解决问题的算法，同时可以通过模拟来检验自己模型的正确性，是比赛时必用的方法）2、数据拟合、参数估计、插值等数据处理算法（比赛中通常会遇到大量的数据需要处理，而处理数据的关键就在于这些算法，通常使用Matlab作为工具）3、线性规划、整数规划、多元规划、二次规划等规划类问题（建模竞赛大多数问题属于最优化问题，很多时候这些问题可以用数学规划算法来描述，通常使用Lindo、Lingo软件实现）4、图论算法（这类算法可以分为很多种，包括最短路、网络流、二分图等算法，涉及到图论的问题可以用这些方法解决，需要认真准备）5、动态规划、回溯搜索、分支定界等计算机算法（这些算法是算法设计中比较常用的方法，很多场合可以用到竞赛中）6、最优化理论的三大非经典算法：模拟退火法、神经网络、遗传算法（这些问题是用来解决一些较困难的最优化问题的算法，对于有些问题非常有帮助，但是算法的实现比较困难，需慎重使用）元胞自动机7、网格算法和穷举法（网格算法和穷举法都是暴力搜索最优点的算法，在很多竞赛题中有应用，当重点讨论模型本身而轻视算法的时候，可以使用这种暴力方案，最好使用一些高级语言作为编程工具）8、一些连续离散化方法（很多问题都是实际来的，数据可以是连续的，而计算机只认的是离散的数据，因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的）9、数值分析算法（如果在比赛中采用高级语言进行编程的话，那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用）10、图象处理算法（赛题中有一类问题与图形有关，即使与图形无关，论文中也应该要不乏图片的，这些图形如何展示以及如何处理就是需要解决的问题，通常使用Matlab进行处理）以上为各类算法的大致介绍，下面的内容是详细讲解，原文措辞详略得当，虽然不是面面俱到，但是已经阐述了主要内容，简略之处还望大家多多讨论。
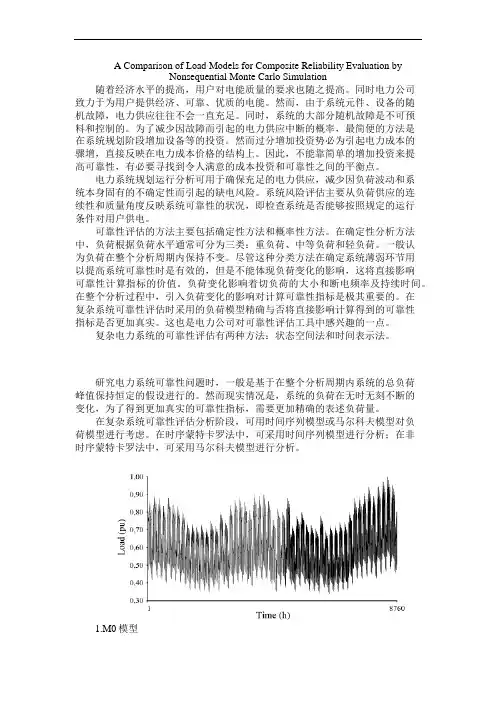
A Comparison of Load Models for Composite Reliability Evaluation byNonsequential Monte Carlo Simulation随着经济水平的提高，用户对电能质量的要求也随之提高。
同时电力公司致力于为用户提供经济、可靠、优质的电能。
然而，由于系统元件、设备的随机故障，电力供应往往不会一直充足。
同时，系统的大部分随机故障是不可预料和控制的。
为了减少因故障而引起的电力供应中断的概率，最简便的方法是在系统规划阶段增加设备等的投资。
然而过分增加投资势必为引起电力成本的骤增，直接反映在电力成本价格的结构上。
因此，不能靠简单的增加投资来提高可靠性，有必要寻找到令人满意的成本投资和可靠性之间的平衡点。
电力系统规划运行分析可用于确保充足的电力供应，减少因负荷波动和系统本身固有的不确定性而引起的缺电风险。
系统风险评估主要从负荷供应的连续性和质量角度反映系统可靠性的状况，即检查系统是否能够按照规定的运行条件对用户供电。
可靠性评估的方法主要包括确定性方法和概率性方法。
在确定性分析方法中，负荷根据负荷水平通常可分为三类：重负荷、中等负荷和轻负荷。
一般认为负荷在整个分析周期内保持不变。
尽管这种分类方法在确定系统薄弱环节用以提高系统可靠性时是有效的，但是不能体现负荷变化的影响，这将直接影响可靠性计算指标的价值。
负荷变化影响着切负荷的大小和断电频率及持续时间。
在整个分析过程中，引入负荷变化的影响对计算可靠性指标是极其重要的。
在复杂系统可靠性评估时采用的负荷模型精确与否将直接影响计算得到的可靠性指标是否更加真实。
这也是电力公司对可靠性评估工具中感兴趣的一点。
复杂电力系统的可靠性评估有两种方法：状态空间法和时间表示法。
研究电力系统可靠性问题时，一般是基于在整个分析周期内系统的总负荷峰值保持恒定的假设进行的。
然而现实情况是，系统的负荷在无时无刻不断的变化，为了得到更加真实的可靠性指标，需要更加精确的表述负荷量。
第42卷第12期原子能科学技术Vol.42,No.12 2008年12月Atomic Energy Science and Technology Dec.2008四种蒙特卡罗程序的比较计算邱 睿,李君利,武 祯,曾 志(清华大学工程物理系,粒子技术与辐射成像教育部重点实验室,高能辐射成像国防重点学科实验室,北京 100084)摘要:为研究4种不同蒙特卡罗程序FL U KA、GEAN T4、EGS(包括EGS4和EGS5版本)的一致性及其差异,利用Crannell实验模型作为算例进行比较计算,并与实验结果进行比较。
分别用4种程序模拟了能量为1G eV的电子束射入圆柱状铝靶中的粒子输运过程,得到了不同半径范围内的能量沉积百分比深度曲线。
比较表明,4种程序得到的曲线基本一致,也与实验数据相符,其中,GEAN T4的结果差异略大;4种程序花费的计算时间有较大差异,经分析,很可能是源于它们对电子输运过程的具体处理方法的不同。
关键词:蒙特卡罗程序;Crannell实验;FL U KA;GEAN T4;EGS中图分类号:TL99 文献标志码:A 文章编号:100026931(2008)1221149204Comparison C alculation of Four Monte2C arlo CodesQ IU Rui,L I J un2li,WU Zhen,ZEN G Zhi(De partment of Physics Engineering,Tsinghua Universit y,Key L aboratory of Particle&Radiation I maging,Minist ry of Education,Key L aboratory of Hi gh Energ y Radiation I maging Fundamental Science f or N ational Def ense,B ei j ing100084,China)Abstract: In order to investigate t he agreement and difference of four different Monte2 Carlo codes FL U KA,GEAN T4and EGS(EGS4and EGS5version),Crannell shower experiment model was used as a benchmark and t he result s from four codes were com2 pared wit h experiment result s.The particle t ransportatio n process when a1GeV elec2 t ron beam hit an aluminum column target was simulated respectively wit h four codes.The energy depo sition dept h curves in different radial ranges were obtained.The com2 parison shows t hat t he curves obtained wit h four codes agree wit h each ot her and con2 form t he experiment result s,and t he result of GEAN T4has a slightly bigger difference.However,t he difference of t he calculation time is big.It may be due to t he different met hods in t he electron t ransport simulation.K ey w ords:Monte2Carlo code;Crannell experiment;FL U KA;GEAN T4;EGS收稿日期:2007208222;修回日期:2007211230基金项目:国家自然科学基金资助项目(10775084);高能质子加速器辐射防护关键问题研究资助项目作者简介:邱 睿(1981—),女,湖北枣阳人,博士后,辐射防护专业 蒙特卡罗方法在研究粒子输运问题的领域得到了非常广泛的应用[1]。
蒙特卡罗方法、分子动力学方法和有限元方法是当前科学研究和工程技术领域中常用的数值计算方法，它们在材料科学、物理化学、工程力学等领域均有着重要的应用。
本文将从这三种方法的基本原理、应用领域和优缺点等方面进行介绍和比较。
一、蒙特卡罗方法蒙特卡罗方法是一种随机模拟的计算方法，主要用于求解概率统计问题和复杂的数学积分。
其基本原理是通过大量的随机样本来近似计算得出结果，具有较高的精度和可靠性。
蒙特卡罗方法的应用领域非常广泛，包括金融工程、通信网络、生物医学、物理模拟等方面，在材料科学领域中也有着重要的应用。
可以利用蒙特卡罗方法模拟材料的热力学性质，计算材料的热容、热传导系数等物理量。
蒙特卡罗方法的优点是能够处理复杂的非线性问题，但由于需要大量的随机样本，计算量较大，耗时较长，且结果受随机性影响较大。
二、分子动力学方法分子动力学方法是一种模拟分子运动的数值计算方法，通过求解牛顿运动方程来模拟分子在空间中的运动轨迹。
分子动力学方法在纳米材料、生物化学、材料加工等领域有着广泛的应用。
可以利用分子动力学方法模拟材料的力学性能、热学性质、表面反应等。
分子动力学方法的优点是能够考虑到分子间相互作用力的影响，较为真实地反映了材料的微观结构和宏观性能，但由于需要求解大量分子的运动轨迹，计算量也较大，且对计算机的性能要求较高。
三、有限元方法有限元方法是一种常用的工程数值计算方法，主要用于求解复杂结构的力学问题和传热问题。
其基本思想是将求解区域划分为有限个小单元，通过建立单元之间的联系，得出整个求解区域的数值解。
有限元方法在工程结构分析、材料成型、热处理过程中有着广泛的应用。
可以利用有限元方法模拟材料的应力分布、变形状态、热应力分析等。
有限元方法的优点是能够较为准确地描述复杂结构的力学和热学行为，计算精度较高，但需要进行网格划分和建立单元之间的关系，工作量较大，且求解非线性和大变形问题时较为困难。
蒙特卡罗方法、分子动力学方法和有限元方法分别在概率统计、分子模拟和结构力学领域有着重要的应用价值，对于不同的研究和工程问题可以选择合适的数值计算方法。
蒙特卡罗方法及应用蒙特卡罗方法是一种基于概率统计的数值计算方法，它在许多实际问题中具有广泛的应用。
本文将介绍如何在没有明确思路的情况下，使用蒙特卡罗方法来解决实际问题，并概述其基本原理、实现步骤、优缺点及应用实例。
当遇到一些复杂的问题，比如在无法列出方程求解的数学问题，或者在需要大量计算的概率统计问题中，我们可能会感到无从下手。
此时，蒙特卡罗方法提供了一种有效的解决方案。
通过使用随机数和概率模型，我们可以对问题进行模拟，并从模拟结果中得出结论。
蒙特卡罗方法的基本原理是利用随机数生成器，产生一组符合特定概率分布的随机数，然后通过这组随机数对问题进行模拟。
具体实现步骤包括：首先，确定问题的概率模型；其次，使用随机数生成器生成一组随机数；然后，通过模拟大量可能情况，得到问题的近似解；最后，对模拟结果进行统计分析，得出结论。
蒙特卡罗方法的优点在于，它可以在一定程度上解决难以列出方程的问题，提供一种可行的计算方法。
此外，蒙特卡罗方法可以处理多维度的问题，并且可以给出近似解，具有一定的鲁棒性。
然而，蒙特卡罗方法也存在一些缺点，比如模拟次数过多可能会导致计算效率低下，而且有时难以确定问题的概率模型。
蒙特卡罗方法在概率领域有广泛的应用，比如在期权定价、估计数学期望、计算积分等领域。
以估计数学期望为例，我们可以通过蒙特卡罗方法生成一组符合特定概率分布的随机数，并计算这些随机数的平均值来估计数学期望。
总之，蒙特卡罗方法为我们提供了一种有效的数值计算方法，可以在没有明确思路的情况下解决许多实际问题。
通过了解蒙特卡罗方法的基本原理、实现步骤、优缺点及应用实例，我们可以更好地理解并应用这种方法。
在实际问题中，我们可以根据具体的情况选择合适的概率模型和随机数生成器，以得到更精确的结果。
我们也需要注意蒙特卡罗方法的局限性，例如在处理高维度问题时可能会出现计算效率低下的问题。
针对这些问题，我们可以尝试使用一些优化技巧或者和其他计算方法结合使用，以提高计算效率。
蒙特卡罗模拟（Monte Carlo Simulation）和历史模拟方法（Historical Simulation）都是在金融风险管理、工程计算以及其他领域中常用的模拟技术，它们的主要异同点如下：相同点：1.随机性：两种方法都依赖于随机性来模拟现实世界的不确定性。
2.风险评估：两者都被广泛用于风险评估，特别是在金融市场风险分析中，如计算金融资产的价值变动、估计潜在损失（如Value at Risk，VaR）等。
3.计算机模拟：这两种方法都需要通过计算机程序生成大量随机数据来模拟未来可能发生的情景。
不同点：1.数据来源：o蒙特卡罗模拟：通过随机数生成器模拟未来可能发生的各种状态，这些状态不一定基于历史数据，而是基于预设的概率分布和模型参数。
o历史模拟：直接使用历史数据来模拟未来情况，假设未来发生的可能性与过去相似。
这种方法假设历史数据可以很好地代表未来的不确定性。
2.模拟过程：o蒙特卡罗模拟：构建模型并设定参数后，反复模拟未来可能出现的各种情景，多次迭代计算期望结果和风险指标。
o历史模拟：收集一段时间的历史数据，然后对这些数据进行重采样（bootstrap）或随机排列以创建大量不同的模拟路径。
3.模型依赖：o蒙特卡罗模拟：通常涉及更多对底层风险因素的模型假设，如资产价格变化服从某种特定分布。
o历史模拟：较少依赖复杂的模型，更多依赖实际历史数据，因此对于非线性关系和极端事件的捕捉可能更为直观，但可能无法很好地处理未曾经历过的极端情况。
4.适应性：o蒙特卡罗模拟：适用于对尚未发生或未来可能发生的新情况建模，特别适合于处理复杂的金融衍生品定价和风险评估。
o历史模拟：更适合于已有充足历史数据可供分析的情况，尤其在市场行为可能具有较强历史趋势和周期性的时候。
5.局限性：o蒙特卡罗模拟：对模型假设的依赖较大，如果假设偏差可能影响模拟结果的准确性。
o历史模拟：依赖于历史数据的质量和完整性，且可能低估极端事件发生的概率（即所谓的“肥尾”问题）。
A Comparison of Load Models for Composite Reliability Evaluation by
Nonsequential Monte Carlo Simulation
随着经济水平的提高，用户对电能质量的要求也随之提高。
同时电力公司
致力于为用户提供经济、可靠、优质的电能。
然而，由于系统元件、设备的随
机故障，电力供应往往不会一直充足。
同时，系统的大部分随机故障是不可预
料和控制的。
为了减少因故障而引起的电力供应中断的概率，最简便的方法是
在系统规划阶段增加设备等的投资。
然而过分增加投资势必为引起电力成本的
骤增，直接反映在电力成本价格的结构上。
因此，不能靠简单的增加投资来提
高可靠性，有必要寻找到令人满意的成本投资和可靠性之间的平衡点。
电力系统规划运行分析可用于确保充足的电力供应，减少因负荷波动和系
统本身固有的不确定性而引起的缺电风险。
系统风险评估主要从负荷供应的连
续性和质量角度反映系统可靠性的状况，即检查系统是否能够按照规定的运行
条件对用户供电。
可靠性评估的方法主要包括确定性方法和概率性方法。
在确定性分析方法中，负荷根据负荷水平通常可分为三类：重负荷、中等负荷和轻负荷。
一般认
为负荷在整个分析周期内保持不变。
尽管这种分类方法在确定系统薄弱环节用
以提高系统可靠性时是有效的，但是不能体现负荷变化的影响，这将直接影响
可靠性计算指标的价值。
负荷变化影响着切负荷的大小和断电频率及持续时间。
在整个分析过程中，引入负荷变化的影响对计算可靠性指标是极其重要的。
在
复杂系统可靠性评估时采用的负荷模型精确与否将直接影响计算得到的可靠性
指标是否更加真实。
这也是电力公司对可靠性评估工具中感兴趣的一点。
复杂电力系统的可靠性评估有两种方法：状态空间法和时间表示法。
研究电力系统可靠性问题时，一般是基于在整个分析周期内系统的总负荷
峰值保持恒定的假设进行的。
然而现实情况是，系统的负荷在无时无刻不断的
变化，为了得到更加真实的可靠性指标，需要更加精确的表述负荷量。
在复杂系统可靠性评估分析阶段，可用时间序列模型或马尔科夫模型对负
荷模型进行考虑。
在时序蒙特卡罗法中，可采用时间序列模型进行分析；在非
时序蒙特卡罗法中，可采用马尔科夫模型进行分析。
1.M0模型
通常情况下，在利用非时序蒙特卡洛法进行可靠性评估时，系统负荷通常
用聚合的马尔科夫模型，利用聚合技术降低时序负荷曲线表示的负荷种类。
巴
西开发的大型电力系统可靠性评估系统NH2程序中采用的就是这种模型。
每年的时序负荷曲线是由8760个小时的总负荷值组成。
利用聚合技术，将
负荷曲线转换为一系列不同的负荷水平，从而获得多种状态的负荷模型。
聚合
到负荷曲线的负荷水平的数量直接影响到计算结果的精确。
聚合状态的数量取
决于负荷曲线的特性和系统本身。
A COMPARISON OF MONTE CARLO SIMULATION FOR COMPOSITE
POWER SYSTEM RELIABILITY TECHNIQUES ASSESSMENT 电力系统的工程师和管理人员对发输电组合系统的可靠性评估拥有相当大
的兴趣。
组合系统的可靠性评估有两种基本方法：枚举解析法和蒙特卡洛模拟法。
蒙特卡罗法一般更灵活，当需要考虑复杂的操作条件和系统（如多降额状态，负荷年表，备用容量运行规则，母线负荷的不确定性，天气因素）等时，
其优越性更加明显。
电力系统可靠性评估中，使用的蒙特卡罗法有两种基本方法，即时序蒙特
卡罗法和非时序蒙特卡洛法。
在非时序蒙特卡洛法中，对所有组件的状态进行
采样，得到一组与时间无关的系统状态。
在时序蒙特卡罗法中，在一个系统运
行周期内对所有组件进行上下不断循环采样，直到执行周期结束为止。
时序蒙
特卡罗法允许配电网可靠性指标以时间序列的形式进行计算。
这种方法相对非
时序蒙特卡罗法而言，所花计算时间更长，编程更复杂。
在发输电组合系统中使用的模型已出现了一些。
时序模拟法是最基本实用
的技术，可提供一些广泛的指标。
它可用于提供预测值，也可作为与其他相近
技术进行比较的基准。
状态采样技术
在状态采样法中（非时序），对所有组件的状态进行采样，得到非时序的
系统状态。
基本抽样方法假设每个组件的状态可通过一个[0，1]均匀分布进行
分类。
在二状态组件中，组件的强迫停运率可表示停电概率(故障率)。
以下开始进行说明，系统状态由矢量S=S1，S2，…，S n表示，S i表示第
i个组件的状态。
集合S包括了系统所有组件的状态(发电机、线路、变压器等)。
用FOR i表示组件的强迫停运率，第i个组件的状态S i利用线性同余法产生的[0，
1]均匀分布的伪随机数x决定。
S i=0(正常状态)x≥FOR i S i=1(故障状态)0≤x<FOR i
它可以计算每个系统状态S相应的发生概率。
利用状态采样技术评估发输电组合系统的充足性(可靠性)步骤可简要概括如下：
1.利用状态抽样技术进行系统状态抽样。
2.如果系统状态正常，不削弱负荷。
如果系统状态处于故障状态，则负荷削弱。
输电线路的功率用直流潮流计算计算得到。
3.对最小化模型进行线性规划，重新分配发电机，防止线路过载和避免负荷削减，如果削弱负荷不可避免，则使总负荷削弱最小。
4.累加充足性指数，重复步骤1-3，直到电力不足期望（EDNS）小于容许
误差。
状态抽样法相对比较简单，产生[0，1]的均匀分布随机数是关键。
它不需
要采样一个连续的分布函数。
状态抽样方法，无需额外使用枚举法估计负荷削
减频率作为负荷削减状态的总和。
这里只有一个频率指数的上限，状态转换采
样技术可提供实际频率指数的估计。
状态转换采样技术
状态转换采样技术，重点研究的是整个系统的状态转换，而不是组件状态
或组件状态的持续时间。
该方法不需要采样所有组件的状态持续时间分布函数，同时用时序方法按时间顺序存储。
因此，计算速度比时序方法快，但比状态抽
样法慢。
在该方法中的一个重要限制条件是，假设所有状态根据时间分布。
混
合系统的充足性评估步骤如下：
1. 仿真过程从正常的系统状态开始，即所有的发电机组和输电线路处在正常状态。
2.如果当前的系统状态处于一个故障状态，则至少有一部分是在停电状态，负荷削减的最小化模型可用来评估这个系统状态是否充足。
否则，下一步可不
使用最小化模型。
3. 用状态转移抽样程序产生一个均匀分布的随机数，用于确定下一个系统状态。
4.重复步骤2，直到满足收敛判据。
时序蒙特卡洛法
顺序或状态持续时间抽样方法是基于元件状态持续时间的概率分布进行抽样。
序贯Monte Carlo方法可以用来模拟各种意外情况和系统中固有的运行特点。
它被认为可以是轻松用来计算实际频率指数和状态持续时间分布函数。
使
用序贯蒙特卡罗法评估混合系统可靠性的主要步骤如下：
1.所有元件（发电机，输电线路）每年的故障时间和修复时间序列是由采
样适当的概率分布产生。
在这一过程中，状态持续时间被假定为按指数分布。
以随机变量T为下标的指数分布的概率密度函数为：
f T t=λe−λt
λ是分布函数的平均值。
使用逆变换法求得随机变量T为：
T=−ln(1−U)/λ
U是(0，1)区间内均匀分布的随机数。
仿真期间，系统所有元件的可用率
均已知。
2.按时间顺序逐时排列负荷模型，假如负荷母线可用，则每条母线上的负
荷加上每次的仿真时间。
3.系统的仿真操作使用线性规划最小化模型进行评估，同时累加充足指数。
4.步骤2-3计算的是年度时序系统状态。
年度充足性指标用F(X j)累加得到。
X j是第j年的时序系统状态；F(X j)是第j年的可靠性指标函数。
例如为了评估LOLP，F(X j)是第j年所有故障状态持续时间的总和除以8736。
5.如果所选择的指标的差值大于收敛水平，重复步骤1-4直到实现收敛。
此方法与其余两种方法相比，需要的计算时间和存储容量更大。
因为它在
一个长的时间跨度内必须为每个元件产生一个随机变量，并将所有元件时序状
态信息进行存储。
负载母线上的负荷随时间变化的序贯仿真应用
早先的研究已有使用IEEE可靠性测试系统（IEEE-RTS）逐时负荷模型对整个系统进行评估。
所提供的负载模型的信息，可用于计算系统的逐时负荷一年按单位，表示在一个时间的时尚，每日，每周和季节模式可以开发。
