origin化学化工,曲线积分实例

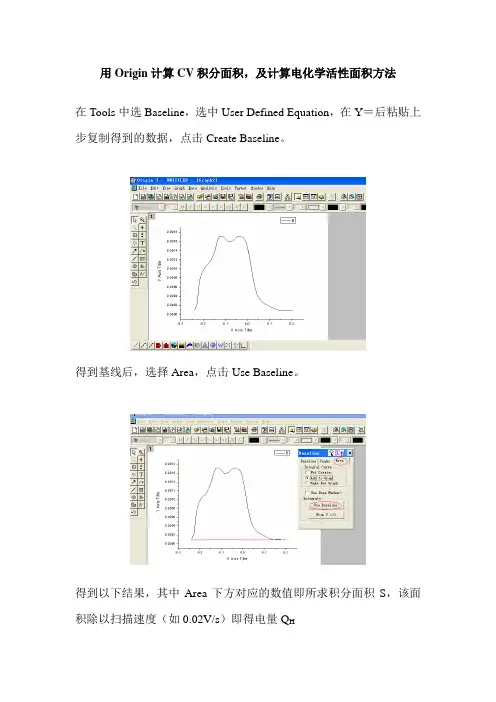
用Origin计算CV积分面积，及计算电化学活性面积方法
在Tools中选Baseline，选中User Defined Equation，在Y＝后粘贴上步复制得到的数据，点击Create Baseline。

得到基线后，选择Area，点击Use Baseline。

得到以下结果，其中Area下方对应的数值即所求积分面积S，该面积除以扫描速度（如0.02V/s）即得电量Q H
Pt 电催化剂的电化学活性表面积EAS(m 2/gPt)可按下式计算：
C
m Q ESA ⋅= 其中，ν
扫速峰面积S =Q m 为电极上的催化剂质量
C 为Pt 对氢的单位吸附电容，= 0.21mC/cm 2
对于具体的计算过程，你自己推倒吧，比较简单，但需要把单位搞清楚，一般计算出来的Pt 黑面积为～10m 2/g ，Pt/C 为几十m 2/g ，如果你算出来的为几百或几m 2/g ，说明你的单位换算错了，重新把公式搞一遍。

数据处理软件Origin在物理化学实验数据处理中的应用许劲毅谢振竑指导老师：沈雪松桂林医学院摘要：应用软件Origin在计算机上对实验数据进行处理(作相图,线性拟合，非线性拟合等)，能提高试验数据处理的准确性和规范性,并能及时了解和判断学生实验结果的正确性和精密度。

关键字：Origin 线性拟合直线回归相图物理化学实验中常见的数据处理有：①公式计算；②相图绘制；③线性拟合；④非线性拟合；⑤求斜率或截距。

在学生实验中，经常要对数据进行定量处理,用手工绘图.例如；在二组分体系相图的绘制中，必须先进行标准曲线的手工绘制,再在标准曲线上进行量取这样手工的数据处理误差大,效率低。

随着计算机技术的发展对实验数据的处理也应计算机化。

一个专门的数据处理软件Origin7.0，可对物理化学实验的数据处理有很大帮助，能提高试验数据处理的准确性和规范性，可提高数据处理的效率.在学生实验中，可很快知道其实验是否成功,而且大大减少实验数据处理的误差。

1. Origin软件的介绍1.1数据作图Origin可绘制散点图，点线图,柱行图，条形三角图以及双Y轴图形等，在物化实验中通常用散点图，点线图及双Y轴图形。

1.2线性拟合当用散点图或用点线图作出曲线后，用菜单栏中的Analysis中的Fit linear或Tools菜单中的Liner Fit可对曲线进行线性拟合.结果记录中显示曲线的公式,斜率,截距和相对误差等。

在处理数据时，可对散点图或点线图的形状选择合适的函数进行拟合。

2. 应用介绍2.1 相图绘制2.1.1二元组分T-X相图的绘制2.1.1.1 苯－乙醇二组分T-X相图的绘制2.1.1.1.1作二元组分的标准曲线下表苯-乙醇溶液折光率测定数据.苯的摩尔分数折光率10% 1.373420% 1.387550% 1.429070% 1.457090% 1.48502.1.1.1.2线性拟合.将数据输入Origin 数据表中，作苯组分-折光率的散点图，再进行选择Analysis菜单中的Fit linea，对该数点图进行线性拟合.得到曲线类的为y=B+Ax, B= -9.75602，A= 7.17622 R(相关系数)=1，SD(标准偏差)=9.95047E-4，P(R2=0的概率)<0.0001表明拟合效果最佳,拟合函数式为y=7.17622x-9.75602。

Origin 是美国OriginLab 公司开发的数据分析和制图软件，目前最新版本为Origin8.0，本文介绍现在实用比较广泛的7.5版本。

Origin 比Excel 具有更强的制图功能，尤其是曲线拟合更加灵活，但是其数据输入，电子表格的绘制没有Excel 方便，不过如果电脑安装了Excel97或更高级别的版本，在Origin 内也可以进行Excel 操作，这样就充分的将Excel 的电子表格功能和Origin 强大的制图功能有机结合起来。

3.1 Origin7.5基本操作3.1.1 Origin7.5界面Origin7.5界面与Windows 软件相似，是一个多文档界面应用程序。

运行Oringin7.5后，就打开一个Project 文件，并带有一个Worksheet 窗口，另外Origin 还提供了Matrix ，Excel ，Layout ，Note ，Gragh 等主要子窗口。

这些子窗口具有不同的作用，Origin7.5界面各个部分名称如图3.1所示标题栏菜单栏Script 窗口Graph 窗口结果显示窗口工具栏Matrix窗口Excel窗口Layout窗口Worksheet窗口Project 窗口状态栏图3.1 Origin7.5界面从图3.1可以看出，Origin 界面包括下列几个部分：1） 标题栏 在界面的顶部，显示当前文件的名称和存放路径2） 菜单栏 在标题栏下方，每个菜单还有许多子菜单，通过菜单可以实现几乎所有Origin7.5的功能3） 工具栏 菜单栏下是工作栏，大部分工具可以在菜单栏中找到相应的命令。

工具栏调出方法：单击菜单View|toolbars 进入“Customize Toobar ”对话框，见图3.2，在“Toolbars ”选项卡中进行选择，名称前带“√”的工具栏在界面显示。

将光标放在一个工具按钮上，则在光标的右下方会出现该工具的名称，在状态栏会出现该光标的功能，如图3.3。

origin化学化工,曲线积分实例摘要：1.引言：Origin化学化工背景介绍2.曲线积分概念阐述3.曲线积分实例详细解析4.实例应用：Origin软件操作演示5.结论：曲线积分在化学化工领域的意义及应用价值正文：【引言】Origin是一款强大的科学绘图和数据分析软件，广泛应用于各个领域，如化学、化工等。

在化学化工研究中，曲线积分是一种重要的数学工具，可以帮助我们更好地理解和分析实验数据。

本文将简要介绍曲线积分的概念，并通过实例详细解析其在Origin化学化工领域的应用。

【曲线积分概念阐述】曲线积分，又称路径积分，是一种数学方法，用于计算函数在曲线上的积分值。

其基本思想是将曲线划分为无数小段，计算每一小段上的函数值与长度的乘积之和。

在化学化工领域，曲线积分常用于计算反应速率、物质传输等方面的物理量。

【曲线积分实例详细解析】以下将以一个简单的反应速率为例，说明曲线积分在Origin中的计算方法。

假设我们有一个反应速率与时间的关系式：r = k[A]，其中k为反应速率常数，[A]为反应物A的浓度。

我们需要计算在一定时间内反应物A的消耗量。

首先，在Origin中绘制反应速率与时间的关系曲线。

然后，选择曲线上的两个时间点（如t1和t2），并计算这两个时间点之间的曲线长度。

假设曲线长度为Δs。

接下来，计算曲线上的反应速率值。

在Origin中，可以使用Curve Fitting工具拟合曲线，得到反应速率与时间的关系式。

将拟合得到的反应速率函数表示为r = f(t)。

最后，根据曲线积分公式，计算反应物A在Δt时间内的消耗量：Δ[A] = ∫r dt = ∫f(t) dt【实例应用：Origin软件操作演示】以下是一个简单的Origin操作演示，用于计算曲线积分。

1.打开Origin软件，新建一个空白文档。

2.在Origin中绘制反应速率与时间的关系曲线。

可以选择绘制散点图或使用Curve Fitting工具直接拟合曲线。

数据处理软件Origin在物理化学实验中的应用①【摘要】本文简要介绍了Origin软件的基本功能和基本使用方法，并以物理化学实验为例介绍如何使用Origin软件处理实验数据、曲线的计算机拟合等。

运用该软件处理实验数据解决了物理化学实验中的数据多、处理麻烦、手工作图误差大等问题。

不仅简化了数据处理的过程，而且还提高了分析结果的准确度，进一步拓展了学生计算机软件应用能力。

【关键词】Origin软件数据处理物理化学实验1 前言《物理化学实验》是高等院校化学及相关专业学生的一门独立基础实验课程。

与其它化学实验课不同，它得到的是一系列实验数据。

学生需对数据进行大量计算，在直角坐标纸上作图。

大部分是画直线，求出截距和斜率，进而求得实验结果的数学表达式;少部分是画曲线，有的需要在曲线上作切线，有的需要对曲线求积分，进而求得实验结果的数学表达式。

学生只根据散点图做直线或曲线，就不可避免地引起主观误差，同一组实验数据不同学生处理，结果相差很大。

个别学生还修改某些偏离较大的实验数据以期得到好的实验结果。

由于实验数据计算过程复杂、作图费事，导致实验报告中经常出现各种错误。

教师批改实验报告时不得不花费大量时间核查其计算结果。

物理化学实验中常见的数据处理的方法有: 运用基本公式计算;用实验数据作图;线性拟合，求截距或斜率;非线性曲线拟合。

目前学生多用坐标纸手工作图;手工拟合直线，求斜率或截距。

这种手工作图的方法不仅费时费力，而且误差较大。

物理化学实验数据处理过程一般为:对实验数据作图或对数据经过计算后作图→作数据点的拟合线→求拟合直线的斜率或曲线上某点的切线→根据斜率求物理量。

这一过程可以用计算机处理完成，并能克服手工绘图费时费力、偶然性较大、误差大的缺点。

Origin软件是Microcal Software公司推出的一个集图形绘制、数据的处理、统计与分析为一体的综合应用系统。

Origin软件从它诞生以来，由于强大的数据处理和图形化功能，已被化学工作者广泛应用。

学术干货再来一波，如何利用Origin实现曲线拟合现实生活中，变量间未必都会有线性关系，比如疾病疗效与疗程长短的关系。

在材料科学的研究中，也会遇到一些非线性的数量关系，那么面对大量的离散点组或者数据，我们如何来透过零散的“外表”来发现它们“真实的内心”呢？今天小编就一步一步告诉大家。

曲线拟合（curve fitting）是指选择适当的曲线类型来拟合观测数据，并用拟合的曲线方程分析两个变量之间的关系。

通过对数据进行曲线拟合，我们不但能找到它的变化规律，还能对数据的变化进行一定程度的预测。

我们将以Origin 8.0为例，为大家详细的讲解利用Origin进行曲线拟合的方法。

本文共分为3个小节，分别是线性回归（直线拟合）、多项式拟合和非线性拟合。

一、线性回归（直线拟合）1.首先打开Origin 8，在A(X)和B(Y)列分别输入对应的横坐标和纵坐标数据，本节中的A(X)列为电流，B(Y)列为电压。

如图1-1所示。

研究的规律是当电阻不变时，电压随着电流增加的情况。

其中，Long Name:名称；Units:单位；Comments:注释。

图1-12.选中A(X)和B(Y)列的全部数据，然后依次Plot→Symbol→Scatter（或者点击左下角的作图，如图1-2所示）。

得到图1-3。

图1-33.根据图1-3可知，电流跟电压是线性关系，所以要进行线性拟合，接下来点击Analysis→Fitting→Fit Linear→Open Dialog...，如图1-4所示，得到图1-5。

图1-54.根据在图1-5的Linear Fit选项卡中单击OK按钮，得到图1-6。

在跳出来的Reminder Message选项卡中单击OK按钮，得到直线的拟合结果报告，如图1-7所示。

得到的电压与电流的函数关系为：y=3.02747x+0.01209，拟合度R2因子达0.99984。

图1-6图1-7二、多项式拟合打开Origin 8，在A(X)和B(Y)列分别输入对应的横坐标和纵坐标数据，如本节中A(X)列为电流，B(X)列为光强度。

ORIGIN 8
胆色素浓
度
(mg/100ml)
5075100125150175200225250
吸光率0.03
9
0.06
1
0.08
7
0.10
7
0.11
9
0.16
3
0.17
9
0.19
4
0.21
3
工程管理器
回归分析：图形窗口激活状态下，选Analysis（分析）菜单下的Fit Polynomial命令（多项式拟合）
回归参数各自的标准误差（Error）、相关系数R、标准偏
差（SD），数据点个数N，R=0
的概率P等。

相关系数R反映了x和y的相关程度，R=1 表示x、y之间严格符合关系
式
窗口类型对应的菜单
Workbook
Graph
Matrix
Excel
workbook 当Excel窗口为Origin当前窗口时，菜单栏同时显示Excel和Origin的菜单，其中File、Plot、Window是Origin菜单，其他为Excel中的菜单。

layout
note
十进制格式
科学记数格式
工程记数格式
有千位分隔符的十进制格式默认的十进制显示数据设置小数点的位置
设置有效数字的位数
0.00.5 1.0 1.5 2.0
-0.4
-0.2
0.0
0.2
0.4
0.60.8
1.0
1.2
s i n X X sinX cosX。

origin化学化工,曲线积分实例摘要：1.曲线积分的概念和应用2.origin 化学化工软件的介绍3.origin 化学化工软件在曲线积分实例中的应用4.结论正文：曲线积分是一种重要的数学工具，广泛应用于各个领域，如物理、化学、工程等。

曲线积分可以用来计算物体的质心、转动惯量等，也可以用来解决化学中的反应速率等问题。

Origin 化学化工软件是一款功能强大的科学计算软件，它集成了数学、统计、图形和数据分析等功能，为科研人员提供了方便的工具。

在曲线积分方面，Origin 化学化工软件提供了直观、易用的操作界面和丰富的函数库，使得用户可以轻松地完成各种复杂的曲线积分计算。

下面，我们通过一个具体的曲线积分实例，来看一下origin 化学化工软件在曲线积分中的应用。

假设我们有一个由两条曲线围成的图形，我们想要计算这个图形的面积。

在origin 化学化工软件中，我们可以通过以下步骤来完成这个任务：首先，我们打开origin 软件，新建一个空白的图形窗口。

然后，我们选择“绘图”功能，在窗口中绘制出两条曲线。

接下来，我们选择“分析”功能，点击“积分”按钮，选择“面积”积分类型。

在弹出的对话框中，我们选择两条曲线的交点作为积分的上下限，然后点击“确定”按钮。

origin 软件就会自动计算出这个图形的面积，并在窗口中显示结果。

通过这个实例，我们可以看到，origin 化学化工软件在曲线积分方面的强大功能和易用性。

无论是计算物理中的质心、转动惯量，还是计算化学中的反应速率，origin 软件都能提供方便、高效的解决方案。

总的来说，曲线积分是一种重要的数学工具，而origin 化学化工软件为我们提供了强大的曲线积分计算功能。

Origin软件在化学工程实验中的应用谢名财（青海大学化工学院，西宁810016）【摘要】物理化学实验和化工原理实验是化学工程专业的基础学科实验。

介绍了运用Origin软件对物理化学和化工原理实验结果进行数据处理和图像绘制的方法。

【期刊名称】云南化工【年(卷),期】2016(043)002【总页数】4【关键词】 Origin；化学工程；曲线切线绘制收稿：2015-12-17物理化学实验和化工原理实验是化学工程专业的基础学科实验，是学生学习物理化学和化工原理课程的重要手段和途径。

这些实验，数据处理麻烦，手工做图误差大，曲线拟合粗糙［1］。

采用Origin软件对实验数据进行处理，不仅提高了数据处理的效率，还具有数据处理精度高、图表美观等特点。

1 Origin软件简介Origin为OriginLab公司开发的、较流行的专业函数绘图软件，是公认的简单易学、操作灵活、功能强大的软件，既可以满足一般用户的制图需要，也可以满足高级用户数据分析、函数拟合的需要［1］。

Origin的数据分析主要包括统计、信号处理、图像处理、峰值分析和曲线拟合等各种完善的数学分析功能。

Origin的绘图是基于模板的，Origin本身提供了几十种二维和三维绘图模板，而且允许用户自己定制模板。

绘图时，只要选择所需要的模板就行。

用户可以自定义数学函数、图形样式和绘图模板，也可以和各种数据库软件、办公软件、图像处理软件等方便的连接，还可以把Origin 图形以多种格式输出到图像文件中，譬如JPEG、GIF、EPS、TIFF等格式［2］。

2 Origin在物理化学实验中的运用在一定温度、压力下，纯液体B和纯液体C的摩尔体积分别为V和V。

两液体的物质的量分别为nB和nC，则混合前系统的体积为nBV+ nCV。

将两液体相互混合形成均相液态混合物后，根据两纯液体性质的不同，混合物的体积（V）可以等于或不等于混合前的体积。

例如：用B、C分别代表H2O（l）和C2H5OH（l），在25℃及常压下，两纯液体的摩尔体积分别为V= 18.09cm3/ mol、V= 58.35cm3/ mol。

origin化学化工,曲线积分实例题
Origin软件是一款强大的数据分析和图形绘制工具，广泛应用于化学、化工、生物等领域。

在化学和化工领域，Origin软件可以用于处理实验数据、绘制各种图表，并进行数据分析和解释。

以下是一个Origin软件进行曲线积分（Curve Integration）的实例：
1. 打开Origin软件，并导入需要进行积分处理的实验数据。

2. 在Origin软件中选择“Plot”菜单，选择适合的图表类型（例如，Line、Scatter等），将实验数据绘制成图表。

3. 在绘制的图表上，右键单击需要积分处理的曲线，选择“Analysis”菜单中的“Integration”选项。

4. 在弹出的对话框中，选择合适的积分范围和积分类型（例如，定积分、不定积分等），并设置其他参数（如积分精度、积分方法等）。

5. 点击“OK”按钮，Origin软件将自动进行积分计算，并将结果以表格形式显示在图表下方。

6. 如果需要进一步处理积分结果，可以对表格进行编辑、计算和格式化等操作。

需要注意的是，曲线积分是一项比较复杂的数据处理操作，需要结合具体实验背景和数据特点进行操作。

在进行曲线积分时，需要选择合适的积分范围和积分类型，并设置合适的参数和方法，以保证积分结果的准确性和可靠性。

origin化学化工,曲线积分实例
摘要：
一、引言
二、曲线积分的概念与性质
三、曲线积分的计算方法
四、曲线积分在化学化工领域的应用实例
五、结论
正文：
一、引言
在我国化学化工领域，曲线积分作为一种重要的数学工具，广泛应用于各种实际问题中。

本文旨在通过介绍曲线积分的相关知识，以及其在化学化工领域的实例，帮助读者更好地理解和应用曲线积分。

二、曲线积分的概念与性质
曲线积分是微积分中的一个重要概念，它是指在给定曲线上，对某一函数进行定积分。

曲线积分具有线性性质、可积性、可微性等性质。

三、曲线积分的计算方法
曲线积分的计算方法主要包括：第一类曲线积分（对数函数、指数函数、三角函数、反三角函数等）和第二类曲线积分（多项式函数、有理函数等）。

此外，还有其他一些特殊类型的曲线积分计算方法。

四、曲线积分在化学化工领域的应用实例
1.分子间势能曲线的积分：在研究分子间相互作用时，需要对势能曲线进
行积分，以得到分子间势能的总体表达式。

2.化学反应速率曲线的积分：在研究化学反应动力学时，需要对反应速率曲线进行积分，以得到反应速率与浓度之间的关系。

3.电化学反应曲线的积分：在研究电化学反应时，需要对电化学反应曲线进行积分，以得到电化学反应的电流与电位之间的关系。

五、结论
曲线积分作为一种重要的数学工具，在化学化工领域具有广泛的应用。

掌握曲线积分的概念、性质和计算方法，有助于更好地理解和解决化学化工问题。