最新人教版高中数学必修4第一章《三角函数的诱导公式》课后训练(第2课时)2
- 格式:doc
- 大小:1.20 MB
- 文档页数:3

高中数学第一章三角函数 1.3.2 三角函数的诱导公式(2)课后习题新人教A版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第一章三角函数1.3.2 三角函数的诱导公式(2)课后习题新人教A版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第一章三角函数1.3.2 三角函数的诱导公式(2)课后习题新人教A版必修4的全部内容。
1。
3。
2 诱导公式(2)一、A组1。
已知sin(π-α)=,则cos等于()A.B。
C。
-D。
—解析:∵sin(π—α)=,∴sin α=.∴cos=-sin α=—.答案:C2。
若α∈,则=()A。
sin α B.-sin αC.cos αD。
-cos α解析:∵α∈,∴sin α〈0,∴=—sin α.答案:B3。
若sin〉0,cos〉0,则角α的终边位于()A.第一象限B。
第二象限C.第三象限D.第四象限解析:∵sin>0,cos>0,∴cos α〉0,sin α<0。
∴角α的终边在第四象限。
答案:D4。
sin(π-2)-cos化简的结果是()A。
0 B。
—1C.2sin 2 D。
—2sin 2解析:sin(π—2)—cos=sin 2-sin 2=0。
答案:A5。
=() A。
—cos αB。
cos αC.sin αD。
—sin α解析:原式===—cos α.答案:A6。
求值:sin2+sin2=.解析:∵-α++α=,∴sin2=sin2=cos2。
∴sin2+sin2=sin2+cos2=1。
答案:17。
若α是三角形内角,且sin=—sin,则α=。

1.3.2 诱导公式(2)一、A组1.已知sin(π-α)=,则cos等于()A. B. C.- D.-解析:∵sin(π-α)=,∴sin α=.∴cos=-sin α=-.答案:C2.若α∈,则=()A.sin αB.-sin αC.cos αD.-cos α解析:∵α∈,∴sin α<0,∴=-sin α.答案:B3.若sin>0,cos>0,则角α的终边位于()A.第一象限B.第二象限C.第三象限D.第四象限解析:∵sin>0,cos>0,∴cos α>0,sin α<0.∴角α的终边在第四象限.4.sin(π-2)-cos化简的结果是()A.0B.-1C.2sin 2D.-2sin 2解析:sin(π-2)-cos=sin 2-sin 2=0.答案:A5.=()A.-cos αB.cos αC.sin αD.-sin α解析:原式===-cos α.答案:A6.求值:sin2+sin2=.解析:∵-α++α=,∴sin2=sin2=cos2.∴sin2+sin2=sin2+cos2=1.7.若α是三角形内角,且sin=-sin,则α=.解析:∵sin=-sin,∴cos α=-.∵0<α<π,∴α=.答案:8.若sin,则cos2=.解析:sin=cos θ=,则cos2=sin2θ=1-cos2θ=1-.答案:9.已知sin,求cos sin的值.解:cos sin=cos sin=sin sin.10.已知f(α)=.(1)证明:f(α)=sin α.(2)若f=-,且α是第二象限角,求tan α.(1)证明:因为f(α)====sin α.(2)解:由sin=-,得cos α=-.又α是第二象限角,所以sin α=,则tan α==-.二、B组1.若sin(3π+α)=-,则cos等于()A.-B.C.D.-解析:∵sin(3π+α)=sin(π+α)=-sin α=-,∴sin α=.∴cos=cos=cos=-sin α=-.答案:A2.A,B,C为△ABC的三个内角,下列关系式中不成立的是()①cos(A+B)=cos C ②cos=sin③tan(A+B)=-tan C ④sin(2A+B+C)=sin AA.①②B.③④C.①④D.②③解析:因为cos(A+B)=-cos C,所以①错;cos=cos=sin,所以②正确;tan(A+B)=tan(π-C)=-tan C,所以③正确;sin(2A+B+C)=sin(π+A)=-sin A,所以④错,故选C.答案:C3.若sin(180°+α)+cos(90°+α)=-a,则cos(270°-α)+2sin(360°-α)的值为()A.-B.-C.D.解析:由已知得,-sin α-sin α=-a,即sin α=.故cos(270°-α)+2sin(360°-α)=-sin α-2sin α=-3sin α=- a.答案:B4.已知sin α是方程5x2-7x-6=0的根,α是第三象限角,则=.解析:由已知得sin α=-.因为α是第三象限角,所以cos α=-,tan α=.所以原式=.答案:5.sin21°+sin22°+sin23°+…+sin289°=.解析:sin21°+sin22°+sin23°+…+sin289°=sin21°+sin22°+sin23°+…+sin245°+cos244°+…+cos 21°=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+sin245°=44+.答案:6α是第二象限角,若cos=-,则是第象限角. 解析:∵cos=-=-=-=-,∴cos<0.又α为第二象限角,∴为第一或第三象限角,∴必为第三象限角.答案:三7.已知α是三角形的内角,且sin α+cos α=.。

1.3 三角函数的诱导公式一、选择题:1.已知sin(4π+α)=23,则sin(43π-α)值为( ) A.21 B. —21 C. 23 D. —23 2.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为( ) A.23 B. 21 C. 23± D. —23 3.化简:)2cos()2sin(21-∙-+ππ得( )A.sin2+cos2B.cos2-sin2C.sin2-cos2D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( )A.sinα=sinβB. sin(α-π2) =sinβC.cosα=cosβD. cos(π2-α) =-cosβ5.设tanθ=-2, 2π-<θ<π2,那么sin 2θ+cos(θ-π2)的值等于( ), A. 51(4+5) B. 51(4-5) C. 51(4±5) D. 51(5-4)二、填空题:6.sin (-317π)= .7.cos(π-x)=23,x ∈(-π,π),则x 的值为 .8.tanα=m ,则=+-+++)cos(-sin()cos(3sin(απα)απ)απ .9.|sinα|=sin (-π+α),则α的取值范围是 .10.若α为锐角,则2|log secαcos (π2-α)= .三、解答题:11.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .12.已知:sin (x+6π)=41,求sin ()67x +π+cos 2(65π-x )的值.13. 求下列三角函数值:(1)sin3π7;(2)cos 4π17;(3)tan (-6π23);(4)sin (-765°).14. 求下列三角函数值:(1)sin 3π4·cos 6π25·tan 4π5; (2)sin [(2n +1)π-3π2].15.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3π)的值.参考答案一、选择题:1.C 2.A 3.C 4.C 5.A二、填空题:6.23 7.±65π 8.11-+m m 9.[(2k-1) π,2k π] 10.2 三、解答题:11.原式=)cos (·sin()cos()n s (sin αα)παπα--+--αi =)cos ?(sin )cos (sin 2αααα--= sinα 12.1611 13.解:(1)sin3π7=sin (2π+3π)=sin 3π=23. (2)cos 4π17=cos (4π+4π)=cos 4π=22. (3)tan (-6π23)=cos (-4π+6π)=cos 6π=23. (4)sin (-765°)=sin [360°×(-2)-45°]=sin (-45°)=-sin45°=-22. 注:利用公式(1)、公式(2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.14.解:(1)sin3π4·cos 6π25·tan 4π5=sin (π+3π)·cos (4π+6π)·tan (π+4π) =(-sin 3π)·cos 6π·tan 4π=(-23)·23·1=-43.(2)sin [(2n +1)π-3π2]=sin (π-3π2)=sin 3π=23. 15.解:f (θ)=θθθθθcos cos 223cos sin cos 2223++-++ =θθθθθcos cos 223cos cos 1cos 2223++-+-+ =θθθθθcos cos 22)cos (cos 2cos 2223++--- =θθθθθcos cos 22)1(cos cos )1(cos 223++--- =θθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 222++--++- =θθθθθcos cos 22)2cos cos 2)(1(cos 22++++- =cos θ-1,∴f (3π)=cos 3π-1=21-1=-21.。

最新人教版高中数学必修四第一章三角函数(三角函数的诱导公式2)同步练习(含解析)一、选择题1.已知f (sin x )=cos 3x ,则f (cos 10°)的值为( )A .-12 B.12 C .-32 D.322.若sin(3π+α)=-12,则cos ⎝ ⎛⎭⎪⎫72π-α等于( ) A .-12 B.12 C.32 D .-323.已知sin ⎝ ⎛⎭⎪⎫α-π4=13,则cos ⎝ ⎛⎭⎪⎫π4+α的值等于( ) A .-13 B.13 C.-223 D.2234.若sin(π+α)+cos ⎝ ⎛⎭⎪⎫π2+α=-m ,则cos ⎝ ⎛⎭⎪⎫32π-α+2sin(2π-α)的值为( ) A .-2m 3 B.2m 3 C .-3m 2 D.3m 25.已知cos ⎝ ⎛⎭⎪⎫π2+φ=32,且|φ|<π2,则tan φ等于( ) A .-33 B.33C .- 3 D.3 6.已知cos(75°+α)=13,则sin(α-15°)+cos(105°-α)的值是( )A.13B.23 C .-13 D .-23二、填空题7.若sin ⎝ ⎛⎭⎪⎫α+π12=13,则cos ⎝ ⎛⎭⎪⎫α+7π12=________. 8.代数式sin 2(A +45°)+sin 2(A -45°)的化简结果是______.9.sin 21°+sin 22°+…+sin 288°+sin 289°=________.10.已知tan(3π+α)=2,则sin (α-3π)+cos (π-α)+sin ⎝ ⎛⎭⎪⎫π2-α-2cos ⎝ ⎛⎭⎪⎫π2+α-sin (-α)+cos (π+α)=________.三、解答题11.求证:tan (2π-α)sin (-2π-α)cos (6π-α)sin ⎝ ⎛⎭⎪⎫α+3π2cos ⎝ ⎛⎭⎪⎫α+3π2=-tan α.12.已知sin ⎝ ⎛⎭⎪⎫-π2-α·cos ⎝ ⎛⎭⎪⎫-5π2-α=60169,且π4<α<π2,求sin α与cos α的值.13.化简:sin ⎝ ⎛⎭⎪⎫4k -14π-α+cos ⎝ ⎛⎭⎪⎫4k +14π-α (k ∈Z ).14.是否存在角α,β,α∈⎝ ⎛⎭⎪⎫-π2,π2,β∈(0,π),使等式 ⎩⎪⎨⎪⎧sin (3π-α)=2cos ⎝ ⎛⎭⎪⎫π2-β3cos (-α)=-2cos (π+β)同时成立. 若存在,求出α,β的值;若不存在,说明理由.参考答案与解析1.A [f (cos 10°)=f (sin 80°)=cos 240°=cos(180°+60°)=-cos 60°=-12.]2.A [∵sin(3π+α)=-sin α=-12,∴sin α=12.∴cos ⎝ ⎛⎭⎪⎫7π2-α=cos ⎝ ⎛⎭⎪⎫32π-α=-cos ⎝ ⎛⎭⎪⎫π2-α=-sin α=-12.] 3.A [cos ⎝ ⎛⎭⎪⎫π4+α=sin ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4+α=sin ⎝ ⎛⎭⎪⎫π4-α=-sin ⎝ ⎛⎭⎪⎫α-π4=-13.] 4.C [∵sin(π+α)+cos ⎝ ⎛⎭⎪⎫π2+α=-sin α-sin α=-m , ∴sin α=m 2.cos ⎝ ⎛⎭⎪⎫32π-α+2sin(2π-α)=-sin α-2sin α=-3sin α=-32m .] 5.C [由cos ⎝ ⎛⎭⎪⎫π2+φ=-sin φ=32,得sin φ=-32, 又∵|φ|<π2,∴φ=-π3,∴tan φ=- 3.] 6.D [sin(α-15°)+cos(105°-α)=sin [(75°+α)-90°]+cos [180°-(75°+α)]=-sin [90°-(75°+α)]-cos(75°+α)=-cos(75°+α)-cos(75°+α)=-2cos(75°+α)=-23.]7.-13解析 cos ⎝ ⎛⎭⎪⎫α+7π12=cos ⎣⎢⎡⎦⎥⎤π2+⎝ ⎛⎭⎪⎫α+π12=-sin ⎝ ⎛⎭⎪⎫α+π12=-13. 8.1解析 原式=sin 2(A +45°)+sin 2(45°-A )=sin 2(A +45°)+cos 2(A +45°)=1. 9.892解析 原式=(sin 21°+sin 289°)+(sin 22°+sin 288°)+…+(sin 244°+sin 246°)+sin 245°=44+12 =892.10.2解析 原式=sin αsin α-cos α=tan αtan α-1=22-1=2. 11.证明 左边=tan (-α)·sin (-α)·cos (-α)sin ⎣⎢⎡⎦⎥⎤2π-⎝ ⎛⎭⎪⎫π2-α·cos ⎣⎢⎡⎦⎥⎤2π-⎝ ⎛⎭⎪⎫π2-α =(-tan α)·(-sin α)·cos αsin ⎣⎢⎡⎦⎥⎤-⎝ ⎛⎭⎪⎫π2-αcos ⎣⎢⎡⎦⎥⎤-⎝ ⎛⎭⎪⎫π2-α =sin 2α-sin ⎝ ⎛⎭⎪⎫π2-αcos ⎝ ⎛⎭⎪⎫π2-α =sin 2α-cos α·sin α=-sin αcos α=-tan α=右边.∴原等式成立.12.解 sin ⎝ ⎛⎭⎪⎫-π2-α=-cos α, cos ⎝ ⎛⎭⎪⎫-5π2-α=cos ⎝ ⎛⎭⎪⎫2π+π2+α=-sin α. ∴sin α·cos α=60169,即2sin α·cos α=120169. ①又∵sin 2α+cos 2α=1, ②①+②得(sin α+cos α)2=289169,②-①得(sin α-cos α)2=49169,又∵α∈⎝ ⎛⎭⎪⎫π4,π2,∴sin α>cos α>0, 即sin α+cos α>0,sin α-cos α>0,∴sin α+cos α=1713, ③sin α-cos α=713, ④③+④得sin α=1213,③-④得cos α=513.13.解 原式=sin ⎣⎢⎡⎦⎥⎤k π-⎝ ⎛⎭⎪⎫π4+α+cos ⎣⎢⎡⎦⎥⎤k π+⎝ ⎛⎭⎪⎫π4-α. 当k 为奇数时,设k =2n +1 (n ∈Z ),则原式=sin ⎣⎢⎡⎦⎥⎤(2n +1)π-⎝ ⎛⎭⎪⎫π4+α+cos ⎣⎢⎡⎦⎥⎤(2n +1)π+⎝ ⎛⎭⎪⎫π4-α =sin ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π4+α+cos ⎣⎢⎡⎦⎥⎤π+⎝ ⎛⎭⎪⎫π4-α =sin ⎝ ⎛⎭⎪⎫π4+α+⎣⎢⎡⎦⎥⎤-cos ⎝ ⎛⎭⎪⎫π4-α =sin ⎝ ⎛⎭⎪⎫π4+α-cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4+α =sin ⎝ ⎛⎭⎪⎫π4+α-sin ⎝ ⎛⎭⎪⎫π4+α=0; 当k 为偶数时,设k =2n (n ∈Z ),则原式=sin ⎣⎢⎡⎦⎥⎤2n π-⎝ ⎛⎭⎪⎫π4+α+cos ⎣⎢⎡⎦⎥⎤2n π+⎝ ⎛⎭⎪⎫π4-α =-sin ⎝ ⎛⎭⎪⎫π4+α+cos ⎝ ⎛⎭⎪⎫π4-α =-sin ⎝ ⎛⎭⎪⎫π4+α+cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4+α =-sin ⎝ ⎛⎭⎪⎫π4+α+sin ⎝ ⎛⎭⎪⎫π4+α=0. 综上所述,原式=0.14.解 由条件,得⎩⎨⎧sin α=2sin β, ①3cos α=2cos β. ②①2+②2,得sin 2α+3cos 2α=2,③又因为sin 2α+sin 2α=1,④由③④得sin 2α=12,即sin α=±22,因为α∈⎝ ⎛⎭⎪⎫-π2,π2,所以α=π4或α=-π4. 当α=π4时,代入②得cos β=32,又β∈(0,π), 所以β=π6,代入①可知符合. 当α=-π4时,代入②得cos β=32,又β∈(0,π), 所以β=π6,代入①可知不符合.综上所述,存在α=π4,β=π6满足条件.。

第一章三角函数1.3 三角函数的诱导公式 第1课时 诱导公式二、三、四课后篇巩固探究1.已知sin (π+θ)=45,则角θ的终边在( )A.第一或第二象限B.第二或第三象限C.第一或第四象限D.第三或第四象限-sinθ=45,所以sinθ=-45,故角θ的终边在第三或第四象限.2.若cos(π-α)=-12,则cos(-2π-α)的值为( )A.12B.±√32C.-12D.±12-α)=-cosα=-12,∴cosα=12.∴cos(-2π-α)=cos(-α)=cosα=12.3.sin (-13π6)-cos (-10π3)-tan (15π4)的值为( )A.-2B.0C.12D.1=-sin (2π+π6)-cos (2π+4π3)-tan (2π+7π4)=-sin π6-cos (π+π3)-tan (2π-π4)=-12+cos π3+tan π4=-12+12+1=1.4.已知tan(π-α)=12,则sinα+cosα2sinα-cosα=( )A.14B.-14C.12D.-12-tanα=12,所以tanα=-12.于是sinα+cosα2sinα-cosα=tanα+12tanα-1=-12+12×(-12)-1=-14.5.若角7π-α的终边与单位圆的交点坐标是(x ,35),则cos(α-2018π)=( ) A.±45B.±35C.45D.-35-α)=35,即sinα=35,于是cosα=±45,故cos(α-π)=cosα=±45.6.√1-2sin (π+2)cos (π-2)等于( )A.sin 2-cos 2B.sin 2+cos 2C.±(sin 2-cos 2)D.cos 2-sin 21-2sin(π+2)cos(π-2)=√1-2sin2cos2=√(sin2-cos2)2=|sin2-cos2|=sin2-cos2.7.记cos(-80°)=k,则tan 100°等于( )A.√1-k2k B.-√1-k2kC.√1-k2D.-√1-k2cos(-80°)=cos80°=k,sin80°=√1-cos280°=√1-k2,∴tan100°=-tan80°=-√1-k2k.故选B.8.已知A=sin(kπ+α)sinα+cos(kπ+α)cosα(k∈Z),则A的值构成的集合是( )A.{1,-1,2,-2}B.{-1,1}C.{2,-2}D.{1,-1,0,2,-2}k为偶数时,A=sinαsinα+cosαcosα=2;当k为奇数时,A=-sinαsinα−cosαcosα=-2.故选C.9.已知sin(45°+α)=513,则sin(135°-α)=.-α)=sin[180°-(45°+α)]=sin(45°+α)=513.10.已知tan (π7+α)=5,则tan (6π7-α)= .(6π7-α)=tan [π-(π7+α)]=-tan (π7+α)=-5.11.设tan(5π+α)=m,则sin (α-3π)+cos (π-α)sin (-α)-cos (π+α)= .=-sinα-cosα-sinα+cosα=-tanα-1-tanα+1=-m -1-m+1=m+1m -1.12.已知π6<α<2π3,cos (α+π3)=m(m≠0),则tan (2π3-α)= .解析由π6<α<2π3,可得α+π3∈(π2,π).因为cos (α+π3)=m<0,所以sin (α+π3)=√1-cos 2(α+π3)=√1-m 2,所以tan (α+π3)=√1-m 2m.所以tan (2π3-α)=tan [π-(α+π3)]=-tan (α+π3)=-√1-m 2m.-√1-m 2m13.已知sin(3π+α)=13,求:sin (180°+α)cos (720°+α)tan (540°+α)sin (-180°+α)tan (900°+α)sin (-180°-α)cos (-180°-α)的值.解∵sin(3π+α)=13,∴sinα=-13.原式=(-sinα)·cosα·tanα·(-sinα)tanα·sinα·(-cosα)=-sinα=13.14.(1)已知sin α是方程5x 2-7x-6=0的根,求cos (α+2π)cos (4π+α)tan 2(2π+α)tan (6π+α)sin (2π+α)sin (8π+α)的值;(2)已知sin(4π+α)=√2sin β,√3cos(6π+α)=√2cos(2π+β),且0<α<π,0<β<π,求α和β的值.因为方程5x 2-7x-6=0的两根为2和-35,所以sinα=-35.由sin 2α+cos 2α=1,得cosα=±√1-sin 2α=±45.当cosα=45时,tanα=-34;当cosα=-45时,tanα=34.所以原式=cosα·cosα·tan 2α·tanαsinα·sinα=tanα=±34.(2)因为sin(4π+α)=√2sinβ, 所以sinα=√2sinβ.①因为√3cos(6π+α)=√2cos(2π+β), 所以√3cosα=√2cosβ.②①2+②2,得sin 2α+3cos 2α=2(sin 2β+cos 2β)=2, 所以cos 2α=12,即cosα=±√22.又0<α<π,所以α=π4或α=3π4.又0<β<π,当α=π4时,由②得β=π6;当α=3π4时,由②得β=5π6.所以α=π4,β=π6或α=3π4,β=5π6.。
高中数学第一章三角函数1.3 三角函数的诱导公式(2)课时训练(含解析)新人教A版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第一章三角函数1.3 三角函数的诱导公式(2)课时训练(含解析)新人教A版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第一章三角函数1.3 三角函数的诱导公式(2)课时训练(含解析)新人教A版必修4的全部内容。
§1.3三角函数的诱导公式(二)课时目标1。
借助单位圆及三角函数定义理解公式五、公式六的推导过程.2。
运用公式五、公式六进行有关计算与证明.1.诱导公式五~六(1)公式五:sin错误!=________;cos错误!=________。
以-α替代公式五中的α,可得公式六.(2)公式六:sin错误!=________;cos错误!=________。
2.诱导公式五~六的记忆错误!-α,错误!+α的三角函数值,等于α的____________三角函数值,前面加上一个把α看成锐角时原函数值的________,记忆口诀为“函数名改变,符号看象限”.一、选择题1.已知f(sin x)=cos 3x,则f(cos 10°)的值为()A.-错误! B。
错误! C.-错误! D。
错误!2.若sin(3π+α)=-错误!,则cos 错误!等于( )A.-错误! B。
错误! C.错误! D.-错误!3.已知sin错误!=错误!,则cos错误!的值等于( )A.-错误! B.错误! C。
错误! D。
错误!4.若sin(π+α)+cos错误!=-m,则cos错误!+2sin(2π-α)的值为( )A.-错误! B.错误! C.-错误! D.错误!5.已知cos错误!=错误!,且|φ|<错误!,则tan φ等于()A.-错误! B。
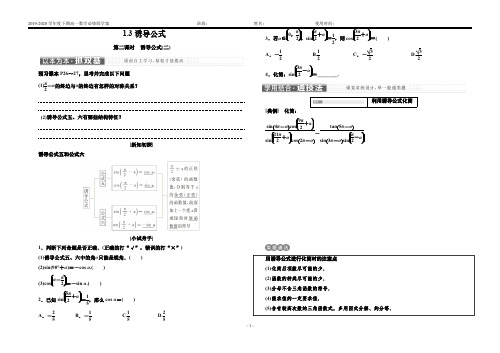
第2课时 诱导公式五、六[核心必知]1.预习教材,问题导入根据以下提纲,预习教材P 26~P 27的内容,回答下列问题. 如图所示,设α是任意角,其终边与单位圆交于点P 1(x ,y ),与角α的终边关于直线y =x 对称的角的终边与单位圆交于点P 2.(1)P 2点的坐标是什么? 提示:P 2(y ,x ).(2)π2-α的终边与角α的终边关于直线y =x 对称吗?它们的正弦、余弦值有何关系?提示:对称.sin ⎝ ⎛⎭⎪⎫π2-α=cos α,cos ⎝ ⎛⎭⎪⎫π2-α=sin α. 2.归纳总结,核心必记 (1)诱导公式五和公式六(2)诱导公式的记忆诱导公式一~六可归纳为k ·π2±α的形式,可概括为“奇变偶不变,符号看象限”:①“变”与“不变”是针对互余关系的函数而言的.②“奇”、“偶”是对诱导公式k ·π2±α中的整数k 来讲的.③“象限”指k ·π2±α中,将α看成锐角时,k ·π2±α所在的象限,根据“一全正,二正弦、三正切,四余弦”的符号规律确定原函数值的符号.[问题思考](1)诱导公式五、六中的α是任意角吗? 提示:是.(2)在△ABC 中,角A 2与角B +C2的三角函数值满足哪些等量关系?提示:∵A +B +C =π,∴A 2=π2-B +C2,∴sin A 2=sin ⎝ ⎛⎭⎪⎫π2-B +C 2=cos B +C 2,cos A 2=cos ⎝ ⎛⎭⎪⎫π2-B +C 2=sin B +C 2.[课前反思](1)诱导公式五: ;(2)诱导公式六: .知识点1化简求值讲一讲1.已知f (α)=sin π-αcos 2π-αcos ⎝⎛⎭⎪⎫-α+3π2cos ⎝ ⎛⎭⎪⎫π2-αsin ()-π-α.(1)化简f (α);(2)若α为第三象限角,且cos ⎝⎛⎭⎪⎫α-3π2=15,求f (α)的值;(3)若α=-31π3,求f (α)的值.[尝试解答] (1)f (α)=sin αcos α()-sin αsin αsin α=-cos α.(2)∵cos ⎝ ⎛⎭⎪⎫α-3π2=-sin α=15,∴sin α=-15, 又∵α为第三象限角,∴cos α=-1-sin 2α=-265,∴f (α)=265.(3)f ⎝ ⎛⎭⎪⎫-31π3=-cos ⎝ ⎛⎭⎪⎫-31π3=-cos ⎝ ⎛⎭⎪⎫-6×2π+5π3 =-cos 5π3=-cos π3=-12.类题·通法三角函数式化简的方法和技巧(1)方法:三角函数式化简的关键是抓住函数名称之间的关系和角之间的关系,据此灵活应用相关的公式及变形,解决问题.(2)技巧:①异名化同名;②异角化同角;③切化弦. 练一练1.已知f (x )=sin 3π-x cos ⎝⎛⎭⎪⎫x -3π2tan x -2πsin ⎝ ⎛⎭⎪⎫π2-x cos ⎝⎛⎭⎪⎫-x -π2tan x -5π.(1)化简f (x );(2)当x =π3时,求f (x )的值;(3)若f (x )=1,求sin ⎝⎛⎭⎪⎫3π2-x cos ⎝ ⎛⎭⎪⎫-x -7π2的值.解:(1)f (x )=sin x -sin x tan xcos x -sin x tan x =tan x .(2)当x =π3时,f (x )=tan π3= 3.(3)若f (x )=1,则tan x =1,所以sin ⎝⎛⎭⎪⎫3π2-x cos ⎝⎛⎭⎪⎫-x -7π2=-cos x sin x =-1tan x =-1.知识点2条件求值问题讲一讲2.(1)已知cos 31°=m ,则sin 239°tan 149°的值是( ) A.1-m2mB.1-m 2C .-1-m 2mD .-1-m 2(2)已知sin ⎝ ⎛⎭⎪⎫π3-α=12,则cos ⎝ ⎛⎭⎪⎫π6+α的值为________. [尝试解答] (1)sin 239°tan 149°=sin(180°+59°)·tan(180°-31°) =-sin 59°(-tan 31°)=-sin(90°-31°)·(-tan 31°) =-cos 31°·(-tan 31°)=sin 31°=1-cos 231°=1-m 2. (2)cos ⎝⎛⎭⎪⎫π6+α=cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π3-α=sin ⎝ ⎛⎭⎪⎫π3-α=12. 答案:(1)B (2)12类题·通法解决条件求值问题的策略(1)解决条件求值问题,首先要仔细观察条件与所求式之间的角,函数名称及有关运算之间的差异及联系.(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.练一练2.已知cos(π+α)=-12,求cos ⎝ ⎛⎭⎪⎫π2+α的值. 解:∵cos(π+α)=-cos α=-12,∴cos α=12,∴α为第一或第四象限角.①若α为第一象限角,则cos ⎝ ⎛⎭⎪⎫π2+α=-sin α=-1-cos 2α=-1-⎝ ⎛⎭⎪⎫122=-32; ②若α为第四象限角,则cos ⎝ ⎛⎭⎪⎫π2+α=-sin α=1-cos 2α=1-⎝ ⎛⎭⎪⎫122=32.知识点3三角恒等式的证明讲一讲3.求证:2sin ⎝⎛⎭⎪⎫θ-3π2cos ⎝ ⎛⎭⎪⎫θ+π2-11-2sin 2π+θ=tan 9π+θ+1tan π+θ-1. [尝试解答] 左边=-2sin ⎝ ⎛⎭⎪⎫3π2-θ·-sin θ-11-2sin 2θ =2sin ⎣⎢⎡⎦⎥⎤π+⎝ ⎛⎭⎪⎫π2-θsin θ-11-2sin 2θ=-2sin ⎝ ⎛⎭⎪⎫π2-θsin θ-11-2sin 2θ=-2cos θsin θ-1cos 2θ+sin 2θ-2sin 2θ=sin θ+cos θ2sin 2θ-cos 2θ=sin θ+cos θsin θ-cos θ,右边=tan 9π+θ+1tan π+θ-1=tan θ+1tan θ-1=sin θ+cos θsin θ-cos θ,∴左边=右边,原式得证.类题·通法三角恒等式的证明策略对于恒等式的证明,应遵循化繁为简的原则,从左边推到右边或从右边推到左边,也可以用左右归一、变更论证的方法.常用定义法、化弦法,拆项拆角法、“1”的代换法、公式变形法,要熟练掌握基本公式,善于从中选择巧妙简捷的方法.练一练3.求证:sin2π-θcos π+θcos ⎝ ⎛⎭⎪⎫π2+θcos ⎝ ⎛⎭⎪⎫11π2-θcos π-θsin 3π-θsin -π-θsin ⎝ ⎛⎭⎪⎫9π2+θ=-tan θ.证明:sin2π-θcos π+θcos ⎝ ⎛⎭⎪⎫π2+θcos ⎝ ⎛⎭⎪⎫11π2-θcos π-θsin 3π-θsin -π-θsin ⎝ ⎛⎭⎪⎫9π2+θ=-sin θ·-cos θ·-sin θ·co s ⎝⎛⎭⎪⎫3π2-θ-cos θ·sin θ·sin θ·si n ⎝ ⎛⎭⎪⎫π2+θ=sin θ·cos θ·sin θ·sin θ-cos θ·sin θ·sin θ·cos θ=-tan θ.[课堂归纳·感悟提升]1.本节课的重点是诱导公式五、六及其应用,难点是利用诱导公式解决条件求值问题. 2.要掌握诱导公式的三个应用(1)利用诱导公式解决化简求值问题,见讲1; (2)利用诱导公式解决条件求值问题,见讲2; (3)利用诱导公式解决三角恒等式的证明问题,见讲3. 3.本节课要掌握一些常见角的变换技巧π6+α=π2-⎝ ⎛⎭⎪⎫π3-α⇔⎝ ⎛⎭⎪⎫π6+α+⎝ ⎛⎭⎪⎫π3-α=π2,π4+α=π2-⎝ ⎛⎭⎪⎫π4-α⇔⎝ ⎛⎭⎪⎫π4+α+⎝⎛⎭⎪⎫π4-α=π2,⎝ ⎛⎭⎪⎫5π6+α-⎝ ⎛⎭⎪⎫π3+α=π2等.。
1.3 三角函数的诱导公式一、选择题: 1.已知sin(4π+α)=23,则sin(43π-α)值为( ) A. 21 B. —21 C. 23 D. —232.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为( ) A. 23 B. 21 C. 23± D. —233.化简:)2cos()2sin(21-∙-+ππ得( )A.sin2+cos2B.cos2-sin2C.sin 2-cos2D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( ) A.sin α=sin β B. sin(α-π2) =sin β C.cos α=cos β D. cos(π2-α) =-cos β5.设tan θ=-2, 2π-<θ<π2,那么sin 2θ+c os(θ-π2)的值等于( ), A. 51(4+5) B. 51(4-5) C. 51(4±5) D. 51(5-4)二、填空题: 6.sin (-317π)= .7.c os(π-x)= 23,x∈(-π,π),则x 的值为 .8.tan α=m ,则=+-+++)cos(-sin()cos(3sin(απα)απ)απ .9.|sin α|=sin (-π+α),则α的取值范围是 .10.若α为锐角,则2|log sec αcos (π2-α)= .三、解答题: 11.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .12.已知:sin (x+6π)=41,求sin ()67x +π+cos 2(65π-x )的值.13. 求下列三角函数值: (1)sin 3π7;(2)cos 4π17;(3)tan (-6π23);(4)sin (-765°).14. 求下列三角函数值: (1)sin3π4²cos 6π25²tan 4π5; (2)sin [(2n +1)π-3π2].15.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3π)的值.参考答案一、选择题:1.C 2.A 3.C 4.C 5.A 二、填空题: 6.237.±65π 8.11-+m m 9.[(2k-1) π,2k π] 10.2三、解答题:11.原式=)cos (·sin()cos()n s (sin αα)παπα--+--αi =)cos ?(sin )cos (sin 2αααα--= sin α12.1611 13.解:(1)sin 3π7=sin (2π+3π)=sin 3π=23. (2)cos4π17=cos (4π+4π)=cos 4π=22.(3)tan (-6π23)=cos (-4π+6π)=cos 6π=23. (4)sin (-765°)=sin [360°³(-2)-45°]=sin (-45°)=-sin45°=-22. 注:利用公式(1)、公式(2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.14.解:(1)sin 3π4²cos 6π25²tan 4π5=sin (π+3π)²cos(4π+6π)²tan(π+4π) =(-sin3π)²cos 6π²tan 4π=(-23)²23²1=-43.(2)sin [(2n +1)π-3π2]=sin (π-3π2)=sin 3π=23. 15.解:f (θ)=θθθθθcos cos 223cos sin cos 2223++-++=θθθθθcos cos 223cos cos 1cos 2223++-+-+=θθθθθcos cos 22)cos (cos 2cos 2223++---=θθθθθcos cos 22)1(cos cos )1(cos 223++---=θθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 222++--++-=θθθθθcos cos 22)2cos cos 2)(1(cos 22++++-=cos θ-1, ∴f (3π)=cos 3π-1=21-1=-21.仅此学习交流之用谢谢。
数学·必修4(人教A 版)1.3 三角函数的诱导公式1.3.2 诱导公式(习题课)基础提升1.已知函数f (x )=cos x 2,则下列等式成立的是( ) A .f (2π-x )=f (x ) B .f (2π+x )=f (x )C .f (-x )=-f (x )D .f (-x )=f (x )解析:对于A ,f (2π-x )=cos 2π-x 2=cos ⎝ ⎛⎭⎪⎫π-x 2=-cos x 2≠f (x ),对于B ,f (2π+x )=cos 2π+x 2=cos ⎝ ⎛⎭⎪⎫π+x 2=-cos x 2≠f (x ). 对于C ,f (-x )=cos -x 2=cos x 2≠-f (x ),故选D.答案:D2.若sin(π+α)+cos ⎝ ⎛⎭⎪⎫π2+α=-m ,则cos ⎝ ⎛⎭⎪⎫3π2-α+2sin(6π-α)的值为( ) A .-2m 3 B .-3m 2 C.2m 3 D.3m 2解析:由sin(π+α)+cos ⎝ ⎛⎭⎪⎫π2+α=-m ,得-sin α-sin α=-m ,即sin α=m 2. ∴cos ⎝ ⎛⎭⎪⎫3π2-α+2sin(6π-α)=-sin α-2sin α=-3sin α=-3m 2.故选B. 答案:B3.已知α∈⎣⎢⎡⎦⎥⎤π2,3π2,tan(α-7π)=-34,sin α+cos α的值等于( ) A .±15 B.15 C .-15 D .-35解析:∵tan(α-7π)=-34,∴tan α=-34, 又α∈⎣⎢⎡⎦⎥⎤π2,3π2,∴α∈⎝ ⎛⎦⎥⎤π2,π.∴sin α=35,cos α=-45. ∴ sin α+cos α=-15.故选C. 答案:C4.已知α为第四象限角且sin(π-α)=-13,则tan α等于________.解析:由sin(π-α)=-13,得sin α=-13,又α为第四象限角,∴cos α=223,tan α=-24. 答案:-24巩固提高5.已知f (x )=⎩⎨⎧ sin πx ,x <0,f (x -1)-1,x >0,则f ⎝ ⎛⎭⎪⎫-116+f ⎝ ⎛⎭⎪⎫116的值为( ) A .-1 B .-3-2C .-2D .-3解析:f ⎝ ⎛⎭⎪⎫-116=sin ⎝ ⎛⎭⎪⎫-11π6=sin π6=12,f ⎝ ⎛⎭⎪⎫116=f ⎝ ⎛⎭⎪⎫56-1=f ⎝ ⎛⎭⎪⎫-16-2=sin ⎝ ⎛⎭⎪⎫-π6-2=-sin π6-2=-12-2,∴f ⎝ ⎛⎭⎪⎫-116+f ⎝ ⎛⎭⎪⎫116=-2.故选C. 答案:C6.|cos α|=cos(π+α),则角α的集合为________.解析:|cos α|=cos(π+α)=-cos α,∴cos α≤0,α=⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ 2k π+π2≤α≤2k π+32π,k ∈Z 答案:B7.已知π<θ<2π, cos(θ-9π)=-35,求tan(10π-θ)的值.解析:由已知,得cos(θ-π)=-35,cos(π-θ)=-35,∴cos θ=35.∵π<θ<2π,∴3π2<θ<2π.∴tan θ=-43. ∴tan(10π-θ)=tan(-θ)=-tan θ=43.8.若sin(x -2π)-cos(π-x )=1-32,x 是第二象限的角.(1)求sin x 与cos x 的值;解析:(1)由已知,得sin x +cos x =1-32, ∴sin x cos x =-34.又x 是第二象限的角, ∴sin x >0,cos x <0.∴sin x -cos x =1-2sin x cos x =2+32=1+32. ∴sin x =12,cos x =-32.(2)求x 的集合.解析:(2)∵sin ⎝ ⎛⎭⎪⎫π-π6=sin π6=12, ∴在⎣⎢⎡⎦⎥⎤π2,π内符合条件的x =5π6. ∴x的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x =2k π+5π6,k ∈Z .。