当前位置：文档之家 › 数字电子技术基础-逻辑代数基础

数字电子技术基础-逻辑代数基础

  • 格式：ppt
  • 大小：2.17 MB
  • 文档页数：77

下载文档原格式

  / 77

合集下载

《数字电子技术基础》第1章.逻辑代数概论.

《数字电子技术基础》第1章.逻辑代数概论.


1.1 数制与数值表示方法
2.二进制正负数的表示法 表1.1.2 4位二进制带符号数的原码、反码和补码
1.1 数制与数值表示方法
3.补码的算术运算
例1.1.8 已知 X1 =0001000，X2 =－0000011,求X1+ X2。
1.1 数制与数值表示方法
例1.1.9 已知 X1 =-0001000，X2 =0001011,求X1+ X2。
1.5 硬件描述语言HDL基础
3.属性
VHDL中的属性使VHDL 程序更加简明扼要、容易 理解，VHDL的属性在时序 电路设计程序中几乎处处 可见，如值类属性的左边 界、右边界、上下边界以 及值类属性的长度，用于 返回数组的边界或长度。
1.5 硬件描述语言HDL基础
4.运算操作符 表1.5.1 VHDL运算操作符
表1.3.3 最小项和最大项关系
1.3.3 逻辑 函数 及其 表示 方法
1.3 逻辑代数基础
4）标准形式
逻辑函数的标准积之和表达式、标准和之积 表达式和真值表一样具有唯一性。 若函数的积之和（与或）表达式中的每一个乘 积项均为最小项，则这种表达式称为标准积之和 表达式，也称最小项表达式。
1.3.3 逻辑 函数 及其 表示 方法
1.4 逻辑函数的化简
例1.4.11 化简F（A,B,C,D） =∑m(3,6,9,11,13)+∑d(1,2,5,7 ,8,15)。 图1.4.11例1.4.11卡诺图解： 画出4变量卡诺图，将最小项1和 无关项“×”填入卡诺图如图 1.4.11所示。合并最小项。与1方 格圈在一起的无关项被当作1，没 有圈的无关项作为0。 写出逻辑函数的最简“与—或” 表达式 图1.4.11 例1.4.11
数字电子技术基础教程

数字电子技术基础教程


第6页/共55页
2.2 逻辑代数的基本定律和规则
反演律 吸收律
A B AB
A AB A
A B A B A (A B) A
A B A B A
(A B)(A B) A
A AB A B
A(A B) AB
冗余律
AB AC BC AB AC
(A＋B)(A＋C)(B C) (A＋B)(A＋C)
F AB
2.或非逻辑
F AB
A
F
&
B
与非门
A
F
B
或非门
3. 与或非逻辑
&
F AB CD
第20页/共55页
异或逻辑与同或逻辑
4.异或逻辑
F A B AB AB
A
=1
F
B
5.同或逻辑 F=A ⊙ B= AB AB
A
=
F
B
AB F
00 0 01 1 10 1 11 0
AB F
00 1 01 0 10 0 11 1
② 任意两个i0最小项之积恒i为0A0B，C任·意AB两C个＝最0大项之
和恒等于1 。
mi m j 0(i j)
Mi M j 1(i j)
③ n 变量的每一个最小（大）项有n 个相邻项
（相邻项是指两个最小项只有一个因子互为反变
量，其余因子均相同，又称为逻辑相邻项）。
第32页/共55页
2.6 逻辑代数的K诺图
ABC ABC ABC
最大项表达式：
F ( A B C)( A B C)( A B C)
第28页/共55页
最大项的Mi表示
n个变量可以构成2n个最大项。最大项用符号Mi表示。与 最小项恰好相反，对于任何一个最大项，只有一组变量 取值使它为0，而变量的其余取值均使它为1。
《数字电子技术基础》读书笔记02逻辑代数基础

《数字电子技术基础》读书笔记02逻辑代数基础

《数字电子技术基础》读书笔记02 逻辑代数基础2.1从布尔代数到逻辑代数1849年英国数学家乔治布尔(George Boole)提出布尔代数，使用数学方法进行逻辑运算。

把布尔代数应用到二值逻辑电路中，即为逻辑代数。

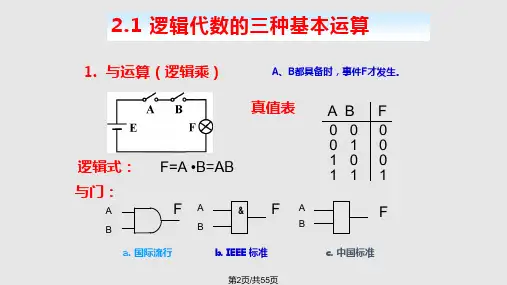
2.2逻辑代数中的运算(想想初等代数中的加减乘除)2.2.1三种基本运算与(AND)：逻辑乘，Y=A B或(OR)：逻辑加，Y=A+B非(NOT)：逻辑求反，Y=Aˊ简单逻辑运算(与、或、非)的两套图形符号，均为IEEE(国际电气与电子工程师协会)和IEC(国际电工协会)认定。

上排为国外教材和EDA软件中普遍使用的特定外形符号；下排为矩形符号。

2.2.2复合逻辑运算(都可以表示为与、或、非的组合)与非(NAND)：先与后非，与的反运算，Y=(A B)ˊ或非(NOR)：先或后非，非的反运算，Y=(A+B)ˊ与或非(AND-NOR)：先与再或再非，Y=(A B+C D)ˊ异或(Exclusive OR)：Y=A⊕B=A Bˊ+AˊB A和B不同，Y为1；A和B相同，Y为0。

当A与B相反时，A Bˊ和AˊB，肯定有一个结果为1，则Y为1。

同或(Exclusive NOR)：Y=A⊙B=A B+AˊBˊA和B相同，Y为1；A和B不同，Y为0。

当A与B相同时，A B和AˊBˊ，肯定有一个结果为1，则Y为1。

同或与同或互为反运算，即两组运算，只要输入相同，一定结果相反。

A⊕B=(A⊙B)ˊA⊙B=(A⊕B)ˊ复合逻辑运算的图像符号和运算符号。

2.3逻辑代数的基本公式和常用公式2.3.1基本公式(见对偶定理)2.3.2若干常用公式(见逻辑函数化简方法之公式化简法)2.4逻辑代数的基本定理2.4.1代入定理(相当于初等代数中的换元)任何一个包含逻辑变量A的逻辑等式中，若以另外一个逻辑式代入式中所有A的位置，则等式依然成立。

2.4.2反演定理对于任意一个逻辑式Y，若将其中所有的""换成"+"，"+"换成""，"0"换成"1"，"1"换成"0"，原变量换成反变量，反变量换成原变量，则得到的结果就是Yˊ。

数字电子技术基础第1章逻辑代数基础PPT演示文稿

数字电子技术基础第1章逻辑代数基础PPT演示文稿


（1-23）
§ 1.1.3码制—信息的编码
路
中
的
信
数字信号
号
时间和幅度都是离散的
（1-5）
模拟信号： 正弦波信号 u
锯齿波信号
u
t t
（1-6）
研究模拟信号时，我们注重电路 输入、输出信号间的大小、相位关系。 相应的电子电路就是模拟电路，包括 交直流放大器、滤波器、信号发生器 等。
在模拟电路中，晶体管一般工作 在放大状态。
（1-7）
数字信号： 数字信号 产品数量的统计。 数字表盘的读数。 数字电路信号： u
（1-11）
一个十进制数数 N可以表示成：
(N)D Ki 10i
i
若在数字电路中采用十进制，必须 要有十个电路状态与十个记数码相对应。 这样将在技术上带来许多困难，而且很 不经济。
（1-12）
（2）二进制： 以二为基数的记数体制
表示数的两个数码：
0, 1 遵循逢二进一，借一当二的规律
（N）B Ki 2i
前言
1.课程特点：数字电路是一门技术基础课程，它是学 习微机原理、接口技术等计算机专业课程的基础。 既有丰富的理论体系，又有很强的实践性。
2.数字电路内容：（1）基础；（2）组合逻辑电路； （3）时序逻辑电路；（4）其它电路。
3.学习重点：（1）在具体的数字电路与分析和设计方 法之间，以分析和设计方法为主；（2）在具体的设 计步骤与所依据的概念和原理之间，以概念和原理 为主；（3）在集成电路的内部原理与外部特性之间， 以外部特性为主。
（1-2）
第一章
电子技术 数字电路部分
逻辑代数基础
（1-3）
第一章 数字电路的基础知识
§1.1 数字电路的基础知识 §1.2 逻辑代数及运算规则 §1.3 逻辑函数的表示法 §1.4 逻辑函数的化简
数字电子技术基础逻辑代数基础

数字电子技术基础逻辑代数基础


与普通代数相似的公式
交换律 A B B A
A B B A
结合律 ( A B) C A (B C)
( A B) C A (B C)
分配律 A(B C) AB AC
普通代数
A BC ( A B) ( A C) 不适用!
[例 2. 3. 1] 证明公式 A BC ( A B)( A C)
各种表示方法之间可以相互转换
•真值表
输入变量
输出
A B C····
遍历所有可能的输 入变量的取值组合
Y1 Y2 ···· 输出对应的取值
• 逻辑式
将输入/输出之间的逻辑关系用与/或/非的运算式
表示就得到逻辑式。
• 逻辑图 用逻辑图形符号表示逻辑运算关系，与逻辑电路的 实现相对应。
• 波形图 将输入变量所有取值可能与对应输出按时间顺序排 列起来画成时间波形。
3. 对偶定理：如果两个表达式相等，则它们的对 偶式也一定相等。
将 Y 中“. ”换成“+”,“+”换成“.” “0” 换成“1”,“1”换成“0”
YD
( 对偶式 )
例如Y1 A(B C) CD Y1D (A BC) (C D)
Y2 ((AB C) D) C Y2D ((( A B) C) D)C
2、逻辑函数的建立
例：举重裁判的例子：设有三个裁判，分别用A,B,C表示，
其中A是主裁判。规定至少有两个裁判确认（其中必须包 含主裁判）时，运动员的试举才算成功。
当用Y表示举重结果时，Y与A,B,C的逻辑关系可表示为：
Y=F(A,B,C) =A(B+C)
2.5.2 逻辑函数的表示方法
数字电子技术教案第3章 逻辑代数基础

数字电子技术教案第3章 逻辑代数基础

重点难点：重点：逻辑函数的表达式描述方法。
难点：任意项和非完全描述函数。
方法步骤：理论讲授、例题讲解、课堂练习、课堂提问。
器材保障：多媒体电脑、投影仪、扩音设备。
教学内容与时间安排：
首先，在黑板上简单举例说明逻辑函数常见的两种描述方式——真值表、表达式，或者叫做“表现形式”。
一、描述方式之一——真值表
本次课小结：
本次课，首先学习了逻辑函数的两种描述方式——真值表和表达式，在 “表达式描述方式”这一部分内容中，又包括表达式的类型、标准的表达式；然后了解了不同描述方式之间的相互转换的方法；最后学习了非完全描述的逻辑函数和任意项。
至此，本课程的第一部分内容已经结束。对这一部分的知识结构、主要内容及学习要求做一个简单的梳理和总结。
(三) 逻辑关系、逻辑函数与数字电路
通过幻灯片上的表格说明三者之间的一一对应关系。
二、常见的逻辑运算
注意强调逻辑关系、逻辑运算和逻辑门之间的联系；注意指出三种逻辑关系、逻辑运算和逻辑门的特点；再次强调逻辑运算与普通代数运算的区别；三种逻辑运算的优先级不同；要求学生认识逻辑门的三套符号，使用国标符号。
1和0的概念是真与假、高与低、导通与截止等对应。
注意三个域之间的对应：逻辑关系、逻辑运算、逻辑门。
注意总结每种逻辑门的特点。
基本定理是等式证明、公式变换的依据。
三条规则熟练掌握应用。
总结知识点，提示知识预习。
内容
备注
《数字电子技术》课程教案
讲课题目：第05讲 逻辑代数（2） —逻辑函数的描述方式
目的要求：1、掌握逻辑函数的两种描述方式——真值表、表达式；2、理解最小项、最大项和任意项的概念。
前面提到，在逻辑函数的真值表中，自变量的每一组取值组合都代表着一个最大项和最小项。如果自变量的某个取值组合令函数值为1，则这个取值组合所代表的最小项就会出现在函数的最小项表达式中；如果自变量的某个取值组合令函数值为0，则这个取值组合所代表的最大项就会出现在函数的最大项表达式中。
数字电子技术--逻辑代数基础知识

数字电子技术--逻辑代数基础知识


十进制转换成十六进制的方法：整数部分除以16，取余数，
读数顺序从下往上；小数部分乘以8，取整数，读数顺序从上
至下。

例如：
27 12.51B.2
10
16
二进制转换成十进制的方法：将二进制数按权展开后，按十 进制数相加。 例如：
11 .0 0 2 0 1 1 1 2 4 1 2 3 0 2 2 1 2 1 1 2 0 0 2 - 1 0 2 - 2 1 2 - 3 2 1 2 7 5 .
例如： 3.1 3 801 01 1 .0 10 2 1
二进制转换成十六进制的方法：以小数点为分界，整数部分
向左、小数部分向右，每4位为一位，不足4位的补0，然后 将每个四位二进制数都用相应的一位十六进制数取代。
例如： 00 10 0 .0 1 1 0 2 1 1 B .2 0 16
十六进制转换成二进制的方法：以小数点为分界，将每位十
解： Y ACD BD AB
ACD BD AB
ACD • BD • AB
与或式 与或非式：先将与或式化成最小项和的形式，然 后直接写成除了这些最小项编号以外的那些编号的最小项的 或非形式。 [例1-6] 试将函数式 YAC BCAB转换成与或非式。
（4）逻辑图 函数式 将逻辑图转换成函数式的方法：从输入到输出分别用相应的 逻辑运算符号取代逻辑图中的逻辑符号即可。
3．逻辑函数的两种标准形式
（1）最小项和的形式 最小项：设m为包含n个因子的乘积项，且这n个因子以原变 量形式或者反变量形式在m中出现且只出现一次，称m为n变 量的一个最小项。n变量共有个2 n 最小项。
六进制数分别用相应的四位二进制数取代。
例如：
1 B .21 600100 .1 010 1 210
数电第二章逻辑代数基础

数电第二章逻辑代数基础


4
A A 0
5
AB B A
11
1 A 1
12
0 A A
13
A A A
14
A A 1
6 A(B C) (A B)C
15 A B B A
7 A(B C) A B AC 16 A (B C) (A B) C
8 ( A B) A B
9
(A) A
17 A B C (A B)(A C) 18 ( A B) A B
返回A 返回B
说明：由表中可以看出
1.关于变量与常数关系的定理
A ·0 = 0 A ·1 = A
A+0=A A+1=1
2. 交换律、结合律、分配律
a. 交换律： AB= BA A + B=B + A
b. 结合律：A（BC） =（ AB）C
A +（ B ＋C）= （A＋B） + C c. 分配律：A( B + C) = AB + AC
☺异或运算的性质
1. 交换律： A B B A
2. 结合律： A (B C) (A B) C
3.分配律： A(B C) AB AC
4. A A 1 A A 0 A1 A A0 A
推论：当n个变量做异或运算时，若有偶数个变量取 “1”时，则函数为“0”；若奇数个变量取1时，则函 数为1.
A + BC = (A + B)(A + C)
链接A
3.逻辑函数独有的基本定理 a. 互补律： A• A 0 A A 1 b. 重叠律：A ·A = A A + A = A
c. 非非律： ( A) A
d. 吸收律：A + A B = A A (A+B) = A
数字电子技术基础 第2章

数字电子技术基础 第2章


证明若干常用公式
21、A+A ·B=A 证明：A(1+B)=A 22、A+A’ ·B=A+B 证明：利用分配律，(A+A’).(A+B)=1.(A+B) 23、A ·B+A ·B’=A 证明：A.(B+B’)=A.1 24、A ·(A+B)=A 证明：A.A+A.B=A+A.B=A(1+B)=A.1=A
1.2 逻辑式列出真值表
将输入变量取值的所有组合状态逐一代入逻辑式求出函数值， 就得到真值表。
例 2.5.2 P32-33
五、各种表示方法间的相互转换
2、逻辑函数式与逻辑图 的相互转换
2.1 给定逻辑函数式转换 为相应的逻辑图
用逻辑图形符号代替逻辑 函数式中的逻辑运算符号 并按运算顺序将它们连接 起来。
1、真值表与逻辑函数式的相互转换 1.1 由真值表写出逻辑函数式
1）找出真值表中使逻辑函数Y=1的那些输入变量取值的组合。 2）每组输入变量取值的组合对应一个乘积项，其中取值为1的
写入原变量，取值为0的写入反变量。 3）将这些乘积项相加，即得Y的逻辑函数式。 例 2.5.1 P32
IEC （International Electrotechnical Commission，国 际电工协会）
异或，同或
异或：
输入A,B 不同时，输出Y为1；输入A,B 相同时，输 出Y为0。
Y=A⊕ B=A· B’+A’ · B
或：
输入A,B 不同时，输出Y为0；输入A,B 相同时，输 出Y为1。
证明若干常用公式
25、A ·B+A’ ·C+B ·C=A ·B+A’ ·C 证明：=A.B+A’.C+B.C(A+A’) =A.B+A’.C+A.B.C+A’.B.C =A.B(1+C)+A’.C.(1+B)=A.B+A’.C 同样可证明：A ·B+A’ ·C+B CD=A ·B+A’ ·C 26、A ·(A ·B)’=A ·B’; A’ ·(A·B)’=A’ 证明：A.(A’+B’)=A.A’+A.B’=A.B’
《数字电子技术基础》——数字逻辑基础.ppt

《数字电子技术基础》——数字逻辑基础.ppt


（3）由数字电路组成的数字系统，抗干扰能力强， 可靠性高， 精确性和稳定性好，便于使用、维护 和进行故障诊断，容易完成实时处理任务。
（4）高速度，低功耗，可编程。
2、数字电路的分类
（1）按集成度分类：数字电路可分为小规模 （SSI）、中规模（MSI）、大规模（LSI）和超 大规模（VLSI）数字集成电路。集成电路从应 用的角度又可分为通用型和专用型两大类型。
数字信号：在时间上和数值上不连续的 （即离散的）信号。
u
t
数字信号波形
对数字信号进行传输、处理的电子线路称 为数字电路。
1.1.2 数字电路的特点与分类
1、数字电路的特点
（1）数字技术能够完成许多复杂的信号处理工作。
（2）数字电路不仅能够完成算术运算，而且能够完 成逻辑运算， 具有逻辑推理和逻辑判断的能力。
约束条件反映了逻辑函数中各逻辑变量之间的制约关系约束条件所含的最小项称为约束项它表示输入变量某些取值组合不允许出现或者不影响逻辑函数的输出因此也被称为无关项任意项一般用d表示i仍为最小项序号填入卡诺图时用表示
数字电子技术基础
国防科技大学出版社
第1章 数字逻辑基础
1.1 概述 1.2 数制及二进制代码 1.3 逻辑代数基础 1.4 逻辑函数及其化简
交换律：
A A
B B BB
A
A
结合律：
( (
A A
B) B)
C
C
A
(B A
C) (B
C)
分配律：
A A
(B B
C) C
A (A
B B)
A (A
C
C)
反演律（摩根定律）：
A
.B
数电 第一章 逻辑代数基础

数电 第一章 逻辑代数基础


文字、数值信息
十进制数的二进制编码 常用十进制数码
十进制数 8421码
0 1 2 3 4 5 6 7 8 9
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001
2421码 0000 0001 0010 0011 0100 1011 1100 1101 1110 1111 有权码
N
B

d 2
i
i
i
0
1
1 1
0 0
1 0
0 1
【例如】 (101.101)2=1×22十0×21十1×20十1×2-1十0×2-2十1×2-3
3.八进制（O）
以8为基数的计数体制，有0、1、2、3、4、5、6、 7共8个数码，逢八进一。
位置计数法 以权展开式
例：741 O
306O
i i
N
O
5211码 0000 0001 0011 0101 0111 1000 1001 1100 1101 1111
余3码 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100
格雷码 0000 0001 0011 0010 0110 1110 1010 1000 1100 0100
课程考核
平时成绩占30% ：考勤、作业、实验； 期末成绩占70% ：期末考试卷面分。
课外作业 为了让大家学完本课程有较大的收获，有以下两 个作业： （1）查询资料，有关自己所学专业和电子技术方面 的新技术、新方法，学习科技小论文的撰写方法，查 询有关资料。 （2）利用计算机，学习电子技术仿真软件的应用— —Multisim
课程设计
利用自己所学的电子技术基本理论知识，综 合设计电子实际应用电路，培养综合设计能力.

数电第一章逻辑代数基础

计数的基数是16，进位规则是“逢十六进一” 任意一个十六进制数D可按“权”展开为：D=ΣkiX16i 如：(2F.8)16=2×161+15×160+8×16-1=(47.5)10 下标16代表十六进制数，有时也用H（Hexadecimal）代
替下标16。
如：2F.8H=47.5D 二进制、十六进制数广泛应用于数字电路
低位
所以：(44.375)10＝(101100.011)2
3.二进制—十六进制转换 十六进制实际上也应属于二进制的范畴 将4位二进制数（恰好有16个状态）看作一个整体时，它的 进位关系正好是“逢十六进一” 所以只要以小数点为界，每4位二进制数为一组（高位不足4 位时，前面补0，低位不足4位时，后面补0），并代之以等值
注意： 不要漏掉 将十进制数展成Σki×2i的形式 0 得到二进制数:knkn-1……k1k0（有小数时还会有k-1……） =1×64+1×32+1×16+1×8+0×4+1×2+1×1 =(1111011)2
例：(123)10=64+32+16+8+0+2+1
或者：采用的方法 — 除2取余、乘2取整 原理：将整数部分和小数部分分别进行转换。 整数部分采用除 2取余法，小数部分采用乘2取整法。转换后再合并。 整数部分采用除2取余法， 先得到的余数为低位，后 得到的余数为高位。
数 字 电 路
车晓镭
第一章 逻辑代数基础
1.1 概述 1.2 逻辑代数的基本运算 1.3 逻辑代数的基本公式和常用公式 1.4 逻辑代数的基本定理 1.5 逻辑函数及其表示方法 1.6 逻辑函数的公式化简 1.7 逻辑函数的卡诺图化简法

数字电子技术--逻辑代数基础

数字电子技术第1秦便霧代敌基础范立南代红艳恩莉刘明丹中国水利水电出版社第1秦便锈代敌基础1 -2逻辑代数►1-1概述1.1.1数字电路和模拟电路物理量的分类：数字量和模拟量。

数字量：是指变化无论在时间上还是数值上都是离散的物理量。

模拟量：是指变化无论在时间上还是数值上都是连续的物理量。

数字信号：用于表示数字量的信号。

模拟信号：用于表示模拟量的信号。

数字电路：工作在数字信号下的电子电路。

模拟电路：工作在模拟信号下的电子电路。

‘專书主要研究数字电路的分析方法、设计方法及其应用1-1-2数制和码制1 ■数制数制：是指多位数码中每一位的构成方法及低位向相邻高位的进位规则。

(1)常用进制十进制：由0、1 ...9十个数码组成，进位规则是逢十进一，计数基数为10,其按权展开式D = 2kixl()i例如:热(27.125)十2 x I。

】+ 7 x 10° +1 x io1 + 2x io-2 +5x io-3二进制：由0、计数基数为2, 1两个数码组成，进位规则是逢二进一，其按权展开式为。

例如:D = Yki><2i(11011.001)2 = 1X 24 +1X 23 + 0 X 22 +1X 21 +1X 2° + o X 21 + 0 X 2-2 +1X 2八进制：由0、计数基数为8, 1...7八个数码组成，进位规则是逢八进一，其按权展开式为。

例如:D二><8Z(33.1) =3X81+3X8°+1X84十六进制：由0、1…9、A、B…F十六个数码组成，进位规则是逢十六进一，计数基数为16,其按权展开式D = Xki><16i例如: (1B.2)I6=1X161+B X16°+2X1610. 125x 20. 250. 25x 2----- 整数0 =K-i0. 50. 5 x 2 ----- 整数o =K-2(2)常用进制之间的转换十进制转换成二进制的方法：整数部分除以2,取余数，读数顺序从下往上；小数部分乘以2,取整数，读数顺序从上至下。

数字电子技术基础：第二章 逻辑代数基础


8. 同或运算： 其布尔表达式为 Y A⊙B (A B) AB AB
符号“⊙”表示同或运算，即两个输入变量值相同 时Y=1，即相同为“1”不同为“0” 。同或运算用同 或门电路来实现，它等价于异或门输出加非门，
其真值表如表2.2.7所示 其门电路的逻辑符号如图2.2.11 所示
表2.2.7 同或逻辑真值表
☺异或运算的性质
1. 交换律： A B B A
2. 结合律： A (B C) (A B) C
3.分配律： A(B C) AB AC
4. A A 1 A A 0 A1 A A0 A
推论：当n个变量做异或运算时，若有偶数个变量取 “1”时，则函数为“0”；若奇数个变量取1时，则函 数为1.
符号“⊕”表示异或运算，即两个输入逻辑变量取
值不同时Y=1，即不同为“1”相同为“0”，异或运算
用异或门电路来实现 其真值表如表2.2.6所示
表2.2.6 异或逻辑真值表 输入 输出
其门电路的逻辑符号如图2.2.10
A
BY
所示
0
00
A B
=1 Y A B
Y
0
11
1
01
1
10
图2.2.10 异或门逻辑符号
A 0
上式说明：当逻辑变量A、B有
0
一个为1时，逻辑函数输出Y就
1
为1。只有A、B全为0，Y才为0。 1
BY
00 11 01 11
其逻辑门符号如图 2.2.4所示，实现或逻辑
A
运算的门电路称为或门。 B
1
Y
A B
Y
图2.2.4 或门逻辑符号
若有n个逻辑变量做或运算，其逻辑式可表示为
Y A1 A2 An

数字电子技术--逻辑代数基础知识

数字电子技术--逻辑代数基础知识数字电子技术是研究和应用逻辑代数基础知识的一门学科。

逻辑代数是数学中的一个分支，它研究命题的逻辑运算和关系。

在数字电子技术中，逻辑代数被用来描述和分析数字电路的行为。

首先，逻辑代数中的基本运算包括逻辑与、逻辑或和逻辑非。

逻辑与运算表示两个输入同时为真时，输出为真；逻辑或运算表示两个输入中至少有一个为真时，输出为真；逻辑非运算表示输入为真时，输出为假，反之亦然。

逻辑代数中的命题通常用0和1表示，其中0代表假，1代表真。

这样，逻辑运算可以用真值表来表示。

真值表是逻辑运算的真值集合的表示形式，通过列举所有可能的输入值和对应的输出值，可以得到逻辑运算的完整描述。

在数字电子技术中，逻辑运算的结果被用来表示一个电路的输出。

电路由逻辑门组成，逻辑门是实现逻辑运算的基本元素。

常见的逻辑门有与门、或门和非门。

与门将两个输入进行逻辑与运算，输出结果与两个输入相同；或门将两个输入进行逻辑或运算，输出结果与两个输入相同；非门将一个输入进行逻辑非运算，输出结果与输入相反。

利用逻辑门，可以构建各种复杂的数字电路，如加法器、计数器和存储器等。

这些电路通过组合不同的逻辑门和使用逻辑代数进行分析和设计，实现了数字信号的存储、处理和传输。

逻辑代数基础知识在数字电子技术中起着重要的作用。

它提供了一种抽象和形式化的方法，用于描述和分析数字电路的行为。

通过逻辑代数的基本运算和规则，可以简化和优化数字电路的设计，提高电路的性能和可靠性。

总而言之，逻辑代数基础知识是数字电子技术的核心内容之一。

它为数字电路的设计和分析提供了基本的工具和方法，使我们能够理解和应用数字电子技术。

通过掌握逻辑代数基础知识，可以更好地理解数字电子技术的原理和应用，为实际问题的解决提供有效的方法。

当我们深入研究数字电子技术时，逻辑代数的基础知识成为我们理解和设计复杂电路的基础。

在数字电路中，逻辑门是数字信号处理的基本组成部分。

通过逻辑代数的运算和规则，我们可以将逻辑门进行组合，从而构建出更为复杂的数字电路。

数字电子技术0-1 逻辑代数基础

第1章 逻辑代数基础
首都师范大学物理系
3 数字电路分类
一、按集成电路规模分类
集成度：每块集成电路芯片中包含的元器件数目
小规模集成电路(Small Scale IC，SSI) 中规模集成电路(Medium Scale IC，MSI) 大规模集成电路(Large Scale IC，LSI) 超大规模集成电路(Very Large Scale IC，VLSI) 特大规模集成电路(Ultra Large Scale IC，ULSI) 巨大规模集成电路(Gigantic Scale IC，GSI）
乘法运算
1001 ×0101 1001 0000
除法运算
1. 1 1… 0 1 0 1) 1 0 0 1 0101 1000 0101
1001
0000 0101101
0110
0101 0010
符号（+/-）数码化 算术运算---数值表示 “0”表示“+” 最高位： “1”表示“-”
一、真值与机器数
三、按电路结构分类
组合逻辑电路（第三章） 时序逻辑电路（第五章）
目录
1.1 概述 1.2 逻辑代数的基本运算 1.3 逻辑代数的基本公式和常用公式 1.4 逻辑代数的基本定理 1.5 逻辑函数及其表示方法 1.6 逻辑函数的公式代数化简法 1.7 逻辑函数的卡诺图化简 1.8 具有无关项的逻辑函数及其化简 本章小结

与非 或非 与或非
异或
同或

其逻辑表达式、 逻辑符号及逻辑真值表如下表所 示。
0
1.3 逻辑代数的基本公式与常用公式
1.3.1 基本公式 1.3.2 若干常用公式
定律名称 1· 0-1律 2·交换律 3·结合律 4·分配律 5·互补律 6·重叠律 7·还原律 8·反演率（摩 根定律） 9· 吸收律

数字电子技术 1 逻辑代数基础

解： 首先将 (1101111.00011)B 分段，然后计算每段的值，可得
（1）转换为八进制数
(1101111.00011)B (001/101/111.000/110)B (157.06)O
（2）转换为十六进制数
(1101111.00011)B (0110/1111.0001/1000)B 6F.18H
375.38 3102 7 101 5100 3101 8102
表示十进制数时，可以在数字的右下角标注10或D，对 于任意一个十进制数 ，都可以按以下形式写出其按权展开式
(N )D an1 10n1 an2 10n2 L a1 101 a0 100 a1 101 a2 102 L am 10m
1.2.3 二进制数的反码、 补码和补码运算
1．二进制数的原码
原码就是符号位加上真值的绝对值，即用第1位表示符号， 其余位表示值。例如，8位二进制数
(1)原 0000 0001
(1)原 1000 0001
所以8位二进制数的取值范围就是[1111 1111，0111 1111]， 即[ 127，127]。
表1-2 不同进制计数制的各种数码
二进制数 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
八进制数 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17
十六进制数 0 1 2 3 4 5 6 7 8 9 A B C D E F
和“除二取余法”进行运算，可得
(29.3125)D (29)D (0.3125)D (11101)B (0.0101)B (11101.0101)B
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
= ( 2
E
8.
6)
H
十六进制转换为二进制正好和上述过程相反
《数字电子技术基础》
三、二进制数算术运算
• 算术运算 二进制数的0/1可以表示数量，进行 加，减，乘，除…等运算 • 二进制数的正、负号也是用0/1表示的。 在定点运算中，最高位为符号位（0为正，1为负） 如 +89 = （0 1011001） -89 = （1 1011001）
《数字电子技术基础》
《数字电子技术基础》
电子课件
郑州大学电子信息工程学院 2018年6月7日
《数字电子技术基础》
第一章
逻辑代数基础
《数字电子技术基础》
1.1 概述 1.1.1 脉冲波形和数字波形
图1.1.1几种常见的脉冲波形，图(a)为 矩形波、图(b)为锯齿波、图(c)为尖峰波、 图(d)为阶梯波。
UH
1
1
1
UL
0 0
0
0
0
t
图1.1.3 矩形脉冲数字表示方法
《数字电子技术基础》
1.1.2 数制和码制
一、数制 ①每一位的构成 ②从低位向高位的进位规则 我们常用到的： 十进制，二进制，八进制，十六进制
《数字电子技术基础》
十进制，二进制，八进制，十六进制
逢二进一
逢八进一
逢十进一
逢十六进一
《数字电子技术基础》
十进制数325.12用位置计数法可以表示为
D10 3 102 2 101 5 100 1101 2 102
任意一个具有n为整数和m为小数的二进制 数表示为
D2 k n1 2 n1 k n2 2 n2 k1 21 k0 20 k 1 2 1 k m 2 m
几种常用的复合逻辑运算
• 与非 或非 与或非
《数字电子技术基础》
几种常用的复合逻辑运算
• 异或 • Y= A B A 0 0 B 0 1 Y 0 1
1
1
0
1
1
0
《数字电子技术基础》
几种常用的复合逻辑运算
• 同或 • Y= A ⊙B A 0 0 B 0 1 Y 1 0
1
1
ห้องสมุดไป่ตู้
0
1
0
1
1.2.2 逻辑代数的运算定律及规则
《数字电子技术基础》
1.2.1 逻辑代数中的三种基本运算
与（AND） 或（OR） 非（NOT）
以A=1表示开关A合上，A=0表示开关A断开； 以Y=1表示灯亮，Y=0表示等不亮； 三种电路的因果关系不同：
《数字电子技术基础》
与
• 条件同时具备，结果发生 • Y=A AND B = A&B=A· B=AB
《数字电子技术基础》
二进制数的补码：
• 最高位为符号位（0为正，1为负） • 正数的补码和它的原码相同 • 负数的补码 = 数值位逐位求反 + 1
如 +5 = （0 0101） -5 = （1 1011）
• 通过补码，将减一个数用加上该数的补码来实现
《数字电子技术基础》
• 7–4=3 • 7 + 8 = 3 （舍弃进位）
（a） （b）
（c）
（d）
图1.1.1 几种常见的脉冲波形
《数字电子技术基础》
脉冲信号的参数
0.9U m
Um tW T
（a）
0.5U m 0.1U m
Um
tr
tW T
tf
（b）
图1.1.2 矩形脉冲参数
《数字电子技术基础》
矩形脉冲数字表示法
通常规定：0表示矩形脉冲的低电平；1表 示矩形脉冲的高电平，如图1.1.3波形所示。
D16 ki 16i
例如：
(E5C7.A2)16 E 163 5 162 C 161 7 160 A 161 2 162
《数字电子技术基础》
二、数制间的转换
各种进制转换为十进制
(1101 .11) 2 2 3 2 2 2 0 2 1 2 2 (13.75) 2
• 4 + 8 = 12 产生进位的模 • 8是-4对模数12的补码
特别要注意的是，运算过程中 所有的数都用补码表示。
《数字电子技术基础》
• 1110 – 0110 = 1000 （14 - 6 = 8） • 1110 + 1010 = 11000 =1000（舍弃进位） （14 + 10 = 8）
十进制转换为二进制
2 2 129 64 2 32 2 16 2 8 2 4 2 2 2 1 0
余1 余0 余0 余0 余0 余0 余0 余1
k0 k1 k2 k3 k4 k5 k6
k7
所以
(129) 10 (10000001 )2
《数字电子技术基础》
二进制转换与十六进制间的转换
(0010, 1110, 1000. 0110)
A 0
0 1 1
B 0
1 0 1
Y 0
0 0 1
《数字电子技术基础》
或
• 条件之一具备，结果发生 • Y= A OR B = A+B A 0 0 B 0 1 Y 0 1
1
1
0
1
1
1
《数字电子技术基础》
非
• 条件不具备，结果发生 • Y A NOT A A 0 1 Y 1 0
《数字电子技术基础》
八进制有0~7个数码，基数为8，它的计数 规则是“逢八进一”。八进制一般表达式为
D8 ki 8i
《数字电子技术基础》
十六进制数的符号有0、1、2、…、8、9、 A、B、C、D、E和F，其中符号0~9与十进制符 号相同，字母A~F表示10~15。十六进制的计数 规则“逢十六进一”，一般表示形式为
0011 )8421BCD
(0100101001 1000 )8421 -BCD (1298 )D
BCD码除842l码外，常用的还有2421码、余3码、 余3循环码、BCD格雷码等等
《数字电子技术基础》
1.2 基本逻辑函数及运算定律
基本概念 逻辑：事物的因果关系 逻辑运算的数学基础：逻辑代数 在二值逻辑中的变量取值： 0/1 逻辑代数中的变量称为逻辑变量，用字 母A、B、C、…表示。其取值只有0或者l两 种。这里的0和1不代表数量大小，而表示两 种不同的逻辑状态，如，电平的高、低；晶 体管的导通、截止；事件的真、假等等。
2 14 4 12 10 8 6
16
• 0110 + 1010 =24 • 1010是- 0110对模24 （16） 的补码
《数字电子技术基础》
四、BCD码（Binary Coded Decimal）
8421BCD码与十进制数之间的转换是直接按位转 换，例如
(29.3) D (0010
1001 .