集合论(习题课)

集合习题课一、集合三要素：确定性、互异性、无序性。

1、若集合A 是由23,,02+-m m m 三个元素组成的集合，且,2A ∈则实数m 为（ ） 2.A 3.B 30.或C 均可3,2,0.C二、集合的表示方法：列举法、描述法、图像法.三、集合的关系：元素与集合的关系用””或““∉∈；集合与集合的关系用”或“⊆“”。

2．下列各式中，正确的是( )A ．23∈{x |x ≤3}B ．23∉{x |x ≤3}C ．23⊆{x |x ≤3}D ．{23}⊄{x |x ≤3}3．已知集合A ＝{x ∈N *|－5≤x ≤5}，则必有( )A ．－1∈AB ．0∈A C.3∈A D ．1∈A1、 一般地，对于两个集合A 、B ，如果集合A 中任意一个元素都是集合B 中的元素，则 称 集合A 是集合B 的子集。

记作B A ⊆.4.满足M a ⊆}{的集合},,,{d c b a M 共有 （ ）5.6个 B.7个 C.8个 D.15个6.已知集{}}{a x x B x x A <=<<=,21，满足A B ，则 （ ）A.2≥aB. 1≤aC.1≥aD. 2≤a7.已知集合}{41>-<=x x x A 或，=B }{32+≤≤a x a x ，若A B ⊆，求实数a 的取值范围.2、 如果集合B A ⊆，但存在元素B x ∈，且A x ∉，则称集合A 是集合B 的真子集.记作：A B.3、 把不含任何元素的集合叫做空集.记作：∅.并规定：空集合是任何集合的子集.4、 如果集合A 中含有n 个元素，则集合A 有n 2个子集。

8.集合}{Z x x x A ∈<≤=且30的真子集的个数为 （ ）A.5B.6C.7D.8四、集合运算1、 集合A 与B 的并集.记作：B A2、 A 与B 的交集.记作：B A .3、全集、补集？{|,}U C A x x U x U =∈∉且9．设集合A ＝{x|2≤x ＜4}，B ＝{x|3x －7≥8－2x}，则A ∪B 等于( )A ．{x|x ≥3}B ．{x|x ≥2}C ．{x|2≤x ＜3}D ．{x|x ≥4}10．集合A ＝{0，2，a}，B ＝{1，2a }．若A ∪B ＝{0，1，2，4，16}，则a 的值为( )A ．0B ．1C ．2D ．411．满足M ⊆{4321,,a a a a }，且M ∩{321,,a a a }＝{21,a a }的集合M 的个数是( )A ．1B ．2C ．3D ．412.已知全集U=R ，集合A={x ︱-2≤x ≤3},B={x ︱x ＜-1或x ＞4｝，那么集合A ∩（CUB ）等于（ ）.A.{x ︱-2≤x ＜4｝B.{x ︱x ≤3或x ≥4}C ．{x ︱-2≤x ＜-1｝ D.{-1︱-1≤x ≤3}13．（12分）已知全集{}6,5,4,3,2,1,0=U ，集合{}41≤<∈=x N x A ，（1）用列举法表示集合A 与B ；（2）求B A ⋂及)(B A C U ⋃。

大学集合论试题及答案一、选择题（每题3分，共30分）1. 集合论的创始人是（）。

A. 康托尔B. 罗素C. 希尔伯特D. 哥德尔2. 集合A和集合B的并集表示为（）。

A. A∩BB. A∪BC. A-BD. A∩B'3. 若集合A是集合B的子集，则表示为（）。

A. A⊆BB. A⊇BC. A⊂BD. A⊃B4. 空集是所有集合的（）。

A. 子集B. 真子集C. 并集D. 交集5. 集合A和集合B的交集表示为（）。

A. A∩BB. A∪BC. A-BD. A∩B'6. 若集合A和集合B的交集为空集，则A和B是（）。

A. 子集B. 真子集C. 互斥的D. 相等的7. 集合的幂集是指（）。

A. 集合的所有子集的集合B. 集合的所有元素的集合C. 集合的所有真子集的集合D. 集合的所有非空子集的集合8. 集合A和集合B的差集表示为（）。

A. A∩BB. A∪BC. A-BD. A∩B'9. 集合的元素个数称为集合的（）。

A. 基数B. 序数C. 秩D. 维数10. 集合论中，无限集合的基数可以是（）。

A. 有限的B. 可数的C. 不可数的D. 以上都是二、填空题（每题2分，共20分）1. 集合{1, 2, 3}的幂集有个元素。

2. 集合{a, b, c}和集合{a, b}的交集是。

3. 集合{1, 2, 3}和集合{2, 3, 4}的并集是。

4. 集合{1, 2, 3}和集合{2, 3, 4}的差集是。

5. 集合{1, 2, 3}的补集在全集U={1, 2, 3, 4, 5}中是。

6. 若集合A={1, 2, 3}，集合B={2, 3, 4}，则A∪B= 。

7. 集合{1, 2, 3}的子集个数是。

8. 集合{1, 2, 3}的真子集个数是。

9. 集合{1, 2, 3}的非空真子集个数是。

10. 若集合A={1, 2, 3}，集合B={2, 3, 4}，则A∩B= 。

三、解答题（每题10分，共50分）1. 证明：若集合A是集合B的子集，且集合B是集合C的子集，则集合A是集合C的子集。

习 题 课例1设{,,}A a b c =，给出A 上的一个二元关系，使其同时不满足自反性、反自反性、对称性、反对称和传递性的二元关系，并画出R 的关系图。

解：{(,),(,),(,),(,)}R a a b c c b a c =，关系图如图所示。

例2 设X 是一个集合，X ＝n ，求：1.X 上的二元关系有多少？()22n 2. X 上的自反的二元关系有多少？ 3. X 上的反自反的二元关系有多少？解：因为把所有的反自反的二元关系的每个都加上对角线上的序对，就变成了自反的关系，因此，自反的与反自反的个数一样多。

即22nn-4. X 上的对称的二元关系有多少？2222n n n nn -++=，故共有222n n+个对称的关系。

5. X 上的反对称的二元关系有多少？22(32)n n n -∙6. X 上既是自反的也是反自反的二元关系的个数；(0)个7.X 上既不是自反的也不是反自反的二元关系有多少？2(2(22))n nn --解：解：可用容斥原理来计算设B 表示所有自反关系构成的集合，C 表示所有反自反关系构成的集合，则22nnB C -==。

而B C φ=，故B C B C =+，从而CC B C S B C S B C =-=--2222222222222(22)n n n n n n n n n n n ----=--=-=-于是，既不是自反的，也不是反自反关系共有22(22)n nn --个。

8.自反的且对称的关系有多少？[此结果与“反自反的且对称的关系有多少？”是一样多]即有222n n -（对角线上全去掉）9.自反的或对称的关系有多少？解：设B 表示自反关系的集合，C 表示对称关系的集合，则自反或对称关系的集合为：22222222n n n n nnB C B C B C +--=+-=+-。

10.X 上既是反自反的也是反对称的二元关系的个数为：223n n -；11.X 上既是对称的也是反对称的关系个数；解：X 上既是对称的也是反对称的关系X R I ⊆，故有2n 。

课程作业——集合论部分•填空题1、集合有两种表示方法，分别为法和法。

2、“使有意义的所有的集合。

”可表示为：。

“大于3而小于或等于7的整数组成的集合”表示为。

3、写出A={a,b,c,d}}的全部子集，真子集为。

4、设A，B是两个集合，A={1，2，3，4}，B={2，3，5}，则A-B= ，r（B）-r（A）= ，r（A）的元素个数为。

5、设，则A-B= ，B-A= ，~A= ，~B= 。

6、全集E={a，b，c，d，e}，A={a，d}，B={a，b，e}，C={b，d}，求（AÇB）È~C= ，r（A）Çr（B）= 。

7、集合运算的基本定律：1）AÇA=A，满足律；2）AÇE=A，满足律；3）~（AÈB）=~AÇ~B，满足律。

8、A和B是任意两个集合，若有序对的第一个元素是A的一个元素，第二个元素是B的一个元素，则所有这样的有序对集合称为集合A和B 的，记作A´B，即A´B= 。

9、设A、B是两个集合，其中A={1，2}，B={a,b,c}，则A×B= ，B×A= ，所以笛卡尔积不满足律。

10、设A、B为两个有限集合，则根据包含排斥定理知：|A∪B|= 。

11、有序对（a,b）=(x,y)的充分条件是。

•单项选择题1、由集合运算定义，下列各式正确的有（）。

•XÍXÈY B.XÊXÈY C.XÍXÇY D.YÍXÇY2、下列命题正确的是（）。

A．fÇ{f}=f B．fÈ{f}=f C．{a}Î{a，b，c} D．fÎ{a，b，c}3、设集合，则（）。

4、下列式子中正确的有（）。

5、设为任意集合，下列命题正确的有（）A、若，则；B、若，则；C、若则；D、若，则6、对于任意集合S，，满足（）A、等幂律B、同一律C、零一律D、互补律7、某个集合的元数为10，可以构成（）个子集。

P3 习题1.11.1.1 解：⑴ {2,3,5,7,11,13,17,19}； ⑵ {e,v,n,i,g}； ⑶ {－3,2}；⑷ {－1}； ⑸ {2,271i +-,271i --}； ⑹ Φ ⑺ 共14项，前四项为极小因式：不能再分解为其它因式的因式：{①x+1，②x -1，③x 2+x+1，④x 2-x+1，①②x 2-1，①③x 3+2x 2+2x+1，①④x 3+1， ②③x 3－1，②④x 3－2x 2+2x －1，③④x 4+x 2+1，①②③x 4+x 3-x+1，①②④x 4－x 3+x －1，①③④x 5+x 4+x 3+x 2+x+1，②③④x 5-x 4+x 3-x 2+x -1)}1.1.2 解 ⑴ {x | x ∈I + , x<80}； ⑵ {x | x ∈I 且∃n ∈I 使x=2n+1}； ⑶ {x | x ∈I 且∃n ∈I 使x=5n}；⑷ {(x,y)| x,y ∈R , x 2+y 2<1}； ⑸ {(ρ,θ)| ρ,θ∈R , ρ>1}； ⑹ {ax+b=0| a,b ∈R 且a ≠0}。

P5 习题1.21.2.1 答：为真的有：⑵、⑷、⑻、⑽，其余为假。

1.2.2 答：为真的有：⑴、⑷，其余为假。

1.2.3 解：A=Φ，B={0}，C={…,-4,-2,0,2,4…}，D={2,4}，E={…,-4,-2,0,2,4…}，F={2,4}， G=Φ，H={…,-4,-2,0,2,4…}。

∴ C=E=H ，D=F ，A=G 。

1.2.4 答：四个全为真。

证明：⑴ 例 A={a} , B={a,A}⑵ 例 B={A} , C={A , B}⑶ 例 A={Φ}⑷ 例 A={a} , B={a,A} , ∴ 2B ={Φ , {a} , {A} , B} ※1.2.5 解 ⑴ 幂集 {Φ} ；幂集的幂集 {Φ,{Φ}}⑵ 幂集 {Φ,{Φ},{a},{Φ,a}}；幂集的幂集 零元素子集 {Φ,单元素子集 {Φ} , {{Φ}} , {{a}} , {{Φ,a}},双元素子集 {Φ,{Φ}} , {Φ,{a}} , {Φ,{Φ,a}} , {{Φ},{a}} , {{Φ},{Φ,a}} , {{a},{Φ,a}} , 三元素子集 {Φ,{Φ},{a}} , {Φ,{Φ},{Φ,a}} , {Φ,{a},{Φ,a}} , {{Φ},{a},{Φ,a}}}， 四元素子集 {Φ,{Φ},{a},{Φ,a}} 。

第五章 图的基本概念习 题 课 11. 画出具有 6、8、10、…、2n 个顶点的三次图；是否有7个顶点的三次图？2. 无向图G 有21条边，12个3度数顶点，其余顶点的度数均为2，求G 的顶点数p 。

解：设图的顶点为p ，根据握手定理：1deg()2pi i v q ==∑，有212)12(2312⨯=-⨯+⨯p ，得15302==p p ，。

3. 下列各无向图中有几个顶点？（1）16条边，每个顶点的度为2；（2）21条边，3个4度顶点，其余的都为3度数顶点；（3）24条边，各顶点的度数相同。

解： 设图的顶点为p ，根据握手定理：（1）1deg()2p i i v q ==∑，即2221632p q ==⨯=；所以16p =，即有16个顶点。

（2）1deg()2p i i v q ==∑，即433(3)222142p q ⨯+⨯-==⨯=，所以13p =。

（3）各点的度数为k ，则1deg()2i pi v q ==∑，即222448k p q ⨯==⨯=，于是① 若1k =，48p =； ② 若2k =，24p =；③ 若3k =，16p =； ④ 若4k =，12p =；⑤ 若6k =，8p =；⑥ 若8k =，16p =； ⑦ 若12k =，4p =；⑧ 若16k =，3p =； ⑨ 若24k =，2p =； ⑩ 若48k =，1p =。

4．设图G 中9个顶点，每个顶点的度不是5就是6。

证明G 中至少有5个6度顶点或至少有6个5度顶点。

证：由握手定理的推论可知，G 中5度顶点数只能是0，2，6，8五种情况，此时6度顶点数分别为9，7，5，3，1个。

以上五种情况都满足至少5个6度顶点或至少6个5度顶点的情况。

5．有n 个药箱，若每两个药箱里有一种相同的药，而每种药恰好放在两个药箱中，问药箱里共有多少种药？[就是求一个完全图n K 的边数(1)(2)/2q p p =--g ]6.设G 是有p 个顶点，q 条边的无向图，各顶点的度数均为3。

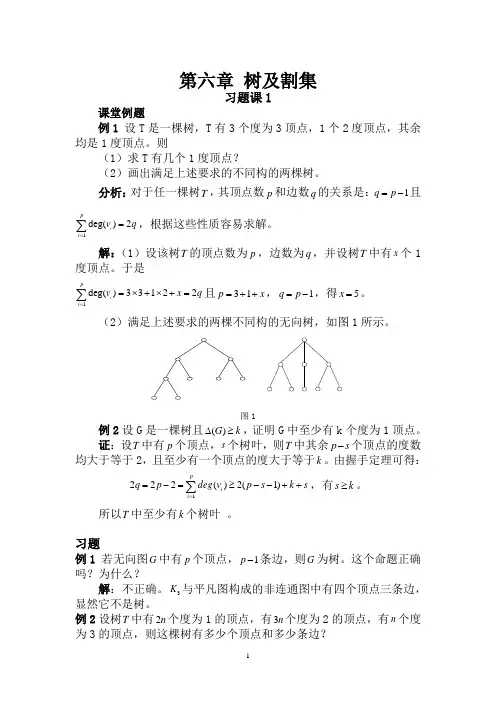
第六章 树及割集习题课1课堂例题例1 设T 是一棵树，T 有3个度为3顶点，1个2度顶点，其余均是1度顶点。

则（1）求T 有几个1度顶点？（2）画出满足上述要求的不同构的两棵树。

分析：对于任一棵树T ，其顶点数p 和边数q 的关系是：1q p =-且1deg()2ipi v q ==∑，根据这些性质容易求解。

解：（1）设该树T 的顶点数为p ，边数为q ，并设树T 中有x 个1度顶点。

于是1deg()33122ipi v x q ==⨯+⨯+=∑且31p x =++，1q p =-，得5x =。

（2）满足上述要求的两棵不同构的无向树，如图1所示。

图1例2设G 是一棵树且()G k ∆≥，证明G 中至少有k 个度为1顶点。

证：设T 中有p 个顶点，s 个树叶，则T 中其余p s -个顶点的度数均大于等于2，且至少有一个顶点的度大于等于k 。

由握手定理可得：1222()2(1)pi i q p deg v p s k s ==-=≥--++∑，有s k ≥。

所以T 中至少有k 个树叶 。

习题例1 若无向图G 中有p 个顶点，1p -条边，则G 为树。

这个命题正确吗？为什么？解：不正确。

3K 与平凡图构成的非连通图中有四个顶点三条边，显然它不是树。

例2设树T 中有2n 个度为1的顶点，有3n 个度为2的顶点，有n 个度为3的顶点，则这棵树有多少个顶点和多少条边？解：设T 有p 个顶点，q 条边，则123161q p n n n n =-=++-=-。

由deg()2v Vv q ∈=∑有：1223322(61)122n n n q n n ⨯+⨯+⨯==-=-，解得：n =2。

故11,12q p ==。

例3证明恰有两个顶点度数为1的树必为一条通路。

证：设T 是一棵具有两个顶点度数为1的(,)p q 树，则1q p =-且1deg()2pii v q ==∑2(1)p =-。

又T 除两个顶点度数为1外，其他顶点度均大于等于2，故211deg()2deg()2(1)p p iii i v v p -===+=-∑∑，即21deg()2(2)p ii v p -==-∑。