行列式典型例题

高等代数《行列式》部分习题及解答例1：决定以下9级排列的逆序数，从而决定它们的奇偶性： 1）.134782695；2）.217986354；3）.987654321. 答：1）. ()134782695=10τ，134782695是一个偶排列；2）. ()217986354=18τ，217986354是一个偶排列； 3）. ()987654321=36τ，987654321是一个偶排列. 例2：写出把排列12435变成排列25341的那些对换.答：()()()()()()()12154,312435214352543125341−−→−−→−−−→.例3：如果排列121...n n x x x x -的逆序数为k ，排列121...n n x x x x -的逆序数是多少？答：()112n n k --例4：按定义计算行列式： 000100201).0100000n n - 010000202).0001000n n -001002003).1000000n n-答：1）.原行列式()()()()1,1,,2,121!1!n n n n n n τ--=-=-2）.原行列式()11!.n n -=-3）.原行列式()()()1221!n n n --=-.例5：由行列式定义计算()212111321111x x x f x x x-=中4x 与3x 的系数，并说明理由. 答：()f x 的展开式中x 的4次项只有一项；2,x x x x ⋅⋅⋅故4x 的系数为2；x 的3次项也只有一项()()213411,x x x τ-⋅⋅⋅故3x 的系数为-1.例6：由111111=0111，证明：奇偶排列各半.证明：由于12n j j j 为奇排列时()()121n j j j τ- 为-1，而偶排列时为1,.设有k 个奇排列和l 个偶排列，则上述行列式()()()()12121212110.n n nnj j j j j j j j j j j j l k ττ=-+-=-=∑∑ 即奇偶排列各占一半.例7：证明1111111112222222222b cc a a b a b c b c c a a b a b c b c c a a b a b c ++++++=+++. 证明：111111111111111111122222222222222222222222.2b cc a a bac aa baa b a cab c b c c a a b a c a a b a a b a c a b c b c c a a b a c a a b a a b a c a b c +++-+++++++=-++=++=+++-++++ 例8：算出行列式：121401211).00210003-；1122).321014-的全部代数余子式. 答：111213142122232431323334414243441).6,0;12,6,0;15,6,3,0;7,0,1, 2.A A A A A A A A A A A A A A A A =-====-=====-=-=====-1112132122233132332).7,12,3;6,4,1;5,5, 5.A A A A A A A A A ==-====-=-== 例9：计算下面的行列式：111121131).12254321-；11112112132).1111321112---；01214201213).135123312121035-- 答：1111111111110115011501151).= 1.011400010012012300120001---------==-=-------原式132).12-3).483-. 例10：计算下列n 级行列式： 0000001).;000000x y x y x yyx1112121222122).n nn n n na b a b a b a b a b a b a b a b a b ---------122222223).;2232222n1231110004)..02200011n n n n-----答：()()110000000000000001).11.000000000000000n n n n xy xy yx y x xy x y x y x y x yy yxxxy++=+-=+-2）.当1n =时，为11a b -；当2n =时，为()()1212a a b b --；当3n ≥时，为零.()12221000222222223).22!223200102220002n n n -==-⋅--（利用第2行（列）的特点）()()11231110001!4).1.02200211n n nn n n---+=---- （从左起，依次将前一列加到后一列） 例11：用克拉默法则解线性方程组1234123412341234232633325323334x x x x x x x x x x x x x x x x -++=⎧⎪-++=⎪⎨--+=⎪⎪-+-=⎩.答：2132333270031123131d --==-≠----，所以可以用克拉默法则求解.又因16132533270;31124131d --==-----22632353270;33123431d ==---32162335270;31323141d --==----42136333570;31133134d --==----所以此线性方程组有唯一解，解为1234 1.x x x x ====例12：求12121212111222,n nnnj j j j j j j j j nj nj nj a a a a a a a a a ∑这里12nj j j ∑是对所有n 级排列求和.答：对每个排列12n j j j ，都有：()()121212121111112122221222121.n n nnj j j n j j j j j j nn n nnnj nj nj a a a a a a a a a a a a a a a a a a τ=- 因为在全部n 级排列中，奇偶排列个数相同，各有!2n 个.所以121212121112220n n nnj j j j j j j j j nj nj nj a a a a a a a a a =∑.例13：计算n 级行列式：12222122221212111.nnn n n nnn n nx x x x x x x x x x x x ---答：作范德蒙德行列式：1212222121111111211211111.n n n n n n n n n n nnn nn n x x x x x x x x D x x x x x x x x ++----++=将这个行列式按最后一列展开，展开式中11n n x -+的系数的()11n n++-倍就是所求行列式D ，因为()111,ji i j n D xx ≤<≤+=-∏所以()()()()11111111.nnn nji k ji k k k i j n i j n D xx x xx x ++==≤<≤+≤<≤+=---=-∑∑∏∏。

第一章 行列式习题1. n 阶行列式D 的值为c ，若将D 的第一列移到最后一列，其余各列依次保持原来的次序向左移动，则得到的行列式值为 。

（1(1)n c --）2. n 阶行列式D 的值为c ，若将D 的所有元素改变符号，得到的行列式值为 。

（(1)n c -）3. 2(1)(2,1,21,2,,1,)(21)0(23)0122k k N k k k k k k k k --+=-++-+++=+?。

4. 由行列式的定义计算行列式413331233626xx x x xx展开式中4x 和3x 的系数。

（3412, 12x x -）（分析：4x 的系数：四个元素中必须全都包含x 。

第一行只能取11a ，第三行只能取33a ，这样第二、四行只能取22a 和44a ，则此项为(1234)411223344(1)4312N a a a a x x x x x -=⋅⋅⋅=。

3x 的系数：(2134)(4231)3331221334441223314(1)(1)3912N N a a a a a a a a x x x -+-=--=-。

）5. 已知1703，3159，975，10959能被13整除，不直接计算行列式17033159097510959的值，证明他是13的倍数。

证明：12341701703170170341000131531593153159410021309709750979754103109510959109510959l c c l c c l c c l +⋅+⋅=⋅+⋅，能被13整除。

注意，以下两个行列式：170317037033159315915909759759751095910959959≠，所以一定要加到最后一列上。

6. 设行列式311252342011133--=--D ，求11213141243A A A A +--及2123242-++M M M 。

（0和-5）解：112131412112423424301011333A A A A -+--==----。

第二讲 行列式综合训练第一部分例2.1 计算行列式，其中对角线上元素都是a ，未写出的元素都是零．n D =11aa解 这道题可以用多种方法进行求解，充分应用了行列式的各种性质． 方法1 利用性质，将行列式化为上三角行列式．nD 11c nc a-⋅=101aaaa-=11()n a a a--=n a -2n a - 方法2 仍然是利用性质，将行列式化为上三角行列式．n D n 1r r -=111a aa --1nc c +=111a aa +-=na -2n a-方法3 利用展开定理，将行列式化成对角行列式．n D 1c 展开=1n aaa -+11001(1)0n n a a+--而 11001(1)0n n aa+--最后列展开=21(1)n +-2n aa -=2n a--n D =1n a a -⋅-2n a -=n a -2n a -方法4 利用公式A O OB=A B ．将最后一行逐行换到第2行，共换了2n -次；将最后一列逐列换到第2列，也共换了2n -次．n D =2(2)(1)n --11a aa=11a a2n aa -=na -2n a-方法5 利用公式A O OB=A B ．例2.2 计算n 阶行列式：11212212nn n n na b a a a a b a D a a a b ++=+ (120n b b b ≠)解 采用升阶（或加边）法．该行列式的各行含有共同的元素12,,,n a a a ，可在保持原行列式值不变的情况下，增加一行一列，适当选择所增行（或列）的元素，使得下一步化简后出现大量的零元素．12112122121000nn n n n na a a ab a a D a a b a a a a b +=++升阶213111n r r r r r r +---=121211001001n na a ab b b --- 1112,,1jj c c b j n -+=+=11121112100000000n na a a a ab b b b b +++=1121(1)nn na ab b b b b +++这个题的特殊情形是121212nn n n a x a a a a x a D a a a x++=+=11()nn i i xx a -=+∑可作为公式记下来．例2.3 计算n 阶行列式：12111111111n na a D a++=+其中120n a a a ≠．解 这道题有多种解法． 方法1 化为上三角行列式nD 12,,i r r i n-==1121111n a a a a a +--112,,j ja c c a j n+==21100nb a a其中11211ni i b a a a ==++∑1111ni i a a =⎛⎫=+ ⎪⎝⎭∑，于是n D 12111nn i i a a a a =⎛⎫=+ ⎪⎝⎭∑．方法2 升阶（或加边）法121111011101110111n na D a a +=++升阶12,3,,1i r r i n -=+=121111100101na a a --- 11111121,2,,1121111111j jni jc c a nn j n i i na a a a a a a a +=+=-=+⎛⎫==+⎪⎝⎭∑∑方法3 递推法．将n D 改写为1211101110111n na a D a ++++=+n =按c 拆开12111111111a a +++1211011011na a a ++由于12111111111a a ++1,,1i n r r i n -=-=12111a a 121n a a a -=1211011011na a a ++n =按c 展开1n n a D -因此n D =1n n a D -121n a a a -+为递推公式，而111D a =+，于是n D =1n n a D -121n a a a -+=12n a a a 11211n n n D a a a a --⎛⎫+ ⎪⎝⎭=12n a a a 2122111n n n n D a a a a a ---⎛⎫++ ⎪⎝⎭==12n a a a 11211n D a a a ⎛⎫+++⎪⎝⎭=12n a a a 121111n a a a ⎛⎫++++⎪⎝⎭例２.4 设343123211211)(------=x x x x x x x f ，证明存在),1,0(∈ζ使0)(='ζf . 证 因为()f x 是关于x 的二次多项式多项式,在[]1,0上连续,(0,1)内可导,且0331221111)0(=------=f ,101(1)1110121f =-=-由罗尔定理知,存在)1,0(∈ζ,使0)(='ζf .例2.5 计算D =222244441111a b c d abcda b c d ．解 这不是范得蒙行列式，但可借助求解范得蒙行列式进行求解．方法1 借助于求解范得蒙行列式的技巧进行求解：从下向上，逐行操作．D 2433221r a r r ar r ar ---=222222222111100()()()0()()()b ac ad a b b a c c a d d a b b a c c a d d a ---------1c 展开=()()()b ac ad a ---222111()()()bcdb b ac c ad d a +++3r 拆开=()()()b a c a d a ---（333111bc d b c d +222111a b c d b c d ）其中333111b c d b c d 23221r b r r br --=222211100()()c bdb c c b d db ----=()()c bd b --11()()c c bd d b ++=()()c b d b --[()()]d d b c c b +-+由于222111bc d b c d 是范德蒙行列式，故222111b c d b c d =()()()c b d b d c --- D =()a b c d +++()()()b a c a d a ---()()()c b d b d c ---方法2 D 213141c c c c c c ---=222222244444441000a b a c a d a a b a c a d a a b a c a d a ---------1r 展开=()()()b ac ad a ---222222111()()()()()()b ac ad ab a b ac a c ad a d a +++++++++2131c c c c --=()()()b ac ad a ---22100()()b ac bd b b a b a x y+--++1c 展开=()()()b ac ad a ---c b d b xy--其中222()()x c b a b c ac bc ab =-+++++，222()()y d b a b c ad bd ab =-+++++D =()a b c d +++()()()b a c a d a ---()()()c b d b d c ---=()a b c d +++()()()a b a c a d ---()()()b c b d c d ---方法3 用升阶法．由于行列式中各列元素缺乏3次幂的元素，在D 中添加3次幂的一 行元素，再添加一列构成5阶范得蒙行列式：5D =22222333334444411111ab c d x a b c d x a b c d x a b c d x 5D 按第5列展开得到的是x 的4次多项式，且3x 的系数为4545(1)A D D +=-=-又利用计算范得蒙行列式的公式得5D =()()()()b a c a d a x a ----()()()c b d b x b ---()()()d c x c x d ---=()()()b a c a d a ---()()c b d b --()d c -[()()()()]x a x b x c x d ----=()()()b a c a d a ---()()c b d b --()d c -43[()]x a b c d x -++++其中3x 的系数为()()()b a c a d a ----()()c b d b --()d c -()a b c d +++由3x 的系数相等得：D =()a b c d +++()()()b a c a d a ---()()()c b d b d c ---例2.6 设4322321143113151||-=A ，计算A 41 + A 42 + A 43 + A 44 = ? 其中A 4j (j= 1, 2, 3, 4)是|A |中元素a 4j 的代数余子式.解 直接求代数余子式的和工作量大．可将414243A A A A +++改写为4142431111A A A A ⋅+⋅+⋅+⋅，故A 41 + A 42 + A 43 + A 44 1111321143113151-=160210231012100-==41602(1)023012+--=62103202061=-- 例2.7 求解方程:11111111()01121111(1)x f x x nx-==---解 方法1()f x 12,,i r r i n-==111100000100(2)xxn x-=---=)2()1()1(1+----n x x x n由题设知0)2()1()1()(1=+---=-n x x x x f n所以2,,1,0121-===-n x x x n 是原方程的解.方法2 由题设知,当2,,2,1,0-=n x 时,由于行列式中有两列对应元素相同,行列式值为零,因此)(x f 可写成)2()1()(+--=n x x Ax x f于是原方程0)2()1()(=+--=n x x Ax x f 的解为:2,,1,0121-===-n x x x n例2.8 计算元素为a ij = | i －j |的n 阶行列式. 解 方法1 由题设知，11a =0，121a =，1,1,n a n =-，故01110212n n n D n n --=--1,1,,2i i r r i n n --=-=11111111n ----1,,1j n c c j n +=-=1211021(1)2(1)20001n n n n n n ------=----其中第一步用的是从最后一行起，逐行减前一行．第二步用的每列加第n 列．方法2 011102120n n n D n n --=--11,2,,111111112i i r r i n n n +-=----=--12,,1001201231j c c j nn n n +=---=---=12(1)2(1)n n n ----例2.9 计算行列式2211112200000000b d b d c a c a D =．解 方法1 按第一列展开：112112000a c D a db b =-0000111122b d c a c d =111122b d c ab a -111122b d c a c d=（22b a -111122b d c a c d ）=（22b a -）22c d （11b a -）11c d方法2 本题也可利用拉普拉斯展开定理进行计算，选定第2、3行，有：11232311(1)a c D d b +++=-2222a c db =（11b a 11dc -）（22b a 22d c -）例2.10 计算2n D =1111nnnna b a b c d c d ，其中未写出的元素都是0．解 方法1 利用公式A O OB=A B ．采用逐行操作，将最后一行逐行和上行进行对换，直到换到第2行（作22n -次相邻对换）；最后一列逐列和上列换，换到第2列（作22n -次相邻对换），得到2n D =2(22)(1)n --1111111100000nn n n n n n n a b c d a b a b c d c d ----=2D 2(1)n D -=()n n n n a d b c -2(1)n D -=()n n n n a d b c -1111()n n n n a d b c -----2(2)n D -==()n n n n a d b c -1111()n n n n a d b c -----1111()a d b c -=1()ni i i i i a d b c =-∏方法2 利用行列式展开定理进行求解．2n D 1r 展开=11111111n n nn n na b a b a c d c d d ----+12(1)nn b +-111111110n n n n na b a b c d c d c ----上面第1个行列式是A O OB的形式，而第2个行列式按第1列展开，所以2n D =2112222(1)n n n n n n n a d D b c D -+----=()n n n n a d b c -2(1)n D - ==1()ni i i i i a d b c =-∏例2.11 计算5100011000110001100011a a aa D a a a a a ---=------． 解 方法１ 采用递推的方法进行求解．5D 125c c c ++=1000010001100011011a a aa a a aaa-------- 1c 展开=100110011011a a a a a a a-------+5100100()(1)11011a a a a a aa a+-------即 51454()(1)D D a a +=+--， 41343()(1)D D a a +=+--，31232()(1)D D a a +=+--， 221D a a =-+故 234551D a a a a a =-+-+-方法2 采用降阶的方法进行求解．5D 12(1)r a r +-=22010011000110001100011a a a a a a a a a a a-+---------213(1)r a a r +-+=2323001011000110001100011a a a a a a a a a a a a a -+--+--------2314(1)r a a a r +-+-=234234000111000110001100011a a a a a a a a a a a a a a a-+-+-+--------- 23415(1)r a a a a r +-+-+=234500001110011000110011a a a a a a aa a a a a-+-+---------1r 展开=2345514(1)(1)(1)a a a a a +-+-+-⋅--=23451a a a a a -+-+-例2.12 证明D n =121100010nn n xxa a a xa ----+=111n n n n x a x a x a --++++证 方法1 递推法 按第1列展开，有D n = x D 1-n +（－1）1+n a n11111n x x x-----= x D 1-n + a n由于D 1= x + a 1，2211xD a x a -=+，于是 D n = x D 1-n + a n =x （x D 2-n +a 1-n ）+ a n =x 2D 2-n + a 1-n x + a n== x 1-n D 1+ a 2x 2-n + + a 1-n x + a n =111n n n n x a x a x a --++++方法2 第2列的x 倍，第3列的x 2倍， ，第n 列的x 1-n 倍分别加到第1列上12c xc n D +=21121010010000n n n n x x x a xa a a xa-----++213c x c += 32121231010000100010n n n n n n x xx a xa x a a a a x a--------+++==111x fx---n r =按展开1(1)n f+-1111n x xx----=f其中111n n n n f a a x a x x --=++++或 D n21123n nc xc x c x c -++++=12210100001000001n n x x fa a ax a -----+1=按c 展开1(1)n f+-1111n x xx----=11(1)(1)n n f +---=f其中111n n n n f a a x a x x --=++++方法3 利用性质，将行列式化为上三角行列式．D n21321111n n c c x c c xc c x-+++=112200000n n nnn n nx x x a a a a a a k xx x---+++n =按c 展开x 1-n k n = x 1-n (1-n n x a + 21--n n x a ++x a 2+a 1+x) =111n n n n a a x a x x --++++方法4n r nD =按展开1(1)n na +-10001001x x ---+21(1)n n a +--000010001x x --+ +212(1)n a --1000001x x --+21(1)()na x -+10000000x x x-=（－1）1+n （－1）1-n a n +（－1）2+n （－1）2-n a 1-n x+ +（－1）12-n （－1）a 2x2-n +（－1）n2( a 1+x) x1-n= 111n n n n a a x a x x --++++例2.13 计算n阶“三对角”行列式Dn=001000101αβαβαβαβαβαβ+++＋解 方法1 递推法．D n1=按c 展开()αβ+D 1-n —(1)00001001n αβαβαβαβ-++1=按r 展开()αβ+D 1-n －αβD 2-n即有递推关系式 D n =()αβ+D 1-n －αβD 2-n (n ≥3) 故 1n n D D α--＝12()n n D D βα---递推得到 1n n D D α--＝12()n n D D βα---＝223()n n D D βα---＝＝221()n D D βα--而1()D αβ=+，2D ＝β+α1αββ+α＝22ααββ++，代入上式得1nn n D D αβ--=1n n n D D αβ-=+ （2.1）由递推公式得1n n n D D αβ-=+＝12()n n n D ααββ--++＝α2D2-n ＋1n n αββ-+＝＝nα＋1n αβ-＋ ＋1n n αββ-+＝时＝，当时，当－－βαβα1)α(n αβαβ111≠⎪⎩⎪⎨⎧++++n n n方法2 把D n 按第1列拆成2个n 阶行列式D n =000100010001ααβαβαβαβαβ++＋＋0010001000001βαβαβαβαβαβαβαβ+++上式右端第一个行列式等于αD 1-n ，而第二个行列式0010001000001βαβαβαβαβαβαβαβ+++12,,i i c ac i n--==0001000010001ββββ=βn于是得递推公式1nn n D D αβ-=+，已与（2.1）式相同．方法3 在方法1中得递推公式D n =()αβ+D 1-n －αβD 2-n又因为当αβ+时 D 1=αβ+=βαβα--2221D αβαβαβ+=+=2()αβ+-αβ=22ααββ++=βαβα--33D 3=βααββααββα+++110=3()αβ+-2αβ()αβ+ = ()αβ+22()αβ+=βαβα--44于是猜想11n n n D αβαβ++-=-，下面用数学归纳法证明．当n=1时，等式成立，假设当n ≤k 时成立． 当n=k+1是，由递推公式得D 1+k =()αβ+D k －αβD 1-k=()αβ+βαβα--++11k k —αββαβα--k k =βαβα--++22k k所以对于n ∈N +，等式都成立．第二部分这一部分的题是与矩阵、向量、特征值等后续内容有关的题，感觉困难的同学可以放到相关内容学习后再看．但应注意考研题中关于行列式内容的出题,往往与后续内容联系较多．例2.14 设A 为3×3矩阵, |A | =－2, 把A 按行分块为123A A A A ⎛⎫ ⎪= ⎪ ⎪⎝⎭, 其中(1,2,3)i A i =是A 的第i 行, 则行列式312122A A A A -=______.解312122A A A A -=312122A A A A -=3212A A A =12322||4A A A A -=-=例2.15 判断题(1) 若B A ，是可乘矩阵，则=AB B A ． （ ） (2) 若B A ，均为n 阶方阵，则A B A B -=-． （ ）解 (1) 错误，因为B A ，不一定是方阵，即不一定有对应的行列式．(2) 错误，例如取3003A ⎛⎫= ⎪⎝⎭，2002B ⎛⎫= ⎪⎝⎭，15A B A B -=≠-=．例2.16 证明:奇数阶反对称矩阵的行列式为零.证 ||||)1(||||||,A A A A A A A nTT-=-=-==-=(n 为奇数). 所以|A | = 0.例2.17 （数四，01，3分）设矩阵111111111111kk A k k ⎛⎫ ⎪⎪= ⎪⎪⎝⎭，且秩()R A =3，则k = 解 由于111111111111k k A kk=124r r r ++=3333111111111k k k k k k k ++++=1111111(3)111111k k kk+=11110100(3)00101k k k k -+--=3(3)(1)k k +-由()R A =3，知A =0，而1k =时，()R A =1，故必有3k =-．例2.18 若B A ，，C 均为3阶可逆方阵，1-=A ，2=B ，计算C B A C T211)(2--．解 C B A C T 211)(2--=23112T CA B C --=223112T C A BC-=22312A B=2例2.19 设3阶方阵B A ，满足方程 E B A B A =--2，试求矩阵B 以及行列式B ，其中101020201A ⎛⎫⎪= ⎪ ⎪-⎝⎭． 解 由E B A B A =--2，得E A B E A +=-)(2，即 ()()A E A E B A E +-=+由于 201030202A E ⎛⎫⎪+= ⎪ ⎪-⎝⎭，180A E +=≠ 001010200A E ⎛⎫ ⎪-= ⎪ ⎪-⎝⎭，20A E -=≠ 111()()()()B A E A E A E A E ---=-++=-1001001/2010010200100--⎛⎫⎛⎫⎪ ⎪== ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭所以2/1||=B ．例2.20 设A 为3阶方阵，A =2，求1*1()32A A --的值． 解 方法1 化为关于*A 的形式进行计算．利用公式111()A A λλ--=，*1A A A-=，1n A A -*=有1*1()32A A --=1*23A A --=**23A A A-=**3A A - =*2A -=3*(2)A -=23(2)A -=32-方法2 化为关于1A -的形式计算． 利用公式111()A A λλ--=，*1A A A -=，1A -=1A，有 1*1()32A A --=1123A A A ---=14A --=3(4)-1A =32-例2.21 （数四，98，3分）设B A ，均为n 阶方阵，A =2，B =-3，求1*2-B A 的值． 解 1*2-BA =1*2-BA n =n21-n AB 1⋅=n 212-n 31-=3212--n例 2.22 若21321,,,,ββααα都是4维列向量，且4阶行列式n =3221,,,αβαα，m =1321,,,βααα，计算4阶行列式32112,,,αααββ+的值．解 如果行列式的列向量组为n ααα,,,21 ，则此行列式可表示为n ααα,,,21 ，利用行列式的性质，有=+21123,,,ββααα3211,,,αααβ+3212,,,αααβ=1231,,,αααβ--3221,,,ααβα=1231,,,αααβ-+1223,,,ααβα=n m -例2.23 计算行列式OB AO B A ，，||||，其中12112(1)121121n n x n x n A x n n x n n -+⎛⎫⎪-+ ⎪⎪=⎪+- ⎪ ⎪+-⎝⎭， 100002000010000B n n ⎛⎫⎪ ⎪⎪=⎪- ⎪ ⎪⎝⎭解 ||A =12112(1)121121n n x n x nxn nx n n-+-++-+-12,,12100000i rri nn n x x x x x x x-=-+-=--1,,1n j c c j n +=-=(1)12120000000n n n x x x x +-+这是逆对角的上三角行列式，所以(1)12(1)(1)()2n n n n n A x x --+=-+ 又!||n B =，故12)1(!)2)1(()1(2-+-++-=n n n n x n x n n O B A O ．注 这里用了公式：若A 为m 阶方阵，B 为n 阶方阵，则O AB O=(1)mn-A B ．例2.24 若A 为n 阶方阵，E 为单位矩阵，满足T AA E =，0A <，求 A E +． 解 方法1 由TAA E =有A E +=T A AA +=()T A E A +=()T A E A +=A ()TE A +=A E A +=A A E +即(1)A -A E +=0，而(1)A -0>，所以A E +=0．方法2 因为 ()TA E A +=TTAA A +=TE A +=A E + 即 A E +A =A E +有(1)A -A E +=0，而(1)A -0>，所以A E +=0．方法 3 由TAA E =知矩阵A 为正交矩阵，即TAA =1，2A =1，又因为0A <，所以有1A =-，故A E +=A 1E A -+=TE A -+=E A -+即2A E +=0，A E +=0．例2.25 若A 为n 阶正定矩阵，E 为n 阶单位矩阵，证明A E +的行列式大于1．证 方法1 因为A 为正定矩阵，因此所有的特征值大于零．设A 的n 个特征值为1,1,2,,i i n λ==，且0i λ>，由特征值的性质知，A E +的n 个特征值为1,1,2,,i i n λ+=，于是1(1)(1)1n λλ++>．方法2 因为正定矩阵是对称矩阵，因此A 可对角阵，且所有的特征值大于零，故存在可逆阵P 有11n P AP λλ-⎛⎫⎪=⎪⎪⎝⎭ （0,1,2,,i i n λ>=）即 11n A P P λλ-⎛⎫⎪= ⎪ ⎪⎝⎭111n A E P P PP λλ--⎛⎫ ⎪+=+⎪ ⎪⎝⎭=1111n P P λλ-+⎛⎫⎪ ⎪ ⎪+⎝⎭ A E +=1111n PP λλ-++=1(1)(1)1n λλ++>例2.26 设11112222aa A nn n n a +⎛⎫⎪+⎪= ⎪⎪+⎝⎭，求A解 利用特征值法进行求解，即利用公式12n A λλλ=．11112222aa A nn n n a +⎛⎫ ⎪+⎪= ⎪⎪+⎝⎭=100000000a ⎛⎫⎪⎪ ⎪⎪⎝⎭+11112222a nn n n a ⎛⎫ ⎪+ ⎪ ⎪⎪+⎝⎭==11112222aE n n nn ⎛⎫ ⎪⎪+ ⎪⎪⎝⎭优秀教案欢迎下载矩阵11112222n n n n⎛⎫⎪⎪⎪⎪⎝⎭的秩为1，由第十三讲的注意（7）知它特征值为11122nna a aλ=++=(1)2n n+，23nλλλ====0所以A特征值为(1),,,2n na a a++，故A=1(1)[]2nn na a-++．。

大学-----行列式经典例题例1计算元素为aij= | i－j|的n阶行列式.解方法1 由题设知，11a=0，121a=，1,1,na n=-，故011102120nnnDn n--=--1,1,,2i ir ri n n--=-=011111111n----1,,1j nc cj n+=-=1211021(1)2(1)020001n nn n nn------=----其中第一步用的是从最后一行起，逐行减前一行．第二步用的每列加第n列．方法2011102120nnnDn n--=--11,2,,1111111120i ir ri nn n+-=----=--12,,1001201231jc cj nn n n+=---=---=12(1)2(1)n n n----例2.设a, b, c是互异的实数, 证明:的充要条件是a + b + c =0.证明: 考察范德蒙行列式:=行列式 即为y 2前的系数. 于是=所以 的充要条件是a + b + c = 0.例3计算Dn =121100010nn n x x a a a x a ----+解： 方法1 递推法 按第1列展开，有D n = x D 1-n +（－1）1+n a n 11111n x x x-----= x D 1-n + a n由于D 1= x + a 1，2211x D a x a -=+，于是D n = x D 1-n + a n =x （x D 2-n +a 1-n ）+ a n =x 2D 2-n +a 1-n x + a n == x1-n D 1+ a 2x2-n + + a 1-n x + a n =111n n n n x a x axa--++++方法2 第2列的x 倍，第3列的x 2倍， ，第n 列的x1-n 倍分别加到第1列上12c xc n D +=21121010010000n n n n x x x a xa a a x a -----++213c x c +=32121231010*******10n n n n n n x xx a xa x a a a a xa--------+++==111x fx---n r =按展开1(1)n f+-1111n x xx----=111n n n n x a x a x a --++++方法3 利用性质，将行列式化为上三角行列式．D n21321111n n c c x c c xc c x-+++=11220000000n n nnn n nx x x a a a a a a k xx x---+++n =按c 展开x1-n k n = x1-n (1-n n xa + 21--n n x a + +x a 2+a 1+x) =111n n n n a a x a x x --++++方法4 n r nD =按展开1(1)n na +-10001001x x---+21(1)n n a +--000010001x x--+ +212(1)n a --1000001x x --+21(1)()na x -+10000000x x x-=（－1）1+n （－1）1-n a n +（－1）2+n （－1）2-n a 1-n x+ +（－1）12-n （－1）a 2x 2-n +（－1）n 2( a 1+x) x 1-n = 111n n n n a a x a x x --++++例4． 计算n 阶行列式：11212212nn n n na b a a a a b a D a a a b ++=+ (120n b b b ≠)解 采用升阶（或加边）法．该行列式的各行含有共同的元素12,,,n a a a ，可在保持原行列式值不变的情况下，增加一行一列，适当选择所增行（或列）的元素，使得下一步化简后出现大量的零元素．12112122121000n n n n n na a a ab a a D a a b a a a a b +=++升阶213111n r r r r r r +---=121211001001n na a ab b b --- 1112,,1j j c c b j n -+=+=11121112100000000n na a a a ab b b b b +++=1121(1)nn na ab b b b b +++这个题的特殊情形是121212nn n n a x a a a a x a D a a a x++=+=11()nn i i xx a -=+∑可作为公式记下来．例5．计算n 阶“三对角”行列式Dn=001000101αβαβαβαβαβαβ+++＋解 方法1 递推法．D n1=按c 展开()αβ+D 1-n —(1)00001001n αβαβαβαβ-++1=按r 展开()αβ+D 1-n －αβD 2-n即有递推关系式 D n =()αβ+D 1-n －αβD 2-n (n ≥3) 故 1n n D D α--＝12()n n D D βα---递推得到 1n n D D α--＝12()n n D D βα---＝223()n n D D βα---＝＝221()n D D βα--而1()D αβ=+，2D ＝β+α1αββ+α＝22ααββ++，代入得1n n n D D αβ--=1n n n D D αβ-=+ （2.1）由递推公式得1n n n D D αβ-=+＝12()n n n D ααββ--++＝α2D2-n ＋1n n αββ-+＝＝nα＋1n αβ-＋ ＋1n n αββ-+＝时＝，当时，当－－βαβα1)α(n αβαβ111≠⎪⎩⎪⎨⎧++++n n n方法2 把D n 按第1列拆成2个n 阶行列式D n =000100010001ααβαβαβαβαβ++＋＋0010001000001βαβαβαβαβαβαβαβ+++上式右端第一个行列式等于αD 1-n ，而第二个行列式0010001000001βαβαβαβαβαβαβαβ+++12,,i i c ac i n--==0001000010001ββββ=βn于是得递推公式1nn n D D αβ-=+，已与（2.1）式相同．方法3 在方法1中得递推公式D n =()αβ+D 1-n －αβD 2-n又因为当αβ+时 D 1=αβ+=βαβα--2221D αβαβαβ+=+=2()αβ+-αβ=22ααββ++=βαβα--33D 3=βααββααββα+++110=3()αβ+-2αβ()αβ+ = ()αβ+22()αβ+=βαβα--44于是猜想11n n n D αβαβ++-=-，下面用数学归纳法证明．当n=1时，等式成立，假设当n ≤k 时成立． 当n=k+1是，由递推公式得D 1+k =()αβ+D k －αβD 1-k=()αβ+βαβα--++11k k —αββαβα--k k =βαβα--++22k k所以对于n ∈N +，等式都成立例6． 计算n 阶行列式：12111111111n na a D a ++=+其中120n a a a ≠．解 这道题有多种解法． 方法1 化为上三角行列式nD 12,,i r r i n-==1121111n a a a a a +--112,,jj a c c a j n+==21100nb a a其中11211ni i b a a a ==++∑1111ni i a a =⎛⎫=+ ⎪⎝⎭∑，于是n D 12111nn i i a a a a =⎛⎫=+ ⎪⎝⎭∑．方法2 升阶（或加边）法121111011101110111n na D a a +=++升阶12,3,,1i r r i n -=+=1211111001001na a a --- 11111121,2,,1121111111j jni jc c a nn j n i i na a a a a a a a +=+=-=+⎛⎫==+ ⎪⎝⎭∑∑方法3 递推法．将n D 改写为1211101110111n na a D a ++++=+n =按c 拆开12111111111a a +++1211011011na a a ++由于12111111111a a ++1,,1i n r r i n -=-=12111a a 121n a a a -=121111011na a a ++n =按c 展开1n n a D -因此n D =1n n a D -121n a a a -+为递推公式，而111D a =+，于是n D =1n n a D -121n a a a -+=12n a a a 11211n n n D a a a a --⎛⎫+ ⎪⎝⎭=12n a a a 2122111n n n n D a a a a a ---⎛⎫++ ⎪⎝⎭==12n a a a 11211n D a a a ⎛⎫+++⎪⎝⎭=12n a a a 121111n a a a ⎛⎫++++⎪⎝⎭。

「线性代数」行列式计算（例题一）
行列式计算，是线性代数中比较基础的一部分内容
工欲善其事，必先利其器
我们得先搞懂行列式计算的几条规则
1、两行（或两列）互换位置，行列式的值变号
2、两行（或两列）相同，行列式的值为零
（1）某行（或列）的元素全为0，行列式的值为0
（2）若两行（或列）的元素对应成比例，行列式的值为0
3、如果行列式某行（或列）是两个元素之和，则可把行列式拆成两个行列式之和
4、把某行（或列）的k倍加到另一行（或列），行列式的值不变
5、行列互换，值不变
这里用到了其中很多条原则
关系到一条重要的公式，上（下）三角形行列式的值等于主对角线元素的乘积。

第二讲 行列式综合训练第一部分例2.1 计算行列式，其中对角线上元素都是a ，未写出的元素都是零．n D =11aa解 这道题可以用多种方法进行求解，充分应用了行列式的各种性质． 方法1 利用性质，将行列式化为上三角行列式．n D 11c nc a-⋅=101a aaa-=11()n a a a--=n a -2n a - 方法2 仍然是利用性质，将行列式化为上三角行列式．n D n 1r r -=111a aa --1nc c +=111a aa +-=na -2n a-方法3 利用展开定理，将行列式化成对角行列式．n D 1c 展开=1n aaa -+11001(1)0n n a a +--而 11001(1)0n n a a+--最后列展开=21(1)n +-2n aa -=2n a--n D =1n a a -⋅-2n a -=n a -2n a -方法4 利用公式A O OB=A B ．将最后一行逐行换到第2行，共换了2n -次；将最后一列逐列换到第2列，也共换了2n -次．n D =2(2)(1)n --11a aa=11a a2n aa -=na -2n a-方法5 利用公式A O OB=A B ．例2.2 计算n 阶行列式：11212212n n n n na b a a a a b a D a a a b ++=+ (120n b b b ≠)解 采用升阶（或加边）法．该行列式的各行含有共同的元素12,,,n a a a ，可在保持原行列式值不变的情况下，增加一行一列，适当选择所增行（或列）的元素，使得下一步化简后出现大量的零元素．1211212212100n n n n n na a a ab a a D a a b a a a a b +=++升阶213111n r r r r r r +---=121211001010n na a ab b b --- 1112,,1jj c c b j n -+=+=111211121000000000n na a a a ab b b b b +++=1121(1)nn na ab b b b b +++这个题的特殊情形是121212n n n n a x a a a a x a D a a a x++=+=11()nn i i xx a -=+∑可作为公式记下来．例2.3 计算n 阶行列式：12111111111n na a Da ++=+其中120n a a a ≠．解 这道题有多种解法． 方法1 化为上三角行列式nD 12,,i r r i n-==1121111na a a a a +--112,,j ja c c a j n+==21100nb a a其中11211n i i b a a a ==++∑1111ni i a a =⎛⎫=+ ⎪⎝⎭∑，于是n D 12111nn i i a a a a =⎛⎫=+ ⎪⎝⎭∑．方法2 升阶（或加边）法121111011101110111n naD a a +=++升阶12,3,,1i r r i n -=+=121111100101na a a --- 11111121,2,,1121111111j jni jc c a nn j n i i na a a a a a a a +=+=-=+⎛⎫==+⎪⎝⎭∑∑方法3 递推法．将n D 改写为1211101110111n na a D a ++++=+n=按c 拆开12111111111a a +++1211011011na a a ++由于12111111111a a ++1,,1i n r r i n -=-=12111a a 121n a a a -=1211011011na a a ++n =按c 展开1n n a D -因此n D =1n n a D -121n a a a -+为递推公式，而111D a =+，于是n D =1n n a D -121n a a a -+=12n a a a 11211n n n D a a a a --⎛⎫+ ⎪⎝⎭=12n a a a 2122111n n n n D a a a a a ---⎛⎫++ ⎪⎝⎭==12n a a a 11211n D a a a ⎛⎫+++⎪⎝⎭=12n a a a 121111n a a a ⎛⎫++++⎪⎝⎭例２.4 设343123211211)(------=x x x x x x x f ，证明存在),1,0(∈ζ使0)(='ζf . 证 因为()f x 是关于x 的二次多项式多项式,在[]1,0上连续,(0,1)内可导,且0331221111)0(=------=f ,101(1)1110121f =-=-由罗尔定理知,存在)1,0(∈ζ,使0)(='ζf .例2.5 计算D =222244441111ab c d a b c d a b c d ． 解 这不是范得蒙行列式，但可借助求解范得蒙行列式进行求解．方法1 借助于求解范得蒙行列式的技巧进行求解：从下向上，逐行操作．D 2433221r a r r ar r ar ---=222222222111100()()()0()()()b ac ad ab b ac c ad d a b b a c c a d d a ---------1c 展开=()()()b ac ad a ---222111()()()b c d b b a c c a d d a +++ 3r 拆开=()()()b a c a d a ---（333111bc d b c d +222111a b c d b c d ）其中333111b cd b c d 23221r b r r br --=222211100()()c bd b c c b d d b ---- =()()c bd b --11()()c c bd d b ++=()()c b d b --[()()]d d b c c b +-+由于222111bcd b c d 是范德蒙行列式，故222111b c d b c d =()()()c b d b d c --- D =()a b c d +++()()()b a c a d a ---()()()c b d b d c --- 方法2 D 213141c c c c c c ---=222222244444441000ab ac ad aa b a c a d a a b a c a d a --------- 1r 展开=()()()b ac ad a ---222222111()()()()()()b ac ad a b a b a c a c a d a d a +++++++++ 2131c c c c --=()()()b ac ad a ---221()()b a c b d b b a b a x y+--++ 1c 展开=()()()b ac ad a ---c b d b xy--其中222()()x c b a b c ac bc ab =-+++++，222()()y d b a b c ad bd ab =-+++++D =()a b c d +++()()()b a c a d a ---()()()c b d b d c ---=()a b c d +++()()()a b a c a d ---()()()b c b d c d ---方法3 用升阶法．由于行列式中各列元素缺乏3次幂的元素，在D 中添加3次幂的一 行元素，再添加一列构成5阶范得蒙行列式：5D =22222333334444411111a b c d x a b c d x a b c d x a b c d x 5D 按第5列展开得到的是x 的4次多项式，且3x 的系数为4545(1)A D D +=-=-又利用计算范得蒙行列式的公式得5D =()()()()b a c a d a x a ----()()()c b d b x b ---()()()d c x c x d ---=()()()b a c a d a ---()()c b d b --()d c -[()()()()]x a x b x c x d ----=()()()b a c a d a ---()()c b d b --()d c -43[()]x a b c d x -++++其中3x 的系数为()()()b a c a d a ----()()c b d b --()d c -()a b c d +++由3x 的系数相等得：D =()a b c d +++()()()b a c a d a ---()()()c b d b d c --- 例2.6 设4322321143113151||-=A ，计算A 41 + A 42 + A 43 + A 44 = ? 其中A 4j (j= 1, 2, 3, 4)是|A |中元素a 4j 的代数余子式.解 直接求代数余子式的和工作量大．可将414243A A A A +++改写为4142431111A A AA ⋅+⋅+⋅+⋅，故A 41 + A 42 + A 43 + A 44 1111321143113151-=1602102310121000-==41602(1)023012+--=62100320261=-- 例2.7 求解方程:11111111()01121111(1)x f x x nx-==---解 方法1()f x 12,,i r r i n-==111100000100(2)x xn x-=---=)2()1()1(1+----n x x x n由题设知0)2()1()1()(1=+---=-n x x x x f n所以2,,1,0121-===-n x x x n 是原方程的解.方法2 由题设知,当2,,2,1,0-=n x 时,由于行列式中有两列对应元素相同,行列式值为零,因此)(x f 可写成)2()1()(+--=n x x Ax x f于是原方程0)2()1()(=+--=n x x Ax x f 的解为:2,,1,0121-===-n x x x n例2.8 计算元素为a ij = | i －j |的n 阶行列式. 解 方法1 由题设知，11a =0，121a =，1,1,n a n =-，故01110212n n n D n n --=--1,1,,2i i r r i n n --=-=11111111n ----1,,1j n c c j n +=-=1211021(1)2(1)20001n n n n n n ------=----其中第一步用的是从最后一行起，逐行减前一行．第二步用的每列加第n 列．方法2 011102120n n n D n n --=--11,2,,111111112i i r r i n n n +-=----=--12,,1001201231j c c j nn n n +=---=---=12(1)2(1)n n n ----例2.9 计算行列式221111220000000b d b d c a c a D =． 解 方法1 按第一列展开：1121120000a c D a d b b =-0000111122b d c a c d =111122b d c ab a -111122b d c a c d=（22b a -111122b d c a c d ）=（22b a -）22c d （11b a -）11c d方法2 本题也可利用拉普拉斯展开定理进行计算，选定第2、3行，有：11232311(1)a c D d b +++=-2222a c db =（11b a 11dc -）（22b a 22d c -）例2.10 计算2n D =1111nnnna b a b c d c d ，其中未写出的元素都是0．解 方法1 利用公式A O OB=A B ．采用逐行操作，将最后一行逐行和上行进行对换，直到换到第2行（作22n -次相邻对换）；最后一列逐列和上列换，换到第2列（作22n -次相邻对换），得到2n D =2(22)(1)n --1111111100000n n n n n n n n a b c d a b a b c d c d ----=2D 2(1)n D -=()n n n n a d b c -2(1)n D -=()n n n n a d b c -1111()n n n n a d b c -----2(2)n D -==()n n n n a d b c -1111()n n n n a d b c -----1111()a d b c -=1()ni i i i i a d b c =-∏方法2 利用行列式展开定理进行求解．2n D 1r 展开=11111111n n nn n na b a b a c d c d d ----+12(1)n n b +-111111110n n n n na b a b c d c d c ----上面第1个行列式是A O OB的形式，而第2个行列式按第1列展开，所以2n D =2112222(1)n n n n n n n a d D b c D -+---- =()n n n n a d b c -2(1)n D - ==1()ni i i i i a d b c =-∏例2.11 计算5100011000110001100011a a aa D a a a a a ---=------． 解 方法１ 采用递推的方法进行求解．5D 125c c c ++=1000010001100011011a a aa a a aaa-------- 1c 展开=1001100110011a a a a a a a -------+51000100()(1)110011a a a a a a aa+------- 即 51454()(1)D D a a +=+--， 41343()(1)D D a a +=+--，31232()(1)D D a a +=+--， 221D a a =-+故 234551D a a a a a =-+-+-方法2 采用降阶的方法进行求解．5D 12(1)r a r +-=2210011000110001100011a a a a a a a a a a a -+---------213(1)r a a r +-+=232301011000110001100011a a a a a a a a a a a a a-+--+--------2314(1)r a a a r +-+-=23423400111000110001100011a a a a a a a a a a a a a a a-+-+-+---------23415(1)r a a a a r +-+-+=23450001110001100011011a a a a a a a a aa a a-+-+---------1r 展开=2345514(1)(1)(1)a a a a a +-+-+-⋅--=23451a a a a a -+-+-例2.12 证明D n =121100010nn n xxa a a xa ----+=111n n n n x a x a x a --++++证 方法1 递推法 按第1列展开，有D n = x D 1-n +（－1）1+n a n11111n xxx-----= x D 1-n + a n由于D 1= x + a 1，2211x D a x a -=+，于是D n = x D 1-n + a n =x （x D 2-n +a 1-n ）+ a n =x 2D 2-n + a 1-n x + a n== x1-n D 1+ a 2x2-n + + a 1-n x + a n =111n n n n x a x a x a --++++方法2 第2列的x 倍，第3列的x 2倍， ，第n 列的x1-n 倍分别加到第1列上12c xc n D +=2112101001000n n n n x x xa xa a a xa -----++213c x c +=3212123110000100010n n n n n n x xx a xa x a a a a x a--------+++==111x fx---n r =按展开1(1)n f+-1111n xxx----=f其中111n n n n f a a x a x x --=++++或 D n21123n nc xc x c x c -++++=122110000100001n n x x fa a ax a -----+1=按c 展开1(1)n f +-1111n x xx----=11(1)(1)n n f +---=f其中111n n n n f a a x a x x --=++++方法3 利用性质，将行列式化为上三角行列式．D n21321111n n c c x c c xc c x-+++=112200000000n n nnn n nx x x a a a a a a k xx x---+++n =按c 展开x1-n k n = x1-n (1-n n x a + 21--n n x a + +x a 2+a 1+x)=111n n n n a a x a x x --++++ 方法4n r nD =按展开1(1)n na +-1000101x x ---+21(1)n n a +--000010001x x --+ +212(1)n a --1000001x x --+21(1)()n a x -+10000000x x x-=（－1）1+n （－1）1-n a n +（－1）2+n （－1）2-n a 1-n x+ +（－1）12-n （－1）a 2x2-n +（－1）n2( a 1+x) x1-n= 111n n n n a a x a x x --++++例2.13 计算n阶“三对角”行列式Dn=001000101αβαβαβαβαβαβ+++＋解 方法1 递推法．D n1=按c 展开()αβ+D 1-n —(1)0000101n αβαβαβαβ-++1=按r 展开()αβ+D 1-n －αβD 2-n即有递推关系式 D n =()αβ+D 1-n －αβD 2-n (n ≥3) 故 1n n D D α--＝12()n n D D βα---递推得到 1n n D D α--＝12()n n D D βα---＝223()n n D D βα---＝＝221()n D D βα--而1()D αβ=+，2D ＝β+α1αββ+α＝22ααββ++，代入上式得1n n n D D αβ--=1n n n D D αβ-=+ （2.1）由递推公式得1n n n D D αβ-=+＝12()n n n D ααββ--++＝α2D2-n ＋1n n αββ-+＝＝n α＋1n αβ-＋ ＋1n nαββ-+＝时＝，当时，当－－βαβα1)α(n αβαβ111≠⎪⎩⎪⎨⎧++++n n n方法2 把D n 按第1列拆成2个n 阶行列式D n =000100010001ααβαβαβαβαβ++＋＋00010001000001βαβαβαβαβαβαβαβ+++上式右端第一个行列式等于αD 1-n ，而第二个行列式00010001000001βαβαβαβαβαβαβαβ+++12,,i i c ac i n--==00010000101ββββ=βn于是得递推公式1n n n D D αβ-=+，已与（2.1）式相同．方法3 在方法1中得递推公式D n =()αβ+D 1-n －αβD 2-n又因为当αβ+时 D 1=αβ+=βαβα--2221D αβαβαβ+=+=2()αβ+-αβ=22ααββ++=βαβα--33 D 3=βααββααββα+++110=3()αβ+-2αβ()αβ+ = ()αβ+22()αβ+=βαβα--44于是猜想11n n n D αβαβ++-=-，下面用数学归纳法证明．当n=1时，等式成立，假设当n ≤k 时成立． 当n=k+1是，由递推公式得D 1+k =()αβ+D k －αβD 1-k=()αβ+βαβα--++11k k —αββαβα--k k =βαβα--++22k k所以对于n ∈N +，等式都成立．第二部分这一部分的题是与矩阵、向量、特征值等后续内容有关的题，感觉困难的同学可以放到相关内容学习后再看．但应注意考研题中关于行列式内容的出题,往往与后续内容联系较多．例2.14 设A 为3×3矩阵, |A | =－2, 把A 按行分块为123A A A A ⎛⎫ ⎪= ⎪ ⎪⎝⎭, 其中(1,2,3)i A i =是A 的第i 行, 则行列式312122A A A A -=______.解312122A A A A -=312122A A A A -=3212A A A =12322||4A A A A -=-=例2.15 判断题(1) 若B A ，是可乘矩阵，则=AB B A ． （ ） (2) 若B A ，均为n 阶方阵，则A B A B -=-． （ ）解 (1) 错误，因为B A ，不一定是方阵，即不一定有对应的行列式．(2) 错误，例如取3003A ⎛⎫= ⎪⎝⎭，2002B ⎛⎫= ⎪⎝⎭，15A B A B -=≠-=．例2.16 证明:奇数阶反对称矩阵的行列式为零.证 ||||)1(||||||,A A A A A A A n T T -=-=-==-=(n 为奇数). 所以|A | = 0.例2.17 （数四，01，3分）设矩阵111111111111kk A k k ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭，且秩()R A =3，则k = 解 由于111111111111k k A k k =124r r r ++=3333111111111k k k k k k k++++=1111111(3)111111k k k k +=11110100(3)00100001k k k k -+-- =3(3)(1)k k +-由()R A =3，知A =0，而1k =时，()R A =1，故必有3k =-．例2.18 若B A ，，C 均为3阶可逆方阵，1-=A ，2=B ，计算C B A C T 211)(2--．解 C B A C T 211)(2--=23112T C A BC -- =223112TC A BC-=22312A B=2例2.19 设3阶方阵B A ，满足方程 E B A B A =--2，试求矩阵B 以及行列式B ，其中101020201A ⎛⎫⎪= ⎪ ⎪-⎝⎭． 解 由E B A B A =--2，得E A B E A +=-)(2，即 ()()A E A E B A E +-=+由于 201030202A E ⎛⎫⎪+= ⎪ ⎪-⎝⎭，180A E +=≠ 001010200A E ⎛⎫ ⎪-= ⎪ ⎪-⎝⎭，20A E -=≠ 111()()()()B A E A E A E A E ---=-++=-1001001/2010010200100--⎛⎫⎛⎫⎪ ⎪== ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭所以2/1||=B ．例2.20 设A 为3阶方阵，A =2，求1*1()32A A --的值． 解 方法1 化为关于*A 的形式进行计算．利用公式111()A A λλ--=，*1A A A-=，1n A A -*=有1*1()32A A --=1*23A A --=**23A A A -=**3A A -=*2A -=3*(2)A -=23(2)A -=32-方法2 化为关于1A -的形式计算． 利用公式111()A A λλ--=，*1A A A -=，1A -=1A，有 1*1()32A A --=1123A A A ---=14A --=3(4)-1A=32- 例2.21 （数四，98，3分）设B A ，均为n 阶方阵，A =2，B =-3，求1*2-B A 的值．解 1*2-BA =1*2-BA n =n21-n AB1⋅=n 212-n 31-=3212--n 例 2.22 若21321,,,,ββααα都是4维列向量，且4阶行列式n =3221,,,αβαα，m =1321,,,βααα，计算4阶行列式32112,,,αααββ+的值．解 如果行列式的列向量组为n ααα,,,21 ，则此行列式可表示为n ααα,,,21 ，利用行列式的性质，有=+21123,,,ββααα3211,,,αααβ+3212,,,αααβ=1231,,,αααβ--3221,,,ααβα=1231,,,αααβ-+1223,,,ααβα=n m -例2.23 计算行列式OB AO B A ，，||||，其中12112(1)121121n n x n x n A x n n x n n -+⎛⎫⎪-+ ⎪⎪=⎪+- ⎪ ⎪+-⎝⎭， 100002000010000B n n ⎛⎫⎪ ⎪⎪=⎪- ⎪ ⎪⎝⎭ 解 ||A =12112(1)121121n n x n x nx n nx n n-+-++-+-12,,12100000ir ri nn n x x x x x x x-=-+-=--1,,1n j c c j n +=-=(1)12120000000n n n x x x x +-+这是逆对角的上三角行列式，所以(1)12(1)(1)()2n n n n n A x x --+=-+ 又!||n B =，故12)1(!)2)1(()1(2-+-++-=n n n n x n x n n O B A O ．注 这里用了公式：若A 为m 阶方阵，B 为n 阶方阵，则O AB O=(1)mn -A B ．例2.24 若A 为n 阶方阵，E 为单位矩阵，满足TAA E =，0A <，求 A E +． 解 方法1 由TAA E =有A E +=T A AA +=()T A E A +=()T A E A +=A ()TE A +=A E A +=A A E +即(1)A -A E +=0，而(1)A -0>，所以A E +=0．方法2 因为 ()T A E A +=T T AA A +=TE A +=A E +即 A E +A =A E +有(1)A -A E +=0，而(1)A -0>，所以A E +=0．方法 3 由TAA E =知矩阵A 为正交矩阵，即T AA =1，2A =1，又因为0A <，所以有1A =-，故A E +=A 1E A -+=T E A -+=E A -+即2A E +=0，A E +=0．例2.25 若A 为n 阶正定矩阵，E 为n 阶单位矩阵，证明A E +的行列式大于1． 证 方法1 因为A 为正定矩阵，因此所有的特征值大于零．设A 的n 个特征值为1,1,2,,i i n λ==，且0i λ>，由特征值的性质知，A E +的n 个特征值为1,1,2,,i i n λ+=，于是1(1)(1)1n λλ++>．方法2 因为正定矩阵是对称矩阵，因此A 可对角阵，且所有的特征值大于零，故存在可逆阵P 有11n P AP λλ-⎛⎫⎪=⎪⎪⎝⎭ （0,1,2,,i i n λ>=）即 11n A P P λλ-⎛⎫⎪= ⎪ ⎪⎝⎭111n A E P P PP λλ--⎛⎫ ⎪+=+⎪ ⎪⎝⎭=1111n P P λλ-+⎛⎫⎪ ⎪ ⎪+⎝⎭A E +=1111n PP λλ-++=1(1)(1)1n λλ++>例2.26 设11112222aa A nn n n a +⎛⎫⎪+⎪= ⎪⎪+⎝⎭，求A解 利用特征值法进行求解，即利用公式12n A λλλ=．11112222aa A nn n n a +⎛⎫ ⎪+⎪= ⎪⎪+⎝⎭=100000000a ⎛⎫⎪⎪ ⎪⎪⎝⎭+11112222a nn n n a ⎛⎫ ⎪+ ⎪ ⎪⎪+⎝⎭==11112222aE n n nn ⎛⎫ ⎪⎪+ ⎪⎪⎝⎭矩阵11112222n n n n⎛⎫⎪⎪⎪⎪⎝⎭的秩为1，由第十三讲的注意（7）知它特征值为11122nna a aλ=++=(1)2n n+，23nλλλ====0所以A特征值为(1),,,2n na a a++，故A=1(1)[]2nn na a-++．21。

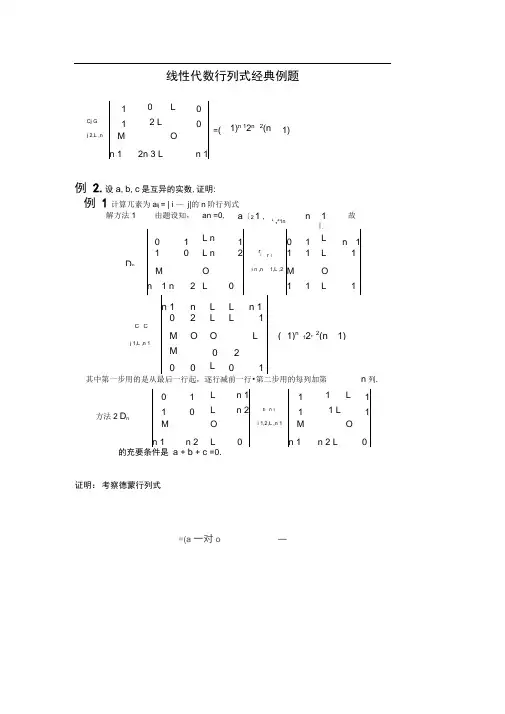
线性代数行列式经典例题例 1计算兀素为a ij = | i — j|的n 阶行列式解方法1由题设知， an =0,a 〔2 1 , L,a1nn 1丄故0 1L n 10 1 L n 11L n2rir 111 L1D nMOi n ,n1,L ,2MOn 1 n2 L 011 L1n 1 n L L n 12L L1C j CnM O OL ( 1)n 12* 2(n 1)j 1,L ,n 1M0 2L 01其中第一步用的是从最后一行起，逐行减前一行•第二步用的每列加第n 列.的充要条件是 a + b + c =0.证明：考察德蒙行列式=(a 一对o—1 L n 111 L 1 1 0L n 2r i r i 1 1 1 L 1 MOi 1,2,L ,n 1M On 1n 2 Ln 1n 2 L方法2 D n10 L 0 Cj G 12 L0 j 2,L ,nM On 12n 3 Ln 11)n 12n 2(n 1) =(例 2.设a , b , c 是互异的实数,证明:1 x行列式即为y 2前的系数•于是所以的充要条件是a + b + c = 0.x 10 K 0 x 1 K MM Ma na n 1a n 2K例3计算D n = 递推法按第 1 0 0 M x a i解：方法1列展开,D n = x D n 1 + (-1) a n =x D n 1+ a n 由于 D 1 = x + a 1, D 2 a 2a 1 2 1+ a n =x(x D n 2 +a n 1)+ a n =x D n 2 + n 1 n 2 a n 1x + a n = L = x D 1 + a 2 x + n n 1 + a n 1 x + a n = x a 1 x a n 1 x a n，第n 列的x n 1倍分别加到第1列上 01 0K C 1 XC 22 x x1 K D n0 0 x KMMMa n xa n 1a n 1a n 2K方法2第2列的x 倍，第3列的x 2倍, 0 0 0M x a 11 0 0 K 2C 1xC30 x 1 0K3 x 0 x 1 KMMMM2 a n xa n 1x a n 2a n 1a n 2a n 3K0 0 0 M x a 10 1x 1 O OfO按r n 展开1)n11 x 1x O Oxna 〔xa n 1x a n方法3利用性质，将行列式化为上三角行列式.1 c Gx 1c 3c2Xx 0 0x 0 0 MM0 0 x M-Cn a na n 1a na n 2a n 1按Cn 展开““ a n 1n 1 dnx k n = x ( —^7 +xa n 1 x0 0 0 M k na 2 + +a 1 +x)x按r n 展开1 方法4D n( 1)n1a nAMX0 K 0 0n 21 K0 0(1) a n1+M MM MK X 1X 1 K0 02 n0 X K0 0+ ( 1) (a 1 x)M M M M 0 0 L 0 X n 1 n=a n a n 1X L a 1X x=(-1) n 1 (- 1) n 1a n + (- 1) 0 K1 K 0+MM M0 KX1X1 K 0 0+ ( 1)2n 1a 20 X K 0 0M MM M0 K1(-1 ) n 2 a n 1X+ (-1) 2n 1(一 1) a 22 + (— 1) 2nn 1(a 1+x) xa n a n 1X L n 1 n a 1x x 例4.计算n 阶行列式: a Ea 2L a n D nqa 2b 2L a n M M Ma 1 a 2L a nb n(解 采用升阶（或加边）法.该行列式的各行含有共同的元素bbL b n 0)a 1,a 2,L , a * ,可在保持原行列式值不变的情况下，增加一行一列，适当选择所增行（或列）的元素，使得下一步化 简后出现大量的零元素.1aa 2 La n1 a 1 a2 L a n 升阶0 a 1a 2 L a n2 r 13 r 11 bi 0 L 0 D n0 aa 2b 2 La n Lrn 1r11 0 b2 L 0 M MMMM M MMaa 2La nb n10 0Lb n彳a1La 1L1 —a 1a 2 a n 1bib 1q — C jb j i0 bi 0 L 0a 1a nj 2丄，n 1L=d b ? L b n (1Ln0 b 2 0b nMM MM0 0 Lb n例5.计算n 阶“三对角”行列式K 0 01K 0 0D n =0 1 + K 0 0M M MMM0 00 K 1解方法1递推法K 0 0按q 展开D n（)D n 1 ―1K 0M M MM MK 1(n 1)按口展开()D n 1 —D n 2即有递推关系式D n=( )D n1 — D n2(n 3)故D nD n1 =(D n 1D n 2 )可作为公式记下来.递推得到D n D n 1 = (D ni2D n 2)= ( D n 2 D n 3)a 1 x a 2D na 1 a 2 xM Ma 1 a 2L a nL a n n 1 /n =x (x ajMi 1 L an X这个题的特殊情形是n 2八=L= (D 2 D i )方法3在方法1中得递推公式D n = () D n 1 — Dn 22 2又因为当时 D 1= = ------------D nD n1n(2.1)由递推公式得D n D n 1 0 = ( D n 2n1)n2 .=aD n 2 +n 1nD 2=(而D 1 (D 2=ap a + B代入得D nD n 1(n当a B 时 当a=B 时1K K 0 0 0 0D n = 01 +K0 0+M M MMMK1K 0 0 1K 0 0 0 1K0 0 MM MMM0 0 0 KK1K 0 0 1K 0 0 0 1K0 0 M M MMM0 0 0 KK10 0 K0 010 K0 0c aq 11K0 0 n =B i 2,L ,nM M MM M 10 0 K1n 1方法2把D n 按第1列拆成2个n 阶行列式上式右端第一个行列式等于aD n 1，而第二个行列式于是得递推公式 D n D n 1 n ，已与(2.1)式相)2n 1 n 1于是猜想D n ------------------ ，下面用数学归纳法证明. 当n=1时，等式成立，假设当 n k 时成立. 当n=k+1是，由递推公式得D k 1 = () D k — Dk 1=(所以对于n N ，等式都成立例6.计算n 阶行列式:D na n其中a n 0 .方法2升阶(或加边)法D 3 =)(=()3-2(4 4a 2解这道题有多种解法. 方法1 化为上三角行列式其中b 1i 2 3i1 a 1 1L1&1c1 丁 C jb1 L1r i r 1a 1a 2aj0 a 22,L ,nM Oj 2,L ,nMOa 1a na n1n1na 1 1于是D na 〔 a ? a n 1i 1a ia ii 1D n. i n0 0方法 由于 因此 升阶D n1c1cj 1aj1,2,L ,n 1递推法.a11r i「11 a 1 1 1 a 11 D n = a n D n 1a ja 2 M2,3,L , n 1a 10 M a 2 Ma 1a na na 2a n1 3ia 11 L 1 01 1 a2 L1 0M MM11L1 a n1 a 11 L 11 a 11 L 01 1 a 2L11 1 a2 L+MMM AM MM 1 1L111La nD n 改写为按c n 拆开L a 2 D na 2 M a^L a n 1 a 11 r i 「na 2M i 1L ，n 1111 L1L 3卫2 L L按c n 展开a n 1a n1为递推公式, a nD n 1而D 1D n =a nD n 1a 1 a 2 L a n 1=a 1a 2L a nD n 1a 1a 2La n 1D n 2=a 1a 2 L a na 1a 2L a n 2a n 1—=L L a nD1 1 1 11 1 =a〔a2 L 3n L = a〔a2 L a n 1 La1 a2 a n a1 a2 a n a〔a?。

第一章 行列式一．行列式的定义和性质1. 余子式ij M 和代数余子式ij A 的定义例1行列式11110111101111------第二行第一列元素的代数余子式21A =（ ）A ．2-B ．1-C ．1D ．2测试点 余子式和代数余子式的概念解析11110111101111------,212121111111(1)10101211101A M +--=-=--=--=--- 答案 B2．行列式按一行或一列展开的公式 1）11,1,2,;(,1,2,)nnijij ij ijij ij nni j A a a A j n A a a A i n ========∑∑2）11 ; 00nn ij ik ij kj i j k j k i A Aa A a A k j k i ====⎧⎧==⎨⎨≠≠⎩⎩∑∑ 例2 设某3阶行列式的第二行元素分别为1,2,3,-对应的余子式分别为3,2,1--则此行列式的值为 . 测试点 行列式按行(列)展开的定理解 212223212223212223(1)23(1)(1)2(1)3(1)D A A A M M M +++=-⋅++=--+-+-34310=---=-例3 已知行列式的第一列的元素为1,4,3,2-，第二列元素的代数余子式为2,3,4,x 问x = .测试点 行列式的任意一行(列)与另一行(列)元素的代数余子式的乘积之和为零. 解 因第一列的元素为1,4,3,2-，第二列元素的代数余子式为2,3,4,x ,故1243(3)420x ⨯+⨯+-⨯+=所以1x =-3．行列式的性质 1）.T A A =2）用数k 乘行列式的某一行（列）所得新行列式＝原行列式的k 倍.推论 3）互换行列式的任意两行（列）所得新行列式等于原行列式的相反数. 推论 4）如果行列式中两行（列）对应元素成比例，则行列式值为0. 5）行列式可以按任一行（列）拆开.6）行列式的某一行（列）的k 倍加到另一行（列）上，所得新行列式与原行列式的值相等.例4 已知1112132122233132333a a a a a a a a a =，那么111213212223313233222222a a a a a a a a a =---（ ） A.24- B.12- C.6-D. 12测试点 行列式的性质解析 1112131112132122232122233132333132332222(2)12.222a a a a a a a a a a a a a a a a a a =⨯-=---- 答案 B 例5设行列式2211b a b a =1，2211c a c a =2，则222111c b a c b a++=（ ）A ．3-B ．1-C ．1D ．3测试点 行列式的性质解111111122222223a b c a b ac a b c a b a c +=+=+ 故应选 D 答案 D二．行列式的计算1．二阶行列式和三角形行列式的计算.2.对一般数字行列式，利用行列式的性质将其降阶以化成二阶行列式或三角形行列式的计算.3．对行列式中有一行或一列中只有一个或两个非零元的情况，用这一行或一列展开. 4．行列式中各行元素之和为一个常数的类型. 5.范德蒙行列式的计算公式例6求4阶行列式1111112113114111的值.测试点 行列式的计算解111411140231131002302103(3)6121101031000311110003--==-=-=---例7计算3阶行列式 .767367949249323123解 (1)(1)(2)(2)(1)(3)1232331002331002032494992004992004090.367677300677300607+-+-=== 例8 计算行列式：x a a aa x a a a ax a a a ax测试点 各行元素之和为常数的行列式的计算技巧.解 333000300030x a a ax a a a a x a a a a a x a a x ax a a x a D a ax a x a ax a x a a a a xx a a axx a+++-====+-+-3(3)().x a x a =+-例9计算行列式000000000 000000n a b a ba D ab b a=测试点 行列式中有一行只有两个元素不为零的行列式的计算和三角形行列式的计算解111111110000000000 ==+(1)(1) 000000n n n n n n n a b a ba D aA bA aMb M a ba bb a++=+-=+-例10计算行列式60001002005006000D =解 36(1)(6)(2)(5)(3)(4)0001100000200200(1)6!0500005060000006D ↔↔↔==-=- 例11设2311248()139********x x x D x =问（1）()D x 中，3x 项的系数＝？（2）方程()0D x =有几个根？试写出所有的根。