微专题 反比例函数中的面积问题 【九年级 中考数学复习】
- 格式:ppt
- 大小:735.50 KB
- 文档页数:14



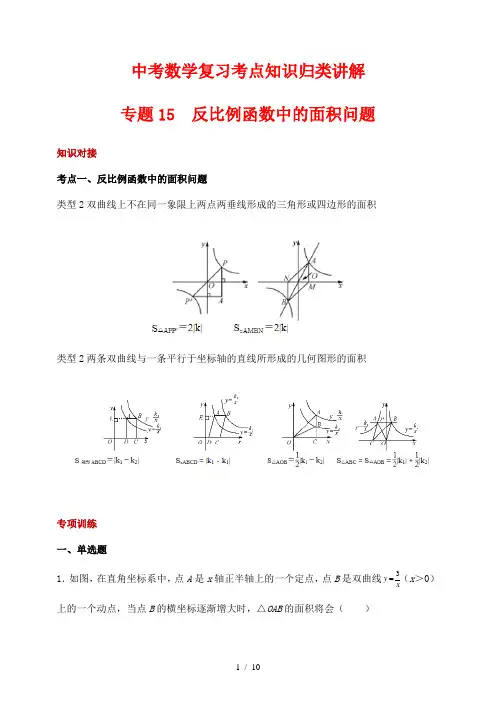
中考数学复习考点知识归类讲解专题15 反比例函数中的面积问题知识对接考点一、反比例函数中的面积问题类型2双曲线上不在同一象限上两点两垂线形成的三角形或四边形的面积类型2两条双曲线与一条平行于坐标轴的直线所形成的几何图形的面积专项训练一、单选题1.如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线3(x>0)yx上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小2.如图所示,点A在反比例函数kyx是的图象上,AM⊥y轴于点M,P是x轴上一动点,当△APM的面积是2时,k的值为()A.4 B.﹣2.C.﹣4 D.﹣23.某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地.当人和木板对湿地的压力一定时,人和木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数,其图象如图,点A在反比例函数图象上,坐标是(8,30),当压强P(Pa)是4800Pa时,木板面积为()m2A.0.5 B.2 C.0.05 D.204.如图,平行四边形OABC的顶点A在x轴的正半轴上,点D(4,3)在对角线OB上,反比例函数y =kx (k >0,x >0)的图象经过C 、D 两点.已知平行四边形OABC 的面积是283,则点B 的坐标为()A .(5,154) B .(6,92)C .(163,4) D .(285,215) 5.如图,点A ,B 分别是反比例函数12y x =-(x <0)和4y x=-(x <0)图象上的点,且AB ∥x 轴,点C 在x 轴上,则△ABC 的面积是()A .4B .5C .6D .86.如图,点A 在曲线到12(0)y x x=>上,点B 在双曲线2(0)k y x x=<上,//AB x 轴,点C 是x 轴上一点,连接AC 、BC ,若ABC 的面积是6,则k 的值()A .6-B .8-C .10-D .12-7.在平面直角坐标系中,反比例函数()120y x x=>的图象经过点()3,A m ,过点A 的直线y=kx +b 与x 轴、y 轴分别交于B 、C 两点若△AOB 的面积为△BOC 的面积的2倍,则k b +的值为()A .83B .43-C .83或0D .43或48.如图,在平面直角坐标系中,平行四边形OABC 的顶点A 在反比例函数y =1x上,顶点B 在反比例函数y =5x上,点C 在x 轴的正半轴上,则平行四边形OABC 的面积是()A .52B .4C .6D .329.如图,在平面直角坐标系中,平行四边形OABC 的顶点B 在反比例函数6y x=上,顶点C 在反比例函数2y x=上,点A 在x 轴的正半轴上,则平行四边形OABC 的面积是()A .3B .4C .5D .610.如图,过反比例函数(0)k y x x=<的图像上的一点P 作PQ x ⊥轴,垂足为Q ,连接PO .若OPQ △的面积是2,则k 的值是()A .4B .4-C .2D .2-二、填空题11.如图,边长为4的正方形ABCD 的对称中心是坐标原点O ,//AB x 轴,//BC y 轴,反比例函数2y x=与2y x=-的图像均与正方形ABCD 的边相交,则图中阴影部分的面积之和是________.12.如图,菱形ABCD 中,120ABC ∠=︒,顶点A ,C 在双曲线()110k y k x=>上,顶点B ,D在双曲线()220k y k x=<上,且BD 经过点O .若122k k +=,则菱形ABCD 面积的最小值是___________.13.如图,在平面直角坐标系xOy 中,菱形AOBC 的一个顶点O 在坐标原点,一边OB 在x 轴的正半轴上,sin∠AOB =45,反比例函数48y x=在第一象限内的图象经过点A ,与BC 交于点F ,则△AOF 的面积等于______________.14.如图,已知A ,B 是反比例函数y =9x(x >0)图象上的两点,AC ⊥x 轴于点C ,OB 交AC 于点D ,若△OCD 的面积是△BCD 的面积的2倍,则△AOD 的面积是_______.15.如图,P 是反比例函数k y x=图象上一点,矩形OAPB 的面积是6,则k =___.三、解答题16.如图,1O 与2O 的直径为2,反比例函数1y x 的图像与两圆分别交于点A ,B ,C ,D ,求图中阴影部分的面积.17.如图,一次函数y =kx +b (k ≠0)与反比例函数y =mx(m ≠0)的图像交于点A 、B ,点B 的横坐标为-4.直线AB 交x 轴于点C ,交y 轴于点D ,过点A 作AE ⊥x 轴于点E ,且OE =2OC =4OD =8.(1)求一次函数和反比例函数的表达式; (2)根据函数图像直接写出不等式kx +b <mx的解集; (3)求△AOB 的面积18.如图,一次函数7y x =-与反比例函数k y x=的图象交于()1,A a 和(),1B b -两点.(1)直接写出a =______,b =_______,k =______;(2)结合图象直接写出关于x 的不等式7kx x -≤-的解集是__________; (3)点(),2C n 在反比例函数k y x=的图象上,连接AC 、BC ,求ABC 的面积. 19.如图,在平面直角坐标系xOy 中,直线AB 与反比例函数my x=交于()2,3A -,()4,B n 两点.(1)求直线AB 和反比例函数的表达式; (2)连接AO ,求AOB 的面积.20.如图,在平面直角坐标系xOy 中,一次函数与反比例函数的图象交于点A (﹣6,﹣3)和B (m ,6),直线AB 交y 轴于点C ,连接OA ,OB .(1)求AOB 的面积;(2)根据图象直接写出,当x 的取值在什么范围内时,反比例函数的值大于一次函数的值.21.如图,一次函数y =kx +b 的图象与反比例函数my x=的图象交于A (﹣2,1),B (1,n )两点.(1)试确定上述反比例函数和一次函数的表达式; (2)当x 为何值时反比例函数值大于一次函数的值; (3)求△AOB 的面积.22.如图,反比例函数()0,0k y k x x=≠>的图象与直线2y x =相交于点C ,过直线2y x =上一点(),8A a 作AB y ⊥轴,垂足为点B ,交反比函数图象于点D ,且4AB BD =. (1)求反比例函数的解析式;(2)若点()2,C b ,求四边形OCDB 的面积.23.如图,在平面直角坐标系xOy 中,一次函数y =x +b 的图象经过点C (0,2),与反比例函数k y x=(x >0)的图象交于点A (1,a ). (1)求一次函数和反比例函数的表达式;(2)一次函数y =x +b 的图象与x 轴交于B 点,求ABO 的面积;(3)设M 是反比例函数ky x=(x >0)图象上一点,N 是直线AB 上一点,若以点O 、M 、C 、N 为顶点的四边形是平行四边形,求点N 的坐标.。
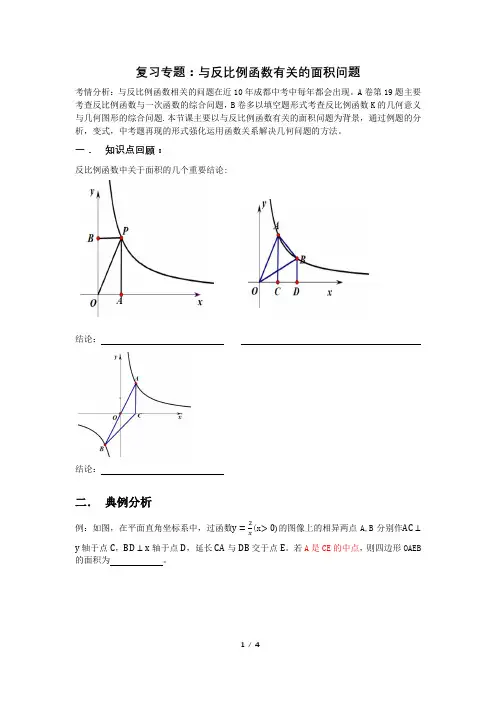
复习专题:与反比例函数有关的面积问题考情分析:与反比例函数相关的问题在近10年成都中考中每年都会出现。
A卷第19题主要考查反比例函数与一次函数的综合问题,B卷多以填空题形式考查反比例函数K的几何意义与几何图形的综合问题.本节课主要以与反比例函数有关的面积问题为背景,通过例题的分析,变式,中考题再现的形式强化运用函数关系解决几何问题的方法。
一.知识点回顾:反比例函数中关于面积的几个重要结论:结论:结论:二.典例分析例:如图,在平面直角坐标系中,过函数(x的图像上的相异两点A,B分别作轴于点,轴于点,延长与交于点。
若A是CE的中点,则四边形OAEB的面积为。
(例图) (变式1图)方法提炼:变式1:把例题中“A是CE的中点”改为“CA:AE=1:2”,此时四边形OAEB的面积为;若改为“CA:AE=1:n”,此时四边形OAEB的面积为。
此题可提炼的结论:。
变式2:如图,在平面直角坐标系中,过函数(x的图像上的相异两点A,B分别作轴于点,轴于点,延长与交于点。
若E的坐标为(2,3),△OAB的面积为,则k的值是。
方法提炼:变式3:如图,在平面直角坐标系中,连接函数(x的图像上的相异两点A,B,延长BA交y 轴于点P,连接AO并延长,交函数(x的图像于点,若已知A点坐标为△PBF的面积是8,则点B的坐标是。
变式4:如图,在反比例函数y=(x>0)的图象上,有点P1、P2、P3、P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1、S2、S3,则S1+S2+S3=()(追问:+= )方法提炼:三、知识巩固1.如图,已知A1,A2,A3,...A n,...是x轴上的点,且OA1=A1A2=A2A3=...=A n﹣1A n (1)分别过点A1,A2,A3,…A n,…作x轴的垂线交反比例函数y=(x>0)的图象于点B1,B2,B3,…,B n,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△B n P n B n+1的面积为S n.则S1+S2+S3+…+S n=.2.如图,双曲线经过四边形OABC的顶点A,C,∠ABC=90°,OC平分OA 与x轴负半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,且点B′恰好落在OA上,则四边形OABC的面积为。


反比例函数中的面积问题利用反比例函数中|k|的几何意义求解与面积有关的问题设P为双曲线上任意一点,过点P作x轴、y轴的垂线PM、PN,垂足分别为M、N,则两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|∴xy=k 故S=|k| 从而得结论1:过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值|k|对于下列三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论,可得出对应的面积的结论为:结论2:在直角三角形ABO中,面积S=结论3:在直角三角形ACB中,面积为S=2|k|结论4:在三角形AMB中,面积为S=|k|一、专题讲解考点一已知面积,求反比例函数的解析式(或比例系数k)【例1】如图,直线OA与反比例函数的图象在第一象限交于A点,AB⊥x轴于点B,△OAB的面积为2,则k=.(2)如图,已知双曲线()经过矩形的边的中点,且四边形的面积为2,则.如图,矩形ABOD 的顶点A是函数与函数在第二象限的交点,轴于B,轴于D,且矩形ABOD的面积为3.(1)求两函数的解析式.(2)求两函数的交点A、C的坐标.(3)若点P是y轴上一动点,且,求点P的坐标.考点二已知反比例函数解析式,求图形的面积【例2】(1)在反比例函数的图象中,阴影部分的面积不等于4的是()A.B.C. D.考点三利用点的坐标及面积公式求面积【例3】如图,已知,是一次函数的图像和反比例函数的图像的两个交点.(1)求反比例函数和一次函数的解析式;(2)求直线与轴的交点的坐标及三角形的面积.如图,直线与反比例函数(<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.(1)试确定反比例函数的关系式;(2)求△AOC的面积.考点四、利用对称性求反比例函数有关的面积问题【例4】已知, A 、B 、C 、D 、E 是反比例函数(x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示)如图,⊙A 和⊙B 都与x 轴和y 轴相切,圆心A 和圆心B 都在反比例函数的图象上,则图中阴影部分的面积等于 .二、 巩固练习: (1) 选择题1、反比例函数xky =的图象如图所示,点M 是该函数图象上一点,MN 垂直于x 轴,垂足是点N ,如果S △MON =2,则k 的值为( )(A)2 (B)-2 (C)4 (D)-42、若A (a 1,b 1),B (a 2,b 2)是反比例函数xy 2-=图象上的两个点,且a 1<a 2,则b 1与b 2的大小关系是( )A .b 1<b 2B .b 1 = b 2C .b 1>b 2D .大小不确定CBA(第7题图)yxO3、函数y x m =+与(0)my m x=≠在同一坐标系内的图象可以是( )(2) 填空题4、如图,反比例函数xy 5=的图象与直线)0(>=k kx y 相交于B 两点,AC ∥y 轴,BC ∥x 轴,则△ABC 的面积等于 个面积单位.(3)解答题5、如图 所示,反比例函数y kx=的图象经过点()Ab -3,,过点A 作AB 垂直x 轴于点B ,△AOB 的面积为3。
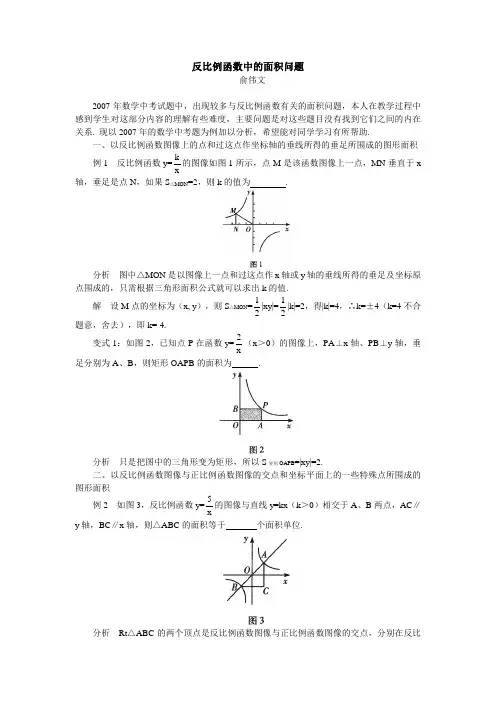
反比例函数中的面积问题俞伟文2007年数学中考试题中,出现较多与反比例函数有关的面积问题,本人在教学过程中感到学生对这部分内容的理解有些难度,主要问题是对这些题目没有找到它们之间的内在关系. 现以2007年的数学中考题为例加以分析,希望能对同学学习有所帮助.一、以反比例函数图像上的点和过这点作坐标轴的垂线所得的垂足所围成的图形面积例1 反比例函数y=xk的图像如图1所示,点M 是该函数图像上一点,MN 垂直于x 轴,垂足是点N ,如果S △MON =2,则k 的值为 .分析 图中△MON 是以图像上一点和过这点作x 轴或y 轴的垂线所得的垂足及坐标原点围成的,只需根据三角形面积公式就可以求出k 的值.解 设M 点的坐标为(x, y ),则S △MON =21|xy|=21|k|=2,得|k|=4,∴k=±4(k=4不合题意,舍去),即k=-4.变式1:如图2,已知点P 在函数y=x2(x >0)的图像上,PA ⊥x 轴、PB ⊥y 轴,垂足分别为A 、B ,则矩形OAPB 的面积为 .分析 只是把图中的三角形变为矩形,所以S 矩形OAPB =|xy|=2.二、以反比例函数图像与正比例函数图像的交点和坐标平面上的一些特殊点所围成的图形面积例2 如图3,反比例函数y=x5的图像与直线y=kx (k >0)相交于A 、B 两点,AC ∥y 轴,BC ∥x 轴,则△ABC 的面积等于 个面积单位.分析 Rt △ABC 的两个顶点是反比例函数图像与正比例函数图像的交点,分别在反比例函数图像的两个分支上,且知道反比例函数图像上的A 、B 两点关于原点成中心对称,∴S △ABC =21|2x ×2y|=2|xy|=10. 变式1. 如图4,直线y=mx 与双曲线y=xk交于点A 、B. 过点A 作AM ⊥x 轴,垂足为点M 连接BM. 若S △ABM =1,则k 的值是( ).A .1 B. m-1 C .2 D. m分析 图形变为反比例函数图像上的A 、B 两点和其中一点与坐标轴的交点所围成的△AMB ,底为|y|,高为|2x|,则S △ABM =21|y ×2x|=|xy|=|k|=1,得k=±1(根据图形知k >0),所以k=1.变式2. 如图5,直线y=mx 与双曲线y=xk交于点A 、B 过点A 、B 分别作AM ⊥x 轴、BN ⊥x 轴,垂足分别为M 、N ,连接BM 、AN. 若S AMBN =1,则k 的值是 .分析 图形变成AMBN ,它的面积实际上就是△ABM 面积的2倍,则SAMBN =2|xy|=2|k|=1,结合图像可知k=21. 三、以反比例函数图像与一次函数图像的交点和坐标原点所围成的图形面积例3 如图6,在直角坐标系xOy 中,一次函数y=k 1x+b 的图像与反比例函数y=xk 2的图像交于A (1,4)、B (3、m )两点.(1)求一次函数的解析式; (2)求△AOB 的面积. 分析 (1)略;(2)△AOB 是以反比例函数图像与一次函数图像的交点和坐标原点所围成的图形,△AOB 面积直接比较难求,可看作S △COD - S △COA - S △BOD . 先求出一次函数的解析式,然后求出一次函数y=k 1x+6的图像与x 轴和y 轴的交点坐标,就可求出S △COD 、S △COA 、S △BOD ,即可求出S △AOB =4×316×21-316×1×21-4×34×21=316.变式1. 如图7,一次函数y=kx+b 的图像与反比例函数y=xm的图像交于A (-2,1),B (1,n )两点.(1)试确定上述反比例函数和一次函数的解析式; (2)求△AOB 的面积. 分析 (1)略:(2)△AOB 也是以反比例函数图像与一次函数图像的交点和坐标原点所围成的图形,只是把△AOB 的面积看作S △COD + S △COA + S △BOD ,即可求得S △AOB =1×1×21+1×1×21+1×1×21=23. 四、以反比例函数图像与其它图形的交点和坐标原点所围成的图形面积例4 如图8,已知双曲线y=xk(x >0)经过矩形OABC 边AB 的中点F ,交BC 于点E ,且四边形OEBF 的面积为2,则k= .分析 这是以反比例函数图像与矩形的交点和坐标原点所围成的图形面积. 四边形OEBF 的面积可看作S 矩形OABC - S △COE - S △AOF ,设F 点的坐标为(x, y ),则E 点的坐标为(21x, 2y ),S 矩形OABC =x ×2y=2xy=2k, S △COE =21x ×2y ×21=21xy=21k ,S △AOF =21xy=21k ,所以S 四边形OEBF =k=2.五、以反比例函数图像上的点与坐标轴围成的图形及一次函数图像与坐标轴围成的图形和面积例5 如图9,D 是反比例函数y=xk(k <0)的图像上一点,过D 作DE ⊥x 轴于E ,DC ⊥y 轴于C ,一次函数y=-x+m 与y=-33x+2的图像都经过点C ,与x 轴分别交于A 、B 两点,四边形DCAE 的面积为4,求k 的值.分析 先求出C (0,2),D (2k,2)和m=2,再求出A (2,0),得S 矩形OCDE =-k ,S △COA =2,所以-k+2=4,得k=-2.。

模型介绍一、反比例函数k 的几何意义1.反比例函数k 的几何意义:如图,在反比例函数图象上任选一点,向两坐标轴作垂线,垂线与坐标轴所围成矩形的面积为k 。
如图二,所围成三角形的面积为2k二、利用k 的几何意义进行面积转化1.如图,直线AB 与反比例函数k y x=(0k ≠)交于A 、B 两点,与x 、y 轴的交点分别为C 、D ,那么OAB OCD OBD OAC S S S S ∆∆∆∆=--,此方法是绝大部分学生选用的方法。
但是,从效率来讲,就比较低2.如图,过点A 、B 作x 轴的垂线,垂足分别为E 、F ,则根据k 的几何意义可得,OBF OAE S S ∆∆=,而OBF OAB OAE ABFE S S S S ∆∆∆+=+梯形,所以OAB ABFE S S ∆=梯形,此方法的好处,在于方便,快捷,不易出错。
【例1】.如图,反比例函数y=在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是8.过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,∴x=2时,y=3;x=6时,y=1,=S△OBD=3,故S△ACOS四边形AODB=×(3+1)×4+3=11,故△AOB的面积是:11﹣3=8.故答案为:8.变式训练【变1-1】.如图,点A在反比例函数(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若,△AOB的面积为12,则k的值为()A.4B.6C.10D.12解:如图,过点A作AD⊥x轴,垂足为D,∵OC∥AD,,∴,∴,k>0,∴k=12,故选:D.【变1-2】.如图,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点,=4,则k的值为16.若E是AB的中点,S△BEF解:设E(a,),则B纵坐标也为,∵E是AB中点,∴F点坐标为(2a,),∴BF=BC﹣FC=﹣=,=4,∵S△BEF∴a•=4,∴k=16.故答案是:16.【例2】.如图,平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为6,4,反比例函数y=(x>0)的图象经过A,B两点,若菱形ABCD的面积为2,则k的值为12.解:解法一:过点A作x轴的垂线,交CB的延长线于点E,∵BC∥x轴,∴AE⊥BC,∵A,B两点在反比例函数y=(x>0)的图象,且纵坐标分别为6,4,∴A(,6),B(,4),∴AE=2,BE=﹣=,∵菱形ABCD的面积为2,∴BC×AE=2,即BC=,∴AB=BC=,在Rt△AEB中,BE===1,∴k=1,∴k=12.解法二:同理知:BE=1,设A(a,6),则B(a+1,4),∴6a=4(a+1),∴a=2,∴k=2×6=12.故答案为12.变式训练【变2-1】.如图,点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,连接OA、OB,则△OAB的面积是()A.9B.8C.7D.6解:∵点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,∴A(4,3),B(2,6),作AD⊥y轴于D,BE⊥y轴于E,=S△BOE=×12=6,∴S△AOD=S△AOD+S梯形ABED﹣S△BOE=S梯形ABED,∵S△OAB=(4+2)×(6﹣3)=9,∴S△AOB故选:A.【变2-2】.如图,在直角坐标系中,O为坐标原点,函数y=与y=(a>b>0)在第一象限的图象分别为曲线C1,C2,点P为曲线C1上的任意一点,过点P作y轴的垂线交C2于点A,作x轴的垂线交C2于点B,则阴影部分的面积S△AOB=a﹣.(结果用a,b表示)解:设B(m,),A(,n),则P(m,n),∵点P为曲线C1上的任意一点,∴mn=a,=mn﹣b﹣b﹣(m﹣)(n﹣)∴阴影部分的面积S△AOB=mn﹣b﹣(mn﹣b﹣b+)=mn﹣b﹣mn+b﹣=a﹣.故答案为:a﹣.1.如图,在△ABC中,AB=AC,点A在反比例函数y=(k>0,x>0)的图象上,点B,C在x轴上,OC=OB,延长AC交y轴于点D,连接BD,若△BCD的面积等于1,则k的值为()A.3B.2C.D.4解:作AE⊥BC于E,连接OA,∵AB=AC,∴CE=BE,∵OC=OB,∴OC=BC=×2CE=CE,∵AE∥OD,∴△COD∽△CEA,∴=()2=4,∵△BCD的面积等于1,OC=OB,=S△BCD=,∴S△COD=4×=1,∴S△CEA∵OC=CE,=S△CEA=,∴S△AOC=+1=,∴S△AOE=k(k>0),∵S△AOE∴k=3,故选:A.2.如图,OC交双曲线y=于点A,且OC:OA=5:3,若矩形ABCD的面积是8,且AB ∥x轴,则k的值是()A.18B.50C.12D.解:延长DA、交x轴于E,∵四边形ABCD是矩形,且AB∥x轴,∴∠CAB=∠AOE,∴DE⊥x轴,CB⊥x轴,∴∠AEO=∠ABC∴△AOE∽△CAB,∴=()2,∵矩形ABCD的面积是8,OC:OA=5:3,∴△ABC的面积为4,AC:OA=2:3,∴=()2=,=9,∴S△AOE∵双曲线y=经过点A,=|k|=9,∴S△AOE∵k>0,∴k=18,故选:A.3.如图,已知点A,B分别在反比例函数y1=﹣和y2=的图象上,若点A是线段OB 的中点,则k的值为()A.﹣8B.8C.﹣2D.﹣4解:设A(a,b),则B(2a,2b),∵点A在反比例函数y1=﹣的图象上,∴ab=﹣2;∵B点在反比例函数y2=的图象上,∴k=2a•2b=4ab=﹣8.故选:A.4.如图,点A(m,n),B(4,)在双曲线y=上,且0<m<n.若△AOB的面积为,则m+n=()A.7B.C.D.3解:∵点A(m,n),B(4,)在双曲线y=上,∴mn=4×=k,∴mn=k=6,∴双曲线为y=,∴n=,作AD⊥x轴于D,BE⊥x轴于E,=S△AOD+S梯形ADEB﹣S△BOE=S梯形ADEB,∵S△AOB∴(+)(4﹣m)=,解得m1=1,m2=﹣16,∵0<m<n.∴m=1,∴n=6,∴m+n=7,故选:A.5.如图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴=3,则S△于点C,BD⊥x轴于点D,连接OA、BC,已知点C(2,0),BD=3,S△BCDAOC为()A.2B.3C.4D.6解:在Rt△BCD中,∵×CD×BD=3,∴×CD×3=3,∴CD=2,∵C(2,0),∴OC=2,∴OD=4,∴B(4,3),∵点B是反比例函数y=(x>0)图象上的点,∴k=12,∵AC⊥x轴,==6,∴S△AOC故选:D.6.如图,平行于y轴的直线分别交y=与y=的图象(部分)于点A、B,点C是y 轴上的动点,则△ABC的面积为()A.k1﹣k2B.(k1﹣k2)C.k2﹣k1D.(k2﹣k1)解:由题意可知,AB=﹣,AB边上的高为x,=×(﹣)•x=(k1﹣k2),∴S△ABC故选:B.7.已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线y=与边BC交于点D、与对角线OB交于中点E,若△OBD的面积为10,则k的值是()A.10B.5C.D.解:设E点的坐标是(x,y),∵E是OB的中点,∴B点的坐标是(2x,2y),则D点的坐标是(,2y),∵△OBD的面积为10,∴×(2x﹣)×2y=10,解得,k=,故选:D.8.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=()A.6B.9C.D.解:∵四边形OCBA是矩形,∴AB=OC,OA=BC,设B点的坐标为(a,b),∵BD=3AD,∴D(,b)∵D、E在反比例函数的图象上,∴=k,设E的坐标为(a,y),∴ay=k∴E(a,),=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣k﹣k﹣••(b﹣)=12,∵S△ODE∴4k﹣k﹣+=12k=故选:D.9.如图,一直线经过原点O,且与反比例函数y=(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=8.解:∵反比例函数与正比例函数的图象相交于A、B两点,∴A、B两点关于原点对称,∴OA=OB,∴△BOC的面积=△AOC的面积=8÷2=4,又∵A是反比例函数y=图象上的点,且AC⊥y轴于点C,∴△AOC的面积=|k|,∴|k|=4,∵k>0,∴k=8.故答案为8.10.如图,若反比例函数y=的图象经过等边三角形POQ的顶点P,则△POQ的边长为2.解:如图,过点P作x轴的垂线于M,∵△POQ为等边三角形,∴OP=OQ,OM=QM=OQ,∵反比例函数的图象经过点P,∴设P(a,)(a>0),则OM=a,OQ=OP=2a,PM=,在Rt△OPM中,PM===a,∴=a,∴a=1(负值舍去),∴OQ=2a=2,故答案为:2.11.如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A作AB∥x 轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.则△OAP 的面积为5.解:过P作MN⊥x轴于M,交AB于N,过A作AD⊥x轴于D,∵A(4,3),∴AD=3,OD=4,∴AO==5,∵AB=AO,∴AB=5,∵AB∥x轴,点B的横坐标是4+5=9,纵坐标是3,即点B的坐标是(9,3),设直线OB的解析式是y=ax,把B点的坐标(9,3)代入得:3=9a,解得:a=,即y=x,∵AB∥x轴,∴MN⊥AB,把A(4,3)代入y=,得k=12,即y=,解方程组得:或,∵点P在第一象限,∴点P的坐标是(6,2),∵A(4,3),AB∥x轴,P(6,2),∴MN=AD=3,PN=3﹣2=1,﹣S△APB=3﹣=5,∴△OAP的面积是S△ABO故答案为:5.12.如图,直线y=x+m与双曲线y=相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC 面积的最小值为6.解:方法一:设A(a,),B(b,),则C(a,).将y=x+m代入y=,得x+m=,整理,得x2+mx﹣3=0,则a+b=﹣m,ab=﹣3,∴(a﹣b)2=(a+b)2﹣4ab=m2+12.=AC•BC∵S△ABC=(﹣)(a﹣b)=••(a﹣b)=(a﹣b)2=(m2+12)=m2+6,∴当m=0时,△ABC的面积有最小值6.故答案为6.方法二:因为y=x+m斜率为1,且BC∥x轴,AC∥y轴,∴∠ABC=∠BAC=45°,∴△ABC为等腰直角三角形,∴AC=BC=AB,=AC•BC=AB2,∴S△ABC当AB最小时,m=0,直线为y=x,联立方程,解得或,∴A(,),B(﹣,﹣),AB=×2=2,=×4×6=6.∴S△ABC最小故答案为:6.13.如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO =AB,点C为斜边OB的中点,反比例函数y=(k>0,x>0)的图象过点C,且交线=6,则k的值为8.段AB于点D,连接CD,OD.若S△OCD解:根据题意设B(m,m),则A(m,0),∵点C为斜边OB的中点,∴C(,),∵反比例函数y=(k>0,x>0)的图象过点C,∴k=•=,∵∠OAB=90°,∴D的横坐标为m,∵反比例函数y=(k>0,x>0)的图象过点D,∴D的纵坐标为,作CE⊥x轴于E,=S△AOD,∵S△COES△OCD=S△COE+S梯形ADCE﹣S△AOD=S梯形ADCE,S△OCD=6,∴(AD+CE)•AE=6,即(+)•(m﹣m)=6,∴m2=32,∴k==8,故答案为:8.解法二:作CE⊥OA于E,∵C为AB的中点,OA=AB,∠OAB=90°,=S△AOD=k,S△AOB=2k,∴S△OEC=k,∴S△BOD∵C为斜边OB的中点,=S△BCD=S△BOD=6,∴S△OCD∴×k=6,∴k=8.故答案为:8.14.如图,在平面直角坐标系中,▱OABC的顶点A,B在第一象限内,顶点C在y轴上,经过点A的反比例函数y=(x>0)的图象交BC于点D.若CD=2BD,▱OABC的面积为15,则k的值为18.解:过点D作DN⊥y轴于N,过点B作BM⊥y轴于M,设OC=a,CN=2b,MN=b,∵▱OABC的面积为15,∴BM=,∴ND=BM=,∴A,D点坐标分别为(,3b),(,a+2b),∴•3b=(a+2b),∴b=a,∴k=•3b=•3×a=18,故答案为:18.15.如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴于点B,点C在x 轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.解:连DC,如图,∵AE=3EC,△ADE的面积为3,∴△CDE的面积为1,∴△ADC的面积为4,设A点坐标为(a,b),则AB=a,OC=2AB=2a,而点D为OB的中点,∴BD=OD=b,=S△ABD+S△ADC+S△ODC,∵S梯形OBAC∴(a+2a)×b=a×b+4+×2a×b,∴ab=,把A(a,b)代入双曲线y=,∴k=ab=.故答案为:.16.如图,已知反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8),B(﹣4,m)两点.(1)求k1,k2,b的值;(2)求△AOB的面积;(3)请直接写出不等式x+b的解.解:(1)∵反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8)、B(﹣4,m),∴k1=8,B(﹣4,﹣2),解方程组,解得;(2)由(1)知一次函数y=k2x+b的图象与y轴的交点坐标为(0,6),=×6×4+×6×1=15;∴S△AOB(3)﹣4≤x<0或x≥1.17.如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB=,反比例函数y=的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为.(1)求反比例函数的解析式;(2)求直线EB的解析式;.(3)求S△OEB解:(1)∵A点的坐标为(a,6),AB⊥x轴,∴AB=6,∵cos∠OAB==,∴,∴OA=10,由勾股定理得:OB=8,∴A(8,6),∴D(8,),∵点D在反比例函数的图象上,∴k=8×=12,∴反比例函数的解析式为:y=;(2)设直线OA的解析式为:y=bx,∵A(8,6),∴8b=6,b=,∴直线OA的解析式为:y=x,则,x=±4,∴E(﹣4,﹣3),设直线BE的解式为:y=mx+n,把B(8,0),E(﹣4,﹣3)代入得:,解得:,∴直线BE的解式为:y=x﹣2;=OB•|y E|=×8×3=12.(3)S△OEB18.如图,直线y=x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=.(1)求反比例函数的解析式;(2)求点B的坐标;.(3)求S△OAB解:(1)∵直线y=x与反比例函数的图象交于点A(3,a),∴a=×3=4,∴点A的坐标为(3,4),∴k=3×4=12,∴反比例函数解析式y=.(2)∵点B在这个反比例函数图象上,设点B坐标为(x,),∵tanα=,∴=,解得:x=±6,∵点B在第一象限,∴x=6,∴点B的坐标为(6,2).(3)设直线OB为y=kx,(k≠0),将点B(6,2)代入得:2=6k,解得:k=,∴OB直线解析式为:y=x.过A点做AC⊥x轴,交OB于点C,如图所示:则点C坐标为(3,1),∴AC=3.S△OAB的面积=S△OAC的面积+S△ACB的面积=×|AC|×6=9.∴△OAB的面积为9.19.已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比=4.例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB (1)求该反比例函数的解析式和直线AB的解析式;(2)若直线AB与双曲线的另一交点为D点,求△ODB的面积.=•|x A|•y B,解:(1)由题意得:S△AOB即×2×y B=4,y B=4,∴B(2,4),设反比例函数的解析式为:y=,把点B的坐标代入得:k=2×4=8,∴y=,设直线AB的解析式为:y=ax+b,把A(﹣2,0)、B(2,4)代入得:,解得:,∴y=x+2;(2)由题意得:x+2=,解得:x1=﹣4,x2=2,∴D(﹣4,﹣2),=S△OAD+S△OAB=×2×2+4=6.∴S△ODB20.如图,在平行四边形OABC中,,点A在x轴上,点D是AB 的中点,反比例函数的图象经过C,D两点.(1)求k的值;(2)求四边形OABC的面积.解:(1)过点C作CE⊥x轴于E,∵∠AOC=45°,∴OE=CE,∴OE2+CE2=OC2∵OC=2,∴OE=CE=2,∴C(2,2),∵反比例函数的图象经过点C点,∴k=2×2=4;(2)过点D作DF⊥x轴于F,∵四边形OABC是平行四边形,∴AB=OC=2,∠DAF=∠AOC=45°,又∵点D是AB的中点,∴AD=,AF=DF,∴AF2+DF2=AD2,∴AF=DF=1,∴D点的纵坐标为1,∵反比例函数的图象过点D点,∴D(4,1),∴OF=4,OA=OF﹣AF=4﹣1=3,∴平行四边形OABC的面积S=OA•CE=3×2=6.21.如图,直线y=6x与双曲线y=(k≠0,且x>0)交于点A,点A的横坐标为2.(1)求点A的坐标及双曲线的解析式;(2)点B是双曲线上的点,且点B的纵坐标是6,连接OB,AB,求△AOB的面积.解:(1)将x=2代入y=6x,得:y=12,∴点A的坐标为(2,12),将A(2,12)代入y=,得:k=24,∴反比例函数的解析式为y=;(2)在y=中y=6时,x=4,∴点B(4,6),而A(2,12),如图,过A作AC⊥y轴,BD⊥x轴,交于点E,则OD=4,OC=12,BD=6,AC=2,AE=2,BE=6,=S矩形OCED﹣S△AOC﹣S△BOD﹣S△ABE∴S△AOB=4×12﹣×2×12﹣×4×6﹣×2×6=48﹣12﹣12﹣6=18.22.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数的图象的两个交点.(1)求反比例函数和一次函数的表达式;(2)求△AOB的面积;(3)若D(x,0)是x轴上原点左侧的一点,且满足,求x的取值范围.解:(1)∵B(2,﹣4)在反比例函数y=的图象上,∴m=﹣8,∴反比例函数的表达式为y=﹣.∵A(﹣4,n)在y=﹣的图象上,∴n=2,∴A(﹣4,2).∵y=kx+b经过A(﹣4,2)和B(2,﹣4),∴,解得∴一次函数的表达式为y=﹣x﹣2.(2)当y=﹣x﹣2=0时,解得x=﹣2.∴点C(﹣2,0),∴OC=2,=S△AOC+S△COB∴S△AOB=×2×2+×2×4=6.(3)根据函数的图象可知:若D(x,0)是x轴上原点左侧的一点,当﹣4<x<0时,满足kx+b﹣<0.23.如图,一次函数y=k1x+b的图象与反比例函数y=(x<0)的图象相交于点A(﹣1,2)、点B(﹣4,n).(1)求此一次函数和反比例函数的表达式;(2)求△AOB的面积;(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.解:(1)∵反比例函数y=(x<0)的图象经过点A(﹣1,2),∴k2=﹣1×2=﹣2,∴反比例函数表达式为:y=﹣,∵反比例y=﹣的图象经过点B(﹣4,n),∴﹣4n=﹣2,解得n=,∴B点坐标为(﹣4,),∵直线y=k1x+b经过点A(﹣1,2),点B(﹣4,),∴,解得:,∴一次函数表达式为:y=+.(2)设直线AB与x轴的交点为C,如图1,当y=0时,x+=0,x=﹣5;∴C点坐标(﹣5,0),∴OC=5.S△AOC=•OC•|y A|=×5×2=5.S△BOC=•OC•|y B|=×5×=.S△AOB=S△AOC﹣S△BOC=5﹣=;(3)如图2,作点A关于x轴的对称点A′,连接A′B,交x轴于点P,此时△PAB的周长最小,∵点A′和A(﹣1,2)关于x轴对称,∴点A′的坐标为(﹣1,﹣2),设直线A′B的表达式为y=ax+c,∵经过点A′(﹣1,﹣2),点B(﹣4,)∴,解得:,∴直线A′B的表达式为:y=﹣x﹣,当y=0时,则x=﹣,∴P点坐标为(﹣,0).24.如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=(x>0)的图象经过线段OC的中点A(3,2),交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;(2)求△OEF的面积;(3)请结合图象直接写出不等式k2x+b>0的解集.解:(1)∵四边形DOBC是矩形,且D(0,4),B(6,0),∴C点坐标为(6,4),∵A点坐标为(3,2),∴k1=3×2=6,∴反比例函数解析式为y=;把x=6代入y=得x=1,则F点的坐标为(6,1);把y=4代入y=得x=,则E点坐标为(,4),把F(6,1)、E(,4)代入y=k2x+b,得,解得,,∴直线EF的解析式为y=﹣x+5;﹣S△ODE﹣S△OBF﹣S△CEF(2)△OEF的面积=S矩形BCDO=4×6﹣×4×﹣×6×1﹣×(6﹣)×(4﹣1)=;(3)由图象得:不等式k2x+b﹣>0的解集为<x<6.25.如图,已知反比例函数y=(m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).(1)求反比例函数与一次函数的表达式;(2)一次函数的图象分别与x轴、y轴交于A、B两点,与反比例函数图象的另一个交点为P,连结OP、OQ.求△OPQ的面积.解:(1)反比例函数y=(m≠0)的图象经过点(1,4),解得m=4,故反比例函数的表达式为y=.一次函数y=﹣x+b的图象与反比例函数的图象相交于点Q(﹣4,n),所以,解得n=﹣1,b=﹣5.∴一次函数的表达式y=﹣x﹣5;(2)由,解得或.∴点P(﹣1,﹣4),在一次函数y=﹣x﹣5中,令y=0,得﹣x﹣5=0,解得x=﹣5,故点A(﹣5,0),S△OPQ=S△OP A﹣S△OAQ=×5×4−×5×1=7.5.26.如图,在平面直角坐标系中,边长为4的等边△OAB的边OB在x轴的负半轴上,反比例函数y=(x<0)的图象经过AB边的中点C,且与OA边交于点D.(1)求k的值;(2)连接OC,CD,求△OCD的面积;(3)若直线y=mx+n与直线CD平行,且与△OAB的边有交点,直接写出n的取值范围.解:(1)∵等边△OAB,∴AB=BO=AO=4,∠ABO=∠BOA=∠OAB=60°,∵点C是AB的中点,∴BC=AC=2,过点C作CM⊥OB,垂足为M,在Rt△BCM中,∠BCM=90°﹣60°=30°,BC=2,∴BM=1,CM=,∴OM=4﹣1=3,∴点C 的坐标为(﹣3,),代入y =得:k =﹣3答:k 的值为﹣3;(2)过点A 作AN ⊥OB ,垂足为N ,由题意得:AN =2CM =2,ON =OB =2,∴A (﹣2,2),设直线OA 的关系式为y =kx ,将A 的坐标代入得:k =﹣,∴直线OA 的关系式为:y =﹣x ,由题意得:,解得:舍去,,∴D (﹣,3)过D 作DE ⊥OB ,垂足为E ,S △OCD =S CMED +S △DOE ﹣S △COM =S CMED =(+3)×(3﹣)=3,答:△OCD 的面积为3.(3)①当与直线CD 平行的直线y =mx +n 过点O 时,此时y =mx +n 的n =0,②当与直线CD 平行的直线y =mx +n 经过点A 时,设直线CD 的关系式为y =ax +b ,把C 、D 坐标代入得:,解得:a =1,b =3+∴直线CD 的关系式为y =x +3+,∵y =mx +n 与直线y =x +3+平行,∴m =1,把A (﹣2,2)代入y =x +n 得:n =2+2因此:0≤n ≤2+2且n .答:n 的取值范围为:0≤n ≤2+2且n ≠3+.。


中考数学专题复习反比例函数面积问题(两点两垂线)学校:___________姓名:___________班级:___________考号:___________评卷人得分一、单选题1.如图,点A是第一象限内双曲线y=mx(m>0)上一点,过点A作AB∥x轴,交双曲线y=nx(n<0)于点B,作AC∥y轴,交双曲线y=nx(n<0)于点C,连接BC.若△ABC的面积为92,则m,n的值不可能是()A.m=19,n=﹣109B.m=14,n=﹣54C.m=1,n=﹣2D.m=4,n=﹣2评卷人得分二、填空题2.如图,直线y=mx与双曲线y=kx交于点A,B,过点A,B分别作AM⊥x轴,BN⊥x轴,垂足分别为M,N,连接BM,AN.若S四边形AMBN=1,则k的值是_______.3.点A,B分别是双曲线(0)ky kx=>上的点,AC y⊥轴正半轴于点C,BD y⊥轴于点D,联结AD,BC,若四边形ACBD是面积为12的平行四边形,则k=________.参考答案:1.A【解析】【分析】设A的坐标为(x,mx),分别表示出点B和点C的坐标,再根据三角形的面积公式得出()2m n=9m-,再将各个选项中的值代入比较,据此进行判断即可.【详解】解:⊥点A是第一象限内双曲线y=mx(m>0)上一点,⊥设A的坐标为(x,mx ),⊥AB∥x轴,AC∥y轴,且B、C两点在y=nx(n<0)上,⊥B的坐标为(nxm ,mx),C的坐标为(x,nx),⊥AB=nxmx-,AC=n-xmx,⊥△ABC的面积为92,⊥19 22 AC BA⨯=,⊥nxmx⎛⎫-⎪⎝⎭n-x⎛⎫⎪⎝⎭mx=9,⊥()2m n=9m-,⊥将m和n的值代入,只有选项A中不符合.故选:A.【点睛】本题考查了反比例函数图像上点的特征,三角形形的面积等知识及综合应用知识、解决问题的能力.2.12【解析】【分析】先证明四边形AMBN是平行四边形,AMBN的面积实际上就是ABM面积的2倍,则S △ABM =12,结合图象可知12k =. 【详解】解:⊥OA =OB ,ON =OM ,⊥四边形AMBN 是平行四边形,⊥S 四边形AMBN =1,⊥S △ABM =12, 设点A 的坐标为(x ,y ),⊥B 的坐标为(−x ,−y ),⊥12×2x ×y =12, ⊥xy =12, ⊥k =xy =12. 故答案是:12.【点睛】 本题主要考查反比例函数与一次函数的交点问题,平行四边形的判定和性质,掌握反比例函数的比例系数等于在它上面的点的横纵坐标的积,是解题的关键.3.6【解析】【分析】首先根据平行四边形的性质得出,OA OB OC OD ==,从而有412AOC ABCD S S ==△四边形,然后根据k 的几何意义求解即可.【详解】如图,⊥点A ,B 分别是双曲线(0)k y k x=>上的点,AC y ⊥轴正半轴于点C ,BD y ⊥轴于点D , //AC BD ∴.⊥四边形ACBD 是面积为12的平行四边形,AC BD ∴=,⊥A ,B 关于原点对称,,OA OB OC OD ∴==,412AOC ABCD S S ∴==△四边形,3AOC S ∴=△,236k ∴=⨯=,故答案为:6.【点睛】本题主要考查平行四边形的性质以及k 的几何意义,掌握平行四边形的性质以及k 的几何意义是解题的关键.。
中考复习专题 反比例函数与图形面积反比例函数问题,许多都是与三角形、四边形等图形的面积联系在一起的,其中常见的有已知反比例函数的解析式,求其图象围成的某一图形的面积;或已知某一图形的面积,求符合条件的反比例函数的解析式等题型。
一、反比例函数与矩形面积。
例1、如图,P 是反比例函数)0(≠=k xk y 的图象 上一点,过P 点分别向x 轴、y 轴作垂线,所得 到的图中阴影部分的面积为6,则这个反比例函数的解析式为( ) A. x y 6-= B. xy 6= C. x y 3-= D. xy 3=例2、如图,已知正方形OABC 的面积为9,点O 为坐标原点,点A 在x 轴上,点C 在y 轴上,点B 在函数x k y =(k >0,x >0)的图象上,点P (n m ,)是函数xk y =(k >0,x >0)的图象上的任意一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为E 、F ,并设矩形OEPF 和正方形OABC 不重合部分的面积为S 。
(1)求B 点坐标和k 的值; (2)当29=S 时,求点P 的坐标。
写出S 与m 的函数关系式变式议练:如图,在反比例函数xy 2=(x >0)的图象上, 有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4。
分别过这些点作x 轴与y 轴的垂线,图中所构成的阴影部分 的面积从左到右依次为S1,S2,S3,则S1+S2+S3= 。
二、反比例函数与三角形面积。
1、反比例函数与直角三角形面积例3、如图,点A 在反比例函数)0(≠=k xk y 的图象上,AB 垂直于x 轴,若S △AOB=4,变式议练1、如图,过反比例函数xy 1=(x >0)的图形上任意两点A 、B 分别作x 轴的垂线,垂足分别为C 、D ,连结OA 、OB 。
设AC 与OB 的交点为E ,△AOE 与梯形ECDB 的面积分别为S1,S2,比较它们的大小,可得( )A. S1>S2B. S1=S2C. S1<S2D. 大小关系不能确定变式议练2、如图,A 、B 是函数xy 1=的图象上关于原点O 对称的任意两点,AC 平行于y 轴,BC 平行于x 轴,△ABC 的面积为S ,则( )A. S=1B. 1<S <2C. S=2D. S >2 2、反比例函数与斜三角形面积例4、如图,函数kx y -=(0≠k )与xy 4-=的图象交于A 、B 两点,过点A 作AC 垂直于y 轴,垂足为点C ,则△BOC 的面积为 。
反比例函数中与面积有关的问题及解答反比例函数解析式及图象的特殊性与面积结合起来,既能考查反比例函数本身的基础知识,又能充分体现数形结合的思想方法,考查涉及的题型广泛,方法灵活,可较好地将知识与能力融合在一起。
下面就反比例函数中与面积有关的问题及解析归纳如下:利用反比例函数中|k|的几何意义求解与面积有关的问题设P为双曲线上任意一点,过点P作x轴、y轴的垂线PM、PN,垂足分别为M、N,则两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|∴xy=k 故S=|k| 从而得结论1:过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值|k|。
对于下列三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论,可得出对应的面积的结论为:k结论2:在直角三角形ABO中,面积S=2结论3:在直角三角形ACB中,面积为S=2|k|结论4:在三角形AMB 中,面积为S=|k|类型之一 k 与三角形的面积※问题1、如图,已知双曲线y=xk(k >0)经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为6,则k=______.答案解析:过D 点作DE⊥x 轴,垂足为E , 由双曲线上点的性质,得S △AOC =S △DOE = 21k, ∵DE⊥x 轴,AB⊥x 轴, ∴DE ∥ AB ,∴△OAB ∽ △OED, 又∵OB=2OD,∴S △OAB =4S △DOE =2k ,由S △OAB -S △OAC =S △OBC ,得2k -21k=6,解得:k=4.故答案为:4.问题2.如图,分别过反比例函数y=x2018(x >0)的图象上任意两点A 、B 作x 轴的垂线,垂足分别为C 、D ,连接OA 、OB ,设△AOC 和△BOD 的面积分别是S 1、S 2,,比较它们的大小,可得A.S 1>S 2B.S 1=S 2C.S 1<S 2D.S 1、S 2大小不确定。
导学案
科目数学课题反比例函数中的面积问题
授课老师班级上课
时间
签审
领导节次
学习目标及
重难点
能用反比例函数解决相关的面积问题。
(重、难)
教学过程
一、解读学习目标
二、知识梳理
模型一:一点一垂线(8min)
1、模型特征反比例函数图象上一点与坐标轴垂线、另一坐标轴上一点(含原点)围成的三角形面积=1/2|k|.
模型示例
2、生理解记忆知识点(2min)
3、针对性练习(5min)
如图,点A在反比例函数y=-4/x的图象上,AM⊥y轴于点M,
点P是x轴上的一点,则△APM的面积是().
模型二:一点两垂线(6min)
1、模型特征反比例函数图象上一点与坐标轴的两条垂线所围成的矩形面积=|k|.
模型示例
2、生理解记忆知识点(2min)
3、针对性练习(5min)
如图,点P在函数y=k/x的图象上,PA⊥x轴于点A,PB⊥y轴于点B,且△APB的面积为4,则k等于().
做题技巧:遇到反比例函数有关的面积问题,尽可能构造与坐标轴平行(垂直)的边,将不易求的面积转化为与k有关系的面积进行计算。
三、当堂检测(8min)
精练本1至3题
四、课堂小结(2min)
1、一点一垂线型
2、一点两垂线型
五、作业布置
试题研究微专题2题4题。