运筹学最短路例2解题步骤

法求解，这里介绍一种有效算法—狄克斯拉（Dijkstra）算法，这一
算法是1959年首次被提出来的。该算法适用于每条弧的权数ωij ≥0 情形。算法的基本思路：从发点vs 出发，有一个假想的流沿网络一 切可能的方向等速前进，遇到新节点后，再继续沿一切可能的方向 继续前进，则最先到达终点vt 的流所走过的路径一定是最短的。为 了实现这一想法，对假想流依次到达的点，依次给予p标号，表示vs 到这些点的最短距离。对于假想流尚未到达的点给予T标号，表示vs 到这些点的最短距离的估计值。具体作法如下：
或v1 →v4。
v1 →vv31→5v36 或
v1 →v4→v6
22
30
41
59
23
16
v2v24→1 v61262
v3v33→1 v6 17 30
v4v42→3 v167 23
v5v51→8 v618 v6
41
31
21
2
6
5
08
7
1
17
2
1
9
32
5
9 3
79
66
11 2 13
431 4
9
1
10
21
p（v2）=3 3
v2
p（v1）=0 v1
p（v3）=4
6
51 1
v4
7 4
v5
v3 2 3
5
v7
26 v6 9
15
v8
T（v4）=min{6,4+1}=5, k（v4 ）=v3
T（v6）=min{7,4+2}=6, k（v6 ）=v3
目前，点v4 具有最小T标号，将其标号改为p标号： p（v4）=5；

最短路问题的求解方法最短路问题是图论中的一个经典问题，它在很多实际应用中都有着重要的作用。

在现实生活中，我们经常需要求解最短路径，比如在地图导航、网络通信、交通运输等领域。

因此，研究最短路问题的求解方法具有重要的理论意义和实际应用价值。

在图论中，最短路问题的求解方法有很多种，其中比较经典的有Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法等。

这些算法各有特点，适用于不同的场景和要求。

下面我们就逐一介绍这些算法的原理和求解方法。

Dijkstra算法是一种用于求解单源最短路径的算法，它采用贪心策略，每次找到当前距离最短的节点进行松弛操作，直到所有节点都被遍历。

Dijkstra算法的时间复杂度为O(V^2)，其中V为节点的个数。

这种算法适用于边权值为正的图，可以求解从单个源点到其他所有点的最短路径。

Bellman-Ford算法是一种用于求解单源最短路径的算法，它可以处理边权值为负的图，并且可以检测负权回路。

Bellman-Ford算法的时间复杂度为O(VE)，其中V为节点的个数，E为边的个数。

这种算法适用于一般情况下的最短路径求解，但是由于其时间复杂度较高，不适用于大规模图的求解。

Floyd-Warshall算法是一种用于求解所有点对最短路径的算法，它可以处理边权值为正或负的图，但是不能检测负权回路。

Floyd-Warshall算法的时间复杂度为O(V^3)，其中V为节点的个数。

这种算法适用于求解图中所有点对之间的最短路径，可以同时求解多个源点到多个目标点的最短路径。

除了上述几种经典的最短路求解算法外，还有一些其他的方法，比如A算法、SPFA算法等。

这些算法在不同的场景和要求下有着各自的优势和局限性，需要根据具体情况进行选择和应用。

在实际应用中，最短路问题的求解方法需要根据具体的场景和要求进行选择，需要综合考虑图的规模、边权值的情况、时间效率等因素。

同时，对于大规模图的求解，还需要考虑算法的优化和并行化问题，以提高求解效率。

现在我们就来构造一个图G，它的顶点就是这10 种情况，G中的边是按照下述原则来连的；如果情况 甲经过一次渡河可以变成情况乙，那么就在情况甲与 乙之间连一条边.
MWSV MWS MWV WSV MS
WV
W
S
V
Ø
例如，MWSV经过一次渡河可以变成WV(人带着羊 过河，左岸留下狼和白菜)，又例如MWV经过一次渡河 可以变为W(人带着白菜过河，留下狼)，或变为V.当 然反过来，W也可以变为MWV(人带着白菜从右岸返回 左岸).
§3.2 求最短有向路的标号法
这一节介绍一种求有向图上最短有向路的方法 ，叫做标号法。
所谓标号,我们是指与图的每一个顶点对应的一个 数(或几个数)．例如设G=(V,A)的顶点集合是V={v1,v2, …,vn}，如果我们能使v1对应一个数b(1)，v2对应数 b(2)，…，vn对应数b(n)，那么，这些数b(i)就称为vi的 标号，当然，在不同的问题中，标号b(i)一般代表不同 的意义.
从上面的简单比较久可以看出，为什么说计算 次数是n的多项式的方法是有效的，而计算次数是 n的指数函数的方法是无效的.另外，也可以看出， 单靠提高计算机的速度还不够，还必须从数学上寻 求有效的计算方法.
现在再回过头来看看标号法好不好.回想一下标 号法的各轮计算，可以看出，它只包含两种运算： 加法与比较大小(比较大小也需要花费时间，所以 也要考虑).加法用于计算k(i,j)，每计算一个k(i,j)进 行一次加法，而且每一条弧最多只计算一次.因此, 如果图中有m条弧，那么至多进行m次加法.对于一 个有n个顶点的简单有向图来说，最多有n(n-1)条 弧(假设从每一个顶点vi出发，都有n-1条弧指向其 他的n-1个顶点)，因此，最多进行n(n-1)次加法， 放宽一点，也可以说，至多进行n2次加法.

年份 购置费 使用年数 维修费
1
2
3
4
5
18 20 21 23 24
0~1 1~2 2~3 3~4 4~5
5
7 12 18 25
方法：将此问题用一个赋权有向图来描述，然后求这个赋权有向图 的最短路。
求解步骤：
1）画赋权有向图：
设 vi 表示第i年初， (vi ,vj )表示第i 年初购买新设备用到第j年初（j-1年底）， 而wi j 表示相应费用， 则5年的一个更新计划相当于从v1 到v6的一条路。 2）求解 （标号法）
v5 29
45
v6
62
算法步骤：
1.给始点v1标号[0，v1] 。
2. ：把顶点集V分成VA ：已标号点集 VB ：未标号点集
3.考虑所有这样的边[vi ，vj] ：其中vi VA ，v j VB ，挑选
其与起点v1距离最短（mindi cij ）的vj，对vj进行标号
4.重复步骤2、3，直至终点vn标上号[dn ，vj],则dn 即为vs到
第三节 最短路问题
例：求网络图中，起点v1到终点v8之间的一条最短
路线。
v2
1
v5
6
2
3
6
v1
v3
2
v9
6 3
10 3
1
2
v8
4
2 v7
v4
10
v6
(一)、 狄克斯拉(Dijkstra)标号算法
Байду номын сангаас
基本思想：从起点vs 开始，逐步给每个结点vj标号[dj ，vi]，其
中dj为起点vs到vj的最短距离， vi为该最短路线上的前一结点。
vj的最短距离，反向追踪可求出最短路。

最短路问题的求解方法最短路问题是图论中的经典问题之一，它在实际生活中有着广泛的应用，比如在交通规划、通信网络、物流配送等领域都有着重要的作用。

在解决最短路问题时，我们需要找到图中两个顶点之间的最短路径，即使得路径上的边的权值之和最小。

针对不同的图，我们可以采用不同的方法来求解最短路问题，下面将介绍几种常见的求解方法。

首先，最简单直接的方法是暴力搜索法。

暴力搜索法适用于小规模的图，它通过穷举所有可能的路径来找到最短路径。

虽然这种方法在理论上是可行的，但是在实际应用中由于时间复杂度过高，通常不适用于大规模的图。

其次，我们可以使用迪杰斯特拉算法来解决最短路问题。

迪杰斯特拉算法是一种贪心算法，它通过逐步扩展离源点距离最短的节点来逐步求解最短路径。

迪杰斯特拉算法的时间复杂度为O(V^2)，其中V为顶点数，因此适用于稠密图。

另外，我们还可以使用贝尔曼-福特算法来求解最短路问题。

贝尔曼-福特算法是一种动态规划算法，它通过多次松弛操作来逐步逼近最短路径。

贝尔曼-福特算法适用于存在负权边的图，但是由于其时间复杂度为O(VE)，因此在稠密图中效率较低。

最后，我们还可以使用Floyd-Warshall算法来解决最短路问题。

Floyd-Warshall算法是一种动态规划算法，它通过逐步考察所有顶点对之间的路径来求解最短路径。

Floyd-Warshall算法的时间复杂度为O(V^3)，因此适用于小规模图。

总的来说，不同的最短路求解方法适用于不同的图，我们需要根据具体的情况来选择合适的方法。

在实际应用中，我们还可以结合启发式算法、并行算法等方法来进一步提高求解效率。

希望本文介绍的内容能够对读者有所帮助，谢谢！。

B）Dijkstra算法和Ford算法都适用于任意边的情况 C）Dijkstra算法仅适用于所有边的权非负的情况，Ford算
法适用于所有边的权为任意实数的情况 D）Dijkstra算法适用于所有边的权为任意实数的情况，
Ford算法适用于所有边的权非负情况
29
OR:SM
试试看——选择题
• 2、以下说法中错误的是（ ）。
4
8
1
v4
vt
1
7
3
6
1
2
v6
7
OR:SM
vs
方式之一：单标号算法
第一步：
T(vs)=∞
v1
2
3
P(vs)=0 vs
9
10
4 7
T(vs)=∞
v2 1
4
3
v3
2
T(vs)=∞
T(vs)=∞
v5
8 1
v4 T(vs)=∞
7
vt T(vs)=∞
6
1
v6
T(vs)=∞
8
OR:SM
方式之一：单标号算法
第二步：
第4年 19 3-4 18
第5年 24 4-5 27
[解]设以vi(i=1,2,3,4,5)表示“第i年初购进一台新设备”这 种状态，以v6表示“第5年末”这种状态；以弧(vi, vj)表示 “第i年初购置的一台设备一直使用到第j年初”这一方案，以
wij表示这一方案所需购置费和维护费之和。于是，该问题就 可归结为从图中找出一条从v1到v6的最短路问题。其网络模型 如下：
本章小结
图论是应用十分广泛的运筹学分支，它已广泛应用在物 理、化学、控制论、信息论、科学管理、电子计算机等 各个领域。

v1
v2
v3
v4
v5
v6
把所有弧的权数计算如下表：
1 1 2 3 4 5 6 2 16 3 22 16 4 30 22 17 5 41 30 23 17 6 59 41 31 23 18
管
理
运
筹
学
2
§2 最短路问题
(继上页) 把权数赋到图中，再用Dijkstra算法求最短路。
59 22 v1 16 v2 30 41 v4 23 41 23 17 v5 31
管 理 运 筹 学
11
§4 最大流问题
二、最大流问题网络图论的解法 对网络上弧的容量的表示作改进。为省去弧的方向，如下图: (a)和 (b)、(c)和(d)的意义相同。 cij cij 0 vi vi vj vj （ a） （ b） cij cij cji v j vi vi vj （cji） （ d） （c） 用以上方法对例6的图的容量标号作改进，得下图
个网络能联通7个学院办公室，并使总的线路长度为最短。
v2 3 1 4 v7 3 v6 5 2 8 v5 v3
7
v4
图11-14
v1 10
3
4
解：此问题实际上是求图11-14的最小生成树，这在例4中已经求得， 也即按照图11-13的(f)设计，可使此网络的总的线路长度为最短，为19 百米。 “管理运筹学软件”有专门的子程序可以解决最小生成树问题。
年份
年初价格
1
11
2
11
3
12
4
12
5
13
设备维修费如下表 使用年数 每年维修 费用 0-1 5 1-2 6 2-3 8 3-4 11 4-5 18
管

如果P是D中从vs到vj的最短路，vi是P中的一点，那么从vs沿P到vi路也是 从vs到vi的最短路。
Dijkstra法的适用条件
求出一点到图中任意点最短路
求解思路
从vs出发，逐步地向外探索最短路。执行过程中，与每个点记下一个数， 它或者表示从vs到该点的最短路的权（称为P(perpetual)标号），或者是 从vs到该点的最短路的权的上界（称为T(temporary)标号），方法的每一 步是去修改T标号，并且把某一个T标号点改为P标号点，从而使D中P标 号顶点多一个，这样最多经过p-1步就可以求出从vs到各点的最短路。
（2）起点发出的流的总和(称为流量)，必须等于终点接收的流的总 和；
（3）各中间点流入的流量之和必须等于从该点流出的流量之和，即 流入的流量之和与流出的流量 之和的差为0，也就是说各中间点只 起转运作用，它既不产出新的物资，也不得截留过境的物资．
Operation Research
网络最大流的基本概念（3）
第八讲
Operation Research
网络最大流的基本概念（6）
增广链的基本概念
第八讲
Operation Research
第八讲
Operation Research
第八讲
Operation Research
实例：寻找图中增广链
第八讲
Operation Research
第八讲
网络最大流的基本概念（7）
运筹学课程
Operation Research
最短路问题
定义
第八讲
求最短路有两种算法，一是求从某一点至其他各点之间最短距离的Dijkstra(狄 克斯屈拉)算法；另一种是求网络图上任意两点之间最短距离的矩阵算法.

根 据 Dijkstra 算 法 ， 可 以 得 出 从 v1 到 v2 最 短路权是2，但是这显然不对，因为从v1到 v2的最短路是(v1, v3, v2)，权是-1。
2
v1
v2
2
-3
vh 3
38
有向图某些权值为负
逐次逼近算法
1、先对图中各个点按照Dijkstra算法标号，称之为第 一次标号，令m=1，转入第二步；
2.5
3
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
h
27
v5
3
5
3
3 0 v1
v2
3
2
v6
2.5
3
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
h
28
v5
3
5
3
3 0 v1
v2
3
v6
2.5
2
53
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
h
29
v5
3
5
3
3 0 v1
v2
3
v6
2.5
2
53
1
2
v3
4 3
4
v7 2
h
60
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 2 2 0 5 5 1 4 0 6 v5 2 3 0 v6 2 2 0
h
61
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 2 2 05 5 1 4 0 6 3 23 0 v6 2 2 0

v1
V1 0 V2 2 V3 5 D = V4 − V5 − V6 − V7 −
பைடு நூலகம்
v2
2 0 2 4 6 − −
v3
5 2 0 1 − 3 −
v4
− 4 1 0 4 1 4
v5
− 6 − 4 0 − 1
v6
− − 3 1 − 0 2
v7
− − − 4 1 2 0
二、最短路算法： 最短路算法：
1． D氏标号法（Dijkstra） 氏标号法（Dijkstra） （1）求解思路 求解思路——从始点出发，逐步顺序 从始点出发， 从始点出发 逐步顺序 地向外探寻，每向外延伸一步都要求是最 地向外探寻，每向外延伸一步都要求是最 短的。 短的。 （2）使用条件 使用条件——网络中所有的弧权均 网络中所有的弧权 网络中所有的弧权均 非负， 非负，即 wij ≥ 0 。
（4） 计算步骤及例：
第三步：若网络图中已无T标号点 标号点， 第三步：若网络图中已无 标号点，停止 计算。否则 令 计算。否则,令 二步。 二步。 此时，要注意将第二步中的 此时，
T ( v j0 ) =
min {T ( v )}
v j ∈s j
,
然后将 标号改成P 然后将 v j0 的T 标号改成 标号 ，转入第
步骤 考察点 T标号点集 标号点集 v1 0
标 v2
标号） 号（ 表P标号） 标号 v3 v4 v5 v6 v7
1 2 3 4 5 6
v1 v2 v3 v4 v6 v5
{v2，…，v7} ， {v3，…，v7} ， {v4，…，v7} ， {v5，v6，v7} {v5，v7} {v7}
2
5 2+2 4

3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 6,2 2
∞,1
v9
6
3
3 4
10 4
v6 2 v7 ∞,1
11,4
∞,1
v8
18
v2 5,3 1
6 2
v1
3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 6,2 2
∞,1
v9
6
3
3 4
10 4
v6 2 v7 9,5
10,5
12,5
v8
19
v2 5,3 1
9
v2 6,1 1
6 2
v1
3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 ∞,1 2
6
3
4 10
4
v6
2
v7
∞,1
∞,1
∞,1
v9
3
∞,1
v8
10
v2 6,1 1
6 2
v1
3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 ∞,1 2
6
3
4 10
4
v6
2
v7
∞,1
∞,1
∞,1
v9
3
∞,1
v8
11
v2 6,1 1
6 2
v1
3
3,1
v3
0,0
6
1
2

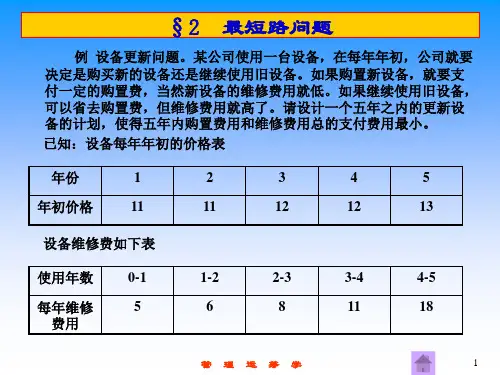
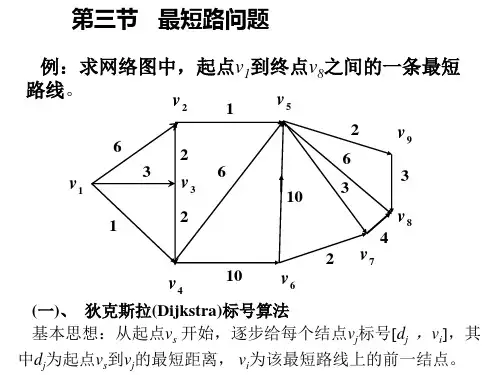
图论——单源最短路一、最短路两点之间的最短路：给定一个带权图，图中两点i与j的最短路是指从i到j的一条路径，这条路径经过的边的权值之和最小。

求单源最短路：给定一个带权图，求图以结点start为起点的单源最短路是指对每一个结点j<>start，求出start到j的最短路。

二、图的存储方式对于求最短路类问题的算法，图的不同存储方式会产生很大的影响，总的来说，图的存储方式有邻接矩阵，邻接表，前向星等几种。

邻接矩阵：这种存储方法需要开设一个V^2的二维数组edge，对于每两个顶点i和j，如果ij有边，则edge[i,j]=w[i,j]，否则edge[i,j]=-1，这里w[i,j]为边Eij的权。

邻接表：邻接表有链表与数组两种实现方式，如果用数组实现，同邻接矩阵一样需要一个V^2的二维数组edge，edge的每个元素包含两个信息：终点和权值。

另有一个数组a记录从指定顶点出发的边数。

对于每个顶点i，edge[i, j](j=1~a[i])表示从i出发的第j条边的终点与权值。

若用链表实现邻接表，我们可以将edge减成一维，在每个edge[i]后面连一条链表，链表上的每个结点都表示由i出发的一条边。

前向星：前向星的存法只需两个一维数组pos与edge，其中edge[i]存储了第i条边的信息，这些边是按照起点由小到大排好序的，而pos[i]则表示以i为起点的第一条边的位置。

这样在edge[pos[i]~pos[i+1]-1]中便可找到从i出发的所有边的信息。

以下的例子显示了这四种存储图的方法：2 4邻接矩阵：邻接表(数组)：邻接表(链表)：edge各种存储方法的比较：#对于稀疏图而言，复杂度约为常数。

*需要一个O(ElogE)的预处理(排序)。

总的来说，邻接矩阵比较好编写，存储方式简单明了，适合中小规模数据；用数组实现的邻接表与邻接矩阵相差不多；用链表实现的邻接表编程复杂度较高，但效率很好，适合各种各样的图论类题目；前向星只对数组进行操作，编写不是很难，同时效率也不错，在不需要修改边的最短路问题中，前向星是遇到大数据时的最佳选择。

v6
9
7
4
1 1 1
1 2 2
1 2 3
1 2 3
1 2 3
1 2
3
10 8
8 6
9
7
5 3 4
0 4 3
4 0 1
3
1
0
1 11
2 2 2
3 3 3
4 4 4
4 5 5
4
5 6
由于D(2) =D(3)，故D(3)中的元素就是vi到vj的 最短距离,D(3)称为最短距离矩阵。
1 1 2 2 3
到其他不直接邻接的节点的最短 距离不会发ห้องสมุดไป่ตู้变化。
②在v1到所有其他节点的最短距离中选择最小的距 离，找到节点 vk，使下式满足：
求 min{T (v j )}
vk
满足
T (vk
)
min{T
v jS
(v
j
)}
令：P(vk ) T (vk )
比较v1到所有其它节点的最短距离，找到 节点vk,并将最小的距离记录在P(vk)中。
的最短路。
（1）使用条件—没有负回路
（2）步骤：
①
令
d 1 j
w1 j，j
2,3,, N，其中
w1 j为起点v1
到 v j 的弧（v1, v j ）的权；
②用下列递推公式进行迭代：
d d k min
j
i
k 1
j
wij
j 2,3,, N
其中，
d k j
表示从起点 v1 到点 v j 走k步
的最短距离；
一、问题的提法及应用背景
（1）问题的提法——寻求网络中两点间 的最短路就是寻求连接这两个点的边的 总权数为最小的通路。（注意：在有向 图中，通路——开的初等链中所有的弧 应是首尾相连的。）

5
5
0
5
V2
3
6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
6
(4)找出所有与v1,v2,v3相邻的未标记的点v4,v5,v6，求出
从v1直接到这些点的距离(v1->v4:7)以及经过v2到这些点 的距离(v1->v2->v4:11;v1->v2->v5:10;v1->v2->v6:8)以及 经过v3到这些点的距离(v1->v3->v4:6;v1->v3->v5:12)找出 这些距离中最短的路径为v1->v3->v4，最短距离为L14=6， 将v4标记为6
3 2 4 1
时间
2 3 3 2
25
0
5
V2
3
6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
(2)找出同v1相邻的未标号的点有v2,v3,v4，求出从
v1到其所有相邻点的距离(v1->v2:5;v1->v3:4;v1>v4:7)，距离最短路径为v1->v3，最短距离为L13=4， 将v3标记为4
0
5
V2
3
6 5 5 V6
5
0
5
V2
3
6 6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
7
(5)找出所有与v1,v2,v3,v4相邻的未标记的点v5,v6，求出

最短路问题的求解方法最短路问题是图论中的一个经典问题，它在现实生活中有着广泛的应用。

在很多实际情况下，我们需要找到两个节点之间的最短路径，以便在最短时间内到达目的地或者以最小的成本进行运输。

因此，求解最短路问题具有重要的意义。

在图论中，最短路问题可以分为单源最短路和多源最短路两种情况。

单源最短路指的是从图中的一个固定节点出发，到达其他所有节点的最短路径；而多源最短路则是求解图中任意两个节点之间的最短路径。

针对这两种情况，我们可以采用不同的算法来求解最短路问题。

其中，最著名的算法包括Dijkstra算法和Floyd-Warshall算法。

Dijkstra算法适用于单源最短路问题，它采用贪心策略，逐步确定从源节点到其他节点的最短路径。

而Floyd-Warshall算法则适用于多源最短路问题，它通过动态规划的方式，计算图中任意两个节点之间的最短路径。

除了这两种经典算法外，还有一些其他方法可以用来求解最短路问题，比如Bellman-Ford算法和SPFA算法。

这些算法各有特点，适用于不同的场景，可以根据具体情况选择合适的算法来解决最短路问题。

在实际应用中，最短路问题常常涉及到大规模的图和复杂的网络结构，因此算法的效率和性能也是非常重要的考量因素。

为了提高算法的求解速度，可以采用一些优化手段，比如使用堆优化的Dijkstra算法、矩阵快速幂优化的Floyd-Warshall算法等。

总之，最短路问题是图论中的一个重要问题，它在实际生活中有着广泛的应用。

通过合理选择算法和优化方法，我们可以高效地求解最短路问题，为实际应用提供有力的支持。

希望本文能够为读者对最短路问题的求解方法有所启发，也希望在未来的实际应用中能够发挥一定的作用。

运筹学最短路问题----------关于旅游路线最短及程序摘要：随着社会的发展，人民的生活水平的提高，旅游逐渐成为一种时尚，越来越多的人喜欢旅游。

而如何才能最经济的旅游也成为人民考虑的一项重要环节，是选择旅游时间最短，旅游花费最少还是旅游路线最短等问题随之出现，如何决策成为一道难题。

然而，如果运用运筹学方法来解决这一系列的问题，那么这些问题就能迎刃而解。

本文以旅游路线最短问题为列，给出问题的解法，确定最短路线，实现优化问题。

关键词：最短路 0-1规划约束条件提出问题:从重庆乘飞机到北京、杭州、桂林、哈尔滨、昆明五个城市做旅游，每个城市去且仅去一次，再回到重庆，问如何安排旅游线路，使总旅程最短。

各城市之间的航线距离如下表：重庆北京杭州桂林哈尔滨昆明重庆0 1640 1500 662 2650 649北京1640 0 1200 1887 1010 2266杭州1500 1200 0 1230 2091 2089桂林662 1887 1230 0 2822 859哈尔滨2650 1010 2091 2822 0 3494昆明649 2266 2089 859 3494 0问题分析：1．这是一个求路线最短的问题，题目给出了两两城市之间的距离，而在最短路线中,这些城市有的两个城市是直接相连接的（即紧接着先后到达的关系），有些城市之间就可能没有这种关系，所以给出的两两城市距离中有些在最后的最短路线距离计算中使用到了，有些则没有用。

这是一个0-1规划的问题，也是一个线性规划的问题。

2．由于每个城市去且仅去一次，最终肯定是形成一个圈的结构，这就导致了这六个城市其中有的两个城市是直接相连的，另外也有两个城市是不连接的。

这就可以考虑设0-1变量，如果两个城市紧接着去旅游的则为1，否则为0。

就如同下图3. 因为每个城市只去一次，所以其中任何一个城市的必有且仅有一条进入路线和一条出去的路线。

解法：为了方便解题，给上面六个城市进行编号，如下表（因为重庆是起点，将其标为1）重庆北京杭州桂林哈尔滨昆明123456假设：设变量x11。

最短路径问题的求解最短路径问题是信息学竞赛中常见的一类中等难题，这是一个非常能联系实际的问题，甚至有时一些看似跟最短路径问题无关的问题也可以归结为最短路径问题。

本文就简要分析一下此类问题的算法，以使大家一起探讨一下该类问题，也使没参加信息学竞赛的同学对信息学竞赛有个简单了解。

下面我们以具体例题来看看这类问题的解法：例1、假设A、B、C、D、E各个城市之间旅费如下图所示。

某人想从城市A 出发游览各城市一遍，而所用费用最少。

试编程序输出结果。

解这类题时同学们往往不得要领，不少同学采用穷举法把所有可能的情况全部列出，再找出其中最短的那条路径；或是采用递归或深度搜索，找出所有路径，再找出最短的那条。

这两种方法可见都是费时非常多的解法，如果城市数目多的话则很可能要超时了。

实际上我们知道，递归、深度搜索等算法一般用于求所有解问题（例如求A 出发每个城市走一遍一共有哪几种走法），而这几种算法对于求最短路径这类最优解问题显然是不合适的，以下介绍的几种算法就要优越很多。

首先，对于这类图我们都应该先建立一个邻接矩阵来存放任意两点间的距离数据，以便在程序中方便调用，如下：const dis:array[1..5,1..5] of integer =( ( 0, 7, 3,10,15),( 7, 0, 5,13,12),( 3, 5, 0, 5,10),(10,13, 5, 0,11),(15,12,10,11, 0));以下是几种解法：一、宽度优先搜索宽度优先搜索并不是一种很优秀的算法，只里只是简单介绍一下它的算法。

具体方法是：1、从A点开始依次展开得到AB、AC、AD、AE四个新结点（第二层结点），当然每个新结点要记录下其距离；2、再次以AB展开得到ABC、ABD、ABE三个新结点（第三层结点），而由AC结点可展开得到ACB、ACD、ACE三个新结点，自然AD可以展开得到ADB、ADC、ADE，AE可以展开得到AEB、AEC、AED等新结点，对于每个结点也须记录下其距离；3、再把第三层结点全部展开，得到所有的第四层结点：ABCD、ABCE、ABDC、ABDE、ABEC、ABED……AEDB、AEDC，每个结点也需记录下其距离；4、再把第四层结点全部展开，得到所有的第五层结点：ABCDE、ABCED、……、AEDBC、AEDCB，每个结点也需记录下其距离；5、到此，所有可能的结点均已展开，而第五层结点中最小的那个就是题目的解了。