大学物理第九章热力学讲解

大学物理中的热力学热能的转化与热力学定律热力学是物理学中研究热能转化与热力学定律的一个重要分支。

热力学研究了热能与其他形式能量之间的转化关系，从而揭示了物质中热现象的本质规律和特性。

在大学物理学习中，了解热力学的基本原理对于理解能量转化和自然界中的热现象非常重要。

一、能量与热力学能量是物质存在时的基本属性，包括热能、机械能、化学能等形式。

热能指的是物质内部由分子振动和相对运动带来的能量。

热力学研究如何将热能转化为其他形式的能量，以及如何实现能量守恒。

二、热力学系统与热力学定律热力学中的系统指的是由一定数量物质和能量组成的系统，可以是封闭的、开放的或孤立的。

热力学定律是通过观察和研究系统中能量的转化和物质的变化得出的。

其中最重要的三条热力学定律分别是热力学第一定律、第二定律和第三定律。

三、热力学第一定律——能量守恒定律热力学第一定律表明能量在一个系统中是守恒的，能量可以转化为其他形式，但总量不变。

这意味着系统所吸收的热量与所做的功等于内能的变化。

即，ΔU = Q - W其中，ΔU表示内能的变化，Q表示系统吸收的热量，W表示系统对外界做的功。

四、热力学第二定律——熵增定律热力学第二定律是关于能量转化方向的定律。

它指出，孤立系统的熵增总是大于等于零，且在实际过程中熵增不会减小。

熵是描述能量分子混乱程度的物理量，熵增表示能量分子无序性的增加。

五、热力学第三定律——绝对零度定律热力学第三定律说明了在绝对零度下，系统的熵为零。

绝对零度是热力学温标的零点，相对于绝对零度，系统的热能全部被完全冻结，内能最小。

六、热力学中的热能转化在热力学中，热能可以通过热传导、热辐射和热对流等过程转化为其他形式的能量。

热传导是指通过物质内部的分子间碰撞，热能从高温区向低温区传递。

热辐射是指物质表面的热能通过辐射传递。

热对流是指通过液体或气体的传流而进行的热能转移过程。

七、热力学的应用热力学的研究在能源转换、工程设计、气候变化、环境保护等方面都有重要应用。

第九章 热力学基础主要内容一.准静态过程（理想过程，在P-V 图中代表一条线） 系统从一个平衡态到另一个平衡态，中间经历的每一状态都可以近似看成平衡态（平衡态在P-V 图中代表一个点）过程。

二.理想气体状态方程：112212PV PV PV C T T T =→=； m PV RT M'=； P nkT = 8.31J R k mol =；231.3810J k k -=⨯；2316.02210A N mol -=⨯；A R N k =三.热力学第一定律Q E W =∆+；dQ dE dW =+…1.气体做功 21V V W Pdv =⎰ （规定气体对外做功>0 ）2.Q （规定气体从外界吸收热量>0，过程量，只有在某个过程中才有意义）3.2121()V m V m m m dE C dT E E C T T M M ''=-=- 或 （状态量，理想气体内能只取决于温度，内能变化公式适用于任意的过程。

）,2V m i C R =，=，P +22m i C R （i 为自由度，单原子分子自由度为3，双原子分子为5，多原子分子为6）， =+，P ,m V m C C R ，气体比热容比：γ=>,,1P m V m C C四.热力学第一定律在理想气体的等值过程和绝热过程中的应用1. 等体过程-2(V m T 2. 等压过程⎧=⋅-=-⎪⎪⎪=∆+=-=⋅∆⎨⎪⎪∆=-∆⎪⎩21212121()()+2()2()=2p m V m m W P V V R TT M m i Q E W C T T P VM mi E C T T P V M;3.等温过程212211T T E E m V m p Q W RTln RTlnM V M p -=⎧⎪''⎨===⎪⎩1. 绝热过程210()V m Q W E C T T ν=⎧⎪⎨=-∆=--⎪⎩绝热方程1PV C γ=， -12V T C γ= ，13P T C γγ--= 。

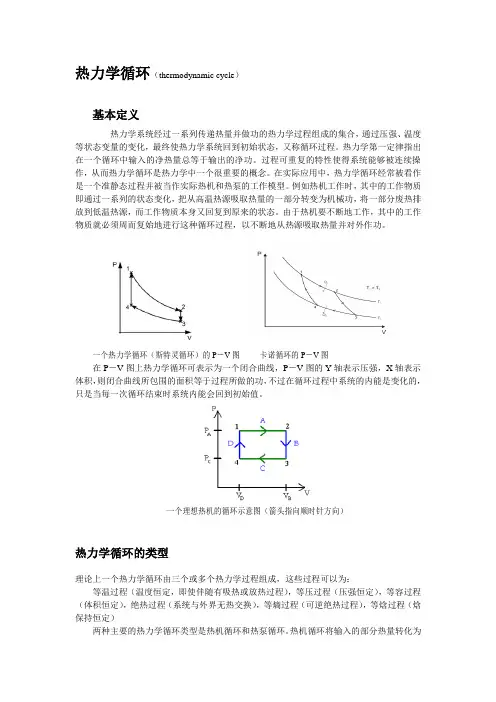
热力学循环（thermodynamic cycle）基本定义热力学系统经过一系列传递热量并做功的热力学过程组成的集合，通过压强、温度等状态变量的变化，最终使热力学系统回到初始状态，又称循环过程。

热力学第一定律指出在一个循环中输入的净热量总等于输出的净功。

过程可重复的特性使得系统能够被连续操作，从而热力学循环是热力学中一个很重要的概念。

在实际应用中，热力学循环经常被看作是一个准静态过程并被当作实际热机和热泵的工作模型。

例如热机工作时，其中的工作物质即通过一系列的状态变化，把从高温热源吸取热量的一部分转变为机械功，将一部分废热排放到低温热源，而工作物质本身又回复到原来的状态。

由于热机要不断地工作，其中的工作物质就必须周而复始地进行这种循环过程，以不断地从热源吸取热量并对外作功。

一个热力学循环（斯特灵循环）的P－V图卡诺循环的P－V图在P－V图上热力学循环可表示为一个闭合曲线，P－V图的Y轴表示压强，X轴表示体积，则闭合曲线所包围的面积等于过程所做的功，不过在循环过程中系统的内能是变化的，只是当每一次循环结束时系统内能会回到初始值。

一个理想热机的循环示意图（箭头指向顺时针方向）热力学循环的类型理论上一个热力学循环由三个或多个热力学过程组成，这些过程可以为：等温过程（温度恒定，即使伴随有吸热或放热过程），等压过程（压强恒定），等容过程（体积恒定），绝热过程（系统与外界无热交换），等熵过程（可逆绝热过程），等焓过程（焓保持恒定）两种主要的热力学循环类型是热机循环和热泵循环。

热机循环将输入的部分热量转化为输出的机械功，而热泵循环通过输入的机械功将热量从低温传向高温。

如果组成循环的全部过程都是可逆的，则称此种循环为可逆循环；如果过程中的任一部分或全部是不可逆的，则称此种循环为不可逆循环。

热机循环将输入的部分热量转化为输出的机械功，而热泵循环通过输入的机械功将热量从低温传向高温。

完全由准静态过程组成的循环能够通过控制来作为热机或热泵循环使用。

第9章 热力学基础本章是热现象的宏观描述—热力学,其主要内容有:平衡态、准静态过程、热量、体积功、内能、热容等概念.热力学第一定律及其对理想气体等值过程、绝热过程和多方过程的应用;循环过程、卡诺循环、热力学第二定律、熵和熵增加原理等.§9.1 热力学系统 理想气体状态方程一、热力学系统人们通常把确定为研究对象的物体或物体系统称为热力学系统(简称为系统),这里所说的物体可以是气体、液体或固体这些宏观物体,在热力系统外部,与系统的状态变化直接有关的一切叫做系统的外界.热力学研究的客体是由大量分子、原子组成的物体或物体系.若系统与外界没有能量和质量的交换,这样的系统称为孤立系统,与外界没有质量交换,但有能量交换的系统,称为封闭系统,既有质量又有能量交换的系统称为开放系统.二、气体的状态参量在力学中研究质点机械运动时,我们用位矢和速度(动量)来描述质点的运动状态.而在讨论由大量作无规则运动的分子构成的气体状态时,位矢和速度(动量)只能用来描述分子运动的微观状态,不能描述整个气体的宏观状态.对一定量的气体,其宏观状态常用气体的体积V 、压强P 和热力学温度T(简称温度)来描述。

P 、V 、T 这三个物理量叫做气体的状态参量,是描述整个气体特征的量,它们均为宏观量,而象分子的质量、速度、能量等则是微观量.三个量中,气体的体积V 是几何参量,是指气体分子所能到达的空间,对于装在容器中的气体,容器的容积就是气体的体积.在国际单位制中,体积的单位是立方米,符号是m 3.气体的压强是力学参量,是作用于容器器壁上单位面积上的正压力.在国际单位制中,压强的单位是帕斯卡，符号为2a a m N 1P 1P ⋅=，，有时也用标准大气压(atm),厘米汞柱高(cmHg)它们之间的关系为a 5P 100131cmHg 76atm 1⨯==.温度T 是物体冷热程度的量度,是热学量.定义温度的科学依据是热力学第零定律要进行温度的测量,必须建立温标,温标是温度的数值表示法.各种各样的温度计都是由各种温标确定的.常用的温标有摄氏温标;而热力学温标是最基本的温标,符号为T ,单位是开尔文(K).1960年国际计量大会规定摄氏温度与热力学温度之间的关系为15273.-=T t三、平衡态气体平衡状态的概念是个非常重要的概念.把一定质量的气体装在一给定体积的容器中,经过足够长的时间后,容器内各部分气体的压强相等.温度相同,此时气体的状态参量具有确定的值.如果容器中的气体与外界没有能量和物质的交换,气体内部也没有任何形式的能量与物质转化(例如没有发生化学变化或原子核的变化等),则气体的状态参量将不随时间而变化,这样的状态叫做平衡状态.应该指出,容器中的气体总不可避免的会与外界发生程度不同的能量和物质交换.所以平衡态只是一个理想的模型.实际中,如果气体状态的变化很微小,可以略去不计时就可以把气体的状态看成是近似平衡态.还应指出,气体的平衡状态只是一种动态平衡,因为,分子的无规则运动是永不停息的.通过气体分子的运动和相互碰撞,在宏观上表现为气体各部分的密度、温度、压力均匀且不随时间变化的平衡态.对于处在平衡态、质量为M 的气体,它的状态可用一组P 、V 、T 值来表示.例如,一组参量值111T V P 、、表示一个状态,另一组参量222T V P 、、表示另一状态,在以P 为纵轴,V 为横轴的P —V 图上,气体的一个平衡状态可以用一个确定的点来表示.如图9.1中的点A（111T V P 、、）或点B （222T V P 、、） . 四、理想气体物态方程实验证明,当一定量的气体处于平衡态时,描述平衡状态的三个参量P 、V 、T 之间存在一定的关系,当其中任意一个参量发生变化时,其他两个参量也将随之改变,即其中一个量是其他两个量的函数,如0==)()(T V P f V P T T 、、或、上述方程就是一定量的气体处于平衡态时气体的物态方程.在中学物理中我们已经知道,一般气体, 在密度不太高,压力不太大(与大气压强相比)和温度不太低(与室温比较)的实验范围内,遵守玻意耳定律,盖·吕萨克定律和查理定律,我们把任何情况下都遵守上述三条实验定律和阿伏伽德罗定律的气体称为理想气体.一般气体在温度不太低,压强不太大时,都可以近似当作理想气体.描述理态气体状态的三个参量P 、V 、T 之间的关系即为理想气体物态方程.可由三个实验定律和阿伏)(111T V P A 、、)(222T V P B 、、P VO 图9.1伽德罗定律导出.对一定质量的理想气体,物态方程的形式为）（摩尔数μ=νμ=M RT M PV (9.1) 式中的M 为气体质量, μ为一摩尔气体的质量,简称摩尔质量,如氧气的摩尔质量13m ol kg 1032--⋅⨯=μ。

热力学循环大学物理实验中热机效率的测量热机效率是一个热力学循环中的重要参数，它衡量了热机的能源利用效率。

在大学物理实验中，测量热机效率是一个常见的实验内容。

本文将介绍热力学循环的基本原理以及如何利用实验方法准确测量热机效率。

一、热力学循环的基本原理热力学循环是指系统经过一系列状态变化后回到原始状态的过程。

在大学物理实验中，常见的热力学循环包括卡诺循环、斯特林循环和内燃机循环等。

其中，卡诺循环是一个理想化的热力学循环，通过卡诺循环的特性可以推导出热机效率的理论最大值。

卡诺循环是由两个等温过程和两个绝热过程组成的。

等温过程是指系统与热源保持恒温接触，通过吸热和放热使得系统温度保持不变。

绝热过程是指系统与外界热源没有热量交换，系统内部没有能量的转移，只有吸热或放热。

通过这样的循环，卡诺循环既能完成代表工作的过程，又能回到初始状态。

根据卡诺循环的原理，热机效率可以通过温度比来计算。

温度比是指热机工作温度与冷源温度的比值。

根据卡诺循环的分析，热机的效率等于1减去温度比。

二、热机效率的测量实验中，我们使用实际的热力学循环来测量热机的效率。

以卡诺循环为例，我们可以通过测量热源和冷源的温度来计算热机效率。

首先，我们需要确定热源和冷源的温度。

热源可以是一个恒温水槽，通过控制加热器的功率来维持一定的温度。

冷源可以是大气温度，利用室温环境即可。

其次，我们需要使用压力传感器来测量工作物质在卡诺循环的不同状态下的压力。

通过压力-体积图可以计算出等温过程和绝热过程的工作面积，并且可以得到卡诺循环的效率。

最后，我们可以利用温差计来测量热源和冷源的实际温度差。

通过将实际温度差与卡诺循环理论温度差进行比较，可以计算出热机的效率。

三、实验中需注意的问题在进行热机效率的测量实验时，还需要注意以下几个问题：1. 实验装置的绝热性：为了准确测量绝热过程的工作面积，需要确保实验装置在工作过程中与外界不发生热量交换。

2. 实验装置的恢复时间：在进行不同温度状态的转换时，需要给予足够的时间让系统达到稳定状态，以保证实验数据的准确性。

大学物理C（2）知识点第九章热力学基础1. 平衡态、态参量、热力学第零定律2.理想气体状态方程3.准静态过程、热量和内能4.热力学第一定律、典型的热力学过程（等容、等压、等温、绝热）教材：P42 9-2，P43 9-3、9-4，P43 9-14；指导：P175 1、2。

5.循环过程、卡诺循环、热机效率教材：P44 9-16，P45 9-17、9-18、9-19；指导：P175 3，P176 4、7。

6．热力学第二定律选择题：P173 1、2、3，P174 4、6、8、10；填空题：P174 1、2、P174 4、5、6。

第十章气体动理论1. 麦克斯韦速率分布律、三种统计速率教材：P92 10-14；指导：P194 2，P194 7。

2.统计规律、理想气体的压强和温度3.理想气体的内能、能量按自由度均分定理教材：P9210-17；指导：P195 3、4。

4.气体分子的平均碰撞频率和平均自由程教材：P9210-18。

5. 熵和熵增加原理选择题：P192 1、3、5，P193 6、7、9，填空题：P193 2，P1936、7、9。

第十一章振动学基础1.简谐运动的基本特征和表述、振动的相位、旋转矢量法教材：P128 11-3、11-4、11-5；指导：P211 3、6。

2.简谐运动的动力学方程教材：P129 11-12；指导：P211 7，P215 1。

3.简谐运动的能量教材：P129 11-14；指导：P215 2。

4.一维简谐运动的合成、拍现象教材：P130 11-16、11-18；指导：P215 3。

选择题：P208 1、3，P209 6、10，P211 1，P212 4，P213 6；填空题：P210 3、4，P213 1、P215 8、9。

第十二章波动学基础1.机械波的基本特征、平面简谐波波函数教材：P178 12-4、12-5、12-6，P179 12-9；指导：P236 3、4、6。

2.波的能量、能流密度3.惠更斯原理、波的衍射4.波的叠加、驻波、相位突变教材：P180 12-13，P181 12-15、12-19；指导：P236 7，P239 2、3。

习 题 九9-1 一系统由图示的状态a 经acb 到达状态b ，系统吸收了320J 热量，系统对外作功126J ． （1）若adb 过程系统对外作功 42J ，问有多少热量传入系统? （2）当系统由b 沿曲线ba 返回状态a ，外界对系统作功84 J ，试问系统是吸热还是放热? 热量是多少? [解] 由热力学第一定律A E Q +∆=得 A Q E -=∆ 在acb 过程中，E E E ∆=-a b J 19412632011=-=-=A Q在adb 过程中，内能变化量与acb 过程相同 因此 J 2364219422=+=+∆=A E Q 在ba 过程中J 2788419433b a 3-=--=+∆-=+-=A E A E E Q由于热量为负值，所以本过程中系统放热．9-2 2mol 氮气由温度为 300K ，压强为510013.1⨯Pa （1atm ）的初态等温地压缩到 510026.2⨯Pa （2atm ）．求气体放出的热量． [解] 在等温过程中气体吸收的热量等于气体对外做的功，所以J 1046.321ln30031.82ln321T ⨯-=⨯⨯⨯===p p RT A Q ν即气体放热为J 1046.33⨯．9-3 一定质量的理想气体的内能E 随体积的变化关系为E - V图上的一条过原点的直线，如图所示．试证此直线表示等压过程．[证明] 设此直线斜率为k ，则此直线方程为kV E = 又E 随温度的关系变化式为 T k T C MM E '=⋅=v m o l所以 T k kV '= 因此 C kk T V ='=（C 为恒量）又由理想气体的状态方程知，C T pV'= （C '为恒量）所以 p 为恒量，即此过程为等压过程．9-4 2mol 氧气由状态1变化到状态2所经历的过程如图所示：（1）沿l →m →2路径．（2）1→2直线．试分别求出两过程中氧气对外作的功、吸收的热量及内能的变化．[解] （1） 在1→m →2这一过程中，做功的大小为该曲线下的面积，氧气对外做负功．()()J 1010.81010013.11050204352121⨯-=⨯⨯⨯-⨯-=--=-V V p A由气体的内能公式T C E V ν=和理想气体的状态方程RT pV ν=得pV i RR i pVRpVC RpVC E 22VV====νν对于氧气5=i ，所以其内能的变化为 ()()J 1027.11010013.15051020252543511221⨯-=⨯⨯⨯⨯-⨯⨯=-=∆-V p V p E此过程吸收的热量为 J 1037.91010.81027.1444111⨯-=⨯-⨯-=+∆=A E Q （2）在从1→2过程中，由图知氧气对外作功为()()()()J 1007.51010013.11050520212143521122⨯-=⨯⨯⨯-⨯+⨯-=-+-=-V V p p A内能的变化 J 1027.1412⨯-=∆=∆E E吸收的热量 J 1034.61007.51027.1444222⨯-=⨯-⨯-=+∆=A E Q9-5 10mol 单原子理想气体在压缩过程中外界对它作功209J ，其温度上升1K ，试求：（1）气体吸收的热量与内能的增量．（2） 此过程中气体的摩尔热容量．[解] （1） 内能的增量为 J 65.124131.82310V =⨯⨯⨯=∆=∆T C E ν气体吸收的热量 J 35.8420965.124-=-=+∆=A E Q （2） 由气体摩尔热容量知 ())K mol J 44.835.841011⋅-=-⨯=∆=TQC ν9-6 将压强为1atm ，体积为33m 101-⨯的氧气（25V R C =）从0℃加热到100℃．试分别求在等体（积）过程和等压过程中各需吸收多少热量．[解] 由理想气体状态方程 RT pV ν= 00RT V p RTpV ==ν在等容过程中吸收的热量为 J 77.9210027310110013.1252535000V V =⨯⨯⨯⨯⨯=∆=∆=-T R RT V p T C Q ν在等压过程中吸收的热量为J 88.12977.92575727V p p =⨯==∆=∆=Q T R T C Q νν9-7 已知氩气的定体（积）比热为)K kg J 314V ⋅=c ，若将氩气看作理想气体，求氩原子的质量．（定体（积）摩尔热容V mol V c M C =）．[解] 由定容摩尔热容量的定义知 R R i C 232V ==因此 VVV m o l 23c Rc C M==氩原子的质量为 kg 1059.63141002.631.823232623V A Amol-⨯=⨯⨯⨯===c N RN Mm9-8 为测定气体的γ（V p C C =）值有时用下列方法：一定量的气体的初始温度、体积和压强为0T 、0V 和0p ，用一根电炉丝对它缓慢加热．两次加热的电流强度和时间相同，第一次保持体积0V 不变，而温度和压强变为1T 和1p ．第二次保持压强0p 不变，而温度和体积变为2T 和1V ．试证明 ()()001001p V V V p p --=γ[证明] 两次加热气体吸收的热量相同，等容过程吸收的热量为()01V 1T T C Q -=ν 等压过程吸收的热量为 ()02p 2T T C Q -=ν 由 21Q Q =可得 ()()02p 01V T T C T T C -=-νν所以 0201Vp T T T T C C --==γ由理想气体状态方程 000RT V p ν= 101RT V p ν= 210RT V p ν= 因此 00101V R p p T T ν-=- 00102p RV V T T ν-=-所以得到 ()()001001p V V V p p --=γ9-9 已知1mol 固体的状态方程为bp aT v v ++=0，内能apT cT E +=，式中0v 、a 、b 、c 均为常量，求该固体的p C 、V C ．[解] 由热力学第一定律可得 V p E A E Q d d d d d +=+= （1） 由已知条件可得 p b T a V d d d += （2） T ap p aT T c E d d d d ++= （3）将（2）、（3）代入（1）得 ()p b T a p T ap p aT T c Q d d d d d d ++++= （4） 在等压过程中，0d =p所以 ()T ap c Q d 2d += 因此 ap c TQ C 2d d p +==在等容过程中 0d =V代入（2）式得 0d d =+p b T a 因此 T ba p d d -=代入（4）式得Tb T a apc T b a b T a p T ap T b a aT T c Qd d d d d d d 2⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-+++⎪⎭⎫ ⎝⎛-+= 所以 bT a ap c TQ C 2V d d -+==9-10 已知范德瓦尔斯气体的内能0V E Va T C E +-=．其中V C 、a 、0E 为常数，试证明其绝热过程方程为()常数=-VC R b V T[证明] 范德瓦尔斯气体的状态方程为 ()RT b V V a p =-⎪⎭⎫⎝⎛+2 （1） 又由已知条件可得 V Va T C E d d d 2V += （2）绝热过程 0d =Q ，由热力学第一定律得 V p A E d d d -=-= （3） 由（2）、（3）式可得 V p V Va T C d d d 2V -=+ （4）由 （1）式可得 2Va bV RT p --=（5）将（5）代入（4）式有 V bV RT V Va V Va T C d d d d 22V --=+整理得 V bV T RTC d 1d V --=积分得()常数=-+b V T RC ln ln V即 ()常数=-RCVT b V这就是范德瓦尔斯气体的绝热过程方程．9-11 如图所示是氮气循环过程，求：（1）一次循环气体对外作的功；（2）循环效率． [解] （1） 一次循环过程气体对外作功的大小为闭合曲线所包围的面积，由图知，其包围的面积为1()()1412V V p p S --= ()()J 100.2101015510335⨯=⨯⨯-⨯-=-该循环对外作功为正，所以 J 100.23⨯=A（2） 该循环过程中，从1→2，2→3为吸收热量过程 1→2为等容过程，吸收热量为()()112212V 125V p V p T T C Q -=-=ν()J 1025.110101511025335⨯=⨯⨯⨯-⨯⨯=-2→3为等压过程，吸收热量为 ()()223323p 227V p V p T T C Q -=-=ν()J 104.1101011051027435⨯=⨯⨯⨯-⨯⨯=-因此吸收的总热量为 J 10525.1421⨯=+=Q Q Q 该循环的效率为 %1.13%10010525.1100.243=⨯⨯⨯==Q A η9-12 一理想气体的循环过程如图所示，其中ca 为绝热过程，点 a 的状态参量为()11,V T ，点b 的状态参量为()22,V T ，理想气体的热容比为γ，求（1）气体在ab 、bc 过程中与外界是否有热交换? 数量是多少?（2）点c 的状态参量；（3）循环的效率．[解] （1） ab 过程是等温过程，系统吸收热量为121T lnV V RT A Q ν==因12V V >，故该过程是吸热过程．bc 过程是等容过程，系统吸收热量为 ()2c V V T T C Q -=ν 因 c T <2T ，故该过程是放热过程． （2） 从图上可看到 2c V V =又 ac 为绝热过程，故根据绝热方程 112111c1c T VV T VV T --⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=γγ又有 γγ11c c V p V p =得到 121211121211c -⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛=γγγννV V V RT V RT V V V V p p（3） ()()[]()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⋅-=--=--=-=--12121V 12111212V 121C 2V TV ln 11ln1ln11V V V V RC V V RT T V V T C V V RT T T C Q Q γγννη9-13 图中闭合曲线为一理想气体的循环过程曲线，其中ab 、cd 为绝热线，bc 为等体（积）线，da 为等压线，试证明其效率为bc ad T T T T ---=γη1式中a T 、b T 、c T 、d T 分别为a 、b 、c 、d 各状态的温度，V p C C =γ．[证明] da 为放热过程，其放出的热量为()a d p 2T T C Q -=νbc 为吸热过程，其吸收的热量为 ()b c V 1T T C Q -=ν 所以其效率为 ()()bc ad b c V a d p 12111T T T T T T C T T C Q Q ---=---=-=γννη9-14 如图所示，AB 、DC 为绝热线，COA 是等温线． 已知系统在COA 过程中放热J 100，OAB 的面积是J 30，ODC 的面积为 J 70，试问在BOD 过程中系统是吸热还是放热?热量是多少?[解] 因COA 是等温线，COA 过程中J 100CA CA -==Q A 又因AB 、DC 为绝热线，AB AB A E -=∆ DC DC A E -=∆ OAB 过程系统作负功，ODC 过程系统作正功，整个循环过程系统作功 3070CA DC BD AB -=+++A A A ABOD 过程中系统吸热A C BD DC AB BD BD 140140E E E E E E A Q -+=∆+∆+∆+=∆+=由于COA 是等温过程，过程中系统内能变化为零，即 0A C =-E E 因此BOD 过程中系统吸热 J 140=Q9-15 一制冷机进行如图所示的循环过程，其中ab 、cd 分别是温度为1T 、2T 的等温线，bc 、da 为等压过程，设工作物质为理想气体．证明这制冷机制冷系数为：12121ln22p p i T T T ++-=ω[证明] ab 为等温过程，吸收热量为12111lnp p RT A Q ν==cd 为等温过程，其放出的热量大小为12222lnp p RT A Q ν==bc 为等压过程，吸收的热量为 ()12p 3T T C Q -=ν da 为等压过程，放出的热量大小为 ()12p 4T T C Q -=ν所以致冷系数 ()()12121314231ln22p p i T T T Q Q Q Q Q Q Q Q Q AQ ++-=+-++=-==吸放吸吸ω9-16 mol 1单原子理想气体，初态压强为1p ，体积为1V ，经等温膨胀使体积增加一倍，然后保持压强不变，使其压缩到原来的体积，最后保持体积不变，使其回到初态． （1）试在V p -图上画出过程曲线；（2）求在整个过程中内能的改变，系统对外作的净功、从外界吸收的净热量以及循环效率．[解] （1） 过程曲线（2） 系统经过循环又回到初态，所以其内能改变量0=∆E a →b 为等温过程，系统对外作正功2ln ln11121V p V V RT A ==νa2p 1p 2V 1V OVb →c 为等压过程，系统对外作负功，其数值大小为()()122111222V V V V p V V p A -=-=过程中总功 ()1112211112119.02ln V p V V V V p V p A A A =--=-=系统从外界吸收的净热量 1119.0V p A Q == a →b 过程吸热为 2ln 1111V p A Q ==c →a 过程中吸收的热量为 ()c a V 2T T C Q -=ν()V p V V V p p V p p 112111121432323=⎪⎪⎭⎫ ⎝⎛-=-=所以 %2.13432ln 19.011111121=+=+=V p V p V p Q Q A η9-17 一可逆卡诺热机低温热源的温度为27℃，热机效率为 40％，它的高温热源的温度是多少? 今欲将热机效率提高到50％，若低温热源保持不变，则高温热源的温度应增加多少度?[解] 可逆卡诺循环的效率为121T T -=η所以 K 5004.01300121=-=-=ηT T若 %50='η，则 K 6005.01300121=-='-='ηT T所以 K 10050060011=-=-'=∆T T T9-18 有一卡诺热机，用29kg 空气为工作物质，高温热源和低温热源的温度分别为C 27o 和C 73-o ，求此热机的效率．若在等温膨胀过程中工作物质的体积增大到2.718倍，则此热机每一循环所作的功是多少?[解] 此热机的效率为 %3.333002001112=-=-=T T η在等温膨胀过程中，吸收的热量为J 1049.2718.2ln 30031.8291029ln631211⨯=⨯⨯⨯⨯==V V RT Q ν又 1Q A =η所以 J 103.81049.231561⨯=⨯⨯==Q A η9-19 在高温热源为127℃、低温热源为27℃之间工作的卡诺热机，一次循环对外作净功为8000J ，今维持低温热源温度不变，提高高温热源的温度，使其一次循环对外做功10000J ，若两次循环该热机都工作在相同的两条绝热线之间，试求： （1）后一卡诺循环的效率．（2）后一卡诺循环的高温热源的温度．[解] （1） 设前一卡诺循环从高温热源吸收热量为1Q ，则有11Q A =η又 414003001112=-=-=T T η所以 J 320004800011=⨯==ηA Q 后一卡诺循环从高温热源吸收热量为J 34000800010000320001211=-+=-+='A A Q Q所以第二个卡诺循环的效率为 %4.29%100340001000012=⨯='='Q A η（2） 第二个卡诺循环的高温热源温度为 K 425294.01300121=-='-='ηT T9-20 一台家用冰箱，放在气温为300K 的房间内，做一盘C 13-o 的冰需从冷冻室取走J 1009.25⨯的热量．设冰箱为理想卡诺制冷机． （1）求做一盘冰所需要的功；（2）若此冰箱能以s J 1009.22⨯的速率取走热量，求所要求的电功率是多少瓦? （3）做一盘冰需时若干?[解] （1） 致冷系数为 2122T T T A Q -==ω因此 ()()J 1022.32602603001009.2452212⨯=-⨯⨯=-=T T T Q A（2） 取走制一盘冰的热量所需要的时间为 s 101009.21009.2325=⨯⨯=t所以电功率为 W 2.32101022.334=⨯==tA P（3） 做一盘冰所需要的时间为 s 103．9-21 绝热容器中间有一无摩擦、绝热的可动活塞，如图所示，活塞两侧各有mol ν的理想气体，5.1=γ，其初态均为0p 、0V 、0T ．现将一通电线圈置入左侧气体中，对气体缓慢加热，左侧气体吸热膨胀推动活塞向右移，使右侧气体压强增加为0375.3p ，求； （1）左侧气体作了多少功?（2）右侧气体的终态温度是多少?（3）左侧气体的终态温度是多少? （4）左侧气体吸收了多少热量?[解] （1） 右侧气体所发生的过程为绝热过程．它对外所做的功的负值就是左侧气体所作的功．所以左侧气体作功为 12200---='-=γV p V p A A又对右侧气体： γγγ202200375.3V p V p V p == 因此 γ102375.3V V =所以 000000122001375.3375.31V p V p V p V p V p A =--=---=γγγ（2） 对右侧气体，由绝热方程知 ()γγγγ----=210010375.3T p T p得到 00325.1375.3T T T ===（3） 左侧气体末态体积为 γ1002001375.32V V V V V V -=-+=得到 00000010011125.525.212375.3375.312375.3T T T V p V V p RV p T =⎪⎭⎫ ⎝⎛-⨯=⎪⎭⎫⎝⎛-==γν（4） 左侧气体吸收热量()()0000V 01V 1125.5V p T T C A T T C A E Q +-=+-=+∆=νν由 000RT V p ν= 知 RV p T ν000=又由 5.1VV Vp =+==C R C C C γ， 得到 R C 2V =所以 00000015.925.42V p V p RV p R Q =+⨯⨯⨯=νν9-22 如图所示，在刚性绝热容器中有一可无摩擦移动而且不漏气的导热隔板，将容器分为A 、B 两部分，各盛有1mol 的He 气和2O 气．初态He 、2O 的温度各为K 300A =T ，K 600B =T ；压强均为atm 1．求：（1）整个系统达到平衡时的温度T 、压强p （氧气可视为刚性理想气体）； （2）He气和2O 气各自熵的变化，系统的熵变．[解] （1） 因中间是导热隔板，过程中两部分气体热量变化和作功的数值都相等，所以内能变化量的数值也相等，且由于初温度不同而末温度相同所以一正一负．因此 ()()T T C T T C '-=-'B VB B A VA A νν解得 K 5.487536005300325232523BA VBVA BVB A VA =+⨯+⨯=++=++='RR RT RT C C T C T C T因平衡时温度、压强都相等，且都是1mol ，所以体积也相等．()A B A A B B B A AA BA B A45021212p RT T p R p RT p RT V V V V =+=⎪⎪⎭⎫ ⎝⎛+=+='='νν 根据理想气体状态方程得到压强为atm 08.114505.478450A =⨯=⋅'=''='p T V T R p ν（2） He 气熵变⎰⎰⎰⎰''+=+==∆T T V V VVR TTC TVp E TQ S AAAd d d d d A VA A He He He ννK J 42.93002600300ln31.83005.487ln31.8232lnln23ABA A=⨯+⨯+⨯⨯=++'=T T T R T T R氧气熵变⎰⎰⎰⎰''+=+==∆T T V V VVR TTC TVp E TQ S BBB222d d d d d B VB B O O O ννK J 70.66002600300ln31.86005.487ln31.8252lnln25-=⨯+⨯+⨯⨯=++'=BBA BT T T R T T R系统的熵变 K J 72.270.642.92O He =-=∆+∆=∆S S S9-23 已知在0℃1mol 的冰溶化为0℃的水需要吸收热量 6000 J ，求： （1）在0℃条件下这些冰化为水时的熵变；（2）0℃时这些水的微观状态数与冰的微观状态数的比． [解] （1） 温度不变时，熵变为 K J 0.222736000d 1d 0====∆⎰⎰Q T TQ S（2） 根据玻尔兹曼熵公式 冰冰Ω=ln k S 水水Ω=ln k S冰水冰水冰水ΩΩ=Ω-Ω=-=∆lnln ln k k k S S S根据（1）结果，得2423106.11038.10.22⨯⨯∆===ΩΩ-ee ekS 冰水9-24 把2mol 的氧从40℃冷却到0℃，若（1）等体（积）冷却；（2）等压冷却．分别求其熵变是多少?[解] 在等容压缩过程中 T C Q d d V ν= 因此 K J 68.5313273ln252d d d 273313VV -=⨯====∆⎰⎰⎰R TT C TTC TQ S νν在等压冷却过程中， T C Q d d p ν=K J 95.7313273ln272d d d 273313pp -=⨯====∆⎰⎰⎰R TT C TTC TQ S νν9-25 取1mol 理想气体，按如图所示的两种过程由状态A 到达状态C ． （1）由A 经等温过程到达状态 C ；（2）由A 经等体（积）过程到达状态B ，再经等压过程到达状态C ． 按上述两种过程计算该系统的熵变A C S S -．已知A C 2V V =，A C 21p p =．[解] （1） 根据理想气体状态方程得 RV p RV p T A A AA A ==ν因此等温过程中熵变为⎰⎰⎰⎰====∆V VRTT T Vp T QTQS C Ad 1d d d AAAν2ln lnd AC AA CAR V V R VV T RT V V ===⎰（2） A →C 与A →B →C 两过程初末状态相同，熵是状态函数，只与初末位置有关，因此两过程熵变相同等于2ln R ．或：根据理想气体状态方程得 A A BB B 211V p RRV p T ⋅==νA →B →C 过程熵变等于A →B 等容过程和B →C 等压过程中熵变的和⎰⎰⎰⎰+=+=+=∆CBB ACBB ATTC TTC TQ TQ S S S d d d d p V 21νν2ln 2ln 2ln p V R C C =+-=。

大学物理热力学知识点汇总热力学是大学物理中的一个重要部分，它研究的是热现象的规律以及与热相关的能量转化和传递。

以下将对大学物理热力学中的关键知识点进行汇总。

一、热力学系统和热力学平衡态热力学系统是指研究的对象，它可以是一个气体、液体或固体，也可以是由多个物体组成的系统。

而热力学平衡态则是指系统的宏观性质在长时间内不随时间变化的状态。

这包括热平衡（系统各部分温度相等）、力学平衡（系统各部分压力相等）、化学平衡（系统内各化学组分的浓度不再变化）。

二、热力学第零定律如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡，那么这两个热力学系统也必定处于热平衡。

这个定律为我们定义了温度的概念，使我们能够通过比较不同系统之间的热平衡来测量温度。

三、热力学第一定律也被称为能量守恒定律，它表明一个热力学系统内能的增量等于外界向它传递的热量与外界对它所做的功之和。

用公式表示为：ΔU ＝ Q ＋ W。

其中，ΔU 是系统内能的变化，Q 是系统吸收的热量，W 是系统对外界所做的功。

在这个定律中，需要注意功的正负。

当系统对外做功时，W 为负；外界对系统做功时，W 为正。

同样，当系统吸收热量时，Q 为正；系统放出热量时，Q 为负。

四、等容过程等容过程是指系统的体积保持不变。

在等容过程中，系统不做功（W ＝ 0），内能的变化等于吸收或放出的热量，即ΔU ＝ Q。

五、等压过程等压过程中系统的压力保持不变。

此时，系统所做的功为 W ＝pΔV，内能的变化和吸收的热量的关系为ΔU ＝Q pΔV 。

六、等温过程等温过程中系统的温度保持不变。

在理想气体的等温过程中，内能不变（ΔU ＝0），系统吸收的热量等于对外界所做的功，即Q ＝W 。

七、绝热过程绝热过程是指系统与外界没有热量交换（Q ＝0）。

在绝热过程中，系统做功导致内能变化，即 W ＝ΔU 。

八、热力学第二定律它有多种表述方式，常见的有克劳修斯表述（热量不能自发地从低温物体传到高温物体）和开尔文表述（不可能从单一热源吸取热量，使之完全变为有用功而不产生其他影响）。

大学物理热力学的基本概念与热平衡定律解释热力学是研究物质的热现象与能量转化规律的学科，在自然科学中具有重要的地位。

热力学的研究对象包括热力学系统、热力学性质以及热力学定律等内容。

本文将介绍热力学的基本概念，并重点解释其中的热平衡定律。

一、热力学的基本概念1. 热力学系统：热力学系统是指研究对象，它可以是一个物体、一组物体或者一个空间范围内的物质。

热力学系统可以分为封闭系统、开放系统和孤立系统等不同类型。

2. 热力学性质：热力学性质是指描述热力学系统状态的物理量，如温度、压强、体积、内能等。

这些性质的变化可以通过热力学过程来描述，例如等温过程、绝热过程等。

3. 热力学定律：热力学定律是指总结和归纳得出的描述热力学现象和规律的定律，如热力学第一定律、热力学第二定律等。

二、热平衡定律的解释热平衡定律是热力学第零定律，它是热力学研究的基础。

热平衡定律的核心概念是热平衡，即两个物体之间不存在热量的净交换。

如果两个物体之间达到了热平衡，它们的温度是相等的。

反之，如果两个物体温度不相等，它们之间会发生热量的传递，直到达到热平衡为止。

热平衡定律可以用以下实例来解释。

假设有两个热力学系统A和B，它们之间没有物质交换，只能通过热交换来达到热平衡。

当A和B接触时，它们会发生热量的交换，直到两个系统的温度相等，称为热平衡状态。

在热平衡状态下，系统A和B的内能之和保持不变，即热平衡状态是一种稳定的状态。

根据热平衡定律，我们可以得出一个重要的推论：如果一个物体与另外两个物体都达到了热平衡，那么这两个物体之间也一定达到了热平衡。

这种传递性质使得热平衡成为一个具有普适性的概念，在热力学的研究中具有重要的应用。

总结起来，热力学的基本概念包括热力学系统、热力学性质和热力学定律。

热平衡定律是热力学研究的基石，它描述了热力学系统中热量传递的规律。

根据热平衡定律，我们可以判断系统是否处于热平衡状态，并通过热平衡状态来描述系统的特性。

热平衡定律的解释为我们理解和应用热力学提供了基础。

第9章 热力学基础本章是热现象的宏观描述—热力学,其主要内容有:平衡态、准静态过程、热量、体积功、内能、热容等概念.热力学第一定律及其对理想气体等值过程、绝热过程和多方过程的应用;循环过程、卡诺循环、热力学第二定律、熵和熵增加原理等.§9.1 热力学系统 理想气体状态方程一、热力学系统人们通常把确定为研究对象的物体或物体系统称为热力学系统(简称为系统),这里所说的物体可以是气体、液体或固体这些宏观物体,在热力系统外部,与系统的状态变化直接有关的一切叫做系统的外界.热力学研究的客体是由大量分子、原子组成的物体或物体系.若系统与外界没有能量和质量的交换,这样的系统称为孤立系统,与外界没有质量交换,但有能量交换的系统,称为封闭系统,既有质量又有能量交换的系统称为开放系统.二、气体的状态参量在力学中研究质点机械运动时,我们用位矢和速度(动量)来描述质点的运动状态.而在讨论由大量作无规则运动的分子构成的气体状态时,位矢和速度(动量)只能用来描述分子运动的微观状态,不能描述整个气体的宏观状态.对一定量的气体,其宏观状态常用气体的体积V 、压强P 和热力学温度T(简称温度)来描述。

P 、V 、T 这三个物理量叫做气体的状态参量,是描述整个气体特征的量,它们均为宏观量,而象分子的质量、速度、能量等则是微观量.三个量中,气体的体积V 是几何参量,是指气体分子所能到达的空间,对于装在容器中的气体,容器的容积就是气体的体积.在国际单位制中,体积的单位是立方米,符号是m 3.气体的压强是力学参量,是作用于容器器壁上单位面积上的正压力.在国际单位制中,压强的单位是帕斯卡，符号为2a a m N 1P 1P ⋅=，，有时也用标准大气压(atm),厘米汞柱高(cmHg)它们之间的关系为a 5P 100131cmHg 76atm 1⨯==.温度T 是物体冷热程度的量度,是热学量.定义温度的科学依据是热力学第零定律要进行温度的测量,必须建立温标,温标是温度的数值表示法.各种各样的温度计都是由各种温标确定的.常用的温标有摄氏温标;而热力学温标是最基本的温标,符号为T ,单位是开尔文(K).1960年国际计量大会规定摄氏温度与热力学温度之间的关系为 15273.-=T t三、平衡态气体平衡状态的概念是个非常重要的概念.把一定质量的气体装在一给定体积的容器中,经过足够长的时间后,容器内各部分气体的压强相等.温度相同,此时气体的状态参量具有确定的值.如果容器中的气体与外界没有能量和物质的交换,气体内部也没有任何形式的能量与物质转化(例如没有发生化学变化或原子核的变化等),则气体的状态参量将不随时间而变化,这样的状态叫做平衡状态.应该指出,容器中的气体总不可避免的会与外界发生程度不同的能量和物质交换.所以平衡态只是一个理想的模型.实际中,如果气体状态的变化很微小,可以略去不计时就可以把气体的状态看成是近似平衡态.还应指出,气体的平衡状态只是一种动态平衡,因为,分子的无规则运动是永不停息的.通过气体分子的运动和相互碰撞,在宏观上表现为气体各部分的密度、温度、压力均匀且不随时间变化的平衡态.对于处在平衡态、质量为M 的气体,它的状态可用一组P 、V 、T 值来表示.例如,一组参量值111T V P 、、表示一个状态,另一组参量222T V P 、、表示另一状态,在以P 为纵轴,V 为横轴的P —V 图上,气体的一个平衡状态可以用一个确定的点来表示.如图9.1中的点A（111T V P 、、）或点B （222T V P 、、） . 四、理想气体物态方程 实验证明,当一定量的气体处于平衡态时,描述平衡状态的三个参量P 、V 、T 之间存在一定的关系,当其中任意一个参量发生变化时,其他两个参量也将随之改变,即其中一个量是其他两个量的函数,如0==)()(T V P f V P T T 、、或、上述方程就是一定量的气体处于平衡态时气体的物态方程.在中学物理中我们已经知道,一般气体, 在密度不太高,压力不太大(与大气压强相比)和温度不太低(与室温比较)的实验范围内,遵守玻意耳定律,盖·吕萨克定律和查理定律,我们把任何情况下都遵守上述三条实验定律和阿伏伽德罗定律的气体称为理想气体.一般气体在温度不太低,压强不太大时,都可以近似当作理想气体.描述理态气体状态的三个参量P 、V 、T 之间的关系即为理想气体物态方程.可由三个实验定律和阿伏伽德罗定律导出.对一定质量的理想气体,物态方程的形式为）（摩尔数μ=νμ=M RT M PV (9.1) )(111T V P A 、、)(222T V P B 、、PVO图9.1式中的M 为气体质量, μ为一摩尔气体的质量,简称摩尔质量,如氧气的摩尔质量13m ol kg 1032--⋅⨯=μ。