武汉科技大学_信号与系统习题精解第12章

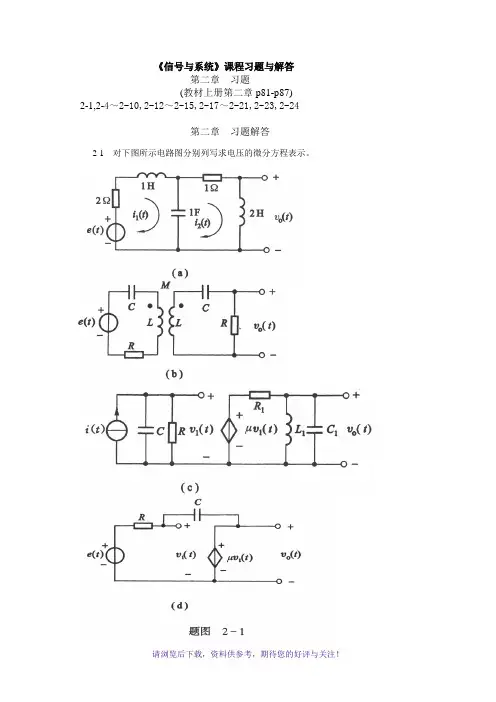
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4～2-10,2-12～2-15,2-17～2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。

图(a)：微分方程：11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图（b ）：微分方程：⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程：dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程：⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件，求系统的零输入响应。

第1章 信号及信号的时域分析1.1本章要点本章在时域范围内讨论信号的分类和信号的基本运算，通过本章的学习，读者应该了解信号的各种分类、定义及相关波形；了解各类常用信号及其性质，掌握几种奇异信号的特性及运算方法；了解和掌握信号的基本运算方法，深刻理解卷积与输入、输出信号和系统之间的物理关系及其性质，为后续课程打下牢固的基础。

1、信号的分类（1）连续信号与离散信号一个信号，如果在连续时间范围内(除有限个间断点外)有定义， 就称该信号在此区间内为连续时间信号，简称连续信号。

仅在离散时间点上有定义的信号称为离散时间信号，简称离散信号。

（2）确定信号与随机信号确定信号是指能够以确定的时间函数表示的信号。

即给定某一时间值，就能得到一个确定的信号值。

随机信号是时间的随机函数，即给定某一时间值，其函数值并不确定的信号。

（3）周期信号与非周期信号对于连续信号)(t f ，若存在0>T ，使得)()(t f rT t f =+，r 为整数，则称)(t f 为周期信号；对于离散信号)(n f ，若存在大于零的整数N ，使得)()(n f rN n f =+，r 为整数，则称)(n f 为周期信号。

不满足周期信号定义的信号称为非周期信号。

① 几个周期信号相加而成的信号的周期问题几个周期信号相加，所产生的信号可能是周期信号，也可能是非周期信号，这主要取决于几个周期信号的周期之间是否存在最小公倍数0T 。

以周期分别为1T 、2T （角频率分别为21,ΩΩ）的两个信号相加产生的信号()t f 为例，如果===ΩΩ211221n n T T 有理数，21,n n 均为整数，则()t f 为周期信号，其周期0T 为 22112211022Ω=Ω===ππn n T n T n T （1-1） ② 离散正（余）弦信号的周期问题时域连续的正（余）弦信号一定是周期信号，但时域离散的正（余）弦信号不一定是周期信号，要求周期N 为正整数。

武汉科技⼤学信号与系统期末试题答卷武汉科技⼤学考试卷（A 卷）课程：信号与系统（闭卷）（2014/05）专业班级姓名学号１．５．信号f （3）求()()dg t h t dt=的傅⾥叶变换。

图⼀解：（1）()[()(1)]f t t t t εε=--（2分）2114分）（3）h(t)（2）2t ()2()[()(2)]h t t t t δεε=---（2分）22112[()](1)2(1)j j e e j j ωωπδωωω--=-+-=--（4分）三、（18分）已知)(t f 的频谱函数为)(ωj F ，其频谱图如图⼆所⽰。

（1）求t j e t f t f 21)2()(-=的频谱函数)(1ωj F 的表达式；（4器H H 所以222()()()222t f t Sa t Sa τττππ==?=（4分）（4）41()()cos ()[(1)(1)]()2A A f t f t t F j F j j F j j G ωωωω=?=++-= （2四、（15分）某LTI 系统保持初始状态不变。

已知当激励为1()()e t t δ=时，其全响应为1()()()t r t t e t δε-=+；当激励为2()()t e t e t ε-=时，其全响应为2()3()t r t e t ε-=。

（1）求系统的单位冲激响应()h t ，说明其因果性；（2）写出描述系统输⼊输出关系的微分⽅程；（3）求当激励为3()()(1)e t t t εε=--时的全响应。

解：（1）设该系统的零输⼊响应为()zi r t ，则由题意，有对两式分别取拉⽒变换，得解之得，1()111H s s ?=-即()()()()(1)()t zi h t t t r t e t δεε-=-??=+?（4分）六、（10分）设计⼀个离散系统，使其输出()y k 是:,1,,1k k k M --+各点输⼊之平均。

（1）确定描述该系统输出()y k 与输⼊()e k 之关系的差分⽅程；（2）求该系统的系统函数)(z H ；（3）当3=M 时，采⽤加法器，标量乘法器和单位延时器画出系统的结构框图，要求尽可能地少⽤单位延时器。

第一章测试1.项目管理的客体是项目的全部任务。

（）A:错B:对答案:B2.确定项目是否可行应在项目规划阶段完成。

（）A:错B:对答案:A3.站务人员售卖车票给顾客的任务属于项目。

（）A:错B:对答案:A4.对项目的可交付成果负主要责任的是项目经理。

（）A:对B:错答案:A5.项目“一次性”的含义是指项目持续的时间很短。

（）A:错B:对答案:A6.随着项目生命期的进展，资源的投入先变小再变大。

（）A:错B:对答案:A7.项目开始时，风险最低，随着任务的不断完成，风险逐渐增多。

（）A:错B:对答案:A8.项目变更所需的花费将随着生命期的推进而增加。

( )A:错B:对答案:B9.任何项目都有明确的起止时间。

( )A:错B:对答案:B10.项目管理的三要素包括时间、成本、范围。

（）A:错答案:A第二章测试1.项目团队成员更关注所属部门的工作，而不是项目的目的，是哪种组织结构，可能会出现的情形。

（）A:职能型B:强矩阵型C:平衡矩阵型D:项目型答案:A2.项目的规模大，同时技术创新性强适合选用哪种组织结构形式。

( )A:强矩阵型B:平衡矩阵型C:项目型D:职能型答案:C3.环境变化不大、技术标准化的小项目，适用于哪种组织结构形式（）A:强矩阵型B:平衡矩阵型C:职能型D:项目型答案:C4.最机动灵活的组织织形式是( )。

A:矩阵型B:职能型C:项目型D:混合型答案:A5.项目经理在哪种组织结构中权力最大。

( )A:强矩阵型B:平衡矩阵型C:职能型组织D:项目型答案:D6.矩阵型组织结构适合于风险较大技术较为复杂的大型项目。

（）A:错B:对答案:B7.项目经理是职能部门领导，才能取得公司总经理对项目的信任。

（）A:错答案:A8.项目组织选择应遵循的原则之一是统一指挥。

（）A:对B:错答案:A9.在项目式组织结构中每个项目成员有两个领导。

（）A:错B:对答案:A10.项目团队成员在项目结束后回到所属的部门，是采用职能型组织结构会出现的情况。

230第10章 无限冲激响应数字滤波器的设计10.1 本章要点1、IIR 数字滤波器设计的基本概念及方法（1）IIR 数字滤波器的性能指标数字滤波器的频率响应)(ωj e H 可表示为：)()()(ωϕωωj j j e e H e H =式中，)(ωj e H 称为幅频特性，表示信号通过滤波器后各频率成分的衰减情况；)(ωϕ称为相频特性，反映各频率成分通过滤波器后在时间上的延时情况。

对IIR 数字滤波器，通常用幅频响应)(ωj e H 来描述性能指标。

需要注意的是数字滤波器的频率响应)(ωj e H 是以π2为周期的，滤波器的低频频带处于π2的整数倍附近，而高频频带处于π的奇数倍附近，这是数字滤波器与模拟滤波器的最大区别。

所以，一般只给出],0[π区间上的性能指标描述。

IIR 低通滤波器的幅频特性如图10-1所示。

图中，p ω和s ω分别称为通带截止频率和阻带截止频率。

通带频率范围为p ωω≤≤0，在通带中要求1)(11≤≤-ωδj e H ；阻带频率范围为πωω≤≤s ，在阻带中要求2)(δω≤j e H ；从p ω到s ω称为过渡带，在过渡带内，幅频响应平滑地从通带下降到阻带。

1δ在具体指标中往往用通带内允许的最大衰减p α表示，2δ用阻带内允许的最小衰减s α表示，p α和s α分别定义为：dB eH e H pj j p )()(lg 200ωα=dB eH e H sj j s )()(lg200ωα=如果将)(0j e H 归一化为1，则p α和s α可分别表示为：dBeH pj p )(lg 20ωα-= dBe H sj s )(lg 20ωα-=231当c p ωω=时，幅度下降到707.022≈，此时dB p 3=α，所以常称c ω为3dB 通带截止频率。

c ω是滤波器设计的重要参数之一。

图10-1 IIR 低通滤波器的幅频特性（2）IIR 数字滤波器的设计方法设计一个数字滤波器，可分为以下3步： ① 根据实际要求确定滤波器的性能指标。

《信号与系统》（第四版）习题解析高等教育2007年8月目录第1章习题解析1第2章习题解析5第3章习题解析14第4章习题解析21第5章习题解析29第6章习题解析39第7章习题解析47第8章习题解析52第1章习题解析1-1题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解(a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t )表示将f ( t )波形展宽。

](a) 2 f (t - 2 )(b) f ( 2t )(c)f (2t ) (d)f (-t +1 )题1-2图解以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图S R S L S C解各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅=tt i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

题1-4图解系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) +f 2( t )，则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有21显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

第6章 系统及系统的时域分析1. 解：由于系统(1)不满足分解性；系统(2)不满足零输入线性；系统(3)不满足零状态线性，故这三个系统都不是线性系统。

对于系统(4)，如果直接观察)(n y ～)(n f 关系，似乎系统既不满足齐次性，也不满足叠加性。

但考虑到令)(n f =0时，系统响应为常数b ，若把它看成是由初始状态引起的零输入响应时，系统仍是满足线性系统条件的，故系统(4)是线性系统。

2. 解：(1) 已知)(t f →)](cos[)(t f a t y f =，设 dd t t t t f t f >-=),()(1，则其零状态响应为)](cos[)](cos[)(11d f t t f a t f a t y -==，显然 )()(1d f f t t y t y -=，故该系统是时不变系统。

(2) 已知)(n f →)()(n bf n y f =，设01),()(n n n n f n f >-=，则其零状态响应为)()()(011n n bf n bf n y f -==，显然 )()(01n n y n y f f -=，故该系统是时不变系统。

3. 解：对于（1）～（4），由于任一时刻的零状态响应均与该时刻以后的输入无关，因此都是因果系统。

而对于（5），系统任一时刻的零状态响应都与该时刻以后的激励有关。

响应在先，激励在后，这在物理系统中是不可能的。

因此，该系统是非因果的。

（6）也是非因果的，因为如果0)(=t f ，0t t < 则有 0)3()(==t f t y f ，3t t <可见在区间003t t t <<上0)(≠t y f ，即零状态出现于激励之前，因而该系统是非因果的。

4. 解：（1）显然，无论激励)(n f 是何种形式的序列，只要它是有界的，那么)(n y f 也是有界的，因果该系统是稳定的。

（2）若)()(t u t f =，显然该激励是有界的，但 t x x u t y tf ==⎰∞-d )()(，0≥t它随时间t 无限增长，故该系统是不稳定的。

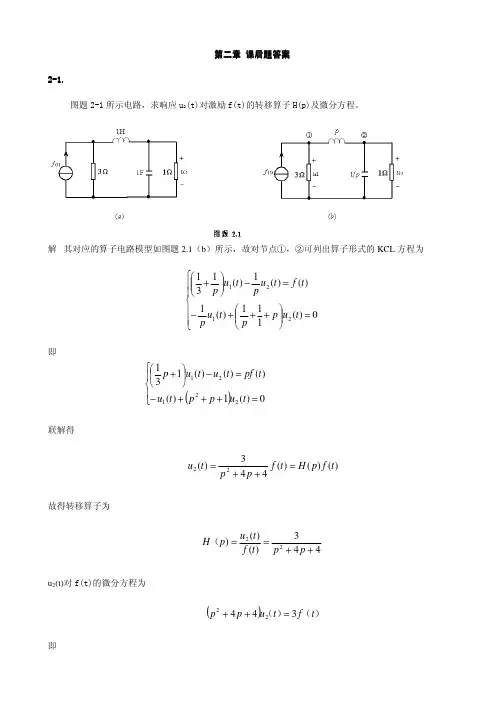
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路，求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。

解 其对应的算子电路模型如图题2.1（b ）所示，故对节点①，②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H （u 2(t)对f(t)的微分方程为()）（）（t f t u p p 34422=++即）（t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路，求响应i(t)对激励f(t)的转移算子H(p)及微分方程。

解 其对应的算子电路模型如图2.2（b）所示。

故得）（）（t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路，已知u C (0-)=1 V, i(0-)=2 A。

求t>0时的零输入响应i(t)和u C (t)。

解 其对应的算子电路模型如图题2.3（b）所示。

故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t)，代入上式化简，即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根（即电路的自然频率）为p 1=-1，p 2=-2。