非惯性系中的质点动力学
- 格式:ppt
- 大小:335.57 KB
- 文档页数:20




4、非惯性系中质点的动能定理惯性参考系中的动能定理只适用于惯性系。
在非惯性参考系中,由于质点的运动微分方程中含有惯性力,因此需要重新推导动能定理。
质点的相对运动动力学基本方程为r d d m t=++Ie IC v F F F 式中e C r2m m m =-=-=-´Ie IC F a F a ωv ,r d d tv 是对时间t 的相对导数r v 上式两端点乘相对位移d ¢r r d d d d d d m t¢¢¢¢×=×+×+×Ie IC v r F r F r F r 注意到,并且科氏惯性力垂直于相对速度,所以IC F r v d 0¢×=IC F r d d r t¢=r v 上式变为:r r d d d m ¢¢×=×+×Ie v v F r F r δW ¢Ie—表示牵连惯性力F Ie 在质点的相对位移上的元功。
δF W ¢—表示力F 在质点的相对位移上的元功。
则有:2r 1d()δδ2F mv W W ¢¢=+Ie 质点在非惯性系中相对动能的增量等于作用于质点上的力与牵连惯性力在相对运动中所作的元功之和。
——质点相对运动动能定理(微分形式)4、非惯性系中质点的动能定理积分上式得22r r01122F mv mv W W ¢¢-=+Ie ——质点相对运动动能定理(积分形式)质点在非惯性系中相对动能的变化等于作用于质点上的力与牵连惯性力在相对路程上所作功的和。
注意:因为在非惯性系中科式惯性力始终垂直于相对速度,因此在相对运动中科式惯性力始终不做功。
例4 已知:一平板与水平面成θ角,板上有一质量为m 的小球,如图所示,若不计摩擦等阻力。
求: (1)平板以多大加速度向右平移时,小球能保持相对静止?(2)若平板又以这个加速度的两倍向右平移时,小球应沿板向上运动。




0 引 言在物理学中,如何选择适当的参照系是非常重要的,在力学中通常选用惯性系,但有时也可选用非惯性系。
功能原理在惯性系中成立,在非惯性系中作适当处理后也成立,有时用它解题很方便。
本文就给出这样的例题。
关于非惯性系参照系中,在《理论力学》中只是研究动力学方程,缺少的是非惯性系中的功能原理。
本文经过推导得出质点系非惯性系的功能原理。
1 功能原理的研究1.1 质点系的动能定理质点系也是实际物体的一种理想模型,它可以当作有限个质点组成的一个系统。
设一个质点系有N 个质点组成,其中第i 个质点的质量为m i ,第j 个质点作用在m i 上的力(内力)为f ij ,这N 个质点以外的其他物体作用在m i 上的合力(外力)为f i ,则由牛顿运动定律()11Ni i i ij ij j dv m f f dt ==+-∑δ (1-1)式中i v 是i m 的速度,而10ij i ji j=⎧=⎨≠⎩, 当, 当δ (1-2)当i m 的位移为i dr 时,以i dr 点乘上式便得()()21211Ni i ij ij i i i j f dr f dr dm v =+-=∑ δ (1-3)将上式对所有的N 个质点求和,便得()21211111N N NN i i ij ij i i i i i j i f dr f dr d m v ====⎛⎫+-= ⎪⎝⎭∑∑∑∑ δ (1-4) 令1Niii dA f dr ==∑ 外, (1-5)()111N Nij ij i i j dA f dr ===-∑∑ 内δ, (1-6)分别代表外力和内力作的功,则(1-4)可写作:2121N i i i dA dA d m v =⎛⎫+= ⎪⎝⎭∑外内。
(1-7)这就是质点系的动能定理。
1.2质点系统的功能原理质点系的内力可以分为保守内力和非保守内力。
例如,质点系内各质点的万有引力是保守内力;质点间的摩擦力是非保守内力。


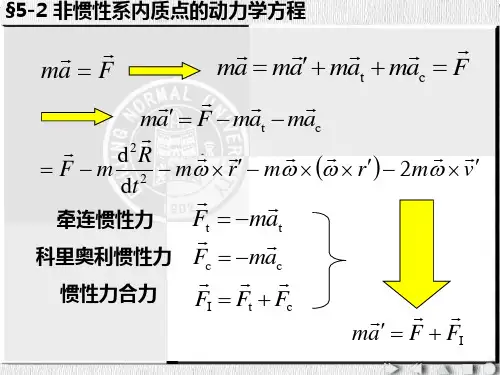
第16章非惯性系中的质点动力学16.1复习笔记一、基本方程1.非惯性系中的质点动力学基本方程(或称为质点相对运动动力学基本方程),其表达式为r Ie ICma F F F =++v v v v 式中,e Ie F ma =-v v ,表示牵连惯性力;C C I F ma =-v v ,表示科氏惯性力。
2.在动参考系内,把非惯性系质点动力学基本方程写成微分形式22Ie IC d d r m F F F t'=++v v v v 3.几种特殊情况(1)当动参考系相对于定参考系作平移时,则C 0a = ,0F =IC ,于是相对运动动力学基本方程为r Iema F F =+v v v (2)当动参考系相对于定参考系作匀速直线平移时,则C 0a = ,e 0a = ,Ie 0F F ==IC,于是相对运动动力学基本方程与相对于惯性参考系的基本方程形式一样,其表达式为r ma F= ①相对于惯性参考系做匀速直线平移的参考系都是惯性参考系。
②发生在惯性参考系本身的任何力学现象,都无助于发现该参考系本身的运动状况,这称为经典力学的相对性原理。
(3)当质点相对于动参考系静止时,则r r 00a υ==v v ,,0F =IC ,所以质点相对静止的平衡方程为F F +=Ie 上式称为质点相对静止的平衡方程,即当质点在非惯性参考系中保持相对静止时,作用在质点上的力与质点的牵连惯性力相互平衡。
(4)当质点相对于动参考系作等速直线运动时,有r 0a =,质点相对平衡方程为0Ie IC F F F ++=v v v 上式称为质点相对平衡方程。
可见在非惯性参考系中,质点相对静止和作等速直线运动时,其平衡条件是不相同的。
二、非惯性系中质点的动能定理1.质点相对运动动能定理的微分形式质点在非惯性系中相对动能的增量,等于作用于质点上的力与牵连惯性力在相对运动中所作的元功之和。
即2r 1d()δδ2F mv W W ''=+Ie 2.质点相对运动动能定理的积分形式质点在非惯性参考系中相对动能的变化,等于作用在质点上的力与牵连惯性力在相对路程上所作的功之和。
非惯性系中的功能原理及应用摘要: 在理论力学中,关于非惯性参照系中动力学问题,从来未涉及到非惯性系中的功能原理。
为此,本文先推证出质点系相对非惯性系的动能定理,再推出质点系相对非惯性系的功能原理及机械能守恒定理,然后再运用此原理解决实际问题。
关键词: 非惯性系;牵连惯性力;科氏惯性力;功能原理;机械能守恒定理The function of the inertial system principle and applicationAbstract: In the theory of mechanics,about the dynamics inertia reference in question never involved in noninertial system function and principle.For this reason this paper first inferred, particle system to a relative non-inertial systems of kinetic energy theorem,and then launch the relative particle noninertial system of function and principle, the last to solve practical problems by using theprinciple.Key words: Noninertial system; Involved the inertial force; Division type inertia force; principle of work and energy; Mechanical energy conservation theorem0 引言处理非惯性参考系中的动力学问题有两种方法,一种是在惯性参考系中考虑问题,然后运用相对运动的关系进行两种坐标参考系之间坐标、速度和加速度诸量的转换,化成非惯性系中的结论。
第三章 非惯性系力学引言:到目前为止,我们对质点的力学现象只是限制在惯性参考系中进行讨论的。
但是在某些实际问题中往往要求我们在非惯性系中研究力学问题。
而牛顿定律a m F =只适用于惯性系,在非惯性系中,它是不能适用的,那么相对于非惯性系中的运动定律要解决的是,质点在怎样的力作用下作怎样的运动,换句话来说,运动定律要解决的问题是,质点的受力情况与运动情况之间的联系。
1、对惯性系来说这种联系已经有了,就是牛顿第二定律a m F =。
提到了质点的受力情况,必须要明确力是物体之间的相互作用,既然力是物体间的互相作用,它与参照系的选择有没有关系?没有关系。
2、对非惯性系质点所受的力仍然为F 。
至于运动情况与参照系的选取却是有关的,对不同的参照系会给出不同的描述。
因此,质点相对惯性系和非惯性系的加速度当然是不同的,为了加以区分,就用a ' 表示质点相对非惯性系的加速度。
此时F 就不等于a m F '= ,F 虽然不等于a m F '= ,那么能不能找出F 与a ' 的关系呢?如果找到了它们之间的关系,也就等于找到了非惯性系中的运动定律,那么我们也就可以在非惯性系中讨论力学问题了。
F 与a '之间的关系总能够找到的。
3、只要能找到a 与a ' 的关系:)(a f a '=,根据运动描述的相对性,这个关系总是可以找到的。
那么根据)(a mf a m F '== 也就可以找到F 与a ' 的关系。
因此根据这条解决问题的途径,在这一章里我们准备要讲的4、内容:是①相对运动;②非惯性系动力学;③然后再做一个大题目——解决地球自转所产生的影响。
下面先讲质点相对运动的描述。
也就是讨论质点相对于两个不同参照系运动之间的关系。
§1. 作平动的参照系一、伽利略变换如右图所示,为叙述方便起见简称OX 坐标系为O 系,假定O 系为惯性系,并认为它是一个固定不动的参照系,就称它为固定坐标系。
包头师范学院本科毕业论文论文题目:非惯性系中动力学问题的讨论院系:物理科学与技术学院专业:物理学姓名:王文隆学号: 0809320007指导教师:鲁毅二〇一二年三月摘要综述了近几十年来国内外学者对非惯性系动力学方面的研究情况 ,以及对非惯性系动力学的实际应用情况。
介绍了在非惯性系中建立动力学方程的方法 ,惯性系中拉格朗日方程在非惯性系中的转换形式 ,以及非惯性系中的能量定理和能量守恒定律的应用等研究成果。
最后 ,概述了一些运用非惯性系动力学的方法来解决非惯性系中的理论和实际工程应用两方面的文献 ,并且对非惯性系的研究和应用进行了展望。
关键词:非惯性系;惯性力;动力学方程;拉格朗日方程;动量定理; 动能定律;守恒定律AbstractAnd under classical mechanics frame, the conservation law, leads into the inertial force concept according to kinetic energy theorem , moment of momenum theorem , mechanical energy in inertia department, equation having infered out now that the sort having translation , having rotating is not that inertia is to be hit by dynamics, priority explains a few representative Mechanics phenomenon in being not an inertia department.Key words:Non- inertia Inertial force Kinetic energy theorem Mechanical energy conserves Apply目录引言 (5)1非惯性系概述 (6)1.1非惯性系 (6)1.2 惯性力 (6)2 动力学方程 (7)2.1 质点动力学方程 (7)2.2 拉格朗日方程 (8)3 能量问题 (9)4 应用研究举例 (9)5 研究展望 (10)参考文献 (11)致谢 (12)非惯性系中动力学问题的讨论引言实际工程中有许多系统处于非惯性系内工作 ,如航空航天、天文和外星空探索等领域的许多转子系统。
质点在非惯性系中的运动飞行员的黑晕和红视现象爬升时:a > 5g俯冲时:a > 2g?北半球由南向北流动的河流对河岸将产生什么作用s as rxzyO 质点相对运动动力学的基本方程Mr′ x ′y ′z ′O′ F惯性参考系- O x y z非惯性参考系- O ´x ´y ´z ´ 绝对运动轨迹 s a -质点M在惯性参考系中的运动轨迹 相对运动轨迹 s r -质点M 在非惯性参考系中的运动轨迹 研究质点在非惯性参考系中 的运动需要先研究质点在惯性 参考系中的运动。
相对位矢 r ´F -作用在质点上的力s as rxzy O Mr′ x ′y ′z ′O′ F对质点M 应用牛顿第二定律Fa =a m 根据加速度合成定理Cr e a a a a a ++=Cr e a a a F m m m ++=C e r a a F a m m m --=ege a F m -=rC gC 2v ωa F ⨯-=-=m m gCge r F F F a ++=mgCge 22d d F F F r ++='tm 非惯性系中质点的运动微分方程质点的质量与质点的相对加速度的乘积等于作用在质点上的外力的合力与牵连惯性力以及科氏力的矢量和。
gCge r F F F a ++=m(1)当动系相对于定系仅作平动时 gCge r F F F a ++=m ger F F a +=m (2)当动系相对于定系作匀速直线平动时Fa =r m (3)当质点相对于动参考系静止时ge =+F F (4)当质点相对于动参考系匀速直线运动时 0gC ge =++F F F 质点相对静止的平衡方程:即质点在非惯性参考系中保持相对 静止时,作用在质点上的力与质点的牵连惯性力相互平衡。
质点相对平衡方程飞机急速爬高时飞行员的黑晕现象爬升时:a > 5g惯性参考系——地球非惯性参考系——飞机动点——血流质点牵连惯性力向下,从心脏流向头部的血流受阻,造成大脑缺血,形成黑晕现象。