第七章重点时程分析步骤弹性恢复力双线型模型弹性恢复力三线型模型
- 格式:ppt
- 大小:198.00 KB
- 文档页数:14

时程分析法定义:由结构基本运动方程沿时间历程进行积分求解结构振动响应的方法。
概述:时程分析法是世纪60年代逐步发展起来的抗震分析方法。
用以进行超高层建筑的抗震分析和工程抗震研究等。
至80年代,已成为多数国家抗震设计规范或规程的分析方法之一。
原理:时程分析法在数学上称步步积分法,抗震设计中也称为“动态设计”。
由结构基本运动方程输入地面加速度记录进行积分求解,以求得整个时间历程的地震反应的方法。
此法输入与结构所在场地相应的地震波作为地震作用,由初始状态开始, 一步一步地逐步积分,直至地震作用终了。
是对工程的基本运动方程,输入对应于工程场地的若干条地震加速度记录或人工加速度时程曲线,通过积分运算求得在地面加速度随时间变化期间结构的内力和变形状态随时间变化的全过程,并以此进行结构构件的界面抗震承载力验算和变形验算。
时程分析法是世纪60年代逐步发展起来的抗震分析方法。
用以进行超高层建筑的抗震分析和工程抗震研究等。
至80年代,已成为多数国家抗震设计规范或规程的分析方法之一。
“时程分析法”是由结构基本运动方程输入地震加速度记录进行积分,求得整个时间历程内结构地震作用效应的一种结构动力计算方法,也为国际通用的动力分析方法。
“时程分析法”常作为计算高层或超高层的一种(补充计算)方法,也就是说满足了规范要求的时候是可以不用它计算结构的。
规范规定:对于特别不规则的建筑、甲类建筑及超过一定高度的高层建筑,宜采用时程分析法进行补充计算。
所以有较多设计人员对应用时程分析法进行抗震设计感到生疏。
近年来,随着高层建筑和复杂结构的发展,时程分析在工程中的应用也越来越广泛了。
地震动输入对结构的地震反应影响非常大。
目前的现状是,输入地震动的选择大多选择为数不多的几条典型记录(如:1940年的El Centro(NS)记录或1952年的Taft记录),国内外进行结构时程分析时所经常采用的几条实际强震记录主要有适用于I类场地的滦河波、适用于II、III类场地的El-Centrol波(1940,N-S)和Taft波(1952,E-w)、适用于IV 类场地的宁河波等。

时程分析法时程分析法又称直接动力法,在数学上又称步步积分法。
顾名思义,是由初始状态开始一步一步积分直到地震作用终了,求出结构在地震作用下从静止到振动以至到达最终状态的全过程。
它与底部剪力法和振型分解反应谱法的最大差别是能计算结构和结构构件在每个时刻的地震反应(内力和变形)。
当用此法进行计算时,系将地震波作为输入。
一般而言地震波的峰值应反映建筑物所在地区的烈度,而其频谱组成反映场地的卓越周期和动力特性。
当地震波的作用较为强烈以至结构某些部位强度达到屈服进入塑性时,时程分析法通过构件刚度的变化可求出弹塑性阶段的结构内力与变形。
这时结构薄弱层间位移可能达到最大值,从而造成结构的破坏,直至倒塌。
作为高层建筑和重要结构抗震设计的一种补充计算,采用时程分析法的主要目的在于检验规范反应谱法的计算结果、弥补反应谱法的不足和进行反应谱法无法做到的结构非弹性地震反应分析。
时程分析法的主要功能有:1)校正由于采用反应谱法振型分解和组合求解结构内力和位移时的误差。
特别是对于周期长达几秒以上的高层建筑,由于设计反应谱在长周期段的人为调整以及计算中对高阶振型的影响估计不足产生的误差。
2)可以计算结构在非弹性阶段的地震反应,对结构进行大震作用下的变形验算,从而确定结构的薄弱层和薄弱部位,以便采取适当的构造措施。
3)可以计算结构和各结构构件在地展作用下每个时刻的地震反应(内力和变形),提供按内力包络值配筋和按地震作用过程每个时刻的内力配筋最大值进行配筋这两种方式。
总的来说,时程分析法具有许多优点,它的计算结果能更真实地反映结构的地震反应,从而能更精确细致地暴露结构的薄弱部位。
时程分析法有关的几个问题:1、恢复力特性曲线;恢复力特性曲线应用于计算必须模型化,常用的有双线型模型与退化三线型模型;退化三线型模型(附图)能较好地反映以弯曲破坏为主的钢筋混凝土构件的的特性,所以适用于此类构件计算。
2、结构计算模型及分析方法;3、地震波的选用;4、时程分析计算结果的处理。

2024年建筑结构抗震分析与减震控制学习心得2024年建筑结构抗震分析与减震控制是我在大学期间的一门重要专业课程。
通过学习和实践,我深刻认识到了抗震设计在保护建筑物和人们生命财产安全方面的重要性。
以下是我对这门课程的学习心得。
首先,这门课程让我更加深入地了解了地震灾害对建筑物的影响以及抗震设计的原理和方法。
我们学习了地震波的基本性质、地震荷载的计算方法,以及材料和结构在地震中的响应机理。
通过学习这些基础知识,我能够更好地理解抗震设计的目标和要求。
同时,我们还学习了各种抗震设计的原理和方法,如增加结构刚度、加固和改造现有结构、采用减震控制技术等。
这些知识对于我未来从事相关工作具有重要意义。
其次,这门课程还培养了我分析和解决问题的能力。
在课堂上,我们不仅学习了理论知识,还进行了大量的实例分析。
通过参与实例分析,我学会了如何快速准确地了解一个建筑物的结构形式和设计参数,并判断其抗震性能。
同时,通过解决实例中的问题,我也积累了一定的实践经验,提升了自己的解决问题的能力。
这对我今后从事实际工作非常有帮助。
另外,这门课程还注重培养学生的实践能力。
我们参观了一些地震风险较高的建筑物,实地调查了其结构形式和材料特性。
通过这样的实践活动,我更加直观地感受到了地震对建筑物的破坏性,并对实际工程中的抗震设计有了更深入的认识。
同时,我们还使用专业软件进行了一些抗震设计的计算和分析。
通过这些实践操作,我掌握了一些常用工具和方法,提高了我的抗震设计能力。
最后,这门课程注重培养了我们的团队合作和沟通能力。
在课堂上,我们经常组成小组进行项目设计和分析。
通过与同学的合作,我学会了尊重他人的意见并协调不同意见之间的矛盾。
同时,在小组讨论中我也学会了更好地表达自己的观点和听取他人的建议。
这些团队合作和沟通的能力对于我今后的职业发展非常重要。
总的来说,2024年建筑结构抗震分析与减震控制是一门非常重要的专业课程。
通过学习和实践,我不仅深化了对抗震设计的理解,还提高了自己的问题分析和解决能力。

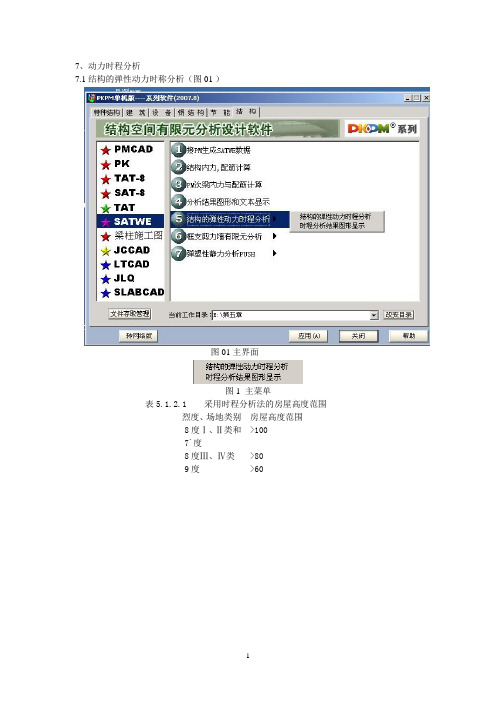
7、动力时程分析7.1结构的弹性动力时称分析(图01 )图01主界面图1 主菜单表5.1.2.1 采用时程分析法的房屋高度范围度、烈度、场地类别房屋高度范围8度Ⅰ、Ⅱ类和>1007`度8度Ⅲ、Ⅳ类>809度>601.1 结构的弹性动力时程分析(图1.1):位置:主菜单\结构的弹性动力时称分析图1 地震波选择操作说明及规范链接:○〈选择地震波〉:选用不少于二组的实际强震记录,一组人工模拟的加速度时程曲线。
见〈建筑抗震设计规范〉[GB50011-2001]第5.1.2条。
○〈地震波信息〉:纵坐标示〈加速度〉,横坐标示记录时间。
○〈峰值加速度值〉:最大值见〈建筑抗震设计规范〉[GB50011-2001]5.1.2条表5.1.2.-2 时程曲线最大值地震影响6度7度8度9度多遇地震18 35(55) 70(110) 140罕遇地震220(310) 4000(510) 620○方向:计算单向地震时,主分量峰值加速度赋正确值,其它赋0;计算双向地震时,主、次分量峰值加速度赋正确值,其它赋0;○楼层剪力、楼层弯矩不分塔统计:应勾选。
1.2分析参数(图1.2):位置:主菜单\分析参数图1.2 弹性动力时程分析参数操作说明及规范链接:○〈地震波主方向与X轴夹角〉:可用90。
○〈主分量峰值加速度〉:○〈次分量峰值加速度〉:○〈垂直分量峰值加速度〉:计算单向地震时,主分量峰值加速度赋正确值,其它赋0;计算双向地震时,主、次分量峰值加速度赋正确值,其它赋0;○〈结构阻尼比〉:钢筋混凝土结构:0.05;小于12层纲结构:0.03;大于12层纲结构:0.035。
○〈第一条地震波放大系数〉:可不放大。
○〈第二条地震波放大系数〉:可不放大。
○〈第三条地震波放大系数〉:可不放大。
2.1、时程分析结果图形显示(图2.1):位置:主菜单\时程分析结果图形显示图2.1.位置菜单2.1.1动力时程分析结果(WDYNA.OUT1):位置:位置菜单\动力时程分析结果WDYNA.OUTWDYNA.OUT动力时程分析结果2.1.2 最大楼层位移曲线(图2.1.2):位置:位置菜单\最大楼层位移曲线图2.1.2最大楼层位移曲线2.1.3 最大层间位移角曲线(图2.1.3):位置:位置菜单\最大层间位移角曲线图2.1.3最大层间位移角曲线2.1.4 最大楼层剪力曲线(图2.1.4):位置:位置菜单\最大楼层剪力曲线图2.1.4最大楼层剪力曲线2.1.5 最大楼层弯矩曲线(图2.1.5):位置:位置菜单\最大楼层弯矩曲线图2.1.5最大楼层弯矩曲线7.2EPDA/PUSH(图02 )图02主界面采用弹塑性静、动力分析范围1、甲类建筑及9度区的乙类建筑;2、7-9度区楼层屈服强度系数小于0.5的框架结构;3、高度大于150m的钢结构;4、采用隔震和消能减震设计的结构;5、9度及8度Ⅲ、Ⅳ类高大厂房的排架见〈建筑抗震设计规范〉[GB50011-2001]5.5.2条1、生成弹塑性静、动力分析数据(图1):位置:主界面\生成弹塑静、动力分析数据图1位置菜单1.1、接力SATWE或PMSAP生成三维弹塑性模型(图1.1.A-C):位置:位置菜单\接力SATWE或PMSAP生成三维弹塑性模型图1.1.A图1.1.B图1.1.C操作说明:○由图A选择单项。

恢复力模型【摘要】恢复力模型是根据大量从试验中获得的恢复力与变形的关系曲线经适当抽象和简化而得到的实用数学模型,是结构构件的抗震性能在结构弹塑性地震反应分析中的具体体现。
本文通过对恢复力模型的进行了简要评述,提出恢复力模型研究存在的问题。
【关键词】:恢复力模型性质适用范围一、恢复力模型简介恢复力模型是根据大量从试验中获得的恢复力与变形的关系曲线经适当抽象和简化而得到的实用数学模型,是结构构件的抗震性能在结构弹塑性地震反应分析中的具体体现。
若仅用于静力非线形分析,恢复力模型一般是指力与变形关系骨架曲线的数学模型;而如果是用于结构的动力非线形时程分析,恢复力模型不仅包含骨架曲线,同时也包括各变形阶段滞回环的数学模型。
大量的试验表明,恢复力特征曲线具有下列主要性质:⑴在一次荷载作用下,应当是向上凸起的曲线。
⑵随着荷载反复次数的增加,变形增大,刚度不断下降,表现为恢复力曲线中的刚度退化现象。
⑶当荷载反向时,曲线趋于前一个荷载的反向点。
⑷随着荷载循环次数的增加,结构逐渐破坏,达到同样变形量的荷载值逐渐减少。
在临近破坏阶段,荷载降低时位移继续增大,出现负刚度。
⑸曲线所包含的面积随变形的增加而增加,而且增加的速度比变形增大的速度快。
⑹当混凝土开裂时,曲线在该点有突变。
二、恢复力模型分类从试验得出的恢复力-变形关系曲线比较复杂,难以直接应用到实际的工程中,一般需要加以简化,得出用数学计算表达的模型。
恢复力性质与梁柱的刚度分布模型密切相关,根据梁柱刚度分布模型的差别,其恢复力模型可分为:材料层次的恢复力模型、截面层次的恢复力模型和构件层次恢复力模型。
同时根据研究的问题是平面结构还是空间结构的不同,恢复力模型可分为:平面结构恢复力模型和空间结构恢复力模型。
根据模型曲线形状,恢复力模型可分为:曲线型和折线型。
1、平面结构恢复力模型平面结构恢复力模型在实际的工程中得到了很广泛的应用。
概况的说,可分为曲线型模型和折线型模型。
恢复力模型恢复力是指结构或构件在外荷载去除后恢复原来形状的能力。
恢复力模型建立在3个层次上:材料恢复力模型、构件恢复力模型和结构恢复力模型。
恢复力模型包括骨架曲线和滞回规则两个部分。
骨架曲线应确定关键参数,且能反映开裂、屈服、破坏等主要特征;滞回规则一般要确定正负向加、卸载过程中的行走路线及强度退化、刚度退化和滑移等特征。
确定恢复力模型的方法有试验拟合法、系统识别法、理论计算法。
恢复力模型分曲线型和折线型,折线型因应用简便而被普遍采用,目前提出的折线型恢复力模型主要有双线型、三线型、四线型、退化双线型、退化三线型、定点指向型和滑移型等。
若仅用于静力非线性分析,恢复力模型一般是指力与变形关系骨架曲线的数学模型;而如果是用于结构的动力非线性时程分析,恢复力模型不仅包含骨架曲线,同时也包括各变形阶段滞回环的数学模型。
1887 年,德国Bauschinger 通过对钢材的拉压试验,指出当钢材在一个方向加荷超过其弹性极限后,对其进行反向加荷的弹性极限将显著降低。
此后钢材的这种现象就称作“包辛格效应”。
Penizen (1962)提出了一种适用于钢材的双线性恢复力模型,考虑了钢材的包辛格效应和应变硬化。
混凝土在重复循环荷载作用下的应力- 应变滞回关系,是钢筋混凝土结构抗震研究中的一个最基本的课题。
在钢筋混凝土结构中,混凝土主要是承受压力,因此混凝土的应力- 应变滞回关系的研究主要是针对混凝土在重复压力作用下的性能。
八十年代以来,考虑到地震作用下混凝土受到较高的应变速率的影响,混凝土本构关系的研究重点主要是对约束混凝土在不同应变速率下的应力-应变全过程进行试验研究,并致力于建立考虑应变速率影响的约束混凝土的应力- 应变关系的数学模型。
在结构的弹塑性地震反应分析中应用最为广泛的是双线性(Bi - linear)模型。
该模型首次由Penizen(1962)根据钢材的试验结果提出,考虑了钢材的包辛格效应和应变硬化。
时程分析时程分析法⼜称直接动⼒法,在数学上⼜称步步积分法。
顾名思义,是由初始状态开始⼀步⼀步积分直到地震作⽤终了,求出结构在地震作⽤下从静⽌到振动以⾄到达最终状态的全过程。
它与底部剪⼒法和振型分解反应谱法的最⼤差别是能计算结构和结构构件在每个时刻的地震反应(内⼒和变形)。
当⽤此法进⾏计算时,系将地震波作为输⼊。
⼀般⽽⾔地震波的峰值应反映建筑物所在地区的烈度,⽽其频谱组成反映场地的卓越周期和动⼒特性。
当地震波的作⽤较为强烈以⾄结构某些部位强度达到屈服进⼊塑性时,时程分析法通过构件刚度的变化可求出弹塑性阶段的结构内⼒与变形。
这时结构薄弱层间位移可能达到最⼤值,从⽽造成结构的破坏,直⾄倒塌。
作为⾼层建筑和重要结构抗震设计的⼀种补充计算,采⽤时程分析法的主要⽬的在于检验规范反应谱法的计算结果、弥补反应谱法的不⾜和进⾏反应谱法⽆法做到的结构⾮弹性地震反应分析。
时程分析法的主要功能有:1)校正由于采⽤反应谱法振型分解和组合求解结构内⼒和位移时的误差。
特别是对于周期长达⼏秒以上的⾼层建筑,由于设计反应谱在长周期段的⼈为调整以及计算中对⾼阶振型的影响估计不⾜产⽣的误差。
2)可以计算结构在⾮弹性阶段的地震反应,对结构进⾏⼤震作⽤下的变形验算,从⽽确定结构的薄弱层和薄弱部位,以便采取适当的构造措施。
3)可以计算结构和各结构构件在地展作⽤下每个时刻的地震反应(内⼒和变形),提供按内⼒包络值配筋和按地震作⽤过程每个时刻的内⼒配筋最⼤值进⾏配筋这两种⽅式。
总的来说,时程分析法具有许多优点,它的计算结果能更真实地反映结构的地震反应,从⽽能更精确细致地暴露结构的薄弱部位。
时程分析法有关的⼏个问题:1、恢复⼒特性曲线;恢复⼒特性曲线应⽤于计算必须模型化,常⽤的有双线型模型与退化三线型模型;退化三线型模型(附图)能较好地反映以弯曲破坏为主的钢筋混凝⼟构件的的特性,所以适⽤于此类构件计算。
2、结构计算模型及分析⽅法;3、地震波的选⽤;4、时程分析计算结果的处理。
恢复力恢复力是指结构或构件在外荷载去除后恢复原来形状的能力。
恢复力模型建立在3个层次上:材料恢复力模型、构件恢复力模型和结构恢复力模型。
恢复力模型包括骨架曲线和滞回规则两个部分。
骨架曲线应确定关键参数,且能反映开裂、屈服、破坏等主要特征;滞回规则一般要确定正负向加、卸载过程中的行走路线及强度退化、刚度退化和滑移等特征。
确定恢复力模型的方法有试验拟合法、系统识别法、理论计算法。
恢复力模型分曲线型和折线型,折线型因应用简便而被普遍采用,目前提出的折线型恢复力模型主要有双线型、三线型、四线型、退化双线型、退化三线型、定点指向型和滑移型等。
若仅用于静力非线性分析,恢复力模型一般是指力与变形关系骨架曲线的数学模型;而如果是用于结构的动力非线性时程分析,恢复力模型不仅包含骨架曲线,同时也包括各变形阶段滞回环的数学模型。
1887 年,德国Bauschinger 通过对钢材的拉压试验,指出当钢材在一个方向加荷超过其弹性极限后,对其进行反向加荷的弹性极限将显著降低。
此后钢材的这种现象就称作“包辛格效应”。
Penizen(1962)提出了一种适用于钢材的双线性恢复力模型,考虑了钢材的包辛格效应和应变硬化。
混凝土在重复循环荷载作用下的应力- 应变滞回关系,是钢筋混凝土结构抗震研究中的一个最基本的课题。
在钢筋混凝土结构中,混凝土主要是承受压力,因此混凝土的应力- 应变滞回关系的研究主要是针对混凝土在重复压力作用下的性能。
八十年代以来,考虑到地震作用下混凝土受到较高的应变速率的影响,混凝土本构关系的研究重点主要是对约束混凝土在不同应变速率下的应力-应变全过程进行试验研究,并致力于建立考虑应变速率影响的约束混凝土的应力- 应变关系的数学模型。
在结构的弹塑性地震反应分析中应用最为广泛的是双线性(Bi - linear)模型。
该模型首次由Penizen(1962)根据钢材的试验结果提出,考虑了钢材的包辛格效应和应变硬化。
由于其简单实用,因而也广泛用于钢筋混凝土结构的弹塑性分析。