沪教课标版六年级下册数学:69 二元一次方程组及其解法
- 格式:ppt
- 大小:715.50 KB
- 文档页数:12

沪教版六年级数学下册第六章二元一次方程组及其解法(2)1.运用加减法解二元一次方程组的思路:运用方法将方程组中转化为从而求得方程组的解。
2.已知3a+2b=4,2a-b=5,则5a+b=3.方程组-=+=﹣中,x的系数的特点是,方程组+=-=中y的系数的特点是,这两个方程组用法解较为简便.4.若|2x-y-1|与(2y+x-8)²互为相反数,则x=,y=5.若5+-与-3﹣是同类项,则m和n的取值是m=,n=6.若==是方程组-=+=的解,则m=,n=7.方程+=-=的解是()A ==B.==C.==D==8.已知==是二元一次方程组+=-=的解,则a-b的值为()A.﹣1B. 1C. 2D. 3 9.用加减消元法解下列方程组(1)+=-=(2)-=+=(3)-=﹣+=﹣(4)+=-=10.已知x、y满足方程组+=+=,则x-y的值是11.解方程组+=-=12.解方程组-=-=13.已知代数式kx+b,当x=2时,代数式的值是﹣3;当x=4时,代数式的值是﹣7.求这个代数式.14.如图,矩形ABCD的周长为14cm,E为AB的中点,以A为圆心、AE长为半径画弧交AD 于点F;以C为圆心、CB长为半径画弧交CD于点G.设AB=x cm,BC=y cm,当DF=DG 时,求x、y的值15、甲、乙两人同时解方程组+=﹣-=由于甲看错了方程①中的m,得到的解为==,乙看错了方程②中的n,得到的解为==,试求m、n的正确值.16.阅读理解解方程组+=-=时,如果设=m,=n,则原方程组可变形为关于m、n的方程组+=-=解这个方程组得到它的解为==﹣,由=5,=﹣4,求得原方程组的解为==﹣利用上述方法解方程组+=-=。
17.方程组+=-=的解是18.解方程组+=-=。
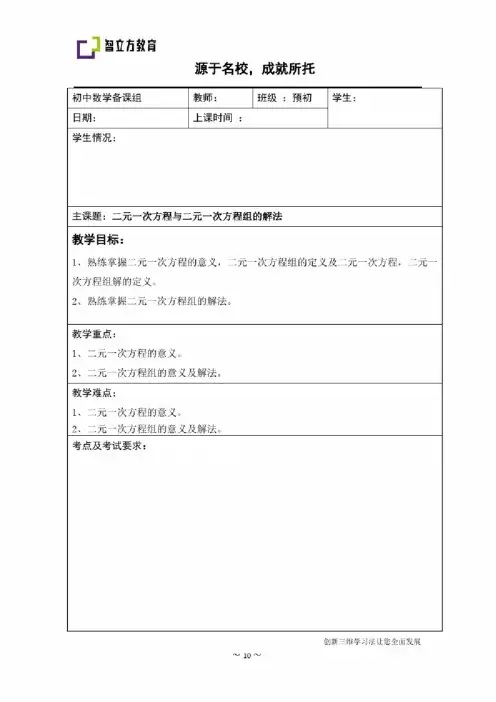
初中数学备课组教师:班级:预初学生:日期:上课时间:学生情况:主课题:二元一次方程与二元一次方程组的解法教学目标:1、熟练掌握二元一次方程的意义,二元一次方程组的定义及二元一次方程,二元一次方程组解的定义。
2、熟练掌握二元一次方程组的解法。
教学重点:1、二元一次方程的意义。
2、二元一次方程组的意义及解法。
教学难点:1、二元一次方程的意义。
2、二元一次方程组的意义及解法。
考点及考试要求:基本内容二元一次方程与二元一次方程组的解法知识精要一、二元一次方程1、含有两个未知数的一次方程叫做二元一次方程.2、使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
3、二元一次方程的解有无数个,二元一次方程的解得全体叫做这个二元一次方程的解集.二、二元一次方程组1、有几个方程组成的一组方程叫做方程组。
如果方程组中含有两个未知数,且含有未知数的项的次数都是一次,那么这样的方程组叫做二元一次方程组,2、在二元一次方程组中,使每个方程都适合的解,叫做二元一次方程组的解.3、三、二元一次方程组的解法1、二元一次方程组的常规解法,是代入消元法和加减消元法。
(注:这两种方法都是从“消元”这个基本思想出发,先把''二元”转化为“一元”把解二元一次方程组的问题归结为解一元一次方程.在“消元”法中,包含了“未知”转化到“己知”的重要数学化归思想。
)2、灵活消元<1)整体代入法(2)先消常数法(3)设参代入法(4)换元法(5)简化系数法热身练习1.下列方程中,是二元一次方程的是(D)I y-2A.3x~2y=4zB.6xy+9=0C.—+4y=6D.4x=----—x 42、下列方程组中,是二元一次方程组的是(A )A.x+y = 4 12« - 3/? = 11B.2x + 3y = 7C.<r =9y = 2.vD.x+y = 8x 2-y = 45b — 4。
= 63、二元一次方程 5a-llb=21( B )A.有且只有-•解B.有无数解C.无解D.有且只有两解Y — 24、若J " 是二元一次方程组的解,则这个方程组是(Cy = —1)x-3y = 52.v+y = 5x = 2y x = 3y +15、在方程2(x + y ) — 3(y 一》)=3中.用含x 的代数式表示),,则 (A )A. y = 5x-3 B.y = -x-3 C. y = 5x +3D. y = -5x - 36. 4x+l=m(x~2)+n(x~5),则 m 、n 的值是( C )m = -4H = -1.c = 4 B.n = 1m = —7D.〃 =3f4x + 3v = 67、二元一次方程组〈 的解是(C )[2x + y = 48、二元一次方程4x-3y+5=0时,用含x 的代数式表示y,则_y = —,用含y的代数式表示x,则A =4S 49、二元一次方程 4x-3y=12> 当、二0, 1, 2, 3 时,y 二-4, -一,一一,0------3 — 3--------------\・=2 I v = i10、方程2x+y 二5的正整数解是 < 。

级数学第二学期-6.9 二元一次方程组及解法-学案(无答案)二元一次方程组及其解法【学习目标】1.了解二元一次方程、二元一次方程组及其解的概念;2.通过了解解二元一次方程组的基本目标:使方程组逐步转化为x=a,y=b的形式,体会消元的思想,掌握解二元一次方程组的代入消元法和加减消元法;并能根据二元一次方程组的具体形式选择适当的解法。
3.掌握三元一次方程组及其解法,进一步体会“消元”思想,能根据三元一次方程组的具体形式选择适当的解法。
【学习重难点】1.二元一次方程组的解法。
2.熟练运用代入法和加减法解二元一次方程组。
【学习过程】一、知识要点梳理知识点一:二元一次方程的概念。
含有两个未知数(一般设为x、y),并且含有未知数的项的次数都是______,像这样的方程叫做____________;如x+y=24,都是____________。
要点诠释:(1)在方程中“元”是指未知数,“二元”就是指方程中______两个未知数。
(2)“未知数的次数为1”是指含有未知数的项(单项式)的次数是______。
如xy的次数是______,所以方程6xy+9=0不是二元一次方程。
(3)二元一次方程的左边和右边都必须是整式。
如方程的左边不是______,所以它就不是二元一次方程。
(4)判断某个方程是不是二元一次方程,一般先把它化为__________________的形式,再根据定义判断,例如:2x+4y=3+2x不是二元一次方程,因为通过移项,原方程变为______,不符合二元一次方程的形式。
知识点二:二元一次方程的解。
级数学第二学期-6.9 二元一次方程组及解法-学案(无答案)能使二元一次方程左右两边的值都____________的两个未知数的值,叫做二元一次方程的解。
由于使二元一次方程的左右两边____________的未知数的值不只一个,故每个二元一次方程都有____________组解。
如……,都是二元一次方程x+y=3的解,我们把有无数组解的这样的方程又称之为____________方程。


二元一次方程组及其解法(1)实验中学张敏一、教材分析:本节课是上海市二期课改教材六年级第二学期课本第五章第九节内容。
在此之前,已经学习过一元一次方程及应用,不等式(组)的解法以及二元一次方程、二元一次方程的解(集)的概念等相关内容,所以学生对方程已经有了一些了解和掌握,这节课的关键是理解方程组解的意义以及消元法解方程组及其这一解题方法所体现出的数学“化归”思想的掌握,解二元一次方程组是为以后的高次方程的解法打下坚实基础,也是后面学习一次函数内容的铺垫,因此学习好二元一次方程组及其解法相当重要。
本节课是二元一次方程组解法的第一节课,学生初次接触方程组的解法,同时思维的重点也集中在如何把未知问题转化为已知问题,把二元问题转化为一元问题。
因此,教学的重点是对转化思想、消元方法的理解,而不是对解法的熟练运用,故在目标中设定为“能用代入消元法解简单的二元一次方程组”.二、学情分析:我校是一所公办学校,虽然地处城镇,但学生也来源于正常的学区划分,有相当一部分农村的学生,故基础相对参差不齐,学习习惯也是不尽相同,而且六年级又是中学阶段的起始年级,学生年龄较小,针对他们喜欢新鲜事物,好动的特点,在平时的教学中,我们利用新教材的特点,尽量激发他们的学习兴趣,抓好双基,逐步培养和提高学生的观察、分析和解决问题的能力,让他们养成学习数学的良好的习惯。
经过前面内容的学习,学生已经掌握了一元一次方程的概念及其解法,而且也了解了二元一次方程及其解的概念,并理解了一元一次不等式组的解集的意义,这样就为本节课的学习提供了很好的知识准备。
由于学生对代数思想的认识不够,缺乏用字母表示数的意识,发现式的变形和依据的能力不强.在用代入法解二元一次方程组时,需要先把其中一个方程变形成用含一个未知数的代数式表示另一个未知数的形式,再利用整体代换的方式替换出一元.这其中所蕴含的式的变形及整体代入思想,都是需要学生理解的.因此,在本节课的教学过程设计中,时刻注意引导学生思维聚焦的方向,通过合理设置有梯度的承接性问题,激发学生的思维,深化学生的思考.并且及时进行阶段性小结,不断完善学生的认知结构,力争做到使学生的思维“发而不散”。


二元一次方程(组)知识精要一、二元一次方程的概念1、二元一次方程:含有_______未知数,并且_________________的方程叫做二元一次方程。
2、二元一次方程的解:使_______________________________的两个未知数的值叫做二元一次方程的解。
3、二元一次方程的解集:二元一次方程的解有________, ______________________叫做二元一次方程的解集。
4、二元一次方程组:如果方程组中含有两个未知数,且含未知数的项的次数都是一次,那么这样的方程组叫做二元一次方程组。
5、二元一次方程组的解:在二元一次方程组中,____________________________,叫做二元一次方程组的解。
二、方程组的解法1、代入消元法:(1)求表示式:从方程组中选一个系数比较简单的方程,将这个方程中的一个未知数用另一个未知数的式子表示出来(2)代入消元:将所得的式子代入另一个方程中,消去一个未知数,得到一个一元一次方程。
(3)求解方程:解得到的一元一次方程(4)回代得解:把求得的一个未知数的值代入先前的表示式,得到另一个未知数的值,从而得到方程组的解。
2、加减消元法:(1)变换系数:方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等(即绝对值不相等),就用适当的数去乘某一个或两个方程的两边,使这个未知数的系数互为相反数或相等(即绝对值相等)(2)加减消元:把两个方程的两边分别相加或相减,消去一个未知数,得到一个以另一个未知数为未知数的一元一次方程。
(3)求解方程:(4)回代得解:热身练习1、下列各式:21(1)233;(2)0;(3)4;3x y x y x y -=-=-= 1(4);2xy = 1(5)32;(6)1;(7)6;(8)523x y y x y z x y x y x++=++=-=- 属于二元一次方程的是2、若4x-5y=0,x≠0,且y≠0,求125125x y x y-+的值。

六年级数学下册 6.9 二元一次方程组及其解法教案沪教版五四制三、二元一次方程组的解法1、二元一次方程组的常规解法,是代入消元法和加减消元法。
(注:这两种方法都是从“消元”这个基本思想出发,先把“二元”转化为“一元”把解二元一次方程组的问题归结为解一元一次方程,在“消元”法中,包含了“未知”转化到“已知”的重要数学化归思想。
)2、灵活消元(1)整体代入法(2)先消常数法(3)设参代入法(4)换元法(5)简化系数法热身练习1、下列方程中,是二元一次方程的是( D )A、3x-2y=4zB、6xy+9=0C、+4y=6D、4x=2、下列方程组中,是二元一次方程组的是( A )A、3、二元一次方程5a-11b=21 ( B )A、有且只有一解B、有无数解C、无解D、有且只有两解4、若是二元一次方程组的解,则这个方程组是( C )A、B、C、D、5、在方程中,用含的代数式表示,则( A )A、B、C、D、6、4x+1=m(x-2)+n(x-5),则m、n的值是( C )B、C、D、7、二元一次方程组的解是( C )A、B、C、D、二元一次方程4x-3y+5=0时,用含x的代数式表示y,则,用含y的代数式表示x,则x= 。
二元一次方程4x-3y=12,当x=0,1,2,3时,y=3)2+|2y+1|=0,则= 。
12、二元一次方程有一个公共解,则m=___1___,n=__-2___。
13、已知是方程的一个解,则。
14、方程组的解是________________。
15、解下列方程组(1)(2)解:解:代数式,当时,它的值是7;当时,它的值是4,试求时代数式的值。
解:由题可得,解得则当时,精解名题例1、如果方程组无解,则a为( B )A、6B、-6C、9D、-9例2、若方程组的解之和:x+y=-5,求k的值,并解此方程组、解:k的值为13例3、解关于x、y的二元一次方程组(1)(2)(1)解:(2)解:设,则原方程组可变形为,解得所以解这个方程组,得:所以原方程组的解是例4、已知方程组,试确定的值,使方程组:(1)有一个解;(2)有无数解;(3)没有解解:(1)当时,(2)时,(3)时,例5、如果方程组和方程组有相同的解,求a,b的值解:由题意得,解得,带入原方程则,,解得。


学科教师辅导讲义授课类型 T –一次方程组的解法 T-一次方程组的应用T-巩固训练,能力提升教学内容 一次方程(组)二元一次方程的概念二元一次方程:含有两个未知数的一次方程。
二元一次方程组:方程组中,含有两个未知数,且含未知数的项的次数是一次的。
二元一次方程(组)的解二元一次方程组的解:使方程组中每一个方程都适合的解。
三元一次方程定义:如果方程组中含有三个未知数,且含有未知数的项的次数都是一次,这样的方程组叫做三元一次方程组。
解三元一次方程组的思想方法是:三元一次方程组−−→−消元二元一次方程组−−→−消元一元一次方程组。
一次方程组的解法:一次方程组的解题方法:1.代入法 :(1)将方程变形成用含一个未知数的代数式来表示另一个未知数的关系式(2)将这个关系式代入另一个方程,消去一个未知数,得到一个一元一次方程.(3)解这个一元一次方程,求得一个未知数的值.(4)将这个求得的未知数的值,再代入关系式求出另一个未知数的值(5)检验2.加减法(1)方程组的两个方程中,如果同一个未知数的系数既不互为相反数,又不相等,那么就用适当的数乘方程的两边,使同一个未知数的系数互为相反数或相等.(2)把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程.(3)解这个一元一次方程,求得一个未知数的值.(4)将这个求得的两个未知数的值代入原方程组的任意一个方程中,求出另一个未知数的值(5)检验一、二元一次方程 例题11.已知x m-1+2y n+1=0是二元一次方程,则m=_______,n=________.(★)我来试一试!1.已知x m+3+4y n —2=0是二元一次方程,则m+n=.例题2我来试一试例题1例题2我来试一试例题1我来试一试例题1我来试一试例题2我来试一试例题3我来试一试一次方程组的应用1.行程问题:1、甲、乙两人相距14千米,两人同时出发,若相向而行,2小时后相遇;若同向而行,甲3.5小时可追上乙,求甲、乙两人的平均速度各是多少?2、A、B两地间的路程为360千米,甲车从A地出发开往B地,每小时行72千米;甲车出发25分钟后,乙车从B地出发开往A地,每小时行48千米。
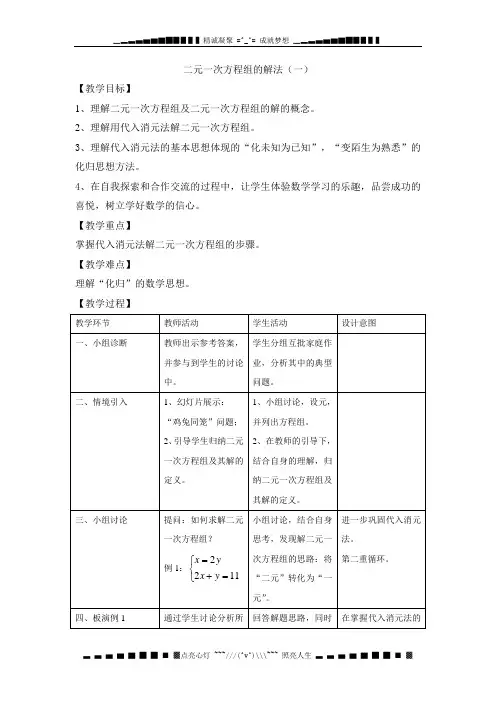
二元一次方程组的解法(一)
【教学目标】
1、理解二元一次方程组及二元一次方程组的解的概念。
2、理解用代入消元法解二元一次方程组。
3、理解代入消元法的基本思想体现的“化未知为已知”,“变陌生为熟悉”的化归思想方法。
4、在自我探索和合作交流的过程中,让学生体验数学学习的乐趣,品尝成功的喜悦,树立学好数学的信心。
【教学重点】
掌握代入消元法解二元一次方程组的步骤。
【教学难点】
理解“化归”的数学思想。
【教学过程】
【教学设计意图】
本节课主要是用小组合作与独立探究相结合的方法,通过对二元一次方程组的学习,初步让学生领悟“化归”的数学思想。
本节课还旨在让学生用规范的数学语言来完善解题格式,提高学生的解题能力。
“自选超市”的设计,主要是通过对不同类型的例题的思考和探究,挖掘问题的本质。
6.9二元一次方程组及其解法(1)知识点归纳1.由几个方程组成的一组方程叫做方程组,如果方程组中含有个未知数,且含未知数的项的次数都是次,那么这样的方程组叫做二元一次方程组.注意:“方程组中含有两个未知数”而不是几个二元一次方程就一定可以组成一个二元次方程组.2.在二元一次方程组中,叫做二元一次方程组的解.3.通过“代入”,将方程组转化为,这种解法叫做代入消元法,简称代入法。
夯实基础一、填空题1.若2a-b=5,a-2b=4,则a-b的值为.2.定义运算“*”:规定x*y=ax+by(其中a,b为常数),若1*1=3,1*(-1)=1,则1*2= .二、选择题3.若方程组,13329.3053{=-=+baba的解是,3.82.1{==ab,则方程组,13)1(3)2(29.30)1(5)2(3{=--+=-++y x y x 的解是 ( )A.,3.62.2{==x yB.,3.82.1{==x yC.,3.102.2{==x yD.,3.102.0{==x y三、解答题4.判断下列方程组是不是二元一次方程组,是的打“√”,不是的打“×”。
(1) ,83212{=-=-y x y x ( )(2) ,64{=-=+z x z y ( )(3) ,761-{=-=y x y ( ) (4),920-{=-=y x xy ( ) 5.解方程组.(1),83-{=-=y x x y (2),1-352-{=+=y x x y(3),2-12{=+=+yxyx(4),213322343{=+=-yxyx6.已知方程组,1,{=-=+yxayx且x=2y,求a的值.强化拓展7.圆珠笔的单价是铅笔的单价的3倍,小明用7元钱买了3支圆珠笔和5支铅笔,求两种笔的单价.(用二元一次方程解).8.方程组,12,2133{=--=+yxmyx的解也是二元一次方程4x+y=17的解,求m的值.9.已知方程组,0-,2023{=+=+ayxyx的解满足x>0,y>0,求整数a的值.10.先阅读,然后解方程组.材料:解方程组)1,(1-)2.(5)(4{=-=--yxyyx时,可由①,得x-y=1,③然后再将③代入②,得4×1-y=5,求得y=-1,从而进一步求得,0.1-{==xy这种方法称为“整体代入”法请用这样的方法解方程组:)1,(2-32)2.(927532{=-=++-yxyyx答案。
上海市静安区实验中学六年级下学期沪教版五四制第六章6.9 二元一次方程组及其解法(word无答案)
一、单选题
(★) 1 . 下列叙述正确的是()
A.方程组不是二元一次方程组
B.方程不是二元一次方程
C.既是方程的解,也是方程的解
D.任何一个二元一次方程组的解都是唯一存在的
二、填空题
(★) 2 . 下列方程组中① ;② ;③ ;④
;⑤ ;是二元一次方程组的是______.(只填序号)
(★) 3 . 在二元一次方程中,若与互为相反数,则=_____.
(★) 4 . 若,则_________.
三、解答题
(★★) 5 . 解下列方程组(用代入法解)
(1);
(2);
(3);
(4);
(5);
(6).
四、填空题
(★) 6 . 用加减法解方程组时,若先求出的值,则应将两个方程_______;若先求出的值,则应将两方程______.
(★★) 7 . 已知方程组,则_______.
(★) 8 . 已知|x﹣1|+(2y+1)2=0,且2x﹣ky=4,则k= _____ .
五、单选题
(★★) 9 . 方程的公共解是()
A.B.C.D.
(★★) 10 . 若│x-2│+(3y+2)2=0,则x+6y的值是()
A.-1B.-2C.-3D.
(★) 11 . 若,则的值是()
A.-1B.0C.1D.2
六、解答题
(★★) 12 . 解下列方程组
(1);
(2).
(★★) 13 . 已知方程组和的解相同,求的值.。