优选高斯定理及应用
- 格式:ppt
- 大小:3.28 MB
- 文档页数:55

高斯定理的原理及应用1. 高斯定理的原理高斯定理是电磁学和流体力学等自然科学领域中十分重要的定理之一,它描述了一个封闭曲面与穿过该曲面的矢量场之间的关系。
根据高斯定理,一个封闭曲面上通过的矢量场的通量等于该曲面所包围的体积的某个性质的总量。
高斯定理可以用数学公式表达为:$$ \\oint_S \\mathbf{F} \\cdot d\\mathbf{S} = \\iiint_V \\left(\ abla \\cdot\\mathbf{F}\\right) dV $$其中,$\\oint_S \\mathbf{F} \\cdot d\\mathbf{S}$表示矢量场$\\mathbf{F}$通过封闭曲面S的通量,$\\iiint_V \\left(\ abla \\cdot\\mathbf{F}\\right) dV$表示矢量场$\\mathbf{F}$在曲面所包围的体积V上的发散。
高斯定理的原理可以简单理解为,一个封闭曲面上通过的矢量场的总量等于该曲面所包围的体积上的性质总量。
这个性质可以是电荷、物质的质量、电场强度等等,具体取决于所研究的领域和问题。
2. 高斯定理的应用高斯定理在物理学、工程学和数学等多个领域都有着广泛的应用。
2.1 电磁学中的应用在电磁学中,高斯定理被广泛应用于求解电荷分布产生的电场。
根据高斯定理,通过一个封闭曲面的电场通量等于该曲面所包围的总电荷。
根据这一原理,我们可以利用高斯定理来计算各种电荷分布产生的电场。
例如,当电荷分布具有对称性时,可以选择合适的高斯面来简化电场计算。
2.2 流体力学中的应用在流体力学中,高斯定理也有着重要的应用。
例如,通过一个封闭曲面的流体流量等于该曲面所包围的总流体质量。
根据这一原理,我们可以利用高斯定理来计算各种流体流动的性质,如质量流率、体积流率等。
高斯定理在流体力学中为我们提供了一种便捷的计算方法。
2.3 数学中的应用在数学中,高斯定理被广泛用于计算多元函数的积分。

静电场中的高斯定理及其应用1高斯定理高斯定理(Gauss’s Law)是物理学中最重要的电荷定律之一,由19世纪哥本哈根学家卡尔·马克斯·高斯于18日本宣言1877年提出。
高斯定理对于理解静电场非常重要,它实际上是一条关系电荷密度和电场的定律,用一般的话来说,它可以用来计算电荷分布情况下的电场外部空间的分布情况。
它可以被表达为:“定积分表示的电荷密度的体积积分等于其相应的电场大小的表面积积分”关于高斯定理的精确表达可以表达为:($\vec{E}·da=\rho·dv$)2应用电荷分布情况下的静电场等电势及电荷等强场的计算应用高斯定理。
其中,电荷分布情况下的静电场的计算是最常见的应用,用来计算空间电场的大小和方向。
具体的做法是选择一个闭合的表面,在此表面上应用高斯定理:($\oint\vec{E}.da=\frac{q_{enclosed}}{\epsilon_0}$)其中,q enclosed是这个表面内封闭的电荷,而$\epsilon_0$是真空介电常数。
由此可以求出该表面上电场的大小及方向。
除此之外,高斯定理也可以用来计算电荷等强场,亦即电荷密度。
由高斯定理,可以得到:($\oint\vec{E}·da=\frac{1}{\epsilon_0}\int\rho·dv$)可以从该等式中看出,积分的表面的表面积积分是由内部的体积积分而产生的,这也就是所谓的电荷等强场原理。
因此,如果电荷的分布情况已经确定,则可以依据上述的高斯定理来求出电荷密度的大小和方向分布情况。
3结论总而言之,高斯定理是物理学中最重要的电荷定律之一,对于理解静电场非常重要。
它可以用来计算电荷分布情况下的电场外部空间的分布情况,也可以用来计算电荷等强场,亦即电荷密度。
因此,高斯定理有着重要的应用价值。

引言概述:在大学物理中,高斯定理是一项重要的物理原理,它描述了电场和磁场的性质。
高斯定理由德国物理学家卡尔·弗里德里希·高斯于18世纪中叶提出,是电磁学的基础之一。
本文将介绍高斯定理的概念、原理及其在电场和磁场中的应用。
正文内容:1. 高斯定理的概念1.1 定义高斯定理是描述电场和磁场分布的一种数学工具,它通过计算电场或磁场通过一个闭合曲面(高斯面)的总通量来研究场的分布。
1.2 数学表达高斯定理可以用数学表达式表示为:∮E·dA = q/ε0,其中∮E·dA表示场在闭合曲面上的总通量,q表示闭合曲面内的电荷量,ε0为真空介电常数。
2. 高斯定理的原理2.1 高斯面的选择高斯定理中的高斯面是根据具体问题选择的,一般情况下我们选择对称性较高的闭合曲面,以简化计算。
2.2 电场线的特性高斯定理的基础是电场线的性质,电场线从正电荷流向负电荷,且与介质边界垂直,通过一个封闭曲面的电场线数目与该封闭曲面内的电荷量有关。
2.3 通量与电场强度高斯定理中的总通量与电场强度呈正相关关系,通过计算总通量可以得到闭合曲面内的电场强度大小。
3. 高斯定理在电场中的应用3.1 点电荷的场分布高斯定理可以用来研究点电荷周围的电场分布,通过选择以点电荷为中心的球面作为高斯面,可以计算出球面内外的电场强度大小。
3.2 均匀带电球壳的场分布对于均匀带电球壳,可以通过选择以球壳为中心的闭合曲面来计算球壳内外的电场分布,根据高斯定理可以得到球壳内外的电场强度大小。
4. 高斯定理在磁场中的应用4.1 磁场的总通量类似于电场,磁场也可以使用高斯定理来描述,通过计算磁场通过闭合曲面的总通量可以了解磁场的分布情况。
4.2 磁场的磁感应强度高斯定理在磁场中的应用可以得到磁场的磁感应强度大小,通过选择合适的闭合曲面,可以计算出曲面内外的磁感应强度。
5. 高斯定理的实际应用5.1 高斯定理在电容器中的应用电容器是电子器件中常见的元件,根据高斯定理,可以计算电容器两极板之间的电场强度,进而了解电容器的性能。


高斯定理的应用
高斯定理是一个重要的数学定理,其应用可以被广泛应用到许多领域。
1. 在机械工程中,高斯定理可以用于解决压力、温度和流量的平均值问题,以及生产高压水管的曲线设计问题。
2. 在电子学中,高斯定理可以用来计算电容器、电阻器和变压器的电流和电压问题。
3. 高斯定理也可以应用到物理学中,可以用来解决牛顿第二定律、动量定理和能量定理等物理学问题。
4. 在热传导方面,高斯定理可以用来计算热量的温度及传播速度,以及热传导系数等问题。
5. 在地理学中,高斯定理可以用来计算地理空间的空间距离和相关性。
6. 在信号处理领域,可以用高斯定理来计算信号的滤波效果以及其他信号处理问题。
7. 在控制系统设计中,高斯定理可以用于控制系统的结构和稳定性设计。
8. 在插值方法中,高斯定理可以用来计算插值和拟合曲线的标准差和精度值。
- 1 -。

高斯定理的应用高斯定理是电磁学和物理学中非常重要的一条定理,它描述了通过一个任意闭合曲面的电场通量与该闭合曲面内的电荷量之间的关系。
这个定理不仅仅在电学领域有着广泛的应用,还可以用于其他领域,比如流体力学和热传导等。
本文将探讨高斯定理的应用,并从几个方面进行论述。
1. 电场分布的计算高斯定理可以用于计算电场在空间中的分布情况。
根据高斯定理,通过一个闭合曲面的电场通量等于该闭合曲面内的电荷量除以真空介电常数。
因此,如果我们已知一个体内的电荷分布情况,通过运用高斯定理可以计算出任意点的电场强度。
这对于理解和分析电场的性质至关重要,可以帮助我们更好地理解电场的行为规律。
例如,假设我们有一个球形体内的均匀带电球体,半径为R,电荷量为Q。
我们可以选取一个球面作为闭合曲面,将高斯定理应用于该球面上。
由于球内电荷均匀分布,球面内的电荷量将与球内电荷量相等。
根据高斯定理,电场通量为闭合曲面内的电荷量除以真空介电常数,即E·4πR^2 = Q/ε0。
通过简单的计算,我们可以得到球心处的电场强度为E = Q/(4πε0R^2)。
2. 电荷分布的确定高斯定理还可以被用于确定电荷分布的情况。
如果我们已知一个空间中存在的电场分布,而且我们希望分析该空间内的电荷分布,高斯定理可以提供有用的信息。
通过选择合适的闭合曲面和确定体内电场的分布情况,我们可以利用高斯定理解出体内电荷的分布特征。
例如,假设我们已知一个无限长的均匀带电导体柱体,电荷密度为λ。
我们可以选择一个圆柱形的闭合曲面,沿着导体的轴线方向,使其穿过导体并将其分为两个平面。
由于导体上的电荷自由分布,电场在导体内是零,因此只有柱体两端面积的电场通量不为零。
根据高斯定理,通过闭合曲面的电场通量等于该曲面内的电荷量除以真空介电常数。
通过简单的计算,我们可以发现,由于导体柱体上的电荷密度均匀,导体两端面积上存在的电荷量与导体表面积成正比。
因此,我们可以确定导体的电荷密度为λ = Q/A。

电场的高斯定理及其应用1. 高斯定理的背景高斯定理,也称为高斯电场定理,是电磁学中的基本定律之一。
它描述了电场通过任意闭合曲面的电通量与该闭合曲面内部的总电荷之间的关系。
这个定理是由德国数学家和物理学家卡尔·弗里德里希·高斯在19世纪初期提出的。
高斯定理在电磁学、物理学和工程学等领域有着广泛的应用。
2. 高斯定理的数学表述高斯定理的数学表述如下:对于任意闭合曲面S,电场通过S的电通量(记作ΦE)与曲面S内部的总电荷(记作q)之间存在以下关系:ΦE = ∫∫S E·dA = q / ε₀其中,E是电场强度,dA是曲面元素的面积向量,ε₀是真空的电介质常数(也称为电常数),其值约为8.85×10^-12 C2/N·m2。
3. 高斯定理的物理意义高斯定理的物理意义可以从两个方面来理解:(1)电场线与闭合曲面的关系:高斯定理说明,对于任意闭合曲面S,电场线通过S的电通量等于曲面S内部的总电荷。
这意味着,无论曲面S如何选择,只要它是闭合的,电场线穿过它的总通量都与曲面内部的电荷有关,而与曲面的形状和位置无关。
(2)电场的分布与电荷的关系:高斯定理表明,电场是通过闭合曲面的电通量的度量,而电通量与曲面内部的总电荷成正比。
这意味着,电场的强度和分布与曲面内部的电荷量有关,而与曲面的具体形状和位置无关。
4. 高斯定理的应用高斯定理在电场分析和计算中有着广泛的应用,下面列举几个常见的应用例子:(1)计算静电场中的电荷分布:通过高斯定理,可以计算静电场中某个闭合曲面内的电荷分布。
只需测量通过该曲面的电通量,然后根据电通量与电荷的关系,可以确定曲面内部的电荷量。
(2)设计电容器和绝缘材料:在电容器和绝缘材料的设计中,高斯定理可以用来分析电场的分布和电荷的积累。
通过合理选择闭合曲面的形状和位置,可以优化电场分布,提高电容器的性能和绝缘材料的可靠性。
(3)研究电磁波的传播:在研究电磁波的传播过程中,高斯定理可以用来分析电磁波在不同介质中的电场分布和电荷的变化。
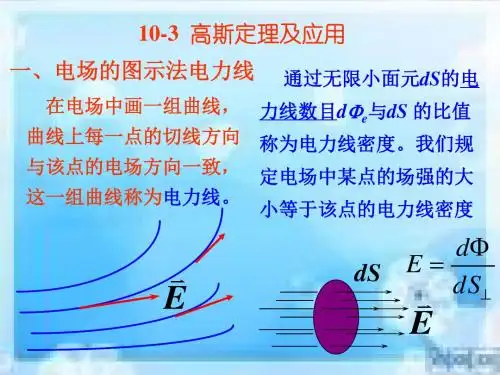

详解高斯定理高斯定理(Gauss theorem),矢量分析的重要定理之一。
它给出,矢量场通过任意闭合曲面的通量(面积分)等于该矢量场的散度在闭合曲面所包围体积内的积分(体积分)。
如果通量恒为零,则矢量场是无源场亦称无散场;如果通量可以不为零,则矢量场是有源场亦称有散场。
高斯定理是比较、区别各种矢量场特征的重要手段之一。
在静电学中,表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。
高斯定律(Gauss' law)表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性,高斯定律也可以应用于其它由平方反比律决定的物理量,例如引力或者辐照度。
穿过一封闭曲面的电通量与封闭曲面所包围的du电荷量成正比。
换一种说法就是,电场强度在一封闭曲面上的面积分与封闭曲面所包围的电荷量成正比。
由于磁力线总是闭合曲线,因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来,否则这条磁力线就不会闭合起来了。
如果对于一个闭合曲面,定义向外为正法线的指向,则进入曲面的磁通量为负,出来的磁通量为正,那么就可以得到通过一个闭合曲面的总磁通量为0。
这个规律类似于电场中的高斯定理,因此也称为高斯定理。
高斯定理的适用范围:1、高斯定理适用于任何静电场。
2、高斯定律(Gauss“law)表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中。
3、因为数学上的相似性,高斯定律也可以应用于其它由平方反比律决定的物理量,例如引力或者辐照度。

高斯定理在力学中的推广及应用
高斯定理(Gauss’s theorem)是创建霍普夫斯基力学的数学基础。
该定理最初是由力学表示的,在推广到其他物理问题中也很有用。
它
的内容是,对于某个区域所有的质量点的外场,其外力总和等于这个
区域内力的积分。
如果把这个定理应用于力学中,可以推广出不同的
有关力学现象的数学模型,从而为解决力学问题提供更有效的解决方案。
高斯定理在力学中的推广和应用有:
(1)运动学中的坐标变换:可以用高斯定理来研究在不同坐标系下同
一物体运动的位置和速度变化情况,这有助于更好地理解物体在不同
坐标系中运动行为。
(2)力学学习中的力定式:可以利用高斯定理来推导着名的力定式,
它给出了一种描述任何物体受力作用时质心上运动行为的公式。
(3)转动力学中的定转矩定律:可以用高斯定理推导定转矩定律,用
来研究各种与转动力学相关的问题,从而更好地理解物体的旋转行为。
(4)势能的传递:高斯定理可以用来理解势能的传递,即可以用来估
算势能的传递方向,以及在物体受力的情况下物体如何发生变形。
(5)热传导场中的温度变化:高斯定理可以用于热传导场中温度变化
的研究,它可以有助于更好地理解热源对物体温度分布的影响。

高斯定理的应用
高斯定理是一个非常重要的物理定理,它描述了电场、磁场和引力场等等几乎所有场的性质。
这个定理的具体内容是:对于一个任意闭合曲面,场在曲面内的通量等于场在曲面外的源强度之和。
这个定理在物理、工程、数学等多个领域都有着广泛的应用。
下面就来探讨一下高斯定理的应用。
1. 电场的应用
在电学中,高斯定理可以用来计算闭合曲面内的电场强度,并且可以方便地计算出点电荷、电偶极子、平面和球面电荷分布等情况下的电场分布,从而解决一些物理问题。
例如,高斯定理可以用来证明库仑定律,即两个电荷之间的相互作用力是与它们之间的距离的平方成反比的。
2. 磁场的应用
在磁学中,高斯定理可以用来计算闭合曲面内的磁场强度,并且也可以计算出不同形状的磁场分布。
例如,高斯定理可以用来计算一个长直导线周围的磁场分布,以及计算一个磁铁的磁场分布等等。
3. 引力场的应用
在引力学中,高斯定理可以用来计算闭合曲面内的引力场强度,并且可以计算出不同形状的质量分布下的引力场分布。
例如,高斯定理可以用来计算出地球的引力场分布,以及计算出三体问题的引力场分布等等。
4. 流体力学的应用
在流体力学中,高斯定理可以用来计算流体在任意闭合曲面上的流量。
例如,高斯定理可以用来计算一个液体管道中的流量,以及计算一个喷泉或水池中的流量等等。
总之,高斯定理是一个非常强大的工具,在物理、工程等多个领域都有着广泛的应用。
通过应用这个定理,我们可以更好地理解和描述自然现象,推动科学的发展。
高斯定理的分类应用引言高斯定理是电磁学中的一个重要定理,它描述了电场或磁场通过一个闭合曲面的总流量等于该闭合曲面内源电荷或源磁荷的总量。
高斯定理被广泛应用于各种领域,包括电磁学、物理学、工程学等。
本文将介绍高斯定理的分类应用,包括电场和磁场的应用。
电场的分类应用高斯定理在电场中有许多应用。
以下是其中一些重要的分类应用:1. 球对称的电荷分布:当电场具有球对称性时,高斯定理可以简化计算。
通过选择一个球面作为闭合曲面,可以利用高斯定理计算球面内的电场强度,而无需计算所有电荷粒子对电场的贡献。
球对称的电荷分布:当电场具有球对称性时,高斯定理可以简化计算。
通过选择一个球面作为闭合曲面,可以利用高斯定理计算球面内的电场强度,而无需计算所有电荷粒子对电场的贡献。
2. 均匀平面电场:高斯定理同样适用于均匀平面电场。
通过选择一个与平面垂直的柱面作为闭合曲面,可以利用高斯定理计算柱面内的电场强度。
均匀平面电场:高斯定理同样适用于均匀平面电场。
通过选择一个与平面垂直的柱面作为闭合曲面,可以利用高斯定理计算柱面内的电场强度。
3. 电场与导体:高斯定理在处理电场与导体相互作用的情况时非常有用。
通过选择一个包围导体的闭合曲面,可以计算导体表面的电场强度。
根据高斯定理,如果导体是不带电的,那么导体表面的电场强度必须为零。
电场与导体:高斯定理在处理电场与导体相互作用的情况时非常有用。
通过选择一个包围导体的闭合曲面,可以计算导体表面的电场强度。
根据高斯定理,如果导体是不带电的,那么导体表面的电场强度必须为零。
磁场的分类应用高斯定理在磁场中的应用相对较少,因为磁荷的存在极其罕见。
然而,在某些情况下,高斯定理也可用于磁场。
1. 磁场的环状对称性:当磁场具有环状对称性时,高斯定理可以简化计算。
通过选择一个垂直于环的平面作为闭合曲面,可以利用高斯定理计算平面内的磁场强度。
磁场的环状对称性:当磁场具有环状对称性时,高斯定理可以简化计算。
高斯定理的理解及应用
高斯定理(Gauss theorem)是德国数学家约翰·卡尔·高斯在1813年提出来的一个定理,它原本是用来分析平面(二维)的几何,高斯定理的定义是这样的:若棋盘上所有的格点的乘积之和为N,则N等于任意一线条上格点的乘积之和。
应用:
1、高斯消元法:高斯消元法是将线性方程组化为行阶梯形矩阵的运算步骤,可以利用高斯定理来解决线性方程组的求解。
2、求和问题:可以利用高斯定理来求解一个序列的和,它可以帮助我们快
速求出数学序列的和,比如等差数列和等比数列的和。
高斯定律及其应用场景高斯定律是电磁学中重要的定律之一,描述了电场与电荷分布之间的关系。
该定律由德国数学家卡尔·弗里德里希·高斯于19世纪初提出,被广泛应用于电磁学领域。
本文将介绍高斯定律的原理及其在不同场景中的应用。
一、高斯定律的原理高斯定律表明了电场的流量与包围电荷的闭合曲面之间的关系。
它可以用以下公式表示:∮E · dA = Q/ε₀其中,∮E · dA表示电场矢量E通过闭合曲面的面积积分,Q表示被包围的总电荷,ε₀表示真空中的介电常数。
根据高斯定律,电场流量正比于被包围电荷的总量,与电场的强度和分布无关。
这一定律在解决各种电荷分布情况下的电场问题时,提供了一种简化计算的方法。
二、高斯定律的应用场景高斯定律在电磁学中有着广泛的应用,以下将介绍其中的几个常见场景。
1. 理想点电荷高斯定律在处理理想点电荷的问题时特别有用。
根据高斯定律,通过以点电荷为中心的任意闭合曲面的电场流量恒定为非零值。
这意味着与点电荷距离越远的曲面,电场流量越小;而与点电荷距离越近的曲面,电场流量越大。
2. 球对称体高斯定律也适用于球对称体的电荷分布。
对于球体内部的任意点,通过以该点为球心的球面的电场流量为零。
这是因为,球体内部的电场矢量在球面上的分量恒定,而由于球面是闭合曲面,因此电场流量为零。
当处理球对称体的电场问题时,高斯定律可以大大简化计算过程。
3. 无限大平面高斯定律在处理无限大平面的电场问题时同样非常有用。
当电场矢量与平面垂直且分布均匀时,通过平面的电场流量在任意闭合曲面上恒定为非零值。
这意味着无论选择何种形状的闭合曲面,都能得到相同的电场流量值,从而简化了计算过程。
4. 电场的对称性高斯定律在处理具有一定对称性的电场问题时也非常方便。
通过选择合适的闭合曲面,可以使计算中的很多电场矢量互相抵消,从而简化了计算过程。
例如,当电场具有球对称性、柱对称性或平面对称性时,可以利用高斯定律快速求解电场分布。
电场的高斯定理与应用电场是物理学中的重要概念,它描述了电荷之间产生的相互作用力。
为了更好地理解和分析电场的性质,科学家们提出了许多定理和公式。
其中,高斯定理是电场研究中的重要工具之一。
本文将通过介绍高斯定理的原理和应用来深入探讨电场的相关知识。
一、高斯定理的原理高斯定理是由物理学家卡尔·弗里德里希·高斯在18世纪发现的。
它表明,电场穿过闭合曲面的通量与被包围电荷量之比等于真空介电常数ε0。
数学表达式如下:Φ = ∮E·dA = Q/ε0其中,Φ表示电场E穿过闭合曲面内的通量,∮表示对闭合曲面的积分运算,E为电场强度,dA为曲面上的微元面积,Q为被包围的电荷量,ε0为真空介电常数。
二、高斯定理的应用高斯定理可以帮助我们计算某个曲面内的电场强度。
下面将介绍两个具体的应用案例。
1. 均匀带电圆板的电场计算假设有一个半径为R,总电荷量为Q的均匀带电圆板,要求在圆板所在平面上的某点P处的电场强度E。
为了求解这个问题,我们选择一个通过圆板且垂直于圆板的闭合曲面S,如图所示。
根据高斯定理,电场穿过闭合曲面的通量与被包围电荷量之比等于真空介电常数ε0,即Φ = Q/ε0。
[插入示意图:闭合曲面与电场方向示意图]由于圆板是均匀带电的,所以它的电荷分布对称。
在圆板上取一个与圆心重合的小面元dA,根据对称性,dA上的电场与圆板法线方向相同,且大小恒定为E。
因此,被积函数E·dA可简化为E·dA = E·dA·cosθ,其中θ为电场线与法线的夹角。
在整个闭合曲面上求和,得到Φ = E∫dA·cosθ。
由于闭合曲面上θ的取值范围为90°,且cosθ在[0,1]区间内取值,因此cosθ可视为常数。
结合积分公式∫dA = A,其中A表示曲面的面积,即Φ =E·A·cosθ。
同时,由高斯定理可得Φ = Q/ε0。
将Φ = E·A·cosθ = Q/ε0带入,整理得到E = Q/ε0A·cosθ。