六年级数学-折扣成数计算

1.一辆自行车1200元，在原价基础上打八折，小明有贵宾卡，还可以再打九折，小明买这辆车花了多少钱?解：1200×80%×90%=864(元)答：小明买这辆车花了864元。

2.小华买来一个MP3，原价150元，实际只花了六折的钱，比原价便宜了多少钱?解：150×(1-60%)=60(元)答：比原价便宜了60元。

3.妈妈在超市买了一套茶具，打了八五折，花了68元。

这套茶具原价是多少元?解：68÷85%=80(元)答：这套茶具原价是80元。

4.书店对学生购书优惠按七五折售书，明明买了一套书花了24元，节省了多少元?解：24÷75%×(1-75%)=8(元)答：节省了8元。

5.孙家庄的果园前年产量为2.1万吨，去年比前年增产二成，去年产量是多少万吨?解：2.1×(1+20%)=2.52(万吨)答：去年的产量是2.52万吨。

6.妈妈以120元的价格买了一套打折服装，比原价便宜40元。

这套服装是打了几折出售的?解：120÷(120+40)=0.75=75%=七五折答：这套服装是打了七五折出售的。

7.去年赵庄共收小麦500吨，今年收的小麦比去年增产三成。

他们把其中的30%运往仓库储存，剩余的运往面粉加工厂，可加工出多少吨面粉?(小麦的岀粉率按85%计算)解：500×(1+30%)×(1-30%)×85%=386.75(吨)答：可加工出386.75吨面粉。

8.六年级一班班主任带领全班46名学生去公园活动，需要购买门票。

门票价格表规定：每人10元，团体票20人以上按九折优惠；50人以上(含50人)按八折优惠。

请你帮他们算一算，他们怎样买票最划算?解：10×(46+1)=470(元)10×90%×47=423(元)50×80%=400(元)答：买50人的团体票最划算。

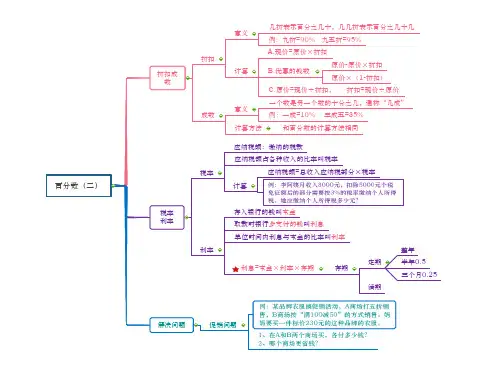
关于百分数的认识和应用，人教版教科书分两步进行。

六年级上册主要编排百分数的认识以及用百分数解决一般性的问题，而本单元主要涉及折扣、成数、税率、利率等百分数的特殊应用，让学生进一步了解百分数在生活中的具体应用，体会百分数与分数之间的内在联系，完善认知结构。

本单元的选材贴近学生生活，直观、有趣，充满时代气息。

教科书依次按照折扣、成数、税率、利率的顺序编排，体现了从简单到综合的层次性。

折扣问题、成数问题都包含了一个数的百分之几、比一个数多(少)百分之几等数量关系，折扣问题与学生的生活实际联系紧密，而成数是表示农业收成方面的术语，或广泛应用于表示各行各业的发展变化情况，学生接触较少。

教科书中涉及成数的实际问题一般是以“增加几成”“减少几成”的形式呈现的，要引导学生将问题转化为“求比一个数多(少)百分之几的数是多少”，同时掌握将成数转化为百分数的方法。

在税率的学习中，教科书着重介绍了应纳税额和税率的含义，揭示了应纳税额、各种收入中应纳税部分与税率三者之间的关系。

在解决实际问题时，教师必须认识到学生感到最困难的并不是计算本身，而是对于税种、应纳税额(一个数)及税率(百分之几)的确定。

教科书在说明储蓄意义的同时，直接介绍了什么是本金、利息、利率以及三者之间的数量关系式，即利息=本金×利率×存期。

由于有存期、利息和本金三个变量，对于学生而言，计算思考的复杂程度大大增加，应用的综合性也更强，在教学时教师应该重视这一问题。

本单元的教学重点是理解掌握折扣、成数、税率和利率的含义，能运用百分数的概念解决生活中的实际问题。

本单元的内容是在学生理解百分数的意义、掌握分数四则混合运算、能用分数四则混合运算解决实际问题、会解决一般性的百分数实际问题的基础上进行教学的。

学生对于折扣、成数、税率、利率等百分数可能会有所了解，但并不能将生活中的这类知识与教科书上的百分数知识相联系，对于知识之间的联系缺乏理解，需要对他们进行规范指导，形成系统性的概念。

第4课时折扣和成数◆教学内容冀教版小学数学六年级上册第62—65页。

◆教学提示几成就是十分之几或百分之几十，三者之间可以互相转化。

解决“成数”问题实际就是求一个数的“十分之几’’或“百分之几”是多少的问题，而解决打折的问题，关键是先将打的折数转化为百分数，再进行解答。

教学中可说出“三成、二成五”等成数，让孩子说出对应的百分数是多少。

之后反过来，由百分数来说出对应的成数，加深二者之间的联系。

◆教学目标1．经历了解商场信息，选择信息提问题并解答“折扣”问题的过程；理解“打折”的含义，会解答有关“折扣”的实际问题。

2．结合具体事例，经历认识“成数”，自主解答有关“成数”的简单实际问题的过程；了解“成数”的含义，会解答有关“成数”的简单实际问题。

3．体会百分数与成数的内在联系以及在现实生活中的广泛应用，获得用数学解决问题的成功体验，丰富学生的生活经验。

重点、难点重点了解“折扣”“成数”的含义，会解答有关“折扣”“成数”的实际问题。

难点了解“折扣”和“成数”的含义，会解答有关“成数”的实际问题。

◆教学准备教师准备：多媒体课件；搜集的有关“折扣”和“成数”的信息。

学生准备：搜集的有关“折扣”和“成数”的信息。

教学过程（一）新课导入：师：要过节了，同学们都很开心，许多商家也很高兴，他们都会看准这一时机，搞许多促销活动。

课前我让大家去了解一些商家的促销手段，有谁来向大家介绍一下你了解的信息?(全班学生交流)师：刚才很多同学都说到了一个新的词“打折”，其实就是降价出售商品，这是商家的一种促销手段。

今天我们先来学习有关“折扣”方面的知识。

(板书课题：折扣)设计意图：数学是一门实用性极强的学科，它源于生活、用于生活，让学生充分了解“折扣”在生活中的广泛应用，体现了数学的应用价值。

（二）新授：1．教学“折扣”。

(1)课件出示商场开业情境图。

师：读图，你们是怎样理解“八五折”和“八折”的?学生讨论后汇报。

生1：“八五折”就是按原价的85％出售。

6年级下册数学第2单元讲解六年级下册数学第二单元学习资料（人教版）一、单元主题。

本单元主要学习百分数（二），包括折扣、成数、税率、利率等与百分数有关的实际生活中的概念和应用。

二、重点知识点。

（一）折扣。

1. 概念。

- 折扣是指商品按原价的百分之几出售，通称“打折”。

例如，几折就表示十分之几，也就是百分之几十。

如八折就是原价的80%，七五折就是原价的75%。

2. 计算方法。

- 已知原价和折扣，求现价：现价 = 原价×折扣。

例如，一件衣服原价100元，打八折出售，那么现价就是100×80% = 80元。

- 已知现价和折扣，求原价：原价 = 现价÷折扣。

例如，一件衣服打六折后售价是60元，那么原价就是60÷60% = 100元。

（二）成数。

1. 概念。

- 成数表示一个数是另一个数的十分之几，通称“几成”。

例如，“一成”就是十分之一，改写成百分数就是10%；“三成五”就是十分之三点五，改写成百分数就是35%。

2. 应用。

- 在农业收成、工业生产等方面经常用到成数。

例如，今年粮食产量比去年增产二成，就是说今年粮食产量是去年的（1 + 20%）=120%。

（三）税率。

1. 概念。

- 应纳税额与各种收入（销售额、营业额……）的比率叫做税率。

2. 计算方法。

- 应纳税额 = 收入×税率。

例如，某商店的营业额是10万元，按照5%的税率纳税，那么应纳税额就是100000×5% = 5000元。

（四）利率。

1. 概念。

- 单位时间（如1年、1月、1日等）内的利息与本金的比率叫做利率。

2. 相关公式。

- 利息 = 本金×利率×存期。

例如，本金1000元，年利率是3.25%，存期2年，那么利息就是1000×3.25%×2 = 65元。

- 本息和=本金 + 利息。

在上面的例子中，本息和就是1000+65 = 1065元。

三、易错点。

数学六年级下册-《折扣和成数》知识讲解折扣问题的解题⽅法折扣问题的解题⽅法问题(1)导⼊(1)爸爸给⼩⾬买了⼀辆⾃⾏车，原价180元，现在商店打⼋五折出售。

买这辆车⽤了多少钱？(2)爸爸买了⼀个随⾝听，原价160元，现在只花了九折的钱，⽐原价便宜了多少钱？（教材8页例1）过程讲解1．解决问题(1)——求⾃⾏车的钱数(1)理解句意：“现在商店打⼋五折出售”的意思就是现在的商品价格是原价的85%。

(2)理解所求问题：“买这辆车⽤了多少钱”就是求原价的85%是多少。

(3)探究解题思路：⾃⾏车原价是单位“1”的量，单位“1”已知，是180元，求180元的85%是多少，⽤乘法计算。

(4)列式解答：180×85%=153（元）答：买这辆车⽤了153元。

2．解决问题(2)——求随⾝听⽐原价便宜的钱数(1)理解句意：“现在只花了九折的钱”是指现在买⼀个随⾝听只花了原价的90%。

(2)理解所求问题：“⽐原价便宜了多少钱”就是求现在⽐原来少花了多少钱。

(3)探究解题⽅法。

⽅法⼀①解题思路：先求出现在买随⾝听所花的钱数（现价），即原价乘折扣。

再⽤原价减去现价，求出⽐原价便宜的钱数。

②列式解答： 160-160×90%=160-144=16(元)⽅法⼆①解题思路：现价是原价的90%，是把原价看作单位“1”，那么现价就⽐原价少1-90% =10%，⽤原价乘10%就是所求问题。

②列式解答： 160×(1-90%)=160×10%=16(元)答：⽐原价便宜了16元。

问题(2)导⼊⽻绒服打折促销期间，王阿姨花了520元钱买了⼀件打六五折的⽻绒服。

这件⽻绒服的原价是多少钱？过程讲解1．读题，理解题意(1)已知条件：⽻绒服现价是520元；打六五折出售。

(2)所求问题：⽻绒服的原价是多少钱？2．探究解题思路已知原价的65%是520元，是把原价看作单位“1”，单位“1”未知，可以列⽅程解答或⽤除法计算。

人教版第二单元《百分数（二）》（一）、折扣和成数1、折扣：用于商品，现价是原价的百分之几，叫做折扣。

通称“打折”。

几折就是十分之几，也就是百分之几十。

解决打折的问题，关键是先将打的折数转化为百分数或分数，然后按照求比一个数多（少）百分之几（几分之几）的数的解题方法进行解答商品现在打八折：现在的售价是原价的80﹪商品现在打六折五：现在的售价是原价的65﹪2、成数：几成就是十分之几，也就是百分之几十。

解决成数的问题，关键是先将成数转化为百分数或分数，然后按照求比一个数多（少）百分之几（几分之几）的数的解题方法进行解答这次衣服的进价增加一成：这次衣服的进价比原来的进价增加10﹪今年小麦的收成是去年的八成五：今年小麦的收成是去年的85﹪（二）、税率和利率1、税率（1）纳税：纳税是根据国家税法的有关规定，按照一定的比率把集体或个人收入的一部分缴纳给国家。

（2）纳税的意义：税收是国家财政收入的主要来源之一。

国家用收来的税款发展经济、科技、教育、文化和国防安全等事业。

（3）应纳税额：缴纳的税款叫做应纳税额。

（4）税率：应纳税额与各种收入的比率叫做税率。

（5）应纳税额的计算方法：应纳税额=总收入×税率收入额=应纳税额÷税率2、利率（1）存款分为活期、整存整取和零存整取等方法。

（2）储蓄的意义：人们常常把暂时不用的钱存入银行或信用社，储蓄起来，这样不仅可以支援国家建设，也使得个人用钱更加安全和有计划，还可以增加一些收入。

（3）本金：存入银行的钱叫做本金。

（4）利息：取款时银行多支付的钱叫做利息。

（5）利率：利息与本金的比值叫做利率。

（6）利息的计算公式：利息＝本金×利率×时间利率＝利息÷时间÷本金×100％（7）注意：如要上利息税（国债和教育储藏的利息不纳税），则：税后利息=利息-利息的应纳税额=利息-利息×利息税率=利息×(1-利息税率)税后利息=本金×利率×时间×(1-利息税率)购物策略：估计费用：根据实际的问题，选择合理的估算策略，进行估算。

六年级折扣成数税率知识点在六年级学习数学的过程中，折扣、成数和税率是我们需要掌握的重要知识点。

本文将简要介绍这些知识点的概念和计算方法，帮助同学们更好地理解和运用。

一、折扣折扣是指商家为促销目的而对商品价格进行的减免。

通常以百分数表示，表示价格打几折。

折扣和折扣后的价格都是以百分数形式给出的，我们需要学会计算折扣和折扣后的价格。

例如，如果商品原价是100元，打8折，那么折扣是80%。

我们可以通过以下公式来计算折扣后的价格：折扣后价格 = 原价 ×折扣所以上述例子中，折扣后的价格是100 × 0.8 = 80元。

同学们可以通过做一些实际的练习题来加深对折扣计算的理解。

二、成数成数是指以百分数形式表示的比例。

例如，80%可以读作80成，90%可以读作90成。

我们需要掌握如何将成数转换为分数、小数和百分数。

1. 将成数转换为分数：将成数的数字部分作为分子，分母为100。

例如，80%可以转换为80/100，即4/5。

2. 将成数转换为小数：将成数的数字部分除以100。

例如，80%可以转换为0.8。

3. 将成数转换为百分数：直接在数字后面加上百分号。

例如，80可以写作80%。

成数在实际生活中广泛应用，我们可以通过举一些例子，如考试的成绩、商场的折扣等来加深对成数的理解。

三、税率税率是指用以计算税额的比例。

在生活中，我们经常遇到各种涉及税率的情况，如增值税、个人所得税等。

学习税率的计算方法，有助于我们在实际生活中更好地理解价格和税收之间的关系。

税率和税额都是以百分数形式给出的，我们需要学会计算税率和税额。

1. 计算税额：将需要计税的金额乘以税率，得到税额。

例如，某商品售价100元，税率为10%，那么税额为100 ×10% = 10元。

2. 计算含税价格：含税价格 = 售价 + 税额。

例如，某商品售价100元，税率为10%，那么含税价格为100 + 10 = 110元。

通过实际的例子和计算练习，我们能够更好地理解税率的概念和计算方法。

六年级数学下册第二单元折扣成数教学内容：人教版六年级数学下册课本第8~9页例1.2及做一做.练习二第1~5题·教学目标：明确折扣的含义.能熟练地把折扣写成分数.百分数.正确解答有关折扣的实际问题·明确成数的含义.能熟练的把成数写成分数.百分数.能正确解答有关成数的实际问题·教学重点：理解“折扣”和“成数”的意义·教学难点：合理.灵活地选择方法.解答有关折扣和成数的实际问题·教学过程：一.创设情境.导入新课圣诞节期间各商家搞了哪些促销活动？谁来说说他们是怎样进行促销的？（学生汇报调查情况·）二.探索交流.解决问题1.教学折扣的含义.会把折扣改写成百分数·（1）刚才大家调查到的打折是商家常用的手段.是一个商业用语.那么你所调查到的打折是什么意思呢？比如说打“七折”.你怎么理解？（2）你们举的例子都很好.老师也搜集到某商场打七折的售价标签·（电脑显示）①大衣.原价：1000元.现价：700元·②围巾.原价：100元.现价：70元·③铅笔盒.原价：10元.现价：？元·④橡皮.原价：1元.现价：？元·（3）动脑筋想一想：如果原价是10元的铅笔盒.打七折.猜一猜现价会是多少？如果原价是1元的橡皮.打七折.现价又是多少？（4）仔细观察.商品在打七折时.原价与现价有一个什么样的关系？带着这样的问题.可以利用计算器.也可以借助课本.四人小组一起试着找到答案·（5）讨论.找规律·A.学生动手操作.计算.并在计算或讨论中发现规律·B.学生汇报寻找的方法：利用计算器.原价乘以70%恰好是标签的售价或现价除以原价大约都是70%；或查书等等·（6）归纳.得定义·A.通过小组讨论.谁能说说打七折是什么意思？打八折是什么意思？打八五折呢？B.概括地讲.打折是什么意思？如果用分母是十的分数.该怎样表示？（“几折”就是十分之几.也就是百分之几十）C.通俗来讲.商店有时降价出售商品.叫做打折扣销售.通称“打折”·几折就是十分之几.也就是百分之几十·如八五折就是85%.九折就是90%·一般情况下.不把折扣写成十分之几这样的分数形式.写成分数时.有时会出现小数（例如八五折就会写成）.不便于计算和理解·2.运用折扣含义解决实际问题·出示问题（1）：爸爸给小雨买了一辆自行车.原价180元.现在商店打八五折出售·买这辆车用了多少钱？①导学生分析题意：打八五折怎么理解？是以谁为单位“1”？②找出数量关系式·先让学生找出单位“1”.然后再找出数量关系式：原价×85%=实际售价③根据数量关系式.学生独立列式解答·④全班交流·根据学生的汇报·出示问题（2）：爸爸买了一个随身听.原价160元.现在只花了九折的钱.比原价便宜了多少钱？①导学生理解题意：只花了九折的钱怎么理解？以谁为单位“1”？②学生试算.独立列式·③全班交流·根据学生的汇报.板书：第一种算法：原价160元.减去现价.就是比原价便宜多少钱·160-160×90%=160-144=16（元）第二种算法：原价160元.现价比原价便宜了（1-90%）·160×(1-90%)=160×10%=16（元）重点引导学生理解第二种算法.知道现价比原价便宜了10%·3.介绍成数的含义.会把成数改写成分数.百分数·（1）刚才大家都说了很多有成数的发展变化情况.那么这些“成数”是什么意思呢？比如说.增产“二成”.你怎么理解？（学生讨论并回答）（成数:表示一个数是另一个数的十分之几.通称“几成”）（2）试说说以下成数表示什么？①出口汽车总量比去年增加三成·这里的“三成”表示什么？②北京出游人数比去年增加两成·这里的两成表示什么？引导学生讨论并回答·4.运用成数的含义解决实际问题·（1）出示教材第9页例2：某工厂去年用电350万千瓦时.今年比去年节电二成五.今年用电多少万千瓦时？（2）分析题目.理解题意：①今年比去年节电二成五怎么理解？是以哪个量为单位“1”？②找出数量关系式·先让学生找出单位“1”.然后再找出数量关系式：今年的用电量=去年的用电量×（1-25%）③根据关系式.学生独立列式解答·全班交流·方法一：350×（1-25%）=350×75%=350×0.75=262.5(万千瓦时)方法二：350×（1-25%）=350×75%=350×75/100=262.5（万千瓦时）三.巩固应用.内化提高1.课本第8页“做一做”·2.课本第9页“做一做”·3.课本第13页练习二第1~5题·四.回顾整理.反思提升通过这节课的学习你有什么收获？。