15微分关系法绘制弯矩与剪力图(精)

多种方法快速绘制剪力图和弯矩图摘要：绘制梁的内力图是材料力学课程的重点问题，也是难点问题，对于初学的学生不易理解。

本文分析了绘制剪力图和弯矩图的多种方法，比较不同方法之间的区别，旨在帮助学生掌握快速绘制剪力图和弯矩图技巧。

关键词：剪力图弯矩图面积法叠加法 1 引言直梁的弯曲变形是杆件受力变形的基本形式之一，在对梁进行强度校核时，根据剪力图和弯矩图中曲线的变化规律，确定等截面弯曲梁的危险截面，因此快速准确绘制剪力图和弯矩图对工程计算非常重要。

绘制剪力图和弯矩图内容复杂，学生较难理解，容易出错。

不同的教材对于剪力图和弯矩图的绘制方法阐述大同小异，主要分为截面法、利用微分关系绘图、叠加法等，在原有绘图方法的基础上，提出自己新的理解，可以有助于学生快速、准确绘制剪力图和弯矩图。

2 直接绘制剪力图和弯矩图例：一外伸梁受力图如图1(a)所示，集中荷载qa/4作用在梁两端，BC梁段受到方向向下大小为q的均匀荷载，CD梁段受到方向向上大小为q的均匀载荷，绘出梁的剪力图和弯矩图。

解：(1)选取整个梁为研究对象，通过平衡方程获得支座反力，FBy=3qa/4，FDy=-qa/4。

(2) 绘制剪力图。

过A点建立水平方向的x轴，竖向的FS轴，方向向上为正。

从原点（0,0）即A+截面（过A点左横截面）开始，初始截面处于自由端，剪力为零。

遇到作用在A点向下的集中载荷，则剪力顺着箭头方向下降qa/4，下降值和集中载荷的大小相同，则对应于A-截面（过A点右横截面）的剪力图坐标为（0，-qa/4)。

AB段无荷载，所以剪力图保持直线，即B+截面处的剪力图坐标为（a，-qa/4)。

在B点处受到约束力FBy的作用，方向向上，B-截面处的剪力图坐标为（a，qa/2)，剪力变化值等于约束力FBy。

BC段梁受到向下均匀载荷的作用，剪力均匀下降，由点B-(a，qa/2)均匀下降到C(2a，-qa/2)，斜率为-q。

CD段的剪力受到向上均匀载荷的作用，剪力均匀上升，由点C(2a，-qa/2)均匀上升到D(3a，qa/2)，斜率为q。

轴，。

以表(a)(c)（1）（2） （3）≤ (4) 以剪力图是平行于轴的直线。

段的剪力为正，故剪力图在轴上方；段剪力为负，故剪力图在轴之下，如图8-12(b )所示。

由式（2）与式（4）可知，弯矩都是的一次方程，所以弯矩图是两段斜直线。

根据式（2）、（4）确定三点，， ，由这三点分别作出段与段的弯矩图，如图8-12(c )。

例8-4 简支梁受集度为的均布载荷作用，如图8-13(a )所示，作此梁的剪力图和弯矩图。

图8-13解 （1）求支反力 由载荷与支反力的对称性可知两个支反力相.即（2）列出剪力方程和弯矩方程 以梁左端为坐标原点，选取坐标系如图所示。

距原点为的任意横截面上的剪力和弯矩分别为x C l x AC x BC x x 0=x 0)(=x M a x =l Fabx M =)(l x =0)(=x M AC BC AB q A x解 （1）求支反力 由静力平衡方程，得（2）列剪力方程和弯矩方程 由于集中力作用在处，全梁内力不能用一个方程来表示，故以为界，分两段列出内力方程段0＜≤ (1)0≤＜ (2)段 ≤＜ (3)≤≤(4) （3） 画剪力图和弯矩图 由式（1）、（3）画出剪力图，见图8-14(b )；由式（2）（4）画出弯矩图，见图8-14(c )。

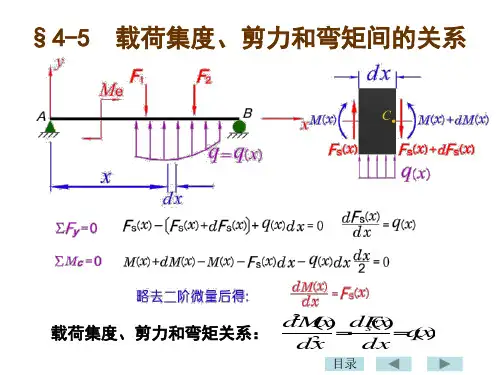
二、弯矩、剪力与分布载荷集度之间的微分关系在例8-4中，若将的表达式对取导数，就得到剪力。

若再将的∑=0)(x M A ∑=0)(x M B m C C AC l mF x F A Q ==)(x a xl m x F x M A ==)(x a BC l mF x F A Q ==)(a x l mx l mm x F x M A -=-=)(a x l )(x M x )(x F Q )(x F Q表达式对取导数，则得到载荷集度。

这里所得到的结果，并不是偶然的。

实际上，在载荷集度、剪力和弯矩之间存在着普遍的微分关系。

现从一般情况出发加以论证。

《机电技术》2010年第3期 机电研究及设计制造利用微分法快速绘制剪力图与弯矩图陈小兰 陈晓波(鄂东职业技术学院，湖北 黄冈 438000)摘 要：本文根据载荷集度、剪力和弯矩三者的微分关系，介绍一种简易快速绘制剪力图和弯矩图的方法——微分关系法，省去了截面法“截、代、平”及建立剪力和弯矩方程的复杂过程，可以高效的、巧妙的绘制出剪力图和弯矩图。

关键词：微分法；剪力图；弯矩图；直梁弯曲中图分类号：TB301 文献标识码：A 文章编号：1672－4801(2010)03－060－03在高职教材《机械设计基础》材料力学这一篇中，直梁的弯曲变形是杆件的基本变形之一，在对梁进行强度和刚度计算时，通常要画出剪力图和弯矩图（即将梁上所有横截面上的剪力和弯矩用函数图象的形式表示出来），以便清楚地看出梁各个横截面上剪力和弯矩的大小、正负以及危险截面（即弯矩最大值所在截面的位置）。

这一节内容往往是学生不容易掌握的，是教学的难点，但是它又是教学的重点，是后面章节尤其是轴的强度校核的基础。

所以学好梁的弯曲变形这一节内容显得非常重要。

而分析梁的弯曲变形主要就是绘制梁的各个横截面上的剪力和弯矩，即绘制剪力图和弯矩图。

因此剪力图和弯矩图的正确快速绘制是分析问题的关键。

本文根据载荷集度、剪力和弯矩三者的微分关系，介绍一种简易快速绘制剪力图和弯矩图的方法——微分关系法，省去了截面法“截、代、平”及建立剪力和弯矩方程的复杂过程，可以高效、巧妙地绘制出剪力图和弯矩图。

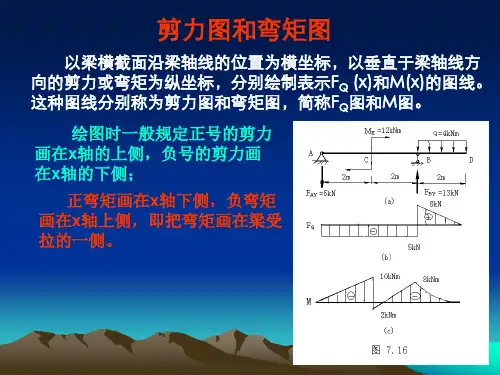
1 微分法绘制剪力图和弯矩图1.1 载荷集度、剪力和弯矩的微分关系载荷集度q 、剪力Q F 、弯矩M 三者存在的微分关系为：弯矩方程的一阶导数等于剪力方程，剪力方程的一阶导数等于载荷集度，即()()(),()Q Q dF x dM x F x q x dx dx==。

根据上式微分关系得出以下推论[1]： (1)在梁的某段，若无载荷作用，即()0q x =，则()Q F x =常数，剪力图是一条与x 轴平行的水平线，而()M x 为一次函数，弯矩图为一条斜直线，斜率为剪力的值。

口诀法在梁内力图绘制中的应用（苏科大土木学院2020.5）弯矩与剪力有这样的关系：弯矩方程比剪力方程高一阶，弯矩方程的一阶导数是剪力方程，弯矩图的在某个截面的斜率值恰恰就是该截面的剪力。

弯矩与剪力、分布荷载之间的微分积分关系，可作为弯矩图绘制的理论依据。

本文以画梁的内力图为例，淡淡形象教学法在力学教学中的应用。

利用形象的口诀同时将弯矩、剪力与荷载集度问的微分关系及梁的内力图的一些特点，文献中的作者们做了大量工作，这里作汇总如下（部分略有改动）。

（1）黄氏口诀[3]：剪力图口诀：剪力跟随载荷走；均布载荷顺着斜；集中力处随着跳；上下看力的方向，遇到力偶剪力不会变。

（要求从左至右画）。

弯矩图口诀：差值等于Q与轴围图的面积；突变朝着同向矢；曲线突向顺着q；顶点正好对零剪。

特征：分段、突变、直线、曲线。

（2）高氏口诀[4]：均布荷载负，剪力下（右下）斜路．弯矩下（下凸）抛物；均布荷载零，剪力直线平，弯矩斜向行；集中力在梁上现．剪力要突变（顺F方向），弯矩定折转（F作用截面出现折角）；力偶作用面，剪力照常现（左右相同），弯矩要突变（顺时针力偶向下突变）。

最大弯矩可能发生在F，零（剪力为零）、F。

变（剪力变号）和紧靠力偶一侧面。

（3）钱氏口诀[5]：剪力图口诀：没有外力，水平线；均布外力，斜直线；集中外力，有突变；集中力偶，不用变。

剪力、弯矩图的相对应口诀：①你无我平，你平我斜，你斜我弯，弯线顶点你为0；②顺流而下，逆流而上，集中力偶来管上；③上尖角、下尖角，外力指向要看好。

（4）网络口诀（作者不详）。

剪力图口诀:外伸端，自由端，没有集中力取零点。

无力梁段Q水平线，集中力偶同样看，均布荷载Q应为斜线，小q正负定增减，集中力处有突变，左顺右逆画竖线，增多少？降多少？集中横力作参考。

弯矩图口诀:弯矩图，较复杂，对照剪图来画它；自由端，铰支端，没有力偶作零点。

剪图水平弯图斜，剪力正负定增减；天上下雨池水满，向上射出弓上箭。