当前位置：文档之家 › 弯曲变形内力图绘制方法

弯曲变形内力图绘制方法

  • 格式：doc
  • 大小：25.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

材料力学刘鸿文第六版最新课件第四章 弯曲内力

材料力学刘鸿文第六版最新课件第四章 弯曲内力

回顾
第三章 扭 转
§3.1 扭转的概念和实例 §3.2 外力偶矩的计算 扭矩和扭矩图 §3.3 纯剪切（薄壁圆筒扭转问题） §3.4 圆轴扭转时的应力 §3.5 圆轴扭转时的变形 §3.6 圆柱形密圈螺旋弹簧的应力和变形 §3.7 非圆截面扭转的概念 §3.8 薄壁杆件的自由扭转
第四章 弯曲内力
M l
e
(l
x2 )
FA
Me
a
b
A
C
x1
x2
l
FS
+
FB
B
Me lx
(3)根据方程画内力图
FS
(
x1
)
M l
e
FS (x2 )
Me l
M x
FA
Me
a
b
A
C
x1
x2
l
FS
+
M
a l
M
e
+
－
b l
M
e
FB
B
Me
lx
(3)根据方程画内力图
FS
(
x1
)
M l
e
FS (x2 )
M
(x1)
M l
Me
l e x1
a l F(lx2 )
FA a F
b
A x1
C
x2
l
FS
bF
+l
－
M
FB (3)根据方程画内力图
B
b
FS (x1) l F
FS
( x2
)
a l
F
x
a l
F
x
FA a F
b

弯曲(1)

弯曲(1)

a
A
b F
C
B
b M FA x1 Fx1 l 0 x1 a
x1 0 时 M 0 x1 a 时 M ab F
x1 x2
ab M F l
a M =- l FX2 +aF a x2 l
直线
ab x2 a 时 M F l x2 l 时 M 0
l
(4). 简支梁受集中力偶 例4：如图所示的简支梁AB，在点C处受集中力偶M0作用， 尺寸a、b和L均为已知，试作此梁的弯矩图。 解： 1.求约束反力 x2
使微段梁两相邻截面发生左上右下的相对错动时,横截面 上的剪力为正 使微段梁弯曲成凹形时的弯矩为正,弯曲成凸形时的弯矩 为负
课本P39
二. 内力分析结果
内力名称：剪力Q和弯矩M 内力计算：
内力数值—剪力数值上等于所求截面任一侧所有 外力的代数和；弯矩数值上等于所求截面任一侧所有 外力对该截面形心力矩的代数和（包括外力偶） 内力符号—左上右下，剪力为正；左顺右逆，弯 矩为正
a M M0 l
M0 M M 0 FA x2 M 0 x2 l
a x2 l
x2 a
x2 l
b M M0 l M 0
剪力和弯矩的规律
剪力和弯矩的规律
弯矩图的规律
1.梁受集中力或集中力偶作用时，弯矩图 为直线，并且在集中力作用处，弯矩发生转 折；在集中力偶作用处，弯矩发生突变，突 变量为集中力偶的大小。 2.梁受到均布载荷作用时，弯矩图为抛物 线，且抛物线的开口方向与均布载荷的方向 一致。 3.梁的两端点若无集中力偶作用，则端点 处的弯矩为0；若有集中力偶作用时，则弯 矩为集中力偶的大小。
变形量 强度计算

工程力学05-杆件的内力图

工程力学05-杆件的内力图
《工程力学》
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
构件内力图概念、画法
杆件基本变形时内力图的表示
内力图沿杆轴线的分布规律 最大内力与危险截面的确定
《工程力学》
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
5.2 轴力图与扭矩图
5.2.2 扭矩图 1）扭转内力分量与扭矩
作用在杆件上的外力偶矩可以向杆轴线简化， 简化的结果若力偶作用面在横截面上，该力偶矩分 量——扭矩 扭矩可以是外力简化，也可以由传递的功率计 算得到 2）功率P、转速n和外力偶矩T P (5-1) T=9549 n (N.m) 式中： P：功率（kW) n：转速（r/min)
d
D MD D
确定控制截面
《工程力学》
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
5.2 轴力图与扭矩图
5.2.2 扭矩图 MA=1146N.m，MB=MC=350N.m，MD=446N.m。 MB MC MA 求各截面扭矩 BC段 SMx= 0 B C A
C
l l MO =2FPl
FP D B
MC C
l
FP
D B
FQC
S M C= 0
解得：
– MC + MO – FP×l =0
FQC=FP MC = MO – FP×l = 2FPl– FPl = FPl

工程力学第八章__直梁弯曲

工程力学第八章__直梁弯曲
作用面内的一条曲线。
（3）构件特征：具有一个以上对称面的等截
面直梁。
§8－1 平面弯曲的力学模型
二、梁的力学模型 1．梁的结构形式 工程中梁的轴 线多为直线。无论截 面形状如何，在计算 简图中的梁，一般均 用与梁轴线重合的一 段直线表示
§8－1 平面弯曲的力学模型
2．梁的支座 梁的支撑情况，要通过分析来确定在载 荷作用平面内支座对梁的约束类型以及相 应的约束反力数目。一般情况下，可将梁 的支承简化为以下三种典型支座之一：
§8－2 弯曲内力——剪力和弯矩
管钳的应用分析
在拧、卸管状零件 时，常常要使用管钳给 管件施加转矩，将管件 拧紧或卸下。当拆卸连 接牢固的管子时，常在 钳柄部分加套管，以增 大转矩。那么，在这种 情况下，钳牙是否会损 坏？
1一固定牙 2一可动牙 3-圆螺母 4一齿条 5一弹簧 6-钳柄 7-销轴
§8－2 弯曲内力——剪力和弯矩
2．改变加载方式，在结构允许的条件下，应 尽可能把集中力改变为分散力
集中力改变为分散力
§8－5 提高梁抗弯强度的主要措施
工程应用
吊车与平板车
吊车简图
平板车过桥
§8－5 提高梁抗弯强度的主要措施
3．增加约束 如图a所示，某变速器 换挡杆1需要加工一个R8的 月牙槽，以往是把月牙槽 铣刀悬挂地装在铣床主轴 上，利用工作台的升降进 行铣削加工。
§8－3
弯曲正应力
2．中性轴与中性层
§8－3 弯曲正应力
二、正应力的分布规律
横截面上各点正应力的大小与该点到中性轴 的距离成正比：

y


max
y max
在中性轴处纤维长度不变，此处 不受力，正应力为零。

材料力学第四版刘鸿文编第04章弯曲内力

材料力学第四版刘鸿文编第04章弯曲内力

FA a F
b
A x1 C x2
l
+
b l
F
FS图
－
Fab
l
M图
+
FB
B
(4)内力图特征
在集中力作用的地方，
剪力图有突变，外力F向
下，剪力图向下变，变化
值=F 值；弯矩图有折角。
a l
F
[例6] 求梁的内力方程并画出内力图。
FA
Me
a
b
A
C
x1
x2
l
(2)写出内力方程
AC段：
FS(x1)FA
M(x1)F1x
1 2
qax
1
F S (x 2 )F q (x 2 a )q2aq(x2 a)
M (x2)F2x 1 2q(x2a)2 12qa2x12q(x2a)2
A x1 B x2
a
F qa 2
FS
qa
2
+
M
q
C 2a
(2)根据方程画内力图
FS
(x1)
qa 2
q2aq(x2a)
FS(x2)
极值点： 令FS(x2)0
即：q2aq(x2a)0
得：
x
0

3 2
a
M 0 85qa2
§4–5 载荷集度、剪力和弯矩间的关系 一、 剪力、弯矩与分布荷载间的关系
取一微段dx， 进行平衡分析。
q(x)
Fy 0 ,
FS(x) q(x)dxF S(x)dF S(x)0
a
2 qa qa 1 qa
3
3
MO0,FA2a1 2q2aM0,
q

土木工程力学基础多学时四单元1直梁弯曲弯曲内力1

土木工程力学基础多学时四单元1直梁弯曲弯曲内力1

三．梁的内力图
例 4－ 2 悬臂梁在自由端受集中力作用如 图4－7所示。试写出梁的剪力方程和弯矩方 程、画出剪力图和弯矩图，并确定梁的最大 剪力和最大弯矩。
剪力方程：Q=P=-Px，各 横截面的弯矩沿轴线呈直 线变化，故可由弯矩方程 确定两点：
x=0, M=0 x=l, M=-Pl
M
max
Pl
三．梁的内力图

例4－3 简支梁受集中力作用如图4－8所示，求 梁的剪力方程和弯矩方程，画出Q、M图并确定最 大剪力和最大弯矩。
例4－4 简支梁受均布荷载作用如图4－9所示，求梁的剪力 方程和弯矩方程，画Q、M图，确定最大剪力和弯矩。
解：（1）计算支座反力
R A RB 1 ql 2
x 0, M 0
x
x l, M 0
1 1 l , M ql 2 2 8
三．梁的内力图
3.单跨梁在简单荷载 作用下的内力图特点 与规律
三．梁的内力图
2．运用简捷作图法绘制梁的剪力图和弯矩图
解：（1）计算支座反力
R A 8kN Rc 20 kN
（2）作剪力图
AB段：梁上无荷载，Q图为一条水平线，
一端为固定铰支座， 另一端为可动铰支座。
一．梁的形式
2.外伸梁
简支梁的一端或两端 伸出支座之外的梁,
一．梁的形式
3.悬臂梁
一端为固定端， 另一端为自由端的梁。
二．梁的内力
1.梁的内力——剪力和弯矩 梁发生弯曲时，横截面上同时存在两个内 力—剪力Q 和弯矩 M 剪力的常用单位为牛顿（N）或千牛顿（kN）， 弯矩的常用单位为牛顿米（N· m）或千牛顿米 （kN· m）。
右 QA ＝R A 8kN

《工程力学》项目9平面弯曲

《工程力学》项目9平面弯曲

项目9 剪切与挤压
• 任务9.4 平面弯曲梁横截面上的应力 • 梁的横截面上只有弯矩而剪力为零的平面弯曲称为纯弯
曲，如图 9-20梁上CD段；而横截面上既有弯矩也有剪力 的平面弯曲称为横力弯曲或剪力弯曲，如图 9-20梁上AC、 DB段。
图 9-20
项目9 剪切与挤压
9.4.1纯弯曲时梁横截面上的应力 1.实验现象 2.假设及推理 • 研究纯弯曲时梁横截面上的应力，可
式（9-2），即可确定截面上的剪力和弯矩为
3
FS2
YA
qa 4
M2
YAa
3 qa2 4
项目9 剪切与挤压
• 3-3截面：将杆件截面右侧的所有的外力给屏蔽起来，如图
9-7（d）所示，取截面的左侧为研究对象，即可确定截面上
的剪力和弯矩为
FS3
YA
P
3 qa qa 4
1 4
qa
M3
YAa
P0
3 4
9-4（b）所示。 外伸梁：梁的支撑情况同简支梁，但梁的一端或两端伸出支座
之外，如图 9-4（c）所示。
图9-4
项目9 剪切与挤压
• 任务9.2 梁弯曲的内力
• 9.2.1梁弯曲内力——剪力和弯矩
• 根据力系的平衡条件，可确定在留 下部分的截面上的内力为平行于横 截面的剪力和作用在纵向对称面内 的内力矩即弯矩。根据平衡方程可 得剪力与弯矩的大小，即
• 为了直观清楚地显示沿梁轴线方向的各截面剪力和 弯矩的变化情况，可绘制剪力图和弯矩图。对剪力 图，正值画在轴线的上侧，负值画在轴线的下侧； 对弯矩图正值画在轴线的下侧，负值画在轴线的上 侧，即弯矩坐标正向向下。
项目9 剪切与挤压
• 【例 9-2】图 9-8（a）所示的简支梁受均布荷载作用，试 作其剪力图和弯矩图。

刘鸿文《材料力学》(第5版)笔记和课后习题(含考研真题)详解-弯曲内力(圣才出品)

刘鸿文《材料力学》(第5版)笔记和课后习题(含考研真题)详解-弯曲内力(圣才出品)
1 / 49
圣才电子书 十万种考研考证电子书、题库视频学习平台

图 4-3
2．载荷的简化 （1）集中载荷：载荷的作用范围远小于杆件轴向尺寸。 （2）分布载荷：沿轴向连续分布在杆件上的载荷，常用 q 表示单位长度上的载荷，称 为载荷集度，如风力、水力、重力。常用的有均布载荷，线性分布载荷。 （3）集中力偶
3．静定梁的基本形式 为方便梁的求解，通常将梁简化，以便得到计算简图。当梁上支反力数目与静力平衡方 程式的数目相同时，即支反力通过静力平衡方程即可完全确定时，称之为静定梁，以下三种 形式的梁均为静定梁。 （1）简支梁：一端为固定铰支座，一端为可动铰支座，如图 4-4 所示。
图 4-4 （2）外伸梁：一端或两端向外伸出的简支梁，如图 4-5 所示。
4.2 课后习题详解
5 / 49
圣才电子书 十万种考研考证电子书、题库视频学习平台

4.1 试求图 4-8 所示各梁中截面 1-1，2-2，3-3 上的剪力和弯矩，这些截面无限接近 于截面 C 或截面 D。设 F，q，a 均为已知。
图 4-8 解：（a）①1-1 截面：沿该截面断开，对右部分进行受力分析，根据平衡条件：
④若
FS
(x)
=
0 ，则
dM (x) dx
=
FS
(x)
=
0
。此时该截面上弯矩有极值（极大值或极小
值）。此外，弯矩的极值还可能出现在集中力和集中力偶作用处截面。
3．外力与内力图的内在联系
（1）斜率规律
剪力图在任一截面处的斜率值等于该截面外力分布载荷的集度值，同理弯矩图图在任一
截面处的斜率值等于该截面剪力值：
圣才电子书

十万种考研考证电子书、题库视频学习平台

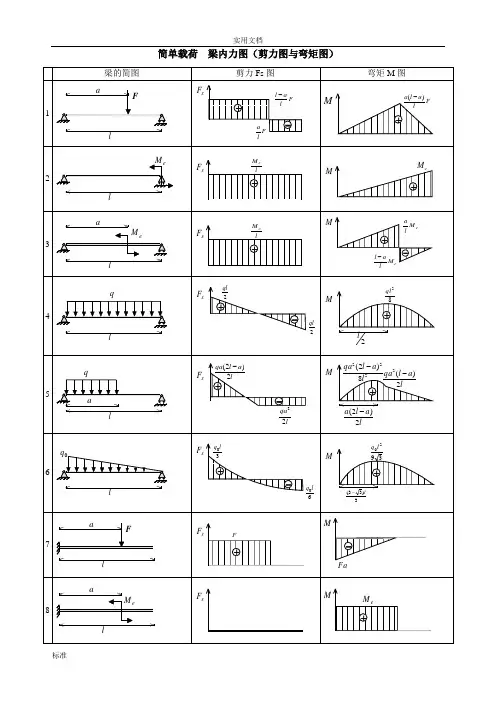
梁 弯矩图 梁 内力图 (剪力图与弯矩图)

梁 弯矩图 梁 内力图 (剪力图与弯矩图)

简单载荷梁内力图（剪力图与弯矩图）表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5标准标准标准标准标准标准标准注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

实用文档2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝11.76kN/m ，每跨各有一集中荷载F ＝29.4kN ，求中间支座的最大弯矩和剪力。

[解] M B 支＝（－0.125×11.76×52）＋（－0.188×29.4×5）＝（－36.75）＋（-27.64）＝－64.39kN ·m V B 左＝（－0.625×11.76×5）＋（－0.688×29.4）＝（－36.75）＋（－20.23）＝－56.98kN[例2] 已知三跨等跨梁l ＝6m ，均布荷载q ＝11.76kN/m ，求边跨最大跨中弯矩。

建筑力学

建筑力学
又由 MB 0 得 F1 5 F2 2 FA 6 0
由①、②得 FA 35kN
FB 25kN
(2)求截面1-1上的内力
在截面1-1处将梁截开，取左段梁为研究对象，画出其受力图如图88（b)，内力 FS1和 M1 均先假设为正的方向，列平衡方程：
由 Fy 0 得 由 M1 0 得
图8-5
剪力的常用单位为N或kN，弯矩的常用单位为N·m，或kN·m
剪力和弯矩的大小，可由左段梁的静力平衡方程求Fs 0
得
Fs FA
由
M0 0
FA a M 0
得
M FA a
据作用如与果反取作右用段力梁的作关为系研，究它对们象与，从同右样段可梁求求得出截m面mm截m面上上的FFSS
第八章 梁的弯曲
a
第一节 梁的平面弯曲
一、弯曲变形和平面弯曲 弯曲是构件变形的基本形式之一。当一杆件 在两端承受一对等值、反向的外力偶作用，且 力偶的作用面与杆件的横截面垂直时，如图81（a），杆件的轴线由直线变为曲线，这种变 形称为弯曲变形，简称弯曲。
（a）
图 8-1
（b）
有时，杆件在一组垂直于杆轴的横向 力作用下也发生弯曲变形，如图8-1（b）， 发生这种弯曲变形时还伴有剪切变形，此 称为剪切弯曲或横向弯曲。
用简易法求内力可以省去画受力图和列平衡方程从而简化计算过程。
例8-3 用简易法求图8-10所示简支梁1-1截面上的剪力和弯矩。
解: (1)求支座反力图8-10 由梁的整体平衡方程求得
FA 8kN
FB 7kN
图8-10
(2)计算1-1截面上的内力 由1-1截面以左部分的外力来计算内力， 根据“顺转剪力正”和“下凸弯矩正”得

第四章 弯曲 (3)

第四章 弯曲 (3)

极轴，q表示截面m–m的位置。
q
x
B
M (q ) Px P(R Rcosq ) PR(1 cosq ) (0 q )
FS (q ) P 1 Psinq (0 q )
N (q ) P q (0 q ) 2 Pcos
M图 R P
A
平面刚架 的内力图
刚结点：受力以后，刚节点处夹角保持不 变。刚节点能承受力与力矩。
平面刚架：是由在同一平面内，不同取向的杆件， 通过杆端相互刚性连结而组成的结构。 A 平面刚架的内力：剪力，弯矩，轴力。
C
B
弯矩图：画在各杆的受拉一側，不注明正、负号。 剪力和轴力图：可画在刚架轴线的任一側（通常正值画在 刚架的外側）。注明正、负号。
例 作图示刚架的弯矩图 解：求支反力 F
计算内力时， A 一般应先求支反力， 由于该图的A端为 一自由端，无需计 算支反力就可计算 弯矩，故此步骤可 省略。
x1
a x2
C
M图
1.5a
Fa Fa
B 作弯矩方程： 如图所示：AC段的坐标原点取在A端。 CB段的坐标原点取在C端。 (0 x1 a) AC： M x1 Fx1 CB： (0 x2 a) M x2 Fx2 作图： 注意：在绘制弯矩图时，我们规定为弯矩图画在杆件受拉的一侧， 即杆件弯曲变形凸入的一侧。由(a)(b)式可见：两段的弯矩方程均 为斜直线，故只要定出A、C、B三点处 的弯矩值即可作出弯矩图。
a q +
q
M x
–
qa2
=
=
2q M1
qa2 2qa2/2
–
x
+
q
+

内力分析的基本方法-截面法

内力分析的基本方法-截面法

得 QE = 0 得 ME = qL2
16
QD
*剪力图和弯矩图 绘制方法1：根据梁的剪力方程和弯矩方程绘制剪力 图和弯矩图。 注意：1、当弯矩图为曲线时，至少要三个控制面 的值一般取两端点和Q=0的截面弯矩值（若无Q = 0 的截面，则取中间截面的弯矩值） 2、弯矩图画在受拉侧，不标正、负
17
绘制方法2：利用荷载与内力间的微分关系运用规律 1、图形：⑴在均布荷载作用区段：Q图为斜直线；M图 为抛物线，抛物线的凸向与q的指向一致。 ⑵在无荷载作用区段：Q图为水平线；M图为斜直线。
10 10
5
(b)
M 图(kN•m)
(c)
10
23
绘制方法3：
MA
A q L
叠加法绘制直杆弯矩图
MB
一、简支梁弯矩图的叠加方法
MA
B
MAB中 1 qL2 MB 8
若MA、MB在杆的两侧，怎么画？
MA MB q
A
MA
MAB中
B MB
＋
A 1 qL2 8
B
MAB中= （ MA ＋ MB）/2
24
MA A
由 y =0，得： FBy +FA - 206 =0 故： FBy=80kN（）
31
q=20kN/m
分别作出 AD 段、DE 段及EB 段受力图
B
2m 2m
10
解： 求支座反力
FC-10-20-30= 0
Ⅱ
A
由
F
y
=0
得：FC= 60 kN（↑）
用截面Ⅰ—Ⅰ将桁架截开，如下图所示：
10kN E Ⅰ 1 20kN 30kN
取右边部分，作受力图如下：

第四章 梁的内力

第四章 梁的内力

q=2kN/m MC B
M C ( F ) 0
l ql 2 M C FB 4.5kN m 2 8
l/4 FSC
FSC
l/2
FB
图4.11
三、用直接法求剪力、弯矩 F=5kN
直接法：梁任一横
截面上的剪力在数 值上等于该截面一
(a)
q=2kN/m
F=5kN
A C l/4 FA l/4
F
A
B
x
例题：作悬臂梁的剪
x
l FS
x
力图和弯矩图。
解：建立坐标系，将坐 标原点取在梁的左端， 写出梁的剪力方程和弯 矩方程 ：
FS图
F
FS (x) F
x
(0 x l) (0 x l)
M(x) Fx
M
M图
x 0时，M(0) 0 x l时， M(l) Fl
FRA
A
x
q
FRB
例题：作如图简支梁
的剪力图和弯矩图。
解：先求两个支反力
FRA FRB ql 2
B
l
FRA
A
q
M(x) FS (x)
建立坐标系，梁的剪力
x
方程和弯矩方程为：
ql FS (x) FRA qx qx (0 x l) 2 x qlx qx 2 M(x) FRA x qx (0 x l) 2 2 2
FRA
A
x
q
FRB
由弯矩方程得弯矩图为一 条二次抛物线。
B
l
x 0,
M 0
ql 2
x =l ,
解：1、求截面C的剪力和弯矩

第二章 杆件的内力与内力图

第二章 杆件的内力与内力图

第二章 杆件的内力与内力图§2-1 杆件内力的概念与杆件变形的基本形式一、杆件的内力与内力分量内力是工程力学中一个非常重要的概念。

内力从广义上讲，是指杆件内部各粒子之间的相互作用力。

显然，无荷载作用时，这种相互作用力也是存在的。

在荷载作用下，杆件内部粒子的排列发生了改变，这时粒子间相互的作用力也发生了改变。

这种由于荷载作用而产生的粒子间相互作用力的改变量，称为附加内力，简称内力。

需要指出的是：受力杆件某横截面上的内力实际上是分布在截面上的各点的分布力系，而工程力学分析杆件某截面上的内力时，一般将分布内力先表示成分布内力向截面的形心简化所得的主矢分量和主矩分量进行求解，而内力的具体分布规律放在下一步（属于本书第二篇中的内容）考虑。

受力杆件横截面上可能存在的内力分量最多有四类六个：轴力N F 、剪力y Q F )(和z Q F )(、扭矩x M 、弯矩y M 和z M 。

轴力N F 是沿杆件轴线方向（与横截面垂直）的内力分量。

剪力y Q F )(和z Q F )(是垂直于杆件轴线方向（与横截面相切）的内力分量。

扭矩xM 是力矩矢量沿杆件轴线方向的内力矩分量。

弯矩y M 和z M 是力矩矢量与杆件轴线方向垂直的内力矩分量。

二、杆件变形的基本形式实际的构件受力后将发生形状、尺寸的改变，构件这种形状、尺寸的改变称为变形。

杆件受力变形的基本形式有四种：轴向拉伸和压缩、扭转、剪切、弯曲。

1、轴向拉伸和压缩变形轴向拉伸和压缩简称为轴向拉压。

其受力特点是：外力沿杆件的轴线方向。

其变形特点是：拉伸——沿轴线方向伸长而横向尺寸缩小，压缩——沿轴线方向缩短而横向尺寸增大，如图4-1所示。

轴向受拉的杆件称为拉杆，轴向受压的杆件压杆。

图2-1 图2-2 土木工程结构中的桁架，由大量的拉压杆组成，如图2-2所示。

内燃机中的连杆、压缩机中的活塞杆等均属此类。

它们都可以简化成图2-1所示的计算简图。

2、剪切变形工程中的拉压杆件有时是由几部分联接而成的。

建筑力学5内力内力图

建筑力学5内力内力图
总结词
弯曲内力是指由于外力作用导致杆件发生弯曲变形而产生的内力，是建筑结构中最常见 的受力形式之一。
详细描述
在建筑结构中，弯曲内力通常用于描述梁、柱等杆件在受到垂直或水平外力作用时发生 的弯曲变形。弯曲内力的分析对于评估结构的承载能力和稳定性至关重要。例如，在桥 梁和高层建筑的梁和柱设计中，弯曲内力的计算和分析是确定截面尺寸、配筋等参数的
重要依据。
03 内力图的绘制方法
轴力图的绘制
总结词
轴力图用于表示杆件在受力过程中沿其轴线方向的受力情况。
详细描述
轴力图是通过将杆件沿轴线方向进行分段，并在每个分段上标出该段的轴力值， 然后将这些值连接起来形成的图形。绘制轴力图时，需要先对杆件进行受力分析 ，确定各段的受力情况，然后根据受力情况计算出各段的轴力值。
内力计算与优化
内力图绘制
根据建筑的使用功能和 设计要求，施加适当的
荷载。
计算各杆件的内力分布， 优化结构布置，降低内
力峰值。
根据计算结果，绘制各 杆件的内力图，为结构
设计提供依据。
06 结论
内力图在建筑力学中的重要性
1 2 3
揭示结构内部பைடு நூலகம்力状态
内力图能够清晰地表示出结构在不同受力情况下 的内部应力分布，有助于设计人员了解结构的受 力特性，从而优化设计。
规律二
规律三
在连续梁的支座处，内力图呈现向上 凸出的形状，表示该处的剪力和轴力 较大。
在连续梁的跨中，内力图呈现向下凸 出的形状，表示该处的弯矩最大。
内力图与外力的关系
01
内力图上的内力是由外力引起的 ，外力的作用点、方向和大小决 定了内力的分布和大小。
02
内力图上的内力分布规律反映了 结构的刚度和承载能力，是判断 结构安全性和稳定性的重要依据 。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

弯曲变形内力图绘制方法
摘要弯曲变形内力图的绘制是材料力学和结构力学的重点和难点,针对学生在学习该部分内容时出现的一些问题,本文提出了求解这种问题的与技巧,应用此方法,绘制内力图简便、快捷,以此更好地提高学生作图效率和教学效果。

关键词弯曲变形;内力图;荷载
1弯曲变形内力图绘制方法介绍
1.1 3个微分关系的应用
在画内力图时,较简捷的方法是运用3个微分关系来处理,即,,,这里,当为常数时,弯矩方程为二次函数,在弯矩图中反映为抛物线。

画抛物线时注意其要点,其对称轴和顶点在处,其开口方向与的方向相反(此时弯矩坐标轴正向与的方向相同)。

1.2 绘制内力图的步骤
一般我们将弯曲变形的内力图分为如下几步进行:
1)计算支反力;
2)分段;
3)计算控制截面内力值;
4)描点、连线。

1.3 杆端荷载的处理
在实际画内力图时,经常会遇到杆端荷载。

对于杆端的集中力,如其使杆端产生顺时针转动,则在该截面处的剪力为正,大小与此集中力相等;反之,剪力为负。

对于杆端的集中力偶,如其使杆端下边缘受拉,则在该截面处的弯矩为正,大小与此集中力偶相等;反之,弯矩为负。

1.4 重要说明
两点说明:画剪力图时,一般是从左向右,这时,向上的外荷载产生正的剪力,向下的外荷载产生负的剪力;画弯矩图时,计算控制截面的弯矩,易将隔离体看作悬
臂梁形式(详见应用举例)。

2应用举例
如图1所示梁的内力图。

1)求支反力(图2所示);
2)分段AB、BC、CD;
3)计算控制截面内力值;
这里只需计算B与C截面弯矩。

计算B截面弯矩时,取AB段为隔离体,其受力与图3所示悬臂梁一致,20kN的集中力使梁上部受拉,60kN的集中力偶使其下部受拉;计算C截面弯矩时,取CD段为隔离体,将其看作图4所示悬臂梁,8kN/m的分布荷载使其上部受拉。

其弯矩分别为
4)描点、连线。

剪力图(图5所示):杆端荷载20kN使A点产生逆时针转动,故此时A右截面的剪力为-20kN,AB段无荷载作用,该段剪力为-20kN,剪力图为水平直线;B支座反力向上,该处右截面剪力为27-20=7(kN);BC段有分布荷载作用,剪力图逐步下降,降至7-8×4=-25(kN);C支座反力向上,该处右截面剪力为41-25=16(kN);CD段有分布荷载作用,剪力图逐步下降,降至16-8×2=0(kN);从另一方面看,D截面无集中力作用,该处剪力也应为0。

弯矩图(图6所示):力偶60kNm使A截面下边缘受拉,该处右截面弯矩为60kNm;B与C截面弯矩分别为20kNm和-16kNm;D截面无集中力偶作用,该处弯矩应为0。

AB段无荷载作用,其弯矩图用斜直线连接;BC段有分布荷载作用,其弯矩图用抛物线连接,抛物线开口与q方向相反,对称轴在剪力为0即E截面处,CE/BE=25/7,CE=3.125m,DE=5.125m,Mmax=ME=41×3.125-8×5.125×5.125/2=2 3.1 (kNm) ;CD段有分布荷载作用,其弯矩图用抛物线连接,抛物线开口与q方向相反,对称轴在剪力为0即D截面处。

3结论
现行材料力学和结构力学教材中,对绘制弯曲变形内力图有一些方法,但笔者觉得本文的方法解决此类问题更有效。

本文介绍的方法可作为相关专业学生学习和教师教学的参考。

参考文献
[1]孙训方,方孝淑,关来泰.材料力学(上册)[M].高等教育出版社,2002.
[2]刘鸿文.材料力学(上册)[M].高等教育出版社,2004.
[3]李廉锟.结构力学(上册)[M].高等教育出版社,2004.
注:本文中所涉及到的图表、注解、公式等内容请以PDF格式阅读原文。