方差分析案例

方差分析案例方差分析（Analysis of Variance, ANOVA）是一种统计方法，用于检验三个或更多样本均值之间的差异是否具有统计学意义。

它广泛应用于社会科学、生物科学、工程学等领域。

下面是一个方差分析的案例，展示了如何使用ANOVA来分析数据。

假设我们想要研究不同教学方法对学生考试成绩的影响。

我们选择了三种不同的教学方法：传统教学法、项目式学习和翻转课堂。

每种方法分别应用于三组学生，每组有20名学生。

在教学结束后，我们收集了所有学生的考试成绩。

首先，我们需要收集数据。

对于每种教学方法，我们记录下每名学生的考试成绩。

这些数据将被用来进行方差分析。

接下来，我们使用统计软件进行ANOVA测试。

在软件中，我们将考试成绩作为因变量输入，教学方法作为自变量输入。

软件将计算出F值和对应的P值。

F值是方差分析中的关键统计量，它反映了不同组间（这里是教学方法）的方差与组内（学生成绩）的方差之间的比例。

如果F值显著大于1，并且对应的P值小于我们设定的显著性水平（通常是0.05），那么我们就可以拒绝原假设，即不同教学方法之间存在显著差异。

假设我们的ANOVA结果显示F值为5.3，P值为0.003。

这意味着我们有足够的证据拒绝原假设，认为至少有一种教学方法与其他方法相比在提高学生考试成绩方面有显著差异。

为了进一步探究哪些教学方法之间存在显著差异，我们可能需要进行事后多重比较测试。

常用的事后测试方法包括Tukey HSD（Honest Significant Difference）测试、Bonferroni校正等。

这些测试可以帮助我们确定哪些特定的教学方法组合之间存在显著差异。

最后，我们将分析结果整理成报告，包括数据收集、分析方法、ANOVA 结果、事后测试结果以及结论。

报告中会详细说明不同教学方法对学生考试成绩的具体影响，并提出可能的解释和建议。

通过这个案例，我们可以看到方差分析是一种强大的工具，可以帮助我们理解不同因素如何影响结果，并为决策提供科学依据。

S P S S-单因素方差分析(A N O V A)案例解析SPSS-单因素方差分析（ANOVA) 案例解析2011-08-30 11:10这几天一直在忙电信网上营业厅用户体验优化改版事情，今天将我最近学习SPSS单因素方差分析（ANOVA)分析，今天希望跟大家交流和分享一下：继续以上一期的样本为例，雌性老鼠和雄性老鼠，在注射毒素后，经过一段时间，观察鼠死亡和存活情况。

研究的问题是：老鼠在注射毒液后，死亡和存活情况，会不会跟性别有关？样本数据如下所示：（a代表雄性老鼠 b代表雌性老鼠 0代表死亡 1 代表活着 tim 代表注射毒液后，经过多长时间，观察结果）点击“分析”——比较均值———单因素AVOVA,如下所示：从上图可以看出，只有“两个变量”可选,对于“组别（性别）”变量不可选，这里可能需进行“转换”对数据重新进行编码，点击“转换”—“重新编码为不同变量”将a,b"分别用8,9进行替换，得到如下结果”此时的8 代表a(雄性老鼠） 9代表b雌性老鼠，我们将“生存结局”变量移入“因变量列表”内，将“性别”移入“因子”框内，点击“两两比较”按钮，如下所示：“勾选“将定方差齐性”下面的 LSD 选项，和“未假定方差齐性”下面的Tamhane's T2选项点击继续点击“选项”按钮，如下所示：勾选“描述性”和“方差同质检验”以及均值图等选项，得到如下结果：结果分析：方差齐性检验结果，“显著性”为0，由于显著性0<0.05 所以，方差齐性不相等，一般情况下，不能够进行方差分析但是对于SPSS来说，即使方差齐性不相等，还是可以进行方差分析的，由于此样本组少于三组，不能够进行多重样本对比从结果来看“单因素 ANOVA”分析结果，显著性0.098，由于0.098>0.05所可以得出结论：生存结局受性别的影响不显著很多人，对这个结果可能存在疑虑，下面我们来进一步进行论证，由于“方差齐性不相等”下我们来进行“非参数检验”检验结果如下所示：（此处采用的是“Kruskal-Wallis "检验方法）通过“Kruskal-Wallis ”检验方法，我们得出“sig=0.098"跟我们先前分析的结果一样，都是0.098，事实得到论证。

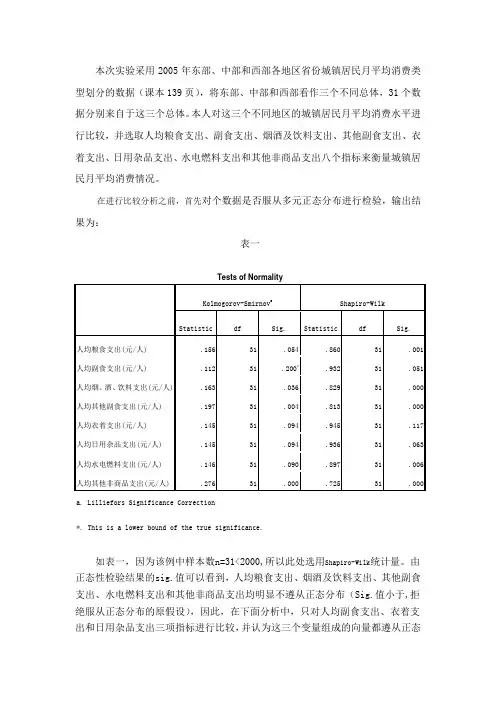
本次实验采用2005年东部、中部和西部各地区省份城镇居民月平均消费类型划分的数据（课本139页），将东部、中部和西部看作三个不同总体，31个数据分别来自于这三个总体。

本人对这三个不同地区的城镇居民月平均消费水平进行比较，并选取人均粮食支出、副食支出、烟酒及饮料支出、其他副食支出、衣着支出、日用杂品支出、水电燃料支出和其他非商品支出八个指标来衡量城镇居民月平均消费情况。

在进行比较分析之前，首先对个数据是否服从多元正态分布进行检验，输出结果为：表一如表一，因为该例中样本数n=31<2000,所以此处选用Shapiro-Wilk统计量。

由正态性检验结果的sig.值可以看到，人均粮食支出、烟酒及饮料支出、其他副食支出、水电燃料支出和其他非商品支出均明显不遵从正态分布（Sig.值小于,拒绝服从正态分布的原假设），因此，在下面分析中，只对人均副食支出、衣着支出和日用杂品支出三项指标进行比较，并认为这三个变量组成的向量都遵从正态分布，并对城镇居民月平均消费状况做出近似的度量。

另外，正态性的检验还可以通过Q-Q图来实现，此时应判别数据点是否与已知直线拟合得好。

如果数据点均落在直线附近，说明拟合得好，服从正态分布，反之，不服从。

具体情况这里不再赘述。

下面进行多因素方差分析：一、多变量检验表二由地区一栏的（即第二栏）所列几个统计量的Sig.值可以看到，无论从那个统计量来看，三个地区的城镇居民月平均消费水平都是有显著差别的（Sig.值小于，拒绝地区取值不同，对Y，即城镇居民月平均消费水平的取值没有显著影响的原假设）。

二、主体间效应检验表三如表三，可以看到三个指标地区一栏的（即第三栏）Sig.值分别为、、，说明三个地区在人均衣着支出指标上没有明显的差别（Sig.值大于，不拒绝地区取值不同，对指标的取值没有显著影响的原假设），反之，而在人均副食支出和日用杂品支出指标上有显著差别。

三、多重比较表四Contrast Results (K Matrix)地区 Simple Contrast aDependent Variable 人均副食支出(元/人)人均日用杂品支出(元/人)人均衣着支出(元/人)Level 1 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..001.036.51795% Confidence Interval for DifferenceLower Bound.173Upper BoundLevel 2 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..668.343.63895% Confidence Interval for DifferenceLower BoundUpper Bound表四Contrast Results (K Matrix)地区 Simple Contrast aDependent Variable 人均副食支出(元/人)人均日用杂品支出(元/人)人均衣着支出(元/人)Level 1 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..001.036.51795% Confidence Interval for DifferenceLower Bound.173Upper BoundLevel 2 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..668.343.63895% Confidence Interval for DifferenceLower BoundUpper Bounda. Reference category = 3如表四，在显著水平下，东部和西部的人均副食支出（Sig.值为）和日用杂品支出（Sig.值为）指标有明显差别(小于，拒绝原假设)，而在人均衣着支出（Sig.值为）指标上没有明显的差别。

SPSS单因素方差分析案例
一、案例简介
本案例主要探讨不同年龄组对对不同种类游戏的不同评价。

采用
SPSS软件进行单因素方差分析，研究对象为50名参与游戏评测的受试者，其中25名为年龄段20-30，25名为年龄段30-40。

每位受试者都被分配3
种不同类型的游戏来评价，评价方式为3分制，值得1，2，3分，分别表
示很差，一般，不错。

二、SPSS分析
1.数据的输入
①打开SPSS软件，点击“文件”-“打开”，选择需要进行分析的数据；
②若原始数据是excel格式，选择“所有的excel文件”，点击“打开”；
③若原始数据是文本格式，选择“所有文本文件”，点击“打开”；
④若原始数据是spss格式，选择“spss 调查”，点击“打开”；
⑤若原始数据是SAS格式，选择“所有SAS文件”，点击“打开”。

2.数据分析
①点击“统计”菜单，在下拉菜单中选择“多元统计分析”；
②在多元统计分析对话框中，在“因变量”栏中选择需要分析的评测
结果；
③在“自变量”栏中选择“受试者的年龄”；
④点击“确定”按钮，开始进行单因素方差分析；
⑤点击“分析”按钮，在下拉菜单中选择“单因素方差分析”；
⑥点击“分析”按钮。

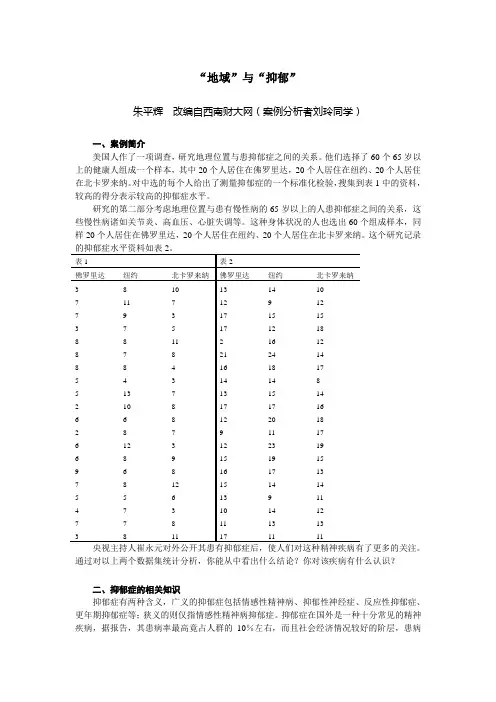
“地域”与“抑郁”朱平辉改编自西南财大网（案例分析者刘玲同学）一、案例简介美国人作了一项调查，研究地理位置与患抑郁症之间的关系。

他们选择了60个65岁以上的健康人组成一个样本，其中20个人居住在佛罗里达，20个人居住在纽约、20个人居住在北卡罗来纳。

对中选的每个人给出了测量抑郁症的一个标准化检验，搜集到表1中的资料，较高的得分表示较高的抑郁症水平。

研究的第二部分考虑地理位置与患有慢性病的65岁以上的人患抑郁症之间的关系，这些慢性病诸如关节炎、高血压、心脏失调等。

这种身体状况的人也选出60个组成样本，同样20个人居住在佛罗里达，20个人居住在纽约、20个人居住在北卡罗来纳。

这个研究记录央视主持人崔永元对外公开其患有抑郁症后，使人们对这种精神疾病有了更多的关注。

通过对以上两个数据集统计分析，你能从中看出什么结论？你对该疾病有什么认识？二、抑郁症的相关知识抑郁症有两种含义，广义的抑郁症包括情感性精神病、抑郁性神经症、反应性抑郁症、更年期抑郁症等；狭义的则仅指情感性精神病抑郁症。

抑郁症在国外是一种十分常见的精神疾病，据报告，其患病率最高竟占人群的10％左右，而且社会经济情况较好的阶层，患病率越高。

世界卫生组织预测，抑郁症将成为21世纪人类的主要杀手。

全世界患有抑郁症的人数在不断增长，而抑郁症患者中有10—15%面临自杀的危险……引起抑郁症的原因有很多，为了了解地理位置对抑郁症是否有影响,我们做如下的案例分析：三、地理位置与患抑郁症之间是否有关系作为对65岁以上的人长期研究的一部分，在纽约洲北部地区的Wentworth医疗中心的社会学专家和内科医生进行了一项研究，以调查地理位置与患抑郁症之间的关系。

选择了60个相当健康的人组成一个样本，其中20人居住在佛罗里达，20人居住在纽约，20人居住在北卡罗米纳。

对中选的人给出了测量抑郁症的一个标准化实验，搜集到表1中的资料，较高的分表示较高的抑郁症水平。

研究的第二部分考虑地理位置与患有慢性病的65岁以上的人患抑郁症之间的关系，这些慢性病诸如关节炎、高血压、心脏失调等。

不同地区公司盈利性差异姜晓兵西安电子科技大学经济与管理学院摘要：本案例收集了重庆、成都和西安等地相同产业的大公司年均资产收益率、股本收益率和营业利润率等盈利性数据，借此研究分析地区对这些盈利性数据是否会产生影响。

地区为品质型变量，三个盈利性指标为数值型变量，问题实质上是探讨品质型变量对数值型变量取值的影响是否显著，因此，运用方差分析方法可对此问题进行详细分析。

关键词：地区，年均资产收益率，股本收益率，营业利润率，方差分析在市场上，微小的差异就能够区分相同产业中不同地区公司的盈利性。

这是因为各地方在资源禀赋方面存在差异，如自然资源获取难易程度、地方政府行政效率、金融市场完备程度、物流交通便捷性等方面的不同。

有人进行了研究以确定重庆、成都和西安等地相同产业的大公司盈利性之间的差异是否具有显著性。

研究人员从这3个地方的服务业中随机抽样了100家大公司。

利用这些公司收集的数据，分别计算了6年内大公司的年均盈利性指标。

反映盈利性的指标有3个：年均资产收益率；股本收益率；营业利润率。

数据如下所示：2 6.40 4.35 3.683 5.63 3.29 3.624 7.69 3.22 4.135 4.10 3.69 3.812 12.05 10.40 10.563 6.89 6.73 10.584 15.20 6.12 9.775 6.02 7.90 10.332 8.76 6.74 5.903 6.37 5.32 5.524 7.08 5.20 1.805 4.75 6.03 0.83案例使用说明一、案例目的与用途本案例主要是用于《应用统计学》课程，也适用于其他经济管理类学科的教学与管理培训。

本案例的教学目的主要在于帮助学员理解、掌握方差分析方法的思路与单因素方差分析、双因素方差分析的具体操作，理清方差分析与假设检验、回归分析三者间的联系与区别。

二、启发思考题1.判断重庆、成都和西安的大公司资产收益率之间存在差异吗？股本收益率和营业利润率呢？2.考虑能否用下面的方法检验上述问题：将每两个地方作为一对，采用一系列的t检验？其错误率如何？假如研究人员在抽样时还抽取了北京、上海、广州和深圳四个地方的公司，采用t检验的方法，需要进行多少次检验？错误率如何？有没有更好的办法？3.是否能够研究地区之外的因素？本研究中只包括了大公司，如何在分析中包括小型规模的公司和中等规模的公司？年份的选择重要吗？有没有可能通过检验来确定不同年份之间资产收益率、股本收益率或营业利润率是否存在具有统计显著性的差异？4.如果设计一个研究，三个地方都包括有小公司、中等规模的公司和大公司，有没有可能通过检验来确定公司规模与地区之间存在交互效应？换言之，假定大公司在重庆的表现良好，而小公司在西安的表现较好。