离散数学期末考试题(附答案和含解析1) - 副本
- 格式:pdf
- 大小:113.38 KB
- 文档页数:4

离散数学期末考试题及答案1.选择题(每题3分,共30分)1. 下列命题中,属于复合命题的是:A. 3是一个奇数,且2是一个偶数B. 如果2是一个素数,那么4也是一个素数C. 不是所有奇数都是素数D. 存在一个整数x,使得x>5且x是一个偶数答案:D2. 已知命题p:草地是绿的,命题q:天空是蓝的。
下列表述可以表示p ∧ ¬q 的是:A. 草地是绿的,天空是蓝的B. 草地不是绿的,天空是蓝的C. 草地是绿的,天空不是蓝的D. 草地不是绿的,天空不是蓝的答案:B3. 设命题p表示“这个数是偶数”,q表示“这个数大于10”。
那么“这个数既是偶数又大于10”可以表示为:A. p ∧ qB. p ∨ qC. ¬p ∧ qD. ¬p ∨ q答案:A4. 下列以下列集合的方式描述,其中哪个是空集∅:A. {x | 0 ≤ x ≤ 1}B. {x | x是一个自然数,x > 10}C. {x | x是一个正偶数,x < 2}D. {x | x是一个负整数,x < -1}答案:C5. 设A = {a, b, c},B = {c, d, e},C = {a, c, e}。
则(A ∪ B) ∩ C等于:A. {a, b, c, d, e}B. {a, c, e}C. {c}D. 空集∅答案:B6. 假设U是全集,A、B、C是U的子集。
则(A ∪ B) ∩ C 的补集是:A. A ∩ B ∩ C的补集B. (A ∪ B) ∩ C的补集C. A ∪ (B ∩ C)的补集D. (A ∩ C) ∩ (B ∩ C)的补集答案:D7. 若关系R为集合A到集合B的一种映射,且|A| = 7,|B| = 4,则R包含的有序对数目为:A. 4B. 7C. 11D. 28答案:D8. 设A={1,2,3},B={4,5,6},则从A到B的映射总数为:A. 3B. 9C. 6D. 18答案:C9. 设A={a,b,c,d,e},则集合A的幂集的元素个数是:A. 2B. 5C. 10D. 32答案:D10. 若f:A→B为满射且g:B→C为单射,则(g ∘ f):A→C为:A. 双射B. 满射C. 单射D. 非单射且非满射答案:A2.简答题(每题10分,共20分)1. 请简要解释什么是关系R的自反性、对称性和传递性。


离散数学期末考试试题(配答案)1. 谓词公式)()(x xQ x xP ∃→∀的前束范式是___________。
2. 设全集{}{}{},5,2,3,2,1,5,4,3,2,1===B A E 则A ∩B =____;=A _____;=B A Y __ _____3. 设{}{}b a B c b a A ,,,,==;则=-)()(B A ρρ__ __________;=-)()(A B ρρ_____ ______。
二.选择题(每小题2分;共10分)1. 与命题公式)(R Q P →→等价的公式是( )(A )R Q P →∨)( (B )R Q P →∧)( (C ))(R Q P ∧→ (D ))(R Q P ∨→ 2. 设集合{}c b a A ,,=;A 上的二元关系{}><><=b b a a R ,,,不具备关系( )性质 (A ) (A)传递性 (B)反对称性 (C)对称性 (D)自反性 三.计算题(共43分)1. 求命题公式r q p ∨∧的主合取范式与主析取范式。
(6分)2. 设集合{}d c b a A ,,,=上的二元关系R 的关系矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛=1000000011010001R M ;求)(),(),(R t R s R r 的关系矩阵;并画出R ;)(),(),(R t R s R r 的关系图。
(10分)5. 试判断),(≤z 是否为格?说明理由。
(5分)(注:什么是格?Z 是整数;格:任两个元素;有最小上界和最大下界的偏序)四.证明题(共37分)1. 用推理规则证明D D A C C B B A ⌝⇒∧⌝⌝⌝∧∨⌝→)(,)(,。
(10分)2. 设R 是实数集;b a b a f R R R f +=→⨯),(,:;ab b a g R R R g =→⨯),(,:。
求证:g f 和都是满射;但不是单射。
(10分)一;1; _ ∃x ∃y¬P(x)∨Q(y)2; {2} {4;5} {1;3;4;5}3; {{c};{a ;c};{b ;c};{a ;b ;c}} Φ_ 二;B D三;解:主合取方式:p ∧q ∨r ⇔(p ∨q ∨r)∧(p ∨¬q ∨r)∧(¬p ∨q ∨r)= ∏0.2.4主析取范式:p ∧q ∨r ⇔(p ∧q ∧r) ∨(p ∧q ∧¬r) ∨(¬p ∧q ∧r) ∨(¬p ∧¬q ∧r) ∨(p ∧¬q ∧r)= ∑1.3.5.6.7 四;1;证明:编号 公式 依据 (1) (¬B∨C )∧¬C 前提 (2) ¬B∨C ;¬C (1) (3) ¬B (2) (4) A →B (3) (5) ¬A (3)(4) (6) ¬(¬A∧D ) 前提 (7) A ∨¬D (6) (8)¬D (5)(6)2;证明:要证f 是满射;即∀y ∈R ;都存在(x1;x2)∈R ×R ;使f (x1;x2)=y ;而f (x1;x2)=x1+x2;可取x1=0;x2=y ;即证得;再证g 是满射;即∀y ∈R ;;都存在(x1;x2)∈R ×R ;使g (x1;x2)=y ;而g (x1;x2)=x1x2;可取x1=1;x2=y ;即证得;最后证f 不是单射;f (x1;x2)=f (x2;x1)取x1≠x2;即证得;同理:g (x1;x2)=g (x2;x1);取x1≠x2;即证得。
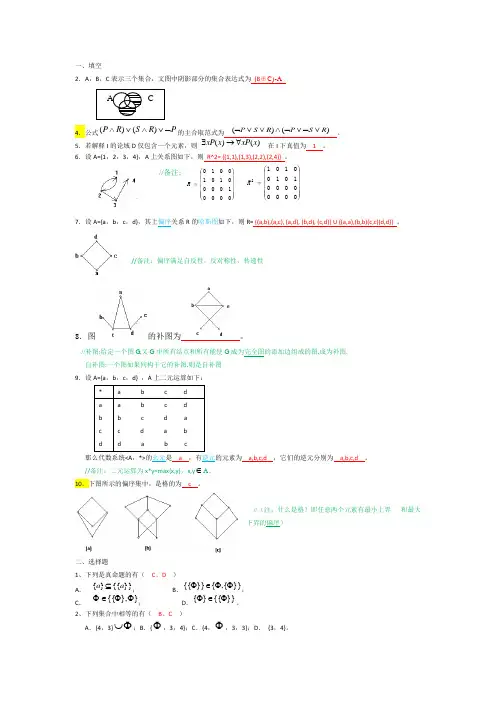
一、填空2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 (B ⊕C)-A4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 )()(R S P R S P ∨⌝∨⌝∧∨∨⌝ 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 1 。
6.设A={1,2,3,4},A 上关系图如下,则 R^2= {(1,1),(1,3),(2,2),(2,4)} 。
//备注:⎪⎪⎪⎪⎪⎭⎫⎝⎛=0000100001010010R⎪⎪⎪⎪⎪⎭⎫⎝⎛=00000000101001012R7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图如下,则R= {(a,b),(a,c), (a,d), (b,d), (c,d)} U {(a,a),(b,b)(c,c)(d,d)} 。
//备注:偏序满足自反性,反对称性,传递性8.图的补图为 。
//补图:给定一个图G ,又G 中所有结点和所有能使G 成为完全图的添加边组成的图,成为补图. 自补图:一个图如果同构于它的补图,则是自补图 9.设A={a ,b ,c ,d} ,A 上二元运算如下:* a b c d a b c da b c d b c d a c d a b d a b c那么代数系统<A ,*>的幺元是 a ,有逆元的元素为 a,b,c,d ,它们的逆元分别为 a,b,c,d 。
//备注:二元运算为x*y=max{x,y},x,y ∈A 。
10.下图所示的偏序集中,是格的为 c 。
//(注:什么是格?即任意两个元素有最小上界 和最大下界的偏序)二、选择题1、下列是真命题的有( C 、D )A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C .}},{{ΦΦ∈Φ; D .}}{{}{Φ∈Φ。
2、下列集合中相等的有( B 、C )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。

离散期末考试题及答案离散数学期末考试题及答案一、选择题(每题2分,共20分)1. 在集合论中,以下哪个符号表示属于关系?A. ∈B. ∉C. ⊆D. ⊂答案:A2. 有限集合A和B的并集,其元素个数最多是A和B元素个数之和,这个性质称为:A. 德摩根定律B. 幂集C. 并集原理D. 子集原理答案:C3. 命题逻辑中,以下哪个命题是真命题?A. (p ∧ ¬p) ∨ qB. (p ∨ ¬p) ∧ qC. (p ∨ q) ∧ ¬pD. (p ∧ q) ∨ ¬p答案:B4. 在图论中,一个无向图的边数至少是顶点数的多少倍才能保证图中至少存在一个环?A. 1B. 2C. 3D. 4答案:B5. 以下哪个算法用于生成一个集合的所有子集?A. 欧拉回路B. 哈密顿回路C. 深度优先搜索D. 子集生成算法答案:D6. 在关系数据库中,以下哪个操作用于删除表中的行?A. SELECTB. INSERTC. UPDATED. DELETE答案:D7. 以下哪个是有限自动机的状态?A. 初始状态B. 终止状态C. 转移状态D. 所有选项答案:D8. 以下哪个是图论中的一个基本定理?A. 欧拉定理B. 哈密顿定理C. 狄拉克定理D. 所有选项答案:D9. 在命题逻辑中,以下哪个是德摩根定律的逆命题?A. ¬(p ∨ q) ≡ ¬p ∧ ¬qB. ¬(p ∧ q) ≡ ¬p ∨ ¬qC. ¬(p ∨ q) ≡ ¬p ∨ ¬qD. ¬(p ∧ q) ≡ ¬p ∧ ¬q答案:B10. 在集合论中,以下哪个操作表示集合的差集?A. ∩B. ∪C. -D. ×答案:C二、填空题(每空3分,共30分)11. 集合{1, 2, 3}的幂集包含________个元素。

离散数学期末考试题及答案一、选择题(每题2分,共20分)1. 以下哪个选项是图的边数与顶点数的关系?A. 边数小于顶点数B. 边数等于顶点数C. 边数大于顶点数D. 边数与顶点数无固定关系答案:D2. 有限自动机的英文缩写是什么?A. FAB. PDAC. TMAD. NFA答案:A3. 布尔代数中,德摩根定律是指什么?A. ¬(A ∧ B) 等于¬ A ∨ ¬ BB. ¬(A ∨ B) 等于¬ A ∧ ¬ BC. A ∧ B 等于¬(A ∨ B)D. A ∨ B 等于¬(¬ A ∧ ¬B)答案:B4. 在命题逻辑中,以下哪个符号表示蕴含?A. ∧B. ∨C. →D. ↔答案:C5. 集合A = {1, 2, 3},B = {2, 3, 4},则A ∪ B等于:A. {1, 2, 3, 4}B. {1, 2, 3}C. {2, 3, 4}D. {1, 3, 4}答案:A6. 以下哪个选项是正确的递归定义?A. 一个数是偶数当且仅当它是2的倍数B. 一个数是偶数当且仅当它不是2的倍数C. 一个数是偶数当且仅当它是另一个偶数加1D. 以上都是正确的递归定义答案:A7. 有向图和无向图的主要区别是什么?A. 有向图的边有方向,无向图的边没有方向B. 有向图的顶点有方向,无向图的顶点没有方向C. 有向图的边可以相交,无向图的边不可以相交D. 有向图可以有环,无向图不可以有环答案:A8. 在命题逻辑中,以下哪个公式是矛盾的?A. A ∧ ¬ AB. A ∨ ¬ AC. A → BD. A ∧ B ∧ ¬ A答案:A9. 以下哪个是图的同义术语?A. 网络B. 矩阵C. 树D. 以上全部答案:A10. 以下哪个命题逻辑公式是有效的?A. (A → B) ∧ (B → A)B. (A ∧ B) → AC. (A ∨ B) → AD. (A ∧ B) → B答案:B二、填空题(每题2分,共20分)11. 在命题逻辑中,_________ 表示一个命题是真的,而 _________ 表示一个命题是假的。

离散数学期末考试题及答案一、选择题(每题2分,共20分)1. 在集合论中,以下哪个选项不是集合的基本运算?A. 并集B. 交集C. 差集D. 乘法答案:D2. 命题逻辑中,以下哪个命题不是基本的逻辑连接词?A. 与(∧)B. 或(∨)C. 非(¬)D. 等于(=)答案:D3. 在图论中,一个图的度数之和等于边数的几倍?A. 1B. 2C. 3D. 4答案:B4. 以下哪个是布尔代数的基本定理?A. 德摩根定律B. 布尔代数的分配律C. 布尔代数的结合律D. 所有选项都是答案:D5. 以下哪个不是组合数学中的计数原理?A. 加法原理B. 乘法原理C. 排列D. 组合答案:C6. 在关系数据库中,以下哪个操作不是基本的数据库操作?A. 选择B. 投影C. 连接D. 排序答案:D7. 以下哪个是有限自动机的组成部分?A. 状态B. 转移C. 输入符号D. 所有选项都是答案:D8. 以下哪个命题逻辑表达式是真命题?A. (p ∧ ¬p) ∨ qB. (p ∨ ¬p) ∧ qC. (p → q) ∧ (q → p)D. (p → q) ∧ (¬p → ¬q)答案:D9. 以下哪个是归纳法证明的基本步骤?A. 基础步骤B. 归纳步骤C. 反证法D. 所有选项都是答案:B10. 以下哪个是图的遍历算法?A. 深度优先搜索(DFS)B. 广度优先搜索(BFS)C. Dijkstra算法D. 所有选项都是答案:A二、简答题(每题10分,共30分)1. 简述命题逻辑中的德摩根定律。
答案:德摩根定律是命题逻辑中描述否定命题的两个重要定律。
它们分别是:- ¬(p ∧ q) ≡ ¬p ∨ ¬q- ¬(p ∨ q) ≡ ¬p ∧ ¬q2. 解释什么是图的连通分量,并给出一个例子。
答案:图的连通分量是指图中最大的连通子图。


离散数学期末考试题及答案一、单项选择题(每题2分,共20分)1. 集合A={1,2,3},B={2,3,4},则A∩B=()。
A. {1,2,3}B. {2,3}C. {2,4}D. {1,4}答案:B2. 命题“若x>0,则x>1”的逆否命题是()。
A. 若x≤0,则x≤1B. 若x≤1,则x≤0C. 若x>1,则x>0D. 若x≤1,则x≤0答案:B3. 函数f: A→B的定义域是集合A,值域是集合B,则()。
A. A⊆BB. A⊂BC. A⊇BD. A⊃B答案:A4. 集合{1,2,3}与集合{3,2,1}是否相等?()。
A. 是B. 否C. 无法确定D. 以上都不对答案:A5. 命题p:“x>0”,则¬p为()。
A. x≤0B. x<0C. x=0D. x<0或x=0答案:A6. 命题“若x>0,则x>1”的逆命题是()。
A. 若x>0,则x>1B. 若x≤1,则x≤0C. 若x>1,则x>0D. 若x≤0,则x≤1答案:C7. 函数f: A→B的定义域是集合A,值域是集合B,则()。
A. A⊆BB. A⊂BC. A⊇BD. A⊃B答案:A8. 集合{1,2,3}与集合{3,2,1}是否相等?()。
A. 是B. 否C. 无法确定D. 以上都不对答案:A9. 命题p:“x>0”,则¬p为()。
A. x≤0B. x<0C. x=0D. x<0或x=0答案:A10. 命题“若x>0,则x>1”的逆命题是()。
A. 若x>0,则x>1B. 若x≤1,则x≤0C. 若x>1,则x>0D. 若x≤0,则x≤1答案:C二、填空题(每题2分,共20分)1. 集合A={1,2,3},B={2,3,4},则A∪B=______。
答案:{1,2,3,4}2. 命题“若x>0,则x>1”的逆否命题是:若x≤1,则x≤0。
安徽大学2006-2007学年第1学期《离散数学》期末考试试卷(A 卷)(时间120分钟)开课院(系、部) 姓名 学号 .一、选择题(每小题2分,共20分)1.下列语句中,哪个是真命题( )A 、42=+x ;B 、我们要努力学习;C 、如果ab 为奇数,那么a 是奇数,或b 是偶数;D 、如果时间流逝不止,你就可以长生不老。
2.下列命题公式中,永真式的是( )A 、P Q P →→)(;B 、P P Q ∧→⌝)(;C 、Q P P ↔⌝∧)(;D 、)(Q P P ∨→。
3.在谓词逻辑中,令)(x F 表示x 是火车;)(y G 表示y 是汽车;),(y x L 表示x 比y 快。
命题“并不是所有的火车比所有的汽车快”的符号表示中哪些是正确的?( ) I.)),()()((y x L y G x F y x →∧∀⌝∀ II.)),()()((y x L y G x F y x ⌝∧∧∃∃III. )),()()((y x L y G x F y x ⌝→∧∃∃A 、仅I ;B 、仅III ;C 、I 和II ;D 、都不对。
4.下列结论正确的是:( )A 、若C AB A =,则C B =; B 、若B A B A ⊆,则B A =;C 、若C A B A =,则C B =;D 、若B A ⊂且D C ⊂,则D B C A ⊂。
5.设φ=1A ,}{2φ=A ,})({3φρ=A ,)(4φρ=A ,以下命题为假的是( ) A 、42A A ∈; B 、31A A ⊆; C 、24A A ⊆; D 、34A A ∈。
6.设R 是集合},,,{d c b a A =上的二元关系,},,,,,,,,,,,{><><><><><><=b d d b a c c a a d d a R 。
下列哪些命题为真?( ) I.R R ⋅是对称的 II. R R ⋅是自反的 III. R R ⋅不是传递的A 、仅I ;B 、仅II ;C 、I 和II ;D 、全真。

离散数学试题(B卷答案1)一、证明题(10分)1)(⌝P∧(⌝Q∧R))∨(Q∧R)∨(P∧R)⇔R证明: 左端⇔(⌝P∧⌝Q∧R)∨((Q∨P)∧R)⇔((⌝P∧⌝Q)∧R))∨((Q∨P)∧R)⇔(⌝(P∨Q)∧R)∨((Q∨P)∧R)⇔(⌝(P∨Q)∨(Q∨P))∧R⇔(⌝(P∨Q)∨(P∨Q))∧R⇔T∧R(置换)⇔R2) ∃x (A(x)→B(x))⇔∀xA(x)→∃xB(x)证明:∃x(A(x)→B(x))⇔∃x(⌝A(x)∨B(x))⇔∃x⌝A(x)∨∃xB(x)⇔⌝∀xA(x)∨∃xB(x)⇔∀xA(x)→∃xB(x)二、求命题公式(P∨(Q∧R))→(P∧Q∧R)的主析取范式和主合取范式(10分)。
证明:(P∨(Q∧R))→(P∧Q∧R)⇔⌝(P∨(Q∧R))∨(P∧Q∧R))⇔(⌝P∧(⌝Q∨⌝R))∨(P∧Q∧R)⇔(⌝P∧⌝Q)∨(⌝P∧⌝R))∨(P∧Q∧R)⇔(⌝P∧⌝Q∧R)∨(⌝P∧⌝Q∧⌝R)∨(⌝P∧Q∧⌝R))∨(⌝P∧⌝Q∧⌝R))∨(P∧Q∧R)⇔m0∨m1∨m2∨m7⇔M3∨M4∨M5∨M6三、推理证明题(10分)1)C∨D, (C∨D)→⌝E,⌝E→(A∧⌝B), (A∧⌝B)→(R∨S)⇒R∨S 证明:(1) (C∨D)→⌝E P(2) ⌝E→(A∧⌝B) P(3) (C∨D)→(A∧⌝B) T(1)(2),I(4) (A∧⌝B)→(R∨S) P(5) (C∨D)→(R∨S) T(3)(4), I(6) C∨D P(7) R∨S T(5),I2) ∀x(P(x)→Q(y)∧R(x)),∃xP(x)⇒Q(y)∧∃x(P(x)∧R(x))证明(1)∃xP(x) P(2)P(a) T(1),ES(3)∀x(P(x)→Q(y)∧R(x)) P(4)P(a)→Q(y)∧R(a) T(3),US(5)Q(y)∧R(a) T(2)(4),I(6)Q(y) T(5),I(7)R(a) T(5),I(8)P(a)∧R(a) T(2)(7),I(9)∃x(P(x)∧R(x)) T(8),EG(10)Q(y)∧∃x(P(x)∧R(x)) T(6)(9),I四、某班有25名学生,其中14人会打篮球,12人会打排球,6人会打篮球和排球,5人会打篮球和网球,还有2人会打这三种球。
离散试卷及答案离散数学试题(A 卷及答案)一、证明题(10分) 1)(P ∧(Q ∧R))∨(Q ∧R)∨(P ∧R)R证明: 左端(P ∧Q ∧R)∨((Q ∨P)∧R)((P ∧Q)∧R))∨((Q ∨P)∧R)((P ∨Q)∧R)∨((Q ∨P)∧R)((P ∨Q)∨(Q ∨P))∧R ((P ∨Q)∨(P ∨Q))∧RT ∧R(置换)R2)x(A(x)B(x))xA(x)xB(x) 证明 :x(A(x)B(x))x(A(x)∨B(x))xA(x)∨xB(x)xA(x)∨xB(x)xA(x)xB(x)二、求命题公式(P ∨(Q ∧R))(P ∧Q ∧R)的主析取范式和主合取范式(10分)证明:(P ∨(Q ∧R))(P ∧Q ∧R)(P ∨(Q ∧R))∨(P ∧Q ∧R))(P ∧(Q ∨R))∨(P ∧Q ∧R) (P ∧Q)∨(P ∧R))∨(P ∧Q ∧R) (P ∧Q ∧R)∨(P ∧Q ∧R)∨(P ∧Q ∧R))∨(P ∧Q ∧R))∨(P ∧Q ∧R) m0∨m1∨m2∨m7 M3∨M4∨M5∨M6三、推理证明题(10分) 1)C ∨D, (C ∨D) E, E (A ∧B), (A ∧B)(R ∨S)R ∨S证明:(1) (C ∨D) E(2) E (A ∧B) (3) (C ∨D)(A ∧B)(4) (A ∧B)(R ∨S)(5) (C ∨D)(R ∨S)(6) C ∨D (7) R ∨S 2) x(P(x)Q(y)∧R(x)),xP(x)Q(y)∧x(P(x)∧R(x)) 证明(1)xP(x)(2)P(a) (3)x(P(x)Q(y)∧R(x)) (4)P(a)Q(y)∧R(a)(5)Q(y)∧R(a) (6)Q(y) (7)R(a) (8)P(a) (9)P(a)∧R(a) (10)x(P(x)∧R(x))(11)Q(y)∧x(P(x)∧R(x))四、设m 是一个取定的正整数,证明:在任取m +1个整数中,至少有两个整数,它们的差是m 的整数倍证明 设1a ,2a ,…,1+m a 为任取的m +1个整数,用m 去除它们所得余数只能是0,1,…,m -1,由抽屉原理可知,1a ,2a ,…,1+m a 这m +1个整数中至少存在两个数s a 和t a ,它们被m 除所得余数相同,因此s a 和t a 的差是m 的整数倍。
离散数学期末考试试题及答案一、选择题(每题4分,共40分)1.下列哪一个不是集合操作? A. 并 B. 交 C. 补 D. 叉积正确答案:D2.下列哪一个不是真命题? A. 1 + 1 = 2 B. 所有的猫都会飞 C. 所有的数都是整数 D. 狗是哺乳动物正确答案:B3.设A = {1, 2, 3},B = {3, 4, 5},则A ∩ B的结果是:A. {1, 2}B. {3}C. {1, 3}D. {4, 5}正确答案:B4.设A = {1, 2, 3},B = {3, 4, 5},则A × B的结果是:A. {(1, 3), (2, 4), (3, 5)}B. {(1, 1), (2, 2), (3, 3)}C. {(3, 3), (3,4), (3, 5)} D. {(3, 1), (3, 2), (3, 3)}正确答案:A5.若n为正整数,则n是偶数的充要条件是: A. n可以被2整除 B. n除以2的余数为1 C. n大于2 D. n的绝对值是偶数正确答案:A6.若A = {1, 2, 3, 4},B = {3, 4, 5},则A - B的结果是:A. {1, 2}B. {3}C. {1, 3, 4}D. {4, 5}正确答案:A7.已知命题P和命题Q,下列哪个是它们的逻辑等价式?A. P ∧ (P ∨ Q) = P B. P ∧ (P ∨ Q) = Q C. P ∨ (P ∨ Q) = P D. P ∨ (P ∨ Q) = Q正确答案:A8.设n为奇数,则n + n的结果是: A. 2n B. n^2 C.n(n+1) D. n(n-1)正确答案:C9.已知集合A = {1, 2, 3, 4},B = {4, 5, 6},C = {6, 7, 8},则(A ∩ B)∩ C的结果是: A. {1, 2, 3} B. {4} C. {6} D. 空集正确答案:D10.若命题P为真,则下列哪个推理是正确的? A. 如果P为真,则Q为真(反证法) B. P与Q都为真(析取引理)C. P蕴含Q(推理法则) D. P等价于Q(假设法)正确答案:A二、解答题(每题10分,共60分)1.证明:任取集合A和B,有(A ∪ B) - B = A - B解答:运用集合的基本运算性质:对任意元素x,x∈ (A ∪ B) - B,即x ∈ (A ∪ B)且x ∉ B。
离散数学期末复习例题讲解一、考核说明考核对象:本课程考核说明适用于国家开放大学开放教育本科电气信息类计算机科学与技术专业的学生.考核依据:本考核说明是以本课程的教学大纲(2015年3月修改)和指定的参考教材为依据制定的.本课程指定的参考教材是由胡俊、顾静相编写,国家开放大学出版社出版的《离散数学(本科)》第2版.考核方式:本课程的考核实行形成性考核和终结性考核相结合的方式.其中终结性考核采用半开卷、笔试方式,试卷满分100分.半开卷考试允许考生携带指定的一张专用A4纸(统一印制),考生可以将自己对全课程学习内容的总结归纳写在这张A4纸上带入考场,作为答卷时参考.考试时间:90分钟.试题类型及结构:单项选择题的分数占15%,填空题的分数占15%,公式翻译题的分数占12%,判断说明题的分数占14%,计算题的分数占36%;证明题的分数占8%.二、例题讲解(一)集合论1.单项选择题(1)若集合A={2,a,{ a },4},则下列表述正确的是( ).A.{a,{ a }}∈A B.{ a }⊆AC.{2}∈A D.∅∈A答:B(2)若集合A={a,b,{1,2 }},B={1,2},则().A.B⊂ A,且B∈A B.B⊄ A,且B∉AC.B ⊂ A,但B∉A D.B∈ A,但B⊄A答:D(3)设集合A = {1, a },则P(A) = ( ).A.{{1}, {a}} B.{∅,{1}, {a}}C.{∅,{1}, {a}, {1, a }} D.{{1}, {a}, {1, a }}答:C(4)设集合A = {1,2,3,4,5,6 }上的二元关系R ={<a , b>⎢a , b∈A , 且a +b = 8},则R具有的性质为().A.对称的B.自反的C.对称和传递的D.反自反和传递的答:A(5)设集合A={1 , 2 , 3 , 4}上的二元关系R = {<1 , 1>,<2 , 2>,<2 , 3>,<4 , 4>},S = {<1 , 1>,<2 , 2>,<2 , 3>,<3 , 2>,<4 , 4>},则S 是R 的( )闭包.A .自反B .传递C .对称D .以上都不对 答:C(6)设集合A = {1 , 2 , 3 , 4 , 5}上的偏序关系的哈斯图如图1所示,若A 的子集B = {3 , 4 , 5}, 则元素3为B 的( ).A .最小上界B .最大下界C .下界D .以上答案都不对 图1 答:A2.填空题(1)设集合A 有n 个元素,那么A 的幂集合P (A )的元素个数为 . 答:2n(2)设集合A ={0,1,2},B ={0,2,4},R 是A 到B 的二元关系,},,{B A y x B y A x y x R ⋂∈∈∈><=且且则R 的集合表示式为 . 答:{<0,0>, <0,2>, <2,0>, <2,2>}(3)设集合A ={a ,b ,c ,d },A 上的二元关系R ={<a , b >, <b , a >, <b , c >, <c , d >},则R 的自反闭包是 .答:r (R )= {<a , b >, <b , a >, <b , c >, <c , d >}∪I A(4)设A ={1, 2, 3, 4, 5, 6, 7, 8},R 是A 上的整除关系,B ={2, 4, 6},则集合B 的最大元、最小元、上界、下界依次为 . 答:无、2、无、2(5)设集合A ={1, 2},B ={a , b },那么集合A 到B 的不同函数的个数有 . 答:4因为:f :{<1, a >, <2, a >}, {<1, b >, <2, b >}{<1, a >, <2, b >}, {<1, b >, <2, a >}3.如果R 1和R 2是A 上的自反关系,判断结论:“R 1-1、R 1∪R 2、R 1⋂R 2是自反的”是否成立?并说明理由. 答:结论成立.因为R 1和R 2是A 上的自反关系,即I A ⊆R 1,I A ⊆R 2. 由逆关系定义和I A ⊆R 1,得I A ⊆ R 1-1;由I A ⊆R 1,I A ⊆R 2,得I A ⊆ R 1∪R 2,I A ⊆ R 1⋂R 2.所以,R 1-1、R 1∪R 2、R 1⋂R 2是自反的.注: R 1-R 2是自反的吗?4.若偏序集<A ,R >的哈斯图如图2所示,则集合 A 的最大元为a ;最小元不存在.答:错a 是集合A 的极大元,最大元不存在. 图2 5.设集合A ={a ,b , { a , b }},B ={{a }, {b }, b },求a f5(1)B ⋂A ; (2)A -B ; (3)A ⨯B . 解:(1)B ⋂A ={a , b , { a , b }}⋂{{a }, {b }, b }={b } (2)A -B = {a , b , { a , b }}-{{a }, {b }, b }={a , { a , b }} (3)A ⨯B ={a , b , { a , b }}⨯{{a }, {b }, b }={<a , {a }>, <a , {b }>, <a , b >,<b , {a }>, <b , {b }>, <b , b >, <{ a , b }, {a }>, <{ a , b }, {b }>, <{ a , b }, b >}6.设A ={0,1,2,3,4},R ={<x ,y >|x ∈A ,y ∈A 且x +y <0},S ={<x ,y >|x ∈A ,y ∈A 且x +y ≤3},试求R ,S ,R ︒S ,R -1,S -1,r (R ),s (R ),t (R ),r (S ),s(S ),t (S ).解:R =∅,S ={<0,0>,<0,1>,<0,2>,<0,3>,<1,0>,<1,1>,<1,2>,<2,0>,<2,1>,<3,0>} R ︒S =∅,R -1=∅,S -1= S ;r (R )= I A ,s (R )= ∅,t (R )= ∅;r (S )=S ∪{<2,2>,<3,3>,<4,4>},s (S )= S ;t (S )= S ∪{<1,3>,<2,2>,<2,3>,<3,1>,<3,2>,<3,3>} 7.试证明集合等式:A ⋃ (B ⋂C )=(A ⋃B ) ⋂ (A ⋃C ).证:若x ∈A ⋃ (B ⋂C ),则x ∈A 或x ∈B ⋂C , 即 x ∈A 或x ∈B 且 x ∈A 或x ∈C . 即x ∈A ⋃B 且 x ∈A ⋃C , 即 x ∈T =(A ⋃B ) ⋂ (A ⋃C ),所以A ⋃ (B ⋂C )⊆ (A ⋃B ) ⋂ (A ⋃C ).反之,若x ∈(A ⋃B ) ⋂ (A ⋃C ),则x ∈A ⋃B 且 x ∈A ⋃C , 即x ∈A 或x ∈B 且 x ∈A 或x ∈C ,即x ∈A 或x ∈B ⋂C , 即x ∈A ⋃ (B ⋂C ),所以(A ⋃B ) ⋂ (A ⋃C )⊆ A ⋃ (B ⋂C ). 因此.A ⋃ (B ⋂C )=(A ⋃B ) ⋂ (A ⋃C ). 8.设R 是集合A 上的对称关系和传递关系,试证明:若对∀a ∈A ,∃b ∈A ,使得<a , b >∈R ,则R 是等价关系.证明:已知R 是对称关系和传递关系,只需证明R 是自反关系. ∀a ∈A ,∃b ∈A ,使得<a , b >∈R ,因为R 是对称的,故<b , a >∈R ; 又R 是传递的,即当<a , b >∈R ,<b , a >∈R ⇒<a , a >∈R ;由元素a 的任意性,知R 是自反的. 所以,R 是等价关系.(二)图论1.单项选择题(1)设图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010010000011100000100则G 的边数为( ).A .5B .6C .3D .4 答:D(2)设图G =<V , E >,则下列结论成立的是 ( ).A .deg(V )=2∣E ∣B .deg(V )=∣E ∣C .E v Vv 2)deg(=∑∈ D .E v Vv =∑∈)deg(答:C(3)设有向图(a )、(b )、(c )与(d )如图3所示,则下列结论成立的是 ( ).图3A .(a )是强连通的B .(b )是强连通的C .(c )是强连通的D .(d )是强连通的答:A(4)给定无向图G 如图4所示,下面给出的结点集子集中,不是点割集的为( ). A .{b , d } B .{d }C .{a , c }D .{g , e } 答:A 图4(5)图G 如图5所示,以下说法正确的是( ). A .{(a , d )}是割边B .{(a , d )}是边割集C .{(d , e )}是边割集D .{(a, d ) ,(a, c )}是边割集答:C 图5 (6)设G 是连通平面图,有v 个结点,e 条边,r 个面,则r = ( ).A .e -v +2B .v +e -2C .e -v -2D .e +v +2 答:A2.填空题(1)已知图G 中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G 的边数是 .答:15 (1⨯1+2⨯2+3⨯3+4⨯4)/2(2)设无向图G =<V ,E >是汉密尔顿图,则V 的任意非空子集V 1,都有 ≤∣V 1∣. 答:W (G - V 1)(3)设无向图G 为欧拉图,则图G 连通且 . 答:每个结点的度数为偶数(4)设图G =<V ,E >,其中|V |=n ,|E |=m .则图G 是树当且仅当G 是连通的,且m = . 答:n -1(5)连通无向图G 有6个顶点9条边,从G 中删去 条边才有可能得到G 的一棵生成树T . 答:4οο οο (a )οο οο (b ) οοοο (c )οοοο(d )a gb d fc e οο ο οο οο ο a ο οο ο ο b c f d e(6)给定一个序列集合{1,01,10,11,001,000},若去掉其中的元素 ,则该序列集合构成前缀码.答:1 3.给定图G (如图6所示): (1)试判断它们是否为欧拉图?并说明理由. (2)若是欧拉图,请写出一条欧拉回路.答:(1)图G 是欧拉图,因为图G 是连通图且每个结点的度数是偶数.(2)欧拉回路为: v 1 e 1 v 2 e 2 v 3 e 3 v 4 e 5v 5 e 7 v 2 e 8v 6 e 6 v 4 e 4v 1 注意:回路是不惟一4.试判断“设G 是一个有5个结点、10条边的连通图,则G 为平面图”是否正确,为什么?答:错误.因为它不满足定理4.3.3,即“设G 是一个有v 个结点e 条边的连通简单平面图,若v ≥3,则e ≤3v -6.”5.设图G =<V ,E >,其中V ={a 1, a 2, a 3, a 4, a 5},E ={(a 1, a 2),(a 2, a 4),(a 3, a 1),(a 4, a 5),(a 5, a 2)}(1)试给出G 的图形表示; (2)求G 的邻接矩阵; (3)求出每个结点的度数; (4)画出其补图的图形. 解:(1)图G 是无向图,图形如图7所示:图7 (2)图G 的邻接矩阵如下:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0101010010000011100100110)(G A(3)结点a 1, a 2, a 3, a 4, a 5的度数分别为:2,3,1,2,2. (4)图G 的补图的如图8所示:图86.图G =<V , E >,其中V ={a , b , c , d , e , f },E ={ (a , b ), (a , c ), (a , e ), (b , d ), (b , e ), (c , e ), (d , e ),ο οο ο οa 1a 2 a 3a 4a 5v 1 v 2 v 3v 4 v 5v 6 e 1 e 2e 3 e 4 e 5 e 6e 7 e 8 οο ο ο ο ο图6 ο ο ο ο οa 1a 2 a 3a 4 a 5οο ο ο οa 1 a 2 a 3a 4a 5(d , f ), (e , f ) },对应边的权值依次为5,2,1,2,6,1,9,3及8.(1)画出G 的图形; (2)写出G 的邻接矩阵;(3)求出G 权最小的生成树及其权值. 解:(1)G 的图形如图9所示:(2)邻接矩阵:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡011000101111110010010001011001010110 图9(3)粗线表示最小的生成树(见图10):最小的生成树的权为:1+1+5+2+3=12. 图107.设有一组权为2,3,6,9,13,15,试 (1)画出相应的最优二叉树; (2)计算它们的权值.解:最优二叉树如图11所示:图11 权值: 2⨯4+3⨯4+6⨯3+9⨯2+13⨯2+15⨯2 =8+12+18+18+26+30 =1128.设G 是一个n 阶无向简单图,n 是大于等于2的奇数.证明图G 与它的补图G 中的奇数度顶点个数相等.证明:设,G V E =<>,,G V E '=<>.则E '是由n 阶无向完全图n K 的边删去E 所得到的.所以对于任意结点u V ∈,u 在G 和G 中的度数之和等于u 在n K 中的度数.由于n 是大于等于2的奇数,从而n K 的每个结点都是偶数度的( 1 (2)n -≥度),于是若u V ∈在G 中是奇数度结点,则它在G 中也是奇数度结点.故图G 与它的补图G 中的奇数度结点个数相等.οο ο ο οc a b e dοf1 5 22 61 9 38 ο ο ο ο οc a b ed οf 15 22 61 938 οοο οο ο ο ο ο32 9 135 6 1115 20 ο ο 48289.设连通图G 有k 个奇数度的结点,证明在图G 中至少要添加2k条边才能使其成为欧拉图.证明:由定理3.1.2,任何图中度数为奇数的结点必是偶数,可知k 是偶数. 又根据定理4.1.1的推论,图G 是欧拉图的充分必要条件是图G 不含奇数度结点.因此只要在每对奇数度结点之间各加一条边,使图G 的所有结点的度数变为偶数,成为欧拉图.故最少要加2k条边到图G 才能使其成为欧拉图.(三)数理逻辑1.单项选择题(1) 下列命题公式是等价公式的为( ).A .⌝P ∧⌝Q ⇔P ∨QB .A →(⌝B →A ) ⇔⌝A →(A →B )C .Q →(P ∨Q ⇔⌝Q ∧(P ∨Q )D .⌝A ∨(A ∧B ) ⇔B 答:B 因为A →(⌝B →A ) ⇔ A →(B ∨A ) ⇔⌝A ∨(B ∨A ) ⇔ A ∨ (⌝A ∨B ) ⇔ A ∨ (A →B )⇔⌝A →(A →B )(2)下列公式 ( )为重言式.A .⌝(⌝P ∨(P ∧Q )) ↔QB .(B →(A ∨B )) ↔(⌝A ∧(A ∨B ))C .A ∧⌝B ↔A ∨BD .(P →(⌝Q →P ))↔(⌝P →(P →Q )) 答:D 因为(P →(⌝Q →P ))⇔⌝P ∨(Q ∨P )) ⇔1 (⌝P →(P →Q )) ⇔P ∨(⌝P ∨Q )) ⇔1 (3)命题公式⌝ (P →Q )的主析取范式是( ). A .Q P ⌝∧ B Q P ∧⌝ C .Q P ∨⌝ D .Q P ⌝∨答:A 因为⌝ (P →Q ) ⇔⌝ (⌝P ∨Q ) ⇔P ∧⌝Q(4)设C (x ): x 是国家级运动员,G (x ): x 是健壮的,则命题“没有一个国家级运动员不是健壮的”可符号化为 ( )A .))()((x G x C x ⌝∧⌝∀B .))()((x G xC x ⌝→⌝∀C .))()((x G x C x ⌝→⌝∃D .))()((x G x C x ⌝∧⌝∃答:D(5)表达式))(),(())(),((z zQ y x R y z Q y x P x ∀→∃∧∨∀中x ∀的辖域是( ). A .P (x , y ) B .P (x , y )∨Q (z ) C .R (x , y ) D .P (x , y )∧R (x , y ) 答:B2.填空题(1)命题公式()P Q P →∨的真值是 . 答:1 因为()P Q P →∨⇔⌝P ∨(Q ∨ P ) ⇔1(2)含有三个命题变项P ,Q ,R 的命题公式P ∧Q 的主析取范式是 . 答:(P ∧Q ∧⌝R )∨( P ∧Q ∧R )因为P ∧Q ⇔ P ∧Q ∧(⌝R ∨R ) ⇔(P ∧Q ∧⌝R )∨( P ∧Q ∧R )(3)设个体域D ={1,2},那么谓词公式)()(y yB x xA ∀∨∃消去量词后的等值式为 . 答:(A (1) ∨A (2))∨(B (1) ∧B (2))(5)谓词命题公式(∀x )(P (x )→Q (x )∨R (x ,y ))中的约束变元为 . 答:x3.请将语句翻译成命题公式: (1)今天不是天晴.(2)你去听课,他也去听课.(3)如果天下雪,则我明天就不去市里. (4)尽管他参加了考试,但他没有通过考试.解:(1)设P :今天是天晴; 命题公式为: ⌝ P .(2)设P :你去听课,Q :他去听课:命题公式为:P ∧Q .(3)设P :天下雪,Q :我明天去市里; 命题公式为:P →⌝Q .(4)设P :他参加了考试,Q :他没有通过考试; 命题公式为:P ∧⌝ Q .4.请将语句翻译成谓词公式: (1)所有人都不去上课. (2)有人不去工作. 解:(1)设P (x ):x 是人,Q (x ):x 去上课.谓词公式为: (∀x )(P (x )→ ┐Q (x )).(2)设P (x ):x 是人,Q (x ):x 去工作,谓词公式为: (∃x )(P (x) ∧┐Q (x )). 5.判断下列各题正误,并说明理由.(1)公式((Q ∧⌝R )→P )∧(⌝P →Q ∨R )↔P ∨R 为永真式.(2)求命题公式(P ∧Q )∧(⌝P ∨⌝R )的真值表,并判断它的类型. 解:(1)该公式是永真式.因为 R P R Q P P R Q ∨↔∨→⌝∧→⌝∧)())((R P R Q P P R Q ∨↔∨∨∧∨∨⌝⇔)()( R P Q Q R P ∨↔∧⌝∨∨⇔)( 1⇔(2)6.判断下列各题正误,并说明理由.(1)公式))(),(()(x xP y x yG x xP ∀→∃→∀是逻辑有效式(永真式).(2)下面的推理是否正确,请给予说明. ① P (a ) P ② (∀x )P (x ) US ① 解:(1)该公式是永真式.因为 ))(),(()(x xP y x yG x xP ∀→∃→∀⇔))(),(()(x xP y x yG x xP ∀∨⌝∃∨⌝∀1)(),()(⇔∀∨⌝∃∨⌝∀⇔x xP y x yG x xP(2)错误.② 应为(∀x )P (x ) UG ① 全称指定规则与全称推广规则不能混淆.7.求公式R Q P →∧)(的析取、合取、主合取\主合取范式. 解:R Q P R Q P ∨∧⌝⇔→∧)()(R Q P ∨⌝∨⌝⇔)(R Q P ∨⌝∨⌝⇔ (析取、合取、主合取范式)⇔(┐P ∧(┐Q ∨Q )∧(┐R ∨R ))∨((┐P ∨P )∧┐Q ∧(┐R ∨R )) ∨((┐P ∨P )∧(┐Q ∨Q )∧R )⇔(┐P ∧┐Q ∧┐R )∨(┐P ∧┐Q ∧R )∨(┐P ∧Q ∧┐R )∨(┐P ∧Q ∧R )∨(P ∧┐Q ∧┐R )∨(P ∧┐Q ∧R )∨(P ∧Q ∧R )(主析取范式)8.用列真值表的方法求命题公式R Q P →→)(的主析取范式.解:列真值表取真值为1的项,所求主析取范式为:(┐P ∧┐Q ∧R )∨(┐P ∧Q ∧R )∨(P ∧┐Q ∧┐R )∨(P ∧┐Q ∧R ) ∨(P ∧Q ∧R )9.试求谓词公式),()),(),()((y x B y x yG y x xH x S x ∨∃→∃∧∀中,∀x ,∃x ,∃y 的辖域,试问G (x , y )和B (x , y )中x ,y 是自由变元,还是约束变元?解:∀x 的辖域:)),(),()((y x yG y x xH x S ∃→∃∧ ∃x 的辖域:H (x ,y )∃y 的辖域:G (x ,y ) G (x , y )中的x ,y 是约束变量,B (x , y )中的x , y 是自由变量. 10.证明命题公式(P →(Q ∨⌝R ))∧⌝P ∧Q 与⌝(P ∨⌝Q )等价. 证:(P →(Q ∨⌝R ))∧⌝P ∧Q ⇔(⌝P ∨(Q ∨⌝R ))∧⌝P ∧Q ⇔(⌝P ∨Q ∨⌝R )∧⌝P ∧Q⇔(⌝P ∧⌝P ∧Q )∨(Q ∧⌝P ∧Q )∨(⌝R ∧⌝P ∧Q ) ⇔(⌝P ∧Q )∨(⌝P ∧Q )∨(⌝P ∧Q ∧⌝R ) ⇔⌝P ∧Q (吸收律) ⇔⌝(P ∨⌝Q ) (摩根律)9.构造推理证明))()(()()(x Q x P x x xQ x xP →∀⇒∀→∃. 分析:前提:)()(x xQ x xP ∀→∃.结论:))()((x Q x P x →∀证:(1) )()(x xQ x xP ∀→∃ P(2) )()(x xQ x xP ∀∨⌝∃ T (1)E(3) )()(x xQ x P x ∀∨⌝∀ T (2) E (量词与否定的关系) (4) ))()((x Q x P x ∨⌝∀(5) ))()((x Q x P x →∀ T (4) E上面这些例题供大家复习参考.。
离散数学复习注意事项:1、第一遍复习一定要认真按考试大纲要求将本学期所学习内容系统复习一遍。
2、第二遍复习按照考试大纲的要求对第一遍复习进行总结。
把大纲中指定的例题及书后习题认真做一做。
检验一下主要内容的掌握情况。
3、第三遍复习把随后发去的练习题认真做一做,检验一下第一遍与第二遍复习情况,要认真理解,注意做题思路与方法。
离散数学综合练习题一、选择题1.下列句子中,()是命题。
A.2是常数。
B.这朵花多好看呀!C.请把门关上!D.下午有会吗?2.令p: 今天下雪了,q:路滑,r:他迟到了。
则命题“下雪路滑,他迟到了”可符号化为()。
A. p q r∨→∧→ B. p q rC. p q r∧∧ D. p q r∨↔3.令:p今天下雪了,:q路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为()。
A.p q∧∧⌝ B.p qC.p q∨⌝ D. p q→⌝4.设()Q x:x会飞,命题“有的鸟不会飞”可符号化为()。
P x:x是鸟,()A. ()(()())⌝∀∧())x P xQ xx P x Q x⌝∀→ B. ()(()C. ()(()())Q x⌝∃∧())x P x Q x⌝∃→ D. ()(()x P x5.设()L x y:x大于等于y;命题“所有整数f x:x的绝对值,(,)P x:x是整数,()的绝对值大于等于0”可符号化为()。
A. (()((),0))∀→x P x L f x∀∧B. (()((),0))x P x L f xC. ()((),0)∀→xP x L f x∀∧ D. ()((),0)xP x L f x6.设()G x:x犯错误,命题“没有不犯错误的人”符号化为()。
F x:x是人,()A.(()())⌝∃→⌝x F x G xx F x G x∀∧B.(()()) C.(()())x F x G x⌝∃∧⌝⌝∃∧D.(()())x F x G x7.下列命题公式不是永真式的是()。
离散数学考试题(后附详细答案)一、命题符号化(共6小题,每小题3分,共计18分)1.用命题逻辑把下列命题符号化a)假如上午不下雨,我去看电影,否则就在家里读书或看报。
b)我今天进城,除非下雨。
c)仅当你走,我将留下。
2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x,总存在y使得xy=1。
c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B,使得f(a)=b.二、简答题(共6道题,共32分)1.求命题公式(P→(Q→R))↔(R→(Q→P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2.设个体域为{1,2,3},求下列命题的真值(4分)a)∀x∃y(x+y=4)b)∃y∀x (x+y=4)3.求∀x(F(x)→G(x))→(∃xF(x)→∃xG(x))的前束范式。
(4分)4.判断下面命题的真假,并说明原因。
(每小题2分,共4分)a)(A⋃B)-C=(A-B) ⋃(A-C)b)若f是从集合A到集合B的入射函数,则|A|≤|B|5.设A是有穷集,|A|=5,问(每小题2分,共4分)a)A上有多少种不同的等价关系?b)从A到A的不同双射函数有多少个?6.设有偏序集<A,≤>,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合,R为实数集合,求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N(写出即可)(6分)三、证明题(共3小题,共计40分)1.使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a)A→(B∧C),(E→⌝F)→⌝C, B→(A∧⌝S)⇒B→Eb)∀x(P(x)→⌝Q(x)), ∀x(Q(x)∨R(x)),∃x⌝R(x) ⇒∃x⌝P(x)2.设R1是A上的等价关系,R2是B上的等价关系,A≠∅且B≠∅,关系R满足:<<x1,y1>,<x2,y2>>∈R,当且仅当< x1, x2>∈R1且<y1,y2>∈R2。