人教版六年级下册数学 9总复习 小升初数学计算能力的有效衔接之追求无缝篇试题(十八)

数不够用了---怎么办？1.仔细思考以下各对量：（1）气温降低4℃与气温为10℃；（2）胜2局与负3局；（3）转盘逆时针转3圈与顺时针转5圈；（4）收入3万元与亏损3万元，其中具有相反意义的量的有（）对。

(提示：①气温下降与气温本身、收入和亏损不是相反的意义。

) A．0 B．1 C．2 D．32.早晨衔衔从家出发，向东跑步1000米，杰杰向西跑步1000米，妈妈说，都是1000米，你们能自己区别出来吗？如果规定向东的方向为正。

你能自己试着表示出来吗？3．某班班学生的平均体重为50千克，其中贝贝重52千克，晶晶重48千克，欢欢重51千克，迎迎重46千克，妮妮重53千克。

如果把平均体重记为0，如何表示这5名同学的体重？4.用直线表示数时，如果表示数a的点在0的左边，那么a一定是（）数；如果表示数b的点在0的右边，则数b一定是（）数；-b一定是（）数。

（提示：-b表示的数是和b相反方向的数，如果b是正数，则-b是负数；如果b是负数，则-b表示正数。

）5.5分钟内背过5个单词为过关，超过的记为正，现有五名同学的成绩记录如下：-3，0，+1，+2，-1．（1）这五个人中有几人过关？（2）他们分别背过了几个单词？6.口算5+6、8+6时，我们很快能得出答案分别是11和14。

负数能加、减吗？下面，我们一起来探究一下吧！比如，-5+（-6）、-8+（+6）怎么计算呢？计算-5+（-6）我们可以这样想：假设向东走为正，则向西走就为负。

-5+（-6）表示先向西走5米，再向西走6米，两次共向西走了11米，用负数表示就是（）米，所以-5+（-6）=（）。

同理，-8+（+6）表示，先向西走8米，再向东走6米，结果离开原来出发点西2米处，所以，-8+（+6）=（）负数的减法也可以这样来理解。

既然负数能加减，那负数能乘除吗？我们一起来探究吧！观察下面左面的算式，你能直接写出右面一组算式的得数吗？3×3=9 3×（-3）=（）3×2=6 3×（-2）=（）5×4=20 5×（-4）=（）通过上面的计算，我发现：一个正数与一个负数相乘，积是（）数，如果是两个负数相乘呢？自己先猜一猜，再试着填空。

人教版六年级数学下册小升初总复习期末测试卷（含答案）班级： 姓名：一、填空。

(共20分)1．一个数是由9个亿，15个万，9个千和7个一组成的数，这个数写作( )，四舍五入到万位约是( )。

2.38的分数单位是( )，再增加( )个这样的单位就是最小的质数。

3．把一根5米长的铁丝平均分成8段，每一段是这根铁丝的( )。

4．5克糖放入20克水中，糖占糖水的( )%。

5．一个3 mm 长的零件画在图纸上是18 cm ，这幅图的比例尺是( )。

6．把0.333，13，33%，0.34，0.4，三成五从左到右依次从大到小排列，排在第四位的数是( )。

7．一个三角形三个内角的度数比是1∶1∶2，这个三角形最大的内角是( )度，其中较短边的长是5 cm ，这个三角形的面积是( )。

8．A ＝2×5×7，B ＝3×3×5×11，那么A 和B 的最大公因数是( )，最小公倍数是( )。

9．14只鸽子飞回了3个鸽巢，那么总有一个鸽巢至少飞入( )只鸽子。

10．一个三位小数取近似值是2.80，这个数最大是()。

11．一个长方体棱长之和是48分米，长是5分米，宽是3分米，这个长方体的表面积是()平方分米，放在桌面上所盖住桌面最小的面积是()平方分米，将它削成一个最大的圆柱的体积是()立方分米。

12．在一个比例中，两个外项互为倒数，其中一个内项是34，另一个内项是()。

二、辨一辨。

(对的画“√”，错的画“×”)(每题1分，共5分)1．大于－2且小于＋2的数只有3个。

() 2．圆的周长一定，直径和圆周率成反比例。

() 3．折线统计图更容易看出数量增减变化的情况。

() 4．圆柱的底面半径和高都扩大为原来的2倍，则体积扩大为原来的8倍。

() 5．林场种100棵树苗，死了3棵，又补种3棵，共成活100棵，成活率为100%。

()三、选一选。

(把正确答案的序号填在括号里)(每题1分，共5分) 1．安妮花图书馆一本《安徒生童话》原价30元，六一儿童节，八折出售，六一儿童节过后恢复原价，需要提价()。

小升初数学计算能力的有效衔接之追求无缝篇（二十）1．商场的自动扶梯以匀速由下往上行驶，两个孩子嫌扶梯走得太慢，于是在行驶的扶梯上，男孩每秒钟向上走2个梯级，女孩每2秒钟向上走3个梯级。

结果男孩用40秒钟到达，女孩用50秒钟到达。

则当该扶梯静止时，可看到的扶梯梯级有( )。

A．80级 B．100级 C．120级 D．140级2．某种物质由液态m变为固态n时，体积缩小5％。

若由固态n变为液态m，它的体积将( )。

A．增大5％B．增大5．2％到5．3％之间C．增大4．8％到4．9％之间 D．以上三种选择都不对3．要配制每100克含盐量17．5克的盐水7千克，需要食盐多少克?( )。

A．125 B．1205 C ．1225 D．0.1254．某次考试有30道判断题，每做对一道题得4分，不做或做错一道题倒扣2分，甲考生得了96分，他做错了几道题?( )。

A．12 B．4C．2 D．65.王霞在计算题时，由于粗心大意，把被减数个位上的3错写成5，把十位上的6错写成0，这样算得差是189。

正确的差是多少？6.小军在做题时，把被减数个位上的3错写成8，把十位上的0错写成6，这样算得的差是198。

正确的差是多少？7.小刚在做题时，把减数个位上的9错写成6，把十位上的3错写成8，这样算得的差是268。

正确的差是多少？8.两数相减，减数减少9，要使差增加16，被减数应有什么变化？9.两个数相除，商是8，余数是600。

如果被除数和除数同时缩小100倍，商是多少？余数是多少？10．有一只猴掉进15米深的井里，每天爬5米滑下4米，后一天比前一天多爬1米，且下滑距离不变，则总共需要( )。

A．3天 B．4天 C．5天 D．6天11．有一个班共有学生100名，各自选一门以上的选修课，选地理的有60名，选物理的有50名，那么地理和物理都选的人数为( )。

A．60 B．50 C．20D．1012、 8．4×2．5+9．7)÷(1．05÷1．5+8．4÷0．28)的值为( )。

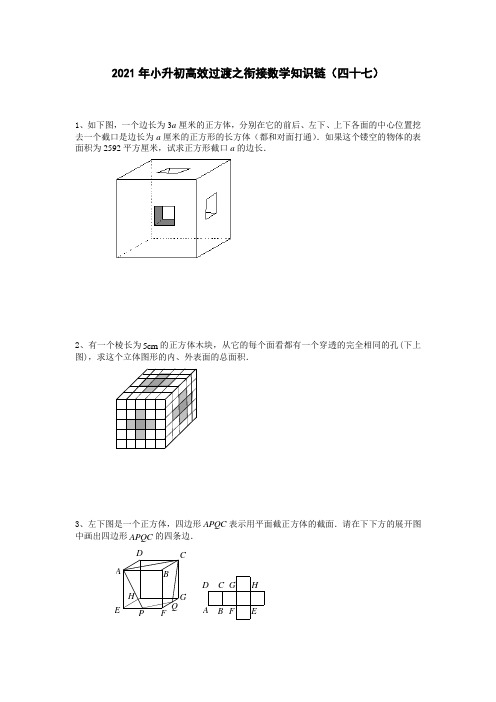
2021年小升初高效过渡之衔接数学知识链（四十七）1、如下图，一个边长为3a厘米的正方体，分别在它的前后、左下、上下各面的中心位置挖去一个截口是边长为a厘米的正方形的长方体（都和对面打通）．如果这个镂空的物体的表面积为2592平方厘米，试求正方形截口a的边长．2、有一个棱长为5cm的正方体木块，从它的每个面看都有一个穿透的完全相同的孔(下上图)，求这个立体图形的内、外表面的总面积．3、左下图是一个正方体，四边形APQC表示用平面截正方体的截面．请在下下方的展开图中画出四边形APQC的四条边．HP FQGBCDEAF EHGD CBA4、如图，用455个棱长为1 的小正方体粘成一个大的长方体，若拆下沿棱的小正方体，则余下371个小正方体，问：所堆成的大长方体的棱长各是多少？拆下沿棱的小正方体后的多面体的表面积是多少？5、大正方体的棱长是小正方体棱长的4倍，那么它的表面积是小正方体表面积的______倍．6、一个大正方体、四个中正方体、四个小正方体拼成如图的立体图形，已知大、中、小三个正方体的棱长分别为5厘米、2厘米、1厘米．那么，这个立体图形的表面积是________平方厘米．7．一项工程，由甲队做30天完成，由乙队做20天完成。

（1）两队合做5天可以完成工程的几分之几？（2）两队合做10天，还剩下工程的几分之几？（3）两队合做几天完成？8．一项工程，由甲工程队修建，需要１２天，由乙工程队修建，需要２０天，两队共同修建需要多少天？9．一项工程，甲队独做８天完成，乙队独做１０天完成，两队合做，多少天完成全部工程的43？10．一项工程，甲、乙合做６天可以完成。

甲独做１８天可以完成，乙独做多少天可以完成？11．小明和小红做游戏，小明拿出一张日历：“我用笔圈出了2×2的一个正方形，它们数字的和是76，你知道我圈出的四个数字中最小的那个数吗？”小红算出的最小的那个数是 ．12．在4点与5点之间，时针与分针成100°时，是4点 分．13．甲、乙两站间距离为284km，一列慢车从甲站开往乙站，每小时行驶48km；慢车驶出1小时后，另有一列快车从乙站开往甲站，每小时行驶70km．问：快车行驶了几小时与慢车相遇？设快车行驶了x小时与慢车相遇，则所列方程为．14．某小组进行个人篮球比赛，并用表格记录了在规定时间内的进球数，后来表格不慎受到了污损．若已知平均每人进球3.5个，则投进3个球的学生有人．15．一条环行跑道长400m，甲在跑道上练习骑自行车，平均每分钟行550m，乙在跑道上练习跑步，平均每分钟跑250m，若两人同时出发，同向而行，则他们经过min后首次相遇．。

2021年小升初高效过渡之衔接数学知识链1、下图是一个812 面积单位的图形．求矩形内的箭形ABCDEFGH 的面积．2、比较图中的两个阴影部分①和②的面积，它们的大小关系______②①3所占的面积是多少？4、如图，每一个小方格的面积都是1平方厘米，那么用粗线围成的图形的面积是多少平方厘米？④③②①⑤⑥5、李师傅利用一张长1.256米、宽0.628米的长方形铁皮做一个水桶的侧面．为了使水桶容积最大，从（）的正方形铁皮中剪出一个圆形的底面最合适．A.边长20厘米B.边长30厘米C.边长40厘米D.边长50厘米6、小王为家人买了四件礼物，最便宜的15元，最贵的30元，那么买这四件礼物总共需要的钱是（）A.75元～105元B.85元～100元C.多于110元7、某月有五个星期三，但这个月的第一天和最后一天不是星期三，这个月的1日是星期（）A.星期二B.星期四C.星期五D.星期六8、如图1第一行是水滴进玻璃容器的示意图（滴水速度相同），如2图第二行表示的是容器中水的高度随滴水时间变化的情况（图中刻度、单位都相同）．下列对应中正确的是（）A.（1）﹣﹣（a）B.（2）﹣﹣（b）C.（3）﹣﹣（c）D.（4）﹣﹣（d）9、口算7.84+0.25= ×3÷×3=1﹣0.72= 6÷6%=10、估算①4.9×697≈②48.03÷3.98≈③10.0001﹣5.997≈④20.3亿+1.9亿≈亿．11、第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一个小方格的面积是1，那么7、2、1三个数字所占的面积之和是多少？12、55的方格纸，小方格的面积是1平方厘米，小方格的顶点称为格点．请你在图上选7个格点，要求其中任意3个格点都不在一条直线上，并且使这7个点用直线连接后所围成的面积尽可能大．那么，所围图形的面积是平方厘米．13．黄玉骑自行车去香山，她先以8千米/时的速度走平路，而后又以4千米/时的速度上坡到达香山，共用了1.5小时，返回时，先以12千米/时的速度下坡，而后以9千米/时的速度度过平路，回到原出发点，共用去55分钟，求从出发点到香山的路程是多少千米？14．某地区住宅用电之电费计算规则如下：每月每户不超过50度时，每度以4元收费；超过50度的部分，每度以5元收费，并规定用电按整数度计算（小数部分舍去）．（1）下表给出了今年3月份A，B两用户的部分用电数据，请将表格数据补充完整，电量（度）电费（元）A240B合计90（2）若假定某月份C用户比D用户多缴电费38元，求C用户该月可能缴的电费为多少？。