第1章 1.5 力的时间和空间积累效应
- 格式:ppt
- 大小:1.96 MB
- 文档页数:68

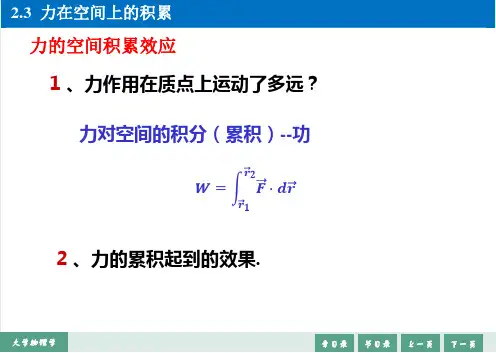
怎么理解力对空间的积累力是物理学的基本概念,它是描述物体运动状态的量。
在我们日常生活中,力也是一个经常被提及的词汇。
力的作用可以对物体产生影响,也可以对我们的身体产生影响。
但是,力还有一个非常重要的作用,那就是对空间的积累。
本文将从以下几个方面来探讨力对空间的积累的意义。
一、力对空间的影响首先,我们需要了解力对空间的影响。
力的作用可以改变物体的位置、形状和速度等。
这些变化会对空间造成影响。
例如,一个重物落地时,它的重力会对地面产生压力,这个压力会使地面产生一个凹陷的形状。
这个凹陷的形状就是力对空间的影响。
此外,力还可以改变空间中物体的运动轨迹。
例如,一个弹簧可以将物体向上弹起,这个弹起的轨迹就是力对空间的影响。
力还可以改变物体的方向和速度,这些变化也会对空间产生影响。
例如,一个车辆在高速行驶时,它的速度和方向会对周围的空间产生影响。
二、力对空间的积累力对空间的影响是不断积累的。
当一个物体受到力的作用时,它会对周围的空间产生影响。
这些影响会随着时间的推移而不断积累,最终形成一个稳定的形态。
例如,一座大桥的建造就是力对空间的积累。
在建造过程中,桥梁承受着巨大的重力和风力,这些力会对周围的空间产生影响。
但是,经过多年的积累,这些影响逐渐稳定下来,形成了一座坚固的大桥。
此外,力对空间的积累还可以表现在自然界中。
例如,一座山峰的形成就是力对空间的积累。
在地球的漫长历史中,地壳运动、地质变化、水流侵蚀等力的作用会不断改变山峰的形态。
但是,这些影响逐渐积累,最终形成了我们看到的山峰。
三、力对空间的美学价值力对空间的积累不仅仅是一个物理过程,它还具有美学价值。
当我们欣赏一座大桥或者一座山峰时,我们所看到的不仅仅是一个物理结构,更是一个经过力对空间积累的艺术品。
例如,一座古老的城墙,它经历了多年的风雨侵蚀和人类的战争摧毁,但它依然屹立在那里,成为城市的标志性建筑。
这个城墙所承载的不仅仅是历史的记忆,更是力对空间积累的美学价值。
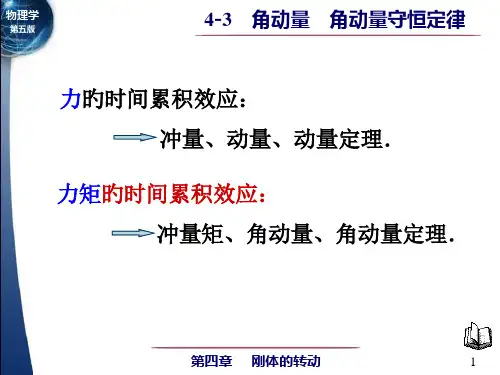

求解力学问题的三把金钥匙——力的三种效应及应用力学是物理学的基础和重要的组成部分,在中学物理教材中,力学知识的核心可以概括为力的三种效应即力的瞬时效应、力的时间积累效应、力的空间积累效应。
力的这三种效应从三个不同的视角揭示了自然界中最普遍的现象之一---运动现象的内在本质及其遵循的规律,为力学问题的解决提供了三种求解方法。
下面就力的三种效应及其应用做以粗浅探讨:1、力的瞬时效应:牛顿第二定律的微分形式为d(mv)/dt=F, mv表示物体的“运动量”,简称动量,d(mv)/dt为动量对时间求导,即动量随时间改变的快慢程度。
在宏观、低速情况下,物体的质量m为定值,d(mv)/dt可写作mdv/dt,dv/dt为速度对时间求导,即速度随时间改变地快慢程度——加速度;如果物体做匀变速运动,加速度为恒量,记做dv/dt=a,则d(mv)/dt=F可写作ma=F,该式就是中学物理教材中牛顿第二定律的数表达式。
F=ma给出了力F与加速度a的瞬时定量关系,称为力的瞬时效应。
应用中可以从物体的受力分析出发,求出物体的加速度a,进而求解位移s、速度v等运动学问题;也可以从分析物体的运动情况出发,求出物体的加速度,进而解决物体的受力问题。
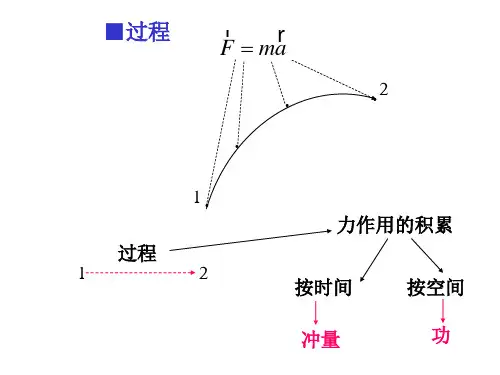
2、力的时间积累效应:力的时间积累效应就是求力F对时间t的积分,由d(mv)/dt=F可得Fdt=mdv则有ʃFdt=ʃmdv 即ʃFdt=mv2-mv1当F为恒力时有F(t2– t1 )= m(v2– v1 ) 即F△t = m△V这就是动量定理:在一段时间内物体动量的变化(m△V),等于物体在同一时间内所受外力的冲量(F△t)。
力的时间积累效应在应用中与力的瞬时效应的应用类似,也是双向的。
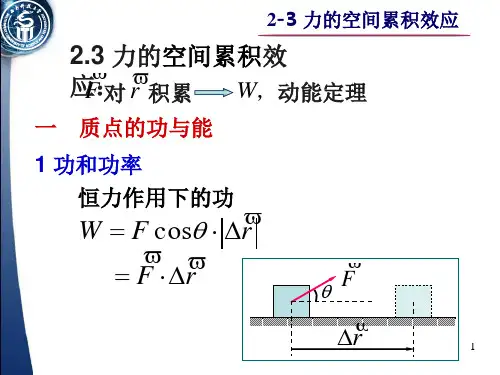
3、力的空间积累效应:力的时间积累效应就是求力对位移的积分,其微分形式为Fds ,由d(mv)/dt=F可得Fds = d(mv)ds/dt ,又ds/dt = v则有Fds = vd (mv) , 对其积分ʃFds =ʃvd(mv) 当F为恒力时有F(s2 – s1) = m(v22– v12)/2这就是动能定理:物体动能的增加,等于外力对物体所做的功。




大学力学第一章知识点总结第一章力学引论1.1 力学的发展历史力学作为物理学的一个重要分支,其发展历史可以追溯到古希腊时期。
古代的力学研究主要集中在物体的静力学和动力学方面,主要代表人物有亚里士多德、阿基米德等。
17世纪以来,伽利略、牛顿等科学家的研究进一步推动了力学的发展,形成了经典力学的基本理论框架。
1.2 力学的研究对象力学的研究对象是宏观物体的运动和相互作用规律。
力学主要关注的问题包括:1) 物体的运动规律:描述物体的位置、速度、加速度等物理量随时间的变化规律;2) 物体的相互作用:研究物体之间的相互作用力、力的性质、大小和方向等。
1.3 力学的基本概念力学的基本概念包括:质点、力、力的合成与分解、质点系等。
1.3.1 质点质点是力学中理想化的物理模型,它具有以下特点:1) 质点的质量可以集中在一个点上;2) 质点的大小可以忽略不计;3) 质点的形状可以忽略不计。
1.3.2 力力是使物体发生形变或者改变运动状态的原因。
根据作用力的性质,力可以分为接触力和非接触力;根据作用力的来源,力可以分为重力、弹力、摩擦力等。
1.3.3 力的合成与分解多个力共同作用在物体上时,可以通过几何方法或者向量加法原理进行力的合成。
而一个力可以分解为多个力的合力,可以用力的正交分解和平行分解法进行。
1.3.4 质点系当研究的物理系统不仅包含一个质点时,就涉及到了质点系的概念。
质点系可以根据质点间的相互作用力和相对位置的不同而表现出不同的特性。
1.4 力学的基本原理力学的基本原理包括牛顿三定律、动量定理和动能定理。
1.4.1 牛顿三定律牛顿三定律是经典力学的基础,包括以下三个定律:1) 牛顿第一定律(惯性定律):若作用于物体的合力为零,则物体将保持静止或匀速直线运动的状态;2) 牛顿第二定律(动力定律):物体的加速度与作用于物体的合外力成正比,与物体的质量成反比,方向与作用力的方向相同;3) 牛顿第三定律(作用与反作用定律):任何一个物体对另一物体施加一个力,必然受到另一物体对它的相等大小、方向相反的力的作用。