数学建模城市垃圾运输问题

A题：垃圾分类处理与清运方案设计深圳市南山区厨余垃圾处理方案设计摘要本文所讨论的是垃圾运输与处理总的整数规划问题。

首先，根据给出的“南山区垃圾转运站分布图”，用几何画板将图形简化，把38个垃圾转运站简化为18个垃圾转运站分布区，并在地图上选取主要干道，确定厨余垃圾处理所需设备数量（只需3个大型设备），根据垃圾站日转运量将18个垃圾转运区划分为3个区域，每个区域建设1个厨余垃圾处理厂，候选点选取在垃圾中转站附近。

其次，用几何画板标记18个点的坐标，并算出18个候选点两两之间的路程。

计算简化图与实际地图比例。

再次，我们确定将厨余垃圾处理厂建在所选的候选点上能使总运费最小。

然后根据设备处理量、设备建设成本、待处理垃圾总量等条件与总成本最小这一目标构建整数规划模型。

在实际建模中合理假设建设3个大型处理厂正本最小，然后利用lingo软件求解，得出处理厂的分布方案。

最后，在问题2中把居民区合理简化为分布点，把所选的主要干道交叉点一齐作为中转站的候选点，参考问题一的步骤，修改了问题已的模型求出新的垃圾中转站方案，在根据这个方案利用问题已的方法与步骤求出新的厨余垃圾处理厂方案与厨余垃圾清运方案。

本文给出的模型可以求解出处理厂的建设数量、规模、位置以及中转站垃圾的运输去向，同时模型的应用性强，可以用来解决本题中的1、2题，并对模型进行了适当修改是指能够适用于其他地区的相关设施建设问题，适用性强。

关键词：最短路、整数线性规划、垃圾中转、lingo软件、几何画板问题重述在垃圾分类收集与处理中，不同类的垃圾有不同的处理方式，简述如下：1）橱余垃圾可以使用脱水干燥处理装置，处理后的干物质运送饲料加工厂做原料。

不同处理规模的设备成本和运行成本（分大型和小型）见附录1说明。

可回收垃圾将收集后分类再利用。

有害垃圾，运送到固废处理中心集中处理。

4）其他不可回收垃圾将运送到填埋场或焚烧场处理。

所有垃圾将从小区运送到附近的转运站，再运送到少数几个垃圾处理中心。

货运公司运输问题数信学院 14 级信计班魏琮【摘要】本文是针对解决某港口对某地区8 个公司所需原材料A、B、C的运输调度问题提出的方案。

首先考虑在满足各个公司的需求的情况下，所需要的运输的最小运输次数，然后根据卸载顺序的约束以及载重费用尽量小的原则，提出了较为合理的优化模型，求出较为优化的调配方案。

针对问题一，在两个大的方面进行分析与优化。

第一方面是对车次安排的优化分析，得出① ~④公司顺时针送货，⑤ ~⑧公司逆时针送货为最佳方案。

第二方面根据车载重相对最大化思想使方案分为两个步骤，第一步先是使每个车次满载并运往同一个公司，第二步采用分批次运输的方案，即在第一批次运输中，我们使 A 材料有优先运输权；在第二批次运输中，我们使 B材料有优先运输权；在第三批次中运输剩下所需的货物。

最后得出耗时最少、费用最少的方案。

耗时为小时，费用为元。

针对问题二，加上两个定理及其推论数学模型与问题一几乎相同，只是空载路径不同。

采取与问题一相同的算法，得出耗时最少，费用最少的方案。

耗时为小时，费用为元。

针对问题三的第一小问，知道货车有 4 吨、 6 吨和 8 吨三种型号。

经过简单的论证，排除了 4 吨货车的使用。

题目没有规定车子不能变向，所以认为车辆可以掉头。

然后仍旧采取① ~④公司顺时针送货，⑤~⑧公司逆时针送货的方案。

最后在满足公司需求量的条件下，采用不同吨位满载运输方案，此方案分为三个步骤：第一，使 8 吨车次满载并运往同一公司；第二， 6 吨位车次满载并运往同一公司；第三，剩下的货物若在 1~6 吨内，则用 6 吨货车运输，若在 7~8 吨内用 8 吨货车运输。

最后得出耗时最少、费用最省的方案。

耗时为小时，费用为元。

一、问题重述某地区有8个公司( 如图一编号①至⑧) ，某天某货运公司要派车将各公司所需的三种原材料A,B,C从某港口( 编号⑨) 分别运往各个公司。

路线是唯一的双向道路( 如图１) 。

货运公司现有一种载重6 吨的运输车，派车有固定成本 20元/ 辆，从港口出车有固定成本为 10元/车次 ( 车辆每出动一次为一车次) 。

垃圾运输调度问题摘要：本文就生活中垃圾车调度问题进行了研究，通过对垃圾站点之间分布位置的分析，建立单目标规划模型，统筹安排了运输车的调度方案。

首先，应该对题设条件提出一定的假设。

其次，对垃圾站点的位置进行分析，并在图中绘制出其(x,y)散点图。

再次，根据题目要求，建立模型，结合已有的模型，对垃圾点之间的位置分布关系进行讨论及证明，从而确定最基本的行车路线原则。

然后，根据上述建立的单目标模型中的约束条件，编写程序，求解出各运输车辆的数量以及最佳的分配方案。

该模型中包含着运输费用、垃圾量、运输车工作时间的累积计算问题，因此，文中以运输车费用最少为目标函数，以运输车载重量的大小、当天必须将所有垃圾清理完、运输车工作时间等为约束条件，以运输车是否从一个垃圾站点到达另一个垃圾站点为决策变量，建立了使得运输费用最小的单目标的非线性规划模型。

并利用MATLAB编程求解，得到满意方案：载重费：2213.37元，空载费：122.4总共花费2335.77元，花费的总时间：15小时18分，一共发车十次，用4辆车来完成任务。

最后，对模型的优缺点进行了分析，并给出了模型的改进意见，对解决实际问题具有一定的指导意义。

关键词：垃圾运输目标规划运输费用MATLAB编程最优方案1.问题提出1.1 基本情况某城区有36个垃圾集中点，每天都要从垃圾处理厂（第37号节点）出发将垃圾运回。

不考虑垃圾的装车时间。

现有一种载重6吨的运输车，运输车平均速度为40公里／小时（夜里运输，不考虑塞车现象）；每台车每日平均工作4小时。

运输车重载运费1.8元/吨公里；运输车空载费用0.4元/公里；并且假定街道方向均平行于坐标轴。

垃圾地理位置坐标如表1所示。

表1 垃圾地理位置坐标数据表1.2 问题要求根据上述基本情况建立的模型中的约束条件，利用计算机编程求解，得出满意的运输车调度方案，包括需要投入多少台运输车，每台车的调度方案以及运营费用。

2.模型建立在建立模型之前，对垃圾车调度问题做一些基本的假设，并给出建立模型时所需要的符号说明，在分析问题的基础上，建立合理优化的模型。

垃圾分类处理与清运方案设计摘要垃圾分类化收集与处理是有利于减少垃圾的产生，有益于环境保护，同时也有利于资源回收与再利用的城市绿色工程。

本文即针对深圳市南山区的分类化垃圾的实现问题建立了相应的数学模型。

首先在垃圾中转站的位置与数量已定的条件下，根据柴油费不超过的数量确定大型垃圾处理中心的数量，然后根据大型垃圾处理中心的数量进行分区，将各个区的垃圾转运站进行比较，求找使总成本最小的坐标位置，确立大型垃圾处理中心的坐标，相应的确立小型垃圾处理中心的位置。

进一步考虑在垃圾转运站的位置和规模不定的情况下，由问题一的求解可知，建设小型垃圾处理中心的位置在偏远地区，并且产生的垃圾总量比较小，只有同时满足才适合建设，否则运往大型垃圾处理中心比较经济。

因此可以将距离比较近的垃圾转运站合并，并建立大型垃圾处理中心，在偏远的地方的并且产生垃圾量比较少的点建立小型垃圾处理中心，偏远但产生垃圾量比较多的点保留垃圾转运站，大型垃圾处理中心进行垃圾处理。

，关键词：灰色模型剔除法递归算法非线性规划和线性规划求最优解数理统计一问题重述深圳垃圾分为四类：橱余垃圾、可回收垃圾、有害垃圾和其他不可回收垃圾，其中对于居民垃圾，基本的分类处理流程如下：在垃圾分类收集与处理中，不同类的垃圾有不同的处理方式，简述如下：1)橱余垃圾。

可以使用脱水干燥处理装置，处理后的干物质运送饲料加工厂做原料。

不同处理规模的设备成本和运行成本（分大型和小型）见附录1说明。

2)回收垃圾。

将收集后分类再利用。

3)有害垃圾。

运送到固废处理中心集中处理。

4)其他不可回收垃圾。

将运送到填埋场或焚烧场处理。

所有垃圾将从小区运送到附近的转运站，再运送到少数几个垃圾处理中心。

显然，1）和2）两项中，经过处理，回收和利用，产生经济效益，而3）和4）只有消耗处理费用，不产生经济效益。

本项研究课题旨在为深圳市的垃圾分类化进程作出贡献。

为此请你们运用数学建模方法对深圳市南山区的分类化垃圾的实现做一些研究，具体的研究目标是：1）、假定现有垃圾转运站规模与位置不变条件下，给出大、小型设备（橱余垃圾）的分布设计，同时在目前的运输装备条件下给出清运路线的具体方案。

垃圾运输问题垃圾运输问题摘要本文对于垃圾运输问题的优化，通过运用目标规划的有关知识对题目给出的坐标数据进行了处理，根据从最远点开始运载垃圾运输费用最低的原则，以及不走回路的前提，采用规划的理论建立了运输车和铲车的调度优化模型，运用MATLAB软件得到了全局最优解，对此类问题的求解提供了一种较优的方案，以达到最少运输费用。

问题（1）包含着垃圾量和运输费用的累积计算问题，因此，文中以运输车所花费用最少为目标函数，以运输车载重量的大小、当天必须将所有垃圾清理完等为约束条件，以运输车是否从一个垃圾站点到达另一个垃圾站点为决策变量，建立了使得运输费用最小的单目标的非线性规划模型。

运用MATLAB求解，得出了最优的运输路线为10条，此时运输所花费用为2335.05元。

通过分析，发现只需6辆运输车（载重量为6吨）即可完成所有任务，且每辆运输车的工作时间均在4个小时左右。

具体结果见文中表3。

问题（2），建立了以运行路径最短为目标的单目标非线性规划模型。

从而求出了使铲车费用最少的3条运行路线，且各条路线的工作时间较均衡。

因此，处理站需投入3台铲车才能完成所有装载任务，且求得铲车所花费用为142.8元，三辆铲车的具体运行路线见文中表4。

文中，我们假定垃圾处理站的运输工作从凌晨0：00开始，根据各铲车的运输路线和所花时间的大小，将铲车和运输车相互配合进行工作的时间做出了详细的安排见表5。

问题（3），要求给出当有载重量为6吨、10吨两种运输车时的最优的调度方案。

基于第（1）问中的模型，修改载重量的约束条件，用MATLAB分别求解，得出两种调度方案，但总的运输费用不变，均为2508.63元；对于方案一，有9条路径，分别需要6吨的运输车2辆；10吨的运输车5辆，各运输车具体的运输线路见文中表8。

对于方案二，有10条路径，分别需要6吨的运输车1辆；10吨的运输车4辆，各运输车具体的运输线路见文中表10。

问题（4），基于问题（1）、问题（2）、问题（3），修改每个站点的垃圾量，用MATLAB分别求解，得到最优的调整方案最后，对模型的优缺点进行了分析，并给出了模型的改进意见，对解决实际问题具有一定的指导意义。

垃圾分类处理与清运方案设计摘要随着社会的快速发展，城市化进程的日益加快，城市垃圾处理问题也随之而来。

近几年，我国大城市的垃圾分类化也已经提到日程上来。

本文主要针对深圳市南山区垃圾的处理问题进行了垃圾分类和清运方案的设计，在合理的假设基础上，建立了合适的数学模型。

问题一，我们优先考虑了最佳经济效益根据现有垃圾转运站规模与位置的资料，给出了大、小型设备（橱余垃圾）的分布设计，同时在目前的运输装备条件下给出清运路线的具体方案。

由于橱余设备的分布之和厨余垃圾量有关，因此只要考虑厨余垃圾的处理过程中的情况就可以。

针对厨余垃圾量，设备的分布可以分为两个大型设备、一个大型设备和多个小型小型设备、全部用小型设备这三种情况。

引入0-1变量，列出目标函数和约束条件后用lingo分别求出了三种情况下后的最优解为：两个大型处理设备，分别建在30和37号转运站。

问题二，分析题目可知，转运站地址将决定小区到其之间的运费，转运站处理厨余垃圾所需的成本、运费，以及处理有害垃圾和不可回收垃圾的运费。

而在环保效益方面，垃圾清运过程将造成垃圾对环境的二次污染。

本题还是先考虑经济效益，最优经济效益的基础上优先考虑环保效益。

我我们按照小区地理位置，综合处理数据后，将小区分为21个片区，每个片区的中心点建立一个转运站。

求出了其最优运费为。

而对于厨余垃圾的处理方式，可以参照第一问的方法求解，最终选择一个大型设备有害垃圾和不可回收垃圾则直接以该转运站到垃圾填埋场或焚烧厂的最短路程为实际路程求解计算。

关键字：清运路线经济效益0-1变量lingo 片区一问题重述随着社会的快速发展，城市化进程的日益加快，城市垃圾处理问题也随之而来。

在发达国家城市已普遍实现了垃圾分类化，近几年，我国大城市的垃圾分类化也已经提到日程上来。

自《关于组织开展城市餐厨废弃物资源化利用和无害化处理试点工作的通知》下达后在北京、上海、重庆和深圳都取得了一定成果。

在深圳，垃圾分橱余垃圾、可回收垃圾、有害垃圾和其他不可回收垃圾这四类，在垃圾分类收集与处理中，不同类的垃圾有不同的处理方式。

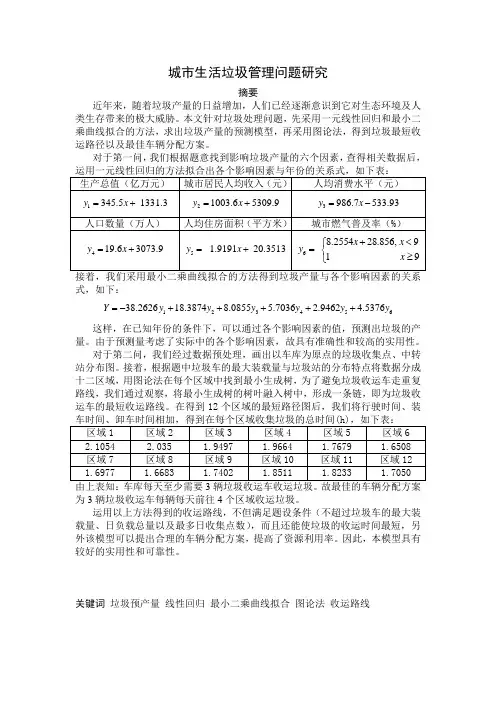
城市生活垃圾管理问题研究摘要近年来，随着垃圾产量的日益增加，人们已经逐渐意识到它对生态环境及人类生存带来的极大威胁。

本文针对垃圾处理问题，先采用一元线性回归和最小二乘曲线拟合的方法，求出垃圾产量的预测模型，再采用图论法，得到垃圾最短收运路径以及最佳车辆分配方案。

对于第一问，我们根据题意找到影响垃圾产量的六个因素，查得相关数据后，式，如下：12345638.262618.38748.0855 5.7036 2.9462 4.5376Y y y y y y y =-+++++这样，在已知年份的条件下，可以通过各个影响因素的值，预测出垃圾的产量。

由于预测量考虑了实际中的各个影响因素，故具有准确性和较高的实用性。

对于第二问，我们经过数据预处理，画出以车库为原点的垃圾收集点、中转站分布图。

接着，根据题中垃圾车的最大装载量与垃圾站的分布特点将数据分成十二区域，用图论法在每个区域中找到最小生成树，为了避免垃圾收运车走重复路线，我们通过观察，将最小生成树的树叶融入树中，形成一条链，即为垃圾收运车的最短收运路线。

在得到12个区域的最短路径图后，我们将行驶时间、装为3辆垃圾收运车每辆每天前往4个区域收运垃圾。

运用以上方法得到的收运路线，不但满足题设条件（不超过垃圾车的最大装载量、日负载总量以及最多日收集点数），而且还能使垃圾的收运时间最短，另外该模型可以提出合理的车辆分配方案，提高了资源利用率。

因此，本模型具有较好的实用性和可靠性。

关键词 垃圾预产量 线性回归 最小二乘曲线拟合 图论法 收运路线1.问题的重述由于人类生产和生活的不断发展而产生的垃圾对生态环境及人类生存带来极大的威胁已逐步成为重要的社会问题。

城市生活垃圾是居民生活、消费过程中产生的废弃物，其年增长速度达8-10%，因此导致城市垃圾的数量日益庞大，并且其组分复杂还处于不断变化中, 使处理费用慢慢升高。

另一方面城市垃圾占用大量土地、污染水体、污染大气、破坏植被, 严重影响城市的市容景观和居民的生活环境[1]。

魅力数模美丽师大浙江师范大学“同梦杯”第八届数学建模竞赛自信创新合作快乐A B论文题目城市垃圾运输问题编号 56组评分监制：浙江师范大学数学建模研究会（2009年5月7日）（说明：评分一栏为评阅人填写，请参赛者不要填写）垃圾运输问题摘要：该题我们的主要解题思路分三阶段：第一阶段，我们先根据题设条件和基本假设画出该题的图。

第二阶段，我们根据图和点的位置关系结合题设，归纳出一些最基本的确定路线的原则：在仔细分析该题后，我们认为该题为一个TSP与VRT相结合的问题。

我们先抛开空载费用，若要把所有的垃圾运回垃圾处理站，这部分有效工的费用为∑2.0＊|Xi|＊Yi(|Xi|为垃圾点Xi到原点的距离,Yi为垃圾点的垃圾量)，是恒定不变的。

只要我们能保证空载路线最小，则所花的时间和费用都最小。

因此解题的关键在于找出一个调度方案，使空载行驶的线路最小。

第三阶段则是编制程序阶段，我们结合下山法逐点搜索，并引入随机生成器。

在出现后继点权值相等难以判断以哪点继续搜索时，由随机生成器确定。

为了让算法更接近人的思维，我们让更靠近父点的子点有更高的几率被作为下一个将去的垃圾点，这也与我们的算法原则对应。

采用计算机模拟搜索的计算方法，搜索出运输车投入辆数以及运输车最佳调配方案，使得在不考虑铲车的情况下运营费用最低。

总运营费用为运输车空载费与实际运输费之和。

问题的解答如下：第一问，求得所需总费用为2496.3元，所需总时间为23小时08分，路线分配图见正文；第二问，求得需4辆铲车，铲车费用为199.0元，分配图及运输车调度表见正文；第三问，运营总费用为：2460.6，其中8吨、6吨、4吨载重量的运输车各需5、2、3辆，路线分配图见正文。

关键词：单目标优化计算机搜索 TSP一、问题的重述某城区有 38 个垃圾集中点，每天都要从垃圾处理厂（第 38 号节点）出发将垃圾运回。

现有一种载重 6 吨的运输车。

每个垃圾点需要用 10 分钟的时间装车，运输车平均速度为 40 公里／小时（夜里运输，不考虑塞车现象）；每台车每日平均工作 4 小时。