六年级分数除法试讲讲义
- 格式:doc
- 大小:179.50 KB
- 文档页数:3


倒数与分数除法1、了解倒数、分数除法的意义教学目的2、掌握计算方法3、会运用在实际冋题中重点:计算方法及实际问题中的运用难点:实际问题中的运用教学内【知识点一】:倒数1、倒数的意义:乘积为1的两个数互为倒数。
(1)、倒数是两个数的关系,它们互相依存,不能单独存在。
单独一个数不能称为倒数。
(必须说清谁是谁的倒数)(2)、判断两个数是否互为倒数的唯一标准是:两数相乘的积是否为“1。
例如:a>b=1则a、b互为倒数。
2、求倒数的方法:①求分数的倒数:交换分子、分母的位置②求整数的倒数:整数分之一。
③求带分数的倒数:先化成假分数,再求倒数。
④求小数的倒数:先化成分数再求倒数。
3、1的倒数是它本身,因为1>=10没有倒数,因为任何数乘0积都是0,且0不能作分母。
非零整数a的倒数为1;分数b的倒数是空。
a a b1真分数的倒数是假分数,真分数的倒数大于1,也大于它本、身。
假分数的倒数小于或等于1。
带分数的倒数小于1。
2用倒数解决问题、(1)用转化的方法解决倒数问题例题1: 一个自然数与它的倒数的和是5.2,这个自然数是多少?小结:已知一个自然数与它的倒数的和,可以把这个和分成整数和纯小数(或真分数)两部分。
整数部分就是这个自然数,纯小数(或真分数)部分就是这个自然数的倒数。
1、用假设的方法比较数的大小3 3 7例题2:如果aX _ = bX— = cX —,且a,b,c均不为0,把a, b,c这三个数按从大到小的顺4 5 3序排列。
(3):用假设的方法解决倒数问题1例题3:两个连续自然数的倒数差是12,求这两个自然数。
小结:解决此类问题,解可以假设其中一个自然数是a,另一个为a+1,再根据题意中的数量关系求【巩固练习二】31、3的倒数是(812、一X()2 ),0.25 和()互为倒数。
18)X 2 = 1X( )= 3 X( )= 17213. 一个自然数与它的倒数的差是21-22,这个数是多少?4 2 14.如果X X - = y X -=z X 1,且X, y,z均不为0,请按照从小到大的顺序排列这三个数。
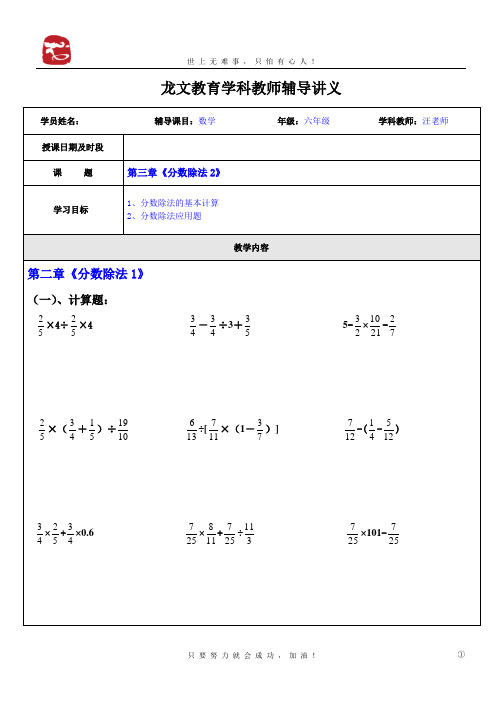
龙文教育学科教师辅导讲义 学员姓名: 辅导课目:数学 年级:六年级 学科教师:汪老师授课日期及时段课 题 第三章《分数除法2》学习目标1、分数除法的基本计算2、分数除法应用题 教学内容第二章《分数除法1》(一)、计算题:52×4÷52×4 43-43÷3+53 5-23×2110-7252×(43+51)÷1019 136÷[117×(1-73)] 127-(41-125)43×52+43×0.6 257×118+257÷311 257×101-257(二)、解方程:3121465÷=+x 87165=+x x 762175=-x x1096552=+x x-85=109 12x=109815 X +512 X = 57 X ÷35 = 512 ×815 3X +1335 = 57(三)、应用题2:(较复杂的分数除法应用题)一、基础知识:1、分数应用题的一般关系式是:表示单位“1”的量(标准量)×分率=分率的对应量。
2、解题思路:① 一道分数应用题中,先根据分率所在的哪个条件,找出并判断“1”。
分率是“谁的”几分之几,谁就是单位“1”(分率是一个不带单位的、不具体的分数,反映的是两个数之间 的一种倍数关系。
)单位“1”的量的判断:根据分率来判断把哪个数量平均分成多少份,哪个数量就是单位“1”。
② 表示单位“1”的量是已知的,则该题用“×”。
表示单位“1”的量是未知的,则该题用“÷”或方程。
③ 解题的关键是:寻找“与数量对应的分率”,“与分率对应的数量”。
二、例题解析:例1、一根140厘米长的绳子,第一次用去它的4/7 ,第二次又用了余下的3/5 ,两次共用去多少厘米?例2、小红看一本书,第一天看了全书的4/7 ,第二天又看了剩下的 3/5,还剩下42页没有看,这本书共有多少页?练一练:某生产队挖一条长300米的水渠,第一天挖了全长的,第二天挖了余下的,第三天恰好挖完,第三天挖了多少米?例3、一瓶油第一次吃了1/5千克,第二次吃了余下的3/4,这时瓶内还有1/5千克,问这瓶油原来有多少千克?例4、某校男生人数比全校学生总数的4/9少25人,女生人数比全校学生总数的4/7 多15人。

分数除法 讲义知识点一、分数除法的意义及运算法则例1、计算(1)20÷310×45 (2)34÷38÷118 (3)(15−16)÷110(4)30÷(14+15) (5)716×45−79÷143(6)310÷0.5×23(7)(43+415)÷15÷16总结:1、除以一个不为0的数,等于乘以它的________。
这样除法问题就可以转化为乘法问题来解决。
2、带分数要转化为_______,小数要转化为_______,再找出它们的倒数。
3、除法没有分配律!乘法才有分配律。
4、注意运算顺序,先乘除,后加减,审题时看清楚。
的倒数是(),()的倒数是0.75.例2、156例3、0.125的倒数是(),3的倒数是()。
性质:○10(1)一个正数乘以一个小于1的数,结果比原来小。
例如10×34○10(2)一个正数乘以一个大于1的数,结果比原来大。
例如10×54性质:○10(1)一个正数除以一个小于1的数,结果比原来_____。
例如10÷34(2)一个正数除以一个大于1的数,结果比原来_____。
例如10÷5○104总结:“将未知的知识转化为已知的知识来解决”、“化难为易”、“化繁为简”这样的思想叫做“化归思想”。
例4、在○里填上>、<或=。
(1)95÷16○95(2)37÷9○37(3)53÷83○53(4)38÷12○38÷2(5)95÷1.5○95÷0.3(6)34÷0.7○34÷4.2知识回顾:乘法和除法互为____运算。
例5、不为0的三个数A、B、C,如果A×B=C,那么C÷B=A,C÷A=B例6、如果3×4=12,那么12÷4=3,12÷3=4分数除法、小数除法、整数除法的意义是相同的...。

章节复习考点讲义(人教版)人教版数学六年级上册章节考点精讲精练第三单元《分数除法》知识点一:倒数的认识1.倒数的意义乘积是1的两个数互为倒数。
倒数具备两个条件:一是两个数;二是乘积是1。
2.互为倒数的两个数特点如果两个数都是分数,那么两个分数的分子和分母正好颠倒了位置;如果一个是整数,则另一个分数的分子是1,分母是这个整数。
3.求一个数倒数的方法知识互联网知识导航(1)通过计算,乘积是1的两个数互为倒数。
(2)交换这个数的分子和分母的位置。
4.特殊的1的倒数是1,0没有倒数。
知识点二:分数除法的计算法则一个数除以一个不等于0的数,等于乘这个数的倒数。
知识点三:分数四则混合运算规律1. 只有乘、除法,按照从左到右的顺序依次进行计算。
2. 在没有括号的算式里,既有加、减法又有乘、除法,要先算乘、除法,再算加、减法。
3. 在一个有小括号的算式里,应该先算小括号里面的,后算小括号外面的。
知识点四:分数除法的应用题1.解决“已知一个数的几分之几是多少,求这个数”的问题,一般方法:方程法:(1)找出单位“1”,设未知量为x;(2)找出题中的等量关系式;(3)列出方程并解答;(4)检验并写出答案。
2. “已知比一个数多(少)几分之几的数是多少,求这数”的问题的解法:方程法:根据题中的等量关系:“单位‘1’的量×(1±几分之几)=已知量”或“单位‘1’的量±单位‘1’的量×几分之几=已知量”,设单位“1”的量为x,列方程解答。
3. 已知两个量的和(差),其中一个量是另一个量的几分之几,求这两个量的问题的解法:有两个量都是未知的,先把谁看作单位“1”都可以,设其中一个量为未知数x,用这个量表示另一个量,然后找出等量关系,列方程解答出一个量,再解答第二个量。
4. 利用抽象的“1”解决实际问题:工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。

六年级数学第二章《分数的除法》讲解一、分数除法的意义及其计算:1、分数除法是分数乘法的逆运算,就是已知两个数的积与其中一个因数,求另一个因数的运算。
除以一个数是乘以这个数的 ,除以几就是乘以这个数的几分之一。
2、比:两个数相除也叫两个数的比。
比表示两个数的关系,可以写成比的形式,也可以用分数表示,但仍读 几比几。
注:10/2=5/1,表示比,读做5比1,10:2=5,5是比值,比值是一个数,可以是整数,分数, 也可以是小数。
1、直接写出得数。
=⨯60154 =⨯3279 =⨯01000999=⨯2332 =÷252 =÷416 =÷83%50 =⨯÷12512532 12×32= 98÷12= 18÷209= 119×3=203×94= 154×1615= 65÷10= 7×145 =409×32= 12÷51= 53÷3= 27÷209=51÷31= 6÷53= 116÷2= 43÷34=2、脱式计算。
能简算的要简算。
135717138⨯+÷ 81978992+⨯+ 2412416112⨯÷⨯44121÷- 511)10354(÷+ 2524)]6131(1[⨯--)6521(65+÷ 69)]4121(87[÷+- (43+61-243)÷241(41-91)×4×9 115÷9+116×91 42÷(61÷92)三、应用题1、求一个数的几分之几是多少。
(1)求一个数的几分之几是多少: 标准量×几几 (分率)=是多少(分率对应的比较量)。
例1:学校买来100千克白菜,吃了45 ,吃了多少千克?(反映整体与部分之间的关系。
六年级分数除法讲解一、分数除法的意义。
1. 与整数除法意义相同。
- 分数除法的意义与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
- 例如:如果(3)/(4)×(2)/(3)=(1)/(2),那么(1)/(2)÷(3)/(4)=(2)/(3),这里(1)/(2)是积,(3)/(4)是其中一个因数,(2)/(3)是要求的另一个因数。
二、分数除法的计算方法。
1. 分数除以整数。
- 分数除以整数(0除外),等于分数乘这个整数的倒数。
- 例如:(4)/(5)÷2=(4)/(5)×(1)/(2)=(4×1)/(5×2)=(2)/(5)。
- 计算时要注意,整数的倒数就是以这个整数为分母,分子为1的分数。
2. 一个数除以分数。
- 一个数除以分数,等于这个数乘分数的倒数。
- 例如:(2)/(3)÷(4)/(5)=(2)/(3)×(5)/(4)=(2×5)/(3×4)=(5)/(6)。
- 这里要先把除数(4)/(5)的分子分母颠倒位置得到它的倒数(5)/(4),然后再按照分数乘法的计算方法进行计算。
3. 带分数除法。
- 先把带分数化成假分数,然后再按照分数除法的计算方法进行计算。
- 例如:1(1)/(3)÷(2)/(3),先把1(1)/(3)化成假分数(4)/(3),然后(4)/(3)÷(2)/(3)=(4)/(3)×(3)/(2) = 2。
三、分数除法的应用。
1. 已知一个数的几分之几是多少,求这个数。
- 这种问题用除法计算。
- 例如:已知一个数的(2)/(5)是10,求这个数。
设这个数为x,则(2)/(5)x = 10,那么x=10÷(2)/(5)=10×(5)/(2)=25。
- 解题思路是根据分数乘法的意义列出方程,然后根据分数除法的计算方法求出未知数。
【知识点一】分数混合运算的运算顺序和计算方法分数混合运算的顺序和整数的运算顺序相同。
一个算式里只有乘除法或只有加减法的,从左往右依次计算;既有乘除法,又有加减法的,先算乘除法,后算加减法;如果有小括号,要先算小括号里面的。
【例1】计算(5115454+÷485367245÷+(727487⨯÷25985798÷-⨯【例2】在⚪里填上“>”“<”或“=”。
【例3】解方程【例4】甲、乙、丙三人赛跑,甲比乙快101,丙比乙慢101,甲的速度是丙的几分之几?【知识点二】简单的“已知一个数的几分之几是多少,求这个数”的问题【知识点三】稍复杂的"已知一个数的几分之几是多少,求这个数"的问题方程解法:①找出单位“1”,未知量设为x;②找出题中的等量关系;③列出方程解答。
算术方法∶①找出单位“1”;②找出已知量和已知量占单位“1”的几分之几;③列出除法算式。
即已知量÷已知量占单位“1”的几分之几=单位“1”的量。
【例1】看图列方程并计算。
【例2】学校参加植树活动,六年级同学共植树123棵,是全校植树棵数的53,全校一共植树多少棵?【例3】一筐鲜鱼连筐重125kg,卖出一半鲜鱼后,又卖出剩下鲜鱼的一半,这时剩的鱼连筐共重35kg,原来这筐鱼重多少千克?【例4】某班学生不满50人,在一次课外活动中,参加球类活动的占全班人数的31,参加绘画的占71,参加唱歌的占21,余下的参加跳舞,参加跳舞的有多少人?【知识点四】已知比一个数多(或少)几分之几的数是多少,求这个数的应用题方程解法:①找出单位“1”,未知量设为x;②找出题中的等量关系;③列出方程解答。
算术方法∶①找出单位“1”;②找出已知量和已知量占单位“1”的几分之几;③列出除法算式。
即已知量÷(1±几分之几)=单位“1”的量。
【例1】看图列方程并计算。
【例2】市污水处理公司投资1800万元改造污水处理系统,比计划投资节约了101,计划投资多少万元?【例3】四年级一班美术小组有25人,比航模小组的人数多41,航模小组有多少人?【知识点五】列方程解含有两个未知数的分数应用题列方程解含有两个未知数的分数应用题,应先找出题中的等量关系式,再设其中一个未知量为x,找x 和另一个未知量之间的关系,再根据等量关系式列出方程。
分数的除法一、分数除法例:1、每盒水果糖重100g,3盒有多重?100×3=300(g)1033101=⨯(kg)怎样改编用除法计算的问题呢?①3盒水果糖重300g,每盒有多重?300÷3=100(g)1013103=÷(kg)②300g水果糖,每盒100g,可以装几盒?300÷100=3(盒)3101103=÷(盒)做一做一、根据乘法算式直接写出除法算式的得数1、2187432=⨯=÷32218()=÷74218()2、1583254=⨯=÷32158()=÷54158100g也可以写成101千克2、把一张纸的54平均分成2份,每份是这张纸的几分之几?自己试着折一折,算一算。
=÷=÷524254=⨯=÷2154254 如果把这张纸的54平均分成3份,每份是这张纸的几分之几?=÷354根据上面的折纸实验和算式,你能发现什么规律?把54平均分成2份,就是把4个51平均分成两份,每份就是两个51,就是52把54 平均分成2份,每份就是54的21,也就是2154⨯3、小明32小时走2km,小红125小时走了65km 。
谁走得快些?小明平均每小时走:322÷想:先求31小时走了多少千米,也就是求2的21,即212⨯。
再求3个31小时走了多少千米,即3212⨯⨯。
32323212322=⨯=⨯⨯=÷(km )小红平均每小时走:)(25126512565km =⨯=÷答:小明走得快。
通过以上两个例子,你发现了什么?分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数。
为什么写成“512⨯” 怎么计算呢?画个图试试吧做一做一、用你发现的规律计算下面各题。
=÷3109=÷283=÷9824 54167÷二、直接写出得数。
(精品教案)《分数除法》讲课稿范文整理的《分数除法》讲课稿范文,仅供参考,欢迎大伙儿阅读。
一.讲教材。
我讲课的内容是人教版课程标准实验教科书六年级上册的分数除法单元中的例1和例2。
例1是分数除法的意义认识,例2是分数除以整数的计算。
在这之前学生差不多掌握了整数除法的意义和分数乘法的意义及计算,而本课的学习将为统一分数除法计算法则打下基础。
例1先是整数除法回忆,再由100克=1/10千克,从而引出分数除法算式,经过类比使学生认识到分数除法的意义与整数除法的意义相同,基本上‘已知两个因数的积和其中一具因数,求另一具因数的运算’。
例2是分数除以整数的计算教学,意在经过让学生举行折纸实验、验证,引导学生将‘图’和‘式’举行对比分析,从而发觉算法,感悟算理,并且也初步感觉数形结合的思想办法。
依照刚刚对教材的明白,本节课的教学目标是:1.明白分数除法的意义与整数除法的意义相同。
2.明白分数除以整数的计算原理,掌握计算办法,并能正确的举行计算。
3.记忆观看、推测、实验、验证和归纳的过程,感觉数形结合的思想办法,并从中进展抽象思维能力。
本课的重点是明白分数除法的意义和分数除以整数的计算办法;本课的难点是分数除法普通算法的明白。
这是因为要将除以一具数转化为乘以它的倒数,在运算形式上由除法转化为乘法,变化较大,而学生往往由于思维的定势,一时别容易同意。
因此本课的关键是怎么引导学生在实验和验证中自主体验和感悟。
二.讲教法、学法。
为了达成教学目标,本课的教学必须贯彻以学生为主体,坚持启示与发觉法相结合的教学办法,引导学生大胆猜想,动手实践,在体验中、在交流中发觉规律。
学习办法上强调以探索学习法为主。
认知结构理论告诉我们,学习是学生积极主动的内化过程。
惟独经过主动参与获得的知识,才是故意义的。
所以,在重难点的学习上,经过折纸实验与验证,数形结合,从而实现真正的明白。
三.讲教学过程。
(一)类比迁移,明白分数除法的意义。
1.乘法意义对比。