深度迭代和参数颜色功能

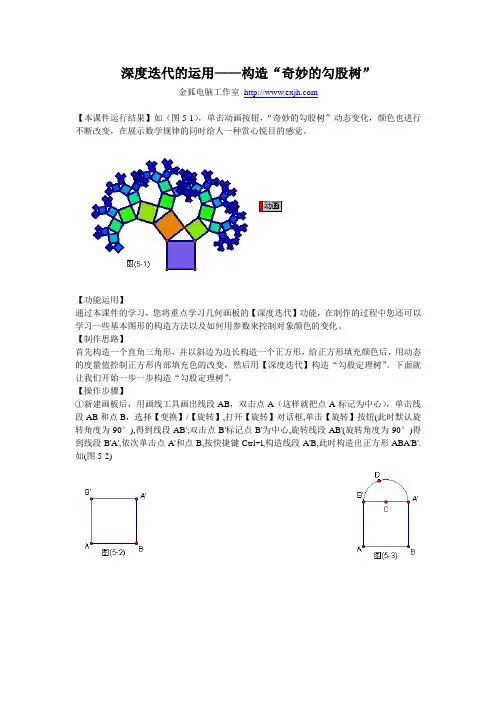
深度迭代的运用——构造“奇妙的勾股树”金狐电脑工作室【本课件运行结果】如（图5-1），单击动画按钮，“奇妙的勾股树”动态变化，颜色也进行不断改变，在展示数学规律的同时给人一种赏心悦目的感觉。

【功能运用】通过本课件的学习，您将重点学习几何画板的【深度迭代】功能，在制作的过程中您还可以学习一些基本图形的构造方法以及如何用参数来控制对象颜色的变化。

【制作思路】首先构造一个直角三角形，并以斜边为边长构造一个正方形，给正方形填充颜色后，用动态的度量值控制正方形内部填充色的改变，然后用【深度迭代】构造“勾股定理树”。

下面就让我们开始一步一步构造“勾股定理树”。

【操作步骤】①新建画板后，用画线工具画出线段AB，双击点A（这样就把点A标记为中心），单击线段AB和点B，选择【变换】/【旋转】,打开【旋转】对话框,单击【旋转】按钮(此时默认旋转角度为90°),得到线段AB';双击点B'标记点B'为中心,旋转线段AB'(旋转角度为90°)得到线段B'A',依次单击点A'和点B,按快捷键Ctrl+l,构造线段A'B,此时构造出正方形ABA'B'.如(图5-2)②单击选中线段A'B',按Ctrl+M 组合键,构造出A'B'的中点C(点C 为选中状态),再依次选中点A'和B'(注意顺序不要搞错啊),选择【构造】/【圆上的弧】,构造出以A'B'为直径的半圆,用画点工具在半圆上画出点D.如图(5-3)③依次单击选中点A 、B 、A'、B'，选择【构造】/【四边形内部】,把正方形填充上颜色;在工作区空白处单击后单击选中点A 、D ，选择【度量】/【距离】得到A 、D 两点间的度量值。

如（图5－4）④依次单击选中正方形的填充色和度量值，选择【显示】/【颜色】/【参数】打开【颜色参数】对话框,按图(5-5)进行设置.(用鼠标托动点D 看看正方形的填充色有什么改变么)(图5-5)(图5-6)⑤选择【图表】/【新建参数】打开【新建参数】对话框,如(图5-6),单击【确定】得到参数t 1=1.⑥依次选中半圆和点C,按组合键Ctrl+H(隐藏它们,为了后面观察方便);依次单击选中点A 、点B 、参数t 1=1.0，按住Shfit 键的同时选择【变换】/【深度迭代】弹出【深度迭代】对话框,如(图5-7)。

encoderparameters详解EncoderParameters是一个用于设置图像编码器参数的类。

在图像处理中，编码器是用于将图像数据转换为特定格式的工具。

EncoderParameters类提供了一种灵活的方式来设置编码器的参数，以便在图像编码过程中进行各种调整和优化。

EncoderParameters类包含一个名为Param的属性，它是一个EncoderParameter数组。

EncoderParameter类用于表示编码器的参数。

每个EncoderParameter对象包含一个名为Encoder的属性，用于指定编码器的类型，以及一个名为Value的属性，用于指定参数的值。

使用EncoderParameters类可以实现许多图像编码的高级功能。

例如，可以使用EncoderParameters类来设置图像的压缩质量、颜色深度、图像格式等。

下面将详细介绍一些常用的EncoderParameters参数。

1. 压缩质量参数（Encoder.Quality）压缩质量参数用于指定图像的压缩质量级别。

它的值范围从0到100，其中0表示最低质量，100表示最高质量。

通过调整压缩质量参数，可以在图像质量和文件大小之间进行平衡。

2. 颜色深度参数（Encoder.ColorDepth）颜色深度参数用于指定图像的颜色深度。

它的值通常为8、16、24或32，表示每个像素使用的位数。

较高的颜色深度可以提供更丰富的颜色表现，但也会增加文件大小。

3. 图像格式参数（Encoder.ImageFormat）图像格式参数用于指定图像的输出格式。

常见的图像格式包括JPEG、PNG、BMP等。

通过设置图像格式参数，可以将图像保存为不同的文件格式。

除了上述常用的参数外，EncoderParameters还支持许多其他参数，如图像的DPI（每英寸点数）、图像的压缩方式、图像的调色板等。

通过灵活使用EncoderParameters类，可以根据具体需求对图像进行精确的编码控制。

几何画板在数学中的学习、教学中的应用重庆市第九十五中学梁勇一、几何画板简介在21世纪，以计算机多媒体和互联网为代表的信息技术已迅速而深刻地改变着人们的工作方式、交往方式、生活方式和思维方式，信息技术正在改变传统的教学内容、教学方式、教学模式与教学观念。

在数学教学中，从课堂教学到课外辅导，从组织练习到成绩的统计评估，从教师备课、同行交流到学生课内外活动的组织，信息技术在推动数学教学改革方面都有着巨大潜力。

《几何画板》就是一个能让老师和学生操作的优秀学科软件，在动态的操作过程中，给学生的比较和抽象活动创造了一种活动的空间和条件。

学生能在活动中理解和掌握抽象的概念。

这样学生获得的才是真正的数学经验，而不只是数学结论。

既然《几何画板》有这样强大的作用，下面我和大家一起分享《几何画板》以及它在数学制卷、教学、命题、解题中的应用。

1、《几何画板》简介《几何画板》软件是由美国Key Curriculum Press公司制作并出版的几何软件,它的全名是《几何画板--21世纪的动态几何》。

《几何画板》是一个适用于几何（平面几何、解析几何、射影几何等）教学的软件平台。

它为老师和学生提供了一个探索几何图形内在关系的环境。

它以点、线、圆为基本元素，通过对这些基本元素的变换、构造、计算、动画、跟踪轨迹等，能显示或构造出其它较为复杂的图形。

2、《几何画板》的基本功能（1）作图《几何画板》在图形绘制上比一般的绘图软件更为精准，更符合数学的严格要求。

我们可以使用工具栏的画点工具、画圆工具、画线工具（线段、射线、直线），作出基本的数学图形。

（2）文字在《几何画板》中可以对各种量进行文本标记和解释，例如对点、线元素的自动习惯性标记，便于在教学过程中的理解。

（3）构造要画某线段的中点，绘制某线的平行线、垂直线等具有一定几何关系的常用图形，可以直接选中所需图形再选择“构造”菜单的相应工具即可构造出来。

（4）变换使用《几何画板》中的“变换”菜单，可按指定值、计算值或动态值任意旋转、平移、缩放原有图形，并在其变化中保持几何关系不变，从而方便我们研究图形的运动和变换等问题。

几何画板中的迭代和带参数的迭代实验报告一、实验目的1、新建参数以及参数动画按钮的制作2、掌握带参数的迭代思想和操作步骤3、学会通过了解父对象和子对象的关系来逆向分析已有的几何画板课件二、实验原理通过带参数的迭代建立参数与图形之间的关系。

制作参数动画按钮时，参数的变化引起图形个数的变化。

三、实验内容运用几何画板逆向分析圆的面积公式推导课件，并将课件还原制作出来。

四、实验课时：8课时五、实验步骤（略）一、方法：分割拼凑法、划曲为直展开法（等腰三角形）、划曲为直展开法（直角三角形）。

二、实施步骤方法一：分割拼凑法1.新建文件新建页：【文件】-【文档选项】-【增加页】-【空白页面】，命名为：圆的面积推导分割拼凑法。

2.构建参数：【数据】—【新建参数】—构建两个参数：半径r=3厘米，t1=6。

【数据】—【计算参数】—【计算2个数据：分别是2*trunc(t1) 和360度/ 2*trunc(t1) 】。

3.做圆和分割圆：选择【点工具】—在空白处做点A—（保持A为选中状态）+选中r—【构造】—【以圆心和半径作圆】—（保持圆为选中状态）【构造】—【圆上的点】（为点B）。

选中参数360度/ 2*trunc(t1) —鼠标右击—【标记角度】，【双击点A+选中点B】—【变换】—【旋转】—【确定】（得到点B’）。

依次选中点A，点B，点B’—【构造】—【圆上的弧】—（保持弧选中状态）【构造】—【弧内部】—【扇形内部】。

选中点B+选中参数2*trunc(t1)—【按住shift 键】—【变换】—【深度迭代】—【将点B迭代到点B’】—【确定】(得到一个分割好扇形的圆)。

4.做分割后的一个扇形：选中点B+选中点B’—【度量】—【距离】—（保持参数选中状态）鼠标右击【标记距离】。

选择【点工具】—在空白处作点C—【变换】—【平移】（按标记距离平移，得到点C’）。

选中点C和点C’+选中参数r —【构造】—【以圆心和半径作圆】—取两圆上面交点D.。

几何画板中的作图功能实验报告一、实验目的1、掌握变换菜单中的迭代思想2、掌握迭代以及带参数的迭代操作步骤3、掌握迭代中的“添加新的映射”的使用方法4、掌握合并点的操作方法二、实验原理1.通过添加新的映射，实现原象到初象的多次映射。

2.颜色参数的使用方法三、实验内容运用几何画板制作“谢尔宾斯三角形”的小课件。

四、实验课时：6课时五、实验步骤（略）①新建页：【文件】-【文档选项】-【增加页】-【空白页面】，命名为：谢尔宾三角形。

②作原像三角形：选择【线段工具】，画出三条线段首尾相接的三角形（目的是这样得到的点是自由点，方便迭代）。

③作迭代初像：选中三角形的三边，【构造】-【中点】④构造三角形内部：【选中点A、B、C】-【构造】-【三角形内部】⑤颜色参数：选中三角形内部，【度量】-【面积】，得到”△ABC的面积”，【选中”△ABC的面积”】-【选中三角形内部】-【显示】-【颜色】-【参数】-【确定】。

⑥建立参数：【数据】-【建立参数】-【确定】，得到参数t1作为迭代深度。

⑦迭代：【选中点A、B、C】-【选中参数t1】—【按住shift键不放】-【变化】-【深度迭代】。

迭代规则：【A→A、B→D、C→E】-【结构】-【添加新的映射】-【A→D、B→B、C→F】-【结构】-【添加新的映射】-【A→E、B→F、C→C】-【显示】-【最终迭代】-【迭代】⑧隐藏原像：【选中原像三角形内部】-【编辑】-【隐藏三角形】，此时拖动A、B、C任一点，内部有颜色的三角形就会改变颜色。

⑨制作参数动画按钮：【选中参数t1】-【编辑】-【操作类按钮】-【动画】-【方向改为：增加】-【范围改为1到5】-【标签改为增加迭代次数】-【确定】。

【选中参数t1】-【编辑】-【操作类按钮】-【动画】-【方向改为：减少】-【范围改为1到5】-【标签改为减少迭代次数】-【确定】。

⑩隐藏不需要显示的对象：选中要隐藏的对象，【编辑】-【操作类按钮】-【显示/隐藏】，点击按钮：【隐藏对象】。

深度学习调参技巧1.数据预处理：在进行调参之前，首先要对数据进行预处理。

这包括数据清洗、缺失值处理、标准化等。

预处理能够提高模型的稳定性和收敛速度。

2.学习率调整：学习率是深度学习中最重要的超参数之一、较小的学习率可能导致模型收敛速度过慢，而较大的学习率可能导致模型无法收敛。

可以通过手动调整学习率或使用学习率衰减策略来寻找最佳学习率。

3.正则化：正则化是一种防止过拟合的技术。

可以通过将L1或L2正则化加入到损失函数中来惩罚模型的复杂度。

通过调整正则化系数，可以调整正则化的强度。

4.批量大小：批量大小是指在训练过程中每次迭代使用的样本数量。

较小的批量大小可能导致模型收敛速度过慢，而较大的批量大小可能导致模型无法收敛。

可以通过试验不同的批量大小来找到最佳的取值。

5.迭代次数：迭代次数是指训练过程中模型进行参数更新的次数。

较小的迭代次数可能导致模型欠拟合，而较大的迭代次数可能导致模型过拟合。

可以通过交叉验证等方法找到最佳的迭代次数。

6.网络结构调整：深度学习的网络结构包括层数、每层的神经元数量、激活函数等。

可以通过调整网络结构来寻找最佳的模型性能。

7. 权重初始化：权重初始化是指在训练过程中为模型的权重赋予初始值。

较好的权重初始化方法可以提高模型的性能和收敛速度。

常用的权重初始化方法有高斯分布初始化、Xavier初始化等。

8. Dropout：Dropout是一种概率性地在神经网络的一些神经元输出为零的方法。

可以通过调整Dropout的概率来防止模型过拟合。

9.数据增强：数据增强是通过对原始数据进行变换和扩充来增加样本数量。

进行数据增强可以增加模型的泛化能力和稳定性。

10.参数：可以使用网格、随机等方法来最佳参数组合。

这种方法会尝试不同的参数组合，并评估每个参数组合的性能。

综上所述，深度学习调参是一个复杂且耗时的过程。

需要结合经验和实验来调整各种参数，并使用评估指标来衡量模型的性能。

通过合适地调整参数，可以达到最佳的模型性能和泛化能力。

《几何画板》新版中的迭代与带参数的迭代应用一、教学目标：知识与技能：理解几何画板中的迭代（Iterate）与带参数的迭代(Iterate To D epth)功能；过程与方法：通过构造分形图形、构造正多边形；构造ICME-7会徽、构造动态勾股定理、构造谢宾斯基三角形、定积分意义的动态演示、构造正弦线等实例，充分理解【变换】菜单下的【迭代】（带参数的迭代）功能。

情感、态度与价值观：培养对几何图形的审美意识和不断追求完美的精神，增强对数学前沿知识的追求意识。

二、教学过程：1．构造分形图案自然界中有许多物体和现象常是它们自身的多次重复，局部与它的整体以某种方式相似。

例如任意一棵大树上的一棵小树枝，它的形状与大树本身相似，这称为自相似性。

还有如海岸线、浮云的边界、波浪起伏的海面、流体的湍流、刚体内的裂缝、山地轮廓等，被经典几何学称为“病态”的被当作个别特例的不规则集被普遍地称为分形。

但这些不光滑曲线或曲面有时比传统几何图形能更好地描述许多自然现象。

1975年，美国的曼德布罗特(B.Manedlbrot)创立了分形几何学用以描述这类曲线，20世纪80年代中期分形几何学得以迅速发展，而今已成为本世纪各个领域中专家学者所注目的前沿焦点学科之一。

新版的《几何画板》中【变换】→迭代（或带参数的迭代）可以制作一些简单的分形图案。

下面就以几何画板4.04（或4.05）来辅于说明。

例1：制作Koch曲线（源文件）（1）画线段AB，以A为中心，缩放点B(固定比为13)，得到'B，把它改为C，再以B为中心，缩放点A，得到'A，把它改为D，隐藏线段AB；（2）双击C点（标记中心），选择点D，旋转60°，得到点E；（3）连接线段AC、CE、ED；（4）【图表】→[新建参数]t，把它的值该为2；（5）依次选择点A、B，t，按Shift键，，选择【变换】→[带参数的迭代]，弹出对话框如图1图1（6）依次选择A、C，按Ctrl＋A，增加一列（对应点），依次选择C、E，再按Ctrl＋A，又增加一列（对应点），依次选择E、D，再按Ctrl＋A，又增加一列（对应点），依次选择D、B，选择“显示”中的最终迭代，如图2所示，单击“迭代”；图2（7）选择参数t，按键盘上的“－”、“＋”可以得到不同迭代次数下的Koch曲线。

如何用好几何画板的深度迭代第一章：迭代的概念和操作迭代是几何画板中一个很有趣的功能，它相当于程序设计的递归算法。

通俗的讲就是用自身的结构来描述自身。

最典型的例子就是对阶乘运算可看作一下的定义：!(1)!(1)!(1)(2)!n n n n n n =⨯--=-⨯- 。

递归算法的特点是书写简单，容易理解，但是运算消耗内存较大。

我们先来了解下面这几个最基本的概念。

迭代：按一定的迭代规则，从原象到初象的反复映射过程。

原象：产生迭代序列的初始对象，通常称为“种子”。

初象：原象经过一系列变换操作而得到的象。

与原象是相对概念。

更具体一点，在代数学中，如计算数列1，3，5，7，9......的第n 项。

我们知道12n n a a -=+，所以迭代的规则就是后一项等于前一项加2。

以1作为原像，3作为初像，迭代一次后得到5，再迭代一次得到7，如此下去得到以下数值序列7 , 9，11, 13, 15......如图1.1所示。

在几何学中，迭代使一组对象产生一组新的对象。

图1.2中A 、B 、C 、D 、E 、F 、G ，各点相距1cm ，那么怎么由A 点和B 点得到其它各点呢？我们可以发现其中的规律就是从左到右，每一个点相当于前面一个点向右平移了1cm 。

所以我们以A 点作为原像，B 点作为初像，迭代一次得到B 点，二次为C 点，以此类推。

所以，迭代像就是迭代操作产生的象的序列，而迭代深度是指迭代的次数。

那么下面我们通过例子来进一步地了解迭代以及相关的概念。

几何画板中迭代的控制方式分为两种，一种是没有参数的迭代，另一种是带参数的迭代，我们称为深度迭代。

两者没有本质的不同，但前者需要手动改变迭代的深度，后者可通过修改参数的值来改变迭代深度。

我们先通过画圆的正n 边形这个例子来看一下它们的区别。

【例1】画圆的内接正7边形。

【分析】由正7边形的特征，我们知道，每一个点都相当于前面的点逆时，抓住这个规律，我们可以用迭代功能来解决。

在几何画板中运用“迭代”构图的几个问题在几何画板中，以“迭代”方式来构图是构图的重要的手段，特别是一些较为复杂的组合图案更是离不开“迭代”功能的运用；“迭代”构图要弄清以下几个方面问题：1.关于迭代迭代可以理解为是不停的代换的意思，简单点说“迭代”就是一种重复操作，将上一步的参数保持不变，再执行一次的意思. （“参数保持不变”在几何画板中可以形象的理解为图形的旋转角度、平移距离、放缩比例等等保持不变）. 迭代分为两种类型：第一种类型是简单迭代：先选中原象（通常是一个点或多个点，亦称原象点） → 然后变换 → 迭代 → 在迭代对话框中选取与原象点相对应的一组或多组映射点（初象点） → 最后按迭代按钮，即可得到固定迭代的图.默认的迭代次数是3次.（后面的图②③④都是简单迭代）第二种类型是深度迭代：按照设定参数确定迭代次数，不用进入迭代菜单，直接控制参数的增减就能控制迭代的深度（次数的多少）.①.构造方法：选中选择你要迭代的原象点、新建的参数按钮并按住Shift 键 → 然后点开“变换”菜单下的迭代自然显示为“深度迭代” → 点击打开“深度迭代”的对话框 → 点入对应的初象点 → 迭代.（见下面的截图①） ②.作用：简化重复作图过程，选定参数按钮后操作“+”、“-”号键可以控制作图重复次数的效果.选中参数按钮后按Shift 键，按“＋”号增加迭代，选中参数按钮直接按“-”号键减少迭代. 若把参数按钮设置动画可以自动增减.2.原象点的确立.原象：产生迭代序列的初始对象（起点的位置），通常称为“种子”.原象点的确定：第一次迭代的出发点为原象点，取决于绘制基本图形的起始条件，原象点必须是自由的点或自由路径上的点（主要不受其它路径控制的端点！“自由”是个关键词，即使在初始对象上任取在该路径活动的点都不算自由点）. 如：正方形ABCD 是由线段AB “变换”（这里是旋转）和“构造”方式得到的，所以线段AB 的端点A B 、可以作为原象点（见组图②）；而线段BC CD DA 、、 以因此其端点C D 、是不能作为迭代关系的原象点.又如选定B C 、后，点B 可以作为建立迭代关系的后原象点，而C 点不能作为原象点.即使在初始对象AB 用点的工具任意取一点都不能作为原象点.再次提醒直接用画板工具栏中的“工具”作出的自由的点或自由路径上的点（不受其它路径控制，比如起始线段的端点）才是原象点，而以别的图形为基础新建立的点不能作为原象点.①3.初象点的确立初象 ：原象经过一系列变换操作而得到的象（第二个点的位置），与原象是相对概念. 初象点的确定：第二次迭代的出发点为初象点，它是和原象点个数相同且相对应的一组点.对于初象点的确立，不管是“变换”、“构造”还是直接用工具作的点，只要以原象为基础的点都可以作为初象点.比如在正方形ABCD 的的边上任意一处取一个点都可以作为原象点对应的初象点（因为它是以正方形的边为基础），但在正方形ABCD 的边之外的空处随便取一个点就不能作为初象点，抓住关键词“以原象为基础作出来点.”注：通过操作发现作为“原象”线段若已经 “构造”和“变换”的第三点，此时选定原象线段的两个端点同时都可以作为初象点，也就是此时的“原象线段”两个端点具有“原象点”和“初象点”的双重特性.组图②：选定A B 、作为原象点，而边的中点E F 、 作为初象点来迭代构图.组图③：直接用线段工具构造出五边形ABCDE ,以线段FG 为长度依次在边上截取AH EI DJ CK BL ====；此时选定A B C D E 、、、、作为原象点，截取的得到点H I J K L 、、、、 作为初象点进行迭代构图.组图④：以线段AB 绕端点B 逆时针旋转108°得到线段AC ，再以取出连线段的中点E F 、 ,连结EF .以点B A 、为原象点，以A C 、为初象点迭代构图，不但可以构造一个正五边形，还可以把其中点五边形同时构造出来，残缺的边可用键盘“+”键补全.4.初象点是怎样把原象点 “迭代”构图的？②④③利用几何画板的“迭代”功能构图，关键是映射点（初象点）与原象点的“迭代”对应关系，在选择对应的初象点是要注意方向；“迭代”出来的图会显示出初象点把原象点的的特性进行重新操作.下面举例来加以说明：例1.已知线段AB ,以 A 为旋转中心逆时针旋转108°得到AC .⑪.若以点B 为原象点，点C 为初象点，则“迭代”出来的图形体现点C 会按点B 绕点A 逆时针旋转108°的特性重新操作,……，依次类推！.（见截图⑤） ⑫.若以点A 为原象点，点C 为初象点，则点C 会成了下一个旋转中心，……； “迭代”出来的图形，点C 会依次把点A 为旋转中心旋转108°的特性体现出来.（见截图⑥）⑬.若以点B A 、 为原象点，点A C 、分别对应为初象点，则点C 成了下一个旋转中心，则“迭代”出来的图形，会把线段AB 绕着点A 逆时针旋转108°得到AC 的特征在点C 处为旋转中心一一体现出来，后面迭代出来图形依然如此.（见截图⑦，因为默认迭代次数为3次，所以恰好为正五边形.）注：若在线段AB AC 、取点连线，会把“连线”同时进行“迭代”，也就是迭代会“映射”原象点和初象点为基础的整个图形，依次类推！如前面组图④的进行“迭代”操作时同时也把中点连成的线段作了“迭代”构造.例2.如图以初始线段AB 为初始线段构造一Rt ⊿ACB ,在斜边AD 任取一点D ；以A C 、为原象点，分别以D B 、 为初象点，会以边DB 对应边DE AB 所在的Rt ⊿ACB 及其填充色进行“迭代”，但迭代图形依次按DB 所占比例缩小 .（见组图⑧.最右边的图用键盘“+”键增加了迭代次数的，有点近似“勾股螺”图案.）⑤⑥C⑦⑧5.关于“添加新的映射”的问题.映射是高中数学的一个概念，是指按某种规则的两个集合中的集合A 的任何一个元素，在集合B 都有唯一的元素与之对应. 在几何画板中最先的从原象点到初象点可以理解为是第一次映射，初象点就是映射点；因此只要还有新的初象点，那么根据需要就可以继续添加新的的映射.下面我举例说明：例：画勾股树.⑪.画一条线段（见图⑨隐藏了字母标签），并且构造一个矩形，以一边（本例取起始线段的对边）为直径作一个半圆，在半圆上取两点，隐藏半圆和圆心点；进行第一次映射点的添加（操作和前面一样，见迭代对话框和图中标示）.⑫.添加新的映射：在图⑨的基础上→ 迭代对话框 → 结构 → 添加新的映射 → 在图中依次点选半圆上的两点入框（见迭代对话框和图⑩标示）. ⑬.继续添加新的映射：在图⑩的基础上 → 迭代对话框 → 结构 → 添加新的映射 → 在图中依次点选半圆上的两点入框（见迭代对话框和图⑪中的标示）.⑭.点击迭代完成构图.组图⑫的左图是最初成图，中图进行增加迭代次数、点的隐藏、颜色和形状姿态调整等等处理，右图进行颜色填充和色彩变化的处理等.上例可以看作画的三个迭代分支的勾股树.当然“添加新的映射”的次数和映射点对应的位置根据设计图案的需要而定，对应点构成的“基本图案”会在对应的⑨⑩映射点处呈现出来（前提是这些“基本图案”是由原象点为基础作出来的）.下面是其它一些迭代构图的效果图：注：昨天在几何画板上画的，比较漂亮！几何画板中的“迭代”构图在制作组合图案和动画制作确实有优势.郑宗平 2017.12.24。

在几何画板中，如何制作自动增减图形变换数目的动画？ 在中学的数学中几何内容占了“半壁江山”，如果利用几何画板的动画功能制作一些视觉效果较好的动画，这对打造高品味的多媒体课件，对学生提高学习数学的兴趣，加强学生对图形性质的认识是有帮助的.几何画板能制作的动画形式还是比较多的，下面以几何画板5.06版简单谈谈制作自动增减图形旋转变换数目的动画，其它的如平移、放缩、反射等可以类推！ 1.制作旋转图形⑴.制作一个三角形△OBC → 双击点O 标记为旋转中心；⑵.选定△OBC （可以不选定点O ） → 变换 → 旋转 → “固定度数”对话框设置好旋转角度和旋转方向（注：若是顺时针旋转在度数前面添一个“-”即可） → 确定即可得到旋转图形说明：①.截图①中的△'''O B C 是由△OBC 绕着点O 顺时针旋转20°得到的； ②.也可以新建参数和其它方式把旋转角度设置为“动态的可变大变小的”.2.新建迭代次数的参数数据 → 新建参数 → 取好名称（这里取“数目”）、填好数据 → 单位（这里勾“无”）确定. 右键参数按钮 → 属性 → 继续在“属性”对话框里设置修改“参数”：数值取好精确度（这里取“单位”化范围、键盘调节等（见图②） → 得到修改后的参数按钮（见示意图③）②①③5.改变原象（就是基础图形，这里是△OBC .）的形状，则旋转和迭代图形会作相应的变化（见下面截图⑥⑦）.如果把“原象△OBC ”的顶点B C 、设置为沿某个路径的动画点，把填充色也设置为“动态变化”的，把点的动画按钮、颜色的动画按钮和迭代参数的动画按钮做成“系列按钮”，将呈现数目增减、图形的变化和颜色的变化等综合性的动画效果，其视觉效果更佳.说明：由于本例在设置迭代次数的参数按钮勾选了“键盘调节”，所以还可以利用键盘的“＋”、“－”来手动调节迭代图数目.其操作是：选定“数目”的参数按钮并按住Shift 键不放，然后按键盘上的“+”号按钮 →“数目”按钮数字增加，且“三角形”数目自动增加；选定“数目”的参数按钮，直接按键盘的“- ”号，→“数目”按钮数字减少，则“三角形”的数目则会减少.郑宗平 2017.12.16 编创⑤ 数目为17④ 数目为6。

深度和颜色对齐原理一、概述在人类视觉感知中，深度和颜色是两个十分重要的信息来源。

深度指的是物体在空间中的距离位置，而颜色则是物体表面对光的反射性质。

深度和颜色的对齐是指在视觉处理中，将深度和颜色的信息进行匹配，以便对物体进行准确的识别和判断。

深度和颜色对齐原理的研究对于计算机视觉、虚拟现实、人机交互等领域具有重要意义。

二、深度和颜色的基本概念1. 深度深度是指物体在空间中的距离位置。

在计算机视觉中，深度通常通过三维重建技术获取，或者通过深度传感器、双目摄像头等设备测量得到。

深度信息对于识别物体形状、距离、大小等具有重要意义。

2. 颜色颜色是物体表面对光的反射性质。

物体的颜色可以通过光谱分布来描述，常用的颜色表示方法有RGB、CMYK等。

颜色信息对于识别物体的外观、表面材质、光照条件等具有重要意义。

三、深度和颜色对齐原理1. 感知对齐深度和颜色在视觉感知中往往是相互关联的。

人类在观察物体时，往往是通过颜色和深度信息共同构建物体的视觉形象。

深度和颜色的对齐原理首先体现在感知上，即人类视觉系统对深度和颜色信息的联合处理。

2. 抽象对齐在计算机视觉领域，深度和颜色的对齐原理也体现在对物体特征的抽象表示上。

通过将深度和颜色信息进行对齐，可以得到更为丰富和准确的物体特征描述。

这对于目标检测、图像分割、姿态估计等任务具有重要意义。

3. 空间对齐深度和颜色信息的对齐涉及到了空间坐标系统的统一。

在三维重建、虚拟现实等应用中，需要将深度和颜色信息进行空间对齐，以便实现真实感强、逼真度高的效果。

4. 时间对齐在动态场景下，深度和颜色信息的对齐也具有重要意义。

通过对深度和颜色信息进行时间对齐，可以实现对动态物体的准确识别和跟踪。

这对于智能交通、安防监控等领域具有重要意义。

四、深度和颜色对齐方法1. 传统方法传统的深度和颜色对齐方法主要是基于多视图几何和图像配准的原理。

通过对深度图和颜色图进行匹配和校正，可以实现它们在空间上的对齐。