蚁群算法及算例

[代码说明]蚁群算法解决VRP问题[算法说明]首先实现一个ant蚂蚁类，用此蚂蚁类实现搜索。

算法按照tsp问题去解决，但是在最后计算路径的时候有区别。

比如有10个城市,城市1是配送站，蚂蚁搜索的得到的路径是1,3,5,9,4,10,2,6,8,7。

计算路径的时候把城市依次放入派送线路中,每放入一个城市前，检查该城市放入后是否会超过车辆最大载重如果没有超过就放入如果超过，就重新开始一条派送路线……直到最后一个城市放完就会得到多条派送路线这样处理比较简单可以把vrp问题转为tsp问题求解但是实际效果还需要验证。

[作者]Wugsh@2011.12.16wuguangsheng@guangsheng.wu@%}%清除所有变量和类的定义clear;clear classes;%蚁群算法参数(全局变量)global ALPHA; %启发因子global BETA; %期望因子global ANT_COUNT; %蚂蚁数量global CITY_COUNT; %城市数量global RHO; %信息素残留系数!!!global IT_COUNT; %迭代次数global DAry; %两两城市间距离global TAry; %两两城市间信息素global CITYW Ary; %城市货物需求量global VW; %车辆最大载重%===================================================================%设置参数变量值ALPHA=1.0;BETA=2.0;RHO=0.95;IT_COUNT=200;VW=100;%=================================================================== %读取数据并根据读取的数据设置其他参数load data.txt; %从文本文件加载数据city_xy_ary=data(:,2:3); %得到城市的坐标数据CITYW Ary=data(:,4); %得到每个城市的货物需求量CITY_COUNT=length(CITYW Ary); %得到城市数量(包括配送站在内)ANT_COUNT=round(CITY_COUNT*2/3)+1; %根据城市数量设置蚂蚁数量,一般设置为城市数量的2/3%MMAS信息素参数%计算最大信息素和最小信息素之间的比值PBest=0.05; %蚂蚁一次搜索找到最优解的概率temp=PBest^(1/CITY_COUNT);TRate=(1-temp)/((CITY_COUNT/2-1)*temp); %最大信息素和最小信息素之间的比值%信息素的最大最小值开始的时候设置成多大无所谓%第一次搜索完成会生成一个最优解,然后用这个解会重新产生最大最小值Tmax=1; %信息素最大值Tmin=Tmax*TRate; %信息素最小值% 计算两两城市间距离DAry=zeros(CITY_COUNT);for i=1:CITY_COUNTfor j=1:CITY_COUNTDAry(i,j)=sqrt((city_xy_ary(i,1)-city_xy_ary(j,1))^2+(city_xy_ary(i,2)-city_xy_ary(j,2))^2);endend% 初始化城市间信息素TAry=zeros(CITY_COUNT);TAry=TAry+Tmax;%===================================================================%初始化随机种子rand('state', sum(100*clock));%另一种方法%rand('twister',sum(100*clock))%定义蚂蚁mayi=ant();Best_Path_Length=10e9; %最佳路径长度，先设置成一个很大的值tm1=datenum(clock); %记录算法开始执行时的时间FoundBetter=0; %一次搜索是否有更优解产生%开始搜索for i=1:IT_COUNTfprintf('开始第%d次搜索, 剩余%d次',i,IT_COUNT-i);FoundBetter=0; %搜索前先置为没有更优解产生for j=1:ANT_COUNT%蚂蚁搜索一次mayi=Search(mayi);%得到蚂蚁搜索路径长度Length_Ary(j)=get(mayi,'path_length');%得到蚂蚁搜索的路径Path_Ary{j}=get(mayi,'path');%保存最优解if (Length_Ary(j) < Best_Path_Length);Best_Path_Length=Length_Ary(j);Best_Path=Path_Ary{j};%有更优解产生,设置标志FoundBetter=1;endend%有更好解产生,进行2-OPT优化if (FoundBetter == 1)fprintf(' , 本次搜索找到更好解!');Best_Path=opt2(Best_Path);Best_Path_Length=PathLength(Best_Path);end%-------------------------------------------------------------%全部蚂蚁搜索完一次，更新环境信息素TAry=TAry*RHO;%只有全局最优蚂蚁释放信息素dbQ=1/Best_Path_Length;for k=2:CITY_COUNTm=Best_Path(k-1); %上一个城市编号n=Best_Path(k); %下一个城市编号%更新路径上的信息素TAry(m,n)=TAry(m,n)+dbQ;TAry(n,m)=TAry(m,n);end%更新最后城市返回出发城市路径上的信息素TAry(n,1)=TAry(n,1)+dbQ;TAry(1,n)=TAry(n,1);%-------------------------------------------------------------%更新完信息素,进行边界检查Tmax=1/((1-RHO)*Best_Path_Length); %信息素最大值Tmin=Tmax*TRate; %信息素最小值for m=1:CITY_COUNTfor n=1:CITY_COUNTif (TAry(m,n)>Tmax)TAry(m,n)=Tmax;endif (TAry(m,n)<Tmin)TAry(m,n)=Tmin;endendend%-------------------------------------------------------------%换行fprintf('\n');endtm2=datenum(clock); %记录算法结束执行时的时间fprintf('\n搜索完成, 用时%.3f秒, 最佳路径长为%.3f , 派送方案如下:：\n\n[1]',(tm2-tm1)*86400,Best_Path_Length);%=================================================================== %输出结果dbW=0;for i=2:CITY_COUNTm=Best_Path(i-1); %上一个城市n=Best_Path(i); %当前城市if (dbW+CITYW Ary(n)>VW) %运送的货物超过限制fprintf(' (满载率: %.1f%%)\n[1]-%d',dbW*100/VW,n);dbW=CITYW Ary(n); %运输的重量等于该城市的需求量else %没有超过限制fprintf('-%d',n);dbW=dbW+CITYWAry(n); %运输的重量加上该城市的需求量endendfprintf(' (满载率: %.1f%%)',dbW*100/VW);fprintf('\n\n');%====== [程序结束]===================================================== %对结果进行2-OPT优化function f=opt2(Line)%数组长度size=length(Line);NewLine=Line; % 返回结果先设置成原来路径Flag=1;while (Flag == 1)Flag=0;for i=1:size-2a=Line(1,1:i); %路径前段b=fliplr(Line(1,i+1:size)); %路径后段倒置c=cat(2,a,b); %新路径%新路径更好就替换if (PathLength(c)<PathLength(NewLine))NewLine=c;Flag=1;fprintf('\n======================= 2-OPT 优化成功! ===');endendend%返回结果f=NewLine;end1 14.5 13.0 0.02 12.8 8.5 0.13 18.4 3.4 0.44 15.4 16.6 1.25 18.9 15.2 1.56 15.5 11.6 0.87 3.9 10.6 1.38 10.6 7.6 1.79 8.6 8.4 0.610 12.5 2.1 1.211 13.8 5.2 0.412 6.7 16.9 0.913 14.8 2.6 1.314 1.8 8.7 1.315 17.1 11.0 1.916 7.4 1.0 1.717 0.2 2.8 1.118 11.9 19.8 1.519 13.2 15.1 1.620 6.4 5.6 1.721 9.6 14.8 1.51 0 0 02 3639 1315 123 4177 2244 134 3712 1399 145 3488 1535 536 3326 1556 457 3238 1229 228 4196 1004 119 4312 790 1110 4386 570 5611 3007 1970 4312 2562 1756 2413 2788 1491 6514 2381 1676 3215 1332 695 5616 3715 1678 6717 3918 2179 6718 4061 2370 2219 3780 2212 3420 3676 2578 5621 4029 2838 2422 4263 2931 2523 3429 1908 2624 3507 2367 4625 3394 2643 8726 3439 3201 3327 2935 3240 2228 3140 3550 2429 2545 2357 5630 2778 2826 2431 2370 2975 4332 1304 2312 12。

蚁群算法概述一、蚁群算法蚁群算法(ant colony optimization, ACO)，又称蚂蚁算法，是一种用来寻找最优解决方案的机率型技术。

它由Marco Dorigo于1992年在他的博士论文中引入，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。

蚂蚁在路径上前进时会根据前边走过的蚂蚁所留下的分泌物选择其要走的路径。

其选择一条路径的概率与该路径上分泌物的强度成正比。

因此，由大量蚂蚁组成的群体的集体行为实际上构成一种学习信息的正反馈现象：某一条路径走过的蚂蚁越多，后面的蚂蚁选择该路径的可能性就越大。

蚂蚁的个体间通过这种信息的交流寻求通向食物的最短路径。

蚁群算法就是根据这一特点，通过模仿蚂蚁的行为，从而实现寻优。

这种算法有别于传统编程模式，其优势在于，避免了冗长的编程和筹划，程序本身是基于一定规则的随机运行来寻找最佳配置。

也就是说，当程序最开始找到目标的时候，路径几乎不可能是最优的，甚至可能是包含了无数错误的选择而极度冗长的。

但是，程序可以通过蚂蚁寻找食物的时候的信息素原理，不断地去修正原来的路线，使整个路线越来越短，也就是说，程序执行的时间越长，所获得的路径就越可能接近最优路径。

这看起来很类似与我们所见的由无数例子进行归纳概括形成最佳路径的过程。

实际上好似是程序的一个自我学习的过程。

3、人工蚂蚁和真实蚂蚁的异同ACO是一种基于群体的、用于求解复杂优化问题的通用搜索技术。

与真实蚂蚁通过外激素的留存/跟随行为进行间接通讯相似，ACO中一群简单的人工蚂蚁（主体）通过信息素（一种分布式的数字信息，与真实蚂蚁释放的外激素相对应）进行间接通讯，并利用该信息和与问题相关的启发式信息逐步构造问题的解。

人工蚂蚁具有双重特性：一方面，他们是真实蚂蚁的抽象，具有真实蚂蚁的特性，另一方面，他们还有一些在真实蚂蚁中找不到的特性，这些新的特性，使人工蚂蚁在解决实际优化问题时，具有更好地搜索较好解的能力。

人工蚂蚁与真实蚂蚁的相同点为：1．都是一群相互协作的个体。

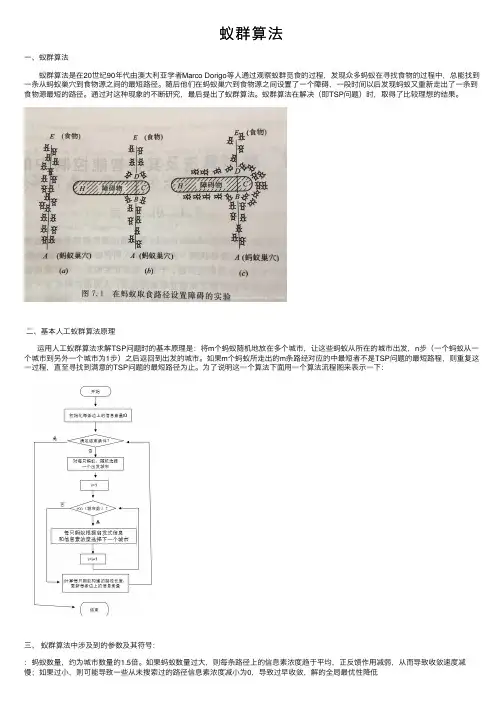
蚁群算法⼀、蚁群算法蚁群算法是在20世纪90年代由澳⼤利亚学者Marco Dorigo等⼈通过观察蚁群觅⾷的过程，发现众多蚂蚁在寻找⾷物的过程中，总能找到⼀条从蚂蚁巢⽳到⾷物源之间的最短路径。

随后他们在蚂蚁巢⽳到⾷物源之间设置了⼀个障碍，⼀段时间以后发现蚂蚁⼜重新⾛出了⼀条到⾷物源最短的路径。

通过对这种现象的不断研究，最后提出了蚁群算法。

蚁群算法在解决（即TSP问题）时，取得了⽐较理想的结果。

⼆、基本⼈⼯蚁群算法原理运⽤⼈⼯蚁群算法求解TSP问题时的基本原理是：将m个蚂蚁随机地放在多个城市，让这些蚂蚁从所在的城市出发，n步（⼀个蚂蚁从⼀个城市到另外⼀个城市为1步）之后返回到出发的城市。

如果m个蚂蚁所⾛出的m条路经对应的中最短者不是TSP问题的最短路程，则重复这⼀过程，直⾄寻找到满意的TSP问题的最短路径为⽌。

为了说明这⼀个算法下⾯⽤⼀个算法流程图来表⽰⼀下：三、蚁群算法中涉及到的参数及其符号：：蚂蚁数量，约为城市数量的1.5倍。

如果蚂蚁数量过⼤，则每条路径上的信息素浓度趋于平均，正反馈作⽤减弱，从⽽导致收敛速度减慢；如果过⼩，则可能导致⼀些从未搜索过的路径信息素浓度减⼩为0，导致过早收敛，解的全局最优性降低：信息素因⼦，反映了蚂蚁运动过程中积累的信息量在指导蚁群搜索中的相对重要程度，取值范围通常在[1, 4]之间。

如果信息素因⼦值设置过⼤，则容易使随机搜索性减弱；其值过⼩容易过早陷⼊局部最优：启发函数因⼦，反映了启发式信息在指导蚁群搜索中的相对重要程度，取值范围在[3, 4.5]之间。

如果值设置过⼤，虽然收敛速度加快，但是易陷⼊局部最优；其值过⼩，蚁群易陷⼊纯粹的随机搜索，很难找到最优解：信息素挥发因⼦，反映了信息素的消失⽔平，相反的反映了信息素的保持⽔平，取值范围通常在[0.2, 0.5]之间。

当取值过⼤时，容易影响随机性和全局最优性；反之，收敛速度降低：信息素常数，表⽰蚂蚁遍历⼀次所有城市所释放的信息素总量。

数据分析知识：数据挖掘中的蚁群算法蚁群算法是一种模拟蚂蚁觅食行为的启发式算法。

它是一种基于群体智能的方法，能够有效地用于数据挖掘和机器学习领域。

本文将介绍蚁群算法的基本原理和应用案例。

一、蚁群算法的基本原理蚁群算法受到了蚂蚁觅食行为的启发。

蚂蚁在觅食过程中会遵循一定的规则，例如在路径上释放信息素，吸引其他蚂蚁前往同一方向；在路径上的信息素浓度较高的路径更容易选择。

蚁群算法利用了这些规则，以一种群体智能的方式搜索解空间。

具体来说，蚁群算法由以下几个步骤组成：1.初始化：定义问题的解空间和初试信息素浓度。

解空间可以是任何基于排列、图形或其他对象的集合，例如TSP问题中的城市序列集合。

信息素浓度矩阵是一个与解空间大小相同的矩阵，用于反映每个解的吸引力。

2.移动规则:蚂蚁在解空间中移动的规则。

通常规则包括根据当前解和信息素浓度选择下一步解以及更新当前解的信息素浓度。

3.信息素更新:蚁群中的蚂蚁经过路径后，更新路径上的信息素浓度。

通常信息素浓度的更新涉及一个挥发系数和一个信息素增量。

4.终止条件:确定蚁群算法的运行时间，例如最大迭代次数或达到特定解的准确度。

蚁群算法是一种群体智能的方法，每只蚂蚁只能看到局部的解。

通过信息素的释放和更新，蚁群最终能够找到全局最优解。

二、蚁群算法的应用案例蚁群算法最常用于解决组合优化问题，例如TSP问题、车辆路径问题和任务分配问题。

下面将介绍蚁群算法在TSP问题和车辆路径问题中的应用。

1. TSP问题TSP问题是一个NP难问题，是指在旅行时，如何有效地走遍所有篮子，使得总的旅行距离最小。

蚁群算法是适用于TSP问题的一种有效的算法。

在每一代，蚂蚁会在城市之间移动，假设当前城市为i，则下一个选择的城市j是基于概率函数计算得到的。

概率函数考虑了当前城市的信息素浓度以及城市之间的距离。

每条路径释放的信息素浓度大小根据路径长度而定。

这样，蚂蚁可以在TSP问题上找到最优解。

2.车辆路径问题车辆路径问题是指在有限时间内如何合理地分配车辆到不同的客户，以最小化送货时间和车辆的旅行距离。

蚁群算法这算是填3年前的⼀个坑吧，已经懒癌晚期了，想必也还是要挣扎下，那今天先从蚁群算法这个坑说起，如果你是要寻找怎么优化蚁群算法，可以直接跳过本⽂，如果你还不了解什么是蚁群算法，或许本⽂能够提起你的兴趣。

如果你同样对遗传算法和粒⼦群算法感兴趣，请查看3年前我对于这两个算法见解的⽂章。

简单蚁群算法模拟实验：这个模拟实验⽐较简单，并没有对信息素、路径选择等做优化，主要是⽅便⼤家查看简单的蚂蚁系统能够带来⼀个什么样的效果,详细说明见后⽂。

什么是蚁群算法按百度百科的话来说，蚁群算法(ant colony optimization, ACO)，⼜称蚂蚁算法，是⼀种⽤来在图中寻找优化路径的机率型算法。

它由Marco Dorigo于1992年在他的博⼠论⽂中提出，其灵感来源于蚂蚁在寻找⾷物过程中发现路径的⾏为。

蚁群算法是⼀种模拟进化算法，初步的研究表明该算法具有许多优良的性质，并且现在已⽤于我们⽣活的⽅⽅⾯⾯。

基本原理蚂蚁在运动过程中，会留下⼀种称为信息素的东西，并且会随着移动的距离，播散的信息素越来越少，所以往往在家或者⾷物的周围，信息素的浓度是最强的，⽽蚂蚁⾃⾝会根据信息素去选择⽅向，当然信息素越浓，被选择的概率也就越⼤，并且信息素本⾝具有⼀定的挥发作⽤。

蚂蚁的运动过程可以简单归纳如下：1. 当周围没有信息素指引时，蚂蚁的运动具有⼀定的惯性，并有⼀定的概率选择其他⽅向2. 当周围有信息素的指引时，按照信息素的浓度强度概率性的选择运动⽅向3. 找⾷物时，蚂蚁留下家相关的A信息素，找家时，蚂蚁留下⾷物相关的B信息素，并随着移动距离的增加，洒播的信息素越来越少4. 随着时间推移，信息素会⾃⾏挥发⼀个简单的例⼦，如果现在有两条通往⾷物的路径，⼀条较长路径A,⼀条较短路径B,虽然刚开始A,B路径上都有蚂蚁，⼜因为B⽐A短，蚂蚁通过B花费的时间较短，随着时间的推移和信息素的挥发，逐渐的B上的信息素浓度会强于A，这时候因为B的浓度⽐A强，越来越多多蚂蚁会选择B，⽽这时候B上的浓度只会越来越强。

蚁群算法蚁群算法⽬录1 蚁群算法基本思想 (1)1.1蚁群算法简介 (1)1.2蚁群⾏为分析 (1)1.3蚁群算法解决优化问题的基本思想 (2)1.4蚁群算法的特点 (2)2 蚁群算法解决TSP问题 (3)2.1关于TSP (3)2.2蚁群算法解决TSP问题基本原理 (3)2.3蚁群算法解决TSP问题基本步骤 (5)3 案例 (6)3.1问题描述 (6)3.2解题思路及步骤 (6)3.3MATLB程序实现 (7)3.1.1 清空环境 (7)3.2.2 导⼊数据 (7)3.3.3 计算城市间相互距离 (7)3.3.4 初始化参数 (7)3.3.5 迭代寻找最佳路径 (7)3.3.6 结果显⽰ (7)3.3.7 绘图 (7)1 蚁群算法基本思想1.1 蚁群算法简介蚁群算法（ant colony algrothrim，ACA）是由意⼤利学者多⾥⼽（Dorigo M）、马聂佐（Maniezzo V ）等⼈于20世纪90初从⽣物进化的机制中受到启发，通过模拟⾃然界蚂蚁搜索路径的⾏为，提出来的⼀种新型的模拟进化算法。

该算法⽤蚁群在搜索⾷物源的过程中所体现出来的寻优能⼒来解决⼀些系统优化中的困难问题，其算法的基本思想是模仿蚂蚁依赖信息素，通过蚂蚁间正反馈的⽅法来引导每个蚂蚁的⾏动。

蚁群算法能够被⽤于解决⼤多数优化问题或者能够转化为优化求解的问题，现在其应⽤领域已扩展到多⽬标优化、数据分类、数据聚类、模式识别、电信QoS管理、⽣物系统建模、流程规划、信号处理、机器⼈控制、决策⽀持以及仿真和系统辩识等⽅⾯。

蚁群算法是群智能理论研究领域的⼀种主要算法。

1.2 蚁群⾏为分析Bm=20t=0 m=10m=10t=11.3 蚁群算法解决优化问题的基本思想⽤蚂蚁的⾏⾛路径表⽰待优化问题的可⾏解，整个蚂蚁群体的所有路径构成待优化问题的解空间。

路径较短的蚂蚁释放的信息量较多，随着时间的推进，较短路径上积累的信息浓度逐渐增⾼，选择该路径的蚂蚁个数愈来愈多。

蚁群算法报告学院:专业:学号:姓名:目录第一部分：蚁群算法原理介绍 (3)1.1蚁群算法的提出 (3)1.2蚁群算法的原理的生物学解释 (3)1.3蚁群算法的数学模型 (3)1.4蚁群算法实现步骤 (5)第二部分：蚁群算法实例--集装箱码头船舶调度模型 (7)2.1集装箱码头船舶调度流程图 (7)2.2算例与MATLAB编程的实现 (7)2.2.1算法实例 (7)2.2.2 Matlab编程 (9)第三章：MATLAB 优化设计工具箱简介 (15)3.1M ATLAB优化工具箱 (15)3.1.1优化工具箱功能： (16)3.2M ATLAB 优化设计工具箱中的函数 (16)3.2.2 方程求解函数 (17)3.2.3最小二乘（曲线拟合）函数 (17)3.2.4 使用函数 (17)3.2.5 大型方法的演示函数 (17)3.2.6 中型方法的延时函数 (18)3.4优化函数简介 (18)3.4.1优化工具箱的常用函数 (18)3.4.2 函数调用格式 (18)3.5模型输入时所需注意的问题 (20)第一部分：蚁群算法原理介绍1.1蚁群算法的提出蚂蚁是地球上最常见、数量最多的昆虫种类之一，常常成群结队地出现于人类的日常生活环境中。

受到自然界中真实蚁群集体行为的启发，意大利学者M.Dorig 。

于20世纪90年代初，在他的博士论文中首次系统地提出了一种基于蚂蚁种群的新型优化算法—蚁群算法}28}(Ant Colony Algorithm, ACA)，并成功地用于求解旅行商问题，自1996年之后的五年时间里，蚁群算法逐渐引起了世界许多国家研究者的关注，其应用领域得到了迅速拓宽。

1.2蚁群算法的原理的生物学解释据观察和研究发现，蚂蚁倾向于朝着信息激素强度高的方向移动。

因此蚂蚁的群体行为便表现出了一种信息激素的正反馈现象。

当某条路径上经过的蚂蚁越多，该路径上存留的信息激素也就越多，以后就会有更多的蚂蚁选择它。

蚁群算法及算例范文蚁群算法的核心思想是通过模拟蚂蚁在路径选择过程中释放的信息素来寻找到达目标的最优路径。

蚂蚁在觅食过程中会释放一种化学物质（信息素），用于标记已经走过的路径。

当其他蚂蚁经过时，会受到这些信息素的影响，从而倾向于选择已经标记过的路径。

通过这种方式，蚂蚁群体能够找到从巢穴到食物的最短路径。

蚁群算法的算例可以参考旅行商问题（TSP，Traveling Salesman Problem）。

旅行商问题是一种经典的组合优化问题，要求在给定的城市之间找到最短的回路，使得每个城市恰好访问一次。

下面是一个应用蚁群算法解决旅行商问题的算例：1.初始化城市和蚂蚁的信息。

2.随机放置若干蚂蚁在城市中。

3.每只蚂蚁根据当前城市和信息素浓度选择下一个城市。

选择过程可以使用蚂蚁选择概率来确定，概率与信息素浓度和距离有关。

假设蚂蚁A 位于城市B，需要选择下一个城市C，蚂蚁选择概率计算公式如下：p(C)=(τ(B,C)^α)*(η(B,C)^β)/Σ[(τ(B,i)^α)*(η(B,i)^β)]其中τ(B,C)表示城市B到城市C之间的信息素浓度，η(B,C)表示城市B到城市C的适应度（与距离相关），α和β是调节信息素和适应度对蚂蚁选择的相对重要性的参数。

4.更新信息素。

当所有蚂蚁行走完成后，根据蚂蚁走过的路径长度更新信息素浓度。

更新公式如下：Δτ(B,C)=Q/L其中Δτ(B,C)表示城市B到城市C之间的信息素增量，Q是常数，L 是蚂蚁行走的路径长度。

5.重复步骤3和步骤4直到满足终止条件。

通常终止条件可以是达到最大迭代次数或者找到最优路径。

6.输出蚂蚁群体找到的最优路径和路径长度。

蚁群算法通过模拟蚂蚁觅食行为，利用信息素的正反馈机制，能够在很短的时间内找到高质量的解。

它被广泛应用于旅行商问题、资源调度问题、网络优化问题等领域。

第三章基本蚁群算法原理3.1 自然界中的蚂蚁在蚂蚁寻找食物的过程中，总能找到一条从蚁穴到随机分布的距离很远的食物源之间的最短路径。

仿生学家经过研究发现，蚂蚁没有视觉，但是在寻找食物的行进过程中，会不断分泌一种化学刺激物——信息素，蚂蚁之间通过它来相互通信。

信息素量与路径长度有关，路径越长，释放的信息素浓度就越低。

信息素可以吸引后来的蚂蚁沿信息素浓度高的路径行进。

某一路径上走过的蚂蚁越多，留下的信息素就越多，后来者选择该路径的概率就越大，蚂蚁个体之间就是通过这种信息的交流搜索食物，这样，由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象，整个蚁群最终会选择出最短路径行进。

图3.1 现实蚂蚁寻找食物如图3.1(a)所示，蚂蚁在点A和E之间的路径上行走，路径突然被出现的障碍物截断，如3.1(b)所示。

因此，蚂蚁从A至E步行至位置B （或以相反的方向在位置D处）必须决定是否要向左或向右转。

一开始蚂蚁按同等概率选择路径，不论路径长短。

第一只蚂蚁到达B点（或D）具有相同的概率向左或向右转。

由于路径BCD比BHD短，以路径BCD第一个到达的蚂蚁比以路径BHD到达的早。

由于一半蚂蚁是以偶然的方式通过DCBA障碍的或者已经通过路径BCD到达的，于是，一个蚂蚁从E 到D返回会在路径DCB上找到一个更强有力的线索。

因此他们极大概率上选择通过路径DCB而不是DHB。

因此，单位时间内通过路径BCD的蚂蚁要比通过路径BHD的蚂蚁多的多，如图3.1(c)。

这将导致较短路径上的信息素量增长地比较长路径上的快得多，因此单一蚂蚁路径的选择很快偏向于较短路径。

最后的结果是很快所有的蚂蚁会选择较短的路径[1]。

不仅如此，作为一种化学物质，信息素还具有挥发性，这使得寻径初期距离较长的路径和长期没有经过的路径对蚂蚁的影响逐渐减小。

可见，在整个寻找食物的过程中，虽然单个蚂蚁的选择能力有限，但是通过信息素的作用是整个蚁群行为具有非常高的自组织性，蚂蚁之间交换着路径信息，最终通过蚁群的集体自催化行为找出最优路径[3,4]。