周期型

第九节低钾型周期性麻痹的护理常规周期性瘫痪是以周期性反复发作的骨骼肌弛缓性瘫痪为特征的一组疾病。

发作时多数与血清钾代谢异常有关。

按发病时的血清钾浓度和症状可分为低血钾型、高血钾型和正常血钾型三型，临床上以低血钾型最常见，其中有部分病例，合并甲状腺功能亢进，称为甲亢性周期性麻痹。

一、护理措施1．发作时应立即急查血钾及心电图，属低钾性周期性瘫痪者立即口服10%氯化钾40～50ml，24小时内再分次口服,总量为10g。

血钾过低者应同时静脉滴注氯化钾2～4克。

2.滴注氯化钾的稀释液以等渗盐水为宜（若需稀释液较多可加用少量5%葡萄糖液），滴速每小时应不超过1克，浓度不超过0.3%。

3.静脉补钾时宜选择粗大血管，因钾盐对血管具有强刺激性。

4.在补钾过程中应密切监测BP、P、尿量、血清钾与心电图的变化，防止发生心律失常及呼吸麻痹。

重症患者应在心电图监护下进行静脉补钾。

5.呼吸困难者应给氧气吸入，必要时辅助人工呼吸。

6.及时复查血钾，根据病情调整补钾量。

补钾宜达有效剂量，不宜过量。

重症缺钾者应在2～3日内补足体内钾。

7.发作期间应卧床休息，发作间期鼓励患者在能耐受的范围内参加适当活动，如有明显的心功能不全时，应限制活动量，以防心肌受损。

8.做好患者心理护理，稳定情绪，使其能以乐观、积极的态度配合各项检查和治疗。

二、出院指导1.平时少吃多餐，限制钠盐的摄入，忌高糖饮食，要多食高钾饮食及饮料，如榨菜、瘦猪肉、鳝鱼、海带、花生、香蕉、桔子水等，多饮茶。

2.免过度疲劳、过饱、受寒、酗酒等诱发因素。

3.发作频繁者可每日口服氯化钾3～6克，或口服乙酰唑胺、安体舒通等预防发作。

4.甲亢性周期性瘫痪患者应积极治疗甲亢，可预防复发。

参考文献：1.王维治.神经病学.北京.人民卫生出版社.2004年7月第5版2.尤黎明.内科护理学.北京.人民卫生出版社.2001年5月第1版3.袁峥.医院神经内科护理常规与临床技术操作工作手册.北京4.杨和平等.疾病护理常规.四川.科学技术出版社.2005年11月第1版。

6.周期型1.电子跳蚤游戏盘是如图所示的678ABC AB AC BC ∆===，，，．如果跳蚤开始时在BC 边的0P 处，02BP =．跳蚤第一步从0P 跳到AC 边的1P （第一次落点)处，且10CP CP =；第二步从1P 跳到AB 边的2P （第一次落点)处，且21AP AP =；第三步从2P 跳到BC 边的3P （第三次落点)处，且32BP BP =；……；跳蚤按上述规则一致跳下去，第n 次落点为n P （n 为正整数），则点2007P 与2010P 之间的距离为______．答案：3解析：根据规律：10826CP CP ==-=，12761AP AP ==-=，23615BP BP ==-=， 34853CP CP ==-=，45734AP AP ==-=⋯，由此可得0303633P P CP CP =-=-=，1441413PP AP AP =-=-=， 2552413P P AP AP =-=-=，…∴200720103P P =．故答案为3．2.如图所示，长为4cm ，宽为3cm 的长方形木板在桌面上做无滑动的翻滚（顺时针方向），木板上点A 位置变化为12A A A →→，由1A 翻滚到2A 时被桌面上一小木块挡住，此时长方形木板的边2A C 与桌面成30︒角，则点A 翻滚到2A 位置时所经过的路径总长度为__________cm ．答案：7π2解析：由1A A →路径为90π55π1802⋅=，由12A A →路径为60π3π180⋅=，因此由12A A A →→总路径为7π2．故答案为：7π2．3.如图，正方形ABCD 边长为2cm ，动点P 从A 点出发，沿正方形的边按逆时针方向运动，当它的运动路程为2013cm 时，线段PA 的长为n 的形式，则n =_____cm ；当点P 第n 次（n 为正整数）到达点D 时，点P 的运动路程为____cm(用含n 的代数式表示)．答案：5；8n-2，-2+8n 解析：先求出正方形的周长，∵边长为2cm . ∴周长为428cm cm ⨯=.再用2013除以8得到201382515÷=L .即此时点P 已经从A 点运动了5cm . 所以点P 的位置在CD 的中点，如图则根据勾股定理225PA AD DP =+=.当点P 第1次到达D 点时，P 的运动路程为8126⨯-=； 当点P 第2次到达D 点时，P 的运动路程为82214⨯-=； 当点P 第3次到达D 点时，P 的运动路程为83222⨯-=； 以此类推，当点P 第n 次到达D 点时，P 的运动路程为82n -.4.如图，菱形ABCD 中，2AB =，60C∠=︒,我们把菱形ABCD 的对称中心O 称作菱形的中心．菱形ABCD 在直线l 上向右作无滑动的 翻滚，每绕着一个顶点旋转60︒叫一次操作，则经过3n （n 为正整数） 次这样的操作菱形中心O 所经过的路径总长为（ ）解析：∵菱形ABCD 中，2AB =，60C ∠=︒，∴ABD △是等边三角形，1BO DO ==，223AO AB BO =-=，第一次旋转的弧长60π33π1803⨯==，∴第一、二次旋转的弧长和60π360π323π1801803⨯⨯=+=，第三次旋转的弧长为：60π11π1803⨯=，故经过3n （n 为正整数）次这样的操作菱形中心O所经过的路径总长为：231(π+π)33n ⨯231π3n +=． 故答案为：3π3，231π3n +．5.观察下列等式：123456733393273813243372932187======⋯=，，，，，， 解答下列问题：234201333333+++⋯+ 的末位数字是（）解析：∵133= ，239= ，3327= ，4381= ，53243= ，63729= ，732187= …∴末尾数，每4个一循环， ∵201345031÷=⋯ ， ∴234201333333+++⋯+的末位数字相当于：37913++++⋯+的末尾数为36.如图，动点P 从()03，出发，沿所示的方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P 第2013 次碰到矩形的边时，点P 的坐标为（ ）A ．()14， B ．()50，C ．()64，D ．()83，答案：D 解析：如下图，动点()03P，沿所示的方向运动，满足反弹时反射角等于入射角， 到①时，点()30P ，；到②时，点()74P ， ；到③时， 点()83P，；到④时，点()50P ， ；到⑤时，点()14P ， ； 到⑥时，点()30P，，此时回到出发点，继续.......， 出现每5 次一循环碰到矩形的边.因为201340253(201354023)=⨯+÷=…… . 所以点P 第2013 次碰到矩形的边时，点P 的坐标为()83，. 故选D .7.我们知道，一元二次方程21x=-没有实数根，即不存在一个实数的平方等于1- ，若我们规定一个新数“”，使其满足21i=- (即方程2-1x =有一个根为)，并且进一步规定: 一切实数可以与新数进行四则运算，且原有的运算律和运算法则仍然成立，于是有2i i =，21i =-，321i i i i i =⋅=-⋅=- ，422()1i i == 那么， 23420122013i i i i i i ++++++……的值为（ ）A ．0B ．1C ．1-D ．i答案：D 解析：由于234110i ii i i i +++=--+=，而2013=4503+1⨯，23420122013=i i i i i i i ++++++…… .8.如图，在直角坐标系中，已知点(3,0)A - 、()04B，，对OAB △ 连续作旋转变换，依次得到1△ 、2△、3△、4△…，则2013△的直角顶点的坐标为(______，______)．答案：8052；0解析：∵(3,0)A - 、()04B ，， ∴223+4=5AB =，由图可知，每三个三角形为一个循环组依次循环，一个循环组前进的长度为：45312++= ，∵20133671÷=，∴2013△的直角顶点是第671个循环组的最后一个三角形的直角顶点， ∵671128052⨯= ，∴2013△的直角顶点的坐标为()80520，．9.根据如图中箭头的指向规律，从2013到2014再到2015 ，箭头的方向是以下图示中的（ ）选项：A ．B ．C ．D ．答案：D解析：由图可知，每4个数为一个循环组依次循环，201345031÷=⋯ ，∴2013是第504个循环组的第2个数，∴从2013到2014再到2015，箭头的方向是．故选D ．10.有一个正六面体骰子，放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动90︒ 算一次，则滚动第2014 次后，骰子朝下一面的点数是______．答案：3解析：观察图象知道点数三和点数四相对，点数二和点数五相对且四次一循环， ∵201445032÷=⋯ ，∴滚动第2014次后与第二次相同， ∴朝下的点数为3 ，11.一列数123,,,n a a a a ⋯ ，其中11a =- ，2111a a =-，3211a a =-，…，111n n a a -=-，则1232004a a a a +++⋯+= ______． 答案： 1002 解析：11a =-，2111=12a a =-，32211a a =-=，43111a a ==--，…，由此可以看出三个数字一循环，20043668÷= ， 则12320041668(12)10022a a a a +++⋯+=⨯-++= ．12.如图，弹性小球从点()0,3P出发，沿所示方向运动，每当小球碰到矩形OABC 的边时反弹，反弹时反射角等于入射角，当小球第1 次碰到矩形的边时的点为1P ，第2次碰到矩形的边时的点为2P ，…，第n 次碰到矩形的边时的点为n P ，则点3P 的坐标是___,点2014P 的坐标是___．答案：8;3;5;0 解析：如图，经过6次反弹后动点回到出发点()0,3 ，当点P 第3次碰到矩形的边时，点P 的坐标为：()8,3 ；∵201463354÷=⋯ ，∴当点P 第2014次碰到矩形的边时为第336个循环组的第4次反弹， 点P 的坐标为()5,0 ．13.在平面直角坐标系中，正方形ABCD 的顶点分别为(11)A ，、(11)B -，、(11)C --，、(11)D -，，y 轴上有一点P ()2,0,作点P 关于点A 的对称点1P ，作1P 关于点B 的对称点2P ，作点2P 关于点C 的对称点3P ，作3P 关于点D 的对称点4P ，作点4P 关于点A 的对称点5P ，作5P 关于点B 的对称点6P ⋅⋅⋅，按如此操作下去，则点2011P 的坐标为（ ）.A ．(02)，B ．(20)，C ．(02)-， D ．(20)-，答案：D解析：找出规律，1P 20（，）202P -（，），320P （-，），4P (02)，，……，4(02)n P ，，41n P +20（，），42n P +02-（，），43n P +20（-，）.而2011除以4余3，所以点2011P 的坐标与3P 坐标相同，为20（-，）.14.观察图中正方形四个顶点所标的数字规律，可知数2011应标在（） A 、第502个正方形的左下角B 、第502个正方形的右下角C 、第503个正方形的左上角D 、第503个正方形的右下角答案：C解析：观察发现：正方形的左下角是4的倍数，左上角是4的倍数余3，右下角是4的倍数余1，右上角是4的倍数余2.2011除以4等于余3，所以数2011应标在第503个正方形的左上角.15.如下表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第2011个格子中的数为（）解析：首先由已知和表求出a 、C 、F ，再观察找出规律求出第2011个格子中的数． 已知其中任意三个相邻格子中所填整数之和都相等， 则，3a Fa F C +=+++，+1abc b c +=+-， 解得1a =-，3C=，按要求排列顺序为，3，1﹣，F ，3，1-，F ，…， 结合已知表得2F=，所以每个小格子中都填入一个整数后排列是：3，1-，2，3，1-，2，…， 其规律是每3个数一个循环.∵20113670÷=余1， ∴第2011个格子中的数为3.故选A .16.一个纸环链，纸环按红黄绿蓝紫的顺序重复排列，截去其中的一部分，剩下部分如图所示，则被截去部分纸环的个数可能是（）解析：从图中知，该纸链是5的倍数，中间截去的是剩下35n +，从选项中数减3为5的倍数者即为所求.因为20133-被5整除，故选D . 17.若123121111 , 1 , 1 , a a a m a a =-=-=-⋅⋅⋅，则2011a 的值为（ ）．（用含m 的代数式表示）解析：根据已知条件，找出题中的规律：2111111 1111111m m m a a m m m m--=-=-=-==----，32111 11111a m m a m=-=-=-+=-， 43111 1a a m=-=-.可见，123 , , , a a a ⋅⋅⋅分别以11m -，11m-，m 循环.而2011 除以3 余1 ，从而2011a 的值与1a 相同，为11m-.18.如下图，在平面直角坐标系中，对ABC △ 进行循环往复的轴对称或中心对称变换，若原来点A 坐标是()2n π，，则经过第2011 次变换后所得的A 点坐标是（ ）．解析：因为变换是循环往复的，补全一个循环；56y ABC ABC −−−−−→∆−−−−−→∆第次第次关于原点对称关于轴对称到第二象限 回到第一象限初始位置因此一个循环要经过6 次变换.而20116335÷＝ ……余1 ，从而ABC △ 经过第2011 次变换与经过第1 次变换得到的位置相同，即在第四象限.因为原来点A 坐标是（2π，n ），根据坐标关于x 轴对称时，横坐标不变纵坐标改变符号的特点，得到经过第2011次变换后所得的A 点坐标是（2π，n -）.19.将1 、2、3、6按如下方式排列．若规定（m n ，）表示第m排从左向右第n 个数，则（54， ）与（157， ）表示的两数之积是（ ）．111122663263323第1排第2排第3排第4排第5排解析：54（，） 从右侧可见为2.下面求157（，） 是几：首先看157（，）是整个排列的第几个数，从排列方式看第1 排1 个数，第2 排2 个数，…… 第m 排m 个数，所以前14 排一共的数目是1214⋯⋯＋＋＋(114)(213)(78)⋯⋯＝＋＋＋＋＋＋715⨯＝105＝ ，因此（157， ）是第1057112＋＝个数.第二看第112 个数是哪个数，因为1 、2、3、6四个数循环，而1124÷ 商余0 ，所以（157，）为6.则（54， ）与（157， ）表示的两数之积是4(5,0)P .20.如图物体从点A 出发，按照A B →（第1步）y （第2步）a E →F G A B →→→→→L的顺序循环运动，则第2011 步到达 点处；答案：D解析：根据循环运动的规律，8步一个循环.而2011 除以8 余3 ，故第2011步到达点D 处.21.如图，将若干个正三角形、正方形和圆按一定规律从左向右排列，那么第2014个图形是______．答案：正方形．解析：由图形看出去掉开头的两个三角形，剩下的由三个正方形，一个三角形，两个圆6个图形为一组，不断循环出现，()2014263352-÷=⋯，所以第2014 个图形是与循环的第二个图形相同是正方形．22.将正方体骰子（相对面上的点数分别为1和6、2和5、3和 4）放置于水平桌面上，如图①．在图②中，将骰子向右翻滚90︒，然后在桌面上按逆时针方向旋转90︒，则完成一次变换．若骰子的初始位置为图①所示的状态，那么按上述规则连续完成10次变换后，骰子朝上一面的点数是（）解析：不难看出经过一次变换后正面朝上的点数是5，经过第二次变换后正面朝上的6点数是，经过第三次变换后正面朝上的点数是3，又回到了起始位置，则三个变换一循环，10次变换即相当于第一次变换的结果故选B.23.如图，圆圈内分别标有0，1，3，…，11这12个数字，电子跳骚每跳一次，可以从一个圆圈跳到相邻的圆圈，现在，一只电子跳骚从标有数字“0”的圆圈开始，按逆时针方向跳了2010次后，落在一个圆圈中，该圆圈所标的数字是______．答案：6解析：根据题意可知是0，1，3121⨯-=，3，4，…，11即12个数是一个循环．因为2010除12余数为6．故该圆圈所标的数字是3224⨯-=．故答案为：6．24.如图，在平面直角坐标系中，以原点O 为圆心的同心圆半径由内向外依次为1，2，3，4，…，同心圆与直线y x =和y x =-分别交于1A ，2A ，3A ，4A ，…，则点31A 的坐标是（ ）．解析：本题考查了解直角三角形，一次函数等知识点的应用，解此题的关键是确定出31A 的位置．根据31473÷=⋯，得出31A 在直线y x =上，在第三象限，且在第8个圆上，求出318OA =，通过解直角三角形即可求出答案．25.如图，菱形ABCD 中，260AB C=∠=︒，,我们把菱形22AB AP BP PC=+⋅的对称中心称作菱形的中心．菱形ABCD 在直线l 上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过3n （n 为正整数）次这样的操作菱形中心O 所经过的路径总长为 ( )解析：从图中可以看出，第一次旋转是以点A 为圆心，那么菱形中心旋转的半径就是OA ，解直角三角形可求出OA 的长，圆心角是60度．第二次还是以点A 为圆心，那么菱形中心旋转的半径就是OA ，圆心角是60度．第三次就是以点B 为旋转中心，OB 为半径，旋转的圆心角为60度．旋转到此菱形就又回到了原图．故这样旋转18次，就是这样的6个弧长的总长，依此计算即可得，进而得出经过3n （n 为正整数）次这样的操作菱形中心O 所经过的路径总长．26.如图，ABC ∆中，2AB AC == ，若P 为BC 的中点,则2AP BP PC +⋅的值为______；若BC边上有100个不同的点1P ，2P ，…，100P ，记2i i i im AP BP PC =+⋅(1i =，2，…，100)，则12m m ++…100m +的值为______．答案：4；400解析：当P 在BC 的中点时，可以得到直角三角形，利用勾股定理证明22AB AP BP PC =+⋅即可；第二个空可作AD BC ⊥于D ．根据勾股定理，得22222()i i i AP AD DP AD BD BP =+=+-，从而求得22iM AD BD =+，即可求解．27.如图所示，圆圈内分别标有1，2，…，12，这12个数字，电子跳蚤每跳一步，可以从一个圆圈逆时针跳到相邻的圆圈，若电子跳蚤所在圆圈的数字为n ，则电子跳蚤连续跳（3-2n ）步作为一次跳跃，例如：电子跳蚤从标有数字1的圆圈需跳3121⨯-=步到标有数字2的圆圈内，完成一次跳跃，第二次则要连续跳3224⨯-=步到达标有数字6的圆圈，…依此规律，若电子跳蚤从①开始，那么第3次能跳到的圆圈内所标的数字为______；第2012次电子跳蚤能跳到的圆圈内所标的数字为______．答案：10；6解析：第一次跳到数字2，第二次跳到数字6，第三次跳到数字10，第四次跳到数字2，…然后每三个一循环，用2012除以3，整除为10，余1为2，余2为6即可确定答案．28.在数学校本活动课上，张老师设计了一个游戏，让电动娃娃在边长为1的正方形的四个顶点上依次跳动．规定：从顶点A出发，每跳动一步的长均为1．第一次顺时针方向跳1步到达顶点D，第二次逆时针方向跳2步到达顶点B，第三次顺时针方向跳3步到达顶点C，第四次逆时针方向跳4步到达顶点C，… ，以此类推，跳动第10次到达的顶点是______，跳动第2012次到达的顶点是______．A B D C答案：B；C解析：先根据每跳一次所到达的顶点，找出其中的规律是每八次一个循环，再用10812÷=⋯，即可求出跳动第10次到达的顶点，用201282514÷=⋯，即可求出跳动第2012次到达的顶点．29.观察下列图形的排列规律（其中☆、□、●分别表示五角星、正方形、圆）●□☆●●□☆●□☆●●□☆●…若第一个图形是圆，则第2009个图形是______．答案：五角星解析：根据题意分析可得：圆、正方形、五角星前七个一组，依次循环；且2009除以7没有余数；故第2009个图形是五角星．30.如图，在平面直角坐标系中，一颗棋子从点P处开始跳动，第一次跳到点P关于x轴的对称点1P处，接着跳到点1P关于y轴的对称点2P处，第三次再跳到点2P关于原点的对称点处，…，如此循环下去．当跳动第2009次时，棋子落点处的坐标是（______,______）．答案：3；-2解析：首先发现点P 的坐标是32-(，)，第一次跳到点P 关于x 轴的对称点1P 处是32--（，），接着跳到点1P 关于y 轴的对称点2P 处是32-（，），第三次再跳到点2P 关于原点的对称点处是32-（，）…，发现3次一循环．又200936692÷=⋯，则落在了(32)-，处．31.如图平面内有公共端点的五条射线,,,,,OA OB OC OD OE 从射线OA 开始，在射线上写出数字1,2,3,4,5； 6,7,8,9,10；…．按此规律，则“12”在射线______上；“2011”在射线______上．答案：OC ；OB解析：∵如图所示可知，每隔一个数正好是连续的有理数，∴11在BO 上，∴“12”在射线CO上；∵每5个数一轮，2011÷5=402余数为1，每5轮顶点正好循环一周，402÷5=80余数为2，∴“2011”与第3轮第一个数的位置相同，即与9的位置相同，∴“2011”在射线BO 上．32.在平面直角坐标系xOy 中，矩形OABC 如图放置，动点P 从(0,3)出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P 第2014次碰到矩形的边时，点P 的坐标为（______,______）答案：5；0解析：依题可知，1(3,0)P ，2(7,4)P ，3(8,3)P ，4(5,0)P ，5(1,4)P ，6(0,3)P， 7(3,0)P ，8(7,4)P ，L L，6个一循环，2014=33546L L ，故2014(5,0)P故答案为：(1,4)，(5,0)．33.如图，矩形BCDE 的各边分别平行于x 轴或y 轴，物体甲和物体乙由点(2,0)A 同时出发，沿矩形BCDE 的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2014次相遇地点的坐标是（_____,_____）答案：-1；1解析：依题可知，甲、乙两物体沿着矩形BCDE 在做环形运动，矩形BCDE 的周长为12，12=41+2秒，每过4秒相遇一次，故第一次在(1,1)-处相遇，第二次在(1,1)--处相遇，第三次在(2,0)处相遇，第四次又在(1,1)-处相遇，故3次一循环，2014=67113L L ，所以第2014次在(1,1)-处相遇． 故答案为：(1,1)-．34.如图，正方形ABCD 的边长为3，点E 、F 分别在边AB 、BC 上，1AE BF ==，小球P 从点E 出发沿直线向点F 运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当小球P 第一次碰到BC 边时，小球P 所经过的路程为__________；当小球P 第一次碰到AD 边时，小球P 所经过的路程为__________；当小球P 第n （n 为正整数）次碰到点F 时，小球P 所经过的路程为__________．解析：22125EF =+=；3555522EFFM +=+=；画图可知，6次一个循环，一个循环周期，P 所经过的路程为3552(5++)=6522， 当小球P 第n （n 为正整数）次碰到点F 时，小球P 所经过的路程为65(1)56555n n -+=-．故答案为：5，552，6555n -．35.如图，在平面直角坐标系xOy 中，点(10)A ，，(20)B ，， 正六边形ABCDEF 沿x 轴正方向无滑动滚动，当点D 第一次落 在x 轴上时，点D 的横坐标为：_____；在运动过程中，点A 的纵坐标的最大值是______；保持上述运动过程，经过(20143)，的正六边形的顶点是_____.解析：因为2014=3356+4⨯， 所以经过(2014,3)的点必然会经过(4,3)．图分别是第二次和第三次滚动后的图形， 可以看出经过(4,3)的点有B 、F 两个， 故经过(2014,3)为B 、F 两个点．故答案为：(4,0)，2，B 或F ．36.将正整数12345,⋅⋅⋅、、、、按以下方式排放：则根据排放规律，从2002到2004的箭头依次为（ ） 解析：200250042,=⨯+Q1 2 3 yx O1234A BCDEF 1 2 3 yx O1234A B C D EF21 / 21∴数2002的位置与数2相同，数2003的位置与数3相同，数2004的位置与数4相同， ∴从2002到2004的箭头依次为,.→↓37.如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由A 点开始按ABCDEFCGA 的顺序沿菱形的边循环运动,行走2010厘米后停下,则这只蚂蚁停在（ ）点．解析：解：∵两个全等菱形的边长为1厘米，∴蚂蚁由A 点开始按ABCDEFCGA 顺序走一圈所走的距离为818⨯=厘米， 201025128=Q L ， ∴当蚂蚁走到第251圈后再走2厘米正好到达C 点。

低钾型周期性瘫痪市儿童医院智胜, 丹)周期性瘫痪又称周期性麻痹( periodic paralysis)是以反复发作的骨骼肌迟缓性瘫痪为特征的一组少见疾病,发作时大都伴有血清钾浓度的改变。

根据血清钾离子浓度的变化可将周期性瘫痪分为低钾型、正常钾型和高钾型3 种类型,其中以低钾型周期性瘫痪( hypokalemic periodic paral2 ysis, hypoKPP)最为常见。

近年来随着对离子通道结构和功能的了解,发现周期性瘫痪是由肌肉细胞膜离子通道基因突变所致的离子通道病( ion channel disease) 。

周期性瘫痪的原发性缺陷并不是血清钾浓度的改变,而是钾代障碍所致。

周期性瘫痪进一步被分为原发性和继发性,本文主要介绍原发性和继发性hypoKPP,并从离子通道病角度更新对hypoKPP 的认识。

1 原发性低钾型周期性瘫痪1. 1 家族性低钾型周期性瘫痪1863 年Cavare 首先描述hypoKPP, 1885 年Goldflam 认为hypoKPP 与遗传有关,故又称为家族性低钾型周期性瘫痪( familial hypokalemic period2 ic paralysis, FhypoKPP) ,我国以散发性hypoKPP 为多见。

1. 1. 1 与hypoKPP 相关的突变基因FhypoKPP 呈常染色体显性遗传,男性100%外显,女性外显率下降。

70%病例的基础缺陷是编码骨骼肌L2型电压门控钙通道α1亚单位( calcium channel α1 subunit, CACNA1S) 基因发生突变, 定位于染色体1q31232 。

CACNA1S基因错义突变可导致钙通道α1 亚单位结构域ⅣS4片段位点1239 上带正电的精氨酸(Arg) 被弱阳性的组氨酸( His) 或不带电荷的甘氨酸( Gly) 替代(Arg1239His/ G1y) , 也可导致钙通道α1亚单位结构域IIS4 片段位点528 上的Arg被His或Gly 替代(Arg528His/ G1y) ; 其中以Arg1239His 和Arg528His 突变常见,Arg1239His 突变较Arg528His 突变首次发病年龄更早且发作时血清钾水平更低。

为确保企业安全生产的长期稳定，降低事故发生概率，提高员工安全意识，特制定本安全长周期型管理制度。

本制度旨在通过系统性的安全管理措施，实现企业安全生产的长周期运行。

二、组织机构与职责1. 安全生产委员会：负责企业安全生产工作的统筹规划、决策和监督。

2. 安全生产部：负责企业安全生产的具体实施、监督和检查。

3. 各部门、车间、班组：负责本部门、本车间、本班组的安全生产管理工作。

三、制度内容1. 安全生产目标（1）实现安全生产零事故；（2）降低事故发生率，确保企业安全生产的长周期运行；（3）提高员工安全意识，培养良好的安全习惯。

2. 安全生产责任制（1）各级领导要高度重视安全生产工作，认真履行安全生产责任制；（2）各部门、车间、班组要明确安全生产责任人，落实安全生产责任；（3）员工要遵守安全生产规章制度，履行安全生产义务。

3. 安全教育培训（1）定期开展安全教育培训，提高员工安全意识和安全技能；（2）对新入职员工进行岗前安全教育培训，确保其具备必要的安全知识和技能；（3）对特种作业人员进行专项安全教育培训，提高其操作技能和安全意识。

4. 安全检查与隐患排查（1）定期开展安全检查，确保安全生产设施设备完好；（2）建立隐患排查治理制度，及时发现和消除安全隐患；（3）对重大安全隐患实行挂牌督办，确保整改到位。

5. 应急管理与救援（1）建立健全应急预案，提高应急处置能力；（2）定期开展应急演练，提高员工应对突发事件的能力；（3）加强应急救援队伍建设，提高应急救援水平。

6. 安全生产考核与奖惩（1）建立安全生产考核制度，对各部门、车间、班组及员工进行考核；（2）对安全生产先进典型进行表彰和奖励；（3）对安全生产责任事故进行严肃查处。

四、实施与监督1. 各部门、车间、班组应认真贯彻执行本制度，确保安全生产各项工作落到实处；2. 安全生产部应加强对本制度的宣传、培训和监督，确保制度有效执行；3. 企业领导应定期检查安全生产工作，对存在的问题及时整改。

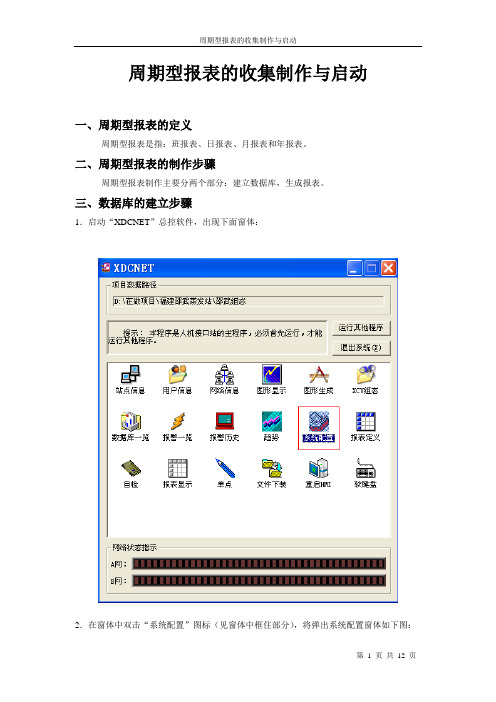
周期型报表的收集制作与启动一、周期型报表的定义周期型报表是指：班报表、日报表、月报表和年报表。

二、周期型报表的制作步骤周期型报表制作主要分两个部分：建立数据库，生成报表。

三、数据库的建立步骤1．启动“XDCNET”总控软件，出现下面窗体：2．在窗体中双击“系统配置”图标（见窗体中框住部分），将弹出系统配置窗体如下图：3．在窗体导航器列表中点击“周期报表收集配置”选项，出现周期报表配置窗体，如下图：你可以根据需要设置数据源和数据库名称。

数据源和数据库名可以相同，也可以直接使用系统默认的数据源和数据库名。

如：将“TabData”作为名称。

4．点击“创建Access数据库”按钮，在你的项目路径下就创建了一个数据源为“TabData”，数据库名为“TabData”的数据库，并出现一个如图所示的数据库文件图标：5．配置数据源数据。

点击“收集测点”按钮，弹出报表收集测点选择窗体：根据所需收集数据的类型（Ax或Dx）和收集属性，在“选择测点”的列表中点中报表所需的测点（如表中P802it测点），点击添加按钮“<<”，则测点P802it就追加到“测点收集”列表中。

6．保存周期报表测点配置。

当所有需要收集的测点都添加到“收集测点”列表中以后，点击“保存”按钮，所有需要收集的测点就被保存到数据库中了。

7．创建数据源。

打开“控制面板”→双击“管理工具”图标→双击“数据源(ODBC)”图标，这时出现如图所示的“数据源管理”窗体：8．在“数据源管理”窗体中点击“添加”按钮，弹出“创建数据源”窗体：在“创建数据源”窗体中选择“Micosoft Access Driver（*.mdb）”驱动程序选项，点击“完成”按钮，弹出如下对话窗体：9．在窗体中“数据源名”内填写我们的数据源名字“TabData”点击“选择”按钮，弹出以下窗体：10．在以上窗体中找到你的数据库“TabData.mdb”所在的项目路径，找到后将出现窗体变为如下显示：11．填写好数据库名“TabData.mdb”，点击“确定”按钮，出现以下窗体：12．继续点击“确定”按钮，出现以下窗体：这时“数据源管理器”中便增加了一项名为“TabData”的数据源。

理学硕士学位论文几类微分方程的概周期型解的存在性和唯一性肖嘉慧哈尔滨理工大学2011年3月国内图书分类号：O177.9理学硕士学位论文几类微分方程的概周期型解的存在性和唯一性硕士研究生：肖嘉慧导师：姚慧丽申请学位级别：理学硕士学科、专业：基础数学所在单位：应用科学学院答辩日期：2011年3月授予学位单位：哈尔滨理工大学Classified Index: O177.9Dissertation for the Master Degree in ScienceThe Existence and Uniqueness of Almost Periodic Type Solutions for Several Classes of DifferentialEquationsCandidate：Xiao JiahuiSupervisor：Yao HuiliAcademic Degree Applied for：Master of Natural Science Specialty：Fundamental MathematicsDate of Oral Examination：March, 2011University：Harbin University of Scienceand Technology哈尔滨理工大学硕士学位论文原创性声明本人郑重声明：此处所提交的硕士学位论文《几类微分方程的概周期型解的存在性和唯一性》，是本人在导师指导下，在哈尔滨理工大学攻读硕士学位期间独立进行研究工作所取得的成果。

据本人所知，论文中除已注明部分外不包含他人已发表或撰写过的研究成果。

对本文研究工作做出贡献的个人和集体，均已在文中以明确方式注明。

本声明的法律结果将完全由本人承担。

作者签名： 日期： 年 月 日哈尔滨理工大学硕士学位论文使用授权书《几类微分方程的概周期型解的存在性和唯一性》系本人在哈尔滨理工大学攻读硕士学位期间在导师指导下完成的硕士学位论文。

一、制度目标1. 建立健全安全管理体系，实现安全管理规范化、标准化。

2. 提高员工安全意识，培养安全文化，营造良好的安全生产氛围。

3. 预防和减少安全事故的发生，保障员工生命财产安全。

二、制度内容1. 安全生产责任制（1）明确各级领导、各部门、各岗位的安全职责，落实安全生产责任制。

（2）建立健全安全生产责任追究制度，对安全生产事故责任人进行严肃处理。

2. 安全教育培训（1）定期组织员工进行安全教育培训，提高员工安全意识和技能。

（2）对新员工进行岗前安全培训，确保其具备必要的安全知识和技能。

（3）开展安全生产知识竞赛、安全技能比武等活动，增强员工安全意识。

3. 安全检查与隐患排查（1）定期开展安全生产大检查，及时发现和消除安全隐患。

（2）建立健全安全隐患排查治理制度，对排查出的隐患进行分类、分级、限时整改。

（3）加强对重点部位、关键环节的安全检查，确保安全生产。

4. 安全生产设备管理（1）加强安全生产设备的管理和维护，确保设备安全运行。

（2）定期对安全生产设备进行检验、检测，发现异常情况立即停机检修。

（3）对老旧、损坏的安全生产设备进行淘汰，确保安全生产。

5. 应急管理与救援（1）制定应急预案，明确应急组织、应急程序、应急措施等。

（2）定期组织应急演练，提高员工应急处置能力。

（3）建立应急救援队伍，确保事故发生时能够迅速有效地进行救援。

6. 安全生产信息报送与处理（1）建立健全安全生产信息报送制度，确保事故信息及时、准确、完整地报送。

（2）对事故信息进行分类、分级，及时进行处理。

（3）对事故原因进行深入分析，制定整改措施，防止类似事故再次发生。

三、制度执行与监督1. 各级领导要高度重视安全生产工作，认真履行安全职责。

2. 安全管理部门要加强对安全全周期型管理制度的执行与监督，确保制度落实到位。

3. 员工要自觉遵守安全全周期型管理制度，积极参与安全生产活动。

4. 对违反安全全周期型管理制度的行为，要严肃处理，确保制度权威。

中考数学专题复习找规律问题之周期型模型学校:___________姓名：___________班级：___________考号：___________评卷人得分一、单选题1．如图，一个机器人从坐标原点O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2点，再向正西方向走9米到达A3点，再向正南方向走12米到达A4点，再向正东方向走15米到达A5点，……．按此规律走下去，当机器人走到A7点时，它的位置可表示为（）（单位长度为1米）A．（-21，18）B．（9，12）C．（-12，12）D．（-21，12）2．如图所示，直线3333y x=+与y轴相交于点D，点A1在直线3333y x=+上，点B1在x轴，且∆OA1B1是等边三角形，记作第一个等边三角形；然后过B1作B1A2∥OA1与直线3333y x=+相交于点A2，点B2在x轴上，再以B1A2为边作等边三角形A2B2B1，记作第二个等边三角形；同样过B2作B2A3∥OA1与直线3333y x=+相交于点A3，点B3在x轴上，再以B2A3为边作等边三角形A3B3B2，记作第三个等边三角形；∥依此类推，则第n个等边三角形的顶点A纵坐标为（）A．1n-B．2n-C．1n-3⨯D．2n-3⨯3．下表中的数字是按一定规律填写的，则a b+的值是（）1235813a34⋯⋯2358132134b⋯⋯A．55B．66C．76D．1104．如图，下列图形都是由几个黑色和白色的正方形按一定规律组成，图∥中有2个黑色正方形，图∥中有5个黑色正方形，图∥中有8个黑色正方形，图∥中有11个黑色正方形，…，依此规律，图n中黑色正方形的个数是（）A．2n B．3n C．21n-D．31n-5．在下面各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（）A．128B．120C．112D．1026．下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第∥个图形中一共有4个小圆圈，第∥个图形中一共有10个小圆圈，第∥个图形中一共有19个小圆圈，…，按此规律排列，则第∥个图形中小圆圈的个数为（）A．31B．46C．64D．857．观察下列三行数：第一行：2、4、6、8、10、12……第二行：3、5、7、9、11、13……第三行：1、4、9、16、25、36……设x、y、z分别为第一、第二、第三行的第100个数，则22x y z-+的值为（）A．9999B．10001C．20199D．200018．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第一次从原点O运动到点1(1,1)P，第二次运动到点2(2,0)P，第三次运动到3(3,2)P-，⋯，按这样的运动规律，第2021次运动后，动点2021P的纵坐标是（）A．1B．2C．2-D．0评卷人得分二、填空题9．根据表中数字的规律，则代数式()x y x--的值是__．2468512177237228x y10．一列数1a，2a，3a，…，na满足11a=-，2111aa=-，3211aa=-，…，111nnaa-=-，则2a=__________；1232020a a a a++++=__________，1232020a a a a⨯⨯⨯⨯=__________．11．如图，1条直线将平面分成两个部分，2条直线最多可以将平面分成4个部分，3条直线最多可以将平面分成7个部分，4条直线最多可以将平面分成11个部分．现有n 条直线最多可以将平面分成2017个部分，则n的值为______．12．如图，在平面直角坐标系中，等腰直角三角形1OAA的直角边OA在x轴上，点1A 在第一象限，且1OA=，以点1A为直角顶点，1OA为一直角边作等腰直角三角形12OA A，再以点2A为直角顶点，2OA为直角边作等腰直角三角形23OA A⋯依此规律，则点2021A的坐标是__．13．如图，在平面直角坐标系中，等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上，且OA1＝A1A2＝1，以OA2为直角边作第二个等腰直角三角形OA2A3，以OA3为直角边作第三个等限直角三角OA3A4，…，依此规律，得到等腰直角三角形OA2020A2021，则点A2021的坐标为_____________．14．用棱长相同的小正方体摆成如图所示的几何体，第1层有1个正方体，第2层有3个正方体，第3层有6个正方体，按图中摆放的方法类推，第20层有_________个正方体15．如图，“海春书局”把WIFI密码做成了数学题．小红在海春书局看书时，思索了一会儿，输入密码，顺利地连接到了“海春书局”的网络，那么她输入的密码是__________．16．观察下面一列单项式：2345,2,4,8,16,x x x x x---⋅⋅⋅，根据你发现的规律写出第100个单项式_______．17．定义一种新运算：“⊗”观察下列各式：232339⊗=⨯+=()313318⊗-=⨯-=4443416⊗=⨯+= ()5353312⊗-=⨯-=，则a b⊗=______（用含a、b的代数式表示）18．如图，直线l为3y x=，过点1(1,0)A作11A B x⊥轴，与直线l交于点1B，以原点O 为圆心，1OB长为半径画圆弧交x轴于点2A；再作22A B x⊥轴，交直线l于点2B，以原点O为圆心，2OB长为半径画圆弧交x轴于点3A；⋯⋯，按此作法进行下去，则点nA 的坐标为__．19．观察一列数：12，34-，56，78-，⋯，按此规律，这一列数的第2022个数为__．20．将黑色圆点按如图所示的规律进行排列：图中黑色圆点的个数依次为：1，3，6，10，……，将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据，则新数据中的第10个数为______，第55个数为______．21．如图，矩形OABC 在平面直角坐标系中，点B 的坐标是（﹣2，1），过点A 作1AB OB ∥，交x 轴于B 1，过点B 1作A 1B 1∥x 轴交直线AC 于A 1，过点A 1作直线121A B AB ∥，交x 轴于B 2，过点B 2作A 2B 2∥x 轴交直线AC 于A 2，……，则A 2021的坐标是 __________________．22．法国著名数学家笛卡尔在蜘蛛戒网的启示下创建了数对与直角坐标系．如图，一只蜘蛛先以O 为起点结六条线OA ，OB ，OC ，OD ，OE ，OF 后，再从线OA 上某点开始按逆时针方向，依次在OA ，OB ，OC ，OD ，OE ，OF ，OA ，OB ，OC ，OD ，…，上结网，若将各线上的结点依次记为1，2，3，4，5，6，7，8，…，那么，第2021个结点在线________上．23．在庆祝建党“100周年”的活动中，某同学用围棋棋子按照某种规律摆成如图所示的“100”字样、如图∥有11个棋子，图∥有16个棋子，按这种规律，则第20个“100”字样的棋子个数是_____．24．一组数1，3，5，7，9，…，用含有n的式子表示这组数中的第n个数：_____．25．已知21＝2，22＝4，23＝8，24＝16，25＝32，26＝64……则22020﹣22019的个位数字是____．26．观察一列有规律的单项式：x，3x2，5x3，7x4，9x5…，它的第n个单项式是______．27．如图，是由一些小圆点组成的图形，第1个图形是由7个小圆点组成，第2个图形是由13个小圆点组成，第3个图形是由19个小圆点组成，…，按照这样的规律，由181个小圆点组成的是第_____个图形．评卷人得分三、解答题28．规律探究：15×15＝1×2×100+25＝225；25×25＝2×3×100+25＝625；35×35＝3×4×100+25＝1225；(1)第4行为；(2)用含n的式子表示规律并证明．29．若干个有规律的数，排列如下：试探究：(1)第2012个数在第几行？这个数是多少？（每行的数都是从左往右数）(2)写出第n行第k个数的代数式；（用含n，k的式子表示）(3)求第2012个数所在行的所有数之和S．30．将连续的奇数1，3，5，7，9，……排成如图所示的数表．(1)写出数表所表示的规律；（至少写出4个）(2)若将方框上下左右移动，可框住另外的9个数．若9个数之和等于297，求方框里中间数是多少？参考答案：1．C 【解析】 【分析】根据题意知：13OA =，1232A A =⨯ ，2333A A =⨯，可得规律：13n n A A n -=，根据规律可以得到A 7的横坐标和纵坐标. 【详解】解：根据题意，得13OA =，1232A A =⨯ ，2333A A =⨯，可得规律：13n n A A n -=，当机器人走到A 7点时，其横坐标为3-9+15-21=-12；纵坐标为6-12+18=12， 故点A7坐标为（-12，12） 故选择：C . 【点睛】本题考查点的坐标变化，根据题意确定横坐标和纵坐标的变化规律是解决问题的关键. 2．D 【解析】 【分析】可设直线与x 轴相交于C 点．通过求交点C 、D 的坐标可求∥DCO =30°．根据题意得△COA 1、△CB 1A 2、△CB 2A 3…都是等腰三角形，且腰长变化有规律．在正三角形中求高即可得解． 【详解】解：设直线与x 轴相交于C 点．令x =0，则y =33；令y =0，则x =-1． ∥OC =1，OD =33．∥tan∥DCO =33OD OC =， ∥∥DCO =30°． ∥∥OA 1B 1是正三角形， ∥∥A 1OB 1=60°． ∥∥CA 1O =∥A 1CO =30°， ∥OA 1=OC =1．∥第一个正三角形的高=1×sin60°=32； 同理可得：第二个正三角形的边长=1+1=2，高=2×sin60°=3； 第三个正三角形的边长=1+1+2=4，高=4×sin60°=23； 第四个正三角形的边长=1+1+2+4=8，高=8×sin60°=43； …第n 个正三角形的边长=2n -1，高=2n -2×3． ∥第n 个正三角形顶点An 的纵坐标是2n -2×3． 故选：D ． 【点睛】本题是一次函数综合题型，主要考查了等腰三角形的性质，一次函数图象上点的坐标特征． 3．C 【解析】 【分析】根据表格可以得到每行数字的排列规律，然后算出a 、b 的值，最后代入求出a +b 的值，即可判断选项． 【详解】观察可得：第一行从第三个数开始，每个数都等于前面两个数的和，第二行的规律与第一行相同．∥81321a =+=，213455b =+= ∥215576a b +=+= 故选C ． 【点睛】此题为数字型规律探索问题，解题关键是发现数字的变化规律．4．D【解析】【分析】观察图中黑色正方形的个数，1n =对应的个数为231=-；2n =对应的个数为561231=-=⨯-；3n =对应的个数为891331=-=⨯-；4n =对应的个数为11121341=-=⨯-；进而可推导出一般性规律．【详解】解：图∥中有231131=-=⨯-个黑色正方形；图∥中有561231=-=⨯-个黑色正方形；图∥中有891331=-=⨯-个黑色正方形；图∥中有11121341=-=⨯-个黑色正方形；依此规律，图n 中有31n -个黑色正方形故选D ．【点睛】本题考查了图形规律的探究．解题的关键在于推导规律．5．A【解析】【分析】观察四个正方形，可得到规律，每个正方形中左上角的数为连续的偶数，右上角的数比左上角的数大3，左下角的数是右上角的数的相反数，右下角的数=右上角的数与左下角的数的绝对值的乘积+左上角的数-1，依此计算即可求解．【详解】解：观察四个正方形，可得到规律：每个正方形中左上角的数为从0开始的连续的偶数，右上角的数比左上角的数大3，左下角的数是右上角的数的相反数，右下角的数=右上角的数与左下角的数的绝对值的乘积+左上角的数-1，∥m =11×11-+8-1=128，故选：A ．【点睛】本题考查了数字的变化规律，能够根据所给表格，发现数字之间的规律是解题的关键． 6．C【解析】【分析】先分别观察给出的四个图形中，小圆圈的个数，找到规律：第n 个图形小圆圈个数为：(1)(2)2n n +++n 2，即可求解本题． 【详解】解：通过观察，得到小圆圈的个数分别是：第∥图形小圆圈个数为：(12)22+⨯+12＝4， 第∥个图形小圆圈个数为：(13)32+⨯+22＝10， 第∥个图形小圆圈个数为：(14)42+⨯+32＝19， 第∥个图形小圆圈个数为：(15)52+⨯+42＝31， …， 所以第n 个图形小圆圈个数为：(1)(2)2n n +++n 2， 第∥个图形小圆圈个数为(61)(62)2+++62＝64； 故选：C ．【点睛】 本题考查的是图形与规律，从图形中读取我们需要的数据，并进行规律的探寻是解题的关键．7．C【解析】【分析】总结第∥，第∥，第∥行的变化规律，分别求出x ，y ，z 的值即可计算．【详解】解：观察第∥行：2、4、6、8、10、12、…∥第100个数为100×2＝200，即x ＝200，观察第∥行：3、5、7、9、11、13、…∥第100个数为100×2+1＝201，观察第∥行：1、4、9、16、25、36、…∥第100个数是1002＝10000，即x ＝200、y ＝201、z ＝10000，∥2x ﹣y +2z ＝20199，故选：C ．【点睛】本题主要考查的是数字的变化规律，总结归纳出变化规律是解题的关键．8．B【解析】【分析】观察图象，结合第一次从原点O 运动到点1(1,1)P ，第二次运动到点2(2,0)P ，第三次运动到3(3,2)P -，⋯，运动后的点的坐标特点，分别得出点P 运动的横坐标和纵坐标的规律，再根据循环规律可得答案．【详解】解：观察图象，结合第一次从原点O 运动到点1(1,1)P ，第二次运动到点2(2,0)P ，第三次运动到3(3,2)P -，⋯，运动后的点的坐标特点，由图象可得纵坐标每6运动组成一个循环：1(1,1)P ，2(2,0)P ，3(3,2)P -，4(4,0)P ，()55,2P ，()66,0P ⋯202163365÷=⋯，∴经过第2021次运动后，动点P 的坐标与5P 坐标相同，为(5,2)，故经过第2021次运动后，动点P 的纵坐标是2．故选：B ．【点睛】本题考查了规律型点的坐标，数形结合并从图象中发现循环规律是解题的关键． 9．-398【解析】【分析】根据图中的规律可得8(1)x y +=，求出x 与y 可得答案．【详解】解：2521=+，12522=⨯+；21741=+，721744=⨯+；23761=+，2283766=⨯+；28165x ∴=+=，6588528y =⨯+=，()65(52865)398x y x --=--=-．故答案为：398-．【点睛】考查了规律型：数字的变化类，关键是由图形得到第二行左边的数比第一行数的平方大1，第二行右边的数=第二行左边的数×第一行的数+第一行的数．10． 12 201721 【解析】【分析】根据题意，可以求出前几项的值，从而发现这列数的变化特点，从而可以求得所求式子的值.【详解】解：由题意可得，当11a =-时，2111111(1)2a a ===---， 321121112a a ===--，43111112a a ===---， …∥2020÷3=673…1，∥123202012017(12)673(1)22a a a a ++++=-++⨯+-=， 67312320201[(1)2](1)12a a a a ⨯⨯⨯⨯=-⨯⨯⨯-=. 故答案为：12，20172， 1. 【点睛】 本题考查了数字的变化类，明确题意，发现数字的变化特点是解题的关键.11．63【解析】【分析】n 条直线最多可将平面分成()11123112S n n n =+++⋯+=++，依此可得等量关系：n 条直线最多可将平面分成2017个部分，列出方程求解即可．【详解】解：依题意有：()11120172n n ++=， 整理得，240320n n +-=，所以()()64630n n +-=，解得164(n =-不合题意舍去)，263n =．答：n 的值为63，故答案为：63．【点睛】本题考查了规律型：图形的变化类，解一元二次方程，得到分成的最多平面数的规律是解决本题的难点．12．()101010102,2--【解析】【分析】首先根据图形的变化得出OAn 的变化规律，判断出点A 2021的所在象限，再求出其坐标即可．【详解】解：由已知，点A 每次旋转转动45°，则转动一周需转动360845︒=︒(次)， 而22111=2OA =+， ()()()222222=2=2OA =+， ()322322=22=2OA =+，…，()=2nn OA (n 为正整数)， 即每次转动点A 到原点的距离变为转动前的2倍，202125285=⨯+，∴点2021A 的在第三象限的角平分线上，∥20212021(2)OA =，设点A 2021(x ,x )，其中x <0，∥()22021222x x ⎡⎤+=⎢⎥⎣⎦， ∥2202122x =，∥220202x =，∥10102x =-，∥点A 2021的坐标是()101010102,2--【点睛】本题是平面直角坐标系下的规律探究题，除了研究动点变化的相关数据规律，还应该注意各个象限内点的坐标符号．13．（0，﹣21010）【解析】【分析】根据题意，利用等腰直角三角形的性质，勾股定理，坐标系中点与象限的关系，确定一部分点的坐标，从坐标中寻找规律，再按规律计算即可．【详解】解：∥等腰直角三角形OA 1A 2的直角边OA 1在y 轴的正半轴上，且OA 1＝A 1A 2＝1， ∥A 1（0，1），A 2（1，1）；根据勾股定理得：OA 2＝2211=2+，∥OA 3＝2OA 2＝2，∥A 3（2，0），A 4（2，﹣2），根据勾股定理得：OA 4＝2222=22+，∥OA 5＝2OA 4＝4，∥A 5（0，﹣4），∥A 6（﹣4，﹣4），根据勾股定理得：OA 6＝2OA 5＝42，∥OA 7＝2OA 6＝8，∥A 7（﹣8，0），A 8（﹣8，﹣8），根据勾股定理得：OA 8＝2OA 7＝82，∥OA 9＝2OA 8＝16，∥A 9（0，16），∥坐标的循环节为8，∥2021÷8＝252…5，∥A 2021的坐标与A 5（0，﹣4）的规律相同，∥﹣4＝﹣22＝5122--，∥A 2021的纵坐标为2021122--＝﹣21010，∥A 2021的坐标为（0，﹣21010），故答案为：（0，﹣21010）．【点睛】本题考查了坐标系中坐标的变化规律，等腰直角三角形的性质，勾股定理，坐标的特点熟练掌握等腰直角三角形的性质，勾股定理灵活运用一般与特殊的思想，构造幂运算是解题的关键．14．210【解析】【分析】根据层数与正方体个数推导一般规律，第n 层有()1231n n +++⋅⋅⋅+-+个正方体，代值计算求解即可．【详解】解：第1层有1个正方体；第2层有123+=个正方体；第3层有12+36+=个正方体；依次类推，可知第n 层有()1231n n +++⋅⋅⋅+-+=(1)2n n +个正方体； ∥第20层有123192200(2021201)+++⋅⋅⋅++=⨯+=个正方体 故答案为：210．【点睛】本题考查了图形下的数字类规律的探究．解题的关键在于总结一般规律．15．167288【解析】【分析】根据前面三个等式，寻找规律解决问题．【详解】解：由三个等式，得到规律： 635⊕⊗＝301545，可知：6×5 3×5 （6＋3）×5，276⊕⊗＝124254，可知：2×6 7×6 （2＋7）×6，834⊕⊗＝321244，可知：8×4 3×4 （8＋3）×4，∥298⊕⊗＝2×8 9×8 （2＋9）×8=167288.故答案为：167288．【点睛】本题考查数字的变化规律，能够根据所给的式子，探索出数字之间的联系是解题的关键． 16．991002x【解析】【分析】根据符号的规律：n 为奇数时，单项式为负号，n 为偶数时，单项式为正号；系数的绝对值的规律：第n 个对应的单项式的系数的绝对值是2n −1；指数的规律：第n 个对应的单项式的x 指数是n ，据此解答即可．解：根据题干单项式，可知：n为奇数时，单项式为负号，n为偶数时，符号为正号，所以第100个单项式为正号；系数的绝对值的规律：第n个对应的单项式的系数的绝对值是2n−1，所以第100个单项式对应的系数的绝对值是299；指数的规律：第n个对应的单项式的x指数是n，所以第100个单项式对应的x指数是100，故第100个单项式是299x100．故答案为：299x100．【点睛】本题考查了单项式表示规律，确定单项式的系数和次数时，把一个单项式分解成数字因数和字母因式的积，是找准单项式的系数和次数的关键．分别找出单项式的系数和次数的规律也是解决此类问题的关键．17．3a+b【解析】【分析】根据所给算式总结规律解答即可．【详解】⊗=⨯+=，解：∥232339()⊗-=⨯-=，313318⊗=⨯+=，4443416()⊗-=⨯-=，5353312∥a b⊗=3a+b，故答案为：3a+b．【点睛】本题考查了规律型-数字的变化类，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．n-18．1(2,0)【解析】依据直线l 为3y x =，点1(1,0)A ，11A B x ⊥轴，可得2(2,0)A ，同理可得，3(4,0)A ，4(8,0)A ，…，依据此规律可得点n A 的坐标为()12,0n -．【详解】解：直线l 为3y x =，点1(1,0)A ，11A B x ⊥轴，∴当1x =时，3y =，即1(1,3)B ，11tan 3A OB ∴∠=，1160AOB ∴∠=︒，1130A B O ∠=︒，1122OB OA ∴==，以原点O 为圆心，1OB 长为半径画圆弧交x 轴于点2A ，2(2,0)A ∴，同理可得，3(4,0)A ，4(8,0)A ，⋯，∴点n A 的坐标为1(2,0)n -，故答案为：1(2,0)n -．【点睛】本题主要考查了一次函数图象上点的坐标特征，以及点的坐标的规律性，解题时注意：直线上任意一点的坐标都满足函数关系式()0y kx b k =+≠，在找规律时，A 点的横坐标的指数与A 所处的位数容易搞错，应注意．19．40434044- 【解析】【分析】根据前几个数的变化规律得到第n 个数为121(1)()2n n n+--，据此即可解答． 【详解】解：观察一列数：12，34-，56，78-，⋯，可得变化规律为：第n 个数为121(1)()2n n n+--， ∥第2022个数是40434044-， 故答案为：40434044-． 【点睛】 本题考查数字类规律探究，仔细观察，找到数字变化规律是解答的关键．20． 120 3486【解析】【分析】首先得到前n 个图形中每个图形中的黑色圆点的个数，得到第n 个图形中的黑色圆点的个数为(1)2n n +，再判断其中能被3整除的数，得到每3个数中，都有2个能被3整除，再计算出第10和55个能被3整除的数所在组为原数列中的个数，代入计算即可．【详解】第∥个图形中的黑色圆点的个数为：1，第∥个图形中的黑色圆点的个数为：2(21)32⨯+=， 第∥个图形中的黑色圆点的个数为：3(31)62⨯+=， 第∥个图形中的黑色圆点的个数为：4(41)102⨯+=， ……第n 个图形中的黑色圆点的个数为(1)2n n ⨯+， ∥这列数为1，3，6，10，15，21，28，36，45，55，66，78，91，...，∥其中每3个数中，都有2个能被3整除，10÷2=5（组），∥第10个能被3整除的数为原数列中的个数为5×3=15（个），∥15(151)2⨯+=120， ∥55÷2=27（组）……1，∥第55个能被3整除的数为原数列中的个数为27×3+2=83（个）∥83(831)2⨯+=3486， 故答案为：120，3486【点睛】此题考查了图形类的规律变化，通过归纳与总结，得到其中的规律是解题关键． 21．（22020﹣2，22021）【解析】【分析】根据平行四边形的性质及判定可得四边形AB 1OB 是平行四边形，从而推出B 1O ＝CO ＝AB ＝2，再根据直线之间的垂直和平行关系以及相似三角形的判定定理得到∥AOC ∥∥A 1B 1C ，∥AOB 1∥∥A 1B 1B 2，∥A 1B 1C ∥∥A 2B 2C ，利用相似三角形的性质解得A 1B 1＝2，B 1B 2＝4，A 2B 2＝4，再根据点的坐标特征寻找出规律，最后运用即可解答．【详解】解：∥四边形OABC 是矩形∥AB ＝CO ，且AB CO ∥，又∥1AB OB ∥，∥四边形AB 1OB 是平行四边形，∥B 1O ＝AB ，∥点B 的坐标是（﹣2，1），∥B 1O ＝CO ＝AB ＝2，∥A 1B 1∥x 轴，∥11A B AO ∥，∥∥AOC ∥∥A 1B 1C ，∥111AO CO A B CB =，即11124A B =，解得A 1B 1＝2， ∥点A 1坐标为（22﹣2，2），又∥11A B AO ∥，∥∥AOB 1∥∥A 1B 1B 2，∥11211OB AO B B A B =＝12， ∥B 1B 2＝4，∥A 2B 2∥x 轴，∥2211A B A B ∥，∥∥A 1B 1C ∥∥A 2B 2C ，∥111222A B CB A B CB ＝48， ∥A 2B 2＝4，∥点A 2（23﹣2，22），以此类推...，A 2021的坐标为（22020﹣2，22021），故答案为：（22020﹣2，22021）．【点睛】本题主要考查了矩形的性质、平行四边形的性质与判定、相似三角形的判定与性质以及坐标规律等知识点，根据坐标特征、总结坐标规律成为解答本题的关键．22．OE【解析】【分析】根据点在射线上的排布顺序发现规律“射线上的数字以6为周期循环”，依此规律即可得出结论．【详解】解：根据数的排布发现：1在OA 上，2在OB 上，3在OC 上，4在OD 上，5在OE 上，6在OF 上，7在OA 上，…，射线上的数字以6为周期循环，∥2021÷6=336……5，∥2021与5在同一条射线上，即2021在射线OE 上．故答案为：OE ．【点睛】本题考查了规律型中的数字的变化类，解题的关键是找出规律“射线上的数字以6为周期循环”．本题属于基础题，难度不大，解决该题型题目时，根据射线上数字的排布找出规律是关键．23．106【解析】找出规律：“1”的规律是：最先3个棋子，以后每次加1，第20个“100”中的“1”有：3+19=22（个）棋子；“0”的规律是：最先4个棋子，以后每次加2个，第20个“100”中的“0”有：4+19×2=42（个）棋子，从而可求得总的棋子数．【详解】由题意得：（3+19）+2×（4+19×2）=106（个）故答案为：106【点睛】本题考查了图形的规律，找出规律是本题的关键．24．21n -##-1+2n【解析】【分析】根据题意得：第1个数为1，第2个数为3221=⨯-，第3个数为5231=⨯-，第4个数为7241=⨯-，第5个数为9251=⨯-，……，由此发现规律，即可求解．【详解】解：根据题意得：第1个数为1，第2个数为3221=⨯-，第3个数为5231=⨯-，第4个数为7241=⨯-，第5个数为9251=⨯-，……，由此发现，第n 个数为21n -．故答案为：21n -【点睛】本题主要考查了数字类规律题，明确题意，准确得到规律是解题的关键．25．8【解析】【分析】通过观察可知每运算四次个位数循环一次，由此可知22020﹣22019的个位数与23的尾数相同．解：∵21＝2，22＝4，23＝8，24＝16，25＝32，26＝64，∴每运算四次个位数循环一次，∵22020﹣22019＝22019（2﹣1）＝22019，∵2019÷4＝504…3，∴22020﹣22019的个位数与23的尾数相同，∴22020﹣22019的个位数字是8，故答案为：8．【点睛】本题考查数字的变化规律，能够通过所给数对个位数的特点，确定个位数的循环规律是解题的关键．26．()21nn x - 【解析】【分析】根据单项式的系数与次数的变化，探索个数与系数、次数的关系的一般性规律即可．【详解】 解：第1个单项式x 中，系数为1，次数为1；第2个单项式23x 中，系数为3，341221=-=⨯-，次数为2；第3个单项式35x 中，系数为5，561321=-=⨯-，次数为3；第4个单项式47x 中，系数为7，781421=-=⨯-，次数为4；第5个单项式59x 中，系数为9，9101521=-=⨯-，次数为5；依次类推，可知第n 个单项式的系数为21n -，次数为n ，单项式为()21nn x - 故答案为：()21nn x -． 【点睛】本题考查了单项式，数字规律的探究．解题的关键在于总结一般性规律．27．30【解析】【分析】首先分析题意，找到规律，并进行推导得出答案．解：观察分析可得：第1个图形有7个小圆点，7＝6+1，第2个图形有13个小圆点，13＝6×2+1，第3个图形有19个小圆点，19＝6×3+1，…，第n个图形小圆点的个数为6n+1，所以6n+1＝181，解得：n＝30．故答案为：30【点睛】本题主要考查了图形类规律题，明确题意，准确得到规律是解题的关键．28．(1)45×45=4×5×100+25=2025(2)（10n+5）2=100n（n+1）+25，证明见解析【解析】【分析】（1）从给出的数据分析得，这些得出的结果最后两位都为25，百位以上2=1×2，6=2×3，12=3×4，…，依此类推得出规律：百位为n×（n+1）．（2）直接利用已知数据变化规律进而得出符合题意的公式．(1)解：根据数据可分析出规律，个位数位5的整数的平方运算结果的最后2位一定是25，百位以上结果则为n×（n+1），∥第4个算式应为45×45=4×5×100+25=2025．(2)规律：（10n+5）2=100n（n+1）+25，证明：∥左边=100n2+100n+25，右边=100n2+100n+25，∥左边=右边，∥（10n+5）2=100n（n+1）+25．【点睛】本题考查规律型中的数字变化问题，本题的规律为个位数位5的整数的平方运算结果的最后2位一定是25，百位以上结果则为n×（n+1），难度一般．29．(1)第63行，这个数为358；(2)（﹣1）n+13k﹣1；(3)63312-．【解析】【分析】每一行的数的个数和行数都是相同的，奇数行的数字都是3n﹣1，偶数行的数字都是（﹣3）n﹣1，统一为（﹣1）n+13n﹣1；（1）设第2012个数在第n行，则1+2+3+…+n＝(1)2n n+，估算得出答案即可；（2）有以上分析直接写出即可；（3）写出第2012个数所在行的所有数，进一步求和即可．(1)解：∥每一行的数的个数和行数都是相同的，奇数行的数字都是3n﹣1，偶数行的数字都是（﹣3）n﹣1，设行数为n，数字个数为k，k=1+2+3+…+n＝(1)2n n+，当n=62时，62+2⨯（621）＝1953；当n=63时，63+2⨯（631）＝2016；∥62+2⨯（621）＝1953＜2012＜63+2⨯（631）＝2016，所以第2012个数在第63行，从左往右数第2012﹣1953＝59个，这个数为358；(2)解：由以上分析可直接写出为（﹣1）n+13k﹣1；(3)解：∥S＝1+3+32+ (362)∥3S＝3+32+…+362+363∥由∥﹣∥得2S＝363﹣1∥S ＝1+3+32+…+362＝63312- ． 【点睛】此题考查数字的变化规律，找出数字之间的联系，得出规律，解决问题．30．(1)见解析(2)方框里中间数是33【解析】【分析】（1）观察所给的数表即可得；（2）设方框里中间数为x ，则另外8个数为2x -，2x +，10x -，10x +，12x -，12x +，8x -，8x +，由题意得，221010121288297x x x x x x x x x -+-+-+++-+++-+++= 进行计算即可得．(1)解：规律有：∥第一列个位数都是1，∥每行只有5个奇数，∥每行相邻两个数的和是2的倍数，∥每列相邻的两个数相差10．(2)解：设方框里中间数为x ，则另外8个数为2x -，2x +，10x -，10x +，12x -，12x +，8x -，8x +，由题意得，221010121288297x x x x x x x x x -+-+-+++-+++-+++=9297x =，33x =，则方框里中间数是33．【点睛】本题考查了数字规律，一元一次方程，解题的关键是理解题意，掌握一元一次方程的应用．。