典型晶体晶胞结构
- 格式:doc
- 大小:554.50 KB
- 文档页数:2

§1-2 常见的晶体结构及其原胞、晶胞1) 简单晶体的简单立方(simple cubic, sc) 它所构成的晶格为布喇菲格子。
例如氧、硫固体。
基元为单一原子结构的晶体叫简单晶体。
其特点有: 三个基矢互相垂直(),重复间距相等,为a,亦称晶格常数。
其晶胞=原胞;体积= ;配位数(第一近邻数) =6。
(见图1-7)图1-7简单立方堆积与简单立方结构单元2) 简单晶体的体心立方( body-centered cubic, bcc ) , 例如,Li,K,Na,Rb,Cs,αFe,Cr,Mo,W,Ta,Ba等。
其特点有:晶胞基矢, 并且,其惯用原胞基矢由从一顶点指向另外三个体心点的矢量构成:(见图1-9 b)(1-2)其体积为;配位数=8;(见图1-8)图1-8体心立方堆积与体心立方结构单元图1-9简单立方晶胞(a)与体心立方晶胞、惯用原胞(b)3) 简单晶体的面心立方( face-centered cubic, fcc ) , 例如,Cu,Ag,Au,Ni,Pd,Pt,Ne, Ar, Xe, Rn, Ca, Sr, Al等。
晶胞基矢,并且每面中心有一格点, 其原胞基矢由从一顶点指向另外三个面心点的矢量构成(见图1-10 b):(1-3)其体积=;配位数=12。
,(见图1-10)图1-10面心立方结构(晶胞)(a)与面心立方惯用原胞(b)4) NaCl结构(Sodium Chloride structure),复式面心立方(互为fcc),配位数=6(图1-11 a)。
表1-1 NaCl结构晶体的常数5) CsCl结构(Cesuim Chloride structure),复式简单立方(互为sc),配位数=8(图1-11 b)。
表1-2 CsCl结构晶体的常数图1-11 NaCl结构和CsCl结构6) 金刚石结构(Diamond structure), 两套fcc格子相互沿对角线位移1/4处套合。
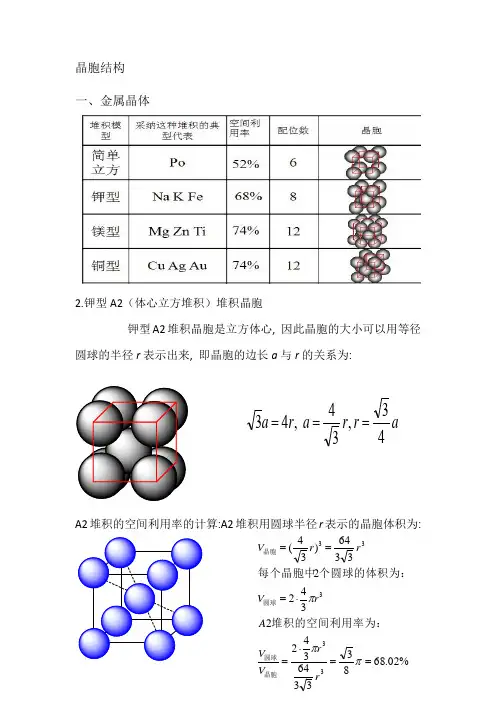
晶胞结构一、金属晶体2.钾型A2(体心立方堆积)堆积晶胞钾型A2堆积晶胞是立方体心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A2堆积的空间利用率的计算:A2堆积用圆球半径r 表示的晶胞体积为:ar r a r a 43,34 ,43===%02.68833364342234223364)34(33333==⋅=⋅===πππr r V V A rV rr V 晶胞圆球圆球晶胞堆积的空间利用率为:个圆球的体积为:每个晶胞中3.六方最密堆积(4)A1(面心立方最密堆积)A1是ABCABCABC······型式的堆积,从这种堆积中可以抽出一个立方面心点阵,因此这种堆积型式的最小单位是一个立方面心晶胞。
A1堆积晶胞是立方面心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A1堆积空间利用率的计算:A1堆积用圆球半径r 表示的晶胞体积为:(5)A4堆积形成晶胞A4堆积晶胞是立方面心点阵结构, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A4堆积的空间利用率的计算:A4堆积用圆球半径r 表示的晶胞体积为: ra r a 22 ,42==%05.742312163441344 4216)22(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为:个圆球的体积为:每个晶胞中ar r a r r a 83,38 ,8243===⨯=%01.34163335123484348 833512)38(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为:个圆球的体积为:每个晶胞中二、原子晶体1.金刚石立体网状结构,每个碳原子形成4个共价键,任意抽出2个共价键,每两个单键归两个六元环所有,而不是只归一个六元环所有(如图所示,红色的两个碳碳单键,可以构成蓝色和紫红色的两个六元环)。

三种晶胞结构的晶体空隙引言晶体是由元素或化合物按照一定规律排列形成的,它们在空间中形成了特定的结构,称为晶体结构。
晶体结构的基本单位是晶胞,而晶胞内的排列方式再决定了晶体的物理和化学性质。
在晶胞结构中,晶体空隙是指晶体中的一些位置没有被原子或离子占据,这些空隙对晶体的性质和应用具有重要影响。
本文将介绍三种晶胞结构中的晶体空隙。
1.面心立方结构的晶体空隙1.1描述面心立方结构是一种常见的晶体结构,其中原子或离子在晶格的每个顶点、每个面心和每个体心都存在。
在这种结构中,晶体空隙主要出现在八面体和四面体的中心,也可以出现在体心和面心位置上。
1.2形成原因在面心立方结构中,由于每个顶点周围有12个近邻原子或离子,导致晶体中的空隙较少。
而八面体和四面体的中心位置是由于晶格点的排列形成的。
这些空隙的形成主要是为了保持晶体结构的稳定性和平衡。
1.3物理性质面心立方结构的晶体空隙对物质的性质具有一定的影响。
首先,空隙使晶体的密度减小,因为没有原子或离子占据这些位置。
此外,晶体中的空隙也影响了晶体的热膨胀性能。
2.体心立方结构的晶体空隙2.1描述体心立方结构是另一种常见的晶体结构,其中晶格的每个顶点都存在原子或离子,而在晶胞的中心位置也存在一个原子或离子。
2.2形成原因在体心立方结构中,晶体空隙出现在八面体的中心。
这是由于晶格点排列的方式导致的。
相比面心立方结构,体心立方结构的空隙相对较少。
2.3物理性质体心立方结构的晶体空隙也会对物质的性质产生一定的影响。
研究发现,空隙的存在会改变晶体的热膨胀性能和导热性能,对材料的力学性能也有一定的影响。
3.立方密堆积结构的晶体空隙3.1描述立方密堆积结构是晶胞结构的一种,它是由最密堆积方式排列的晶格点组成的。
在这种结构中,每个晶胞的顶点位置都存在原子或离子。
3.2形成原因立方密堆积结构中的晶体空隙主要出现在六方环状空隙和四方环状空隙,这是由晶格点排列的方式所决定的。
3.3物理性质立方密堆积结构的晶体空隙对材料的性质有一定影响。

金属中常见的三种晶体结构
金属是人类理解和感知宇宙规律的基础,我们日常生活中实用性最好的材料就是金属。
而
金属的晶体结构是深入研究金属的重要方面,也是决定金属特性的基础之一。
因此,今天
我们就来讨论金属中常见的三种晶体结构:六方晶格、面心立方晶格和菱形晶格。
六方晶格是最常见的金属晶体结构形式,是对称分布最均匀、最节约空间的结构。
它内部
是由晶胞堆积构成,每个晶胞由六颗原子构成,其条形运动立方体形状形成六个晶面。
这
种晶体结构可以满足大多数金属原子的包裹,也是大多数金属表面及体内的晶体结构形式。
面心立方晶格结构是一种复杂的晶体结构,在它的晶胞内部分布着八颗原子,分布方式是
四个原子均匀的放置于晶胞的八个顶点,另外四颗原子均匀的放置于晶胞的六个棱面中间,这种特别的原子分布使晶粒有了更高的密度。
它是一种特殊的光学结构,通常在失去平衡的金属表面形成,并影响金属的光学性质。
菱形晶格结构是四颗原子布置而成的基本晶胞,菱形晶格的核心由四个六面体构成,每一
个六面体都可以由四个原子组成,因此在晶胞中有四颗原子存在。
这种晶体结构的优点是
比较均匀的原子分布,原子离聚力也更大,可以定义更长的晶格参数,可以表示物理和化
学性质。
总而言之,金属中常见的三种晶体结构就是六方晶格、面心立方晶格和菱形晶格,他们各有自身的特点,这些特点直接体现在金属的结构和性能上,研究它们可以揭示金属的秘密,从而使我们更好地应用金属。

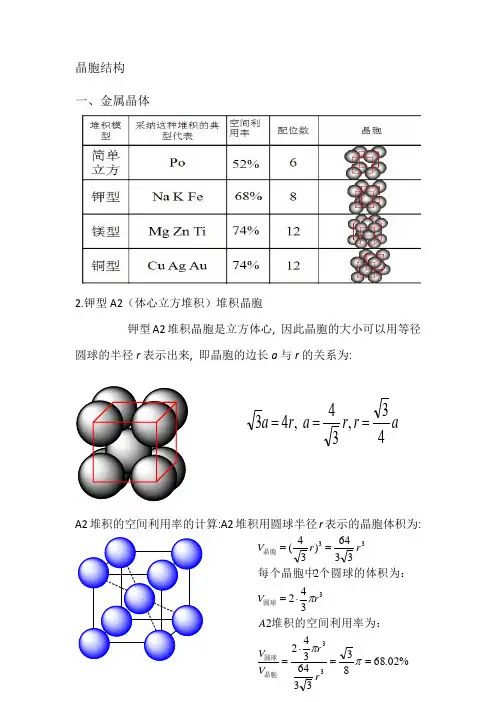
晶胞结构一、金属晶体2.钾型A2(体心立方堆积)堆积晶胞钾型A2堆积晶胞是立方体心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A2堆积的空间利用率的计算:A2堆积用圆球半径r 表示的晶胞体积为:ar r a r a 43,34 ,43===%02.68833364342234223364)34(33333==⋅=⋅===πππr r V V A rV rr V 晶胞圆球圆球晶胞堆积的空间利用率为:个圆球的体积为:每个晶胞中3.六方最密堆积(4)A1(面心立方最密堆积)A1是ABCABCABC······型式的堆积,从这种堆积中可以抽出一个立方面心点阵,因此这种堆积型式的最小单位是一个立方面心晶胞。
A1堆积晶胞是立方面心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A1堆积空间利用率的计算:A1堆积用圆球半径r 表示的晶胞体积为:(5)A4堆积形成晶胞A4堆积晶胞是立方面心点阵结构, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A4堆积的空间利用率的计算:A4堆积用圆球半径r 表示的晶胞体积为: ra r a 22 ,42==%05.742312163441344 4216)22(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为:个圆球的体积为:每个晶胞中ar r a r r a 83,38 ,8243===⨯=%01.34163335123484348 833512)38(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为:个圆球的体积为:每个晶胞中二、原子晶体1.金刚石立体网状结构,每个碳原子形成4个共价键,任意抽出2个共价键,每两个单键归两个六元环所有,而不是只归一个六元环所有(如图所示,红色的两个碳碳单键,可以构成蓝色和紫红色的两个六元环)。
常见晶胞结构最强整理常见晶体结构及其详解晶体晶体结构晶体详解原⼦晶体⾦刚⽯(1)每个碳采取杂化⽅式与4个碳以共价键结合,形成结构,键⾓均为 (2)最⼩碳环由个C 组成且六原⼦不在同⼀平⾯内,平均每个碳原⼦被个六元环共⽤,每根C -C 键被个六元环共⽤。
(3)每个C 参与4条C -C 键的形成, C 原⼦个数与C -C 键数之⽐为 ,1mol ⾦刚⽯中,碳碳键为 molSiO 2(1)每⼀个硅原⼦紧邻个氧原⼦,每⼀个氧原⼦紧邻个硅原⼦,形成了由Si-O 键(极性或⾮极性)键构成的元环的最⼩环状结构。
⼀个环上有个硅原⼦,个氧原⼦(2)1mol SiO 2中,硅氧键为 molSiC每个C 原⼦最近的Si 原⼦有个,每个C 原⼦最近的C 原⼦有个分⼦晶体⼲冰(1)⼀个⼆氧化碳晶胞中含有个⼆氧化碳分⼦(2)8个CO 2分⼦构成⽴⽅体且在6个⾯⼼⼜各占据1个CO 2分⼦ (3)每个CO 2分⼦周围等距且紧邻的CO 2分⼦有个冰⼀个⽔分⼦形成个氢键,平均1mol 冰中含有 mol 氢键C 60(1)⾜球烯的分⼦是由60个碳原⼦构成的,空间构型有12个正五边形,20个正六边形(2)⼀个C 60分⼦中含有根单键,根双键 (3)C 60晶胞中与⼀个C 60最近的C 60分⼦有个(与⼲冰的晶胞相似)离⼦晶体NaCl (型)(1)每个Na +周围等距且紧邻的Cl -有个,每个Cl -周围等距且紧邻的Na +有个。
每个Na +周围等距且紧邻的Na +有个,同理Cl -也然。
(2)每个晶胞中含个Na +和4个Cl -。
CsCl (型)(1)每个Cs +周围等距且紧邻的Cl -有个,每个Cl -周围等距且紧邻的Cs +有个。
(2)左图为个晶胞;右图为⼀个晶胞,每个晶胞中含个Cs +,个Cl -。
CaF 21、1个晶胞中含有个Ca 2+,个F -,Ca 2+的配位数为个,F -配位数为个2、Ca 2+周围等距离最近的Ca 2+ 个,F —周围等距离最近的F — 个⾦属晶体简单⽴⽅堆积典型代表空间利⽤率配位数为体⼼⽴⽅堆积典型代表空间利⽤率配位数为⾯⼼⽴⽅堆积典型代表空间利⽤率配位数为六⽅最密堆积典型代表空间利⽤率配位数为混合晶体⽯墨1、碳原⼦的杂化⽅式为,键⾓为2、⽯墨晶体的⽚层结构中,每个六元碳环含有个碳原⼦数,每个六元碳环所含有的共价健数是个3、⽯墨同层C 原⼦间以连接,熔化需要破坏碳碳之间作⽤⼒,故熔沸点较⾼;层与层之间的作⽤⼒为,作⽤⼒⽐较弱,故⽯墨的硬度较低。


典型的晶体结构1。
铁铁原子可形成两种体心立方晶胞晶体:910℃以下为α-Fe,高于1400℃时为δ-Fe。
在这两种温度之间可形成γ-面心立方晶。
这三种晶体相中,只有γ-Fe能溶解少许C。
问:1.体心立方晶胞中的面的中心上的空隙是什么对称?如果外来粒子占用这个空隙,则外来粒子与宿主离子最大可能的半径比是多少?2.在体心立方晶胞中,如果某空隙的坐标为(0,a/2,a/4),它的对称性如何?占据该空隙的外来粒子与宿主离子的最大半径比为多少?3.假设在转化温度之下,这α-Fe和γ-F两种晶型的最相邻原子的距离是相等的,求γ铁与α铁在转化温度下的密度比。
4.为什么只有γ-Fe才能溶解少许的C?在体心立方晶胞中,处于中心的原子与处于角上的原子是相接触的,角上的原子相互之间不接触。
a=(4/3)r。
①②③1.两个立方晶胞中心相距为a,也等于2r+2r h[如图①],这里r h是空隙“X”的半径,a=2r +2r h=(4/3)r r h/r=0。
115(2分)面对角线(2a)比体心之间的距离要长,因此该空隙形状是一个缩短的八面体,称扭曲八面体。
(1分)2.已知体心上的两个原子(A和B)以及连接两个晶体底面的两个角上原子[图②中C和D].连接顶部原子的线的中心到连接底部原子的线的中心的距离为a/2;在顶部原子下面的底部原子构成晶胞的一半.空隙“h”位于连线的一半处,这也是由对称性所要求的。
所以我们要考虑的直角三角形一个边长为a/2,另一边长为a/4[图③],所以斜边为16/5a。
(1分) r+r h=16/5a=3/5r r h/r=0。
291(2分)3.密度比=42︰33=1。
09(2分)4.C原子体积较大,不能填充在体心立方的任何空隙中,但可能填充在面心立方结构的八面体空隙中(r h/r=0.414)。
(2分)2。
四氧化三铁科学研究表明,Fe3O4是由Fe2+、Fe3+、O2-通过离子键而组成的复杂离子晶体。

几种常见晶体结构分析河北省宣化县第一中学 栾春武 邮编 075131栾春武:中学高级教师,张家口市中级职称评委会委员。
河北省化学学会会员。
市骨干教师、市优秀班主任、模范教师、优秀共产党员、劳动模范、县十佳班主任。
联系电话: E-mail :一、氯化钠、氯化铯晶体——离子晶体由于离子键无饱和性与方向性,所以离子晶体中无单个分子存在。
阴阳离子在晶体中按一定的规则排列,使整个晶体不显电性且能量最低。
离子的配位数分析如下:离子数目的计算:在每一个结构单元(晶胞)中,处于不同位置的微粒在该单元中所占的份额也有所不同,一般的规律是:顶点上的微粒属于该单元中所占的份额为18,棱上的微粒属于该单元中所占的份额为14,面上的微粒属于该单元中所占的份额为12,中心位置上(嚷里边)的微粒才完全属于该单元,即所占的份额为1。
1.氯化钠晶体中每个Na +周围有6个Cl -,每个Cl -周围有6个Na +,与一个Na +距离最近且相等的Cl -围成的空间构型为正八面体。
每个Na +周围与其最近且距离相等的Na +有12个。
见图1。
| 晶胞中平均Cl -个数:8×18 + 6×12 = 4;晶胞中平均Na +个数:1 + 12×14 = 4因此NaCl 的一个晶胞中含有4个NaCl (4个Na +和4个Cl -)。
2.氯化铯晶体中每个Cs +周围有8个Cl -,每个Cl -周围有8个Cs +,与一个Cs +距离最近且相等的Cs +有6个。
晶胞中平均Cs +个数:1;晶胞中平均Cl -个数:8×18 = 1。
因此CsCl 的一个晶胞中含有1个CsCl (1个Cs +和1个Cl -)。
二、金刚石、二氧化硅——原子晶体1.金刚石是一种正四面体的空间网状结构。
每个C 原子以共价键与4个C 原子紧邻,因而整个晶体中无单个分子存在。
由共价键构成的最小环结构中有6个碳原子,不在同一个平面上,每个C 原子被12个六元环共用,每C —C 键共6个环,因此六元环中的平均C 原子数为6×112 = 12 ,平均C —C 键数为6×16 = 1。

氯化钠晶体CsCI 晶体(注意:右侧小立方体为CsCI 晶胞;左侧为8个晶胞)(1) CsCI 晶胞中每个Cs+等距离且最近的CP (即Cs+配位数) 为8个csci 晶胞中每个cr 等距离且最近的cs+(即cr 配位数)为8个,这几个Cs+在空间构成的几何构型为正方体。
(2)在每个Cs+周围与它最近的且距离相等的Cs+有6个这几个Cs+在空间构成的几何构型为正八面体。
CaF2晶体(1) ) CX+立方最密堆积,F 填充在全部四面体空隙中。
(2) C aF2晶胞中每个Ca?+等距离且最近的F (即CO 配位数)为8个CaF?晶胞中每个F 等距离且最近的Ca 2+ (即F 配位数)为4个 (3) 一个晶胞内由均摊法计算出一个晶胞内占有的Ca?+4个;占有的F8个。
离子晶体•cr ocr(3)有的 Cs+1个;占有的CIT 个一个晶胞内由均摊法计算出一个晶胞内占 NaCI 晶胞中每个Na+等距离且最近的CI-(即Na+配位数)为6个(ZnS晶体:(1)1个ZnS晶胞中,有4个,有4个Zr>(2 )Zm的配位数为4个,S2一的配位数为OZn ■舊原子晶体金刚石金刚石晶胞 金刚石晶胞分位置注释(1) 金刚石晶体a 、每个金刚石晶胞中含有8个碳原子,最小的碳环为6元环,并且不在同一平面(实际为椅式结构),碳原子为sp3杂化,每个C 以共价键跟相邻的_4_个C 结合,形成正四面 体°键角109° 28'b 、 每个碳原子被"个六元环共用,每个共价键被6个六元环共用c 、 12g 金刚石中有2mol 共价键,碳原子与共价键之比为上一(2) Si 晶体由于Si 与碳同主族,晶体Si 的结构同金刚石的结构。
将金刚石晶胞中的 C 原子全部换成Si 原子,健长稍长些便可得到晶体硅的晶胞。
(3)某些非金属化合物【SiO2、SiC (金刚砂)、BN (氮化硼)、Si3N4等】例如SiC 将金刚石晶胞中的一个C 原子周围与之连接的4个C 原子全部换成Si 原子,键长 稍长些便可得到SiC 的晶胞。
金刚石的晶胞构型
金刚石结构:原子晶体、碳同素异形体。
金刚石是正八面体结构。
c碳原子按四面体成键方式互相连接,组成无限的三维骨架,是典型的原子晶体,每个碳原子都以sp3杂化轨道与另外4个碳原子形成共价键,构成正四面体。
金刚石结构的原型是金刚石的晶体结构。
在金刚石晶体中,每个碳原子的4个价电子以sp3杂化的方式,形成4个完全等同的原子轨道,与最相邻的4个碳原子形成共价键。
这4个共价键之间的角度都成正比,约为.28度,准确值,这样构成由5个碳原子形成的正四面体结构单元,其中4个碳原子坐落于正四面体的顶点,1个碳原子坐落于正四面体的中心。
因为共价键难以变形,c-c键能大,所以金刚石硬度和熔点都很高,化学稳定性好。
共价键中的电子被束缚在化学键中不能参与导电,所以金刚石是绝缘体,不导电。
1.3 典型的晶体结构,晶向、晶面的表示一. 晶体结构的表达方法二. 晶向、晶面和它们的标志三. 晶面间距四. 典型晶体结构五. 多晶型现象和结构相变参考黄昆书 1.3 节,Kittel8版 1.3 1.4 节一.晶体结构的表达方法指出晶体所属的点阵、晶系、点群和空间群类型是在不同层次上对晶体结构做描述。
以NaCl 为例说明。
面心立方点阵说明了它属于立方晶系,可以用a=b=c, α=β=γ=90°面心立方晶胞表示其原子周期排列特点。
点群为O h ,说明了它的外形具有的宏观对称性。
空间群为O h 5-F m3m ,指出了它的原子排列规律。
至此我们才可以说对NaCl 晶体的几何结构特点有了比较充分的认识。
NaCl结构中的原子排列NaCl晶体为八面体群的说明:O h,它的每个原子都处在不同原子组成的8面体体心位置。
考虑它的晶场时就要注意到这个特点。
点群对称操作:体对角线是3重轴;3 条棱边是4重轴;棱对角线是2重轴,体心是反演中心。
z但有些元素晶体和所有化合物晶体,其最小重复单位(基元)至少包含2个或2 个以上的原子,它们的每一个原子虽然都构成同样的点阵类型(即同样的周期排列方式),但绘成晶胞时,要绘出基元原子之间位置上的相互关系,所以是同样的点阵类型的叠加,我们称这些晶体具有复式晶格。
例如:CsCl晶体是两个原子各自构成简立方点阵后,沿晶胞对角线方向移动二分之一距离的叠加。
NaCl晶体是两个原子各自形成一个面心立方点阵后,沿立方边方向移动二分之一晶胞边长距离的叠加。
上述复式晶格中,每种原子自身是等价的,有完全相同的环境,但两类原子是不等价的,它们的几何环境是完全不同的。
二. 晶向、晶面和它们的标志:晶体的一个基本特点是各向异性,沿晶格的不同方向晶体的性质不同,因此有必要识别和标志晶格中的不同方向。
点阵的格点可以分列在一系列平行的直线系上,这些直线系称作晶列。
同一点阵可以形成不同的晶列,每一个晶列定义一个方向,称作晶向。
常见晶体结构图彩图己烷C6 H12: 碳原子以sp2杂化与相邻两个碳原子碳环s骨架,与2个H 成C-H 键。
二茂铁Fe(C5 H5 )2: 上下环戊烯阴离子各以六个π 电子参与成键,与Fe对称性匹配的d3p3轨道形成六个分子轨道,Fe其余的三个价轨道为非键的孤对电子占据。
B12H122-: 12 个B 形成封闭的三角二十面体,每个B 还与1 个H 形成B-H 键。
C20H20: 每个C 以sp3杂化与相邻的 3 个C 、1 个H 形成s 键,整个碳笼为正十二面体。
C60: 每个C 以sp2杂化与相邻的 3 个C 形成球形多面体s 骨架(12 个五边形与20 个六边形),还有 1 个垂直于曲面的p 轨道与其他p 轨道形成1 个离域的大p 键。
石墨层内 C 以共价键与相邻的 3 个C 形成平面骨架,层之间为范德华力。
金剛石:为A4 结构,每个C 以sp3杂化与相邻的4 个C 形成四面体配位,晶胞中有8 个C 原子。
NaCl 晶体属面心立方点阵,Na+与Cl-的配位数均为6。
Cl-作立方最密堆积,Na+填在Cl-形成的八面体空隙中。
每个晶胞含有4个Cl-和4个Na+,Cl-位于晶胞顶点与面心位置,Na+位于体心与棱心位置。
立方ZnS 晶体中,S 原子作立方最密堆积,Zn 原子填在一半的四面体空隙中,形成立方面心点阵,晶胞中含个S 原子4 个Zn 原子;六方ZnS 晶体中,S 原子作六方最密堆积,Zn 原子填在一半的四面体空隙中,形成六方点阵,晶胞中含个S 原子4 个Zn 原子。
CaF2晶体属立方面心点阵,F-作简单立方堆积,Ca2+数目比F-少一半,填了一半的立方体空隙,每一个Ca2+由八个F-配位,而每个F-有 4 个Ca2+配位,每个CaF2晶胞有 4 个Ca2+和8 个F-原子。
金红石(TiO2)为简单四方结构,Ti4+处在略为变形的氧八面体中,即氧离子作假六方堆积,Ti4+填在它的准八面体空隙中,Ti4+配位数为 6 ,O2-与3 个Ti4+配位( 3 个Ti4+几乎形成等边三角形)。
十二晶体结构
是一种特殊的结晶形态,也被称作十二面体晶胞。
这种结构的
晶胞由十二个六角形构成,看起来非常美丽。
但是除了其美观,
对于材料科学和化学领域来说也是非常重要的。
最早发现的实例是铝石墨烯(Al13C4)的分子团簇。
这种分子
团簇的晶胞由13个铝原子和4个碳原子构成,形状类似于一个球。
这种结构是一种几何立体的体系,具有极高的强度和超弹性。
这
些特性使得其在纳米材料和生物医学领域有着广泛的应用。
除了铝石墨烯,还在其他材料中被广泛应用。
比如氢化物、卤
素化合物和碱金属化合物等。
在这些材料中,的特性主要体现在
其高度对称性和其调节热导率的能力。
这在材料的制造和应用过
程中都有着非常重要的意义。
举例来说,氢化镧(LaH10)和氢化铈(CeH10)这两种化合
物都具有。
这种结构中的La和Ce原子占据了中心位置,而氢原
子则填充在晶胞的角落处。
这种结构的特性使得氢化镧成为了一
种具有潜力的超导材料,并能够用于制造高温超导电缆和超导磁体。
而氢化铈则可以用于制造高强度的磁体,因为能够调节热传导,从而使得其在高温下仍能保持磁场的稳定性。
总的来说,是一种具有非常特殊性质的结晶形态。
除了在材料
科学和化学领域的应用之外,在生物医学领域也有着潜在的应用。
拥有这种结构之后,材料可以具有极高的强度,超弹性和优异的
传热性能。
可以预见,在以后的发展中,将会在各种领域发挥着
更加重要的作用。
典型晶体晶胞结构
原子晶体分子晶体混合型晶体
离子晶体
金属晶体
1.元素Cu的一种氯化物晶体的晶胞结构如图13所示,该氯化物的化学式
是,它可与浓盐酸发生非氧化还原反应,生成配合物
H n WCl3,反应的化学方程式为。
2.(2011山东高考)
CaO与NaCl的晶胞同为面心立方结构,已知CaO晶体密度为
ag·cm-3,A
N表示阿伏加德罗常数,则
CaO晶胞体积为cm3。
3.(2011新课标全国)六方氮化硼BN在高温高压下,可以转化为立方氮化硼,其结构与金刚石相似,硬度与金刚石相当,晶苞边长为361.5pm,立方氮化硼晶胞中含有______各氮原子、________各硼原子,立方氮化硼的密度是_______g·cm-3(只要求列算式,不必计算出数
值,阿伏伽德罗常数为N A )。
描述晶体结构的基本单元叫做晶胞,金刚石晶胞是立方体,其中8个顶点有8个碳原子, 6个面各有6个碳原子,立方体内部还有4个碳原子,如图所示。
所以金刚石的一个晶胞中含有的碳原子数=8×1/8+6×1/2+4=8,因此立方氮化硼晶胞中应该含有4个N 和4个B 原子。
由于立方氮化硼的一个晶胞中含有4个N 和4个B 原子,其质量是
g 2510
02.6423⨯⨯是,立方体的体积是(361.5cm)3,因此立方氮化硼的密度是
g·cm -3。
4.(4)元素金(Au )处于周期表中的第六周期,与Cu 同族,Au 原子最外层电子排布式为______;一种铜合金晶体具有立方最密堆积的结构,在晶胞中Cu 原子处于面心,Au 原子处于顶点位置,则该合金中Cu 原子与Au 原子数量之比为_______;该晶体中,原子之间的作用力是________;(4)Au 电子排布或类比Cu ,只是电子层多两层,由于是面心立方,晶胞内N (Cu )=6×21=3,N (Au )=8×8
1=1;
(5)上述晶体具有储氢功能,氢原子可进入到由Cu 原子与Au 原子构成的四面体空隙中。
若将Cu 原子与Au 原子等同看待,该晶体储氢后的晶胞结构为CaF 2的结构相似,该晶体储氢后的化学式应为_____。
H 8AuCu 3
5.(2010山东卷)铅、钡、氧形成的某化合物的晶胞结构是:Pb 4+处于立方晶胞顶点,Ba 2+
处于晶胞中心,O 2-处于晶胞棱边中心,该化合物化学式为 ,每个Ba 2+与 个O 2-配位。
6.(4)
2CaC 晶体的晶胞结构与NaCl 晶体的相似(如右图所示),但2CaC 晶体
中含有的中哑铃形22C -的存在,使晶胞沿一个方向拉长。
2CaC 晶体中1个2Ca
+周围距离最近的22C -数目为 。
7.(09江苏卷21 A )③在1个Cu 2O 晶胞中(结构如图所示),所包
含的Cu 原子数目为 。