解二元一次方程组的方法——加减法

第7课时 二元一次方程组解法复习1、解方程组：⎩⎨⎧=+=-1424723y x y x 时，要先观察方程组的特点，再确定解方程组的方法。

因为方程①中的 与方程②中的 互为相反数，所以当两个方程相加时，就可以消去单项式中所含的这个未知数。

根据以上思路，在下面解出这个方程组。

解：⎩⎨⎧=+=-1424723y x y x2、解方程组：⎩⎨⎧=+=+622823y x y x 时，先观察它的特点，发现：方程①、方程②中都含有相同的单项式 ，这样的两个方程相减时，就可消去这个单项式所含的未知数。

根据以上思路，在下面解出这个方程组。

解：⎩⎨⎧=+=+622823y x y x3、解方程组：⎩⎨⎧=+=+122573y x y x 时，发现两个方程中既没有相同的单项式，也没有互为相反数的单项式。

因此两个方程不能直接相加或相减。

但可以在其中一个方程两边乘以一个数，从而使得两个方程有相同的单项式。

因为5x 不是3x 倍数，但2y 是y 的2倍，所以，可以用方程①乘以2，得到 ，从而组成新的方程组：⎩⎨⎧=+=+12251426y x y x 以便可以直接使用加减消元法。

根据以上思路，在下面解出这个方程组。

① ②① ②① ②解：⎩⎨⎧=+=+122573y x y x4、解方程组：⎩⎨⎧=+-=+12373y x y x 时，发现两个方程中既没有相同的单项式，也没有互为相反数的单项式。

因此两个方程不能直接 。

但可以在其中一个方程两边乘以一个数，从而使得两个方程有相同的单项式。

因为3y 不是2y 的倍数，但－3x 是x 的3倍，所以，可以用方程①乘以3，得到 ，从而组成新的方程组：⎩⎨⎧=+-=+1232193y x y x 以便可以直接使用加减消元法。

根据以上思路，在下面解出这个方程组。

解：⎩⎨⎧=+-=+12373y x y x5、解方程组：⎩⎨⎧=+=+7231252y x y x 时，发现3x 不是2x 的倍数，5y 也不是2y 的倍数，但我们可以使两个方程都分别乘一个数，都变成它们的公倍数。

加减法解方程的一般步骤
【题目】：
用加减法解方程组的一般步骤是什么？
【答案】：
用加减法消元的一般步骤为：
①在二元一次方程组中，若有同一个未知数的系数相同(或互为相反数)，则可直接相减(或相加)，消去一个未知数。

②在二元一次方程组中，若不存在①中的情况，可选择一个适当的数去乘方程的两边，使其中一个未知数的系数相同(或互为相反数)，再把方程两边分别相减(或相加)，消去一个未知数，得到一元一次方程。

③解这个一元一次方程。

④将求出的一元一次方程的解代入原方程组系数比较简单的方程，求另一个未知数的值。

⑤把求得的两个未知数的值用大括号联立起来，这就是二元一次方程组的解。

用加减法解二元一次方程组的步骤嘿，咱今儿个就来讲讲用加减法解二元一次方程组的步骤，这可是数学里挺重要的一块儿呢！咱先得搞清楚啥是二元一次方程组，不就是有两个未知数，然后每个未知数都是一次方的一堆等式嘛。

就好像生活里的一些难题，有两个关键因素在那儿搅和。

那怎么用加减法来搞定它呢？就好比咱收拾房间，得一步步来。

第一步，观察方程组里的两个方程，看看那些未知数的系数有没有啥特别的。

要是有一个未知数的系数在两个方程里正好相等或者互为相反数，那可就太棒啦！这就像找到了收拾房间的关键入口一样。

第二步，要是系数相等，那就把两个方程相减；要是互为相反数，那就相加。

这就好像把房间里相似的东西归归类，或者把相反的东西区分开。

第三步，经过这么一加一减，嘿，其中一个未知数就被消掉啦！就像把房间里的一堆杂物清理掉了，一下子清爽了不少。

第四步，解出剩下的那个未知数的值。

这就好比终于找到了房间里最重要的那件东西。

第五步，再把这个解出来的值代回到原来的方程里，就能求出另一个未知数的值啦！这就像根据找到的关键东西，又顺藤摸瓜找到了其他相关的东西。

比如说有个方程组，x + 2y = 5，2x - y = 1。

你看，这里的 y 的系数2 和-1 不就是互为相反数嘛！那咱就把这两个方程相加，一下子就把 y 给消掉了，就能求出 x 啦！然后再代回去求出 y，这不就大功告成了嘛！用加减法解二元一次方程组，就像是在数学的迷宫里找路，每一步都得走得稳稳当当。

虽然有时候可能会遇到一些小麻烦，比如系数不太好处理啥的，但咱别怕呀！多琢磨琢磨，总能找到解决办法的。

这就跟咱过日子一样，遇到问题别怕，一步步去解决，总能把日子过得顺顺当当的。

数学的世界多奇妙呀，这加减法解方程组就是其中一个小小的精彩之处。

咱可得好好掌握，以后遇到更难的数学问题也不怕啦！你说是不是呀？所以呀，大家可得把这步骤好好记住咯，在数学的海洋里畅游吧！。

加减法解二元一次方程组的一般步骤嘿，咱今儿来聊聊加减法解二元一次方程组的一般步骤哈。

你看啊，这二元一次方程组就好像是个小怪兽，咱得想办法把它给搞定咯。

那加减法呢，就是咱手中的厉害武器。

先来说说第一步，观察方程组中两个方程里同一个未知数的系数。

要是它们相等或者互为相反数，那可就太棒啦，就像找到了小怪兽的弱点一样。

比如说，一个方程里的 x 系数是 3，另一个方程里的 x 系数是-3，这不就巧了嘛。

接着呢，就可以把这两个方程相加或者相减啦。

这就好比给小怪兽致命一击呀！相加或者相减之后，嘿，其中一个未知数就消掉啦，是不是很神奇？这时候不就变成一元一次方程了嘛，一元一次方程咱总会解吧。

然后呢，解出这个一元一次方程，得到一个未知数的值。

就好像终于打败了小怪兽的一部分。

最后，再把这个解代回到原来的方程组里，去求出另一个未知数的值。

哇塞，这不就把整个小怪兽都打败啦。

你想想，这像不像我们玩游戏打怪物呀，得一步步找到方法，才能取得胜利。

要是一开始就乱了阵脚，那可不行哟。

再比如说，方程组里一个方程是 2x+y=5，另一个是 2x-y=1，这不是很明显嘛，y 的系数互为相反数呀，那就把这两个方程一加，y 就没啦，直接就能求出 x 啦。

然后再代回去求出 y，多简单呀。

咱可不能小瞧这加减法解二元一次方程组呀，它在很多地方都能派上大用场呢。

比如解决一些实际问题，像计算买东西花了多少钱呀，或者安排活动的人数呀之类的。

所以说呀，大家一定要好好掌握这个方法哟，它可是我们数学世界里的一把好武器呢！以后遇到二元一次方程组，咱就不用怕啦，直接用加减法把它拿下。

大家说是不是呀？嘿嘿！。

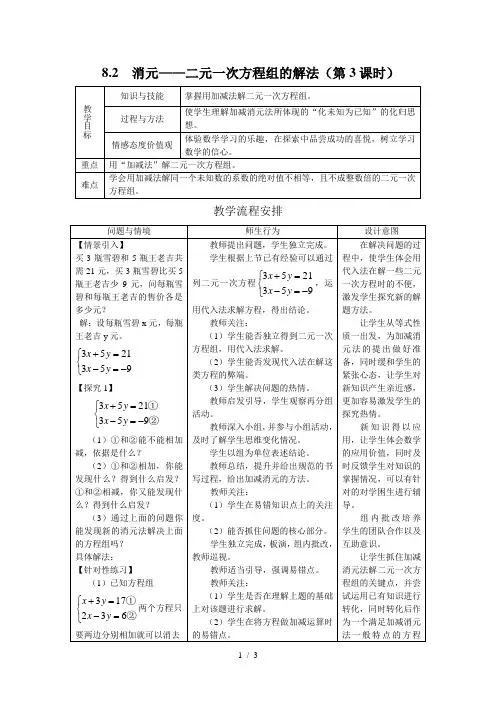
8.2 消元——二元一次方程组的解法（第3课时）教学目标知识与技能掌握用加减法解二元一次方程组。

过程与方法 使学生理解加减消元法所体现的“化未知为已知”的化归思想。

情感态度价值观体验数学学习的乐趣，在探索中品尝成功的喜悦，树立学习数学的信心。

重点 用“加减法”解二元一次方程组。

难点学会用加减法解同一个未知数的系数的绝对值不相等，且不成整数倍的二元一次方程组。

教学流程安排问题与情境师生行为设计意图【情景引入】买3瓶雪碧和5瓶王老吉共需21元，买3瓶雪碧比买5瓶王老吉少9元，问每瓶雪碧和每瓶王老吉的售价各是多少元？解：设每瓶雪碧x 元，每瓶王老吉y 元。

⎩⎨⎧-=-=+9532153y x y x 【探究1】⎩⎨⎧-=-=+②①9532153y x y x （1）①和②能不能相加减，依据是什么？（2）①和②相加，你能发现什么？得到什么启发？①和②相减，你又能发现什么？得到什么启发？（3）通过上面的问题你能发现新的消元法解决上面的方程组吗？ 具体解法： 【针对性练习】 （1）已知方程组⎩⎨⎧=-=+②①632173y x y x 两个方程只要两边分别相加就可以消去教师提出问题，学生独立完成。

学生根据上节已有经验可以通过列二元一次方程⎩⎨⎧-=-=+9532153y x y x ，运用代入法求解方程，得出结论。

教师关注： （1）学生能否独立得到二元一次方程组，用代入法求解。

（2）学生能否发现代入法在解这类方程的弊端。

（3）学生解决问题的热情。

教师启发引导，学生观察再分组活动。

教师深入小组，并参与小组活动，及时了解学生思维变化情况。

学生以组为单位表述结论。

教师总结，提升并给出规范的书写过程，给出加减消元的方法。

教师关注： （1）学生在易错知识点上的关注度。

（2）能否抓住问题的核心部分。

学生独立完成，板演，组内批改，教师巡视。

教师适当引导，强调易错点。

教师关注： （1）学生是否在理解上题的基础上对该题进行求解。