解一元一次方程——同解方程精选试题附答案

解一元一次方程经典题库及答案一．解答题（共30小题）1．（2005•宁德）解方程：2x+1=72．3．（1）解方程：4﹣x=3（2﹣x）；（2）解方程：．4．解方程：．5．解方程（1）4（x﹣1）﹣3（20﹣x）=5（x﹣2）；（2）x﹣=2﹣．6．（1）解方程：3（x﹣1）=2x+3；（2）解方程：=x﹣．7．﹣（1﹣2x）=（3x+1）8．解方程：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+1；（2）．9．解方程：．10．解方程：（1）4x﹣3（4﹣x）=2；（2）（x﹣1）=2﹣（x+2）．11．计算：（1）计算：（2）解方程：12．解方程：13．解方程：（1）（2）14．解方程：（1）5（2x+1）﹣2（2x﹣3）=6 （2）+2（3）[3（x﹣）+]=5x﹣115．（A类）解方程：5x﹣2=7x+8；（B类）解方程：（x﹣1）﹣（x+5）=﹣；（C类）解方程：．16．解方程（1）3（x+6）=9﹣5（1﹣2x）（2）（3）（4）17．解方程：（1）解方程：4x﹣3（5﹣x）=13（2）解方程：x﹣﹣318．（1）计算：﹣42×+|﹣2|3×（﹣）3（2）计算：﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]（3）解方程：4x﹣3（5﹣x）=2；（4）解方程：．19．（1）计算：（1﹣2﹣4）×；（2）计算：÷；（3）解方程：3x+3=2x+7；（4）解方程：．20．解方程（1）﹣0.2（x﹣5）=1；（2）．21．解方程：（x+3）﹣2（x﹣1）=9﹣3x．22．8x﹣3=9+5x．5x+2（3x﹣7）=9﹣4（2+x）．．．23．解下列方程：（1）0.5x﹣0.7=5.2﹣1.3（x﹣1）；（2）=﹣2．24．解方程：（1）﹣0.5+3x=10；（2）3x+8=2x+6；（3）2x+3（x+1）=5﹣4（x﹣1）；（4）．25．解方程：．26．解方程：（1）10x﹣12=5x+15；（2）27．解方程：（1）8y﹣3（3y+2）=7（2）．28．当k为什么数时，式子比的值少3．29．解下列方程：（II）．30．解方程：．6.2.4解一元一次方程（三）参考答案与试题解析一．解答题（共30小题）1．（2005•宁德）解方程：2x+1=7考点：解一元一次方程．专题：计算题；压轴题．分析：此题直接通过移项，合并同类项，系数化为1可求解．解答：解：原方程可化为：2x=7﹣1合并得：2x=6系数化为1得：x=3点评：解一元一次方程，一般要通过去分母，去括号，移项，合并同类项，未知数的系数化为1等步骤，把一个一元一次方程“转化”成x=a的形式．2．考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：左右同乘12可得：3[2x﹣（x﹣1）]=8（x﹣1），化简可得：3x+3=8x﹣8，移项可得：5x=11，解可得x=．故原方程的解为x=．点评：若是分式方程，先同分母，转化为整式方程后，再移项化简，解方程可得答案．3．（1）解方程：4﹣x=3（2﹣x）；（2）解方程：．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，然后再移项、合并同类型，最后化系数为1，得出方程的解；（2）题的方程中含有分数系数，应先对各式进行化简、整理，然后再按（1）的步骤求解．解答：解：（1）去括号得：4﹣x=6﹣3x，移项得：﹣x+3x=6﹣4，合并得：2x=2，系数化为1得：x=1．（2）去分母得：5（x﹣1）﹣2（x+1）=2，去括号得：5x﹣5﹣2x﹣2=2，移项得：5x﹣2x=2+5+2，合并得：3x=9，系数化1得：x=3．点评：（1）本题易在去分母、去括号和移项中出现错误，还可能会在解题前产生害怕心理．因为看到小数、分数比较多，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果．（2）本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍，值不变．这一性质在今后常会用到．4．解方程：．考点：解一元一次方程．专题：计算题．分析：此题两边都含有分数，分母不相同，如果直接通分，有一定的难度，但将方程左右同时乘以公分母6，难度就会降低．解答：解：去分母得：3（2﹣x）﹣18=2x﹣（2x+3），去括号得：6﹣3x﹣18=﹣3，移项合并得：﹣3x=9，∴x=﹣3．点评：本题易在去分母和移项中出现错误，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果．5．解方程（1）4（x﹣1）﹣3（20﹣x）=5（x﹣2）；（2）x﹣=2﹣．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项、合并同类项、化系数为1，从而得到方程的解；（2）先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：（1）去括号得：4x﹣4﹣60+3x=5x﹣10（2分）移项得：4x+3x﹣5x=4+60﹣10（3分）合并得：2x=54（5分）系数化为1得：x=27；（6分）（2）去分母得：6x﹣3（x﹣1）=12﹣2（x+2）（2分）去括号得：6x﹣3x+3=12﹣2x﹣4（3分）移项得：6x﹣3x+2x=12﹣4﹣3（4分）合并得：5x=5（5分）系数化为1得：x=1．（6分）点评：去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．去括号时要注意符号的变化．6．（1）解方程：3（x﹣1）=2x+3；（2）解方程：=x﹣．考点：解一元一次方程．专题：计算题．分析：（1）是简单的一元一次方程，通过移项，系数化为1即可得到；（2）是较为复杂的去分母，本题方程两边都含有分数系数，如果直接通分，有一定的难度，但对每一个式子先进行化简、整理为整数形式，难度就会降低．解答：解：（1）3x﹣3=2x+33x﹣2x=3+3x=6；（2）方程两边都乘以6得：x+3=6x﹣3（x﹣1）x+3=6x﹣3x+3x﹣6x+3x=3﹣3﹣2x=0∴x=0．点评：本题易在去分母、去括号和移项中出现错误，还可能会在解题前不知如何寻找公分母，怎样合并同类项，怎样化简，所以要学会分开进行，从而达到分解难点的效果．去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．7．﹣（1﹣2x）=（3x+1）考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：﹣7（1﹣2x）=3×2（3x+1）﹣7+14x=18x+6﹣4x=13x=﹣．点评：解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为1．此题去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．8．解方程：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+1；（2）．考点：解一元一次方程．专题：计算题．分析：（1）可采用去括号，移项，合并同类项，系数化1的方式进行；（2）本题方程两边都含有分数系数，如果直接通分，有一定的难度，但对每一个式子先进行化简、整理为整数形式，难度就会降低．解答：解：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+13x﹣7=4x﹣2∴x=﹣5；（2）原方程可化为：去分母得：40x+60=5（18﹣18x）﹣3（15﹣30x），去括号得：40x+60=90﹣90x﹣45+90x，移项、合并得：40x=﹣15，系数化为1得：x=．点评：（1）本题易在去分母、去括号和移项中出现错误，还可能会在解题前产生害怕心理．因为看到小数、分数比较多，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果；（2）本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍，值不变．这一性质在今后常会用到．9．解方程：．考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：，去分母得：2x﹣（3x+1）=6﹣3（x﹣1），去括号得：2x﹣3x﹣1=6﹣3x+3，移项、合并同类项得：2x=10，系数化为1得：x=5．点评：去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．10．解方程：（1）4x﹣3（4﹣x）=2；（2）（x﹣1）=2﹣（x+2）．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项，合并同类项，系数化1，即可求出方程的解；（2）先去分母，再去括号，移项，合并同类项，系数化1可求出方程的解．解答：解：（1）4x﹣3（4﹣x）=2去括号，得4x﹣12+3x=2移项，合并同类项7x=14系数化1，得x=2．（2）（x﹣1）=2﹣（x+2）去分母，得5（x﹣1）=20﹣2（x+2）去括号，得5x﹣5=20﹣2x﹣4移项、合并同类项，得7x=21系数化1，得x=3．点评：（1）此题主要是去括号，移项，合并同类项，系数化1．（2）方程两边每一项都要乘各分母的最小公倍数，方程两边每一项都要乘各分母的最小公倍数，切勿漏乘不含有分母的项，另外分数线有两层意义，一方面它是除号，另一方面它又代表着括号，所以在去分母时，应该将分子用括号括上．11．计算：（1）计算：（2）解方程：考点：解一元一次方程；有理数的混合运算．专题：计算题．分析：（1）根据有理数的混合运算法则计算：先算乘方、后算乘除、再算加减；（2）两边同时乘以最简公分母4，即可去掉分母．解答：解：（1）原式=，=，=．（2）去分母得：2（x﹣1）﹣（3x﹣1）=﹣4，解得：x=3．点评：解答此题要注意：（1）去分母时最好先去中括号、再去小括号，以减少去括号带来的符号变化次数；（2）去分母就是方程两边同时乘以分母的最简公分母．12．解方程：考点：解一元一次方程．专题：计算题．分析：（1）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．（2）解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、化系数为1．解答：解：（1）去分母得：3（3x﹣1）+18=1﹣5x，去括号得：9x﹣3+18=1﹣5x，移项、合并得：14x=﹣14，系数化为1得：x=﹣1；（2）去括号得：x﹣x+1=x，移项、合并同类项得：x=﹣1，系数化为1得：x=﹣．点评：本题考查解一元一次方程，正确掌握解一元一次方程的一般步骤，注意移项要变号、去分母时“1”也要乘以最小公倍数．13．解方程：（1）（2）考点：解一元一次方程．专题：计算题．分析：（1）去分母、去括号、移项、合并同类项、化系数为1．（2）去分母、去括号、移项、合并同类项、化系数为1．解答：（1）解：去分母得：5（3x+1）﹣2×10=3x﹣2﹣2（2x+3），去括号得：15x+5﹣20=3x﹣2﹣4x﹣6，移项得：15x+x=﹣8+15，合并得：16x=7，解得：；（2）解：，4（x﹣1）﹣18（x+1）=﹣36，4x﹣4﹣18x﹣18=﹣36，﹣14x=﹣14，x=1．点评：本题考查解一元一次方程，正确掌握解一元一次方程的一般步骤，注意移项要变号、去分母时“1”也要乘以最小公倍数．14．解方程：（1）5（2x+1）﹣2（2x﹣3）=6 （2）+2（3）[3（x﹣）+]=5x﹣1考点：解一元一次方程．专题：计算题．分析：（2）通过去括号、移项、合并同类项、系数化为1，解得x的值；（3）乘最小公倍数去分母即可；（4）主要是去括号，也可以把分数转化成整数进行计算．解答：解：（1）去括号得：10x+5﹣4x+6=6移项、合并得：6x=﹣5，方程两边都除以6，得x=﹣；（2）去分母得：3（x﹣2）=2（4﹣3x）+24，去括号得：3x﹣6=8﹣6x+24，移项、合并得：9x=38，方程两边都除以9，得x=；（3）整理得：[3（x﹣）+]=5x﹣1，4x﹣2+1=5x﹣1，移项、合并得：x=0．点评：一元一次方程的解法：一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤，把一个一元一次方程“转化”成x=a的形式．解题时，要灵活运用这些步骤．15．（A类）解方程：5x﹣2=7x+8；（B类）解方程：（x﹣1）﹣（x+5）=﹣；（C类）解方程：．考点：解一元一次方程．专题：计算题．分析：通过去分母、去括号、移项、系数化为1等方法，求得各方程的解．解答：解：A类：5x﹣2=7x+8移项：5x﹣7x=8+2化简：﹣2x=10即：x=﹣5；B类：（x﹣1）﹣（x+5）=﹣去括号：x﹣﹣x﹣5=﹣化简：x=5即：x=﹣；C类：﹣=1去分母：3（4﹣x）﹣2（2x+1）=6去括号：12﹣3x﹣4x﹣2=6化简：﹣7x=﹣4即：x=．点评：本题主要考查一元一次方程的解法，比较简单，但要细心运算．16．解方程（1）3（x+6）=9﹣5（1﹣2x）（2）（3）（4）考点：解一元一次方程．专题：计算题．分析：（1）去括号以后，移项，合并同类项，系数化为1即可求解；（2）（3）首先去掉分母，再去括号以后，移项，合并同类项，系数化为1以后即可求解；（4）首先根据分数的基本性质，把第一项分母中的0.3化为整数，再去分母，求解．解答：解：（1）去括号得：3x+18=9﹣5+10x移项得：3x﹣10x=9﹣5﹣18合并同类项得：﹣7x=﹣14则x=2；（2）去分母得：2x+1=x+3﹣5移项，合并同类项得：x=﹣3；（3）去分母得：10y+2（y+2）=20﹣5（y﹣1）去括号得：10y+2y+4=20﹣5y+5移项，合并同类项得：17y=21系数化为1得：；（4）原方程可以变形为：﹣5x=﹣1去分母得：17+20x﹣15x=﹣3移项，合并同类项得：5x=﹣20系数化为1得：x=﹣4．点评：解方程的过程中要注意每步的依据，这几个题目都是基础的题目，需要熟练掌握．17．解方程：（1）解方程：4x﹣3（5﹣x）=13（2）解方程：x﹣﹣3考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项，化系数为1，从而得到方程的解．（2）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：（1）去括号得：4x﹣15+3x=13，移项合并得：7x=28，系数化为1得：得x=4；（2）原式变形为x+3=，去分母得：5（2x﹣5）+3（x﹣2）=15（x+3），去括号得10x﹣25+3x﹣6=15x+45，移项合并得﹣2x=76，系数化为1得：x=﹣38．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．18．（1）计算：﹣42×+|﹣2|3×（﹣）3（2）计算：﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]（3）解方程：4x﹣3（5﹣x）=2；（4）解方程：．考点：解一元一次方程；有理数的混合运算．分析：（1）利用平方和立方的定义进行计算．（2）按四则混合运算的顺序进行计算．（3）主要是去括号，移项合并．（4）两边同乘最小公倍数去分母，再求值．解答：解：（1）﹣42×+|﹣2|3×（﹣）3==﹣1﹣1=﹣2．（2）﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]====．（3）解方程：4x﹣3（5﹣x）=2去括号，得4x﹣15+3x）=2移项，得4x+3x=2+15合并同类项，得7x=17系数化为1，得．（4）解方程：去分母，得15x﹣3（x﹣2）=5（2x﹣5）﹣3×15去括号，得15x﹣3x+6=10x﹣25﹣45移项，得15x﹣3x﹣10x=﹣25﹣45﹣6合并同类项，得2x=﹣76系数化为1，得x=﹣38．点评：前两道题考查了学生有理数的混合运算，后两道考查了学生解一元一次方程的能力．19．（1）计算：（1﹣2﹣4）×；（2）计算：÷；（3）解方程：3x+3=2x+7；（4）解方程：．考点：解一元一次方程；有理数的混合运算．专题：计算题．分析：（1）和（2）要熟练掌握有理数的混合运算；（3）和（4）首先熟悉解一元一次方程的步骤：去分母，去括号，移项，合并同类项，系数化为1．解答：解：（1）（1﹣2﹣4）×=﹣=﹣13；（2）原式=﹣1×（﹣4﹣2）×（﹣）=6×（﹣）=﹣9；（3）解方程：3x+3=2x+7移项，得3x﹣2x=7﹣3合并同类项，得x=4；（4）解方程：去分母，得6（x+15）=15﹣10（x﹣7）去括号，得6x+90=15﹣10x+70移项，得6x+10x=15+70﹣90合并同类项，得16x=﹣5系数化为1，得x=．点评：（1）和（2）要注意符号的处理；（4）要特别注意去分母的时候不要发生数字漏乘的现象，熟练掌握去括号法则以及合并同类项法则．20．解方程（1）﹣0.2（x﹣5）=1；（2）．考点：解一元一次方程．分析：（1）通过去括号、移项、系数化为1等过程，求得x的值；（2）通过去分母以及去括号、移项、系数化为1等过程，求得x的值．解答：解：（1）﹣0.2（x﹣5）=1；去括号得：﹣0.2x+1=1，∴﹣0.2x=0，∴x=0；（2）．去分母得：2（x﹣2）+6x=9（3x+5）﹣（1﹣2x），∴﹣21x=48，∴x=﹣．点评：此题主要考查了一元一次方程解法，解一元一次方程常见的过程有去括号、移项、系数化为1等．21．解方程：（x+3）﹣2（x﹣1）=9﹣3x．考点：解一元一次方程．专题：计算题．分析：先去括号得x+3﹣2x+2=9﹣3x，然后移项、合并同类得到2x=4，然后把x的系数化为1即可．解答：解：去括号得x+3﹣2x+2=9﹣3x，移项得x﹣2x+3x=9﹣3﹣2，合并得2x=4，系数化为1得x=2．点评：本题考查了解一元一次方程：先去分母，再去括号，接着移项，把含未知数的项移到方程左边，不含未知数的项移到方程右边，然后合并同类项，最后把未知数的系数化为1得到原方程的解．22．8x﹣3=9+5x．5x+2（3x﹣7）=9﹣4（2+x）．．．考点：解一元一次方程．专题：方程思想．分析：本题是解4个不同的一元一次方程，第一个通过移项、合并同类项及系数化1求解．第二个先去括号再通过移项、合并同类项及系数化1求解．第三个先去分母再同第二个．第四个先分子分母乘以10，再同第三个求解．解答：8x﹣3=9+5x，解：8x﹣5x=9+3，3x=12，∴x=4．∴x=4是原方程的解；5x+2（3x﹣7）=9﹣4（2+x），解：5x+6x﹣14=9﹣8﹣4x，5x+6x+4x=9﹣8+14，15x=15，∴x=1．∴x=1是原方程的解．．解：3（x﹣1）﹣2（2x+1）=12，3x﹣3﹣4x﹣2=12，3x﹣4x=12+3+2，﹣x=17，∴x=﹣17．∴x=﹣17是原方程的解．，解：，5（10x﹣3）=4（10x+1）+40，50x﹣15=40x+4+40，50x﹣40x=4+40+15，10x=59，∴x=．∴x=是原方程的解．点评：此题考查的知识点是解一元一次方程，关键是注意解方程时的每一步都要认真仔细，如移项时要变符号．23．解下列方程：（1）0.5x﹣0.7=5.2﹣1.3（x﹣1）；（2）=﹣2．考点：解一元一次方程．分析：（1）首先去括号，然后移项、合并同类项，系数化成1，即可求解；（2）首先去分母，然后去括号，移项、合并同类项，系数化成1，即可求解解答：解：（1）去括号，得：0.5x﹣0.7=5.2﹣1.3x+1.3移项，得：0.5x+1.3x=5.2+1.3+0.7合并同类项，得：1.8x=7.2，则x=4；（2）去分母得：7（1﹣2x）=3（3x+1）﹣42，去括号，得：7﹣14x=9x+3﹣42，移项，得：﹣14x﹣9x=3﹣42﹣7，合并同类项，得：﹣23x=﹣46，则x=2．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．24．解方程：（1）﹣0.5+3x=10；（2）3x+8=2x+6；（3）2x+3（x+1）=5﹣4（x﹣1）；（4）．考点：解一元一次方程．分析：（1）移项，合并同类项，然后系数化成1即可求解；（2）移项，合并同类项，然后系数化成1即可求解；（3）去括号、移项，合并同类项，然后系数化成1即可求解；（4）首先去分母，然后去括号、移项，合并同类项，然后系数化成1即可求解．解答：解：（1）3x=10.5，x=3.5；（2）3x﹣2x=6﹣8，x=﹣2；（3）2x+3x+3=5﹣4x+4，2x+3x+4x=5+4﹣3，9x=6，x=；（4）2（x+1）+6=3（3x﹣2），2x+2+6=9x﹣6，2x﹣9x=﹣6﹣2﹣6，﹣7x=﹣14，x=2．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．25．解方程：．考点：解一元一次方程．专题：计算题．分析：方程两边乘以10去分母后，去括号，移项合并，将x系数化为1，即可求出解．解答：解：去分母得：5（3x﹣1）﹣2（5x﹣6）=2，去括号得：15x﹣5﹣10x+12=2，移项合并得：5x=﹣5，解得：x=﹣1．点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1，求出解．26．解方程：（1）10x﹣12=5x+15；（2）考点：解一元一次方程．专题：计算题．分析：（1）先移项，再合并同类项，最后化系数为1，从而得到方程的解；（2）先去括号，再移项、合并同类项，最后化系数为1，从而得到方程的解．解答：解：（1）移项，得10x﹣5x=12+15，合并同类项，得5x=27，方程的两边同时除以5，得x=；（2）去括号，得=，方程的两边同时乘以6，得x+1=4x﹣2，移项、合并同类项，得3x=3，方程的两边同时除以3，得x=1．点评：本题考查解一元一次方程，解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．27．解方程：（1）8y﹣3（3y+2）=7（2）．考点：解一元一次方程．专题：计算题．分析：（1）根据一元一次方程的解法，去括号，移项，合并同类项，系数化为1即可得解；（2）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，合并同类项，系数化为1，从而得到方程的解．解答：解：（1）去括号得，8y﹣9y﹣6=7，移项、合并得，﹣y=13，系数化为1得，y=﹣13；（2）去分母得，3（3x﹣1）﹣12=2（5x﹣7），去括号得，9x﹣3﹣12=10x﹣14，移项得，9x﹣10x=﹣14+3+12，合并同类项得，﹣x=1，系数化为1得，x=﹣1．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．28．当k为什么数时，式子比的值少3．考点：解一元一次方程．专题：计算题．分析：先根据题意列出方程，再根据一元一次方程的解法，去分母，去括号，移项，合并同类项，系数化为1即可得解．解答：解：依题意，得=+3，去分母得，5（2k+1）=3（17﹣k）+45，去括号得，10k+5=51﹣3k+45，移项得，10k+3k=51+45﹣5，合并同类项得，13k=91，系数化为1得，k=7，∴当k=7时，式子比的值少3．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．29．解下列方程：（I）12y﹣2.5y=7.5y+5（II）．考点：解一元一次方程．专题：计算题．分析：（Ⅰ）根据一元一次方程的解法，移项，合并同类项，系数化为1即可得解；（Ⅱ）是一个带分母的方程，所以要先去分母，再去括号，最后移项，合并同类项，系数化为1，从而得到方程的解．解答：解：（Ⅰ）移项得，12y﹣2.5y﹣7.5y=5，合并同类项得，2y=5，系数化为1得，y=2.5；（Ⅱ）去分母得，5（x+1）﹣10=（3x﹣2）﹣2（2x+3），去括号得，5x+5﹣10=3x﹣2﹣4x﹣6，移项得，5x﹣3x+4x=﹣2﹣6﹣5+10，合并同类项得，6x=﹣3，系数化为1得，x=﹣．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．30．解方程：．考点：解一元一次方程．专题：计算题．分析：由于方程的分子、分母均有小数，利用分数的基本性质，分子、分母同时扩大相同的倍数，可将小数化成整数．解答：解：原方程变形为，（3分）去分母，得3×（30x﹣11）﹣4×（40x﹣2）=2×（16﹣70x），（4分）去括号，得90x﹣33﹣160x+8=32﹣140x，（5分）移项，得90x﹣160x+140x=32+33﹣8，（6分）合并同类项，得70x=57，（7分）系数化为1，得．（8分）点评：本题考查一元一次方程的解法．解一元一次方程的一般步骤：去分母，去括号，移项，合并同类项，系数化为1．本题的难点在于方程的分子、分母均有小数，将小数化成整数不同于去分母，不是方程两边同乘一个数，而是将分子、分母同乘一个数．。

解一元一次方程练习题及答案过程一．解答题 1．解方程：2x+1=．3．解方程：4﹣x=3；解方程：．4．解方程：．5．解方程4﹣3=5；x﹣=2﹣．6．解方程：3=2x+3；解方程：=x﹣．7．﹣=8．解方程：5﹣2=3+x+1；．9．解方程：．110．解方程：4x﹣3=2； =2﹣．11．计算：计算：解方程：12．解方程：13．解方程：14．解方程：5﹣2=+2[3+]=5x﹣115．解方程：5x﹣2=7x+8；解方程：﹣=﹣；解方程：．16．解方程3=9﹣5217．解方程：解方程：4x﹣3=13解方程：x﹣﹣318．计算：﹣42×+|﹣2|3×3计算：﹣12﹣|0.5﹣|÷×[﹣2﹣2]解方程：4x﹣3=2；解方程：．19．计算：×；计算：÷；3解方程：3x+3=2x+7；解方程：．20．解方程﹣0.2=1；．21．解方程：﹣2=9﹣3x． 22．8x﹣3=9+5x．5x+2=9﹣4．．．23．解下列方程：0.5x﹣0.7=5.2﹣1.3；=﹣2．24．解方程：﹣0.5+3x=10；43x+8=2x+6；2x+3=5﹣4；．25．解方程：．26．解方程：10x﹣12=5x+15；27．解方程：8y﹣3=7．28．当k为什么数时，式子比的值少3．29．解下列方程： 12y﹣2.5y=7.5y+．30．解方程：．5解一元一次方程一、慧眼识金 1．某数的15等于4与这个数的45的差,那么这个数是．4-45-52．若3?2x?11?3x，则x?4的值为．８-８-４４３．若a?b，则①a?13?b?13；②13a?14b；③?34a??34b；④3a?1?3b?1中，正确的有．１个２个３个４个４．下列方程中，解是x??1的是． ?2?12?2?411x?1?52５．下列方程中，变形正确的是．由x?3?4得x?4? 由3=x?2得x?3? 由2-x?5得x?5? 由5?x?2得x?5?26．对于“x?y?a?b”，下列移项正确的是． x?b?y?ax?a?y?ba?x?y?ba?x?b?y ．某同学在解关于x 的方程5a?x?13时，误将?x看作?x，得到方程的解为x??2，则原方程的解为． x??3x?0x?2x?1８．小丽的年龄乘以3再减去3是18，那么小丽现在的年龄为． 7岁8岁16岁32岁二、画龙点睛1．在x?3，x?5，x?10中，是方程x?x?42?3的解．２．若m是3x?2?2x?1的解，则30m?10的值是．３．当x? 时，代数式12与13的差为１０．４．如果5m?14与m?14互为相反数，则m的值为．?6?0是关于x的一元一次方程，则a? ．５．已知方程xa?1６．如果3x?1?2x?3成立，则x的正数解为．７．已知3x?8?x4?a的解满足x?2?0，则1a? ．８．若2x3?2k?2k?4是关于x的一元一次方程，则k?，x?．三、考考你的基本功１．解下列方程?7x?6?22?6x； ?4x?3??5x?2；4x?5?3x；y?7??3y?5．2．x?2是方程ax?4?0的解，检验x?3是不是方程2ax?5?3x?4a的解．3．已知x4．如果?四、同步大闯关方程4x?2m?3x?1和方程3x?2m?4x?1的解相同，求m 的值和方程的解．关于x的方程mx?n?2x?3中，m、n是常数，请你给m、n赋值，并解此时关于x的方程．x3?y4?z6?3，求3x?4y?6z的值．2m?3?6?m是关于x的一元一次方程，试求代数式2008的值．解一元一次方程一、相信你都能选对 1、下列方程中是一元一次方程的是x?12A、x-y=200B、3x-200C、x+x=1D、2x?2=32、下列四组变形中，属于去括号的是1A.5x+3=0,则5x=-B.2x =,则x = 12C.3x-=5,则3x+4x-2=D.5x=1+4,则5x=53、某同学在方程5x-1=□x+3时，把□处的数字看错了，解得x=-4/3,该同学把□看成了A.3B.-C.D. -314、方程x - = +x的解是11A.-2;B.2;C.-2;D.25、下列解方程去分母正确的是x?1?1?x2A.由3,得2x - 1 = -x;x?2B.由2y?1?3x?24y3??1,得2 -x - = -3y?16?yC.由24x??,得3y + =y -y + 1 -y;D.由5?1?y?43,得12x - 1 =y +06、某件商品连续两次9折降价销售,降价后每件商品售价为a元,则该商品每件原价为aaA.0.92aB.1.12aC.1.1D.0.817、一个两位数，个位数字与十位数字的和是9，如果将个位数字与十位数字对调后所得的新数比原数大9，则原来的两位数为 A．5B．2C．7D．458、一个长方形的周长为2cm，这个长方形的长减少1 cm，宽增加cm，就可成为一个正方形，设长方形的长为xcm，可列方程A．x?1?? B．x?1??2C．x?1??2D．x?1??二、相信你填得又快又准、去括号且合并含有相同字母的项：3x+2=8y-6= 10、x =和x = -中,________是方程x - =的解.2?k?111、若代数式3的值是1,则k = _________.3?2x2?x12、当x=________时，式子2与3互为相反数.13、小明买了20本练习本，店主给他八折优惠，结果便宜1.6元，每本练习本的标价是元。

解一元一次方程经典题库及答案一．解答题（共30小题）1．（2005•宁德）解方程：2x+1=72．3．（1）解方程：4﹣x=3（2﹣x）；（2）解方程：．4．解方程：．5．解方程（1）4（x﹣1）﹣3（20﹣x）=5（x﹣2）；（2）x﹣=2﹣．6．（1）解方程：3（x﹣1）=2x+3；（2）解方程：=x﹣．7．﹣（1﹣2x）=（3x+1）8．解方程：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+1；（2）．9．解方程：．10．解方程：（1）4x﹣3（4﹣x）=2；（2）（x﹣1）=2﹣（x+2）．11．计算：（1）计算：（2）解方程：12．解方程：13．解方程：（1）（2）14．解方程：（1）5（2x+1）﹣2（2x﹣3）=6 （2）+2（3）[3（x﹣）+]=5x﹣115．（A类）解方程：5x﹣2=7x+8；（B类）解方程：（x﹣1）﹣（x+5）=﹣；（C类）解方程：．16．解方程（1）3（x+6）=9﹣5（1﹣2x）（2）（3）（4）17．解方程：（1）解方程：4x﹣3（5﹣x）=13（2）解方程：x﹣﹣318．（1）计算：﹣42×+|﹣2|3×（﹣）3（2）计算：﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]（3）解方程：4x﹣3（5﹣x）=2；（4）解方程：．19．（1）计算：（1﹣2﹣4）×；（2）计算：÷；（3）解方程：3x+3=2x+7；（4）解方程：．20．解方程（1）﹣0.2（x﹣5）=1；（2）．21．解方程：（x+3）﹣2（x﹣1）=9﹣3x．22．8x﹣3=9+5x．5x+2（3x﹣7）=9﹣4（2+x）．．．23．解下列方程：（1）0.5x﹣0.7=5.2﹣1.3（x﹣1）；（2）=﹣2．24．解方程：（1）﹣0.5+3x=10；（2）3x+8=2x+6；（3）2x+3（x+1）=5﹣4（x﹣1）；（4）．25．解方程：．26．解方程：（1）10x﹣12=5x+15；（2）27．解方程：（1）8y﹣3（3y+2）=7（2）．28．当k为什么数时，式子比的值少3．29．解下列方程：（II）．30．解方程：．6.2.4解一元一次方程（三）参考答案与试题解析一．解答题（共30小题）1．（2005•宁德）解方程：2x+1=7考点：解一元一次方程．专题：计算题；压轴题．分析：此题直接通过移项，合并同类项，系数化为1可求解．解答：解：原方程可化为：2x=7﹣1合并得：2x=6系数化为1得：x=3点评：解一元一次方程，一般要通过去分母，去括号，移项，合并同类项，未知数的系数化为1等步骤，把一个一元一次方程“转化”成x=a的形式．2．考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：左右同乘12可得：3[2x﹣（x﹣1）]=8（x﹣1），化简可得：3x+3=8x﹣8，移项可得：5x=11，解可得x=．故原方程的解为x=．点评：若是分式方程，先同分母，转化为整式方程后，再移项化简，解方程可得答案．3．（1）解方程：4﹣x=3（2﹣x）；（2）解方程：．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，然后再移项、合并同类型，最后化系数为1，得出方程的解；（2）题的方程中含有分数系数，应先对各式进行化简、整理，然后再按（1）的步骤求解．解答：解：（1）去括号得：4﹣x=6﹣3x，移项得：﹣x+3x=6﹣4，合并得：2x=2，系数化为1得：x=1．（2）去分母得：5（x﹣1）﹣2（x+1）=2，去括号得：5x﹣5﹣2x﹣2=2，移项得：5x﹣2x=2+5+2，合并得：3x=9，系数化1得：x=3．点评：（1）本题易在去分母、去括号和移项中出现错误，还可能会在解题前产生害怕心理．因为看到小数、分数比较多，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果．（2）本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍，值不变．这一性质在今后常会用到．4．解方程：．考点：解一元一次方程．专题：计算题．分析：此题两边都含有分数，分母不相同，如果直接通分，有一定的难度，但将方程左右同时乘以公分母6，难度就会降低．解答：解：去分母得：3（2﹣x）﹣18=2x﹣（2x+3），去括号得：6﹣3x﹣18=﹣3，移项合并得：﹣3x=9，∴x=﹣3．点评：本题易在去分母和移项中出现错误，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果．5．解方程（1）4（x﹣1）﹣3（20﹣x）=5（x﹣2）；（2）x﹣=2﹣．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项、合并同类项、化系数为1，从而得到方程的解；（2）先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：（1）去括号得：4x﹣4﹣60+3x=5x﹣10（2分）移项得：4x+3x﹣5x=4+60﹣10（3分）合并得：2x=54（5分）系数化为1得：x=27；（6分）（2）去分母得：6x﹣3（x﹣1）=12﹣2（x+2）（2分）去括号得：6x﹣3x+3=12﹣2x﹣4（3分）移项得：6x﹣3x+2x=12﹣4﹣3（4分）合并得：5x=5（5分）系数化为1得：x=1．（6分）点评：去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．去括号时要注意符号的变化．6．（1）解方程：3（x﹣1）=2x+3；（2）解方程：=x﹣．考点：解一元一次方程．专题：计算题．分析：（1）是简单的一元一次方程，通过移项，系数化为1即可得到；（2）是较为复杂的去分母，本题方程两边都含有分数系数，如果直接通分，有一定的难度，但对每一个式子先进行化简、整理为整数形式，难度就会降低．解答：解：（1）3x﹣3=2x+33x﹣2x=3+3x=6；（2）方程两边都乘以6得：x+3=6x﹣3（x﹣1）x+3=6x﹣3x+3x﹣6x+3x=3﹣3﹣2x=0∴x=0．点评：本题易在去分母、去括号和移项中出现错误，还可能会在解题前不知如何寻找公分母，怎样合并同类项，怎样化简，所以要学会分开进行，从而达到分解难点的效果．去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．7．﹣（1﹣2x）=（3x+1）考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：﹣7（1﹣2x）=3×2（3x+1）﹣7+14x=18x+6﹣4x=13x=﹣．点评：解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为1．此题去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．8．解方程：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+1；（2）．考点：解一元一次方程．专题：计算题．分析：（1）可采用去括号，移项，合并同类项，系数化1的方式进行；（2）本题方程两边都含有分数系数，如果直接通分，有一定的难度，但对每一个式子先进行化简、整理为整数形式，难度就会降低．解答：解：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+13x﹣7=4x﹣2∴x=﹣5；（2）原方程可化为：去分母得：40x+60=5（18﹣18x）﹣3（15﹣30x），去括号得：40x+60=90﹣90x﹣45+90x，移项、合并得：40x=﹣15，系数化为1得：x=．点评：（1）本题易在去分母、去括号和移项中出现错误，还可能会在解题前产生害怕心理．因为看到小数、分数比较多，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果；（2）本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍，值不变．这一性质在今后常会用到．9．解方程：．考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：，去分母得：2x﹣（3x+1）=6﹣3（x﹣1），去括号得：2x﹣3x﹣1=6﹣3x+3，移项、合并同类项得：2x=10，系数化为1得：x=5．点评：去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．10．解方程：（1）4x﹣3（4﹣x）=2；（2）（x﹣1）=2﹣（x+2）．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项，合并同类项，系数化1，即可求出方程的解；（2）先去分母，再去括号，移项，合并同类项，系数化1可求出方程的解．解答：解：（1）4x﹣3（4﹣x）=2去括号，得4x﹣12+3x=2移项，合并同类项7x=14系数化1，得x=2．（2）（x﹣1）=2﹣（x+2）去分母，得5（x﹣1）=20﹣2（x+2）去括号，得5x﹣5=20﹣2x﹣4移项、合并同类项，得7x=21系数化1，得x=3．点评：（1）此题主要是去括号，移项，合并同类项，系数化1．（2）方程两边每一项都要乘各分母的最小公倍数，方程两边每一项都要乘各分母的最小公倍数，切勿漏乘不含有分母的项，另外分数线有两层意义，一方面它是除号，另一方面它又代表着括号，所以在去分母时，应该将分子用括号括上．11．计算：（1）计算：（2）解方程：考点：解一元一次方程；有理数的混合运算．专题：计算题．分析：（1）根据有理数的混合运算法则计算：先算乘方、后算乘除、再算加减；（2）两边同时乘以最简公分母4，即可去掉分母．解答：解：（1）原式=，=，=．（2）去分母得：2（x﹣1）﹣（3x﹣1）=﹣4，解得：x=3．点评：解答此题要注意：（1）去分母时最好先去中括号、再去小括号，以减少去括号带来的符号变化次数；（2）去分母就是方程两边同时乘以分母的最简公分母．12．解方程：考点：解一元一次方程．专题：计算题．分析：（1）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．（2）解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、化系数为1．解答：解：（1）去分母得：3（3x﹣1）+18=1﹣5x，去括号得：9x﹣3+18=1﹣5x，移项、合并得：14x=﹣14，系数化为1得：x=﹣1；（2）去括号得：x﹣x+1=x，移项、合并同类项得：x=﹣1，系数化为1得：x=﹣．点评：本题考查解一元一次方程，正确掌握解一元一次方程的一般步骤，注意移项要变号、去分母时“1”也要乘以最小公倍数．13．解方程：（1）（2）考点：解一元一次方程．专题：计算题．分析：（1）去分母、去括号、移项、合并同类项、化系数为1．（2）去分母、去括号、移项、合并同类项、化系数为1．解答：（1）解：去分母得：5（3x+1）﹣2×10=3x﹣2﹣2（2x+3），去括号得：15x+5﹣20=3x﹣2﹣4x﹣6，移项得：15x+x=﹣8+15，合并得：16x=7，解得：；（2）解：，4（x﹣1）﹣18（x+1）=﹣36，4x﹣4﹣18x﹣18=﹣36，﹣14x=﹣14，x=1．点评：本题考查解一元一次方程，正确掌握解一元一次方程的一般步骤，注意移项要变号、去分母时“1”也要乘以最小公倍数．14．解方程：（1）5（2x+1）﹣2（2x﹣3）=6 （2）+2（3）[3（x﹣）+]=5x﹣1考点：解一元一次方程．专题：计算题．分析：（2）通过去括号、移项、合并同类项、系数化为1，解得x的值；（3）乘最小公倍数去分母即可；（4）主要是去括号，也可以把分数转化成整数进行计算．解答：解：（1）去括号得：10x+5﹣4x+6=6移项、合并得：6x=﹣5，方程两边都除以6，得x=﹣；（2）去分母得：3（x﹣2）=2（4﹣3x）+24，去括号得：3x﹣6=8﹣6x+24，移项、合并得：9x=38，方程两边都除以9，得x=；（3）整理得：[3（x﹣）+]=5x﹣1，4x﹣2+1=5x﹣1，移项、合并得：x=0．点评：一元一次方程的解法：一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤，把一个一元一次方程“转化”成x=a的形式．解题时，要灵活运用这些步骤．15．（A类）解方程：5x﹣2=7x+8；（B类）解方程：（x﹣1）﹣（x+5）=﹣；（C类）解方程：．考点：解一元一次方程．专题：计算题．分析：通过去分母、去括号、移项、系数化为1等方法，求得各方程的解．解答：解：A类：5x﹣2=7x+8移项：5x﹣7x=8+2化简：﹣2x=10即：x=﹣5；B类：（x﹣1）﹣（x+5）=﹣去括号：x﹣﹣x﹣5=﹣化简：x=5即：x=﹣；C类：﹣=1去分母：3（4﹣x）﹣2（2x+1）=6去括号：12﹣3x﹣4x﹣2=6化简：﹣7x=﹣4即：x=．点评：本题主要考查一元一次方程的解法，比较简单，但要细心运算．16．解方程（1）3（x+6）=9﹣5（1﹣2x）（2）（3）（4）考点：解一元一次方程．专题：计算题．分析：（1）去括号以后，移项，合并同类项，系数化为1即可求解；（2）（3）首先去掉分母，再去括号以后，移项，合并同类项，系数化为1以后即可求解；（4）首先根据分数的基本性质，把第一项分母中的0.3化为整数，再去分母，求解．解答：解：（1）去括号得：3x+18=9﹣5+10x移项得：3x﹣10x=9﹣5﹣18合并同类项得：﹣7x=﹣14则x=2；（2）去分母得：2x+1=x+3﹣5移项，合并同类项得：x=﹣3；（3）去分母得：10y+2（y+2）=20﹣5（y﹣1）去括号得：10y+2y+4=20﹣5y+5移项，合并同类项得：17y=21系数化为1得：；（4）原方程可以变形为：﹣5x=﹣1去分母得：17+20x﹣15x=﹣3移项，合并同类项得：5x=﹣20系数化为1得：x=﹣4．点评：解方程的过程中要注意每步的依据，这几个题目都是基础的题目，需要熟练掌握．17．解方程：（1）解方程：4x﹣3（5﹣x）=13（2）解方程：x﹣﹣3考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项，化系数为1，从而得到方程的解．（2）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：（1）去括号得：4x﹣15+3x=13，移项合并得：7x=28，系数化为1得：得x=4；（2）原式变形为x+3=，去分母得：5（2x﹣5）+3（x﹣2）=15（x+3），去括号得10x﹣25+3x﹣6=15x+45，移项合并得﹣2x=76，系数化为1得：x=﹣38．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．18．（1）计算：﹣42×+|﹣2|3×（﹣）3（2）计算：﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]（3）解方程：4x﹣3（5﹣x）=2；（4）解方程：．考点：解一元一次方程；有理数的混合运算．分析：（1）利用平方和立方的定义进行计算．（2）按四则混合运算的顺序进行计算．（3）主要是去括号，移项合并．（4）两边同乘最小公倍数去分母，再求值．解答：解：（1）﹣42×+|﹣2|3×（﹣）3==﹣1﹣1=﹣2．（2）﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]====．（3）解方程：4x﹣3（5﹣x）=2去括号，得4x﹣15+3x）=2移项，得4x+3x=2+15合并同类项，得7x=17系数化为1，得．（4）解方程：去分母，得15x﹣3（x﹣2）=5（2x﹣5）﹣3×15去括号，得15x﹣3x+6=10x﹣25﹣45移项，得15x﹣3x﹣10x=﹣25﹣45﹣6合并同类项，得2x=﹣76系数化为1，得x=﹣38．点评：前两道题考查了学生有理数的混合运算，后两道考查了学生解一元一次方程的能力．19．（1）计算：（1﹣2﹣4）×；（2）计算：÷；（3）解方程：3x+3=2x+7；（4）解方程：．考点：解一元一次方程；有理数的混合运算．专题：计算题．分析：（1）和（2）要熟练掌握有理数的混合运算；（3）和（4）首先熟悉解一元一次方程的步骤：去分母，去括号，移项，合并同类项，系数化为1．解答：解：（1）（1﹣2﹣4）×=﹣=﹣13；（2）原式=﹣1×（﹣4﹣2）×（﹣）=6×（﹣）=﹣9；（3）解方程：3x+3=2x+7移项，得3x﹣2x=7﹣3合并同类项，得x=4；（4）解方程：去分母，得6（x+15）=15﹣10（x﹣7）去括号，得6x+90=15﹣10x+70移项，得6x+10x=15+70﹣90合并同类项，得16x=﹣5系数化为1，得x=．点评：（1）和（2）要注意符号的处理；（4）要特别注意去分母的时候不要发生数字漏乘的现象，熟练掌握去括号法则以及合并同类项法则．20．解方程（1）﹣0.2（x﹣5）=1；（2）．考点：解一元一次方程．分析：（1）通过去括号、移项、系数化为1等过程，求得x的值；（2）通过去分母以及去括号、移项、系数化为1等过程，求得x的值．解答：解：（1）﹣0.2（x﹣5）=1；去括号得：﹣0.2x+1=1，∴﹣0.2x=0，∴x=0；（2）．去分母得：2（x﹣2）+6x=9（3x+5）﹣（1﹣2x），∴﹣21x=48，∴x=﹣．点评：此题主要考查了一元一次方程解法，解一元一次方程常见的过程有去括号、移项、系数化为1等．21．解方程：（x+3）﹣2（x﹣1）=9﹣3x．考点：解一元一次方程．专题：计算题．分析：先去括号得x+3﹣2x+2=9﹣3x，然后移项、合并同类得到2x=4，然后把x的系数化为1即可．解答：解：去括号得x+3﹣2x+2=9﹣3x，移项得x﹣2x+3x=9﹣3﹣2，合并得2x=4，系数化为1得x=2．点评：本题考查了解一元一次方程：先去分母，再去括号，接着移项，把含未知数的项移到方程左边，不含未知数的项移到方程右边，然后合并同类项，最后把未知数的系数化为1得到原方程的解．22．8x﹣3=9+5x．5x+2（3x﹣7）=9﹣4（2+x）．．．考点：解一元一次方程．专题：方程思想．分析：本题是解4个不同的一元一次方程，第一个通过移项、合并同类项及系数化1求解．第二个先去括号再通过移项、合并同类项及系数化1求解．第三个先去分母再同第二个．第四个先分子分母乘以10，再同第三个求解．解答：8x﹣3=9+5x，解：8x﹣5x=9+3，3x=12，∴x=4．∴x=4是原方程的解；5x+2（3x﹣7）=9﹣4（2+x），解：5x+6x﹣14=9﹣8﹣4x，5x+6x+4x=9﹣8+14，15x=15，∴x=1．∴x=1是原方程的解．．解：3（x﹣1）﹣2（2x+1）=12，3x﹣3﹣4x﹣2=12，3x﹣4x=12+3+2，﹣x=17，∴x=﹣17．∴x=﹣17是原方程的解．，解：，5（10x﹣3）=4（10x+1）+40，50x﹣15=40x+4+40，50x﹣40x=4+40+15，10x=59，∴x=．∴x=是原方程的解．点评：此题考查的知识点是解一元一次方程，关键是注意解方程时的每一步都要认真仔细，如移项时要变符号．23．解下列方程：（1）0.5x﹣0.7=5.2﹣1.3（x﹣1）；（2）=﹣2．考点：解一元一次方程．分析：（1）首先去括号，然后移项、合并同类项，系数化成1，即可求解；（2）首先去分母，然后去括号，移项、合并同类项，系数化成1，即可求解解答：解：（1）去括号，得：0.5x﹣0.7=5.2﹣1.3x+1.3移项，得：0.5x+1.3x=5.2+1.3+0.7合并同类项，得：1.8x=7.2，则x=4；（2）去分母得：7（1﹣2x）=3（3x+1）﹣42，去括号，得：7﹣14x=9x+3﹣42，移项，得：﹣14x﹣9x=3﹣42﹣7，合并同类项，得：﹣23x=﹣46，则x=2．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．24．解方程：（1）﹣0.5+3x=10；（2）3x+8=2x+6；（3）2x+3（x+1）=5﹣4（x﹣1）；（4）．考点：解一元一次方程．分析：（1）移项，合并同类项，然后系数化成1即可求解；（2）移项，合并同类项，然后系数化成1即可求解；（3）去括号、移项，合并同类项，然后系数化成1即可求解；（4）首先去分母，然后去括号、移项，合并同类项，然后系数化成1即可求解．解答：解：（1）3x=10.5，x=3.5；（2）3x﹣2x=6﹣8，x=﹣2；（3）2x+3x+3=5﹣4x+4，2x+3x+4x=5+4﹣3，9x=6，x=；（4）2（x+1）+6=3（3x﹣2），2x+2+6=9x﹣6，2x﹣9x=﹣6﹣2﹣6，﹣7x=﹣14，x=2．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．25．解方程：．考点：解一元一次方程．专题：计算题．分析：方程两边乘以10去分母后，去括号，移项合并，将x系数化为1，即可求出解．解答：解：去分母得：5（3x﹣1）﹣2（5x﹣6）=2，去括号得：15x﹣5﹣10x+12=2，移项合并得：5x=﹣5，解得：x=﹣1．点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1，求出解．26．解方程：（1）10x﹣12=5x+15；（2）考点：解一元一次方程．专题：计算题．分析：（1）先移项，再合并同类项，最后化系数为1，从而得到方程的解；（2）先去括号，再移项、合并同类项，最后化系数为1，从而得到方程的解．解答：解：（1）移项，得10x﹣5x=12+15，合并同类项，得5x=27，方程的两边同时除以5，得x=；（2）去括号，得=，方程的两边同时乘以6，得x+1=4x﹣2，移项、合并同类项，得3x=3，方程的两边同时除以3，得x=1．点评：本题考查解一元一次方程，解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．27．解方程：（1）8y﹣3（3y+2）=7（2）．考点：解一元一次方程．专题：计算题．分析：（1）根据一元一次方程的解法，去括号，移项，合并同类项，系数化为1即可得解；（2）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，合并同类项，系数化为1，从而得到方程的解．解答：解：（1）去括号得，8y﹣9y﹣6=7，移项、合并得，﹣y=13，系数化为1得，y=﹣13；（2）去分母得，3（3x﹣1）﹣12=2（5x﹣7），去括号得，9x﹣3﹣12=10x﹣14，移项得，9x﹣10x=﹣14+3+12，合并同类项得，﹣x=1，系数化为1得，x=﹣1．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．28．当k为什么数时，式子比的值少3．考点：解一元一次方程．专题：计算题．分析：先根据题意列出方程，再根据一元一次方程的解法，去分母，去括号，移项，合并同类项，系数化为1即可得解．解答：解：依题意，得=+3，去分母得，5（2k+1）=3（17﹣k）+45，去括号得，10k+5=51﹣3k+45，移项得，10k+3k=51+45﹣5，合并同类项得，13k=91，系数化为1得，k=7，∴当k=7时，式子比的值少3．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．29．解下列方程：（I）12y﹣2.5y=7.5y+5（II）．考点：解一元一次方程．专题：计算题．分析：（Ⅰ）根据一元一次方程的解法，移项，合并同类项，系数化为1即可得解；（Ⅱ）是一个带分母的方程，所以要先去分母，再去括号，最后移项，合并同类项，系数化为1，从而得到方程的解．解答：解：（Ⅰ）移项得，12y﹣2.5y﹣7.5y=5，合并同类项得，2y=5，系数化为1得，y=2.5；（Ⅱ）去分母得，5（x+1）﹣10=（3x﹣2）﹣2（2x+3），去括号得，5x+5﹣10=3x﹣2﹣4x﹣6，移项得，5x﹣3x+4x=﹣2﹣6﹣5+10，合并同类项得，6x=﹣3，系数化为1得，x=﹣．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．30．解方程：．考点：解一元一次方程．专题：计算题．分析：由于方程的分子、分母均有小数，利用分数的基本性质，分子、分母同时扩大相同的倍数，可将小数化成整数．解答：解：原方程变形为，（3分）去分母，得3×（30x﹣11）﹣4×（40x﹣2）=2×（16﹣70x），（4分）去括号，得90x﹣33﹣160x+8=32﹣140x，（5分）移项，得90x﹣160x+140x=32+33﹣8，（6分）合并同类项，得70x=57，（7分）系数化为1，得．（8分）点评：本题考查一元一次方程的解法．解一元一次方程的一般步骤：去分母，去括号，移项，合并同类项，系数化为1．本题的难点在于方程的分子、分母均有小数，将小数化成整数不同于去分母，不是方程两边同乘一个数，而是将分子、分母同乘一个数．。

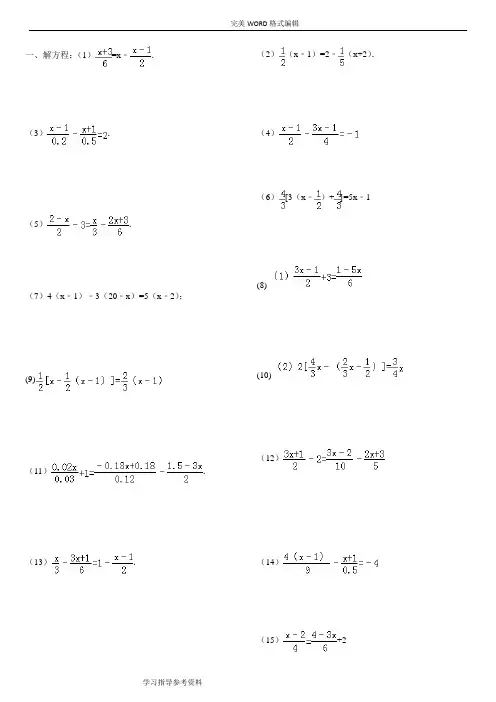
一、解方程：（1）=x ﹣．（3）．（5）．（7）4（x﹣1）﹣3（20﹣x ）=5（x﹣2）；(9)（11）．（13）．（2）（x﹣1）=2﹣（x+2）．（4）（6）[3（x﹣）+]=5x﹣1 (8)(10)（12）（14）（17）（19）x﹣﹣3（21）．（23）．20．解方程（1）．（2）．（I8）12y﹣2.5y=7.5y+5（20）．（22）．二、计算：（1）(2)÷（4）﹣42×+|﹣2|3×（﹣）3（5）当k为什么数时，式子比的值少3．6.2.4解一元一次方程（三）参考答案与试题解析一．解答题（共30小题）1．（2005•宁德）解方程：2x+1=7考点：解一元一次方程．专题：计算题；压轴题．分析：此题直接通过移项，合并同类项，系数化为1可求解．解答：解：原方程可化为：2x=7﹣1 合并得：2x=6系数化为1得：x=3点评：解一元一次方程，一般要通过去分母，去括号，移项，合并同类项，未知数的系数化为1等步骤，把一个一元一次方程“转化”成x=a的形式．2．考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：左右同乘12可得：3[2x﹣（x﹣1）]=8（x﹣1），化简可得：3x+3=8x﹣8，移项可得：5x=11，解可得x=．故原方程的解为x=．点评：若是分式方程，先同分母，转化为整式方程后，再移项化简，解方程可得答案．3．（1）解方程：4﹣x=3（2﹣x）；（2）解方程：．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，然后再移项、合并同类型，最后化系数为1，得出方程的解；移项得：﹣x+3x=6﹣4，合并得：2x=2，系数化为1得：x=1．（2）去分母得：5（x﹣1）﹣2（x+1）=2，去括号得：5x﹣5﹣2x﹣2=2，移项得：5x﹣2x=2+5+2，合并得：3x=9，系数化1得：x=3．点评：（1）本题易在去分母、去括号和移项中出现错误，还可能会在解题前产生害怕心理．因为看到小数、分数比较多，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果．（2）本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍，值不变．这一性质在今后常会用到．4．解方程：．考点：解一元一次方程．专题：计算题．分析：此题两边都含有分数，分母不相同，如果直接通分，有一定的难度，但将方程左右同时乘以公分母6，难度就会降低．解答：解：去分母得：3（2﹣x）﹣18=2x﹣（2x+3），去括号得：6﹣3x﹣18=﹣3，移项合并得：﹣3x=9，∴x=﹣3．点评：本题易在去分母和移项中出现错误，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果．5．解方程（1）4（x﹣1）﹣3（20﹣x）=5（x﹣2）；（2）x﹣=2﹣．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项、合并同类项、化系数为1，从而得到方程的解；（2）先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：（1）去括号得：4x﹣4﹣60+3x=5x﹣10（2分）移项得：4x+3x﹣5x=4+60﹣10（3分）合并得：2x=54（5分）系数化为1得：x=27；（6分）（2）去分母得：6x﹣3（x﹣1）=12﹣2（x+2）（2分）去括号得：6x﹣3x+3=12﹣2x﹣4（3分）移项得：6x﹣3x+2x=12﹣4﹣3（4分）合并得：5x=5（5分）多项式）作为一个整体加上括号．去括号时要注意符号的变化．6．（1）解方程：3（x﹣1）=2x+3；（2）解方程：=x﹣．考点：解一元一次方程．专题：计算题．分析：（1）是简单的一元一次方程，通过移项，系数化为1即可得到；（2）是较为复杂的去分母，本题方程两边都含有分数系数，如果直接通分，有一定的难度，但对每一个式子先进行化简、整理为整数形式，难度就会降低．解答：解：（1）3x﹣3=2x+33x﹣2x=3+3x=6；（2）方程两边都乘以6得：x+3=6x﹣3（x﹣1）x+3=6x﹣3x+3x﹣6x+3x=3﹣3﹣2x=0∴x=0．点评：本题易在去分母、去括号和移项中出现错误，还可能会在解题前不知如何寻找公分母，怎样合并同类项，怎样化简，所以要学会分开进行，从而达到分解难点的效果．去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．7．﹣（1﹣2x）=（3x+1）考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：﹣7（1﹣2x）=3×2（3x+1）﹣7+14x=18x+6﹣4x=13x=﹣．点评：解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为1．此题去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．8．解方程：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+1；（2）．点：专题：计算题．分析：（1）可采用去括号，移项，合并同类项，系数化1的方式进行；（2）本题方程两边都含有分数系数，如果直接通分，有一定的难度，但对每一个式子先进行化简、整理为整数形式，难度就会降低．解答：解：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+13x﹣7=4x﹣2∴x=﹣5；（2）原方程可化为：去分母得：40x+60=5（18﹣18x）﹣3（15﹣30x），去括号得：40x+60=90﹣90x﹣45+90x，移项、合并得：40x=﹣15，系数化为1得：x=．点评：（1）本题易在去分母、去括号和移项中出现错误，还可能会在解题前产生害怕心理．因为看到小数、分数比较多，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果；（2）本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍，值不变．这一性质在今后常会用到．9．解方程：．考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：，去分母得：2x﹣（3x+1）=6﹣3（x﹣1），去括号得：2x﹣3x﹣1=6﹣3x+3，移项、合并同系数化为1得：x=5．点评：去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．10．解方程：（1）4x﹣3（4﹣x）=2；（2）（x﹣1）=2﹣（x+2）．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项，合并同类项，系数化1，即可求出方程的解；（2）先去分母，再去括号，移项，合并同类项，系数化1可求出方程的解．解答：解：（1）4x﹣3（4﹣x）=2去括号，得4x﹣12+3x=2移项，合并同类项7x=14系数化1，得x=2．（2）（x﹣1）=2﹣（x+2）去分母，得5去括号，得5x﹣5=20﹣2x﹣4移项、合并同类项，得7x=21系数化1，得x=3．点评：（1）此题主要是去括号，移项，合并同类项，系数化1．（2）方程两边每一项都要乘各分母的最小公倍数，方程两边每一项都要乘各分母的最小公倍数，切勿漏乘不含有分母的项，另外分数线有两层意义，一方面它是除号，另一方面它又代表着括号，所以在去分母时，应该将分子用括号括上．11．计算：（1）计算：（2）解方程：考点：解一元一次方程；有理数的混合运算．专题：计算题．分析：（1）根据有理数的混合运算法则计减；（2）两边同时乘以最简公分母4，即可去掉分母．解答：解：（1）原式=，=，=．（2）去分母得：2（x﹣1）﹣（3x﹣1）=﹣4，解得：x=3．点评：解答此题要注意：（1）去分母时最好先去中括号、再去小括号，以减少去括号带来的符号变化次数；（2）去分母就是方程两边同时乘以分母的最简公分母．12．解方程：考点：解一元一次方程．专题：计算题．分析：（1）这是一个带分母的方程，所以要为1，从而得到方程的解．（2）解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、化系数为1．解答：解：（1）去分母得：3（3x﹣1）+18=1﹣5x，去括号得：9x﹣3+18=1﹣5x，移项、合并得：14x=﹣14，系数化为1得：x=﹣1；（2）去括号得：x﹣x+1=x，移项、合并同类项得：x=﹣1，系数化为1得：x=﹣．点评：本题考查解一元一次方程，正确掌握解一元一次方程的一般步骤，注意移项要变号、去分母时“1”也要乘以最小公倍数．13．解方程：（2）考点：解一元一次方程．专题：计算题．分析：（1）去分母、去括号、移项、合并同类项、化系数为1．（2）去分母、去括号、移项、合并同类项、化系数为1．解答：（1）解：去分母得：5（3x+1）﹣2×10=3x﹣2﹣2（2x+3），去括号得：15x+5﹣20=3x﹣2﹣4x﹣6，移项得：15x+x=﹣8+15，合并得：16x=7，解得：；（2）解：，4（x﹣1）﹣18（x+1）=﹣36，4x﹣4﹣18x﹣18=﹣36，﹣14x=﹣14，x=1．点评：本题考查解一元一次方程，正确掌握解一元一次方程的一般步骤，注意移项要变号、去分母时“1”也要乘以最小公倍数．14．解方程：（1）5（2x+1）﹣2（2x﹣3）=6 （2）+2（3）[3（x﹣）+]=5x﹣1考点：解一元一次方程．专题：计算题．分析：（2）通过去括号、移项、合并同类项、系数化为1，解得x的值；（3）乘最小公倍数去分母即可；（4）主要是去括号，也可以把分数转化成整数进行计算．解答：解：（1）去括号得：10x+5﹣4x+6=6移项、合并得：6x=﹣5，方程两边都除以6，得x=﹣；（2）去分母得：3（x﹣2）=2（4﹣3x）+24，去括号得：3x﹣6=8﹣6x+24，移项、合并得：9x=38，方程两边都除以9，得x=；（3）整理得：[3（x﹣）+]=5x﹣1，4x﹣2+1=5x﹣1，移项、合并得：x=0．点评：一元一次方程的解法：一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤，把一个一元一次方程“转化”成x=a的形式．解题时，要灵活运用这些步骤．15．（A类）解方程：5x﹣2=7x+8；（B类）解方程：（x﹣1）﹣（x+5）=﹣；（C类）解方程：．考点：解一元一次方程．专题：计算题．分析：通过去分母、去括号、移项、系数化为1等方法，求得各方程的解．解答：解：A类：5x﹣2=7x+8移项：5x﹣7x=8+2化简：﹣2x=10即：x=﹣5；B类：（x﹣1）﹣（x+5）=﹣去括号：x﹣﹣x﹣5=﹣化简：x=5即：x=﹣；C类：﹣=1去分母：3（4﹣x）﹣2（2x+1）=6去括号：12﹣3x﹣4x﹣2=6化简：﹣7x=﹣4即：x=．点评：本题主要考查一元一次方程的解法，比较简单，但要细心运算．16．解方程（1）3（x+6）=9﹣5（1﹣2x）（2）（3）（4）考点：解一元一次方程．专题：计算题．分析：（1）去括号以后，移项，合并同类项，系数化为1即可求解；（2）（3）首先去掉分母，再去括号以后，移项，合并同类项，系数化为1以后即可求解；（4）首先根据分数的基本性质，把第一项分母中的0.3化为整数，再去分母，求解．解答：解：（1）去括号得：3x+18=9﹣5+10x 移项得：3x﹣10x=9﹣5﹣18合并同类项得：﹣7x=﹣14则x=2；（2）去分母得：2x+1=x+3﹣5移项，合并同类项得：x=﹣3；（3）去分母得：10y+2（y+2）=20﹣5（y﹣1）去括号得：10y+2y+4=20﹣5y+5移项，合并同类项得：17y=21系数化为1得：；（4）原方程可以变形为：﹣5x=﹣1去分母得：17+20x﹣15x=﹣3移项，合并同类项得：5x=﹣20系数化为1得：x=﹣4．解方程的过程中要注意每步的依据，这几个题目都是基础的题目，需要熟练掌握．点评：17．解方程：（1）解方程：4x﹣3（5﹣x）=13（2）解方程：x﹣﹣3考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项，化系数为1，从而得到方程的解．（2）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：（1）去括号得：4x﹣15+3x=13，移项合并得：7x=28，系数化为1得：得x=4；（2）原式变形为x+3=，去分母得：5（2x﹣5）+3（x﹣2）=15（x+3），去括号得10x﹣25+3x﹣6=15x+45，移项合并得﹣2x=76，系数化为1得：x=﹣38．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．18．（1）计算：﹣42×+|﹣2|3×（﹣）3（2）计算：﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]（3）解方程：4x﹣3（5﹣x）=2；（4）解方程：．考点：解一元一次方程；有理数的混合运算．分析：（1）利用平方和立方的定义进行计算．（2）按四则混合运算的顺序进行计算．（3）主要是去括号，移项合并．乘最小公倍数去分母，再求值．解答：解：（1）﹣42×+|﹣2|3×（﹣）3==﹣1﹣1=﹣2．（2）﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]====．（3）解方程：4x﹣3（5﹣x）=2去括号，得4x﹣15+3x）=2移项，得4x+3x=2+15合并同类项，得7x=17系数化为1，得．（4）解方程：去分母，得15x﹣3（x﹣﹣3×15去括号，得15x﹣3x+6=10x﹣25﹣45移项，得15x﹣3x﹣10x=﹣25﹣45﹣6合并同类项，得2x=﹣76系数化为1，得x=﹣38．点评：前两道题考查了学生有理数的混合运算，后两道考查了学生解一元一次方程的能力．19．（1）计算：（1﹣2﹣4）×；（2）计算：÷；（3）解方程：3x+3=2x+7；（4）解方程：．考点：解一元一次方程；有理数的混合运算．专题：计算题．分析：（1）和（2）要熟练掌握有理数的混合运算；（3）和（4）首先熟悉解一元一次方程的步骤：去分母，去括号，移项，合并同类项，系数化为1．解答：解：（1）（1﹣2﹣4）×=﹣=﹣13；（2）原式=﹣1×（﹣4﹣2）×（﹣）=6×（﹣）=﹣9；（3）解方程：3x+3=2x+7移项，得3x﹣2x=7﹣3合并同类项，得x=4；（4）解方程：去分母，得6（x+15）=15﹣10（x﹣7）去括号，得6x+90=15﹣10x+70移项，得6x+10x=15+70﹣90合并同类项，得16x=﹣5系数化为1，得x=．点评：（1）和（2）要注意符号的处理；（4）要特别注意去分母的时候不要发生数字漏乘的现象，熟练掌握去括号法则以及合并同类项法则．20．解方程（1）﹣0.2（x﹣5）=1；（2）．考点：解一元一次方程．分析：（1）通过去括号、移项、系数化为1等过程，求得x的值；（2）通过去分母以及去括号、移项、系数化为1等过程，求得x的值．解答：解：（1）﹣0.2（x﹣5）=1；去括号得：﹣0.2x+1=1，∴﹣0.2x=0，∴x=0；（2）．去分母得：2（x﹣2）+6x=9（3x+5）﹣（1﹣2x），∴﹣21x=48，∴x=﹣．点评：此题主要考查了一元一次方程解法，解一元一次方程常见的过程有去括号、移项、系数化为1等．21．解方程：（x+3）﹣2（x﹣1）=9﹣3x．考点：解一元一次方程．专题：计算题．分析：先去括号得x+3﹣2x+2=9﹣3x，然后移项、合并同类得到2x=4，然后把x的系数化为1即可．解答：解：去括号得x+3﹣2x+2=9﹣3x，移项得x﹣2x+3x=9﹣3﹣2，合并得2x=4，系数化为1得x=2．点评：本题考查了解一元一次方程：先去分母，再去括号，接着移项，把含未知数的项移到方程左边，不含未知数的项移到方程右边，然后合并同类项，最后把未知数的系数化为1得到原方程的解．22．8x﹣3=9+5x．5x+2（3x﹣7）=9﹣4（2+x）．．．考点：解一元一次方程．专题：方程思想．分析：本题是解4个不同的一元一次方程，第一个通过移项、合并同类项及系数化1求解．第二个先去括号再通过移项、合并同类项及系数化1求解．第三个先去分母再同第二个．第四个先分子分母乘以10，再同第三个求解．解答：8x﹣3=9+5x，解：8x﹣5x=9+3，3x=12，∴x=4．∴x=4是原方程的解；5x+2（3x﹣7）=9﹣4（2+x），解：5x+6x﹣14=9﹣8﹣4x，5x+6x+4x=9﹣8+14，15x=15，∴x=1．∴x=1是原方程的解．．解：3（x﹣1）﹣2（2x+1）=12，3x﹣3﹣4x﹣2=12，3x﹣4x=12+3+2，﹣x=17，∴x=﹣17．∴x=﹣17是原方程的解．，解：，5（10x﹣3）=4（10x+1）+40，50x﹣15=40x+4+40，50x﹣40x=4+40+15，10x=59，∴x=．∴x=是原方程的解．点评：此题考查的知识点是解一元一次方程，关键是注意解方程时的每一步都要认真仔细，如移项时要变符号．23．解下列方程：（1）0.5x﹣0.7=5.2﹣1.3（x﹣1）；（2）=﹣2．考点：解一元一次方程．分析：（1）首先去括号，然后移项、合并同类项，系数化成1，即可求解；（2）首先去分母，然后去括号，移项、合并同类项，系数化成1，即可求解解答：解：（1）去括号，得：0.5x﹣0.7=5.2﹣1.3x+1.3移项，得：0.5x+1.3x=5.2+1.3+0.7合并同类项，得：1.8x=7.2，则x=4；（2）去分母得：7（1﹣2x）=3（3x+1）﹣42，去括号，得：7﹣14x=9x+3﹣42，移项，得：﹣14x﹣9x=3﹣42﹣7，合并同类项，得：﹣23x=﹣46，则x=2．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．24．解方程：（1）﹣0.5+3x=10；（2）3x+8=2x+6；（3）2x+3（x+1）=5﹣4（x﹣1）；（4）．考点：解一元一次方程．分析：（1）移项，合并同类项，然后系数化成1即可求解；（2）移项，合并同类项，然后系数化成1即可求解；（3）去括号、移项，合并同类项，然后系数化成1即可求解；（4）首先去分母，然后去括号、移项，合并同类项，然后系数化成1即可求解．解答：解：（1）3x=10.5，x=3.5；（2）3x﹣2x=6﹣8，x=﹣2；（3）2x+3x+3=5﹣4x+4，2x+3x+4x=5+4﹣3，9x=6，x=；（4）2（x+1）+6=3（3x﹣2），2x+2+6=9x﹣6，2x﹣9x=﹣6﹣2﹣6，﹣7x=﹣14，x=2．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．25．解方程：．考点：解一元一次方程．专题：计算题．分析：方程两边乘以10去分母后，去括号，移项合并，将x系数化为1，即可求出解．解答：解：去分母得：5（3x﹣1）﹣2（5x﹣6）=2，去括号得：15x﹣5﹣10x+12=2，移项合并得：5x=﹣5，解得：x=﹣1．点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1，求出解．26．解方程：（1）10x﹣12=5x+15；（2）考点：解一元一次方程．专题：计算题．分析：（1）先移项，再合并同类项，最后化系数为1，从而得到方程的解；（2）先去括号，再移项、合并同类项，最后化系数为1，从而得到方程的解．解答：解：（1）移项，得10x﹣5x=12+15，合并同类项，得5x=27，方程的两边同时除以5，得x=；（2）去括号，得=，方程的两边同时乘以6，得x+1=4x﹣2，移项、合并同类项，得3x=3，方程的两边同时除以3，得x=1．点评：本题考查解一元一次方程，解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．27．解方程：（1）8y﹣3（3y+2）=7（2）．考点：解一元一次方程．专题：计算题．分析：（1）根据一元一次方程的解法，去括号，移项，合并同类项，系数化为1即可得解；（2）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，合并同类项，系数化为1，从而得到方程的解．解答：解：（1）去括号得，8y﹣9y﹣6=7，移项、合并得，﹣y=13，系数化为1得，y=﹣13；（2）去分母得，3（3x﹣1）﹣12=2（5x﹣7），去括号得，9x﹣3﹣12=10x﹣14，移项得，9x﹣10x=﹣14+3+12，合并同类项得，﹣x=1，系数化为1得，x=﹣1．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．28．当k为什么数时，式子比的值少3．考点：解一元一次方程．专题：计算题．分析：先根据题意列出方程，再根据一元一次方程的解法，去分母，去括号，移项，合并同类项，系数化为1即可得解．解答：解：依题意，得=+3，去分母得，5（2k+1）=3（17﹣k）+45，去括号得，10k+5=51﹣3k+45，移项得，10k+3k=51+45﹣5，合并同类项得，13k=91，系数化为1得，k=7，∴当k=7时，式子比的值少3．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．29．解下列方程：（I）12y﹣2.5y=7.5y+5（II）．考点：解一元一次方程．专题：计算题．分析：（Ⅰ）根据一元一次方程的解法，移项，合并同类项，系数化为1即可得解；（Ⅱ）是一个带分母的方程，所以要先去分母，再去括号，最后移项，合并同类项，系数化为1，从而得到方程的解．解答：解：（Ⅰ）移项得，12y﹣2.5y﹣7.5y=5，合并同类项得，2y=5，系数化为1得，y=2.5；（Ⅱ）去分母得，5（x+1）﹣10=（3x﹣2）﹣2（2x+3），去括号得，5x+5﹣10=3x﹣2﹣4x﹣6，移项得，5x﹣3x+4x=﹣2﹣6﹣5+10，合并同类项得，6x=﹣3，系数化为1得，x=﹣．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．30．解方程：．考点：解一元一次方程．专题：计算题．分析：由于方程的分子、分母均有小数，利用分数的基本性质，分子、分母同时扩大相同的倍数，可将小数化成整数．解答：解：原方程变形为，（3分）去分母，得3×（30x﹣11）﹣4×（40x﹣2）=2×（16﹣70x），（4分）去括号，得90x﹣33﹣160x+8=32﹣140x，（5分）移项，得90x﹣160x+140x=32+33﹣8，（6分）合并同类项，得70x=57，（7分）系数化为1，得．（8分）点评：本题考查一元一次方程的解法．解一元一次方程的一般步骤：去分母，去括号，移项，合并同类项，系数化为1．本题的难点在于方程的分子、分母均有小数，将小数化成整数不同于去分母，不是方程两边同乘一个数，而是将分子、分母同乘一个数．。

初中数学一元一次方程精选试题（含答案和解析）一.选择题1.（2018·湖北省恩施·3分）一商店在某一时间以每件120元的价格卖出两件衣服.其中一件盈利20%.另一件亏损20%.在这次买卖中.这家商店（）A．不盈不亏 B．盈利20元C．亏损10元D．亏损30元【分析】设两件衣服的进价分别为x、y元.根据利润=销售收入﹣进价.即可分别得出关于x、y的一元一次方程.解之即可得出x、y的值.再用240﹣两件衣服的进价后即可找出结论．【解答】解：设两件衣服的进价分别为x、y元.根据题意得：120﹣x=20%x.y﹣120=20%y.解得：x=100.y=150.∴120+120﹣100﹣150=﹣10（元）．故选：C．【点评】本题考查了一元一次方程的应用.找准等量关系.正确列出一元一次方程是解题的关键．2.(2018湖南省邵阳市)（3分）程大位是我国明朝商人.珠算发明家．他60岁时完成的《直指算法统宗》是东方古代数学名著.详述了传统的珠算规则.确立了算盘用法．书中有如下问题：一百馒头一百僧.大僧三个更无争.小僧三人分一个.大小和尚得几丁．意思是：有100个和尚分100个馒头.如果大和尚1人分3个.小和尚3人分1个.正好分完.大、小和尚各有多少人.下列求解结果正确的是（）A．大和尚25人.小和尚75人 B．大和尚75人.小和尚25人C．大和尚50人.小和尚50人 D．大、小和尚各100人【分析】根据100个和尚分100个馒头.正好分完．大和尚一人分3个.小和尚3人分一个得到等量关系为：大和尚的人数+小和尚的人数=100.大和尚分得的馒头数+小和尚分得的馒头数=100.依此列出方程即可．【解答】解：设大和尚有x人.则小和尚有（100﹣x）人.根据题意得：3x+=100.解得x=25则100﹣x=100﹣25=75（人）所以.大和尚25人.小和尚75人．故选：A．【点评】本题考查了一元一次方程的应用.关键以和尚数和馒头数作为等量关系列出方程．二.填空题1.（2018·湖北江汉油田、潜江市、天门市、仙桃市·3分）某公司积极开展“爱心扶贫”的公益活动.现准备将6000件生活物资发往A.B两个贫困地区.其中发往A区的物资比B区的物资的1.5倍少1000件.则发往A区的生活物资为3200 件．【分析】设发往B区的生活物资为x件.则发往A区的生活物资为（1.5x﹣1000）件.根据发往A.B两区的物资共6000件.即可得出关于x的一元一次方程.解之即可得出结论．【解答】解：设发往B区的生活物资为x件.则发往A区的生活物资为（1.5x﹣1000）件.根据题意得：x+1.5x﹣1000=6000.解得：x=2800.∴1.5x﹣1000=3200．答：发往A区的生活物资为3200件．故答案为：3200．【点评】本题考查了一元一次方程的应用.找准等量关系.正确列出一元一次方程是解题的关键．3.（2018•上海•4分）方程组的解是.．【分析】方程组中的两个方程相加.即可得出一个一元二次方程.求出方程的解.再代入求出y即可．【解答】解：②+①得：x2+x=2.解得：x=﹣2或1.把x=﹣2代入①得：y=﹣2.把x=1代入①得：y=1.所以原方程组的解为..故答案为：.．【点评】本题考查了解高次方程组.能把二元二次方程组转化成一元二次方程是解此题的关键．三.解答题1.（2018•广东•7分）某公司购买了一批A.B型芯片.其中A型芯片的单价比B型芯片的单价少9元.已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等．（1）求该公司购买的A.B型芯片的单价各是多少元？（2）若两种芯片共购买了200条.且购买的总费用为6280元.求购买了多少条A型芯片？【分析】（1）设B型芯片的单价为x元/条.则A型芯片的单价为（x ﹣9）元/条.根据数量=总价÷单价结合用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.即可得出关于x的分式方程.解之经检验后即可得出结论；（2）设购买a条A型芯片.则购买（200﹣a）条B型芯片.根据总价=单价×数量.即可得出关于a的一元一次方程.解之即可得出结论．【解答】解：（1）设B型芯片的单价为x元/条.则A型芯片的单价为（x﹣9）元/条.根据题意得：=.解得：x=35.经检验.x=35是原方程的解.∴x﹣9=26．答：A型芯片的单价为26元/条.B型芯片的单价为35元/条．（2）设购买a条A型芯片.则购买（200﹣a）条B型芯片.根据题意得：26a+35（200﹣a）=6280.解得：a=80．答：购买了80条A型芯片．【点评】本题考查了分式方程的应用以及一元一次方程的应用.解题的关键是：（1）找准等量关系.正确列出分式方程；（2）找准等量关系.正确列出一元一次方程．2.（2018•海南•8分）“绿水青山就是金山银山”.海南省委省政府高度重视环境生态保护.截至2017年底.全省建立国家级、省级和市县级自然保护区共49个.其中国家级10个.省级比市县级多5个．问省级和市县级自然保护区各多少个？【分析】设市县级自然保护区有x个.则省级自然保护区有（x+5）个.根据国家级、省级和市县级自然保护区共49个.即可得出关于x的一元一次方程.解之即可得出结论．【解答】解：设市县级自然保护区有x个.则省级自然保护区有（x+5）个.根据题意得：10+x+5+x=49.解得：x=17.∴x+5=22．答：省级自然保护区有22个.市县级自然保护区有17个．【点评】本题考查了一元一次方程的应用.找准等量关系.正确列出一元一次方程是解题的关键．3.（2018湖南张家界5.00分）列方程解应用题《九章算术》中有“盈不足术”的问题.原文如下：“今有共買羊.人出五.不足四十五；人出七.不足三．问人数、羊價各幾何？”题意是：若干人共同出资买羊.每人出5元.则差45元；每人出7元.则差3元．求人数和羊价各是多少？【分析】可设买羊人数为未知数.等量关系为：5×买羊人数+45=7×买羊人数+3.把相关数值代入可求得买羊人数.代入方程的等号左边可得羊价．【解答】解：设买羊为x人.则羊价为（5x+45）元钱.5x+45=7x+3.x=21（人）.5×21+45=150（员）.答：买羊人数为21人.羊价为150元．【点评】本题考查了一元一次方程的应用.找准等量关系.正确列出一元一次方程是解题的关键．。

精品资料欢迎下载6.2.4解一元一次方程（三）一．解答题（共30小题）1．（2005•宁德）解方程：2x+1=72．3．（1）解方程：4﹣x=3（2﹣x）；（2）解方程：．4．解方程：．5．解方程（1）4（x﹣1）﹣3（20﹣x）=5（x﹣2）；（2）x ﹣=2﹣．6．（1）解方程：3（x﹣1）=2x+3；（2）解方程：=x ﹣．7．﹣（1﹣2x）=（3x+1）8．解方程：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+1；（2）．9．解方程：．10．解方程：（1）4x﹣3（4﹣x）=2；（2）（x﹣1）=2﹣（x+2）．11．计算：（1）计算：（2）解方程：12．解方程：13．解方程：（1）（2）14．解方程：（1）5（2x+1）﹣2（2x﹣3）=6 （2）+2（3）[3（x ﹣）+]=5x﹣115．（A类）解方程：5x﹣2=7x+8；（B 类）解方程：（x﹣1）﹣（x+5）=﹣；（C 类）解方程：．16．解方程（1）3（x+6）=9﹣5（1﹣2x）（2）（3）（4）17．解方程：（1）解方程：4x﹣3（5﹣x）=13 （2）解方程：x ﹣﹣318．（1）计算：﹣42×+|﹣2|3×（﹣）3（2）计算：﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]（3）解方程：4x﹣3（5﹣x）=2；（4）解方程：．19．（1）计算：（1﹣2﹣4）×；（2）计算：（3）解方程：3x+3=2x+7；（4）解方程：．20．解方程（1）﹣0.2（x﹣5）=1；（2）．21．解方程：（x+3）﹣2（x﹣1）=9﹣3x．22．8x﹣3=9+5x．5x+2（3x﹣7）=9﹣4（2+x）．．．23．解下列方程：（1）0.5x﹣0.7=5.2﹣1.3（x﹣1）；（2）=﹣2．24．解方程：（2）3x+8=2x+6；（3）2x+3（x+1）=5﹣4（x﹣1）；（4）．25．解方程：．26．解方程：（1）10x﹣12=5x+15；（2）27．解方程：（2）．28．当k 为什么数时，式子比的值少3．29．解下列方程：（I）12y﹣2.5y=7.5y+5（II ）．30．解方程：．6.2.4解一元一次方程（三）参考答案与试题解析一．解答题（共30小题）1．（2005•宁德）解方程：2x+1=7考点：解一元一次方程．专题：计算题；压轴题．分析：此题直接通过移项，合并同类项，系数化为1可求解．解答：解：原方程可化为：2x=7﹣1合并得：2x=6系数化为1得：x=32．考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：左右同乘12可得：3[2x﹣（x﹣1）]=8（x﹣1），化简可得：3x+3=8x﹣8，移项可得：5x=11，解可得x=．故原方程的解为x=．点评：若是分式方程，先同分母，转化为整式方程后，再移项化简，解方程可得答案．3．（1）解方程：4﹣x=3（2﹣x）；（2）解方程：．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，然后再移项、合并同类型，最后化系数为1，得出方程的解；（2）题的方程中含有分数系数，应先对各式进行化简、整理，然后再按（1）的步骤求解．解答：解：（1）去括号得：4﹣x=6﹣3x，移项得：﹣x+3x=6﹣4，合并得：2x=2，系数化为1得：x=1．（2）去分母得：5（x﹣1）﹣2（x+1）=2，去括号得：5x﹣5﹣2x﹣2=2，移项得：5x﹣2x=2+5+2，合并得：3x=9，比较多，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果．（2）本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍，值不变．这一性质在今后常会用到．4．解方程：．考点：解一元一次方程．专题：计算题．分析：此题两边都含有分数，分母不相同，如果直接通分，有一定的难度，但将方程左右同时乘以公分母6，难度就会降低．解答：解：去分母得：3（2﹣x）﹣18=2x﹣（2x+3），去括号得：6﹣3x﹣18=﹣3，移项合并得：﹣3x=9，∴x=﹣3．点评：本题易在去分母和移项中出现错误，学生往往不知如何寻找公分母，怎样合并同类项，怎样化简，所以我们要教会学生分开进行，从而达到分解难点的效果．5．解方程（1）4（x﹣1）﹣3（20﹣x）=5（x﹣2）；（2）x﹣=2﹣．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项、合并同类项、化系数为1，从而得到方程的解；（2）先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：（1）去括号得：4x﹣4﹣60+3x=5x﹣10（2分）移项得：4x+3x﹣5x=4+60﹣10（3分）合并得：2x=54（5分）系数化为1得：x=27；（6分）（2）去分母得：6x﹣3（x﹣1）=12﹣2（x+2）（2分）去括号得：6x﹣3x+3=12﹣2x﹣4（3分）移项得：6x﹣3x+2x=12﹣4﹣3（4分）合并得：5x=5（5分）系数化为1得：x=1．（6分）点评：去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．去括号时要注意符号的变化．6．（1）解方程：3（x﹣1）=2x+3；（2）解方程：=x﹣．考点：解一元一次方程．专题：计算题．分析：（1）是简单的一元一次方程，通过移项，系数化为1即可得到；解答：解：（1）3x﹣3=2x+33x﹣2x=3+3x=6；（2）方程两边都乘以6得：x+3=6x﹣3（x﹣1）x+3=6x﹣3x+3x﹣6x+3x=3﹣3﹣2x=0∴x=0．点评：本题易在去分母、去括号和移项中出现错误，还可能会在解题前不知如何寻找公分母，怎样合并同类项，怎样化简，所以要学会分开进行，从而达到分解难点的效果．去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．7．﹣（1﹣2x）=（3x+1）考点：解一元一次方程．专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：﹣7（1﹣2x）=3×2（3x+1）﹣7+14x=18x+6﹣4x=13x=﹣．点评：解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为1．此题去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．8．解方程：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+1；（2）．考点：解一元一次方程．专题：计算题．分析：（1）可采用去括号，移项，合并同类项，系数化1的方式进行；（2）本题方程两边都含有分数系数，如果直接通分，有一定的难度，但对每一个式子先进行化简、整理为整数形式，难度就会降低．解答：解：（1）5（x﹣1）﹣2（x+1）=3（x﹣1）+x+13x﹣7=4x﹣2∴x=﹣5；（2）原方程可化为：去分母得：40x+60=5（18﹣18x）﹣3（15﹣30x），去括号得：40x+60=90﹣90x﹣45+90x，移项、合并得：40x=﹣15，系数化为1得：x=．达到分解难点的效果；（2）本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍，值不变．这一性质在今后常会用到．9．解方程：．考点：解一元一次方程．1184454专题：计算题．分析：这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：，去分母得：2x﹣（3x+1）=6﹣3（x﹣1），去括号得：2x﹣3x﹣1=6﹣3x+3，移项、合并同类项得：2x=10，系数化为1得：x=5．点评：去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．10．解方程：（1）4x﹣3（4﹣x）=2；（2）（x﹣1）=2﹣（x+2）．考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项，合并同类项，系数化1，即可求出方程的解；（2）先去分母，再去括号，移项，合并同类项，系数化1可求出方程的解．解答：解：（1）4x﹣3（4﹣x）=2去括号，得4x﹣12+3x=2移项，合并同类项7x=14系数化1，得x=2．（2）（x﹣1）=2﹣（x+2）去分母，得5（x﹣1）=20﹣2（x+2）去括号，得5x﹣5=20﹣2x﹣4移项、合并同类项，得7x=21系数化1，得x=3．点评：（1）此题主要是去括号，移项，合并同类项，系数化1．（2）方程两边每一项都要乘各分母的最小公倍数，方程两边每一项都要乘各分母的最小公倍数，切勿漏乘不含有分母的项，另外分数线有两层意义，一方面它是除号，另一方面它又代表着括号，所以在去分母时，应该将分子用括号括上．11．计算：（2）解方程：考点：解一元一次方程；有理数的混合运算．专题：计算题．分析：（1）根据有理数的混合运算法则计算：先算乘方、后算乘除、再算加减；（2）两边同时乘以最简公分母4，即可去掉分母．解答：解：（1）原式=，=，=．（2）去分母得：2（x﹣1）﹣（3x﹣1）=﹣4，解得：x=3．点评：解答此题要注意：（1）去分母时最好先去中括号、再去小括号，以减少去括号带来的符号变化次数；（2）去分母就是方程两边同时乘以分母的最简公分母．12．解方程：考点：解一元一次方程．专题：计算题．分析：（1）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．（2）解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、化系数为1．解答：解：（1）去分母得：3（3x﹣1）+18=1﹣5x，去括号得：9x﹣3+18=1﹣5x，移项、合并得：14x=﹣14，系数化为1得：x=﹣1；（2）去括号得：x﹣x+1=x，移项、合并同类项得：x=﹣1，系数化为1得：x=﹣．点评：本题考查解一元一次方程，正确掌握解一元一次方程的一般步骤，注意移项要变号、去分母时“1”也要乘以最小公倍数．13．解方程：（1）（2）分析：（1）去分母、去括号、移项、合并同类项、化系数为1．（2）去分母、去括号、移项、合并同类项、化系数为1．解答：（1）解：去分母得：5（3x+1）﹣2×10=3x﹣2﹣2（2x+3），去括号得：15x+5﹣20=3x﹣2﹣4x﹣6，移项得：15x+x=﹣8+15，合并得：16x=7，解得：；（2）解：，4（x﹣1）﹣18（x+1）=﹣36，4x﹣4﹣18x﹣18=﹣36，﹣14x=﹣14，x=1．点评：本题考查解一元一次方程，正确掌握解一元一次方程的一般步骤，注意移项要变号、去分母时“1”也要乘以最小公倍数．14．解方程：（1）5（2x+1）﹣2（2x﹣3）=6（2）+2（3）[3（x﹣）+]=5x﹣1考点：解一元一次方程．专题：计算题．分析：（2）通过去括号、移项、合并同类项、系数化为1，解得x的值；（3）乘最小公倍数去分母即可；（4）主要是去括号，也可以把分数转化成整数进行计算．解答：解：（1）去括号得：10x+5﹣4x+6=6移项、合并得：6x=﹣5，方程两边都除以6，得x=﹣；（2）去分母得：3（x﹣2）=2（4﹣3x）+24，去括号得：3x﹣6=8﹣6x+24，移项、合并得：9x=38，方程两边都除以9，得x=；（3）整理得：[3（x﹣）+]=5x﹣1，4x﹣2+1=5x﹣1，移项、合并得：x=0．点评：一元一次方程的解法：一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤，把一个一元一次方程“转化”成x=a的形式．解题时，要灵活运用这些步骤．15．（A类）解方程：5x﹣2=7x+8；（B类）解方程：（x﹣1）﹣（x+5）=﹣；（C类）解方程：．考点：解一元一次方程．专题：计算题．分析：通过去分母、去括号、移项、系数化为1等方法，求得各方程的解．解答：解：A类：5x﹣2=7x+8移项：5x﹣7x=8+2化简：﹣2x=10即：x=﹣5；B类：（x﹣1）﹣（x+5）=﹣去括号：x﹣﹣x﹣5=﹣化简：x=5即：x=﹣；C类：﹣=1去分母：3（4﹣x）﹣2（2x+1）=6去括号：12﹣3x﹣4x﹣2=6化简：﹣7x=﹣4即：x=．点评：本题主要考查一元一次方程的解法，比较简单，但要细心运算．16．解方程（1）3（x+6）=9﹣5（1﹣2x）（2）（3）（4）考点：解一元一次方程．专题：计算题．分析：（1）去括号以后，移项，合并同类项，系数化为1即可求解；（2）（3）首先去掉分母，再去括号以后，移项，合并同类项，系数化为1以后即可求解；（4）首先根据分数的基本性质，把第一项分母中的0.3化为整数，再去分母，求解．解答：解：（1）去括号得：3x+18=9﹣5+10x移项得：3x﹣10x=9﹣5﹣18合并同类项得：﹣7x=﹣14则x=2；（2）去分母得：2x+1=x+3﹣5移项，合并同类项得：x=﹣3；（3）去分母得：10y+2（y+2）=20﹣5（y﹣1）去括号得：10y+2y+4=20﹣5y+5移项，合并同类项得：17y=21系数化为1得：；（4）原方程可以变形为：﹣5x=﹣1去分母得：17+20x﹣15x=﹣3移项，合并同类项得：5x=﹣20系数化为1得：x=﹣4．点评：解方程的过程中要注意每步的依据，这几个题目都是基础的题目，需要熟练掌握．17．解方程：（1）解方程：4x﹣3（5﹣x）=13（2）解方程：x﹣﹣3考点：解一元一次方程．专题：计算题．分析：（1）先去括号，再移项，化系数为1，从而得到方程的解．（2）这是一个带分母的方程，所以要先去分母，再去括号，最后移项，化系数为1，从而得到方程的解．解答：解：（1）去括号得：4x﹣15+3x=13，移项合并得：7x=28，系数化为1得：得x=4；（2）原式变形为x+3=，去分母得：5（2x﹣5）+3（x﹣2）=15（x+3），去括号得10x﹣25+3x﹣6=15x+45，移项合并得﹣2x=76，系数化为1得：x=﹣38．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．18．（1）计算：﹣42×+|﹣2|3×（﹣）3（2）计算：﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]（3）解方程：4x﹣3（5﹣x）=2；（4）解方程：．考点：解一元一次方程；有理数的混合运算．分析：（1）利用平方和立方的定义进行计算．（2）按四则混合运算的顺序进行计算．（3）主要是去括号，移项合并．（4）两边同乘最小公倍数去分母，再求值．解答：解：（1）﹣42×+|﹣2|3×（﹣）3==﹣1﹣1=﹣2．（2）﹣12﹣|0.5﹣|÷×[﹣2﹣（﹣3）2]====．（3）解方程：4x﹣3（5﹣x）=2去括号，得4x﹣15+3x）=2移项，得4x+3x=2+15合并同类项，得7x=17系数化为1，得．（4）解方程：去分母，得15x﹣3（x﹣2）=5（2x﹣5）﹣3×15去括号，得15x﹣3x+6=10x﹣25﹣45移项，得15x﹣3x﹣10x=﹣25﹣45﹣6合并同类项，得2x=﹣76系数化为1，得x=﹣38．点评：前两道题考查了学生有理数的混合运算，后两道考查了学生解一元一次方程的能力．19．（1）计算：（1﹣2﹣4）×；（2）计算：÷；（3）解方程：3x+3=2x+7；（4）解方程：．考点：解一元一次方程；有理数的混合运算．专题：计算题．分析：（1）和（2）要熟练掌握有理数的混合运算；（3）和（4）首先熟悉解一元一次方程的步骤：去分母，去括号，移项，合并同类项，系数化为1．解答：解：（1）（1﹣2﹣4）×=﹣=﹣13；（2）原式=﹣1×（﹣4﹣2）×（﹣）=6×（﹣）=﹣9；（3）解方程：3x+3=2x+7移项，得3x﹣2x=7﹣3合并同类项，得x=4；（4）解方程：去分母，得6（x+15）=15﹣10（x﹣7）去括号，得6x+90=15﹣10x+70移项，得6x+10x=15+70﹣90合并同类项，得16x=﹣5系数化为1，得x=．点评：（1）和（2）要注意符号的处理；（4）要特别注意去分母的时候不要发生数字漏乘的现象，熟练掌握去括号法则以及合并同类项法则．20．解方程（1）﹣0.2（x﹣5）=1；（2）．考点：解一元一次方程．分析：（1）通过去括号、移项、系数化为1等过程，求得x的值；（2）通过去分母以及去括号、移项、系数化为1等过程，求得x的值．解答：解：（1）﹣0.2（x﹣5）=1；去括号得：﹣0.2x+1=1，∴﹣0.2x=0，∴x=0；（2）．去分母得：2（x﹣2）+6x=9（3x+5）﹣（1﹣2x），∴﹣21x=48，∴x=﹣．点评：此题主要考查了一元一次方程解法，解一元一次方程常见的过程有去括号、移项、系数化为1等．21．解方程：（x+3）﹣2（x﹣1）=9﹣3x．考点：解一元一次方程．专题：计算题．分析：先去括号得x+3﹣2x+2=9﹣3x，然后移项、合并同类得到2x=4，然后把x的系数化为1即可．解答：解：去括号得x+3﹣2x+2=9﹣3x，移项得x﹣2x+3x=9﹣3﹣2，合并得2x=4，系数化为1得x=2．点评：本题考查了解一元一次方程：先去分母，再去括号，接着移项，把含未知数的项移到方程左边，不含未知数的项移到方程右边，然后合并同类项，最后把未知数的系数化为1得到原方程的解．22．8x﹣3=9+5x．5x+2（3x﹣7）=9﹣4（2+x）．．．考点：解一元一次方程．专题：方程思想．分析：本题是解4个不同的一元一次方程，第一个通过移项、合并同类项及系数化1求解．第二个先去括号再通过移项、合并同类项及系数化1求解．第三个先去分母再同第二个．第四个先分子分母乘以10，再同第三个求解．解答：8x﹣3=9+5x，解：8x﹣5x=9+3，3x=12，∴x=4．∴x=4是原方程的解；5x+2（3x﹣7）=9﹣4（2+x），解：5x+6x﹣14=9﹣8﹣4x，5x+6x+4x=9﹣8+14，15x=15，∴x=1．∴x=1是原方程的解．．解：3（x﹣1）﹣2（2x+1）=12，3x﹣3﹣4x﹣2=12，3x﹣4x=12+3+2，﹣x=17，∴x=﹣17．∴x=﹣17是原方程的解．，解：，5（10x﹣3）=4（10x+1）+40，50x﹣15=40x+4+40，50x﹣40x=4+40+15，10x=59，∴x=．∴x=是原方程的解．点评：此题考查的知识点是解一元一次方程，关键是注意解方程时的每一步都要认真仔细，如移项时要变符号．23．解下列方程：（1）0.5x﹣0.7=5.2﹣1.3（x﹣1）；（2）=﹣2．考点：解一元一次方程．分析：（1）首先去括号，然后移项、合并同类项，系数化成1，即可求解；（2）首先去分母，然后去括号，移项、合并同类项，系数化成1，即可求解解答：解：（1）去括号，得：0.5x﹣0.7=5.2﹣1.3x+1.3移项，得：0.5x+1.3x=5.2+1.3+0.7合并同类项，得：1.8x=7.2，则x=4；（2）去分母得：7（1﹣2x）=3（3x+1）﹣42，去括号，得：7﹣14x=9x+3﹣42，移项，得：﹣14x﹣9x=3﹣42﹣7，合并同类项，得：﹣23x=﹣46，则x=2．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．24．解方程：（1）﹣0.5+3x=10；（2）3x+8=2x+6；（3）2x+3（x+1）=5﹣4（x﹣1）；（4）．考点：解一元一次方程．分析：（1）移项，合并同类项，然后系数化成1即可求解；（2）移项，合并同类项，然后系数化成1即可求解；（3）去括号、移项，合并同类项，然后系数化成1即可求解；（4）首先去分母，然后去括号、移项，合并同类项，然后系数化成1即可求解．解答：解：（1）3x=10.5，x=3.5；（2）3x﹣2x=6﹣8，x=﹣2；（3）2x+3x+3=5﹣4x+4，2x+3x+4x=5+4﹣3，9x=6，x=；（4）2（x+1）+6=3（3x﹣2），2x+2+6=9x﹣6，2x﹣9x=﹣6﹣2﹣6，﹣7x=﹣14，x=2．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．25．解方程：．考点：解一元一次方程．专题：计算题．分析：方程两边乘以10去分母后，去括号，移项合并，将x系数化为1，即可求出解．解答：解：去分母得：5（3x﹣1）﹣2（5x﹣6）=2，去括号得：15x﹣5﹣10x+12=2，移项合并得：5x=﹣5，解得：x=﹣1．点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1，求出解．26．解方程：（1）10x﹣12=5x+15；（2）考点：解一元一次方程．专题：计算题．解答：解：（1）移项，得10x﹣5x=12+15，合并同类项，得5x=27，方程的两边同时除以5，得x=；（2）去括号，得=，方程的两边同时乘以6，得x+1=4x﹣2，移项、合并同类项，得3x=3，方程的两边同时除以3，得x=1．点评：本题考查解一元一次方程，解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、化系数为1．注意移项要变号．27．解方程：（1）8y﹣3（3y+2）=7（2）．解答：解：（1）去括号得，8y﹣9y﹣6=7，移项、合并得，﹣y=13，系数化为1得，y=﹣13；（2）去分母得，3（3x﹣1）﹣12=2（5x﹣7），去括号得，9x﹣3﹣12=10x﹣14，移项得，9x﹣10x=﹣14+3+12，合并同类项得，﹣x=1，系数化为1得，x=﹣1．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．28．当k为什么数时，式子比的值少3．考点：解一元一次方程．专题：计算题．解答：解：依题意，得=+3，去分母得，5（2k+1）=3（17﹣k）+45，去括号得，10k+5=51﹣3k+45，移项得，10k+3k=51+45﹣5，合并同类项得，13k=91，系数化为1得，k=7，∴当k=7时，式子比的值少3．29．解下列方程：（I）12y﹣2.5y=7.5y+5（II）．考点：解一元一次方程．专题：计算题．解答：解：（Ⅰ）移项得，12y﹣2.5y﹣7.5y=5，合并同类项得，2y=5，系数化为1得，y=2.5；（Ⅱ）去分母得，5（x+1）﹣10=（3x﹣2）﹣2（2x+3），去括号得，5x+5﹣10=3x﹣2﹣4x﹣6，移项得，5x﹣3x+4x=﹣2﹣6﹣5+10，合并同类项得，6x=﹣3，系数化为1得，x=﹣．。

解一元一次方程去括号同步测试题含答案1.一元一次方程是形如ax+b=0的方程，所以选项中只有B和D是一元一次方程。

答案为B和D。

2.将方程化简得(m+2)x(m-1)=8，移项得(m+2)x(m-1)-8=0，根据一元二次方程的求解公式，解得x=2或x=-2.所以选项C错误，答案为A或C。

3.将方程化简得5x-2=4，移项得5x=6，系数化为1得x=6/5.所以答案为A。

4.将方程化简得3x-4=-2x+1，移项得5x=5，系数化为1得x=1.所以选项D错误，答案为A、B或C。

5.将方程化简得4(2-x)-4(x+1)=60，解得x=-7.所以答案为D。

6.一元一次方程是形如ax+b=0的方程，所以只有①和③是一元一次方程。

所以答案为A。

7.将方程化简得14x-7-12x+3=11，合并同类项得2x-4=0，系数化为1得x=2.所以选项B错误，答案为A、C或D。

8.将方程化简得x=3，所以选项B正确，答案为B。

9.将方程化简得mx+2=2m+2x，移项得(m-2)x=2(m-1)，所以|x|-1=2/(m-2)。

因为绝对值的取值范围是非负实数，所以m-2不等于0，解得m=4或10.所以答案为D。

10.将式子化简得(m-1)x^2=3，移项得x^2=3/(m-1)，所以m-1不等于0且m不等于1，解得m=4.所以答案为4.11.将式子化简得10-5y=5+3y，移项得8y=5，系数化为1得y=5/8.所以答案为5/8.12.将代数式化简得2x+6=-3x+3，移项得5x=-3，系数化为1得x=-3/5.所以答案为-3/5.13.去括号得2x+6-5+5x=3x-3，合并同类项得7x=4，系数化为1得x=4/7.所以第一空是4/7.移项并合并同类项得7x-5=3，系数化为1得x=8/7.所以第二空是8/7.将x=8/7代入原方程得到左边为-2，右边为2，符号相反，所以第三空是-2.14.将2x^3(4k-1)y^2+xy^2化简得(8k-1)x^3y^2+xy^2，要使其仍为单项式，则x^3的次数必须等于1，即3=1，所以x=0.所以答案为0.。

完整版)解一元一次方程习题精选附答案6.2.4 解一元一次方程一、解答题（共30小题）1.解方程：2x+1=7.2.删除此题。

3.（1）解方程：4-x=3(2-x)；2）解方程：删除此题。

4.解方程：删除此题。

5.解方程：1）4(x-1)-3(20-x)=5(x-2)；2）x-1=2(x+1)。

6.（1）解方程：3(x-1)=2x+3；2）解方程：x-1=3(x-2)。

7.-1+2x=3x+1.8.解方程：1）5(x-1)-2(x+1)=3(x-1)+x+1；2）删除此题。

9.解方程：删除此题。

10.解方程：1）4x-3(4-x)=2；2）(x-1)+2=2-(x+2)。

11.（1）计算：删除此题。

2）解方程：删除此题。

12.解方程：删除此题。

13.解方程：1）删除此题。

2）删除此题。

14.解方程：1）5(2x+1)-2(2x-3)=6；2）x+2；3）3(x-1)+2=5x-1.15.（A类）解方程：5x-2=7x+8；B类）解方程：(x-1)-(x+5)=-2；C类）解方程：删除此题。

16.解方程：1）3(x+6)=9-5(1-2x)；2）删除此题；3）删除此题；4）删除此题。

17.解方程：1）4x-3(5-x)=13；2）x+3.18.（1）计算：-42x+|-2|3x(-1)；2）计算：-12-|0.5-2|÷2×[-2-(-3)2]；3）4x-3(5-x)=2；4）(x+1)+2=4(x-1)。

19.（1）计算：-1-2-4×(-2)；2）计算：-6÷2；3）3x+3=2x+7；4）2x-3=5x+1.20.解方程：1）-0.2(x-5)=1；2）删除此题。

21.解方程：(x+3)-2(x-1)=9-3x。

22.8x-3=9+5x；5x+2(3x-7)=9-4(2+x)。

23.解下列方程：1）0.5x-0.7=5.2-1.3(x-1)；2）x+3=-2.24.解方程：1）-0.5+3x=10；2）x= -1；3）5x+3=1；4）删除此题。

初中数学解一元一次方程精选计算题专题训练含答案姓名：__________ 班级：__________考号：__________一、计算题（共38题）1、解方程：2、计算：.3、4、利用等式的性质解下列方程：5、解方程：6、7、 x﹣4=2﹣5x8、9、解方程： 9-10x=10-9x10、解方程：11、－2(x－1)=4．12、解关于x的方程b（a＋x）－a＝（2b＋1）x＋ab（a≠0）.13、解下列方程2y+l=5y+714、 2x+4=-1215、16、－2(x－1)=4．17、 3x-7+4x=6x-218、 -19、20、 4－2（1－x）＝－2x21、解方程：22、23、 5x-6=3x+224、;25、;26、用等式的性质解方程3x+1=7．27、解下列方程：12-3(9-x)=5(x-4)-7(7-x); 28、；29、y-=y+330、31、32、.33、34、；35、 ax-1=bx36、 5(x－1)－2(x+1)=3(x－1)+x+1；37、38、============参考答案============一、计算题1、 X=22、分析：,,=1.解：原式.点拨：根据零指数幂、负整数指数幂的运算规律计算即可.3、-----3分4、 x＝4.5、6、解：（1）原方程可化为：……2分,解得：………4分7、移项合并得：6x=6，解得：x=1；8、 .解：(1)合并同类项，得2x＝6.系数化为1，得x＝3.9、解：9-10=10x-9x x=-110、11、 x=－112、解：适当去括号，得ab＋bx－a＝（2b＋1）x＋ab，移项，得bx－（2b＋1）x＝a＋ab－ab，合并同类项，得（b－2b－1）x＝a，即－（b＋1）x＝a，当b≠－1时，有b＋1 ≠0，方程的解为x＝．当b＝－1 时，有b＋1＝0，又因为a≠0，所以方程无解．（想一想，若a＝0，则如何？13、14、解：X=-815、 x=1y=-116、 x=－117、 x=518、 x= -2219、解：…………………………2分………………………………2分………………………………1分20、 4－2（1－x）＝－2x解：4－2＋2ｘ＝－2ｘ2ｘ＋2ｘ＝2－4……2′4ｘ＝－2………3′ｘ＝…………4′21、22、23、 x=424、（一）解：去分母，得2x - 20 = 60 +3x-移项，得 2x-3x = 60 +20合并同类项，得- x = 80化简，得x = - 80解：移项，得合并同类项化简，得x = - 8025、解：去括号，得 4x– 4 = 2 – 6x -12移项，得 4x + 6x = 2 -12 + 4合并同类项 10x = - 6化简，得26、【考点】等式的性质．【分析】根据等式的性质，可得答案．【解答】解：方程两边都减去1，得3x+1﹣1=7﹣1，化简，得3x=6两边除以3，得x=2．【点评】本题考查了等式的性质，利用等式的性质是解题关键．27、解:去括号，合并-15+3x=12x-69，移项合并，得9x=54,解得x=6;28、；29、解：X=-2130、解: x=3Y=431、32、去分母，…………1分去括号，移项，…………2分合并，…………3分…………5分33、 t=-934、解：先把系数化为整数，得，再去分母，两边都乘以60，得，去括号，合并同类项，得，；35、当a≠b时,方程有惟一解x=；当a=b时,方程无解；36、解：∵5(x－1)－2(x+1)=3(x－1)+x+1∴3x－7 = 3x－3+x+1∴x =－537、＝2；38、。

解一元一次方程——同解方程精选试题附答案6.2.6同解方程完成时间：20min 一．选择题（共9小题）1．已知关于x 的方程7x+3k=12与7x+3=0的解相同，则k 的值为（ ） A ． ﹣3 B ．3 C ．﹣5 D ．52．关于x 的方程x+a=2x ﹣3与2x ﹣b=x 有相同的解，则a 、b 的关系为（ ）A ． a ﹣b=3B ．b ﹣a=3 C ．b+a=3 D ．b+a+3=03．已知方程4x=8与x ﹣k=1的解相同，则4k 2﹣1的值为（ ） A ． 1 B ．3 C ．8 D ．174．吴云科和孟家福是七年级四班的两名爱好数学的优等生，在学完第三章《一元一次方程》后，吴云科对孟家福说：“方程与方程的解相同，你能求出k 的值吗？”孟家福用笔算了一下给出正确答案，聪明的你知道是哪个吗？（ ）其中同解的两个方程是（ ） A ． （1）与（2） B ． （1）与（3） C ． （1）与（4） D ． （2）与（4）二．填空题（共15小题）10．方程x+2=3的解也是方程ax ﹣5=8的解时，则a= _________ ．11．已知关于x 的方程+3=x 与方程3﹣2x=1的解相同，则m 2= _________ ．12．若方程2x ﹣3=11与关于x 的方程4x+5=3k 有相同的解，则k 的值是 _________ ．13．已知关于x 的方程5x+3k=24与5x+3=0的解相同，则k 的值为 _________ ．14．已知方程3（x+3）﹣1=2x 的解与关于x 的方程的解相同，则m 2﹣2m+1的值为 _________ ．15．已知关于x 的方程=x+与=3x ﹣2的解相同，则m=_________ ．16．如果关于x的方程和方程的解相同，那么k的值_________．17．如果方程与方程3x﹣2a=0的解相同，则a 3=_________．18．方程ax2+3x2b﹣1+cy=2是关于x的一元一次方程，则a+b+c= _________；如果关于x的方程2x+1=﹣3和方程=0的解相同，那么k=_________．19．若3x﹣4=﹣1与ax﹣b+1=﹣c有相同的解，则（a﹣b+c）2009=_________．20．若以为未知数的方程3x=5x﹣8和有相同的解，则a=_________．21．已知方程2x﹣3=+x的解满足|x|﹣1=0，则m_________．22．关于x的方程3x=9与x+4=k的解相同，则代数式1﹣2|k|的值为_________．23．关于x的方程3mx+7=0和2 x+3n=0是同解方程，那么（mn）2=_________．24．已知：一元一次方程2x﹣2=3的解是方程的解，则m=_________．三．解答题（共6小题）25．已知：关于x的方程4x﹣k=2与3（2+x）=2k的解相同，求k的值及相同的解．26．已知关于x的方程2x+1=a和2x+2=0的解相同，求的值．27．若关于x的方程2x﹣3=1和=k﹣3x有相同的解，求k 的值．28．如果方程的解与方程4y﹣（3m+1）=6y+2m﹣1的解相同，求式子的值．29．方程4+2（x﹣1）=0的解与关于x的方程的解相同，求k的值．30．当k为何值时，方程与方程有相同的解？6.2.6同解方程参考答案与试题解析一．选择题（共9小题）1．已知关于x 的方程7x+3k=12与7x+3=0的解相同，则k 的值为（ ） A ． ﹣ 3 B ．3 C ．﹣ 5 D ．5考点：同解方程．专题：计算题．分析： 先解方程7x+3=0，可得x=﹣，根据同解的定义可得x=﹣也是7x+3k=12的解，再把x=﹣代入7x+3k=12中即可求k ．解答： 解：解方程7x+3=0得，x=﹣， ∵7x+3k=12与7x+3=0的解相同，∴x=﹣也是7x+3k=12的解，再把x=﹣代入7x+3k=12中，得7×（﹣）+3k=12，解得k=5． 故选D ．点本题考查了同解方程的定义，解题的关键是先求出x ．评：2．关于x 的方程x+a=2x ﹣3与2x ﹣b=x 有相同的解，则a 、b 的关系为（ ）A ． a ﹣b=3B ． b ﹣a=3C ．b+a=3 D ．b+a+3=0考点：同解方程．分析： 求出两个方程的解，根据已知得出两个解相等，即可求出答案． 解答： 解：x+a=2x ﹣3， x﹣2x=﹣3﹣a ， ﹣x=﹣3﹣a ， 则x=3+a ， 2x ﹣b=x ， x=b ，∵关于x 的方程x+a=2x ﹣3与2x ﹣b=x 有相同的解， ∴3+a=b ， ∴b ﹣a=3， 故选B ．点评： 本题考查了对同解方程的理解，关键是求出3+a=b ，题目比较好，难度适中．3．已知方程4x=8与x ﹣k=1的解相同，则4k 2﹣1的值为（ ） A ． 1 B ．3 C ．8 D ．17考点：同解方程．专题：计算题． 分析： 先解出方程4x=8的解，然后代入求出k 的值，进而可得出答案． 解答： 解：解方程4x=8， 得：x=2，把x=2代入x ﹣k=1， 得：k=1， ∴4k 2﹣1=3． 故选B ．点评： 本题考查同解方程的知识，比较简单，解决本题的关键是理解方程解的定义，注意细心运算．4．吴云科和孟家福是七年级四班的两名爱好数学的优等生，在学完第三章《一元一次方程》后，吴云科对孟家福说：“方程与方程的解相同，你能求出k 的值吗？”孟家福用笔算了一下给出正确答案，聪明的你知道是哪个吗？（ ） A ． 0 B ．2 C ．1 D ．﹣1考点：同解方程．专题： 方程思想． 分析：先解方程，得x=1，因为这个解也是方程的解，根据方程的解的定义，把x 代入方程中求出k 的值．解答：解： 12﹣2（x ﹣1）=3（1﹣x ）+6（3﹣x ）解得：x=1． 把x=1代入方程得：4﹣=3k ﹣，12﹣k ﹣2=9k ， 解得：k=1． 故选C ．点本题考查了同解方程，解题的关键是正确解一元一次评： 方程．理解方程的解的定义，就是能够使方程左右两边相等的未知数的值．5．如果方程x=1与2x+a=ax 的解相同，则a 的值是（ ） A ． 2 B ．﹣2 C ．3 D ．﹣3考点：同解方程．专题：计算题． 分析： 可以分别解出两方程的解，两解相等，就得到关于a 的方程，从而可以求出a 的值． 解答： 解：解第一个方程得：x=3， 解第二个方程得：x=∴=3解得：a=3 故选C ．点评： 本题解决的关键是能够求解关于x 的方程，要能正确理解方程解的含义．6．下列方程中与方程3x=x+1的解相同的是（ ）A2x=4 B 2x=4x ﹣C5x+3=6 D6x ﹣． ． 1 ． ． 15x=3考点：同解方程．专题：计算题． 分析：求得题目中各个方程的解，即可作出判断． 解答： 解：方程3x=x+1的解是x=． A、解是x=2，故错误； B 、解是x=，故正确；C 、解是x=，故错误；D 、解是x=﹣，故错误． 故选B ．点评： 本题主要考查了一元一次方程的解法，正确解方程是解题的关键．7．如果方程6x+3a=22与方程3x+5=11的解相同，那么a=（ ） A ． B ．C ．﹣ D ．﹣考点：同解方程．专题：计算题． 分析： 先通过方程3x+5=11求得x 的值，因为方程6x+3a=22与方程3x+5=11的解相同，把x 的值代入方程6x+3a=22，即可求得a 的值． 解答： 解：3x+5=11，移项，得3x=11﹣5， 合并同类项，得3x=6，系数化为1，得x=2， 把x=2代入6x+3a=22中， 得6×2+3a=22，∴a=， 故选B ．点评： 解一元一次方程的一般步骤是去分母，去括号，移项，合并同类项，移项时要变号．因为两方程解相同，把求得x 的值代入方程，即可求得常数项的值．8．在方程：①3x ﹣=1；②；③6x ﹣5=2x ﹣3；④x+=2x 中，与方程2x=1的解相同的方程有（ ）A ． 1个B ．2个 C ．3个 D ．4个考点：同解方程．专计算题．题：分析： 求出方程2x=1的解是x=，要判断x=是否是方程的解，就是把它代入方程的左右两边，看是否相等．解答： 解：方程2x=1的解是x=A 、把x=代入3x ﹣=1，左边=﹣=1，左边=右边，因而x=是方程3x ﹣=1的解，即与方程2x=1的解相同．B 、把x=代入，左边=（+1）=，左边=右边，因而x=是方程的解，即与方程2x=1的解相同．C 、把x=代入6x ﹣5=2x ﹣3，左边=3﹣5=﹣2，右边=1﹣3=﹣2，左边=右边，因而x=是方程6x ﹣5=2x ﹣3的解，即与方程2x=1的解相同．D 、把x=代入x+=2x ，左边=+=1，右边=2×=1，因而左边=右边，因而x=是方程6x ﹣5=2x ﹣3的解，即与方程2x=1的解相同．四个方程都与2x=1的解相同． 故选D ．点评： 本题主要考查判断一个数是否是方程的解的方法．9．有4个关于x 方程：（1）x ﹣2=﹣1 （2）（x ﹣2）+（x ﹣1）=﹣1+（x ﹣1）（3）x=0 （4）其中同解的两个方程是（ ）A ． （1）与（2）B ． （1）与（3）C ． （1）与（4）D ． （2）与（4）考点：同解方程．分析： （1）移项可解出x 的值．（2）先去括号在移项合并可得出x 的值．（3）直接可得出x 的值．（4）直接移项即可，注意分式有意义的条件． 解答： 解：（1）方程的解为x=1，（2）方程的解为x=1，（3）方程的解为x=0，（4）方程无解．∴只有（1）（2）是同解方程． 故选A ．点评： 本题考查同解方程的知识，关键是正确求出4个方程的解，难度不大，注意要细心运算．二．填空题（共15小题）10．方程x+2=3的解也是方程ax ﹣5=8的解时，则a= 13 ．考点：同解方程．专题：计算题． 分首先解出方程x+2=3的解，代入方程ax ﹣5=8中求析： 出a 的值即可． 解答： 解：x+2=3，解得x=1； 把x=1代入ax ﹣5=8中， 得a ﹣5=8， 解得a=13．点评： 本题的关键是正确解一元一次方程．理解方程的解的定义，就是能够使方程左右两边相等的未知数的值．11．已知关于x 的方程+3=x 与方程3﹣2x=1的解相同，则m 2= 16 ． 考点：同解方程．分析：首先解出方程3﹣2x=1的解，然后把方程的解代入方程+3=x 求出m ，即可求出m 2． 解答： 解：解方程3﹣2x=1得： x=1，把x=1代入方程+3=x 得：+3=1， 解得：m=﹣4， 则m 2=16． 故答案为：16． 点本题考查了同解方程的知识，解答本题的关键是理解评： 方程解得定义．12．若方程2x ﹣3=11与关于x 的方程4x+5=3k 有相同的解，则k 的值是 11 ．考点： 同解方程；解一元一次方程．专题：计算题． 分析： 先解方程2x ﹣3=11求出x 的值，把解得的值代入方程4x+5=3k ，就可以得到一个关于k 的方程，解方程就可以求出k 的值．解答： 解：解方程2x ﹣3=11得：x=7， 把x=7代入4x+5=3k ，得：28+5=3k ，解得：k=11． 故答案为：11．点评： 本题考查同解方程的知识，已知条件中涉及到方程的解，把方程的解代入原方程，转化为关于字母系数a 的方程进行求解．13．已知关于x 的方程5x+3k=24与5x+3=0的解相同，则k 的值为 9 ．考同解方程．点：专题：计算题． 分析： 首先根据5x+3=0得到5x=﹣3，再把5x=﹣3代入5x+3k=24求出k 的值即可． 解答： 解：∵5x+3=0， ∴5x=﹣3， ∵方程5x+3k=24与5x+3=0的解相同， ∴﹣3+3k=34， 解得k=9， 故答案为9．点评： 本题考查了同解方程．解一元一次方程的一般步骤是去分母，去括号，移项，合并同类项，移项时要变号．因为两方程解相同，把求得x 的值代入方程，即可求得常数项的值．14．已知方程3（x+3）﹣1=2x 的解与关于x 的方程的解相同，则m 2﹣2m+1的值为 25 ．考点：同解方程．分析： 先求出方程3（x+3）﹣1=2x 的解，再根据方程3（x+3）﹣1=2x 的解与关于x 的方程的解相同，把x 的值代入方程中，求出m 的值，再把m 的值代入要求的式子，即可得出答案．解答： 解：3（x+3）﹣1=2x ， 3x+9﹣1﹣2x=0，x=﹣8，∵方程3（x+3）﹣1=2x 的解与关于x 的方程的解相同，∴把x=﹣8代入方程得： 3×（﹣8）+m=﹣27，解得：m=﹣4，把m=﹣4代入m 2﹣2m+1得：（﹣4）2﹣2×（﹣4）+1=16+8+1=25；故答案为：25．点评： 此题考查了同解方程，关键是能够求出关于x 的方程，根据同解的定义建立方程，求出m 的值．15．已知关于x 的方程=x+与=3x ﹣2的解相同，则m=﹣ ．考点：同解方程． 分析： 先求出方程=3x ﹣2的解，然后把x 的值代入方程=x+求出m 的值．解解：解方程=3x ﹣2，答： 得：x=1，把x=1代入方程=x+得： =1+， 解得：m=﹣．故答案为：﹣．点评： 本题考查了同解方程，解答本题的关键是能够求解关于x 的方程，要正确理解方程解的含义．16．如果关于x 的方程和方程的解相同，那么k 的值．考点：同解方程． 分析：本题可先根据一元一次方程解出x 的值，再根据解相同，将x 的值代入二元一次方程中，即可解出k 的值． 解答： 解：解方程得： x=﹣，把x=﹣代入方程得：2﹣=0， 解得：k=5；故答案为：5．点评： 本题考查了二元一次方程与一元一次方程的综合运用．运用代入法，将解出的x 的值代入二元一次方程，可解出k 的值．17．如果方程与方程3x ﹣2a=0的解相同，则a 3= ．考点：同解方程． 分析： 根据第一个方程即可求得x=﹣；然后根据同解方程的定义，将其代入第二个方程，列出关于a 的方程；最后通过解关于a 的方程求得a 的值后，把a 的值代入所求的代数式并求值．解答： 解：∵x+=0，∴x=﹣；根据题意得3×（﹣）﹣2a=0，解得a=﹣，∴a 3==．故答案是：． 点评：本题考查了同解方程．使方程左右两边相等的未知数的值是该方程的解．因此检验一个数是否为相应的方程的解，就是把这个数代替方程中的未知数，看左右两边的值是否相等，如果左边=右边，那么这个数就是该方程的解；反之，这个数就不是该方程的解．18．方程ax 2+3x 2b ﹣1+cy=2是关于x 的一元一次方程，则a+b+c= 1 ；如果关于x 的方程2x+1=﹣3和方程=0的解相同，那么k= ﹣2 ．考点：同解方程；一元一次方程的定义． 专题：计算题．分析： 根据一元一次方程的定义可得出a=0，b=1，c=0，然后计算即可a+b+c ；先解出2x+1=3的值，然后代入可得出k ．解答： 解：∵方程ax 2+3x 2b ﹣1+cy=2是关于x 的一元一次方程， ∴a=0，2b ﹣1=1，c=0，解得：a=0，b=1，c=0，故可得a+b+c=1；方程2x+1=﹣3的解为：x=﹣2，代入可得：=0，解得：k=﹣2．故答案为：1、﹣2．点评： 此题考查了同解方程的知识，关键是掌握使方程左右两边相等的未知数的值是该方程的解，难度一般．19．若3x ﹣4=﹣1与ax ﹣b+1=﹣c 有相同的解，则（a ﹣b+c ）2009= ﹣1 ．考点：同解方程．专题：计算题；整体思想．分析： 答题时首先解出一元一次方程的解，把一元一次方程的解代入另一个方程中，求得a ﹣b+c 的值．解答： 解：∵3x ﹣4=﹣1与ax ﹣b+1=﹣c 有相同的解， ∴x=1也是ax ﹣b+1=﹣c 的解， ∴a ﹣b+c=﹣1，∴（a ﹣b+c ）2009=﹣1．点评： 本题主要考查解一元一次方程，利用整体法求值是解答本题的关键．20．若以为未知数的方程3x=5x ﹣8和有相同的解，则a=．考点：同解方程． 专题：计算题．分析：解方程3x=5x ﹣8就可以求出方程的解，这个解也是方程的解，根据方程的解的定义，把这个解代入就可以求出a 的值．解答： 解：首先解方程3x=5x ﹣8得：x=4；把x=4代入方程，得到2+4a=a ﹣5； 解得：a=﹣．点评： 本题的关键是正确解一元一次方程以及同解方程的意义．理解方程的解的定义，就是能够使方程左右两边相等的未知数的值．21．已知方程2x ﹣3=+x 的解满足|x|﹣1=0，则m ﹣6或﹣12 ．考点：同解方程．分析：通过解绝对值方程可以求得x=±1．然后把x 的值分别代入方程2x ﹣3=+x 来求m 的值． 解答： 解：由|x|﹣1=0，得x=±1．．当x=1时，由，得，解得m=﹣6； 当x=﹣1时，由，得，解得m=﹣12． 综上可知，m=﹣6或﹣12．故答案是：﹣6或﹣12．点评： 本题考查了同解方程的定义．如果第一个方程的解都是第二个方程的解，并且第二个方程的解也都是第一个方程的解，那么这两个方程叫做同解方程．22．关于x 的方程3x=9与x+4=k 的解相同，则代数式1﹣2|k|的值为 ﹣13 ．考点：同解方程．专题：计算题．分析： 根据3x=9与x+4=k 的解相同可得出k 的值，代入即可得出答案．解答： 解：3x=9，解得：x=3，将x=3代入x+4=k 可得：3+4=k ，k=7，∴1﹣2|k|=﹣13．故填：﹣13．点评： 本题考查同解方程的定义，难度不大，理解同解的概念是关键．23．关于x 的方程3mx+7=0和2 x+3n=0是同解方程，那么（mn ）2= ．考点：同解方程；代数式求值．分分别解出两个方程的解，使这两个解相等，即可得出析： m n 的值，从而可得出答案．解答： 解：由3mx+7=0与2x+3n=0是关于x 的同解方程，可知m ≠0，n ≠0解得 ∴，．故填：2．点评： 本题考查了同解方程的知识，属于比较简单的题目，注意掌握解答此类题目的方法．24．已知：一元一次方程2x ﹣2=3的解是方程的解，则m= ．考点： 同解方程． 分析： 先求出方程2x ﹣2=3的解，然后把x 的值代入方程，求解m 的值． 解答： 解：解方程2x ﹣2=3得：x=，把x=，代入方程， 得，m+=4，解得：m=．故答案为：．点评： 本题考查了同解方程，解决本题的关键是能够求解关于x 的方程，要正确理解方程解的含义．三．解答题（共6小题）25．已知：关于x 的方程4x ﹣k=2与3（2+x ）=2k 的解相同，求k 的值及相同的解．考点： 同解方程．专题：计算题．分析： 由已知关于x 的方程4x ﹣k=2与3（2+x ）=2k 的解相同，所以得关于x 、k 的方程组，解方程组即可． 解答： 解：已知：关于x 的方程4x ﹣k=2与3（2+x ）=2k 的解相同，∴， 解得，，所以k 的值为6，相同的解为2．点评： 此题考查的知识点是同解方程，本题解决的关键是能够求解关于x 的方程，根据同解的定义建立方程组．26．已知关于x 的方程2x+1=a 和2x+2=0的解相同，求的值．考点：同解方程．专题：计算题．分析： 先求出方程2x+2=0的解，代入方程2x+1=a 求出a 的值，代入代数式即可得出答案．解答： 解：2x+2=0，解得：x=﹣1，将x=﹣1代入2x+1=a ，得a=﹣1，则=1﹣1=0．点评： 本题考查了同解方程的知识，关键是理解方程解得含义，另外在代入计算时要细心，不要出错．27．若关于x 的方程2x ﹣3=1和=k ﹣3x 有相同的解，求k的值．考点：同解方程． 分析： 求出方程2x ﹣3=1中x 的值，再把k 当作已知条件求出方程=k ﹣3x 中x 的值，再根据两方程有相同的解列出关于k 的方程，求出k 的值即可．解答： 解：解方程2x ﹣3=1得，x=2，解方程=k ﹣3x 得，x=k ，∵两方成有相同的解，∴k=2，解得k=．点评： 本题考查的是同解方程，熟知如果两个方程的解相同，那么这两个方程叫做同解方程是解答此题的关键．28．如果方程的解与方程4y ﹣（3m+1）=6y+2m ﹣1的解相同，求式子的值．考点：同解方程． 分析： 求出方程的解y=10，代入第二个方程求出m=﹣4，代入求出即可．解答： 解：，2（y ﹣4）﹣48=﹣3（y+2），2y ﹣8﹣48=﹣3y ﹣6，5y=50，y=10，即方程4y ﹣（3m+1）=6y+2m ﹣1的解也是y=10， 代入得：40﹣（3m+1）=60+2m ﹣1，m=﹣4， 所以=4﹣=．点本题考查了一元一次方程的解，解一元一次方程，求评： 出代数式的值的应用，关键是求出y 、m 的值．29．方程4+2（x ﹣1）=0的解与关于x 的方程的解相同，求k 的值．考点：同解方程． 专题：方程思想．分析： 先求方程4+2（x ﹣1）=0的解，再代入，求得k 的值．解答： 解：解方程4+2（x ﹣1）=0，得x=﹣1，把x=﹣1代入， 得﹣3k ﹣2=﹣2， 解得k=﹣．点评： 此题主要考查了一元一次方程解的定义．解答此题的关键是熟知方程组有公共解的含义，考查了学生对题意的理解能力．30．当k 为何值时，方程与方程有相同的解？考点：同解方程．分析： 先解第二个方程，得x 的值，因为这个解也是第一个方程的解，根据方程的解的定义，把x 代入第一个方程中求出k 的值．解答： 解：解方程，得x=1，把x=1代入方程，得4﹣，解得k=﹣13，∴当k=﹣13时，方程与方程有相同的解．点评： 此题考查同解方程，关键是正确解方程的解的定义，就是能够使方程左右两边相等的未知数的值．。

人教版七年级数学上册第三章解一元一次方程——合并同类项与移项复习题（含答案)如果单项式2a mx y 与235a nx y --是关于x ，y 的单项式，且它们是同类项：（1）求()2002722a -的值；（2）若2amx y 235a nxy --=0，且xy ≠0，求200325m n ⎛⎫- ⎪⎝⎭的值．【答案】(1)1；(2)-1 【解析】 【分析】(1)先根据它们是同类项，列式23a a -=，求得a 的值，再代入求值即可； (2)由0xy ≠，得250m n +=，即25m n =-，再代入求值即可．【详解】∵单项式2a mx y 与235a nx y --是关于x ，y 的单项式，且它们是同类项， ∴23a a -=，解得3a =， (1)()2002722a -()20022122=-1=；(2)∵2a mx y 235a nx y --=0，且3a =，∴32mx y 35nx y -=0，即()3250m n x y -=，∵0xy ≠，∴250m n -=，即25m n =，∴200325m n ⎛⎫- ⎪⎝⎭200355n n ⎛⎫=- ⎪⎝⎭1=-．【点睛】本题考查了解一元一次方程以及同类项的概念，解题的关键是掌握解一元一次方程和同类项的概念．52．如图，点A 和点B 在数轴上对应的数分别为a 和b ，且()2680a b ++-=．（1）求线段AB 的长；（2）点C 在数轴上所对应的数为x ，且x 是方程24425x x --=+的解，点D 在线段AB 上，并且BD AD -BC =，请求出点D 在数轴上所对应的数；（3）在（2）的条件下，线段AD 和BC 分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动，运动时间为t 秒，M 为线段AD 的中点，N 为线段BC 的中点，若12MN =，求t 的值．【答案】(1) =4AB 1；(2)点D 在数轴上所对应的数为2-；(3)当t=3秒或 =27t 秒时线段=12MN ． 【解析】 【分析】（1）根据平方的非负性，绝对值的非负性求出a=-6，b=8，得到OA=6，OB=8，即可求出AB ；（2）解方程求出x=14，得到点C 在数轴上所对应的数为14，设点D 在数轴上所对应的数为y ，根据BD AD -BC =，列式求出y ；（3）根据中点得到运动前M N ，两点在数轴上所对应的数分别为-4,11，运动t 秒后M N ，两点在数轴上所对应的数分别为-4+6t,11+5t ，再分M 、N 相遇前，相遇后两种情况分别列方程求出t.【详解】(1)解：∵2(6)0,80a b +≥-≥，且2(6)80a b ++-=， ∴2(6)0,80a b +=-=，∴a+6=0，b-8=0， ∴a=-6，b=8， ∴OA=6，OB=8， ∴AB=OA+OB=6+8=14， (2)解方程24425x x --=+，得 14x ＝，∴点C 在数轴上所对应的数为14，设点D 在数轴上所对应的数为y 点D 在线段AB 上，且BD AD BC -＝，()66,8,1486AD y y BD y BC ∴--=+=＝＝－＝－， ()866y y ∴-－（+）＝， 解这个方程，得2y ＝－，∴点D 在数轴上所对应的数为2-．(3)解：由(2)得A D B C ，，，四点在数轴上所对应的数分别为： 62814--，，，．∴运动前M N ，两点在数轴上所对应的数分别为-4,11，则运动 t 秒后M N ，两点在数轴上所对应的数分别为-4+6t,11+5t ,12MN ＝∴①线段AD 没有追上线段BC 时有：(11+5t)-(-4+6t)=12解得：3t ＝ ；①线段AD 追上线段BC 后有：(-4+6t)-(11+5t)=12， 解得：27t ＝，∴综合上述：当t=3秒或27t ＝秒时线段12MN ＝．【点睛】此题考查线段的和差计算，平方及绝对值的非负性，数轴上两点之间的距离，数轴上动点问题，利用一元一次方程解决图形问题，注意分类讨论的解题思想.53．已知2|2|(53)0n m ++-=，求关于x 的方程1043mx x n +=+的解。

6.2.4解一元一次方程一．选择题（共30小题）1．（2013•海南）若代数式x+3的值为2，则x等于（）A．1B．﹣1 C．5D．﹣52．（2008•自贡）方程3x+6=0的解的相反数是（）A．2B．﹣2 C．3D．﹣33．（2011•新疆）已知：a=﹣a，则数a等于（）A．0B．﹣1 C．1D．不确定4．（2008•十堰）把方程3x+去分母正确的是（）A．18x+2（2x﹣1）=18﹣3（x+1）B．3x+（2x﹣1）=3﹣（x+1）C．18x+（2x﹣1）=18﹣（x+1）D．3x+2（2x﹣1）=3﹣3（x+1）5．（2007•台湾）解方程（3x+2）+2[（x﹣1）﹣（2x+1）]=6，得x=（）A．2B．4C．6D．86．（2011•台湾）若（a﹣1）：7=4：5，则10a+8之值为何（）A．54 B．66 C．74 D．807．（2005•杭州）若2005﹣200.5=x﹣20.05，那么x等于（）A．1814.55 B．1824.55 C．1774.55 D．1784.558．（2006•乌兰察布）我们来定义一种运算：=ad﹣bc．例如=2×5﹣3×4=﹣2；再如=3x﹣2，按照这种定义，当x满足（）时，．A．B．C．D．9．（2008•宣武区一模）对于实数a，b，c，d规定一种运算：，如﹣0×2=﹣2，那么时，x=（）A．B．C．D．10．式子6+x与x+1的和是31，则x的值是（）A．﹣12 B．12 C．13 D．﹣1911．若代数式4x﹣7与代数式5（x+）的值相等，则x的值是（）A．﹣9 B．1C．﹣5 D．312．解方程时，去分母正确的是（）A．（3x﹣5）﹣2（1﹣x）=4 B．（3x﹣5）﹣2（1﹣x）=1 C．（3x﹣5）﹣（1﹣x）=4 D．（3x﹣5）﹣2﹣2x=413．下列方程变形正确的是（）A．由﹣2x=3得x=B．由得x+3（x﹣1）=2（x+3）C．由得D．由﹣2+3x=4x得4x﹣3x=﹣214．下列方程变形正确的是（）A．由=0得x﹣1=5 B．由﹣1=0得x﹣1=0C．由=1得x﹣1=5D．由﹣1=1得x﹣5=115．方程可变形为（）A．B．C．D．16．代数式与m﹣的值互为相反数，则m的值为（）A．B．﹣C．﹣D．17．在解方程时，下列变形正确的是（）A．B．C．D．18．下列方程去括号正确的是（）A．由2x﹣3（4﹣2x）=6得2x﹣12﹣2x=6 B．由2x﹣3（4﹣2x）=6得2x﹣12﹣6x=6 C．由2x﹣3（4﹣2x）=6得2x﹣12+6x=6 D．由2x﹣3（4﹣2x）=6得2x﹣12﹣6x=619．将方程2x﹣=﹣1去分母，正确的是（）A．2x﹣1﹣x=﹣1 B．2x﹣1+x=﹣5 C．10x﹣1+x=﹣5 D．2x=﹣120．把方程的分母化为整数，以下变形正确的是（）A．B．C．D．21．下列解方程去分母正确的是（）A．由，去分母，得2x﹣1=3﹣3xB．由去分母，得2（x﹣2）﹣3x﹣2=﹣4C．由，去分母，得3y+3=2y﹣3y+1﹣6yD．由﹣1=，去分母，得12y﹣1=5y+2022．在解方程时，去分母正确的是（）A．3x+2（2x+1）=3﹣3（x﹣1）B．18x﹣（2x+1）=l8﹣（x﹣1）C．3x+（2x+1）=3﹣（x﹣1） D．18x﹣2（2x+1）=18﹣3（x﹣1）23．在解方程时，去分母正确的是（）A7（1﹣2x）=3（3x+1）﹣3 B．1﹣2x=（3x+1）﹣3 C．1﹣2x=（3x+1）﹣63 D．7（1﹣2x）=3（3x+1）﹣63．24．在梯形面积公式中，已知a=3，b=4，s=21，则h为（）A．3B．6C．73.5 D．1.525．下列方程变形正确的是（）A．方程3x﹣2=2x﹣1移项，得3x﹣2x=﹣1﹣2B．方程3﹣x=2﹣5（x﹣1）去括号，得3﹣x=2﹣5x﹣1C．方程可化为3x=6D．方程系数化为1，得x=﹣126．下列方程的变形正确的是（）A．3x﹣6=5，得3x=5﹣6 B．﹣1=，的4x_1﹣6=3xC．5=x+3，得x=5﹣3 D．+1=，得2x+1=x27．小明解方程去分母时．方程右边的﹣3忘记乘6．因而求出的解为x=2，问原方程正确的解为（）A．x=5 B．x=7 C．x=﹣13 D．x=﹣l28．若与﹣互为倒数，则x的值是（）A．B．﹣C．D．﹣29．解方程3﹣5（x+2）=x去括号正确的是（）A．3﹣x+2=x B．3﹣5x﹣10=x C．3﹣5x+10=x D．3﹣x﹣2=x 30．如果等式，那么△表示的数是（）A．﹣3 B．3C．0D．2014年2月cccgir的初中数学组卷参考答案与试题解析一．选择题（共30小题）1．（2013•海南）若代数式x+3的值为2，则x等于（）A．1B．﹣1 C．5D．﹣5考点：解一元一次方程．分析：根据题意，列出关于x的一元一次方程x+3=2，通过解该方程可以求得x的值．解答：解：由题意，得x+3=2，移项，得x=﹣1．故选B．点评：本题考查解一元一次方程的解法；解一元一次方程常见的过程有去括号、移项、系数化为1等．2．（2008•自贡）方程3x+6=0的解的相反数是（）A．2B．﹣2 C．3D．﹣3考点：解一元一次方程；相反数．专题：计算题．分析：先要求得3x+6=0的解，通过移项，系数化为1得出x的值，再去求它的相反数．解答：解：方程3x+6=0移项得，3x=﹣6，系数化为1得，x=﹣2；则：﹣2的相反数是2．故选A．点评：解一元一次方程的一般步骤是去分母，去括号，移项，合并同类项，移项时要变号，系数化为1．3．（2011•新疆）已知：a=﹣a，则数a等于（）A．0B．﹣1 C．1D．不确定考点：解一元一次方程．专题：探究型．分析：先将等式两边的代数式移到同一边，然后合并，最后解出a的值．解答：解：因为a=﹣a，所以a+a=0，即2a=0，则a=0，故选：A．点评：此题考查的知识点是解一元一次方程，关键是通过移项求解．4．（2008•十堰）把方程3x+去分母正确的是（）A．18x+2（2x﹣1）=18﹣3（x+1）B．3x+（2x﹣1）=3﹣（x+1）C．18x+（2x﹣1）=18﹣（x+1）D．3x+2（2x﹣1）=3﹣3（x+1）考点：解一元一次方程．分析：同时乘以各分母的最小公倍数，去除分母可得出答案．解答：解：去分母得：18x+2（2x﹣1）=18﹣3（x+1）．故选A．点评：本题考查了解一元一次方程的步骤：去分母、去括号、移项、合并同类项和系数化为1，在去分母时一定要注意：不要漏乘方程的每一项．5．（2007•台湾）解方程（3x+2）+2[（x﹣1）﹣（2x+1）]=6，得x=（）A．2B．4C．6D．8考点：解一元一次方程．专题：计算题．分析：先去小括号，再去中括号，移项合并，最后化系数为1，从而得到方程的解．解答：解：去括号得：3x+2+2x﹣2﹣4x﹣2=6，移项合并得：x=8，故选D．点评：本题考查解一元一次方程，解一元一次方程的一般步骤是去分母，去括号，移项，合并同类项，化系数为1．注意先去小括号，再去中括号．6．（2011•台湾）若（a﹣1）：7=4：5，则10a+8之值为何（）A．54 B．66 C．74 D．80考点：解一元一次方程；代数式求值．专题：方程思想．分析：首先由（a﹣1）：7=4：5求出a的值，然后将求得a的值代入10a+8即可得出答案．解答：解：（a﹣1）：7=4：5，即5（a﹣1）=28，去括号、移项得：5a=33，系数化1得：a=，把a=代入10a+8得：10×+8=74，故选：C．点评：此题考查的知识点是解一元一次方程和代数式求值，解题的关键是先把已知化为一元一次方程，解方程求a，再代入求值．7．（2005•杭州）若2005﹣200.5=x﹣20.05，那么x等于（）A．1814.55 B．1824.55 C．1774.55 D．1784.55考点：解一元一次方程．专题：计算题．分析：求x的值，需要对方程进行移项，注意在移项的过程中符号的变化．解答：解：方程2005﹣200.5=x﹣20.05移项得：x=2005﹣200.5+20.05，合并同类项得：x=1824.55；故答案选B．点评：解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项，移项时要变号．8．（2006•乌兰察布）我们来定义一种运算：=ad﹣bc．例如=2×5﹣3×4=﹣2；再如=3x﹣2，按照这种定义，当x满足（）时，．A．B．C．D．考点：解一元一次方程．专题：计算题；压轴题；新定义．分析：首先看清这种运算的规则，将转化为一元一次方程2（﹣1）﹣2x=（x﹣1）﹣（﹣4）×，通过去括号、移项、系数化为1等过程，求得x的值．解答：解：根据运算的规则：，可化简为：2（﹣1）﹣2x=（x﹣1）﹣（﹣4）×，化简可得﹣2x=3；即x=﹣．故选A．点评：本题立意新颖，借助新运算，实际考查解一元一次方程的解法；解一元一次方程常见的过程有去括号、移项、系数化为1等．9．（2008•宣武区一模）对于实数a，b，c，d规定一种运算：，如﹣0×2=﹣2，那么时，x=（）A．B．C．D．考点：解一元一次方程．专题：新定义．分析：由：，可知时列出方程2×5﹣【﹣4×（3﹣x）】=25，即可求解．解答：解：由：，可知时，2×5﹣【﹣4×（3﹣x）】=25，去括号得：22﹣25=4x，系数化为1得，x=﹣．故选D．点评： 此题主要考查学生对解一元一次方程的理解和掌握，难度不大，关键是找出其中的运算规律，然后即可得出答案．10．式子6+x 与x+1的和是31，则x 的值是（ ） A ． ﹣12 B ． 12 C ． 13 D ． ﹣19考点： 解一元一次方程． 专题： 计算题．分析： 式子6+x 与x+1的和是31，即（6+x ）+（x+1）=31，解即可． 解答： 解：根据题意得：（6+x ）+（x+1）=31，化简得：2x=24， 解得：x=12． 故选B ．点评： 本题考查解一元一次方程的解法．解一元一次方程常见的思路有通分、移项、左右同乘除等．11．若代数式4x ﹣7与代数式5（x+）的值相等，则x 的值是（ ） A ． ﹣9 B ． 1 C ． ﹣5 D ． 3考点： 解一元一次方程． 专题： 计算题． 分析： 根据题意建立等量关系，解方程求x 即可． 解答：解：依题意得：4x ﹣7=5（x+）4x ﹣7=5x+2解得：x=﹣9． 故选A ． 点评： 本题考查了根据题意中的等量关系，列方程、解方程的基本知识． 12．解方程时，去分母正确的是（ ）A ． （3x ﹣5）﹣2（1﹣x ）=4B ． （3x ﹣5）﹣2（1﹣x ）=1C ． （3x ﹣5）﹣（1﹣x ）=4D ． （3x ﹣5）﹣2﹣2x=4考点： 解一元一次方程． 专题： 计算题． 分析：方程去分母时，方程两端同乘各分母的最小公倍数4，即可得解．解答： 解：去分母得：（3x ﹣5）﹣2（1﹣x ）=4． 故选A ． 点评： 去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．13．下列方程变形正确的是（ ） A ．由﹣2x=3得x= B ． 由得x+3（x ﹣1）=2（x+3）C．由得D．由﹣2+3x=4x得4x﹣3x=﹣2考点：解一元一次方程；等式的性质．专题：计算题．分析：分别对所给的四个方程利用等式性质进行变形，可以找出正确答案．解答：解：A、系数化为1得，x=﹣，故错误；B、去分母得，6x+3（x﹣1）=2（x+3），故错误；C、根据分式的基本性质得，=0.5，故错误；D、移项得，﹣2=4x﹣3x，即4x﹣3x=﹣2，故正确．故选D．点评：解一元一次方程的步骤是：去分母、去括号、移项、合并同类项、系数化为1．注意等式性质的运用．14．下列方程变形正确的是（）A．由=0得x﹣1=5 B．由﹣1=0得x﹣1=0C．由=1得x﹣1=5D．由﹣1=1得x﹣5=1考点：解一元一次方程．专题：计算题．分析：分别对四个式子去分母即可，注意不要漏乘．解答：解：A、由=0，去分母得，x﹣1=0；B、由﹣1=0，去分母，得x﹣5=0；C、由=1，去分母得，x﹣1=5；D、由﹣1=1，去分母，得x﹣5=5．故选C．点评：去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．15．方程可变形为（）A．B．C．D．考点：解一元一次方程．专题：计算题．分析：对所给的方程左边利用分式的基本性质进行变形，可以找出正确答案．解答：解：根据分式的基本性质得：．故选D．点评：本题主要考查了分式的基本性质，分式的分子与分母同时扩大或缩小相同的倍数，分式的大小不变．16．代数式与m﹣的值互为相反数，则m的值为（）A．B．﹣C．﹣D．考点：解一元一次方程．分析：由于代数式与m﹣的值互为相反数，由此得到+m﹣=0，解此方程即可求解．解答：解：∵代数式与m﹣的值互为相反数，∴+m﹣=0，∴m=﹣．故选B．点评：本题主要考查了解一元一次方程，立意新颖，借助相反数，实际考查解一元一次方程的解法；解一元一次方程常见的过程有去括号、移项、系数化为1等．17．在解方程时，下列变形正确的是（）A．B．C．D．考点：解一元一次方程．专题：计算题．分析：根据分式的性质，将分式的分母化为整数即可．解答：解：分式的分母化为整数，得y﹣=1．故选B．点评：本题考查了解一元一次方程，将分式的分母化为整数利用了分式的基本性质．18．下列方程去括号正确的是（）A．由2x﹣3（4﹣2x）=6得2x﹣12﹣2x=6 B．由2x﹣3（4﹣2x）=6得2x﹣12﹣6x=6 C．由2x﹣3（4﹣2x）=6得2x﹣12+6x=6 D．由2x﹣3（4﹣2x）=6得2x﹣12﹣6x=6考点：解一元一次方程．分析：方程利用去括号法则计算即可得到结果．解答：解：由2x﹣3（4﹣2x）=6，去括号得：2x﹣12+6x=6．故选C点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1，求出解．19．将方程2x﹣=﹣1去分母，正确的是（）A．2x﹣1﹣x=﹣1 B．2x﹣1+x=﹣5 C．10x﹣1+x=﹣5 D．2x=﹣1考点：解一元一次方程．分析：方程两边都乘以5整理即可得解．解答：解：方程两边都乘以5，去分母得，10x﹣1+x=﹣5．故选C．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项．20．把方程的分母化为整数，以下变形正确的是（）A．B．C．D．考点：解一元一次方程．专题：计算题．分析：把方程中的分子与分母同时乘以一个数，使分母变为整数即可．解答：解：把的分子分母同时乘以10，的分子分母同时乘以100得，=﹣1，即=﹣1．故选A．点评：本题考查的是解一元一次方程，在解答此类题目时要注意把方程中分母化为整数再求解．21．下列解方程去分母正确的是（）A．由，去分母，得2x﹣1=3﹣3xB．由去分母，得2（x﹣2）﹣3x﹣2=﹣4C．由，去分母，得3y+3=2y﹣3y+1﹣6yD．由﹣1=，去分母，得12y﹣1=5y+20考点：解一元一次方程．专题：方程思想．分析：将各选项分别乘以分母的最小公倍数去分母，可得出答案．解答：解：A、不含分母的项漏乘以各分母的最小公倍数6，错误；B、的分子作为一个整体没有加上括号，错误；C、正确；D、不含分母的项漏乘以各分母的最小公倍数15，错误．故选C．点评：考查了解一元一次方程，去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号．22．在解方程时，去分母正确的是（）A．3x+2（2x+1）=3﹣3（x﹣1）B．18x﹣（2x+1）=l8﹣（x﹣1）C．3x+（2x+1）=3﹣（x﹣1）D．18x﹣2（2x+1）=18﹣3（x﹣1）考点：解一元一次方程．专题：计算题．分析：本题只需将方程两边同时乘以各分母的最小公倍数6，在去分母的过程中注意分数线有括号的作用，以及去分母时不能漏乘没有分母的项．解答：解：方程两边同时乘以6得：18x﹣2（2x+1）=18﹣3（x﹣1）．故选D．点评：本题考查了解一元一次方程，在去分母的过程中注意分数线起到括号的作用，并注意不能漏乘没有分母的项．23．在解方程时，去分母正确的是（）B．1﹣2x=（3x+1）﹣3 C．1﹣2x=（3x+1）﹣63 D．7（1﹣2x）=3（3x+1）﹣63 A．7（1﹣2x）=3（3x+1）﹣3考点：解一元一次方程．专题：计算题．分析：方程两边乘以21去分母得到结果，即可做出判断．解答：解：去分母得：7（1﹣2x）=3（3x+1）﹣63．故选D．点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1，求出解．24．在梯形面积公式中，已知a=3，b=4，s=21，则h为（）A．3B．6C．73.5 D．1.5考点：解一元一次方程．专题：计算题．分析：先把a=3，b=4，s=21代入梯形的面积公式，再根据解一元一次方程的一般步骤求出h的值即可．解答：解：∵a=3，b=4，s=21，∴21=（3+4）h，即21=h，解得h=6．故选B．点评：本题考查的是解一元一次方程，熟知解一元一次方程的一般步骤是解答此题的关键．25．下列方程变形正确的是（）A．方程3x﹣2=2x﹣1移项，得3x﹣2x=﹣1﹣2B．方程3﹣x=2﹣5（x﹣1）去括号，得3﹣x=2﹣5x﹣1C．方程可化为3x=6D．方程系数化为1，得x=﹣1考点：解一元一次方程．专题：计算题．分析：利用去分母，去括号，移项合并，以及分数的性质计算，判断即可得到结果．解答：解：A、方程3x﹣2=2x﹣1移项，得3x﹣2x=﹣1+2，本选项错误；B、方程3﹣x=2﹣5（x﹣1）去括号，得3﹣x=2﹣5x+5，本选项错误；C、方程﹣=1，化简得：﹣=5x﹣5﹣2x=1，即3x=6，本选项正确；D、方程x=﹣系数化为1，得：x=﹣，本选项错误，故选C．点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项，合并，将未知数系数化为1，求出解．26．下列方程的变形正确的是（）A．3x﹣6=5，得3x=5﹣6 B．﹣1=，的4x_1﹣6=3xC．5=x+3，得x=5﹣3 D．+1=，得2x+1=x考点：解一元一次方程．专题：计算题．分析： A、移项得到结果，即可做出判断；B、去分母得到结果，即可做出判断；C、移项得到结果，即可做出判断；D、去分母得到结果，即可做出判断．解答：解：A、3x﹣6=5，移项得：3x=5+6，本选项错误；B、去分母得：2（2x﹣1）﹣6=3x，本选项错误；C、移项得：x=5﹣3，本选项正确；D、去分母得：2x+4=x，本选项错误，故选C点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将x系数化为1，求出解．27．小明解方程去分母时．方程右边的﹣3忘记乘6．因而求出的解为x=2，问原方程正确的解为（）A．x=5 B．x=7 C．x=﹣13 D．x=﹣l考点：解一元一次方程．专题：计算题．分析：先把错误的解法得到的x的值代入方程求出a的值，然后根据一元一次方程的解法，先去分母，再去括号，最后移项，合并同类项，从而得到方程的解．解答：解：∵方程右边的﹣3忘记乘6，求出的解为x=2，∴2（2×2﹣1）=3（2+a）﹣3，解得a=1，所以，方程为=﹣3，去分母得，2（2x﹣1）=3（x+1）﹣18，去括号得，4x﹣2=3x+3﹣18，移项得，4x﹣3x=3﹣18+2，合并同类项得，x=﹣13．故选C．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号，本题先根据错误的思路列式求出a的值是解题的关键．28．若与﹣互为倒数，则x的值是（）A．B．﹣C．D．﹣考点：解一元一次方程．专题：计算题．分析：先根据互为倒数列式，两数相乘等于1，然后再根据一元一次方程的解法，去分母，去括号，最后移项，化系数为1，从而得到方程x的值．解答：解：根据题意若×（﹣）=1，去分母得，7（5x﹣1）=﹣18，去括号得，35x﹣7=﹣18，移项、合并得，35x=﹣11，系数化为1得，x=﹣．故选D．点评：本题主要考查了解一元一次方程，注意在去分母时，方程两端同乘各分母的最小公倍数时，不要漏乘没有分母的项，同时要把分子（如果是一个多项式）作为一个整体加上括号，根据题意正确列出方程是解题的关键．29．解方程3﹣5（x+2）=x去括号正确的是（）A．3﹣x+2=x B．3﹣5x﹣10=x C．3﹣5x+10=x D．3﹣x﹣2=x考点：解一元一次方程；去括号与添括号．分析：去括号时，注意符号的变化，不要漏乘括号里的每一项．解答：解：去括号得：3﹣5x﹣10=x，故选B．点评：去括号时，运用乘法的分配律，先把括号前的数字与括号里各项相乘，再运用括号前是”+“，去括号后，括号里的各项都不改变符号；括号前是”﹣“，去括号后，括号里的各项都改变符号．30．如果等式，那么△表示的数是（）A．﹣3 B．3C．0D．考点：解一元一次方程．专题：计算题．分析：根据0除以任何一个不为0的数等于0，得出（﹣3）﹣△=0，求出即可．解答：解：∵[（﹣3）﹣△]÷（﹣6）=0，∴（﹣3）﹣△=0，∴△=﹣3，故选A．点评：本题考查了一元一次方程的应用，解此题的关键是根据题意得出（﹣3）﹣△=0，求出关于△的方程的解．。

6.2.6同解方程完成时间：20min一．选择题（共9小题）1．已知关于x的方程7x+3k=12与7x+3=0的解相同，则k的值为（）A﹣3 B．3C．﹣5 D．52．关于x的方程x+a=2x﹣3与2x﹣b=x有相同的解，则a、b的关系为（）A．a﹣b=3 B．b﹣a=3 C．b+a=3 D．b+a+3=03．已知方程4x=8与x﹣k=1的解相同，则4k2﹣1的值为（）A．1B．3C．8D．174．吴云科和孟家福是七年级四班的两名爱好数学的优等生，在学完第三章《一元一次方程》后，吴云科对孟家福说：“方程与方程的解相同，你能求出k的值吗？”孟家福用笔算了一下给出正确答案，聪明的你知道是哪个吗？（）A．0B．2C．1D．﹣15．如果方程x=1与2x+a=ax的解相同，则a的值是（）A．2B．﹣2 C．3D．﹣36．下列方程中与方程3x=x+1的解相同的是（）A．2x=4 B．2x=4x﹣1 C．5x+3=6 D．6x﹣15x=37．如果方程6x+3a=22与方程3x+5=11的解相同，那么a=（）A．B．C．﹣D．﹣8．在方程：①3x﹣=1；②；③6x﹣5=2x﹣3；④x+=2x中，与方程2x=1的解相同的方程有（）A．1个B．2个C．3个D．4个9．有4个关于x方程：（1）x﹣2=﹣1 （2）（x﹣2）+（x﹣1）=﹣1+（x﹣1）（3）x=0 （4）其中同解的两个方程是（）A．（1）与（2）B．（1）与（3）C．（1）与（4）D．（2）与（4）二．填空题（共15小题）10．方程x+2=3的解也是方程ax﹣5=8的解时，则a=_________．11．已知关于x的方程+3=x与方程3﹣2x=1的解相同，则m2=_________．12．若方程2x﹣3=11与关于x的方程4x+5=3k有相同的解，则k的值是_________．13．已知关于x的方程5x+3k=24与5x+3=0的解相同，则k的值为_________．14．已知方程3（x+3）﹣1=2x的解与关于x的方程的解相同，则m2﹣2m+1的值为_________．15．已知关于x的方程=x+与=3x﹣2的解相同，则m=_________．16．如果关于x的方程和方程的解相同，那么k的值_________．17．如果方程与方程3x﹣2a=0的解相同，则a3=_________．18．方程ax2+3x2b﹣1+cy=2是关于x的一元一次方程，则a+b+c=_________；如果关于x的方程2x+1=﹣3和方程=0的解相同，那么k=_________．19．若3x﹣4=﹣1与ax﹣b+1=﹣c有相同的解，则（a﹣b+c）2009=_________．20．若以为未知数的方程3x=5x﹣8和有相同的解，则a=_________．21．已知方程2x﹣3=+x的解满足|x|﹣1=0，则m_________．22．关于x的方程3x=9与x+4=k的解相同，则代数式1﹣2|k|的值为_________．23．关于x的方程3mx+7=0和2 x+3n=0是同解方程，那么（mn）2=_________．24．已知：一元一次方程2x﹣2=3的解是方程的解，则m=_________．三．解答题（共6小题）25．已知：关于x的方程4x﹣k=2与3（2+x）=2k的解相同，求k的值及相同的解．26．已知关于x的方程2x+1=a和2x+2=0的解相同，求的值．27．若关于x的方程2x﹣3=1和=k﹣3x有相同的解，求k的值．28．如果方程的解与方程4y﹣（3m+1）=6y+2m﹣1的解相同，求式子的值．29．方程4+2（x﹣1）=0的解与关于x的方程的解相同，求k的值．30．当k为何值时，方程与方程有相同的解？6.2.6同解方程参考答案与试题解析一．选择题（共9小题）1．已知关于x的方程7x+3k=12与7x+3=0的解相同，则k的值为（）A．﹣3 B．3C．﹣5 D．5考点：同解方程．专题：计算题．分析：先解方程7x+3=0，可得x=﹣，根据同解的定义可得x=﹣也是7x+3k=12的解，再把x=﹣代入7x+3k=12中即可求k．解答：解：解方程7x+3=0得，x=﹣，∵7x+3k=12与7x+3=0的解相同，∴x=﹣也是7x+3k=12的解，再把x=﹣代入7x+3k=12中，得7×（﹣）+3k=12，解得k=5．故选D．点评：本题考查了同解方程的定义，解题的关键是先求出x．2．关于x的方程x+a=2x﹣3与2x﹣b=x有相同的解，则a、b的关系为（）A．a﹣b=3 B．b﹣a=3 C．b+a=3 D．b+a+3=0考点：同解方程．分析：求出两个方程的解，根据已知得出两个解相等，即可求出答案．解答：解：x+a=2x﹣3，x﹣2x=﹣3﹣a，﹣x=﹣3﹣a，则x=3+a，2x﹣b=x，x=b，∵关于x的方程x+a=2x﹣3与2x﹣b=x有相同的解，∴3+a=b，∴b﹣a=3，故选B．点评：本题考查了对同解方程的理解，关键是求出3+a=b，题目比较好，难度适中．3．已知方程4x=8与x﹣k=1的解相同，则4k2﹣1的值为（）A．1B．3C．8D．17考点：同解方程．专题：计算题．分析：先解出方程4x=8的解，然后代入求出k的值，进而可得出答案．解答：解：解方程4x=8，得：x=2，把x=2代入x﹣k=1，得：k=1，∴4k2﹣1=3．故选B．点评：本题考查同解方程的知识，比较简单，解决本题的关键是理解方程解的定义，注意细心运算．4．吴云科和孟家福是七年级四班的两名爱好数学的优等生，在学完第三章《一元一次方程》后，吴云科对孟家福说：“方程与方程的解相同，你能求出k的值吗？”孟家福用笔算了一下给出正确答案，聪明的你知道是哪个吗？（）A．0B．2C．1D．﹣1考点：同解方程．专题：方程思想．分析：先解方程，得x=1，因为这个解也是方程的解，根据方程的解的定义，把x代入方程中求出k的值．解答：解：12﹣2（x﹣1）=3（1﹣x）+6（3﹣x）解得：x=1．把x=1代入方程得：4﹣=3k﹣，12﹣k﹣2=9k，解得：k=1．故选C．点评：本题考查了同解方程，解题的关键是正确解一元一次方程．理解方程的解的定义，就是能够使方程左右两边相等的未知数的值．5．如果方程x=1与2x+a=ax的解相同，则a的值是（）A．2B．﹣2 C．3D．﹣3考点：同解方程．专题：计算题．分析：可以分别解出两方程的解，两解相等，就得到关于a的方程，从而可以求出a的值．解答：解：解第一个方程得：x=3，解第二个方程得：x=∴=3解得：a=3故选C．点评：本题解决的关键是能够求解关于x的方程，要能正确理解方程解的含义．6．下列方程中与方程3x=x+1的解相同的是（）A．2x=4 B．2x=4x﹣1 C．5x+3=6 D．6x﹣15x=3考点：同解方程．专题：计算题．分析：求得题目中各个方程的解，即可作出判断．解答：解：方程3x=x+1的解是x=．A、解是x=2，故错误；B、解是x=，故正确；C、解是x=，故错误；D、解是x=﹣，故错误．故选B．点评：本题主要考查了一元一次方程的解法，正确解方程是解题的关键．7．如果方程6x+3a=22与方程3x+5=11的解相同，那么a=（）A．B．C．﹣D．﹣考点：同解方程．专题：计算题．分析：先通过方程3x+5=11求得x的值，因为方程6x+3a=22与方程3x+5=11的解相同，把x的值代入方程6x+3a=22，即可求得a的值．解答：解：3x+5=11，移项，得3x=11﹣5，合并同类项，得3x=6，系数化为1，得x=2，把x=2代入6x+3a=22中，得6×2+3a=22，∴a=，故选B．点评：解一元一次方程的一般步骤是去分母，去括号，移项，合并同类项，移项时要变号．因为两方程解相同，把求得x的值代入方程，即可求得常数项的值．8．在方程：①3x﹣=1；②；③6x﹣5=2x﹣3；④x+=2x中，与方程2x=1的解相同的方程有（）A．1个B．2个C．3个D．4个考点：同解方程．专题：计算题．分析：求出方程2x=1的解是x=，要判断x=是否是方程的解，就是把它代入方程的左右两边，看是否相等．解答：解：方程2x=1的解是x=A、把x=代入3x﹣=1，左边=﹣=1，左边=右边，因而x=是方程3x﹣=1的解，即与方程2x=1的解相同．B、把x=代入，左边=（+1）=，左边=右边，因而x=是方程的解，即与方程2x=1的解相同．C、把x=代入6x﹣5=2x﹣3，左边=3﹣5=﹣2，右边=1﹣3=﹣2，左边=右边，因而x=是方程6x﹣5=2x﹣3的解，即与方程2x=1的解相同．D、把x=代入x+=2x，左边=+=1，右边=2×=1，因而左边=右边，因而x=是方程6x﹣5=2x﹣3的解，即与方程2x=1的解相同．四个方程都与2x=1的解相同．故选D．点评：本题主要考查判断一个数是否是方程的解的方法．9．有4个关于x方程：（1）x﹣2=﹣1 （2）（x﹣2）+（x﹣1）=﹣1+（x﹣1）（3）x=0 （4）其中同解的两个方程是（）A．（1）与（2）B．（1）与（3）C．（1）与（4）D．（2）与（4）考点：同解方程．分析：（1）移项可解出x的值．（2）先去括号在移项合并可得出x的值．（3）直接可得出x的值．（4）直接移项即可，注意分式有意义的条件．解答：解：（1）方程的解为x=1，（2）方程的解为x=1，（3）方程的解为x=0，（4）方程无解．∴只有（1）（2）是同解方程．故选A．点评：本题考查同解方程的知识，关键是正确求出4个方程的解，难度不大，注意要细心运算．二．填空题（共15小题）10．方程x+2=3的解也是方程ax﹣5=8的解时，则a=13．考点：同解方程．专题：计算题．分析：首先解出方程x+2=3的解，代入方程ax﹣5=8中求出a的值即可．解答：解：x+2=3，解得x=1；把x=1代入ax﹣5=8中，得a﹣5=8，解得a=13．点评：本题的关键是正确解一元一次方程．理解方程的解的定义，就是能够使方程左右两边相等的未知数的值．11．已知关于x的方程+3=x与方程3﹣2x=1的解相同，则m2=16．考点：同解方程．分析：首先解出方程3﹣2x=1的解，然后把方程的解代入方程+3=x求出m，即可求出m2．解答：解：解方程3﹣2x=1得：x=1，把x=1代入方程+3=x得：+3=1，解得：m=﹣4，则m2=16．故答案为：16．点评：本题考查了同解方程的知识，解答本题的关键是理解方程解得定义．12．若方程2x﹣3=11与关于x的方程4x+5=3k有相同的解，则k的值是11．考点：同解方程；解一元一次方程．专题：计算题．分析：先解方程2x﹣3=11求出x的值，把解得的值代入方程4x+5=3k，就可以得到一个关于k的方程，解方程就可以求出k的值．解答：解：解方程2x﹣3=11得：x=7，把x=7代入4x+5=3k，得：28+5=3k，解得：k=11．故答案为：11．点评：本题考查同解方程的知识，已知条件中涉及到方程的解，把方程的解代入原方程，转化为关于字母系数a 的方程进行求解．13．已知关于x的方程5x+3k=24与5x+3=0的解相同，则k的值为9．考点：同解方程．专题：计算题．分析：首先根据5x+3=0得到5x=﹣3，再把5x=﹣3代入5x+3k=24求出k的值即可．解答：解：∵5x+3=0，∴5x=﹣3，∵方程5x+3k=24与5x+3=0的解相同，∴﹣3+3k=34，解得k=9，故答案为9．点评：本题考查了同解方程．解一元一次方程的一般步骤是去分母，去括号，移项，合并同类项，移项时要变号．因为两方程解相同，把求得x的值代入方程，即可求得常数项的值．14．已知方程3（x+3）﹣1=2x的解与关于x的方程的解相同，则m2﹣2m+1的值为25．考点：同解方程．分析：先求出方程3（x+3）﹣1=2x的解，再根据方程3（x+3）﹣1=2x的解与关于x的方程的解相同，把x的值代入方程中，求出m的值，再把m的值代入要求的式子，即可得出答案．解答：解：3（x+3）﹣1=2x，3x+9﹣1﹣2x=0，x=﹣8，∵方程3（x+3）﹣1=2x的解与关于x的方程的解相同，∴把x=﹣8代入方程得：3×（﹣8）+m=﹣27，解得：m=﹣4，把m=﹣4代入m2﹣2m+1得：（﹣4）2﹣2×（﹣4）+1=16+8+1=25；故答案为：25．点评：此题考查了同解方程，关键是能够求出关于x的方程，根据同解的定义建立方程，求出m的值．15．已知关于x的方程=x+与=3x﹣2的解相同，则m=﹣．考点：同解方程．分析：先求出方程=3x﹣2的解，然后把x的值代入方程=x+求出m的值．解答：解：解方程=3x﹣2，得：x=1，把x=1代入方程=x+得：=1+，解得：m=﹣．故答案为：﹣．点评：本题考查了同解方程，解答本题的关键是能够求解关于x的方程，要正确理解方程解的含义．16．如果关于x的方程和方程的解相同，那么k的值．考点：同解方程．分析：本题可先根据一元一次方程解出x的值，再根据解相同，将x的值代入二元一次方程中，即可解出k的值．解答：解：解方程得：x=﹣，把x=﹣代入方程得：2﹣=0，解得：k=5；故答案为：5．点评：本题考查了二元一次方程与一元一次方程的综合运用．运用代入法，将解出的x的值代入二元一次方程，可解出k的值．17．如果方程与方程3x﹣2a=0的解相同，则a3=．考点：同解方程．分析：根据第一个方程即可求得x=﹣；然后根据同解方程的定义，将其代入第二个方程，列出关于a的方程；最后通过解关于a的方程求得a的值后，把a的值代入所求的代数式并求值．解答：解：∵x+=0，∴x=﹣；根据题意得3×（﹣）﹣2a=0，解得a=﹣，∴a3==．故答案是：．点评：本题考查了同解方程．使方程左右两边相等的未知数的值是该方程的解．因此检验一个数是否为相应的方程的解，就是把这个数代替方程中的未知数，看左右两边的值是否相等，如果左边=右边，那么这个数就是该方程的解；反之，这个数就不是该方程的解．18．方程ax2+3x2b﹣1+cy=2是关于x的一元一次方程，则a+b+c=1；如果关于x的方程2x+1=﹣3和方程=0的解相同，那么k=﹣2．考点：同解方程；一元一次方程的定义．专题：计算题．分析：根据一元一次方程的定义可得出a=0，b=1，c=0，然后计算即可a+b+c；先解出2x+1=3的值，然后代入可得出k．解答：解：∵方程ax2+3x2b﹣1+cy=2是关于x的一元一次方程，∴a=0，2b﹣1=1，c=0，解得：a=0，b=1，c=0，故可得a+b+c=1；方程2x+1=﹣3的解为：x=﹣2，代入可得：=0，解得：k=﹣2．故答案为：1、﹣2．点评：此题考查了同解方程的知识，关键是掌握使方程左右两边相等的未知数的值是该方程的解，难度一般．19．若3x﹣4=﹣1与ax﹣b+1=﹣c有相同的解，则（a﹣b+c）2009=﹣1．考点：同解方程．专题：计算题；整体思想．分析：答题时首先解出一元一次方程的解，把一元一次方程的解代入另一个方程中，求得a﹣b+c的值．解答：解：∵3x﹣4=﹣1与ax﹣b+1=﹣c有相同的解，∴x=1也是ax﹣b+1=﹣c的解，∴a﹣b+c=﹣1，∴（a﹣b+c）2009=﹣1．点评：本题主要考查解一元一次方程，利用整体法求值是解答本题的关键．20．若以为未知数的方程3x=5x﹣8和有相同的解，则a=．考点：同解方程．专题：计算题．分析：解方程3x=5x﹣8就可以求出方程的解，这个解也是方程的解，根据方程的解的定义，把这个解代入就可以求出a的值．解答：解：首先解方程3x=5x﹣8得：x=4；把x=4代入方程，得到2+4a=a﹣5；解得：a=﹣．点评：本题的关键是正确解一元一次方程以及同解方程的意义．理解方程的解的定义，就是能够使方程左右两边相等的未知数的值．21．已知方程2x﹣3=+x的解满足|x|﹣1=0，则m﹣6或﹣12．考点：同解方程．分析：通过解绝对值方程可以求得x=±1．然后把x的值分别代入方程2x﹣3=+x来求m的值．解答：解：由|x|﹣1=0，得x=±1．．当x=1时，由，得，解得m=﹣6；当x=﹣1时，由，得，解得m=﹣12．综上可知，m=﹣6或﹣12．故答案是：﹣6或﹣12．点评：本题考查了同解方程的定义．如果第一个方程的解都是第二个方程的解，并且第二个方程的解也都是第一个方程的解，那么这两个方程叫做同解方程．22．关于x的方程3x=9与x+4=k的解相同，则代数式1﹣2|k|的值为﹣13．考点：同解方程．专题：计算题．分析：根据3x=9与x+4=k的解相同可得出k的值，代入即可得出答案．解答：解：3x=9，解得：x=3，将x=3代入x+4=k可得：3+4=k，k=7，∴1﹣2|k|=﹣13．故填：﹣13．点评：本题考查同解方程的定义，难度不大，理解同解的概念是关键．23．关于x的方程3mx+7=0和2 x+3n=0是同解方程，那么（mn）2=．考点：同解方程；代数式求值．分析：分别解出两个方程的解，使这两个解相等，即可得出mn的值，从而可得出答案．解答：解：由3mx+7=0与2x+3n=0是关于x的同解方程，可知m≠0，n≠0解得∴，．故填：2．点评：本题考查了同解方程的知识，属于比较简单的题目，注意掌握解答此类题目的方法．24．已知：一元一次方程2x﹣2=3的解是方程的解，则m=．考点：同解方程．分析：先求出方程2x﹣2=3的解，然后把x的值代入方程，求解m的值．解答：解：解方程2x﹣2=3得：x=，把x=，代入方程，得，m+=4，解得：m=．故答案为：．点评：本题考查了同解方程，解决本题的关键是能够求解关于x的方程，要正确理解方程解的含义．三．解答题（共6小题）25．已知：关于x的方程4x﹣k=2与3（2+x）=2k的解相同，求k的值及相同的解．考点：同解方程．专题：计算题．分析：由已知关于x的方程4x﹣k=2与3（2+x）=2k的解相同，所以得关于x、k的方程组，解方程组即可．解答：解：已知：关于x的方程4x﹣k=2与3（2+x）=2k的解相同，∴，解得，，所以k的值为6，相同的解为2．点评：此题考查的知识点是同解方程，本题解决的关键是能够求解关于x的方程，根据同解的定义建立方程组．26．已知关于x的方程2x+1=a和2x+2=0的解相同，求的值．考点：同解方程．专题：计算题．分析：先求出方程2x+2=0的解，代入方程2x+1=a求出a的值，代入代数式即可得出答案．解答：解：2x+2=0，解得：x=﹣1，将x=﹣1代入2x+1=a，得a=﹣1，则=1﹣1=0．点评：本题考查了同解方程的知识，关键是理解方程解得含义，另外在代入计算时要细心，不要出错．27．若关于x的方程2x﹣3=1和=k﹣3x有相同的解，求k的值．考点：同解方程．分析：求出方程2x﹣3=1中x的值，再把k当作已知条件求出方程=k﹣3x中x的值，再根据两方程有相同的解列出关于k的方程，求出k的值即可．解答：解：解方程2x﹣3=1得，x=2，解方程=k﹣3x得，x=k，∵两方成有相同的解，∴k=2，解得k=．点评：本题考查的是同解方程，熟知如果两个方程的解相同，那么这两个方程叫做同解方程是解答此题的关键．28．如果方程的解与方程4y﹣（3m+1）=6y+2m﹣1的解相同，求式子的值．考点：同解方程．分析：求出方程的解y=10，代入第二个方程求出m=﹣4，代入求出即可．解答：解：，2（y﹣4）﹣48=﹣3（y+2），2y﹣8﹣48=﹣3y﹣6，5y=50，y=10，即方程4y﹣（3m+1）=6y+2m﹣1的解也是y=10，代入得：40﹣（3m+1）=60+2m﹣1，m=﹣4，所以=4﹣=．点评：本题考查了一元一次方程的解，解一元一次方程，求出代数式的值的应用，关键是求出y、m的值．29．方程4+2（x﹣1）=0的解与关于x的方程的解相同，求k的值．考点：同解方程．专题：方程思想．分析：先求方程4+2（x﹣1）=0的解，再代入，求得k的值．解答：解：解方程4+2（x﹣1）=0，得x=﹣1，把x=﹣1代入，得﹣3k﹣2=﹣2，解得k=﹣．点评：此题主要考查了一元一次方程解的定义．解答此题的关键是熟知方程组有公共解的含义，考查了学生对题意的理解能力．30．当k为何值时，方程与方程有相同的解？考点：同解方程．分析：先解第二个方程，得x的值，因为这个解也是第一个方程的解，根据方程的解的定义，把x代入第一个方程中求出k的值．解答：解：解方程，得x=1，把x=1代入方程，得4﹣，解得k=﹣13，∴当k=﹣13时，方程与方程有相同的解．点评：此题考查同解方程，关键是正确解方程的解的定义，就是能够使方程左右两边相等的未知数的值．。

一元一次方程习题精选附答案6.2.4 解一元一次方程（三）一、解答题（共30小题）1.解方程：2x+1=72.删除此题3.1）解方程：4-x=3(2-x)；2）解方程：删除此题4.解方程：删除此题5.解方程1）4(x-1)-3(20-x)=5(x-2)；2）x-1=2(x-3)。

6.1）解方程：3(x-1)=2x+3；2）解方程：x-1=1/x。

7.-1+2x=3x+18.解方程：5(x-1)-2(x+1)=3(x-1)+x+1；9.解方程：删除此题10.1）4x-3(4-x)=2；2）(x-1)+2=2-(x+2)。

11.1）计算：删除此题2）解方程：删除此题12.解方程：删除此题13.1）删除此题2）删除此题14.1）5(2x+1)-2(2x-3)=6；2）删除此题3）3(x-1)+|x-2|=5x-1.15.A类）解方程：5x-2=7x+8；B类）解方程：(x-1)-(x+5)=-2；C类）解方程：删除此题16.1）3(x+6)=9-5(1-2x)；2）删除此题17.1）4x-3(5-x)=13；2）x+3=2x-3.18.1）计算：-42×|-2|÷(3-|3|)；2）计算：-12-|0.5-|-2-(-3)|÷2；3）解方程：4x-3(5-x)=2；4）解方程：删除此题19.1）计算：-7×(-1/3)÷(4/5)；2）删除此题3）解方程：3x+3=2x+7；4）解方程：6x-2=4x+10.20.1）-0.2(x-5)=1；2）删除此题21.解方程：4x+5=9.22.3x=-12.23.1）0.5x-0.7=5.2-1.3(x-1)；2）5x+2(3x-7)=9-4(2+x)；3）2x+3(x+1)=5-4(x-1)；4）删除此题24.解方程：x=21/6.25.解方程：-2x+5=3x+4.26.1）5x=27；2）删除此题27.解方程：x^2+3x-4=0.28.当k=3时，式子比值少3.29.I）7.5y=14；II）删除此题。