《原子物理与量子力学》第十,十一章部分习题解答

格式：ppt
大小：306.50 KB
文档页数：12

下载文档原格式

原子物理学课后习题答案

第一章原子的基本状况1.1 若卢瑟福散射用的α粒子是放射性物质镭'C 放射的，其动能为67.6810⨯电子伏特。

散射物质是原子序数79Z =的金箔。

试问散射角150οθ=所对应的瞄准距离b 多大？解：根据卢瑟福散射公式：20222442K Mv ctgb b Ze Zeαθπεπε==得到：2192150152212619079(1.6010) 3.97104(48.8510)(7.681010)Ze ctg ctg b K οθαπεπ---⨯⨯===⨯⨯⨯⨯⨯⨯米式中212K Mv α=是α粒子的功能。

1.2已知散射角为θ的α粒子与散射核的最短距离为220121()(1)4sinmZe r Mv θπε=+，试问上题α粒子与散射的金原子核之间的最短距离m r 多大？解：将1.1题中各量代入m r 的表达式，得：2min202121()(1)4sin Ze r Mv θπε=+ 1929619479(1.6010)1910(1)7.6810 1.6010sin 75ο--⨯⨯⨯=⨯⨯⨯+⨯⨯⨯143.0210-=⨯米1.3 若用动能为1兆电子伏特的质子射向金箔。

问质子与金箔。

问质子与金箔原子核可能达到的最小距离多大？又问如果用同样能量的氘核（氘核带一个e +电荷而质量是质子的两倍，是氢的一种同位素的原子核）代替质子，其与金箔原子核的最小距离多大？解：当入射粒子与靶核对心碰撞时，散射角为180ο。

当入射粒子的动能全部转化为两粒子间的势能时，两粒子间的作用距离最小。

根据上面的分析可得：220min124p Ze Mv K r πε==，故有：2min 04p Ze r K πε=19291361979(1.6010)910 1.141010 1.6010---⨯⨯=⨯⨯=⨯⨯⨯米由上式看出：min r 与入射粒子的质量无关，所以当用相同能量质量和相同电量得到核代替质子时，其与靶核的作用的最小距离仍为131.1410-⨯米。

大学物理知识总结习题答案(第十章)量子物理基础

大学物理知识总结习题答案（第十章）量子物理基础第十章量子物理基础第十章量子物理基础本章提要1.光的量子性质物体由于自身具有一定温度而以电磁波的形式向周围发射能量的现象称热辐射。

在任何温度下，它都能完全吸收照射在其表面的各种波长的光（电磁波），因此这个物体被称为绝对黑体，简称黑体。

单位时间内物体单位表面积发出的包括所有波长在内的电磁波的辐射功率，称为辐射出射度。

2.维恩位移定律在不同的热力学温度t下，单色辐射本领的实验曲线存在一个峰值波长λm，维恩从热力学理论导出t和λm满足如下关系λmt=b其中b是维恩常量。

3.斯特凡·波尔兹曼定律斯忒藩―玻尔兹曼定律表明黑体的辐射出射度m与温t的关系Mt4其中s为斯忒藩―玻尔兹曼常量。

对于一般的物体Mt4e称发射率。

4.黑体辐射黑体辐射不是连续地辐射能量，而是一份份地辐射能量，并且每一份能量与电磁波的频率?成正比，这种能量分立的现象被称为能量的量子化，每一份最小能量e=hv被称为一个量子。

黑体辐射的能量为e=nhv，其中n＝1，2，3，…，等正整数，h为普朗克常数。

普朗克黑体辐射公式简称普朗克公式2πhc21ml(t)=λ5ehc/λKT-1第10章量子物理基础光是以光速运动的粒子流，这些粒子称为光量子，简称光子。

一个光子具有的能量为e?h?。

5.颗粒挥发性德布罗意认为实物粒子也具有波粒二象性，它的能量e、动量p跟和它相联系的波的频率?、波长?满足以下关系Emc2？Hhλ这两个公式称为德布罗意公式或德布罗意假设。

与实物粒子相联系的波称为P=Mu=材料波或德布罗意波。

dxdpxh或者dedth这一关系叫做不确定关系。

其中为位置不确定量、动量不确定量、能量不确定量、时间不确定量。

物质波是代表空间中粒子概率分布的概率波。

6．薛定谔方程及其应用微粒子的运动状态需要用波函数来描述，波函数通常用y来表示。

一般来说，y是空间和时间的函数，即y=y（x，y，Z，t）。

原子物理习题解答

) =13.6 ev∗
= 12.75 ev
光子的能量为 12.75 ev，依据E2 = p2 c 2 + E0 2 考虑到光子的静止能量为 0，对应的动量为 E 2 − E0 2 = c2 E2 E 12.75 ev = = m c = 光子 c2 c c
p=
因为 m光子 c = M原子 V反冲 V反冲 = = m光子 c M原子
E=ℎ + �� 2
�� 2
��
1
⇒ �� = 0.29 ��
By
ghrui
3
1.2
动能 T=0.87 Mev 的质子轰击静止的汞核，当散
��
射角�� =
时，求它们之间的最小距离和瞄准距离。
=
=12.4 KeV∙ c −1
By
ghrui
14
2.9 下列各粒子限制在限度 L 的一维盒中，请利用海森伯不确定关系式估计它们具有的最小动能：（1）电子限制在 L=1Å的盒子中；（2）电子限制在 L=10 fm（原子核尺寸）的盒子中， 1 fm=��−�� ；（3）中子（静止能量为 940MeV）限制在 L=10 fm 的盒子中；（ 4 ）质量为 L=��−�� 的盒子中；
解：透入距离
1 k2
= =
ℏ 2m(v 0 −E) 6.63 ∗10 −34
2.3.14 ∗ 2∗9.1∗10 −31 ∗4∗1.6∗10 −19
=0.097 Å
By
ghrui

量子力学课后习题答案

Wnl (r)dr Rnl2 (r)r 2dr
例如：对于基态 n 1, l 0
W10 (r) R102 (r)r 2

4 a03
r e2 2r / a0
求最可几半径
R e 2 r / a0
10
a03 / 2
dW10 (r) 4 (2r 2 r 2 )e2r / a0
x)

k
2
2
(
x)

0
其解为 2 (x) Asin kx B cos kx
根据波函数的标准条件确定系数A、B，由连续性条件，得
2 (0) 1(0) B 0
2 (a) 3 (a) Asin ka 0
A0
sin ka 0
ka n
(n 1, 2, 3,)
[1 r
eikr
r
(1 r
eikr )

1 r
eikr
r
(1 r
eikr )]er
i1 1 11 1 1

2
[ r
(
r2
ik
) r

r
(
r2
ik
r )]er

k
r2
er
J1与er 同向。 1 表示向外传播的球面波。
习题
(2)
J2

i
2
(
2
* 2
2*
解：U (x)与t 无关，是定态问题
薛定谔方程为

2
2
d2 dx2

(x) U (x) (x)

E (x)
在各区域的具体形式为：
x0

原子物理和量子力学

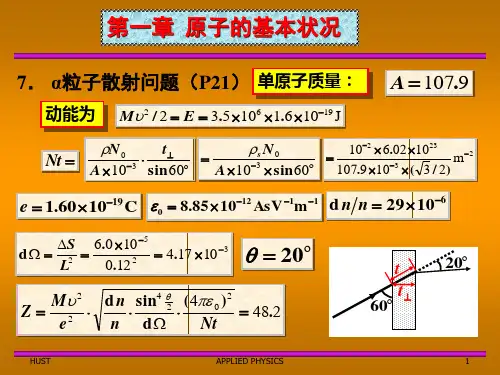
原子物理与量子力学习题参考答案目录原子物理学（褚圣麟编） (1)第一章原子的基本状况 (1)7．α粒子散射问题（P21） (1)第二章原子的能级和辐射 (1)5．能量比较（P76） (1)7．电子偶素（P76） (1)8．对应原理（P77） (1)9．类氢体系能级公式应用（P77） (1)11．Stern-Gerlach实验（P77） (2)第三章量子力学初步 (2)3．de Broglie公式（P113） (2)第四章碱金属原子 (2)2．Na原子光谱公式（P143） (2)4．Li原子的能级跃迁（P143） (2)7．Na原子的精细结构（P144） (2)8．精细结构应用（P144） (3)第五章多电子原子 (3)2．角动量合成法则（P168） (3)3．LS耦合（P168） (3)7．Landé间隔定则（P169） (4)第六章磁场中的原子 (4)2．磁场中的跃迁（P197） (4)3．Zeeman效应（P197） (4)7．磁场中的原子能级（P197） (5)8．Stern-Gerlach实验与原子状态（P197） (5)10．顺磁共振（P198） (5)第七章原子的壳层结构 (6)3．原子结构（P218） (6)第八章X射线 (6)2．反射式光栅衍射（P249） (6)3．光栅衍射（P249） (6)量子力学教程（周世勋编） (7)第一章绪论 (7)1.1 黑体辐射（P15） (7)1.4 量子化通则（P16） (7)第二章波函数和Schrödinger方程 (8)2.3 一维无限深势阱（P52） (8)2.6 对称性（P52） (8)2.7 有限深势阱（P52） (9)第三章力学量 (10)3.5 转子的运动（P101） (10)3.7 一维粒子动量的取值分布（P101） (10)3.8 无限深势阱中粒子能量的取值分布（P101） (11)3.12 测不准关系（P102） (11)第四章态和力学量的表象 (12)4.2 力学量的矩阵表示（P130） (12)4.5 久期方程与本征值方程的应用（P130） (13)第五章微扰理论 (16)5.3 非简并定态微扰公式的运用（P172） (16)5.5 含时微扰理论的应用（P173） (16)第七章自旋与全同粒子 (17)7.1 Pauli算符的对易关系（P241） (17)7.2 自旋算符的性质（P241） (17)7.3 自旋算符x、y分量的本征态（P241） (17)7.4 任意方向自旋算符的特点（P241） (17)7.5 任意态中轨道角动量和自旋角动量的取值（P241） (18)7.6 Bose子系的态函数（P241） (19)原子物理与量子力学习题 (20)一、波函数几率解释的应用 (20)二、态叠加原理的应用 (20)三、态叠加原理与力学量的取值 (20)四、对易关系 (21)五、角动量特性 (22)1原子物理学（褚圣麟编）第一章原子的基本状况7．α粒子散射问题（P21）J 106.1105.3221962-⨯⨯⨯⨯==E M υ232323030m )2/3(109.1071002.61060sin 1060sin 10----⊥-⨯⨯⨯⨯=⨯⨯=⋅⨯=A N t A N Nt s ρρ C 1060.119-⨯=e ，11120m AsV 1085.8---⨯=ε，61029-⨯=n dn32521017.412.0100.6--⨯=⨯==ΩL dS d ， 20=θ 2.48)4(sin 202422=⋅Ω⋅⋅=Nt d n dn eM Z πευθ第二章原子的能级和辐射5．能量比较（P76）Li Li Li Li v hcR hcR E E hv E )427()211(32212=-⋅=-==H e H e H e H e hcR hcR E E 4)1/2(0221=⋅=-=++∞ +∞>H e v E E ，可以使He +的电子电离。

《原子物理学》部分习题解答(杨福家)

Bz dD z m v
gJ
2
z g J B
氢原子基态氯原子基态
2
3 2 3
S1/ 2 P3 / 2

1 S ( S 1) L ( L 1) 2 2 J ( J 1)
两束
四束
2
gJ
1 S ( S 1) L ( L 1) 4 2 2 J ( J 1) 3
pc
E k ( E k 2m0c ) E k
2
所以
E k m in p m in c 6 2 M eV
4－2 解：原子态
2
D3/2
1 2 , J 3 2
可得
gJ 3 2
L 2, S
mJ
1 2
,
3 2
1 S ( S 1) L ( L 1) 4 2 J ( J 1) 5
Ek Ek
3.1keV 0.0094keV
3－3 解：
Ek m0 c 0.511MeV
2
若按非相对论处理
Ek 1 2 m0 v ，有
2
1 2
m0 v m0 c
2
2
v 2c
显然不合理，需要用相对论来处理。
E Ek m0 c 2m0c
2 2
又E mc m0 c
有磁场
m mg
1 2
3
S
1
0
1
0
2
g 2
h 0
3
P0
0
0
m 2 g 2 m1 g 1
2
0
2
相邻谱线的频率差
c

原子核物理(卢希庭)课后习题答案全

1063是常数为其中已知书上第四页上课讲的公式271066qbvm个子能级分裂为个子能级分裂为个子能级由谱线分裂为邻能级的间距比为分裂成四条子能级相解出解出17对于核的基态具有最小最小值最大值满足下列关系原子核同位旋量子数的最低激发态由题意可知量差原子质量单位已知三种标准双线的质1212h12m1212c4m16o16233abc111核磁共振时原子核吸收磁场的能量引起能级间跃迁这种跃迁时核能级间的跃迁吗
2

t T1
2
解：由A N P (1 e T1 ln(1 A ) P 2 知t
t
) P (1 e
) P (1 2 ln 2)ln 2 2.696 ln(1 0.95)
11.65 d
2.6、实验测得纯235U样品的放射性比活度为80.0Bq· mg－1，试求235U的半衰期。解：

解：A N P(1 e t ) P(1 e
t ln 2 T1
2
) 5 108 (1 e

100.693 2.579
) 4.66 108 Bq
2-4
人工放射性的生长，放射性核素的特征量
t T1 / 2
解：由A(t ) P(1 2
8
)得
10 2.579
4 2 1 3
1
fm 2.33 fm
1 3
对于对于
107 47 238 92
Ag，R 1.45 107 U，R 1.45 238
1
fm 6.88 fm fm 8.99 fm
3
1-5, 实验测得 241 Am和 243 Am的原子光谱的超精细结构由六条谱线.，解：由已知条件知原子的总角动量量子数可以取6个值又电子总角动量j>核的自旋I 5 2 5 2

中科院原子物理学习题答案

问题六：什么是原子核衰变？
答案：原子核衰变是指原子核自发地转变为另一个核的过程。原子核衰变可以分为α衰变、β衰变和γ衰变。α衰变是指原子核放出一个α粒子（由两个质子和两个中子组成）；β衰变是指原子核放出一个β粒子（电子或正电子）；γ衰变是指原子核放出γ射线（高能光子）。原子核衰变是放射性衰变的基础。
中科院原子物理学习题答案
中科院原子物理学习题答案
原子物理是物理学的一个重要分支，研究原子和原子核的性质、结构和相互作用。在中科院原子物理学习中，学生们经常会遇到一些难题，下面将给出一些常见问题的答案，希望能帮助到大家。
问题一：什么是原子？
答案：原子是物质的基本单位，由原子核和围绕核旋转的电子组成。原子核由质子和中子组成，质子带正电荷，中子不带电荷。电子带负电荷，数量与质子相等，使得原子整体电荷为零。原子的大小约为10^-10米。
问题七：什么是原子核裂变？
答案：原子核裂变是指重核（如铀、钚等）被中子轰击后分裂成两个或更多的轻核的过程。原子核裂变是一种放出大量能量的反应，被广泛应用于核能产生和核武器。原子核裂变的副产物还包括中子，这些中子可以继续引发更多的裂变反应。
以上是中科院原子物理学习题的一些答案，希望对大家的学习有所帮助。原子物理是一门深奥而有趣的学科，通过学习和研究原子的性质和相互作用，我们可以更好地理解物质的本质和宇宙的奥秘。
问题二：原子核中的质子和中子分别具有什么性质？
答案：质子和中子都是由夸克组成的。质子带正电荷，质量约为1.67×10^-27千克；中子不带电荷，质量约为1.67×10^-27千克。质子和中子都具有自旋和同位旋，自旋是粒子的内禀角动量，同位旋是同位素的标志。
问题三：原子பைடு நூலகம்能级结构是什么？
答案：原子的能级结构是指原子中电子的能级分布。根据量子力学的理论，电子在原子中的能量是离散的，只能取特定的值。这些特定值被称为能级，每个能级可以容纳一定数量的电子。电子在能级之间跃迁时会吸收或放出特定频率的光子，产生光谱。

原子物理学课后习题答案第10章

第十章原子核10.1 n H 1011和的质量分别是1.0078252和1.0086654质量单位，算出C 126中每个核子的平均结合能（1原子量单位=2/5.931c MeV ）.解：原子核的结合能为：MeV m Nm ZE E A H 5.931)(⨯-+= 核子的平均结合能为：AE E =0 MeV MeV m Nm ZE AE A n H 680.75.931)(1=⨯-+=∴ 10.2 从下列各粒子的质量数据中选用需要的数值，算出Si 3014中每个核子的平均结合能：007825.1,973786.29008665.1,014102.2,000548.01130141021→→→→→H Si n H e解：MeV MeV m Nm Zm AA E E ASi n H 520.85.931)(110110=⨯-+==10.3Th 23290放射α射线成为αR 22888.从含有1克Th 23290的一片薄膜测得每秒放射4100粒α粒子,试计算出Th 23290的半衰期为10104.1⨯年.解:根据放射性衰变规律:t e N Nλ-=0如果在短时间dt 内有dN 个核衰变,则衰变率dt dN /必定与当时存在的总原子核数目N 成正比,即:t e N N dtdNλλλ-==-0 此式可写成: 0N dtdN e t-=-λλ……（1）其中2023023''0102612321002.6,232,1002.6,1;1,4100⨯=⨯⨯==⨯=⨯===--=-N A N AN N t dt dN N dt dNe t 故克克秒λλ将各已知量代入（1）式，得：182010264110264100⨯=⨯=-λλe……（2）因为Th 23290的半衰期为10104.1⨯年，所以可视λ为很小，因此可以将λ+e 展成级数，取前两项即有：λλ+≈+1e这样（2）式变为：181026411⨯=+λλ 由此得：年秒秒101818104.110438.02ln /1058.1⨯=⨯==⨯=-λλT所以,Th 23290的半衰期为10104.1⨯年.10.4 在考古工作中,可以从古生物遗骸中C 14的含量推算古生物到现在的时间t .设ρ是古生物遗骸中C 14和C 12存量之比,0ρ是空气中C 14和C 12存量之比,是推导出下列公式:2ln )/ln(0ρρTt =式中T 为C 14的半衰期.推证:设古生物中C 12的含量为)(12C N ;刚死时的古生物中C 14的含量为)(140C N ;现在古生物遗骸中C 14的含量为)(14C N ;根据衰变规律,有:t e C N C N λ-=)()(14014由题意知: )()(1214C N C N =ρ;古生物刚死时C 14的含量与C 12的含量之比与空气二者之比相等, )()(121400C N C N =ρ 所以:t e λρρ=0因此得:2ln )/ln(ln 1ln000ρρρρλρρλTt t ==∴=10.5 核力在原子核大小的距离内有很强的吸引力，它克服了质子间的（元素氢除外，那里只有一粒质子）库仑推斥力的作用而使原子核结合着，足见在原子核中核力的作用超过质子间的库仑推斥力作用；从质子间推斥力的大小可以忽略地了解到核力大小的低限。

《原子物理与量子力学》一至三章部分习题解答

2.7 有限深势阱（P52）有限深势阱（）
（1）势场为）（2）定态） Schrödinger方程为 Schrödinger方程为 E<U0时
（3）方程的解为）
HUST APPLIED PHYSICS 13
（4）利用标准条件定解（单值、有限、连续）利用标准条件定解（单值、有限、连续）单值条件满足。单值条件满足。再考虑连续性，续性，得有限
必须同时成立
HUST APPLIED PHYSICS 14
或者
10
（5）体系的定态分两种情况）
10
10
0
0
0
−10 0
0.5
E ((×10 ) E × 10
−8
−16 −8
1
能级均为分立能级
HUST
−10 0
0.5
E (× 10 )
1
−10 0
0.5
APPLIED PHYSICS
E ((× 10 ) E × 10
第一章原子的基本状况
7． α粒子散射问题（P21）单原子质量：．粒子散射问题粒子散射问题（）单原子质量：
动能为
60
t t⊥
20
HUST
APPLIED PHYSICS
1
第二章原子的能级和辐射
8．对应原理（P77）．对应原理（）
转动频率为
HUST
APPLIED PHYSICS
2
9．类氢体系能级公式应用（P77）．类氢体系能级公式应用（）
1.4 量子化通则（P16）量子化通则（）
（1）一维谐振子）势能为
Bohr-Sommerfeld量子化条件Hale Waihona Puke 量子化条件令HUST

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

11
5.3非简并定态微扰公式的运用（P172）非简并定态微扰公式的运用（）
已知
HUST
APPLIED PHYSICS
12
HUST
APPL程为
的本征值方程， Lx 的本征值方程，如下
HUST
APPLIED PHYSICS
2
HUST
APPLIED PHYSICS
3
STLz→Lx
对角化过程就是L 表象向L 对角化过程就是Lx 由Lz表象向Lx表象的变换过程 Lz表象中 z 对应本征值表象中L
7
（1））的本征态中分析L （1）在Lz的本征态中分析Lx的取值情况 Lx在Lx表象中的本征态为：表象中的本征态为：由表象变换公式L 由表象变换公式 z 的本征态表象下为：在Lx表象下为：
HUST
APPLIED PHYSICS
8
由以上展开式系数可得L 由以上展开式系数可得 x的取值及取值几率
HUST APPLIED PHYSICS 9
（2））
的本征态中分析L （2）在Lx的本征态中分析Lz的取值情况
同理可得L 同理可得 x其他本征态的情况
HUST
APPLIED PHYSICS
10
（3））表象中表示L 及其本征态。（3）在Lx表象中表示Lz及其本征态。
HUST
APPLIED PHYSICS
h,0,−h
的本征态为：的本征态为：
将 Lx 的本征态在Lz 的本征态的本征态在L 上展开，表象中L 上展开，则 Lz 表象中 Lx 对应的本征态为：的本征态为：
HUST
APPLIED PHYSICS
4
Lz表象到 x表象的么正变换矩阵为：表象到L 表象的么正变换矩阵为：
Lx在Lx表象中的表示为：表象中的表示为：
第十、第十、十一章表象和微扰
P130 4.5 的共同表象中求L 的本征值和本征函数，在 L2， Lz的共同表象中求Lx， Ly的本征值和本征函数，并将L 对角化且：并将Lx，Ly对角化且：的本征态中分析L 的取值情况；（1）在Lz的本征态中分析Lx的取值情况；的本征态中分析L 的取值情况；（2）在Lx的本征态中分析Lz的取值情况；（3）在Lx表象中表示Lz及其本征态。表象中表示L 及其本征态。在L2，Lz的共同表象中
HUST
APPLIED PHYSICS
5
同理 L y 的久期方程为
Lz表象中对应本征值
的本征态为： h,0,−h 的本征态为：
HUST
APPLIED PHYSICS
6
Lz表象到 y表象的么正变换矩阵为：表象到L 表象的么正变换矩阵为：
，
Ly在Ly表象中的表示为：表象中的表示为：
HUST
APPLIED PHYSICS