CODATA物理常数(物理化学常数部分)

( 1) 气体运动论方法 首先估算阿伏加德罗常数的是 Loschmidt, 他是 根据气体分子运动论来确定阿伏加德罗常数, 由分 子本身的体积和分子平均自由程推算出阿伏加德罗 常数 N A = 4. 1 @ 1022 mol- 1 。 ( 2) 布朗运动方法 布朗运动表明了液体分子的运动, 根据分子的 布朗运动, Perrin 测定 的阿伏 加德罗 常数 为 N A = 7. 05 @ 1023 mol- 1 。 ( 3) 电子电荷方法 测量电子电荷, 可以通过法拉第常数 F 计算出 阿伏加德罗常数为N A = FPe= 6. 064 @ 1023 mol- 1 。 ( 4) 黑体辐射方法 通过黑体辐射可确定波尔兹曼常数 k , 从波尔 兹曼常数 k 和气体通用常数 R , 可获得阿伏加德罗 常数为 N A = RPk= 6. 175 @ 1023 mol- 1 。 ( 5) A粒子计数方法 Rutherford 和 Geiger 对 镭源放 射 A 粒子进行 计 数, 他们测量出镭元 素放射 A粒子数 的剂量为 3. 4 @ 1010个Pg#s, 对单个原子进行逐个计数显然提供了 确定阿伏加德罗常数的方法, 由此导出阿伏加德罗 常数为 N A = 6. 1 @ 1023 mol- 1 。
通过阿伏加德罗常数可以直接将宏观物理量和
微观物理量联系起来。若阿伏加德罗常数 N A 测量 相对不确定度达到 1 @ 10- 8 , 就有理由以一 定数量 的原子重新定义质量单位千克, 替代目前唯一使用 的人造实物基本单位千克原器。
312 功率天平法 采用功率 天平( watt balance) 法[ 10 ] 测定普朗 克
20 世纪 70 年代前用 X 射线晶体密度法确定的 阿伏加德罗常数准确度大约为 70 @ 10- 6, 这一结果 足以显示由密立根导出的电子电荷的误差达0. 2% 。 X 射线晶体密度 法测定取得的突 破之一是在 1974 年由 R. D. Deslattes 采 用 X 射 线光 学 组合 干 涉仪 ( COXI) 方法取得的。

玻尔兹曼常数玻尔兹曼常数概念释义：符号为k或kB，是有关于温度及能量的⼀个物理常数。

★玻尔兹曼常量系热⼒学的⼀个基本常量，“K”数值为：K=1.3806505 ×10^-23J/K我们都知道，⽔往低处流，因为重⼒在起作⽤。

重⼒也是⼀种⼒，在起作⽤的时候，常常让⼈感觉它来⾃于地球的中⼼。

然⽽，在近代科学萌芽之前，并⾮每⼀种现象都能够像“⽔往低处流”⼀样得到合理的解释。

⽐如，“在⼀杯热⽔中就会融化的冰块为何永远⽆法在⼀杯温⽔中⾃动形成”这样的问题，就始终是19世纪物理学研究中的难题。

问题的答案，最终由奥地利物理学家路德维格·玻尔兹曼给出。

他在研究中发现：热能在⼀杯温⽔的分⼦间消散的⽅式，要⽐在⼀杯加了冰块的热⽔中更多。

从玻尔兹曼的研究中可以看到，⾃然界是⼀个稳健的玩家，它在绝⼤多数情况下都会选择最有可能的⽅式⾏事。

波尔兹曼常数就说明了这⼀点：⽆序总是多过于有序，搞乱⼀间屋⼦的⽅法总是多过收拾整洁，随意融化⼀块冰的难度总是低于让它依照有序的结构凝结。

此外，包含了玻尔兹曼常数的玻尔兹曼熵⽅程，也解释了“感觉会出错，⼀定会出错”的墨菲法则：并不是什么邪恶的⼒量导致你⾛向错误和失败，仅仅只是因为事情变坏的可能性在数量上远远多于变好⽽已。

热⼒学常数编辑玻尔兹曼常量系热⼒学的⼀个基本常量，记为“K”，数值为：K=1.3806488(13)×10^-23J/K[1] ，玻尔兹曼常量可以推导得到，理想⽓体常数R等于玻尔兹曼常数乘以阿伏伽德罗常数。

推导过程编辑从⽓体动理论的观点来看，理想⽓体是最简单的⽓体，其微观模型有三条假设：1.分⼦本⾝的⼤⼩⽐分⼦间的平均距离⼩得多，分⼦可视为质点，它们遵从⽜顿运动定律。

2.分⼦与分⼦间或分⼦与器壁间的碰撞是完全弹性的。

3.除碰撞瞬间外，分⼦间的相互作⽤⼒可忽略不计，重⼒的影响也可忽略不计。

因此在相邻两次碰撞之间，分⼦做匀速直线运动。

单个分⼦在⼀次碰撞中对器壁上单位⾯积的冲量：I=2m·vxvx为x⽅向上的速度分量.这⼀次碰撞的时间为2a╱vx，故单位时间内的碰撞次数为vx╱2a。

来确定 例如由公式(A-3)给出的换算关系 可以写成 1C = c esu 10cm/s
(5-1)
这就意味着两个单位的换算系数同真空光速联系在一起 如果真空光速的测量值有所改
变 那么换算系数就会变化 这就在单位制换算中出现了不确定度 好在国际单位制中真空
光速具有精确值(即定义 秒 以后 用真空光速来定义 米 ) 所以这种不确定度在国际
(2-1)
F
=
q1q2 r2
(2-1')
所以量纲和单位都有很大区别 在国际制中 电流是基本量纲 而由公式(2-1')可以看
出 静电制不需要新的基本量纲 为此静电制电量的量纲就是 L3/2M1/2T−1 它具有一个新的
单位 esu 称为静电单位电量(或称静电库仑) 其值为 1dyn1/2cm
不同单位制中的单位可以互相转换 这里给出从 esu 转换成库仑(C)的方法
1关于单位制物理常数和不确定度的资料黄晨2004年9月email联系地址复旦大学化学系表面化学实验室morningyellowelephantbasenet一一国际单位制国际单位制si和高斯单位制和高斯单位制cgs的力学量纲和单位的力学量纲和单位力学物理定律在国际单位制简称国际制米克秒制记作cgs中具有相同的形式所以所有的力学量都具有相同的量纲的次方数记作si和高斯单位制简称高斯制并且它们都以长度另外这两个单位之间的换算也相当方便又称为厘质量和时间作为基本量纲都是10物理量长度质量时间频率力能量功率压强量纲lmtt?1lmt?2l2mt?2l2mt?3l?1mt?2国际制单位m米kg千克s秒hz赫兹n牛顿j焦耳w瓦特pa帕斯卡表1高斯制单位cm厘米g克s秒hz赫兹dyn达因erg耳格ergsdyncm2换算关系1m102cm1kg103g1n105dyn1j107erg1w107ergs1pa10dyncm2力学量纲和单位二二静电制静电制cgse量纲和单位量纲和单位高斯制在电磁学中具两套单位制它是电动力学中最常用的单位制是国际单位制的理论基础静电学中最基本的定律是库仑定律际制的形式是一套以库仑定律为基础另一套以安培定律为基础称为静电制称为电磁制记作cgse记作cgsm它而该定律在国际制和静电制中有着不同的形式国202r14qqf21这里而电磁制则是0是真空中的介电常数其数值为8854187810?12c2nm2221rqqf21所以量纲和单位都有很大区别静电制不需要新的基本量纲单位esu称为静电单位电量或称静电库仑不同单位制中的单位可以互相转换1设1cxesu2根据公式a13把r1m102cm在国际制中为此静电制电量的量纲就是其值为1dyn12cm这里给出从esu转换成库仑c的方法电流是基本量纲而由公式21可以看l32m12t?1它具有一个新的出当r1mq1q2xesuq1q21c时f89875518109nf89875518109n898755181014dyn代入公2式a2得x2997924581094得出结论1c299792458109esu11esu33356409610?10c2222公式22和22是国际制单位和高斯制单位相互转换的基本公式注1由于等式两边采取的单位制不同所以这样的等号在数学上是不严格的三三电磁制电磁制cgsm量纲和单位量纲和单位静磁学中最基本的定律是安培定律国际制的形式是lii2其数值

地球的基本数据（1980大地测量标准系统）1979年12月在澳大利亚召开的国际大地测量协会（IAG）大会通过了以下列最新大地测量常数为依据的“1980大地测量标准系统”：真空中的光速c=(299792458±1.2)m·s–1万有引力常数 G=（6672±4.1）×10–14 m3·s–2·kg –1地球自转角速度（概略值）ω=7292115×10–11rad·s–1包含大气层在内的地心引力常数GM=(39860047±5) ×107· m3·s–2=（35±0.3）×107· m3·s–2纯大气层的地心引力常数 GMA力学形状系数（不包括因潮汐所引起的永久变形）=(108263 ±0.5) ×10–8J2=(–254±1) ×10–8J3J=(–162±1) ×10–84=(–23±1) ×10–8J5=(55±1) ×10–8J6地球赤道半径a=(6378137±2)m赤道上的标准重力 r=(978033±1) ×10–5m·s–2e扁率 1/f=(298257±1) ×10–3=（6263686±3）×10 m2·s–1大地水准面上的位势ω三轴参数（概略值）=90000赤道椭圆扁率 1/f1=15°（西经）赤道面椭圆的长轴轴向λ1重力潮汐常数（现用值）δ=1.16c和G的数值及标准误差引自“CODATA物理常数系统（1973）”。

其它常数的标准误差均为实际精度。

ω值所给出的数据准确到最后一位。

组合常数在物理学中的应用文献综述前言国际科学技术数据委员会(CODATA1998年推荐的基本物理化学常数及其组合量为175个，其中在最常用的常数简表中，包含18个常数和2个组合量，还有2个常用的非国际单位制的转换因子，共计22个。

不过在谈到基本物理常数时，人们总是首先想到以下8个基本物理常数：光速常数C ，电子电荷e ，普朗克常数h ，万有引力常数G ，电子静止质量，质子静止质量，阿伏加德罗常数N ，和玻尔兹曼常数k 。

这是因为它们出现得比较早，所起的作用也比较重要和人们经常使用的缘故。

此外，由这些基本物理常数组成的一些复合量，如精细结构常数α = e 2／4εo πћc ，玻尔半径ao =4εo πћ2/me e 2，法拉第F=NA e 等，总是严格地以相同的形式出现在许多物理定律和方程之中，代表着一定的物理意义，因此这种组合本身也就成了基本物理常数。

仔细分析175个常数可以发现，它们绝大多数是由一些更基本的常数组合而成的，所以也叫做“导出常数”。

人们在精密的理论方法之外, 寻求以物理常数为基础的较为简捷地获得数量结果的其它方法, 包括量纲分析法、数量级的估算、对称性的考虑、守恒量的利用、极限情形和特例的讨论、简化模型的选取、概念方法, 以及相似和类比等等 . 使用这些定性、半定量方法时, 如果选取恰当的组合常数并正确地使用它们, 不仅能使问题的分析简便、快捷, 而且各个物理量间的关系也非常清楚。

彭双艳（毕节学院学报,2009）在《原子物理中组合常数的应用》一文中，用组合常数方法给出了原子物理学中玻尔理论的全部结果，并讨论了组合常数方法的使用原则与优点。

高丽丽. 宋文福. 何训（通化师范学院学报，20O4）在《组合常数方法在原子物理学中的应用》一文中，通过计算精细结构常数、电子的经典半径、电子的康普顿波长、玻尔原子的轨道半径、电子轨道运动的速度、原子的能量、里德伯常数、原子的角动量、原子的磁矩总结出组合常数方法主要是依据定性与半定量物理学方法中的量纲分析法．只是在选主定参量时包括前面所用的三个组合常数，因此称之为组合常数方法．并介绍组合常数方法可以作为一种普遍的方法，它所具备的优点。

阿伏伽德罗常数的数值是阿伏伽德罗常数是化学中的一个重要常数，通常表示为Avogadro's Number，常缩写为NA，是指每摩尔物质中所含有的粒子数，也就是物质的分子或原子数。

在SI国际单位制中，阿伏伽德罗常数的数值为6.02214076×1023个/摩尔，取自2019年CODATA推荐值。

阿伏伽德罗常数是由意大利化学家洛伦佐·阿伏伽德罗在19世纪提出的，他借助道尔顿的原子假说推论出了分子间存在一个比例常数，这个常数就是今天所称的阿伏伽德罗常数。

它描述了化学体系中物质的数量与其它物理化学属性（如质量、体积等）之间的联系，因此阿伏伽德罗常数在化学、物理、材料科学和生命科学等领域都有广泛的应用。

在化学反应和化学建模中，阿伏伽德罗常数是计算摩尔量、摩尔质量、摩尔体积、分子量等数值的基础；在物理学中，它被用于描述物质粒子的统计物理特性，如热力学平衡、分子速度分布、光谱特性等；在材料科学中，阿伏伽德罗常数用于研究材料的微观结构、能量、光学性质等；在生命科学中，阿伏伽德罗常数是计算生物大分子以及细胞、组织等生物体系中的物质量、物质浓度和物质转运过程的重要参数。

阿伏伽德罗常数的实际测量是基于质量和计数两种方式，其实验测量方法包括光子计数法、X射线衍射法、散射法、介电恒定法等。

以光子计数法为例，实验装置测量样品在光束中的散射光强度，并用缩放系数校正，计算出样品中光子激发事件的数量，进而求解出阿伏伽德罗常数。

总之，阿伏伽德罗常数作为描述物质量的重要参数，已经成为现代物理化学和生物化学中的标志性常数之一，其数值的确定和精确度，将对落实国际单位制、深化物理化学和生命科学等领域的研究和应用产生重要影响。

关于单位制
物理常数和不确定度的资料
黄晨 * 2004年9月初稿 2005年11月修订 (* 联系地址 复旦大学化学系表面化学实验室 eMail webmaster@)
一 国际单位制(SI)和高斯单位制(CGS)的力学量纲和单位
力学物理定律在国际单位制(简称国际制 记作 SI)和高斯单位制(简称高斯制 又称为厘 米克秒制 记作 CGS)中具有相同的形式 并且它们都以长度 质量和时间作为基本量纲 所以所有的力学量都具有相同的量纲 另外 这两个单位之间的换算也相当方便 都是 10 的次方数 物理量 长度 质量 时间 频率 力 能量 功率 压强 量纲 L M T T−1 LMT−2 L2MT−2 L2MT−3 L−1MT−2 国际制单位 高斯制单位 m(米) cm(厘米) kg(千克) g(克) s(秒) s(秒) Hz(赫兹) Hz(赫兹) N(牛顿) dyn(达因) J(焦耳) erg(耳格) erg/s W(瓦特) dyn/cm2 Pa(帕斯卡) 表 1 力学量纲和单位 换算关系 1m = 102cm 1kg = 103g 1N = 105dyn 1J = 107erg 1W = 107erg/s 1Pa = 10dyn/cm2
2
式(4-1) 而是差了 4π 即 1Oe = 103/4π A/m 在高斯制统一静电制和电磁制公式时 电学量全部用静电制单位 磁学量全部用电磁制 单位 电磁学公式中如果同时含有电学量和磁学量 通常会引入常数 c 所以 静电制单位 和电磁制单位的换算比例通常总是真空光速(2.99792458×1010)的若干次方 如果静电制单位 和电磁制单位的量纲之比为 L−nTn 那么两者的换算关系就是 (4-2) 1 静电制单位(esu) = (2.99792458×1010)n 电磁制单位(emu) −2 −1 4 2 例如 国际制中电容单位 F 的量纲为 L M T I 要把它转化为静电制单位 cm(esu) 首 先要经过电磁制单位(cm/s2)−1(emu) 关系是 1F = 10−9(cm/s2)−1(emu) 由于电容在电磁制中的 量纲 L−1T2 和静电制中的量纲 L 之比为 L−2T2 所以两个单位值的比例应该是 1(cm/s2)−1(emu) = 8.98755179×1020cm(esu) 最后 1F = 8.98755179×1011esu(F) 物理量 电量 电流 电位 电阻 电导 电容 电感 磁感应通量 磁感应强度 磁场强度 国际制 静电制 1C 2.99792458×109esu 1A 2.99792458×109esu/s 1V 3.33564096×10−3erg/esu 1.11265005×10−12(cm/s)−1 1Ω 1S 8.98755179×1011cm/s 1F 8.98755179×1011cm 1H 1.11265005×10−12(cm/s2)−1 1Wb 1T 1A/m 表 3 电磁学物理量的单位换算 (注 1Mx/cm2 = 1Gs = 1Oe = 1emu/cm) 电磁制 0.1emu⋅s 0.1emu 8 10 erg/emu⋅s 109Байду номын сангаасm/s 10−9(cm/s)−1 10−9(cm/s2)−1 109cm 108Mx 104Gs 4π×10−3Oe

标准大气压 (standardatmosphere)
101325
原子质量单位 (atomicmassunit)m(12C)/12
amu
1灡660538782(83)x10-27
单暋暋位 相对标准不确定度 (Unit) (Relativestd灡uncert灡ur) 6灡8暳10-10
m-1
6灡6暳10-12
物暋暋质 密度(kg/m3) 物质
密 度 (kg/m3)
铝
2灡669暳103
水
1灡000暳103
铜
8灡96暳103
水银
13灡55暳103
铁
7灡874暳103 无水甘油 1灡260暳103
银
10灡5暳103 无水乙醇 0灡7894暳103
金
19灡32暳103 蓖麻油 0灡957暳103
钨
19灡30暳103 钟表油 0灡981暳103
10-10牛顿,则此时的电流为1 安培
热力学温度
Thermodynamic tempera灢
T
ture
开 [尔 文 ] Kelvin
K
暋1 开尔文是水三相点热力学温度的1/273灡16
214
续上表
物理量名称
物质的量 Amountofsubstance
表示符号 单位名称 单位符号 v 或n 摩[尔]mole mol
N/A2
精 确 (exact)
G
6灡67428(67)暳10-11
m3/(kg·s2)
1灡0暳10-4
普朗克常量 planckconstant
电子电荷 elementarycharge 磁通量子 (magneticfluxquantum)h/2e 电子质量 electron mass

关于单位制 物理常数和不确定度的资料
黄晨 * 2004 年 9 月 (* 联系地址 复旦大学化学系表面化学实验室 eMail morning_yellow@)
一 国际单位制(SI)和高斯单位制(CGS)的力学量纲和单位
力学物理定律在国际单位制(简称国际制 记作 SI)和高斯单位制(简称高斯制 又称为厘 米克秒制 记作 CGS)中具有相同的形式 并且它们都以长度 质量和时间作为基本量纲 所以所有的力学量都具有相同的量纲 另外 这两个单位之间的换算也相当方便 都是 10 的次方数
它是电动力学中最常用的单位制 另一套以安培定律为基础 称为电磁制 记作 CGSM 它
是国际单位制的理论基础
静电学中最基本的定律是库仑定律 而该定律在国际制和静电制中有着不同的形式 国
际制的形式是
这里 ε0 是真空中的介电常数 而电磁制则是
F
=
q1q2 4πε0r 2
其数值为 8.8541878×10−12C2/Nm2
如果静电制单位和电磁制单位的量纲之比为 L−nTn 那么两者的换算关系就是
1 静电制单位 = (2.99792458×1010)n 电磁制单位
(4-3)
例如 国际制中电容单位 F 的量纲为 L−2M−1T4I2 要把它转化为静电制单位 cm 首先要
经过电磁制单位 cm/s2 关系是 1F(SI) = 10−9(cm/s2)−1(CGSM) 由于电容在电磁制中的量纲
制和高斯制之间并不存在 但是在某些单位之间 例如能量单位 J 和 eV 就相差一个基本
电荷 e/C 该常数的不确定度就是这两个单位比值的不确定度 根据这个道理 同一物理常
数在不同单位下具有不一样的不确定度 例如基本电荷 用 C(库仑)时不确定度为 0.09ppm

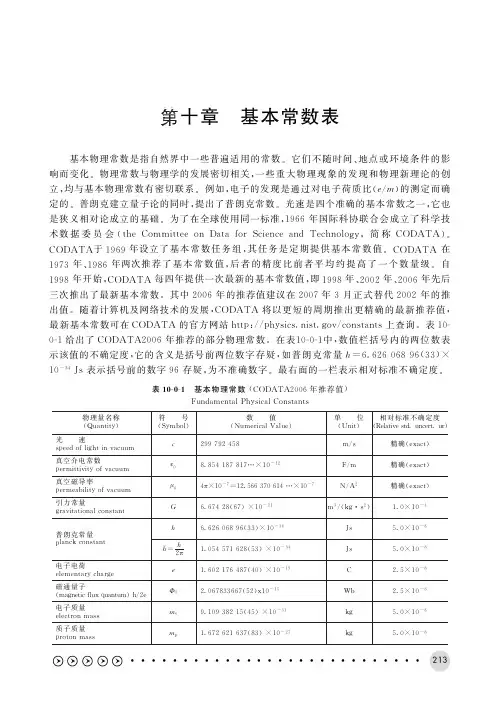
地球的基本数据（1980大地测量标准系统）1979年12月在澳大利亚召开的国际大地测量协会（IAG）大会通过了以下列最新大地测量常数为依据的“1980大地测量标准系统”：真空中的光速c=(299792458±1.2)m·s–1万有引力常数 G=（6672±4.1）×10–14 m3·s–2·kg –1地球自转角速度（概略值）ω=7292115×10–11rad·s–1包含大气层在内的地心引力常数GM=(39860047±5) ×107· m3·s–2=（35±0.3）×107· m3·s–2纯大气层的地心引力常数 GMA力学形状系数（不包括因潮汐所引起的永久变形）J=(108263 ±0.5) ×10–82=(–254±1) ×10–8J3J=(–162±1) ×10–84=(–23±1) ×10–8J5J=(55±1) ×10–86地球赤道半径a=(6378137±2)m赤道上的标准重力 r=(978033±1) ×10–5m·s–2e扁率 1/f=(298257±1) ×10–3=（6263686±3）×10 m2·s–1大地水准面上的位势ω三轴参数（概略值）=90000赤道椭圆扁率 1/f1赤道面椭圆的长轴轴向λ=15°（西经）1重力潮汐常数（现用值）δ=1.16c和G的数值及标准误差引自“CODATA物理常数系统（1973）”。

其它常数的标准误差均为实际精度。

ω值所给出的数据准确到最后一位。

地球的编年史碧声地质年代表也在与时俱进。

我们来探寻一下它诉说的故事，和它自己的故事。

常用化合物物理化学常数表
序号
化学名
分子式
CAS
分子量
熔点 （℃）
沸点（℃）
密度 闪点 （℃） （kg/m3)
折光率
纯度(%)
爆炸极限 (体积)
毒性
腐蚀性
#REF! #REF! #REF! 11 1 #REF! 1 #REF! #REF! 42 38 #REF! 14 1 2 #REF! 2 #REF!
50-00-0 67-56-1 75-05-8 420-04-2 75-07-0 1975/4/7 64-18-6 60-34-4 64-17-5 7803-57-8 124-41-4 765-30-0 60-35-5 107-31-3 64-19-7 57-13-6 67-63-0 141-43-5
99 99.99
———
刺激 刺激 有毒、刺激 有毒、刺激 有毒、刺激 腐蚀
（CH3）2NCOCH3 127-19-5 HBF4 16872-11-0 C4H8O2 (CH3)3COCH3 （CH3）2CHC2H4OH CuCN HOOCCOOH C3H6O3 C4H10O2 C4H10O2 C3H8O3 C3H5ClO C4H9Cl C6H5NH2 C6H7N C5H6N2 C5H6N2 C6H5F C5H8N2 C4H2O3 123-91-1 1634-04-4 123-51-3 544-92-3 144-62-7 110-88-3 110-71-4 110-63-4 56-81-5 106-89-8 109-69-3 62-53-3 108-89-4 462-08-8 109-08-0 462-06-6 1739-84-0 108-31-6
15 #REF! 16 #REF! #REF! 17 18 19 20 21 22 23 9 #REF! 24 #REF! 25 #REF! 26 #REF! #REF! #REF! #REF! #REF! #REF! 16 #REF! 27 #REF! #REF!

PrefaceFundamental Physical Constants: 1998Peter J. Mohr and Barry N. TaylorNational Institute of standards and Technology, Gaithersburg, MD 20899-8401This table gives the 1998 self-consistent set of values of the basic constants and conversion factors of physics and chemistry recommended by the Committee on Data for Science and Technology (CODATA) for international use. Further, it describes in detail the adjustment of the values of the subset of constants on which the complete 1998 set of recommended values is based. The 1998 set replaces its immediate predecessor recommended by CODATA in 1986. The new adjustment, which takes into account all of the data available through 31 December 1998, is a significant advance over its 1986 counterpart. The 1998 adjustment was carried out by P. J. Mohr and B. N. Taylor of the National Institute of Standards and Technology (NIST) under the auspices of the CODATA Task Group on Fundamental Constants. The standard uncertainties (i.e., estimated standard deviations) of the new recommended values are in most cases about 1/5 to 1/12 and in some cases 1/160 times the standard uncertainties of the corresponding 1986 values. Moreover, in almost all cases the absolute values of the differences between the 1998 values and the corresponding 1986 values are less than twice the standard uncertainties of the 1986 values.The Task Group was established in 1969 with the aim of periodically providing the scientific and technological communities with a self-consistent set of internationally recommended values of the fundamental physical constants based on all applicable information available at a given point in time. The first set was published in 1973 and was followed by a revised set first published in 1986; the current 1998 set first appeared in 1999. In the future, the CODATA Task Group plans to take advantage of the high level of automation developed for the current set in order to issue a new set of recommended values at least every four years.Relative std. Quantity Symbol Value Unit uncert.u ra Value recommended by the Particle Data Group,Caso et al.,Eur.Phys.J.C3(1-4),1-794(1998).b Based on the ratio of the masses of the W and Z bosons mW/m Z recommended by the Particle Data Group(Caso et al.,1998).The value for sin2θW they recommend,which is based on a particular variant of the modified minimal subtraction(。

法拉第常数
(faraday constant)
F=NAe
9.648456x104C/mol
摩尔气体常数(mLeabharlann lar gas constant)
R
8.31441 J/(K·mol)
玻尔兹曼常数
(boltzmann constant)
k
1.380662x 10-23J/K
理想气体在标准状态下的摩尔体积
[molar volume, ideal gas
哈特利能量
(hartree energy)
Eh
27.2116 eV
环流量子
(quantum of circulation)
h/me
7.27389x10-4J·s/kg
电子质量(electron mass)
me
9.10953x10-31kg
质子质量(proton mass)
mp
1.672649x10-27kg
中子质量(neutron mass)
mn
1.674954x10-27kg
物理化学常数(physicochemical constants)
阿伏加德罗常数
(avogadro constant)
NA或L
6.022045x1023/mol
原子质量单位
(atomic mass unit)
amu
1.660566x10-27kg
常用的基本物化常数
类别(Sort)
量的名称(Quantity)
符号(Symbol)
数值(Value)
普通常数
(general constants)
真空中光速
(speed of light in vacuum)

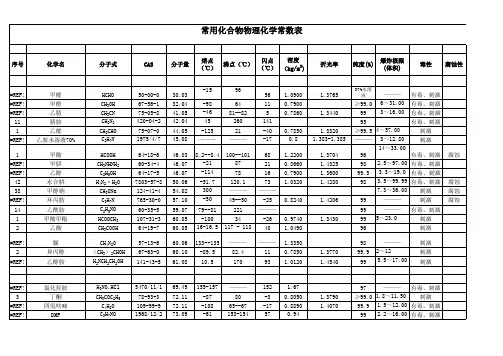
常用有机溶剂的物理常数常用有机溶剂的物理常数溶剂mp bp D420n D20εR D μAcetic acid 乙酸17 118 1.0491.3716 6.15 12.9 1.68Acetone 丙酮-95560.7881.358720.7 16.2 2.85Acetonitrile 乙腈-44820.7821.344137.5 11.1 3.45Anisole 苯甲醚-3 1540.9941.5170 4.33 33 1.38Benzene 苯5 800.8791.5011 2.27 26.2 0.00Bromobenzene 溴苯-31156 1.4951.5580 5.17 33.7 1.55Carbon disulfide 二硫化碳-11246 1.2741.6295 2.6 21.3 0.00Carbon tetrachloride 四氯化碳-2377 1.5941.4601 2.24 25.8 0.00Chlorobenzene 氯苯-46132 1.1061.5248 5.62 31.2 1.54Chloroform 氯仿-6461 1.4891.4458 4.81 21 1.15Cyclohexane 环己烷6 810.7781.4262 2.02 27.7 0.00Dibutyl ether 丁醚-981420.7691.3992 3.1 40.8 1.18o –Dichlorobenzene 邻二氯苯-17181 1.3061.55149.93 35.9 2.271,2-Dichloroethane 1，2-二氯乙烷-3684 1.2531.444810.36 21 1.86Dichloromethane 二氯乙烷-9540 1.3261.42418.93 16 1.55Diethylamine 二乙胺-50560.7071.3864 3.6 24.3 0.92Diethyl ether 乙醚-117350.7131.3524 4.33 22.1 1.301,2-Dimethoxyethane 1，2-二甲氧基-68850.8631.37967.2 24.1 1.71 乙烷N,N –Dimethylacetamide N，N-二甲-201660.9371.438437.8 24.2 3.72 基乙酰胺N,N –Dimethylformamide-601520.9451.430536.7 19.9 3.86 N，N-二甲基甲酰胺Dimethyl sulfoxide二甲基亚砜19 189 1.0961.478346.7 20.1 3.901,4-Dioxane 1，4-二氧六环12 101 1.0341.4224 2.25 21.6 0.45Ethanol 乙醇-114780.7891.361424.5 12.8 1.69Ethyl acetate 乙酸乙酯-84770.9011.3724 6.02 22.3 1.88Ethyl benzoate 苯甲酸乙酯-35213 1.0501.5052 6.02 42.5 2.00Formamide 甲酰胺3 211 1.1331.4475111.0 10.6 3.37Hexamethylphosphoramide 7 235 1.0271.458830.0 47.7 5.54Isopropyl alcohol 异丙醇-90820.7861.377217.9 17.5 1.66isopropyl ether 异丙醚-6068 1.36Methanol 甲醇-98650.7911.328432.7 8.2 1.702-Methyl-2-propanol 2-甲基-2-丙26 820.7861.387710.9 22.2 1.66醇Nitrobenzene 硝基苯6 211 1.2041.556234.82 32.7 4.02 Nitromethane 硝基甲烷-28101 1.1371.381735.87 12.5 3.54 Pyridine 吡啶-421150.9831.510212.4 24.1 2.37 tert-butyl alcohol叔丁醇25.582.5 1.3878Tetrahydrofuran 四氢呋喃-109660.8881.40727.58 19.9 1.75 Toluene 甲苯-951110.8671.4969 2.38 31.1 0.43 Trichloroethylene 三氯乙烯-8687 1.4651.4767 3.4 25.5 0.81 Triethylamine 三乙胺-115900.7261.4010 2.42 33.1 0.87 Trifluoroacetic acid 三氟乙酸-1572 1.4891.28508.55 13.7 2.26 2,2,2-Trifluoroethanol 2，2，2--4477 1.3841.29108.55 12.4 2.52 三氟乙醇Water 水0 1000.9981.333080.1 3.7 1.82 o -Xylene 邻二甲苯-251440.8801.5054 2.57 35.8 0.62 mp 熔点bp 沸点D 密度n D折射率ε介电厂数R D摩尔折射率μ偶极矩。

codata 2018 物理常量
Codata 2018是国际上公认的物理常数和相关数值的权威参考
资料。

它由国际纯粹与应用物理学家学会（IUPAP）和国际纯粹与应
用化学家学会（IUPAC）共同发布。

Codata 2018提供了一系列精确
的物理常数，这些常数在物理、化学、工程等领域中具有重要的应
用价值。

Codata 2018包含了一系列基本物理常数，例如电子的质量、
电荷、普朗克常数、光速等。

这些常数对于研究者在各个领域进行
精密测量和实验具有重要意义。

通过Codata 2018提供的数值，科
学家们可以在其研究中准确地使用这些物理常数，从而保证其研究
结果的准确性和可比性。

除了基本的物理常数外，Codata 2018还包含了一些其他重要
的物理数据，例如原子质量、晶体结构数据、核衰变参数等。

这些
数据对于原子物理、核物理、材料科学等领域的研究具有重要意义。

Codata 2018的发布标志着国际科学界对于物理常数和相关数
据的共识和标准化。

研究者们可以通过Codata 2018获得最新的、
最精确的物理常数数值，从而推动各个领域的科学研究和技术发展。

总的来说，Codata 2018作为物理常数和相关数据的权威参考资料，为科学研究和工程技术提供了重要的支持和依据。

科学家们可以通过Codata 2018获得准确的物理常数数值，从而推动科学研究和技术创新的发展。

7.1×10－10
中子康普顿波长
λCn
1.3195909068×10－15
m
8.2×10－10
里德伯常量
R∞
1.0973731568527×107
m－1
6.6×10－12
电子磁矩
μe
－9.28476377×10－24
J·T-1
2.5×10－8
质子磁矩
μp
1.410606662×10－26
J·T-1
2.6×10－8
阿伏加德罗常数
NA
6.02214179×1023
mol－1
5.0×10－8
普适气体常量
R
8.314472
J/(mol·K)
1.7×10－6
玻尔兹曼常数
k
1.3806504×10－23
J/K
1.7×10－6
气体摩尔体积(p=100kPa)
Vm
22.710953×103
m3·mol-1
9.1×10-7
斯塔藩·玻尔兹曼常数
h
6.62606896×10－34
J·s
5.0×10－8
约化普朗克常数
ℏ=h/2π
1.054571726×10－35
J·s
4.4×10－8
普朗克长度
lP
1.616199×10－35
m
6.0×100－44
s
6.0×10－5
●电磁常数
电磁常数
物理量
符号
数值
单位
相对标准不确定度
σ
5.670373×10－8
W·m-2·K-4
3.6×10-6
第一辐射常数
c1
3.74177153×10－16

甲醇安托因常数1. 什么是甲醇安托因常数？甲醇安托因常数是描述甲醇在溶剂中溶解度的物理量。

安托因常数通常由一个单位体积的溶剂中所能溶解的物质的质量来表示。

在这种情况下，甲醇安托因常数表示在特定温度下，单位体积的溶剂中可以溶解多少甲醇。

2. 甲醇安托因常数的意义和应用甲醇安托因常数在化学和工程领域有着广泛的应用。

它可以用来评估和预测不同条件下甲醇在溶剂中的溶解度，从而为实验设计、工艺优化和产品开发提供依据。

具体来说，甲醇安托因常数可以用于以下方面：a) 溶液浓度计算通过知道某个温度下的甲醇溶液中的安托因常数，可以根据给定的质量或体积计算出相应浓度的甲醇。

这对于实验室研究和工业生产都非常重要。

b) 溶解度预测通过甲醇安托因常数的值，可以预测在不同温度和压力下甲醇在溶剂中的溶解度。

这对于了解溶液的相行为、物质传递和反应速率等方面都有重要意义。

c) 选择合适的溶剂甲醇安托因常数可以用来比较不同溶剂对甲醇的溶解能力。

根据安托因常数的大小，可以选择最适合特定实验或工艺条件的溶剂。

3. 甲醇安托因常数的测定方法甲醇安托因常数可以通过实验测定获得。

一种常用的方法是利用滴定法或称量法，将一定体积的溶液与已知浓度的标准溶液进行反应，根据反应前后标准溶液中物质质量或体积变化来计算出甲醇在该溶剂中的安托因常数。

另外，也可以使用理论模型来估算甲醇安托因常数。

这些模型通常基于统计力学原理和经验参数，并结合实验数据进行拟合。

这种方法适用于无法直接测定安托因常数的情况，或者用于快速预测溶解度。

4. 影响甲醇安托因常数的因素甲醇安托因常数受到多种因素的影响，包括温度、压力、溶剂性质、溶质浓度等。

a) 温度温度是影响甲醇安托因常数的主要因素之一。

一般来说，随着温度的升高，甲醇在溶剂中的溶解度会降低。

这是由于温度升高导致分子热运动增加，使得分子间相互作用减弱，从而降低了溶质在溶剂中的溶解能力。

b) 压力压力对甲醇安托因常数的影响相对较小。