物理化学部分答案

1. 在恒压下，某理想气体的体积随温度的变化率=∂∂P TV)(；而在恒容条件下，某范德华气体的压力随温度的变化率=∂∂V Tp)(()b V R m - 。

（2分）2. 实际气体在节流膨胀过程中（pV 之积变大），则其Q ＝ 0，ΔH ＝ 0，ΔU < 0，ΔS > 0。

（从“>、<、＝或无法确定” 中选一填入）。

（2分）。

3. 1 mol N 2(g)(设为理想气体)在300 K 恒温下从2 dm 3可逆膨胀到40 dm 3，则其体积功W r = 20ln RT -。

4. 一带活塞的气缸中，放有1 mol 温度为300K 、压力为 100 kPa 的理想气体。

在绝热情况下于活塞上突然施加200 kPa 的压力，达平衡后，此过程的∆S > 0；如果始态相同，在保持温度不变条件下于活塞上突然施加200 kPa 的压力，达平衡后，此过程的∆S < 0。

（从“>0、<0、=0或无法确定”中选一填入）5. 根据热力学基本方程，可写出=∂∂V T A )(S -； =∂∂T p S )( pT V ⎪⎭⎫⎝⎛∂∂-。

6. 在一定温度下，p B * > p A *，由纯液态物质A 和B 形成理想液态混合物，当气-液两相达到平衡时，气相组成y B 总是 > 液相组成x B （从“>、<、= 或无法确定”中选一填入）。

7． 液体B 和液体C 可形成理想液态混合物。

在常压及298 K 下，向总量n = 10 mol ，组成为x C = 0.4的B 、C 液态混合物中加入14 mol 的纯液体C ，形成新的混合物，则混合过程的∆mix G = － 16.77 kJ ；∆mix S = 56.25 J K -1 。

8．在一个抽空的容器中放入过量的NH 4I(s)和NH 4Cl(s)并发生下列反应：)()()(34g HI g NH s I NH += )()()(34g HCl g NH s Cl NH +=此平衡系统的相数P = 3 ；组分数C = 2 ；自由度数F = 1 。

第一章气体的pVT 关系1-1物质的体膨胀系数V α与等温压缩系数T κ的定义如下：1 1TT p V p V V T V V ⎪⎪⎭⎫⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂=κα 试导出理想气体的V α、T κ与压力、温度的关系？解：对于理想气体，pV=nRT111 )/(11-=⋅=⋅=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂=T TVV p nR V T p nRT V T V V p p V α 1211 )/(11-=⋅=⋅=⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂-=p p V V pnRT V p p nRT V p V V T T T κ 1-2 气柜内有121.6kPa 、27℃的氯乙烯（C 2H 3Cl ）气体300m 3，若以每小时90kg 的流量输往使用车间，试问贮存的气体能用多少小时？解：设氯乙烯为理想气体，气柜内氯乙烯的物质的量为mol RT pV n 623.1461815.300314.8300106.1213=⨯⨯⨯==每小时90kg 的流量折合p 摩尔数为 133153.144145.621090109032-⋅=⨯=⨯=h mol M v Cl H Cn/v=（14618.623÷1441.153）=10.144小时1-3 0℃、101.325kPa 的条件常称为气体的标准状况。

试求甲烷在标准状况下的密度。

解：33714.015.273314.81016101325444--⋅=⨯⨯⨯=⋅=⋅=m kg M RT p M V n CH CH CHρ 1-4 一抽成真空的球形容器，质量为25.0000g 。

充以4℃水之后，总质量为125.0000g 。

若改用充以25℃、13.33kPa 的某碳氢化合物气体，则总质量为25.0163g 。

试估算该气体的摩尔质量。

解：先求容器的容积33)(0000.10010000.100000.250000.1252cm cm Vl O H ==-=ρ n=m/M=pV/RTmol g pV RTm M ⋅=⨯-⨯⨯==-31.301013330)0000.250163.25(15.298314.841-5 两个体积均为V 的玻璃球泡之间用细管连接，泡内密封着标准状况条件下的空气。

《物理化学》复习题一、选择题：1.体系的状态改变了，其内能值（ ）A 必定改变B 必定不变状态与内能无关 2.μ=0 3. （ ）A. 不变B. 可能增大或减小C. 总是减小4.T, p, W ‘=0≥0 C. (dG)T,V, W=0≤0 D. (dG) T, V, W ‘=0≥0 5.A. (dA)T, p, W ‘=0≤0B. (dA) T, p, W ‘=0≥ T, V, W ‘=0≥0 6.下述哪一种说法正确？ 因为A. 恒压过程中,焓不再是状态函数B. 恒压过程中,焓变不能量度体系对外所做的功 D. 恒压过程中, ΔU 不一定为零 7. NOCl 2（g ）＝NO （g ） + Cl 2（g ）为吸热反应，改变下列哪个因素会使平衡向右移动。

（ ）增大压力 C. 降低温度 D. 恒温、恒容下充入惰性气体 8. ）A. 溶液中溶剂化学势较纯溶剂化学势增大B. 沸点降低C. 蒸气压升高 9．ΔA=0 的过程应满足的条件是 （ ）C. 等温等容且非体积功为零的过程10.ΔG=0 的过程应满足的条件是 （ ） C. 等温等容且非体积功为零的过程D. 等温等容且非体积功为零的可逆过程 11. 300K 将1molZn Q p ，恒容反应热效应为Q v ，则Q p -Q v = J 。

无法判定12．已知FeO(s)+C(s)=CO(g)+Fe(s)，反应的Δr H m 0为正，Δr S m 0为正（设Δr H m 0和Δr S m 0不随温度而变化）A. 高温有利B. 低温有利与压力无关13．化学反应 N 2(g) +3H 2(g) = 2NH 3(g)A. 3NH 2H 2N μμμ==B. 032=++3NH 2H 2N μμμC. NH 2H 2N μμμ32==14. 某化学反应的方程式为2A →P ，则在动力学研究中表明该反应为 （ ）A.二级反应B.基元反应C.双分子反应15. 已知298 K 时， Hg 2Cl 2 + 2e - === 2Hg + 2Cl -， E 1 AgCl + e - === Ag + Cl -， E 2= 0.2224 V 。

物理化学第二版习题答案【篇一：物理化学核心教程课后答案完整版(第二版学生版)】ss=txt>二、概念题1. 答：（d）热力学能是状态的单值函数，其绝对值无法测量。

2. 答：（c）气体膨胀对外作功，热力学能下降。

3. 答：（b）大气对系统作功，热力学能升高。

4. 答：（a）过程（1）中，系统要对外作功，相变所吸的热较多。

5. 答：（a）对冰箱作的电功全转化为热了。

7. 答：（c）对于理想气体而言，内能仅仅是温度的单值函数，经真空绝热膨胀后，内能不变，因此体系温度不变。

8. 答：（c）由气体状态方程pvm= rt+bp可知此实际气体的内能只是温度的函数，经真空绝热膨胀后，内能不变，因此体系温度不变（状态方程中无压力校正项，说明该气体膨胀时，不需克服分子间引力，所以恒温膨胀时，热力学能不变）。

9. 答：（b）式适用于不作非膨胀功的等压过程。

757，cv =rcp=r ，这是双原子分子的特征。

522?n2molv210. （b）1.40=??16. 答：由气体状态方程pvm= rt+bp可知此实际气体的内能与压力和体积无关，则此实际气体的内能只是温度的函数。

三、习题1. （1）一系统的热力学能增加了100kj，从环境吸收了40kj的热，计算系统与环境的功的交换量；（2）如果该系统在膨胀过程中对环境做了20kj的功，同时吸收了20kj的热，计算系统热力学能的变化值。

2. 在300 k时，有 10 mol理想气体，始态压力为 1000 kpa。

计算在等温下，下列三个过程做膨胀功：（1）在100 kpa压力下体积胀大1 dm3 ；p?nrtvp2 (?p2?nrtnrt?－) = - nrt?1??? p2p1p1??100）= -22.45 kj 1000= -nrtln（3）∵ w = -?pdv =-?v1nrtdvvv2p1= -nrtln v1p21000= -57.43 kj 1003. 在373 k恒温条件下，计算1 mol理想气体在下列四个过程中所做的膨胀功。

物理化学模拟题一、选择题（30分，每题2分）1. 热力学第三定律可以表示为┈┈┈┈┈┈┈┈┈┈┈┈┈( ) (A).在0K 时，任何晶体的熵等于零(B).在0K 时，任何完整晶体的熵等于零 (C).在0℃时，任何晶体的熵等于零 (D).在0℃时，任何完整晶体的熵等于零2. 理想气体从状态p 1,V 1,T 等温膨胀到p 2,V 2,T ，此过程的ΔA 与ΔG 的关系为┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( ) (A). ΔA >ΔG (B). ΔA <ΔG （C ）. ΔA =ΔG (D).无法确定 3．一定量的理想气体，从同一初态分别经历等温可逆膨胀、绝热可逆膨胀到具有相同压力的终态，终态体积分别为V 1、V 2。

┈┈┈( ) (A). V 1 < V 2(B). V 1 = V 2（C ）. V 1 > V 2 (D). 无法确定4．方程 mmV T H T P βαβα∆∆=d d 适用于以下哪个过程┈┈┈┈┈┈┈┈┈┈┈┈┈( )(A).NH 4Cl(s)= NH 3(g)+ HCl(g) (B).NH 4Cl(s)溶于水形成溶液 (C).H 2O (s)= H 2O (l) (D).H 2和O 2化合为水 5. 两液体的饱和蒸汽压分别为p *A ，p *B ，它们混合形成理想溶液，液相组成为x ，气相组成为y ，若 p*A > p *B ，则：┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( )(A) y A > x A (B) y A > y B (C) x A > y A (D) y B > y A 6. 在通常情况下，对于二组分物系能平衡共存的最多相为：┈┈┈┈┈┈( )(A) 1 (B) 2 (C) 3 (D) 47. 25℃时水的饱和蒸气压为3.168kPa, 此时液态水的标准生成吉布斯自由能 Δf G m 为－237.19kJ ·mol －1，则水蒸气的标准生成吉布斯自由能为：┈┈┈( ) (A) －245.76kJ ·mol －1 (B) －229.34kJ ·mol －1 (C) －245.04kJ ·mol －1 (D) －228.60kJ ·mol －18. 已知反应 3O 2(g) = 2O 3(g) 在25℃时θm r H ∆ =-280J ·mol -1，则对该反应有利的条件是：┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( ) (A) 升温升压 (B) 升温降压 (C) 降温升压 (D) 降温降压 9. 298K 0.01mol•kg -1的CaCl 2水溶液中，CaCl 2的离子平均活度系数γ±为( )（A ）0.847 （B ）0.791 （C ）0.889 （D ）0.66610. 某反应表观速率常数k 与基元步骤速率常数间的关系为21412)(k kk k =，则表观活化能与各基元步骤活化能的关系为┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( )（A ）E=E 2+21(E 1－E 4) （B ）E=E 2+21(E 1+E 4) （C ）E=E 2+E 1－E 4 （D ）E=E 2(41E E)2111. 由MgCO 3(s)、BaCO 3(s)、BaO(s)、MgO(s)及CO 2(g)构成的一个平衡系统，其独立组分数和自由度分别为┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( ) (A) 5，3 (B) 4，2 (C) 3，1 (D) 3，0 12. 同一温度和压力下，一定量某物质的熵值存在┈┈┈┈( ) (A).s l g S S S 〈〈 (B). s l g S S S 〉〉 (C). s l g S S S == (D). s l g S S S =〉13.某反应物的速率常数为0.099min -1,反应物初始浓度为0.2mol·dm -3,则反应的半衰期为┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( )(A). 7 min (B). 1.01 min (C). 4.04 min (D).50.5 min14.在α、β这两相中均含有A 、B 两种物质，当达到相平衡时下列化学势关系中正确的是┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( )(A). ααμμB A = (B). βαμμA A = (C). αβμμB A = (D). ββμμB A =15.已知电极反应(1) Cu e Cu →++22 ，E 1 =0.34V (2) ++→+Cu e Cu 2，E2=0.167V则Cu e Cu →++的标准电极电势E 3为┈┈┈┈┈┈┈┈┈( ) (A).0.507V (B). 0.513V (C). 0.173V (D). 0.267V二、填空题（10分，每题2分）1、25℃时,0.5molA 与0.5molB 形成理想液态混合物,则混合过程的 ΔS=________。

第一章气体的pVT性质1.1物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的，与压力、温度的关系。

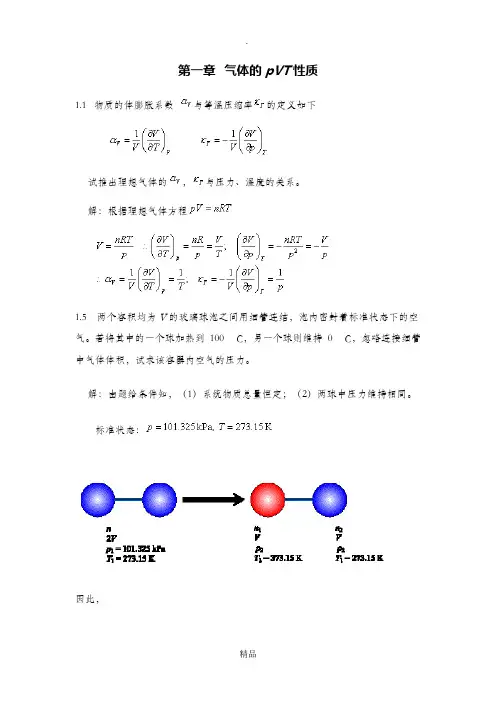
解：根据理想气体方程1.5两个容积均为V的玻璃球泡之间用细管连结，泡内密封着标准状态下的空气。

若将其中的一个球加热到100 C，另一个球则维持0 C，忽略连接细管中气体体积，试求该容器内空气的压力。

解：由题给条件知，（1）系统物质总量恒定；（2）两球中压力维持相同。

标准状态：因此，1.9 如图所示，一带隔板的容器内，两侧分别有同温同压的氢气与氮气，二者均可视为理想气体。

（1）保持容器内温度恒定时抽去隔板，且隔板本身的体积可忽略不计，试求两种气体混合后的压力。

（2）隔板抽取前后，H2及N2的摩尔体积是否相同？（3）隔板抽取后，混合气体中H2及N2的分压立之比以及它们的分体积各为若干？解：（1）等温混合后即在上述条件下混合，系统的压力认为。

（2）混合气体中某组分的摩尔体积怎样定义？（3）根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气，为进行实验时确保安全，采用同样温度的纯氮进行置换，步骤如下：向釜内通氮气直到4倍于空气的压力，尔后将釜内混合气体排出直至恢复常压。

重复三次。

求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。

解：分析：每次通氮气后至排气恢复至常压p，混合气体的摩尔分数不变。

设第一次充氮气前，系统中氧的摩尔分数为，充氮气后，系统中氧的摩尔分数为，则，。

重复上面的过程，第n次充氮气后，系统的摩尔分数为，因此。

1.13 今有0 C，40.530 kPa的N2气体，分别用理想气体状态方程及van der Waals 方程计算其摩尔体积。

实验值为。

解：用理想气体状态方程计算用van der Waals计算，查表得知，对于N2气（附录七），用MatLab fzero函数求得该方程的解为也可以用直接迭代法，，取初值，迭代十次结果1.16 25 C时饱和了水蒸气的湿乙炔气体（即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压）总压力为138.7 kPa，于恒定总压下冷却到10 C，使部分水蒸气凝结为水。

物理化学作业答案第一章热力学第一定律一、判断题（正确打√，错误打×）1. 由于p和V都是状态函数，则pV也是状态函数。

（√ ）2. 状态函数改变后，状态一定改变。

（√ ）3. 孤立系统内发生的一切变化过程，其 U Δ必定为零。

（√ ）4. 温度越高，Q值越大。

（×）5. 等压过程是指系统在变化过程中系统的压力等于环境的压力。

（×）6. 不做非体积功是指系统的始态和终态的体积相同。

（×）7. 在标准状态下，最稳定单质的焓值等于零。

（×）8. O2 （g）的标准摩尔燃烧焓等于零。

（√ ）9. H2O（l）的标准摩尔燃烧焓等于零。

（√ ）10. H2和O2在绝热钢瓶中发生反应的U △ 等于零。

（√）二、选择题（选1个答案）1. 是状态函数。

（ A ）A．G B．△U C．W D．Q2. 不是状态函数。

（ D ）A．H B．U C．S D．△G3. 具有广度性质。

（ B ）A．T B、U C．P D．ρ（密度）4. 具有强度性质。

（ D ）A．S B．V C．G D．η（粘度）5. 的标准摩尔生成焓等于零。

（ A ）A．C（石墨） B．C（金刚石） C．CO2 D．CO6．的标准摩尔燃烧焓等于零。

（ C ）A．C（石墨） B．C（金刚石） C．CO2 D．CO7. 理想气体在外压为 101.325kPa 下的等温膨胀，该过程的。

（ A ）A．Q>0 B．Q<0 C．△U>0 D．△U<08. 101.325kPa和 273.15K的水等温等压变为冰，该过程的。

（ D ）A．Q>0 B．△U=0 C．△H>0 D．△H<09. 下列叙述中不属于状态函数特征的是。

（ C ）A．系统变化时，状态函数的改变值只由系统的始、终态决定。

B．系统状态确定后，状态函数的值也确定。

C．状态函数均有加和性。

D．经循环过程，状态函数的值不变。

物理化学习题及答案第一章热力学第一定律选择题1．热力学第一定律ΔU=Q+W 只适用于(A) 单纯状态变化(B) 相变化(C) 化学变化(D) 封闭物系的任何变化答案：D2．关于热和功, 下面的说法中, 不正确的是(A) 功和热只出现于系统状态变化的过程中, 只存在于系统和环境间的界面上 (B) 只有在封闭系统发生的过程中, 功和热才有明确的意义(C) 功和热不是能量, 而是能量传递的两种形式, 可称之为被交换的能量(D) 在封闭系统中发生的过程中, 如果内能不变, 则功和热对系统的影响必互相抵消答案：B2．关于焓的性质, 下列说法中正确的是(A) 焓是系统内含的热能, 所以常称它为热焓(B) 焓是能量, 它遵守热力学第一定律(C) 系统的焓值等于内能加体积功 (D) 焓的增量只与系统的始末态有关答案：D。

因焓是状态函数。

3．涉及焓的下列说法中正确的是(A) 单质的焓值均等于零(B) 在等温过程中焓变为零(C) 在绝热可逆过程中焓变为零(D) 化学反应中系统的焓变不一定大于内能变化答案：D。

因为焓变ΔH=ΔU+Δ(pV)，可以看出若Δ(pV)＜0则ΔH＜ΔU。

4．下列哪个封闭体系的内能和焓仅是温度的函数(A) 理想溶液 (B) 稀溶液 (C) 所有气体 (D) 理想气体答案：D5．与物质的生成热有关的下列表述中不正确的是(A) 标准状态下单质的生成热都规定为零 (B) 化合物的生成热一定不为零 (C) 很多物质的生成热都不能用实验直接测量(D) 通常所使用的物质的标准生成热数据实际上都是相对值答案：A。

按规定，标准态下最稳定单质的生成热为零。

6．dU=CvdT及dUm=Cv,mdT适用的条件完整地说应当是 (A) 等容过程(B)无化学反应和相变的等容过程(C) 组成不变的均相系统的等容过程(D) 无化学反应和相变且不做非体积功的任何等容过程及无反应和相变而且系统内能只与温度有关的非等容过程答案：D7．下列过程中, 系统内能变化不为零的是(A) 不可逆循环过程(B) 可逆循环过程 (C) 两种理想气体的混合过程(D) 纯液体的真空蒸发过程答案：D。

第一章热力学第一定律选择题1．热力学第一定律ΔU=Q+W 只适用于（）(A) 单纯状态变化 (B) 相变化 (C) 化学变化 (D) 封闭物系的任何变化答案：D2．关于热和功, 下面的说法中, 不正确的是(A) 功和热只出现于系统状态变化的过程中, 只存在于系统和环境间的界面上(B) 只有在封闭系统发生的过程中, 功和热才有明确的意义(C) 功和热不是能量, 而是能量传递的两种形式, 可称之为被交换的能量2(C) D。

因焓3(D) (pV) 45(A)(D)6．(D)7(A)答案：D W＝0，故由热力学第一定律ΔU＝Q＋W得ΔU＝Q，蒸发过程需吸热Q＞0，故ΔU＞0。

8．第一类永动机不能制造成功的原因是（）(A) 能量不能创造也不能消灭 (B) 实际过程中功的损失无法避免 (C) 能量传递的形式只有热和功 (D) 热不能全部转换成功答案：A9．盖斯定律包含了两个重要问题, 即（）(A) 热力学第一定律和热力学第三定律 (B) 热力学第一定律及热的基本性质(C) 热力学第三定律及热的基本性质 (D) 热力学第一定律及状态函数的基本特征答案：D10．当某化学反应ΔrCp,m ＜0,则该过程的()r m H T ∆$随温度升高而（ ）(A) 下降 (B) 升高 (C) 不变 (D) 无规律 答案：A 。

根据Kirchhoff 公式,()/r m r p m d H T dT C ∆=∆$可以看出。

11．在下面涉及盖斯定律的表述中, 不正确的是（ ）(A) 对在等温等压且不做非体积功的条件下, 发生的各个化学反应过程和相变过程, 可使用盖斯定律(B) 对在等温等容且不做功的条件下, 发生的各个化学反应过程, 可使用盖斯定律(C) 同一物质在盖斯定律涉及的几个反应中都出现时, 只要无溶解等现象, 相态不同也可加减(D) 利用盖斯定律求某个反应的热效应时可引入一些别的反应,设想一些中间步骤, 无论实际反应是否按这些中间步骤进行都可以12答案：C ＝Q ，说13(A) 答案：C （D ）等B14(A)15(A) ∑＋∑Wi ，16．与物质的燃烧热有关的下列表述中不正确的是(A) 可燃性物质的燃烧热都不为零 (B) 物质的燃烧热都可测定，所以物质的标准摩尔燃烧焓不是相对值(C) 同一可燃性物质处于不同状态时,其燃烧热不同 (D) 同一可燃性物质处于不同温度下,其燃烧热之值不同答案：B 。

思考题解答1. 判断下列说法是否正确，为什么？(1) 在一给定的系统中，独立组分数是一个确定的数。

(2) 单组分系统的物种数一定等于1。

(3) 相律适用于任何相平衡系统。

(4) 在相平衡系统中，如果每一相中的物种数不相等，则相律不成立。

解答：(1) 对。

(2) 错。

组份数等于1。

(3) 错。

在有电场、重力场、磁场或渗透质存在时，不适用，必须加以修正。

(4) 错。

由相律得出的结论与每一相中的物种数无关。

2. 指出下列平衡系统中的组分数，相数，及自由度数。

(1) I2(S)与其蒸气成平衡；(2) CaCO3(s)与其分解产物CaO(s)和CO2(g)成平衡；(3) NH4HS(s)放入一抽空的容器中，并与其分解产物NH3(g)和H2S(g)成平衡；(4) 取任意量的NH3(g)和H2S(g)与NH4HS(s)成平衡；(5) I2作为溶质在两不互溶液体H2O和CCl4中达到分配平衡(凝聚系统)。

解答：(1) C = 1；Φ= 2；f = 1 – 2 + 2 = 1(2) C = 2；(∵S = 3；R = 1，∴C = 3－1 = 2)；Φ= 3；f = 2 – 3 + 2 = 1(3) C = S－R－R' = 3－1－1=1(浓度限制条件，产物NH3(g):H2S(g) = 1:1)；Φ= 2；f = 1(4) C = 3－1 = 2；Φ= 2；f = 2(5) C = 3；Φ= 2；f = C－Φ+ 1=3 – 2 + 1 = 2(凝聚相可以不考虑压力的影响)3. 证明：(1) 在一定温度下，某浓度的NaCl水溶液只有一个确定的蒸气压；(2) 在一定温度下，草酸钙分解为碳酸钙和一氧化碳时只能有一个确定的CO压力。

解答：(1) Φ= 2，浓度一定，C = 1，温度一定，则f = 1 – 2 + 1 = 0。

(2) Φ= 3，C = 2，当T一定时，f = 2 – 3 + 1 = 0。

4. Na2CO3与水可形成三种水合物Na2CO3·H2O(s)，Na2CO3·7H2O(s)和Na2CO3·10H2O(s)。