工程流体力学(闻建龙)课后答案(部分)

第1章 绪论【1-1】500cm 3的某种液体，在天平上称得其质量为0.453kg ，试求其密度和相对密度。

【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 相对密度330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水，在温度不变的条件下，当压强从98000Pa 增加到4.9×105Pa 时，体积减少1L 。

求水的压缩系数和弹性系数。

【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃，流量为60m 3/h 的水流入加热器，如果水的体积膨胀系数βt =0.00055K -1，问加热到80℃后从加热器中流出时的体积流量变为多少？ 【解】根据膨胀系数1t dV V dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。

罐装时液面上压强为98000Pa 。

封闭后由于温度变化升高了20℃，此时汽油的蒸汽压力为17640Pa 。

若汽油的膨胀系数为0.0006K -1，弹性系数为13.72×106Pa ，（1）试计算由于压力温度变化所增加的体积，（2）问灌装时汽油的体积最多不应超过桶体积的百分之多少？【解】（1）由1β=-=P pdV Vdp E可得，由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积，可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT（2）因为∆∆tp V V ，相比之下可以忽略由压力变化引起的体积改变，则由 200L β+=t V V dT得1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板，其水平运动速度为u =1m/s ，δ=10mm ，油品的粘度μ=0.9807Pa ·s ，求作用在平板单位面积上的阻力。

第1章 绪论【1-1】500cm 3的某种液体，在天平上称得其质量为0.453kg ，试求其密度和相对密度。

【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯相对密度 330.906100.9061.010w ρδρ⨯===⨯【1-2】体积为5m 3的水，在温度不变的条件下，当压强从98000Pa 增加到4.9×105Pa 时，体积减少1L 。

求水的压缩系数和弹性系数。

【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃，流量为60m 3/h 的水流入加热器，如果水的体积膨胀系数βt =0.00055K -1，问加热到80℃后从加热器中流出时的体积流量变为多少？【解】根据膨胀系数1t dVV dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。

罐装时液面上压强为98000Pa 。

封闭后由于温度变化升高了20℃，此时汽油的蒸汽压力为17640Pa 。

若汽油的膨胀系数为0.0006K -1，弹性系数为13.72×106Pa ，（1）试计算由于压力温度变化所增加的体积，（2）问灌装时汽油的体积最多不应超过桶体积的百分之多少？【解】（1）由1β=-=P p dV Vdp E可得，由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E由于温度变化而增加的体积，可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT（2）因为∆∆t p V V ?，相比之下可以忽略由压力变化引起的体积改变，则 由 200L β+=t V V dT 得 1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板，其水平运动速度为u =1m/s ，δ=10mm ，油品的粘度μ=0.9807Pa ·s ，求作用在平板单位面积上的阻力。

《工程流体力学》课后习题答案孔珑第四版第2章流体及其物理性质 (4)2-1 (4)2-3 (4)2-4 (6)2-5 (6)2-6 (6)2-7 (7)2-8 (7)2-9 (8)2-11 (8)2-12 (9)2-13 (9)2-14 (10)2-15 (10)2-16 (11)第3章流体静力学 (12)3-1 (12)3-2 (12)3-3 (13)3-5 (13)3-6 (14)3-9 (14)3-10 (15)3-21 (18)3-22 (19)3-23 (20)3-25 (20)3-27 (20)第4章流体运动学及动力学基础 (22)4-2 (22)4-5 (22)4-6 (23)4-8 (23)4-11 (24)4-12 (24)4-14 (25)4-22 (25)4-24 (26)4-26 (27)第6章作业 (28)6-1 (28)6-3 (28)6-7 (29)6-10 (29)6-11 (29)6-12 (30)6-17 (31)第2章流体及其物理性质2-1已知某种物质的密度ρ=2.94g/cm3，试求它的相对密度d。

【2.94】解：ρ=2.94g/cm3=2940kg/m3，相对密度d=2940/1000=2.942-2已知某厂1号炉水平烟道中烟气组分的百分数为，α(CO2)=13.5%α(SO2)=0.3%，α(O2)=5.2%，α(N2)=76%，α(H2O)=5%。

试求烟气的密度。

解：查课表7页表2-1，可知ρ(CO2)=1.976kg/m3，ρ(SO2)=2.927kg/m3，ρ(O2)=1.429kg/m3，ρ(N2)=1.251kg/m3，ρ(H2O)=1.976kg/m3，ρ(CO2)=1.976kg/m3，3ρ=∑i iαρ=341.1kg/m2-3上题中烟气的实测温度t=170℃，实测静计示压强Pe=1432Pa，当地大气压Pa=100858Pa。

试求工作状态下烟气的密度和运动粘度。

闻建龙主编的《工程流体力学》习题参考答案第一章 绪论1-1 物质就是按什么原则分为固体与液体两大类的？解:从物质受力与运动的特性将物质分成两大类:不能抵抗切向力,在切向力作用下可以无限的变形(流动),这类物质称为流体。

如空气、水等。

而在同等条件下,固体则产生有限的变形。

因此,可以说:流体不管就是液体还就是气体,在无论多么小的剪应力(切向)作用下都能发生连续不断的变形。

与此相反,固体的变形与作用的应力成比例,经一段时间变形后将达到平衡,而不会无限增加。

1-2 何谓连续介质假设？引入连续介质模型的目的就是什么？在解决流动问题时,应用连续介质模型的条件就是什么？解:1753年,欧拉首次采用连续介质作为流体宏观流动模型,即不考虑流体分子的存在,把真实的流体瞧成就是由无限多流体质点组成的稠密而无间隙的连续介质,甚至在流体与固体边壁距离接近零的极限情况也认为如此,这个假设叫流体连续介质假设或稠密性假设。

流体连续性假设就是流体力学中第一个根本性假设,将真实流体瞧成为连续介质,意味着流体的一切宏观物理量,如密度、压力、速度等,都可瞧成时间与空间位置的连续函数,使我们有可能用数学分析来讨论与解决流体力学问题。

在一些特定情况下,连续介质假设就是不成立的,例如:航天器在高空稀薄气体中飞行,超声速气流中激波前后,血液在微血管(1μm)内的流动。

1-3 底面积为25.1m 的薄板在液面上水平移动(图1-3),其移动速度为s m 16,液层厚度为mm 4,当液体分别为C 020的水与C 020时密度为3856m kg 的原油时,移动平板所需的力各为多大？题1-3图解:20℃ 水:s Pa ⋅⨯=-3101μ20℃,3/856m kg =ρ, 原油:s Pa ⋅⨯='-3102.7μ水:233/410416101m N u=⨯⨯=⋅=--δμτ N A F 65.14=⨯=⋅=τ油: 233/8.2810416102.7m N u =⨯⨯=⋅'=--δμτ N A F 2.435.18.28=⨯=⋅=τ1-4 在相距mm 40=δ的两平行平板间充满动力粘度s Pa ⋅=7.0μ液体(图1-4),液体中有一边长为mm a 60=的正方形薄板以s m u 15=的速度水平移动,由于粘性带动液体运动,假设沿垂直方向速度大小的分布规律就是直线。

第1章 绪论【1-1】500cm 3的某种液体，在天平上称得其质量为0.453kg ，试求其密度和相对密度。

【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 相对密度330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水，在温度不变的条件下，当压强从98000Pa 增加到4.9×105Pa 时，体积减少1L 。

求水的压缩系数和弹性系数。

【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃，流量为60m 3/h 的水流入加热器，如果水的体积膨胀系数βt =0.00055K -1，问加热到80℃后从加热器中流出时的体积流量变为多少？【解】根据膨胀系数1t dVV dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。

罐装时液面上压强为98000Pa 。

封闭后由于温度变化升高了20℃，此时汽油的蒸汽压力为17640Pa 。

若汽油的膨胀系数为0.0006K -1，弹性系数为13.72×106Pa ，（1）试计算由于压力温度变化所增加的体积，（2）问灌装时汽油的体积最多不应超过桶体积的百分之多少？【解】（1）由1β=-=P pdV Vdp E可得，由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积，可由1β=t t dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT（2）因为∆∆tp VV ，相比之下可以忽略由压力变化引起的体积改变，则由 200L β+=tV V dT得1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板，其水平运动速度为u =1m/s ，δ=10mm ，油品的粘度μ=0.9807Pa ·s ，求作用在平板单位面积上的阻力。

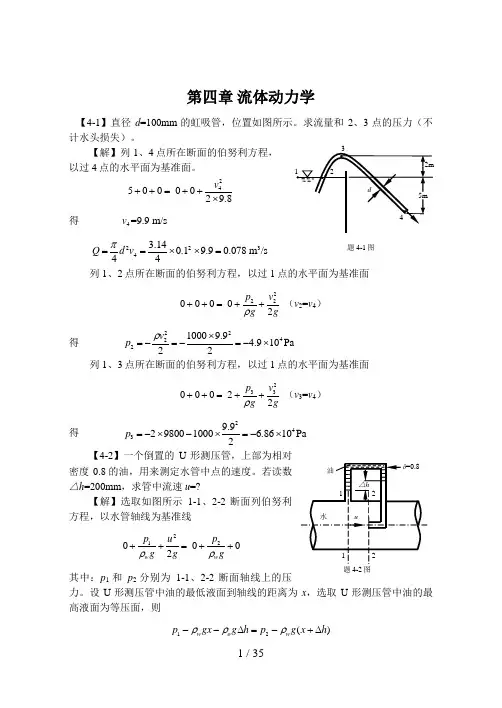
第四章 流体动力学【4-1】直径d =100mm 的虹吸管，位置如图所示。

求流量和2、3点的压力（不计水头损失）。

【解】列1、4点所在断面的伯努利方程，以过4点的水平面为基准面。

24500 0029.8v ++=++⨯得 4 =9.9 m/s v 2234 3.140.19.90.078 m /s 44π==⨯⨯=Q d v列1、2点所在断面的伯努利方程，以过1点的水平面为基准面222000 02p v g gρ++=++ （v 2=v 4）得 2242210009.9 4.910Pa 22ρ⨯=-=-=-⨯v p列1、3点所在断面的伯努利方程，以过1点的水平面为基准面233000 22p v g gρ++=++ （v 3=v 4）得 2439.9298001000 6.8610Pa 2=-⨯-⨯=-⨯p【4-2】一个倒置的U 形测压管，上部为相对密度0.8的油，用来测定水管中点的速度。

若读数△h =200mm ，求管中流速u =?【解】选取如图所示1-1、2-2断面列伯努利方程，以水管轴线为基准线212 0 002w w p p u g g gρρ++=++其中：p 1和p 2分别为1-1、2-2断面轴线上的压力。

设U 形测压管中油的最低液面到轴线的距离为x ，选取U 形测压管中油的最高液面为等压面，则12()w o w p gx g h p g x h ρρρ--∆=-+∆题 4-1图21()w o p p g h ρρ-=-∆则0.885m/s u ==【4-3】图示为一文丘里管和压力计，试推导体积流量和压力计读数之间的关系式。

当z 1=z 2时，ρ=1000kg/m 3，ρH =13.6×103kg/m 3，d 1=500mm ，d 2=50mm ，H =0.4m ，流量系数α=0.9时，求Q =？ 【解】列1-1、2-2断面的伯努利方程、以过1-1断面中心点的水平线为基准线。

闻建龙主编的《工程流体力学》习题参考答案第一章 绪论1-1 物质是按什么原则分为固体和液体两大类的？解：从物质受力和运动的特性将物质分成两大类：不能抵抗切向力，在切向力作用下可以无限的变形（流动），这类物质称为流体。

如空气、水等。

而在同等条件下，固体则产生有限的变形。

因此，可以说：流体不管是液体还是气体，在无论多么小的剪应力（切向）作用下都能发生连续不断的变形。

与此相反，固体的变形与作用的应力成比例，经一段时间变形后将达到平衡，而不会无限增加。

1-2 何谓连续介质假设？引入连续介质模型的目的是什么？在解决流动问题时，应用连续介质模型的条件是什么？解：1753年，欧拉首次采用连续介质作为流体宏观流动模型，即不考虑流体分子的存在，把真实的流体看成是由无限多流体质点组成的稠密而无间隙的连续介质，甚至在流体与固体边壁距离接近零的极限情况也认为如此，这个假设叫流体连续介质假设或稠密性假设。

流体连续性假设是流体力学中第一个根本性假设，将真实流体看成为连续介质，意味着流体的一切宏观物理量，如密度、压力、速度等，都可看成时间和空间位置的连续函数，使我们有可能用数学分析来讨论和解决流体力学问题。

在一些特定情况下，连续介质假设是不成立的，例如：航天器在高空稀薄气体中飞行，超声速气流中激波前后，血液在微血管（1μm ）内的流动。

1-3 底面积为25.1m 的薄板在液面上水平移动（图1-3），其移动速度为s m 16，液层厚度为mm 4，当液体分别为C 020的水和C 020时密度为3856m kg 的原油时，移动平板所需的力各为多大？题1-3图解：20℃ 水：s Pa ⋅⨯=-3101μ20℃，3/856m kg =ρ， 原油：s Pa ⋅⨯='-3102.7μ水：233/410416101m N u=⨯⨯=⋅=--δμτ 油： 233/8.2810416102.7m N u =⨯⨯=⋅'=--δμτ 1-4 在相距mm 40=δ的两平行平板间充满动力粘度s Pa ⋅=7.0μ液体（图1-4），液体中有一边长为mm a60=的正方形薄板以s m u 15=的速度水平移动，由于粘性带动液体运动，假设沿垂直方向速度大小的分布规律是直线。