2020—2021学年湘教版数学七年级下册5.1.1《轴对称图形》同步练习

5.1轴对称图形一、选择题(本大题共8小题)1.下面有4个汽车标致图案，其中不是轴对称图形的是（）A． B． C． D．2.点M（1，2）关于x轴对称的点的坐标为（）A．（﹣1，﹣2）B．（﹣1，2）C．（1，﹣2）D．（2，﹣1）3.已知以下四个图形：①角；②线段；③直角三角形；④正方形．在这四个图形中是轴对称图形的共有（）A．1个B．2个C．3个D．4个4.假设等腰三角形的周长为26cm，一边为11cm，那么腰长为（）A．11cm B．7.5cm C．11cm或7.5cm D．以上都不对5.在△ABC中，∠ACB=90°，∠B=30°，CD⊥AB于D，假设AC=6，那么BD等于（）A．6 B．3 C．9 D．126.如图，∠3=30°，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必需保证∠1的度数为（）A．30° B．45° C．60° D．75°7.等腰三角形ABC在直角坐标系中，底边的两头点坐标是（﹣2，0），（6，0），那么其极点的坐标，能确信的是（）A．横坐标B．纵坐标C．横坐标及纵坐标D．横坐标或纵坐标8.如图，点P是∠AOB外的一点，点M，N别离是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN 上，点P关于OB的对称点R落在MN的延长线上．假设PM=2.5cm，PN=3cm，MN=4cm，那么线段QR的长为（）A．4.5cm B．5.5cm C．6.5cm D．7cm二、填空题(本大题共6小题)9.假设点P的坐标为（3，2），那么点P关于y轴的对称点是．10.假设小红站在镜子前面看到她的运动衣上的号码是508，那么她的运动衣上的实际号码是．11.如图，是4×4正方形网格，其中已有3个小正方形涂成了黑色，此刻从剩余的13个白色小正方形当选出一个涂成黑色，使涂成黑色的四个小正方形所组成的图形是轴对称图形，那么如此的白色小正方形有个．12.在△ABC中，点D在BC边上，∠ADB=45°，BD=2，把△ABD沿AD翻折180°，点B落在点B′处，那么BB′的长等于．13.如图，有一个英语单词，四个字母都关于直线l对称，请在试卷上补全字母，在答题卡上写出那个单词所指的物品．14.如下图，点P为∠AOB内一点，别离作出P点关于OA、OB的对称点P1，P2，连接P1P2交OA于M，交OB于N，P1P2=15，那么△PMN的周长为．三、计算题(本大题共4小题)15.如图，已知三角形ABC和直线l，作出三角形ABC关于直线l的对称图形．16.如图，△ABC和△A′B′C′关于直线m对称．（1）结合图形指出对称点；（2）连接AA′，直线m与线段AA′有什么关系？17.如图，在公路EF的一旁有A，B两个农场，现需在EF上找一点M向A，B两农场各修一条公路，请问点M选在何处，可使路程和AM+BM最短？在图中标出该点．18.花边中的图案以正方形为基础，由圆弧或圆组成，仿照例图①，请你为班级黑板报设计一条花边，要求：（1）只需画出组成花边的一个图案，不写画法，不需配文字；（2）以所给的正方形为基础，用圆弧或圆画出；（3）图案应有美感；（4）与例图不同．参考答案：一、选择题(本大题共8小题)1. D分析：依照轴对称图形的概念结合4个汽车标志图案的形状求解．解：由轴对称图形的概念可知第1个，第2个，第3个都是轴对称图形．第4个不是轴对称图形，是中心对称图形．应选D．2. C分析：依照关于x轴对称的点，横坐标相同，纵坐标互为相反数，可得答案．解：点M（1，2）关于x轴对称的点的坐标为（1，﹣2），应选：C．3. C分析：依照轴对称图形的概念求解．解：①是轴对称图形；②是轴对称图形；③不是轴对称图形；④是轴对称图形．应选C．4.C分析：分边11cm是腰长与底边两种情形讨论求解．解：①11cm是腰长时，腰长为11cm，②11cm是底边时，腰长=（26﹣11）=7.5cm，因此，腰长是11cm或7.5cm．应选C．5. C分析：求出∠ACD=30°，再依照直角三角形30°角所对的直角边等于斜边的一半求出AD、AB，然后依照BD=AB ﹣AD计算即可得解．解：∵∠ACB=90°，CD⊥AB，∴∠ACD=∠B=30°，∵AC=6，∴AD=AC=×6=3，AB=2AC=2×6=12，∴BD=AB﹣AD=12﹣3=9．应选C．6.C分析：要使白球反弹后能将黑球直接撞入袋中，那么∠2=60°，依照∠一、∠2对称，那么能求出∠1的度数．解：要使白球反弹后能将黑球直接撞入袋中，∠2+∠3=90°，∵∠3=30°，∴∠2=60°，∴∠1=60°．应选：C．7.A分析：因为关于等腰三角形来讲存在“三线合一”，因此定点的横坐标正益处于底边的两头点的正中间，因此能够确信其横坐标，而纵坐标能够有很多个．解：因为底边两头点的坐标明白，而等腰三角形的横坐标正好在两头点中间，故能够求出横坐标，但由于腰不明白，因此纵坐标无法确信．应选A．8. A分析：利用轴对称图形的性质得出PM=MQ，PN=NR，进而利用MN=4cm，得出NQ的长，即可得出QR的长．解：∵点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上，∴PM=MQ，PN=NR，∵PM=2.5cm，PN=3cm，MN=4cm，∴RN=3cm，MQ=2.5cm，即NQ=MN﹣MQ=4﹣2.5=1.5（cm），那么线段QR的长为：RN+NQ=3+1.5=4.5（cm）．应选：A．二、填空题(本大题共6小题)9.分析：依照关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变可得答案．解：点P的坐标为（3，2），那么点P关于y轴的对称点是（﹣3，2），故答案为：（﹣3，2）．10.分析：利用镜面对称的性质求解．镜面对称的性质：在平面镜中的像与现实中的事物恰好顺序倒置，且关于镜面对称．解：依照镜面对称的性质，分析可得“508”与“802”成轴对称，故她的运动衣上的实际号码是802．故答案为：802．11.分析：依照轴对称图形的概念求解即可．解：如下图，有4个位置使之成为轴对称图形．故答案为：4．12.分析：作出图形，依照翻折变换的性质可得BD=B′D，∠ADB=∠ADB′，然后求出△BDB′是等腰直角三角形，再依照等腰直角三角形的斜边等于直角边的倍解答．解：如图，∵△ABD沿AD翻折180°点B落在点B′处，∴BD=B′D=2，∠ADB=∠ADB′=45°，∴∠BDB′=45°+45°=90°，∴△BDB′是等腰直角三角形，∴BB′=BD=2．故答案为：2．13.分析：依照轴对称图形的性质，组成图形，即可解答．解：如图，那个单词所指的物品是书．故答案为：书．14.分析：P点关于OA的对称是点P1，P点关于OB的对称点P2，故有PM=P1M，PN=P2N．解：∵P点关于OA的对称是点P1，P点关于OB的对称点P2，∴PM=P1M，PN=P2N．∴△PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2=15．故答案为：15三、计算题(本大题共4小题)15.分析：作出A关于l的对称点A′，B关于l的对称点B′，C关于l的对称点C′，连接A′、B′、C′即可．解：16.分析：（1）△ABC和△A′B′C′关于直线m对称，那么对应极点为对称轴；（2）对称轴是两个对称点的连线的垂直平分线．解：（1）∵△ABC和△A′B′C′关于直线m对称，∴C的对称点为C′，B的对称点为B′，A的对称点为A′．（2）连接AA′，直线m⊥AA′，如图：17.分析：作出A点关于EF的对称点A′，进而连接A′B交EF于点M，进而得出答案．解：如下图：M点即为所求，现在AM+BM最短．18.分析：依照题意画出轴对称图形即可．解：如下图：．。

新课标2017-2018学年湘教版七年级数学下册轴对称与旋转(45分钟100分)一、选择题(每小题4分,共28分)1.下列各图中不是轴对称图形的是( )2.(2013·山西中考)如图,正方形地砖的图案是轴对称图形,该图形的对称轴有( )A.1条B.2条C.4条D.8条3.一个图形无论经过平移还是旋转,有以下说法( )①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.A.①②③B.①②④C.①③④D.②③④4.(2013·株洲中考)下列四种图形都是轴对称图形,其中对称轴条数最多的图形是( )A.等边三角形B.长方形C.菱形D.正方形5.(2013·重庆中考)如图,长方形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE 的长为( )A.6cmB.4cmC.2 cmD.1cm6.如图是某公司商品标志图案,则下列说法:①图案是按照轴对称设计的;②图案是按照旋转设计的;③图案的外层“S”是按旋转设计的;④图案的内层“A”是按轴对称设计的.其中正确的是( )A.1个B.2个C.3个D.4个7.如图所示,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是( )A.150°B.300°C.210°D.330°二、填空题(每小题5分,共25分)8.如图,AB左边是计算器上的数字“5”,若以直线AB为对称轴,那么它的轴对称图形是数字.9.图1绕点O顺时针旋转90°到达图的位置;图1绕点O顺时针旋转°到达图3的位置;图3绕点O逆时针旋转90°到达图的位置;图3绕点O顺时针旋转180°到达图的位置.10.(2013·广州中考)如图,Rt△ABC的斜边AB=16,Rt△ABC绕点O顺时针旋转后得到Rt△A'B'C',则Rt△A'B'C'的斜边A'B'上的中线C'D的长度为.11.如图,线段AB,CD关于直线EF对称,则AC⊥,BO'= .12.图中有五个是相同图形的不同摆法,有一个是与众不同的,它是图.三、解答题(共47分)13.(11分)在图中,请你自由选择8个小方块,设计一幅具有对称美的图案,并画出它的一条对称轴.14.(12分)(2013·茂名中考)在网格纸上按以下要求作图,不用写作法:(1)作出“小旗子”向右平移6格后的图案.(2)作出“小旗子”绕O点按逆时针方向旋转90°后的图案.15.(11分)作图题:在方格纸中,将△ABC向右平移3个单位得到△A1B1C1,画出△A1B1C1.16.(13分)我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做旋转,这个定点称为旋转中心.(1)如图①,△ABC与△DEF能完全重合,△DEF能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心,若不能,试简要说明理由.(2)如图②,△ABC与△MNK能完全重合,△MNK能否由△ABC通过一次旋转得到?若能,请用直尺和圆规画出旋转中心,若不能,试简要说明理由.(保留必要的作图痕迹)答案解析1.【解析】选A.如图,将A中图形沿任意直线折叠,直线两旁部分都不能完全重合,所以该图形不是轴对称图形;将B中图形折叠,直线两旁部分能够完全重合,可判断该图形是轴对称图形;将C中图形折叠,直线两旁部分能够完全重合,可判断该图形是轴对称图形;将D中图形折叠,直线两旁部分能够完全重合,可判断该图形是轴对称图形,综上,不是轴对称图形的应是A中图形.2. 【解析】选C.该图案的对称轴为过两组对边中点的直线和对角线所在的直线,共4条.3.【解析】选D.平移后对应线段平行(或在一条直线上),对应线段相等,对应角相等,图形的形状和大小没有发生变化;旋转后对应线段一般不平行,对应线段相等,对应角相等,图形的形状和大小没有发生变化.4.【解析】选D.等边三角形有3条对称轴;长方形、菱形有2条对称轴;正方形有4条对称轴.5.【解析】选C.由折叠可知,∠BAE=∠B1AE,所以∠BAE=∠B1AE=45°,又因为∠B=90°,所以∠AEB=45°,所以BE=AB=6cm,所以CE=BC-BE=8-6=2(cm).6.【解析】选B.该图形的设计既运用了旋转,又运用了轴对称,③④是正确的.7. 【解析】选B.因为CF是六边形ABCDEF的对称轴,所以∠AFE=2∠AFC,∠BCD=2∠BCF.所以∠AFE+∠BCD=2(∠AFC+∠BCF)=300°.8.【解析】根据轴对称图形的定义可知,数字“5”的轴对称图形是数字2. 答案:29.【解析】图1绕点O顺时针旋转90°到达图4的位置;图1绕点O顺时针旋转180°到达图3的位置;图3绕点O逆时针旋转90°到达图4的位置;图3绕点O顺时针旋转180°到达图1的位置.答案:4 180 4 110.【解析】因为△A'B'C'是由△ABC绕点O旋转而来,所以△A'B'C'也为直角三角形,A'B'=AB=16,所以C'D=A'B'=×16=8.答案:811.【解析】根据对称的性质,可知点A和点C为对应点,所以AC⊥EF;点B 和点D为对应点,所以BO'=DO'.答案:EF DO'12.【解析】(1)逆时针旋转90°得(2),(2)逆时针旋转90°得(4),(4)逆时针旋转90°得(5).答案:(3)13.【解析】画图如下(答案不唯一):14.【解析】(1),(2)如图所示.15.【解析】分别找出△ABC向右平移3个单位后对应的关键点,然后顺次连接即可.如图:所画△A1B1C1即为所求.16.【解析】(1)能.如图所示.点O1就是所求作的旋转中心.(2)能.如图所示.点O2就是所求作的旋转中心.。

第5章轴对称同步练习题姓名：__________ 班级：__________考号：__________一、单选题（共10题；共30分）1.下列图形中，是轴对称图形的是（）A. B. C. D.2.过新年时，小华家的窗户上贴着如图所示的美丽的剪纸图案，它的对称轴有( )A. 0条B. 4条C. 8条D. 16条3.在下列图形中，只利用没有刻度的直尺将无法作出其对称轴的是（）A. 矩形B. 菱形C. 等腰梯形D. 正六边形4.等边三角形的对称轴有（）A. 1 条B. 2条C. 3条D. 4条5.如图所示，将矩形纸片ABCD（图①）按如下步骤操作：（1）以过点A的直线为折痕折叠纸片，使点B 恰好落在AD边上，折痕与BC边交于点E（如图②）；（2）以过点E的直线为折痕折叠纸片，使点A落在BC边上，折痕EF交AD边于点F（如图③）；那么∠AEF的度数为（）A. 60°B. 67.5°C. 72°D. 75°6.如图，将一张矩形纸片沿对角线剪开得到两个直角三角形纸片，将这两个直角三角形纸片通过图形变换构成以下四个图形，这四个图形中是中心对称图形的是（）A. B. C. D.7.如图，ABCD是矩形纸片，翻折∠B，∠D，使AD，BC边与对角线AC重叠，且顶点B，D恰好落在同一点O上，折痕分别是CE，AF，则等于（）A. B. 2 C. 1.5 D.8.小明将一正方形纸片画分成16个全等的小正方形，且如图所示为他将其中四个小正方形涂成灰色的情形．若小明想再将一小正方形涂成灰色，使此纸片上的灰色区域成为线对称图形，则此小正方形的位置为何？（）A. 第一列第四行B. 第二列第一行C. 第三列第三行D. 第四列第一行9.如图，对角线AC将正方形ABCD分成两个等腰三角形，点E，F将对角线AC三等分，且AC=15，点P在正方形的边上，则满足PE+PF=5 的点P的个数是( )A. 0B. 4C. 8D. 1610.如图，∠MON内有一点P，P点关于OM的轴对称点是G，P点关于ON的轴对称点是H，GH分别交OM、ON于A、B点，若∠MON=35°，则∠GOH=（）A. 60°B. 70°C. 80°D. 90°二、填空题（共8题；共24分）11.点P（a，2）和点Q（4，b）关于x轴对称，则a+b=________12.下列各组图：① ；② ；③ ；④ 其中，左右两个图形能成轴对称的是________（填序号）．13.如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=4，M是AB边上一动点，N是AC边上的一动点，则MN+MC的最小值为________．14.如图，将边长为16cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长是________cm．15.如图，已知矩形ABCD沿对角线BD折叠，记点C的对应点为C′，若∠ADC′＝20°，则∠BDC的度数为________。

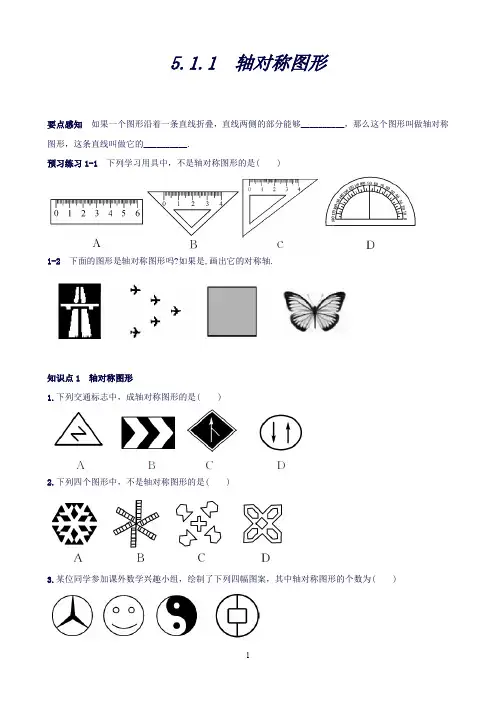
5.1.1 轴对称图形要点感知如果一个图形沿着一条直线折叠，直线两侧的部分能够__________，那么这个图形叫做轴对称图形，这条直线叫做它的__________.预习练习1-1 下列学习用具中，不是轴对称图形的是( )1-2下面的图形是轴对称图形吗?如果是,画出它的对称轴.知识点1 轴对称图形1.下列交通标志中，成轴对称图形的是( )2.下列四个图形中，不是轴对称图形的是( )3.某位同学参加课外数学兴趣小组，绘制了下列四幅图案，其中轴对称图形的个数为( )A．1个 B．2个 C．3个 D．4个4.下列说法中错误的是( )A.教室里的黑板是轴对称图形B.扑克牌中的梅花图案是轴对称图形C.五星红旗的五角星图案不是轴对称图形D.英文字母印刷体大写“W”是轴对称图形知识点2 对称轴5.如图，正方形地砖的图案是轴对称图形，该图形的对称轴有( )A.1条B.2条C.4条D.8条6.下列“数字”图形中，有且仅有一条对称轴的是( )7.下列关于轴对称图形的对称轴的说法中正确的是( )A.轴对称图形的对称轴只能是一条B.轴对称图形的对称轴一定是线段C.轴对称图形的对称轴可以有多条D.轴对称图形的对称轴一定是射线8.下图中的五角星有几条对称轴？请作出这些对称轴.9.下列图形中，不是轴对称图形的是( )10.永州的文化底蕴深厚，永州人民的生活健康向上，如瑶族长鼓舞，东安武术，宁远举重等，下面的四幅简笔画是从永州的文化活动中抽象出来的，其中是轴对称图形的是( )11.下列四句话中的文字有三句具有对称规律，其中没有这种规律的一句是( )A.上海自来水来自海上B.有志者事竟成C.清水池里池水清D.蜜蜂酿蜂蜜12.正方形的对称轴的条数为( )A．1 B．2 C．3 D．413.下列四个图形：其中是轴对称图形，且对称轴的条数为2的图形的个数是( )A．1 B．2 C．3 D．414.如图，正三角形网格中，已有两个小正三角形被涂黑，再将图中其余小正三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形的方法有__________种.15.如图，从我们今天这节课学习的知识来考虑，哪一个与其他三个不同？请指出这个图形，并简述你的理由.16.分别找出具有一条对称轴、两条对称轴、三条对称轴、四条对称轴的几何图形，并画出来(包括对称轴).17.我们把形如abba的四位数称为“对称数”，如1 991、2 002等，试问在1 000～2 000之间有几个“对称数”？18.请在下面这一组图形符号中找出它们所蕴含的内在规律，然后在横线上的空白处填上恰当的图案.19.一天，小明发现如果将4棵树栽于正方形的四个顶点上，如图(1)所示，恰好构成一个对称图形.你还能找到其他两种栽树的方法，也使其组成一个轴对称图形吗？请在图（2）、（3）上表示出来.如果是栽5棵树，又如何呢？6棵、7棵呢？请分别在图（4）、（5）、（6）上表示出来.参考答案要点感知互相重合对称轴预习练习1-1 C1-2略.1.B2.B3.C4.C5.C6.A7.C8.有5条对称轴.图略.9.C 10.C 11.B 12.D 13.C 14.315.图形②.理由是：图形②不是轴对称图形.16.答案不唯一，图略.17.有1 001，1 111，1 221，1 331，…，1 991，共10个.18.每个图形是由各数字和它的轴对称数字组成的轴对称图形.图略.19.答案不唯一，如图所示.。

《轴对称图形》同步练习一．选择题（共5小题，每题6分）1.下列图形中，是轴对称图形的是（）A．B．C．D．2.下列图案是轴对称图形的是（）A. B. C. D.3．如图，∠3=30°，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证∠1的度数为（）A．30°B．45°C．60°D．75°4．下列四个图案中，具有一个共有性质．则下面四个数字中，满足上述性质的一个是（）A．6 B．7 C．8 D．95．把26个英文字母按规律分成5组，现在还有5个字母D、M、Q、X、Z，请你按原规律补上，其顺序依次为（）（1）F，R，P，J，L，G，（）（2）H，I，O，（）（3）N，S，（）（4）B，C，K，E，（）（5）V，A，T，Y，W，U，（）A．Q，X，Z，M，D B．D，M，Q，Z，XC．Z，X，M，D，Q D．Q，X，Z，D，M二．填空题（共5小题，每题6分）6．观察下图中各组图形，其中成轴对称的为（只写序号1，2等）．7．在直线、角、线段、等边三角形四个图形中，对称轴最多的是，它有条对称轴；最少的是，它有条对称轴．8．26个英文字母中，有很多都具有轴对称结构，请你写出其中具有轴对称结构的字母（至少3个）．9．数的计算中有一些有趣的对称形式，如：12×231=132×21；仿照上面的形式填空，并判断等式是否成立：（1）12×462=×（），（2）18×891=×（）．10．如图，在一个规格为6×12（即6×12个小正方形）的球台上，有两个小球A，B．若击打小球A，经过球台边的反弹后，恰好击中小球B，那么小球A击出时，应瞄准球台边上的点．（P1至P4点）三．解答题（共2小题，每题20分）11．指出下列图形中的轴对称图形，是轴对称图形的指出对称轴．12．燕子风筝的骨架如图所示，它是以直线L为对称轴的轴对称图形．已知∠1=∠4=45°，求∠2和∠5的度数．试题解析一．选择题1．A【分析】根据轴对称图形的概念对各选项分析判断即可得解．【解答】解：A、不是轴对称图形，故本选项错误；B、不是轴对称图形，故本选项错误；C、不是轴对称图形，故本选项错误；D、是轴对称图形，故本选项正确．故选A．【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．2．C【解答】解：A．此图形不是轴对称图形，不合题意；B．此图形不是轴对称图形，不合题意；C．此图形是轴对称图形，符合题意；D．此图形不是轴对称图形，不合题意．故选C．【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．3．C【分析】要使白球反弹后能将黑球直接撞入袋中，则∠2=60°，根据∠1、∠2对称，则能求出∠1的度数．【解答】解：要使白球反弹后能将黑球直接撞入袋中，∠2+∠3=90°，∵∠3=30°，∴∠2=60°，∴∠1=60°．故选：C．【点评】本题是考查图形的对称、旋转、分割以及分类的数学思想．4．C【分析】题目中的四个图形都是轴对称图形，据此即可作出判断．【解答】四个图形都是轴对称图形，在6，7，8，9中是轴对称图形的只有8．故选：C．【点评】本题主要考查了对称图形的性质，正确理解题目中各个图形之间的关系是解题关键．5．D【分析】分析各组的对称性与字母D、M、Q、X、Z，的对称性，即可作出判断．【解答】解：（1）不是对称图形，5个子母中不是对称图形的只有：Q，Z；（2）有两条对称轴，并且两对称轴互相垂直，则规律相同的是：X；（3）不是轴对称图形，相同规律的还有Z；（4）是轴对称图形，对称轴是一条水平的直线，满足规律的是：D；（5）是轴对称图形，对称轴是竖直的直线，满足规律的是：M．故各个空，顺序依次为：Q，X，Z，D，M．故选：D．【点评】本题主要考查了图形的对称性，正确找到各组数规律是解决本题的关键．二．填空题6．①②④【分析】认真观察所给的图形，按照直线两旁的部分是否能够互相重合来判断是否符合要求．【解答】解：3中的伞把不对称，故填①②④故填①②④【点评】本题考查了生活中的轴对称问题；轴对称的关键是寻找对称轴，观察直线两边图象折叠后可重合是正确解答本题的关键．7．直线、无数、角、1．【分析】分别确定直线、角、线段、等边三角形四个图形中对称轴的条数即可作出判断．【解答】解：直线：任何与直线垂直的直线都是直线的对称轴，有无数条对称轴；角的对称轴是角的角平分线所在的直线，只有一条对称轴；线段的对称轴是线段的中垂线和本身，有两条对称轴；等边三角形的对称轴是各边的中垂线，有3条对称轴．故：对称轴最多的是直线，它有无数条对称轴；最少的是，它有1条对称轴．故答案是：直线、无数、角、1．【点评】本题主要考查了轴对称图形的定义，对定义的理解是解题的关键．8．答案不唯一，如：A，B，C【分析】轴对称图形就是把图形的一部分沿着一条直线对折，能够与另一部分重合，这样的图形就是轴对称图形，据此即可作出判断．答案不唯一．【解答】解：答案不唯一，如：A，B，C．故答案是：A、B，C．【点评】本题主要考查了轴对称图形的定义，对定义的理解是解题的关键．【点评】本题主要考查了数的计算，正确理解对称形式是解决本题的关键．10．【分析】认真读题，作出点A关于P1P2所在直线的对称点A′，连接A′B与P1P2的交点即为应瞄准的点．【解答】解：如图，应瞄准球台边上的点P2．【点评】本题考查了生活中的轴对称现象问题；解决本题的关键是理解击球问题属于求最短路线问题．三．解答题11．【分析】根据轴对称图形的定义，即可作出判断．【解答】解：根据轴对称图形的定义可知：第一个、第二个、第四个图形都是轴对称图形．对称轴如图：【点评】本题主要考查了轴对称图形的定义，正确理解轴对称图形的定义是解决本题的关键．12．【分析】利用对顶角的定义以及轴对称图形的性质求出即可．【解答】解：∵风筝的骨架如图所示，它是以直线L为对称轴的轴对称图形，∠1=∠4=45°，∴∠1=∠2=45°（对顶角相等），∠5=∠4=45°．【点评】此题主要考查了生活中的轴对称现象，利用轴对称图形的性质求出是解题关键．。

湘教版七年级（下）中考题单元试卷：第5章轴对称图形（01）一、选择题（共22小题）1. 下列各组线段的长为边，能组成三角形的是（）A.2cm，3cm，4cmB.2cm，3cm，5cmC.2cm，5cm，10cmD.8cm，4cm，4cm2. 下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是()A.1，2，6B.2，2，4C.1，2，3D.2，3，43. 下列线段能构成三角形的是()A.2，2，4B.3，4，5C.1，2，3D.2，3，64. 一个三角形的三条边长分别为1、2、x，则x的取值范围是（）A.1≤x≤3B.1<x≤3C.1≤x<3D.1<x<35. 如果一个三角形的两边长分别为2和5，则第三边长可能是( )A.2B.3C.5D.86. 如果一个三角形的两边长分别为2和4，则第三边长可能是（）A.2B.4C.6D.87. 下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（）A.1，2，1B.1，2，2C.1，2，3D.1，2，48. 下列四个图形中，线段BE是△ABC的高的是（）A. B.C. D.9. 过△ABC的顶点A，作BC边上的高，以下作法正确的是( )A. B.C. D.10. 下列图形中具有稳定性的是（）A.正三角形B.正方形C.正五边形D.正六边形11. 下列图形具有稳定性的是（）A.正方形B.矩形C.平行四边形D.直角三角形12. 三角形三条中线的交点叫做三角形的（）A.内心B.外心C.中心D.重心13. 已知△ABC中，AB=6，BC=4，那么边AC的长可能是下列哪个值（）A.11B.5C.2D.114. 下列长度的三条线段能组成三角形的是（）A.1，2，3B.1，√2，3C.3，4，8D.4，5，615. 下列各组数可能是一个三角形的边长的是()A.1，2，4B.4，5，9C.4，6，8D.5，5，1116. 已知三角形两边长分别为3和9，则此三角形的第三边的长可能是（）A.4B.5C.11D.1517. 已知三角形两边长分别为3和8，则该三角形第三边的长可能是（）A.5B.10C.11D.1218. 长为9，6，5，4的四根木条，选其中三根组成三角形，选法有（）A.1种B.2种C.3种D.4种19. 已知三角形两边的长分别是4和10，则此三角形第三边的长可能是( )A.5B.6C.12D.1620. 下列长度的三条线段能组成三角形的是（）A.5，6，10B.5，6，11C.3，4，8D.4a，4a，8a(a>0)21. 如图，D为△ABC内部一点，E、F两点分别在AB、BC上，且四边形DEBF为矩形，直线CD交AB于G点．若CF=6，BF=9，AG=8，则△ADC的面积为何？（）A.16B.24C.36D.5422. 如图，有一△ABC，今以B为圆心，AB长为半径画弧，交BC于D点，以C为圆心，AC长为半径画弧，交BC于E点．若∠B=40∘，∠C=36∘，则关于AD、AE、BE、CD的大小关系，下列何者正确？（）A.AD=AEB.AD<AEC.BE=CDD.BE<CD 二、填空题（共8小题）如图，△ABC的三边的中线AD，BE，CF的公共点为G，且AG：GD=2：1.若S△ABC=12，则图中阴影部分的面积是________.各边长度都是整数、最大边长为8的三角形共有________个．若a、b、c为三角形的三边，且a、b满足√a2−9+(b−2)2＝0，则第三边c的取值范围是________．若一个三角形三边长分别为2，3，x，则x的值可以为________（只需填一个整数）如图，在△ABC中，BD，CE分别是边AC，AB上的中线，BD与CE相交于点O，则OBOD=________．一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为________．如图，D、E分别是△ABC边AB、BC上的点，AD=2BD，BE=CE，设△ADC的面积为S1，△ACE的面积为S2，若S△ABC=6，则S1−S2的值为________．如图，A，B，C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积________．参考答案与试题解析湘教版七年级（下）中考题单元试卷：第5章轴对称图形（01）一、选择题（共22小题）1.【答案】A【考点】三角形三边关系【解析】根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边．即可求解．【解答】解：根据三角形任意两边的和大于第三边，可知A、2+3>4，能组成三角形，故正确；B、2+3=5，不能组成三角形，故错误；C、2+5<10，不能够组成三角形，故错误；D、4+4=8，不能组成三角形，故错误.故选A．【点评】本题考查了能够组成三角形三边的条件，其实用两条较短的线段相加，如果大于最长的那条就能够组成三角形．2.【答案】D【考点】三角形三边关系【解析】根据三角形的三边关系：三角形两边之和大于第三边，计算两个较小的边的和，看看是否大于第三边即可．【解答】解：A，1+2<6，不能组成三角形，故此选项错误；B，2+2=4，不能组成三角形，故此选项错误；C，1+2=3，不能组成三角形，故此选项错误；D，2+3>4，能组成三角形，故此选项正确；故选D．【点评】此题主要考查了三角形的三边关系，关键是掌握三角形的三边关系定理．3.【答案】B【考点】三角形三边关系【解析】根据三角形的任意两边之和大于第三边，对各选项的数据进行判断即可．【解答】解：A，2+2=4，不能构成三角形，故A选项错误；B，3+4>5，能构成三角形，故B选项正确；C，1+2=3，不能构成三角形，故C选项错误；D，2+3<6，不能构成三角形，故D选项错误．故选B．【点评】本题考查了三角形的三边关系，熟记三角形的任意两边之和大于第三边，两边之差小于第三边是解题的关键．4.【答案】D【考点】三角形三边关系【解析】已知两边，则第三边的长度应是大于两边的差而小于两边的和，这样就可求出第三边长的范围．【解答】解：根据题意得：2−1<x<2+1，即1<x<3．故选D．【点评】考查了三角形三边关系，本题需要理解的是如何根据已知的两条边求第三边的范围．5.【答案】C【考点】三角形三边关系【解析】根据在三角形中任意两边之和>第三边，任意两边之差<第三边；可求第三边长的范围，再选出答案．【解答】解：设第三边长为x.由三角形三边关系定理，得5−2<x<5+2，即3<x<7，所以第三边长可能是5.故选C.【点评】本题考查了三角形三边关系，此题实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．6.【答案】B【考点】三角形三边关系【解析】已知三角形的两边长分别为2和4，根据在三角形中任意两边之和>第三边，任意两边之差<第三边；即可求第三边长的范围．【解答】解：设第三边长为x，则由三角形三边关系定理得4−2<x<4+2，即2<x<6．因此，本题的第三边应满足2<x<6，把各项代入不等式符合的即为答案．2，6，8都不符合不等式2<x<6，只有4符合不等式．故选B．【点评】本题考查了三角形三边关系，此题实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．7.【答案】B【考点】三角形三边关系【解析】根据三角形的三边关系：三角形两边之和大于第三边，计算两个较小的边的和，看看是否大于第三边即可．【解答】A、1+1＝2，不能组成三角形，故A选项错误；B、1+2>2，能组成三角形，故B选项正确；C、1+2＝3，不能组成三角形，故C选项错误；D、1+2<4，不能组成三角形，故D选项错误；【点评】此题主要考查了三角形的三边关系，关键是掌握三角形的三边关系定理．8.【答案】D【考点】三角形的角平分线、中线和高三角形的高【解析】根据三角形高的画法知，过点B作AC边上的高，垂足为E，其中线段BE是△ABC的高，再结合图形进行判断．【解答】解：三角形的高是指从三角形的一个顶点向对边作垂线，连接顶点与垂足之间的线段，线段BE是△ABC的高的图是选项D．故选D．【点评】本题主要考查了三角形的高，三角形的高是指从三角形的一个顶点向对边作垂线，连接顶点与垂足之间的线段．熟记定义是解题的关键．9.【答案】A【考点】三角形的角平分线、中线和高三角形的高【解析】根据三角形高线的定义：过三角形的顶点向对边引垂线，顶点和垂足之间的线段叫做三角形的高线解答．【解答】解：由高线的定义，知A选项正确；选项B、C、D未过顶点A，故不正确.故选A.【点评】本题考查了三角形的角平分线、中线、高线，熟记高线的定义是解题的关键．10.【答案】A【考点】三角形的稳定性【解析】直接根据三角形具有稳定性进行解答即可．【解答】∵三角形具有稳定性，∴A正确，B、C、D错误．【点评】本题考查的是三角形的稳定性，熟知三角形三边的长度确定后，三角形的形状和大小就能唯一确定下来，故三角形具有稳定性是解答此题的关键．11.【答案】D【考点】多边形三角形的稳定性【解析】根据三角形具有稳定性，四边形具有不稳定性进行判断．【解答】解：直角三角形具有稳定性．故选D．【点评】此题考查了三角形的稳定性和四边形的不稳定性，正确掌握三角形的性质是解题关键．12.【答案】D【考点】三角形的重心【解析】根据三角形的重心概念作出回答，结合选项得出结果．【解答】解：三角形的重心是三角形三条中线的交点．故选D．【点评】考查了三角形的重心的概念．三角形的外心是三角形的三条垂直平分线的交点；三角形的内心是三角形的三条角平分线的交点．13.【答案】B【考点】三角形三边关系【解析】根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边列出不等式即可．【解答】解：根据三角形的三边关系，6−4<AC<6+4，即2<AC<10，符合条件的只有5，故选：B．【点评】本题考查的是三角形的三边关系，掌握三角形形成的条件：任意两边之和大于第三边，任意两边之差小于第三边是解题的关键．14.【答案】D【考点】三角形三边关系【解析】根据三角形的三边满足任意两边之和大于第三边来进行判断．【解答】解：A、1+2=3，不能组成三角形，故本选项错误；B、1+√2<3，不能组成三角形，故本选项错误；C、3+4<8，不能组成三角形，故本选项错误；D、4+5>6，能组成三角形，故本选项正确．故选D．【点评】本题考查了能够组成三角形三边的条件，简便方法是：用两条较短的线段相加，如果大于最长的那条线段就能够组成三角形．15.【答案】C【考点】三角形三边关系【解析】看哪个选项中两条较小的边的和大于最大的边即可．【解答】解：A，因为1+2<4，所以本组数不能构成三角形，故本选项错误；B，因为4+5=9，所以本组数不能构成三角形，故本选项错误；C，因为4+6>8，所以本组数可以构成三角形，故本选项正确；D，因为5+5<11，所以本组数不能构成三角形，故本选项错误.故选C.【点评】本题主要考查了三角形的三边关系定理：任意两边之和大于第三边，只要满足两短边的和大于最长的边，就可以构成三角形．16.【答案】C【考点】三角形三边关系【解析】已知三角形的两边长分别为3和9，根据在三角形中任意两边之和>第三边，任意两边之差<第三边；即可求第三边长的范围．【解答】解：设第三边长为x，则由三角形三边关系定理得9−3<x<9+3，即6<x<12．因此，本题的第三边应满足6<x<12，把各项代入不等式符合的即为答案．只有11符合不等式，故答案为11．故选C．【点评】此类求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．17.【答案】B【考点】三角形三边关系【解析】根据三角形的第三边大于两边之差，而小于两边之和求得第三边的取值范围，再进一步选择．【解答】解：根据三角形的三边关系，得第三边大于：8−3=5，而小于：3+8=11．则此三角形的第三边可能是：10．故选B．【点评】本题考查了三角形的三边关系，即三角形的第三边大于两边之差，而小于两边之和，此题基础题，比较简单．18.【答案】C【考点】三角形三边关系【解析】要把四条线段的所有组合列出来，再根据三角形的三边关系判断能组成三角形的组数．【解答】解：四根木条的所有组合：9，6，5和9，6，4和9，5，4和6，5，4；根据三角形的三边关系，得能组成三角形的有9，6，5和9，6，4和6，5，4．故选C．【点评】本题考查了三角形的三边关系，熟记三角形的任意两边之和大于第三边，两边之差小于第三边是解题的关键．19.【答案】C【考点】三角形三边关系【解析】设第三边的长为x，再由三角形的三边关系即可得出结论．【解答】解：设第三边的长为x，∵三角形两边的长分别是4和10，∴10−4<x<10+4，即6<x<14．故选C.【点评】本题考查的是三角形的三边关系，熟知三角形任意两边之和大于第三边，任意两边之差小于第三边是解答此题的关键．20.【答案】A【考点】三角形三边关系【解析】根据三角形的三边关系对各选项进行逐一分析即可．【解答】A、∵10−5<6<10+5，∴三条线段能构成三角形，故本选项正确；B、∵11−5＝6，∴三条线段不能构成三角形，故本选项错误；C、∵3+4＝7<8，∴三条线段不能构成三角形，故本选项错误；D、∵4a+4a＝8a，∴三条线段不能构成三角形，故本选项错误．【点评】本题考查的是三角形的三边关系，熟知三角形任意两边之和大于第三边，任意两边差小于第三边是解答此题的关键．21.【答案】B【考点】三角形的面积矩形的性质【解析】由于S△ADC=S△AGC−S△ADG，根据矩形的性质和三角形的面积公式计算即可求解．【解答】解：S△ADC=S△AGC−S△ADG=12×AG×BC−12×AG×BF=1×8×(6+9)−1×8×9=60−36=24．故选：B．【点评】考查了三角形的面积和矩形的性质，本题关键是活用三角形面积公式进行计算．22.【答案】D【考点】三角形三边关系【解析】由∠C<∠B利用大角对大边得到AB<AC，进一步得到BE+ED<ED+CD，从而得到BE<CD．【解答】解：∵∠C<∠B，∴AB<AC，∵AB=BD AC=EC∴BE+ED<ED+CD，∴BE<CD．故选：D．【点评】考查了三角形的三边关系，解题的关键是正确的理解题意，了解大边对大角．二、填空题（共8小题）【答案】4【考点】三角形的中线三角形的面积【解析】根据三角形的中线把三角形的面积分成相等的两部分，知△ABC的面积即为阴影部分的面积的3倍．【解答】解：∵△ABC的三条中线AD，BE，CF交于点G，∴S△CGE=S△AGE=12S△ACG=13S△ACF，S△BGF=S△BGD=13S△BCF，S△ACF=S△BCF=12S△ABC=12×12=6，∴S△CGE=13S△ACF=13×6=2，S△BGF=13S△BCF=13×6=2，∴S阴影=S△CGE +S△BGF=4．故阴影部分的面积为4．故答案为：4．【点评】根据三角形的中线把三角形的面积分成相等的两部分.该图中，S△BGF=S△BGD，S△CGD=S△CGE，S△AGF=S△AGE.【答案】20【考点】三角形三边关系【解析】利用三角形三边关系进而得出符合题意的答案即可．【解答】∵各边长度都是整数、最大边长为8，∴三边长可以为：1，8，8；2，7，8；2，8，8；3，6，8；3，7，8；3，8，8；4，5，8；4，6，8；4，7，8；4，8，8；5，5，8；5，6，8；5，7，8；5，8，8；6，6，8；6，7，8；6，8，8；7，7，8；7，8，8；8，8，8；故各边长度都是整数、最大边长为8的三角形共有20个．【点评】此题主要考查了三角形三边关系，正确分类讨论得出是解题关键．【答案】1<c<5【考点】三角形三边关系非负数的性质：偶次方非负数的性质：算术平方根【解析】根据非负数的性质列式求出a、b，再根据三角形的任意两边之和大于第三边，两边之差小于第三边求解即可．【解答】解：由题意得，a2−9＝0，b−2＝0，解得a＝3，b＝2，∵3−2＝1，3+2＝5，∴1<c<5．故答案为：1<c<5．【点评】本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0；三角形的三边关系．【答案】4【考点】三角形三边关系【解析】根据三角形的三边关系：三角形两边之和大于第三边，三角形的两边差小于第三边可得x的取值范围．【解答】解：根据三角形的三边关系可得：3−2<x<3+2，即：1<x<5，所以x可取整数4．故答案为：4．【点评】此题主要考查了三角形的三边关系，关键是掌握第三边的范围是：大于已知的两边的差，而小于两边的和．【答案】2【考点】三角形的重心相似三角形的性质与判定【解析】根据三角形的重心到顶点的距离等于到对边中点的距离的2倍列式进行计算即可求解．【解答】证明：∵△ABC的中线BD、CE相交于点O，∴点O是△ABC的重心，∴OBOD=2．故答案为：2．【点评】本题主要考查了三角形的重心的性质，熟记三角形的重心到顶点的距离等于到对边中点的距离的2倍是解题的关键．【答案】8【考点】三角形三边关系【解析】首先设第三边长为x，根据三角形的三边关系可得3−2<x<3+2，然后再确定x的值，进而可得周长．【解答】解：设第三边长为x，∵两边长分别是2和3，∴3−2<x<3+2，即：1<x<5，∵第三边长为奇数，∴x＝3，∴这个三角形的周长为2+3+3＝8.故答案为：8.【点评】此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边，三角形的两边差小于第三边．【答案】1【考点】三角形的面积【解析】根据等底等高的三角形的面积相等求出△AEC的面积，再根据等高的三角形的面积的比等于底边的比求出△ACD的面积，然后根据S1−S2=S△ACD−S△ACE计算即可得解．【解答】解：∵BE=CE，∴S△ACE=12S△ABC=12×6=3，∵AD=2BD，∴S△ACD=21+2S△ABC=23×6=4，∴S1−S2=S△ACD−S△ACE=4−3=1．故答案为：1．【点评】本题考查了三角形的面积，主要利用了等底等高的三角形的面积相等，等高的三角形的面积的比等于底边的比，需熟记．【答案】7【考点】三角形的面积【解析】连接AB1，BC1，CA1，根据等底等高的三角形的面积相等求出△ABB1，△A1AB1的面积，从而求出△A1BB1的面积，同理可求△B1CC1的面积，△A1AC1的面积，然后相加即可得解．【解答】解：如图，连接AB1，BC1，CA1，∵A，B分别是线段A1B，B1C的中点，∴S△ABB1=S△ABC=1，S△A1AB1=S△ABB1=1，∴S△A1BB1=S△A1AB1+S△ABB1=1+1=2，同理：S△B1CC1=2，S△A1AC1=2，∴△A1B1C1的面积=S△A1BB1+S△B1CC1+S△A1AC1+S△ABC=2+2+2+1=7．故答案为：7．【点评】本题考查了三角形的面积，主要利用了等底等高的三角形的面积相等，作辅助线把三角形进行分割是解题的关键．。

湘教版数学七年级下册第5章轴对称与旋转单元测试卷（含答案）一、填空题(每小题3分，共24分)1．汉字中、天、日、田等都可看作是轴对称图形，请你再写出一个这样的汉字：____．2．如图，下列图片中，是由图片(1)平移得到的，是由图片(1)旋转得到的，是由图片(1)轴对称得到的．（第2题图）3．如图，AD是三角形ABC的对称轴，AC＝8 cm，DC＝4 cm，则三角形ABC的周长为 cm.（第3题图）（第4题图）4．如图所示的图案是由三个叶片组成，绕点O旋转120°后可以与自身重合．若每个叶片的面积为4cm2，∠AOB为120°，则图中阴影部分的面积之和为 cm2.5．在三角形ABC中，∠A＝90°，将三角形ABC绕A点沿顺时针方向旋转85°，得到三角形AEF，点B，点C分别对应点E，点F，则下列结论：①∠BAE＝85°；②AC＝AF；③EF＝BC；④∠EAF＝85°.其中正确的是 (填序号)．6．将长方形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′＝60°，则∠AED的大小是 .（第6题图）（第7题图）7．如图，将三角形ABC绕着点C按顺时针方向旋转20°，B点落在B′位置，A点落在A′位置，若AC⊥A′B′，则∠BAC的度数是70°.8．如图，在正方形方格中，阴影部分是涂黑7个小正方形所形成的图案，再将方格内空白的一个小正方形涂黑，使得到的新图案成为一个轴对称图形的涂法有种．（第8题图）二、选择题(每小题3分，共30分)9．在一些汉字的美术字中，有的是轴对称图形．下面四个美术字中可以看作轴对称图形的是( )10．将图形按顺时针方向旋转90°得到的图形是( )11．如图是一个风筝的图案，它是轴对称图形，量得∠B＝30°，则∠E的度数为( )A．30° B．35°C．40° D．45°（第11题图）（第12题图）12．如图，直线a与直线b交于点A，与直线c交于点B，∠1＝120°，∠2＝45°，若使直线b与直线c平行，则可将直线b绕点A逆时针旋转( )A．15° B．30°C．45° D．60°13．下列四个图形中，若以其中一部分作为基本图形，无论用旋转还是平移都不能得到的图形是( )14．如图，直线MN是四边形AMBN的对称轴，点P是直线MN上的点，下列判断错误的是( ) A．AM＝BM B．AP＝BNC．∠MAP＝∠MBP D．∠ANM＝∠BNM（第14题图）（第15题图）15．如图，将直角三角形AOB绕点O逆时针旋转得到直角三角形COD，若∠AOB＝90°，∠BOC ＝130°，则∠AOD的度数为( )A．40° B．50° C．60° D．30°16．将一张长方形的纸对折，然后用笔尖在上面扎出“B”，再把它铺平，你可见到的是下列图形中的（）17．如图，在三角形ABC中，BC＝4，其面积为12，AD⊥BC.将三角形ABC绕点A旋转到三角形AB′C′的位置，使得AC⊥B′C′于点D′，则AD′的长度为( ) A．6 B．8 C．10 D．12（第17题图）（第18题图）18．如图，8×8方格纸上的两条对称轴EF，MN相交于中心点O，对三角形ABC分别作下列变换：①以点O为中心逆时针方向旋转180°；②先以A为中心顺时针方向旋转90°，再向右平移4格、向上平移4格；③先以直线MN为对称轴作轴对称图形，再向上平移4格，再以点A的对应点为中心顺时针方向旋转90°.其中，能将三角形ABC变换成三角形PQR的是( )A．①② B．①③ C．②③ D．①②③三、解答题(共66分)19．(10分)我们在学完“平移、轴对称、旋转”三种图形的变换后，可以进行进一步研究，请根据示例图形，完成下表.20.(10分)如图，在边长为1个单位长度的小正方形组成的12×12网格中，给出了四边形ABCD的两条边AB与BC，且四边形ABCD是一个轴对称图形，其对称轴为直线AC.(1)试在图中标出点D，并画出该四边形的另两条边；(2)将四边形ABCD向下平移5个单位，画出平移后得到的四边形A′B′C′D′.（第20题图）21．(10分)如图，在三角形ABC中，∠ACB＝90°，沿CD折叠三角形CBD，使点B恰好落在AC边上的点E处．若∠A＝22°，求∠BDC的度数(提示：三角形的内角和等于180°)．（第21题图）22．(12分)在三角形ABC中，∠ACB＝90°，∠B＝30°，将三角形ABC绕顶点C顺时针旋转，旋转角为θ(0°<θ<180°)，得到三角形A′B′C.如图，当AB∥CB′时，设A′B′与CB相交于点D.试求∠A′DC的度数(提示：三角形的内角和等于180°)．（第22题图）23．(12分)某公司为了节约开支，购买了质量相同的两种颜色的残缺地砖，准备用来装修地面，现已加工成如图①所示的等腰直角三角形，王聪同学设计了如图②所示的四种图案．（第23题图）(1)你喜欢哪种图案？并简述该图案的形成过程；(2)请你利用所学过的知识再设计三幅与上述不同的图案．24．(12分)四边形ABCD是正方形，三角形ADF旋转一定角度后得到三角形ABE，如图所示，如果AF＝4，AB＝7.(1)指出旋转中心和旋转角度；(2)求DE的长度；(3)BE与DF的位置关系如何？请说明理由(提示：三角形的内角和等于180°)．（第24题图）参考答案与解析一、1．平(答案不唯一) 2.(5) (2)和(3) (4) 3．24 4.4 5.①②③ 6.60°7.70° 8.3二、9．D 10.D 11.A 12.A 13.C 14．B 15.B 16.C 17.A 18.C三、19．解：(1)AB ＝A ′B ′，AB ∥A ′B ′(2分)(2)AB ＝A ′B ′ 对称轴l 上(6分)(3)AA ′∥BB ′，l 垂直平分AA ′，BB ′(8分)(4)OA ＝OA ′，OB ＝OB ′，∠AOA ′＝∠BOB ′(10分)20．解：(1)如答图．(5分)(2)如答图的四边形A ′B ′C ′D ′即为所要画的四边形．(10分)（第20题答图）21．解：∵∠ACB ＝90°，∠A ＝22°，∴∠B ＝68°.(3分)由折叠的性质知，∠BCD ＝∠ECD ＝12∠ACB ＝45°.(6分)在三角形BCD 中，∠B ＝68°，∠BCD ＝45°，∴∠BDC ＝180°－∠B －∠BCD ＝180°－68°－45°＝67°.(10分)22．解：∵三角形A ′B ′C 是由三角形ABC 经过旋转得到的，∴∠A ′CB ′＝∠ACB ＝90°，∠B ′＝∠B ＝30°.又∵AB ∥CB ′，∴∠BCB ′＝∠B ＝30°.(6分)∴∠A ′CD ＝∠A ′CB ′－∠BCB ′＝90°－30°＝60°，(8分)∠A ′＝180°－∠A ′CB ′－∠B ′＝60°.(10分)∴∠A ′DC ＝180°－∠A ′－∠A ′CD ＝180°－60°－60°＝60°.(12分)23．解：(1)我喜欢图案(4)．图案(4)的形成过程是：以同行或同列的两个小正方形组成的长方形为“基本图案”，绕大正方形的中心旋转180°.(答案不唯一)(6分)(2)如图所示．(12分)（第23题答图）24．解：(1)旋转中心为点A，旋转角度为90°.(4分)(2)由题意，可得AE＝AF＝4，AD＝AB＝7，∴DE＝AD－AE＝7－4＝3.(8分)(3)BE⊥DF.(9分)理由如下：延长BE交DF于点G，由旋转的性质得∠ADF＝∠ABE，∠FAD ＝∠DAB＝90°，∴∠F＋∠ADF＝90°，∴∠ABE＋∠F＝90°，∴∠BGF＝90°.即BE与DF 互相垂直．(12分)。