2020年湖南省雅礼中学高三1-6次月考 文科数学(试卷含答案)

大联考雅礼中学2024届高三月考试卷（一）数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共8页.时量120分钟，满分150分.第Ⅰ卷一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合{}2|log 4Mx x =<，{}|21N x x =≥，则M N ∩=（）A.{}08x x ≤< B. 182xx≤<C.{}216x x ≤< D. 1162xx≤<2.记等差数列{a n }的前n 项和为S n .若a 6＝16，S 5＝35，则{a n }的公差为（ ）A.3B.2C.－2D.－33.已知1z ，2z 是关于x 的方程2220x x +=−的两个根.若11i z =+，则2z =（ ）A.B.1C.D.24.函数sin exx xy =的图象大致为（）A. B.C. D.5.已知220x kx m +−<的解集为()(),11t t −<−，则k m +的值为（ ）A 1B.2C.-1D.-2.6. 古代数学家刘徽编撰的《重差》是中国最早的一部测量学著作，也为地图学提供了数学基础，根据刘徽的《重差》测量一个球体建筑的高度，已知点A 是球体建筑物与水平地面的接触点（切点），地面上B ，C 两点与点A 在同一条直线上，且在点A 的同侧，若在B ，C 处分别测量球体建筑物的最大仰角为60°和20°，且BC =100m ，则该球体建筑物的高度约为（ ）（cos10°≈0.985）A. 45.25mB. 50.76mC. 56.74mD. 58.60m7. 已知定义域是R 的函数()f x 满足：x ∀∈R ，()()40f x f x ++−=，()1f x +为偶函数，()11f =，则()2023f =（ ）A. 1B. -1C. 2D. -38. 如今中国被誉为基建狂魔，可谓是逢山开路，遇水架桥.公路里程､高铁里程双双都是世界第一.建设过程中研制出用于基建的大型龙门吊､平衡盾构机等国之重器更是世界领先.如图是某重器上一零件结构模型，中间最大球为正四面体ABCD 的内切球，中等球与最大球和正四面体三个面均相切，最小球与中等球和正四面体三个面均相切，已知正四面体ABCD棱长为，则模型中九个球的表面积和为（ ）A 6πB. 9πC.31π4D. 21π二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分.9. 下列命题为真命题的是（ ） A. 若2sin 23α=，则21cos 46πα +=B. 函数()2sin 23f x x π=+的图象向右平移6π个单位长度得到函数()2sin 26g x x π=+的图象.C. 函数()2sin cos cos 26f x x x x π=+−单调递增区间为(),36k k k Z ππππ−++∈D. ()22tan 1tan xf x x =−的最小正周期为2π 10. 如图所示，该几何体由一个直三棱柱111ABC A B C -和一个四棱锥11D ACC A −组成，12AB BC AC AA ====，则下列说法正确的是（ ）A. 若AD AC ⊥，则1AD A C ⊥B. 若平面11A C D 与平面ACD 的交线为l ，则AC //lC. 三棱柱111ABC A B C -的外接球的表面积为143πD. 当该几何体有外接球时，点D 到平面11ACC A11. 同学们，你们是否注意到，自然下垂的铁链；空旷的田野上，两根电线杆之间的电线；峡谷的上空，横跨深洞的观光索道的钢索.这些现象中都有相似的曲线形态.事实上，这些曲线在数学上常常被称为悬链线.悬链线的相关理论在工程、航海、光学等方面有广泛的应用.在恰当的坐标系中，这类函数的表达式可以为()e e x x f x a b −=+（其中a ，b 是非零常数，无理数e 2.71828⋅⋅⋅），对于函数()f x 以下结论正确的是（ ）A. a b =是函数()f x 为偶函数的充分不必要条件；B. 0a b +=是函数()f x 为奇函数的充要条件；C. 如果0ab <，那么()f x 为单调函数；D. 如果0ab >，那么函数()f x 存极值点.12. 设等比数列{}n a 的公比为q ，其前n 项和为n S ，前n 项积为n T ，且满足条件11a >，202220231a a >⋅，()()20222023110a a −⋅−<，则下列选项正确的是（ ）的在A. {}n a 为递减数列B. 202220231S S +<C. 2022T 是数列{}Tn 中的最大项D. 40451T >第Ⅱ卷三、填空题：本题共4小题，每小题5分，共20分.13. 已知(2,),(3,1)a b λ=−=，若()a b b +⊥ ，则a = ______ .14. 已知函数51,2()24,2xx f x x x −≤ =−>，则函数()()g x f x =的零点个数为______. 15. 已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则平面α截此正方体所得截面面积的最大值为______.16. 如图1所示，古筝有多根弦，每根弦下有一个雁柱，雁柱用于调整音高和音质.图2是根据图1绘制的古筝弦及其雁柱的简易平面图.在图2中，每根弦都垂直于x 轴，相邻两根弦间的距离为1，雁柱所在曲线的方程为 1.1x y =，第n 根弦（n ∈N ，从左数首根弦在y 轴上，称为第0根弦）分别与雁柱曲线和直线l ：1y x =+交于点(),n n n A x y 和(),n n n B x y ′′，则20n n n y y =′=∑______.（参考数据：取221.18.14=.）四、解答题：本题共6小题，共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.17. 如图，在直三棱柱111ABC A B C -中，2CACB ==，AB =13AA =，M 为AB 的中点.（1）证明：1//AC 平面1B CM ； （2）求点A 到平面1B CM 的距离.18. 记锐角ABC 的内角,,A B C 的对边分别为,,a b c �已知sin()sin()cos cos A B A C B C−−=．（1）求证：B C =； （2）若sin 1a C =，求2211a b+的最大值． 19. 甲、乙足球爱好者为了提高球技，两人轮流进行点球训练（每人各踢一次为一轮），在相同的条件下，每轮甲、乙两人在同一位置，一人踢球另一人扑球，甲先踢，每人踢一次球，两人有1人进球另一人不进球，进球者得1分，不进球者得1−分；两人都进球或都不进球，两人均得0分，设甲、乙每次踢球命中的概率均为12，甲扑到乙踢出球的概率为12，乙扑到甲踢出球的概率13，且各次踢球互不影响． （1）经过1轮踢球，记甲的得分为X ，求X 的分布列及数学期望； （2）求经过3轮踢球累计得分后，甲得分高于乙得分的概率． 20. 已知数列{}n a 中，10a =，()12n n a a n n N∗+=+∈.（1）令11n n n b a a +=−+，求证：数列{}n b 是等比数列； （2）令3nn n a c =，当n c 取得最大值时，求n 的值．21. 已知双曲线2222:1(0,0)x y E a b a b−=>>的焦距为10，且经过点M ．A ，B 为双曲线E 的左、右顶点，P 为直线2x =上的动点，连接P A ，PB 交双曲线E 于点C ，D （不同于A ，B ）． （1）求双曲线E 的标准方程．（2）直线CD 是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由．22. 设函数()()2cos 102x f x x x =−+≥.（1）求()f x 的最值；（2）令()sin g x x =，()g x 图象上有一点列()*11,1,2,...,,22i i i A g i n n =∈N ，若直线1i i A A +的斜率为()1,2,...,1i k i n =−，证明：1217 (6)n k k k n −+++>−.的大联考雅礼中学2024届高三月考试卷（一）数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共8页.时量120分钟，满分150分.第Ⅰ卷一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若集合{}2|log 4Mx x =<，{}|21N x x =≥，则M N ∩=（ ）A. {}08x x ≤< B. 182xx≤<C. {}216x x ≤<D. 1162xx≤<【答案】D 【解析】【分析】直接解出集合,M N ，再求交集即可.详解】{}{}2|log 4|016Mx x x x =<=<<，1|2N x x=≥ ，则1162M N x x ∩=≤<.故选：D.2. 记等差数列{a n }的前n 项和为S n .若a 6＝16，S 5＝35，则{a n }的公差为（ ） A. 3 B. 2C. －2D. －3【答案】A 【解析】【分析】由题得a 3＝7，设等差数列的公差为d ，解方程组11+27516a d a d = += 即得解.【详解】解：由等差数列性质可知，S 5＝152a a +×5＝5a 3＝35，解得a 3＝7， 设等差数列的公差为d ，所以11+27516a d a d = += ，解之得3d =.故选：A.3. 已知1z ，2z 是关于x 的方程2220x x +=−的两个根.若11i z =+，则2z =（ ）【A.B. 1C.D. 2【答案】C 【解析】【分析】由1z ，2z 是关于x 的方程2220x x +=−的两个根，由韦达定理求出2z ，再由复数的模长公式求解即可.【详解】法一：由1z ，2z 是关于x 的方程2220x x +=−的两个根，得122z z +=， 所以()21221i 1i z z =−=−+=−，所以21i z =−=法二：由1z ，2z 是关于x 的方程2220x x +=−的两个根，得122z z ⋅=， 所以21221i z z ==+，所以2221i 1i z ===++.故选：C . 4. 函数sin exx xy =的图象大致为（ ） A. B.C. D.【答案】D 【解析】【分析】分析函数sin exx xy =的奇偶性及其在()0,π上的函数值符号，结合排除法可得出合适的选项. 【详解】令()sin e x x xf x =，该函数的定义域为R ，()()()sin sin e ex xx x x x f x f x −−−−===，所以，函数sin exx xy =为偶函数，排除AB 选项， 当0πx <<时，sin 0x >，则sin 0exx xy >，排除C 选项. 故选：D.5. 已知220x kx m +−<的解集为()(),11t t −<−，则k m +的值为（ ） A. 1 B. 2C. -1D. -2【答案】B 【解析】【分析】由题知=1x −为方程220x kx m +−=的一个根，由韦达定理即可得出答案. 【详解】因为220x kx m +−<的解集为()(),11t t −<−， 所以=1x −为方程220x kx m +−=的一个根， 所以2k m +=． 故选:B ．6. 古代数学家刘徽编撰的《重差》是中国最早的一部测量学著作，也为地图学提供了数学基础，根据刘徽的《重差》测量一个球体建筑的高度，已知点A 是球体建筑物与水平地面的接触点（切点），地面上B ，C 两点与点A 在同一条直线上，且在点A 的同侧，若在B ，C 处分别测量球体建筑物的最大仰角为60°和20°，且BC =100m ，则该球体建筑物的高度约为（ ）（cos10°≈0.985）A. 45.25mB. 50.76mC. 56.74mD. 58.60m【答案】B 【解析】【分析】数形结合，根据三角函数解三角形求解即可；【详解】设球的半径为R ，,tan10R ABAC=，100tan10RBC =−=− ， 25250.760.985RR ==， 故选:B.7. 已知定义域是R 的函数()f x 满足：x ∀∈R ，()()40f x f x ++−=，()1f x +为偶函数，()11f =，则()2023f =（ ）A. 1B. -1C. 2D. -3【答案】B 【解析】【分析】根据对称性可得函数具有周期性，根据周期可将()()()2023311f f f ==−=−. 【详解】因为()1f x +为偶函数，所以()f x 的图象关于直线1x =对称，所以()()2=f x f x −，又由()()40f x f x ++−=，得()()4f x f x +=−−，所以()()()846f x f x f x +=−−−=−+，所以()()2f x f x +=−，所以()()4f x f x +=，故()f x 的周期为4，所以()()()2023311f f f ==−=−．故选:B ．8. 如今中国被誉为基建狂魔，可谓是逢山开路，遇水架桥.公路里程､高铁里程双双都是世界第一.建设过程中研制出用于基建的大型龙门吊､平衡盾构机等国之重器更是世界领先.如图是某重器上一零件结构模型，中间最大球为正四面体ABCD 的内切球，中等球与最大球和正四面体三个面均相切，最小球与中等球和正四面体三个面均相切，已知正四面体ABCD 棱长为，则模型中九个球的表面积和为（ ）A. 6πB. 9πC.31π4D. 21π【答案】B 【解析】【分析】作出辅助线，先求出正四面体的内切球半径，再利用三个球的半径之间的关系得到另外两个球的半径，得到答案.【详解】如图，取BC 的中点E ，连接DE ，AE，则CE BE ==，AE DE ==，过点A 作AF ⊥底面BCD ，垂足在DE 上，且2DF EF =，所以DF EF=4AF =，点O 为最大球球心，连接DO 并延长，交AE 于点M ，则DM ⊥AE ， 设最大球的半径为R ，则OF OM R ==， 因为Rt AOM △∽Rt AEF ，所以AO OMAE EF==1R =， 即1OM OF ==，则413AO =−=，故1sin 3OM EAF AO ∠== 设最小球的球心为J ，中间球的球心为K ，则两球均与直线AE 相切，设切点分别为,H G ， 连接,HJ KG ，则,HJ KG 分别为最小球和中间球的半径，长度分别设为,a b ，则33,33AJ HJ a AK GK b ====，则33JK AK AJ b a =−=−， 又JK a b =+，所以33b a a b −=+，解得2b a =，又33OK R b AO AK b =+=−=−，故432b R =−=，解得12b =， 所以14a =， 模型中九个球的表面积和为2224π4π44π44π4ππ9πR b a +×+×=++=.故选：B【点睛】解决与球有关的内切或外接的问题时，解题的关键是确定球心的位置．对于外切的问题要注意球心到各个面的距离相等且都为球半径；对于球的内接几何体的问题，注意球心到各个顶点的距离相等，解题时要构造出由球心到截面圆的垂线段、小圆的半径和球半径组成的直角三角形，利用勾股定理求得球的的半径二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分.9. 下列命题为真命题的是（ ） A. 若2sin 23α=，则21cos 46πα +=B. 函数()2sin 23f x x π=+的图象向右平移6π个单位长度得到函数()2sin 26g x x π=+的图象 C. 函数()2sin cos cos 26f x x x x π=+−的单调递增区间为(),36k k k Z ππππ−++∈D. ()22tan 1tan xf x x =−的最小正周期为2π 【答案】ACD 【解析】【分析】利用二倍角公式和诱导公式可求得2cos 4πα+，知A 正确； 根据三角函数平移变换可求得()2sin 2g x x =，知B 错误；利用三角恒等变换公式化简得到()f x 解析式，利用整体对应的方式可求得单调递增区间，知C 正确； 利用二倍角公式化简得到()f x ，由正切型函数的周期性可求得结果知D 正确.【详解】对于A ，21cos 21sin 212cos 4226παπαα++−+===，A 正确； 对于B ，()f x 向右平移6π个单位长度得：2sin 26f x x π−=，即()2sin 2g x x =，B 错误；对于C ，()13sin 22sin 2sin 222226f x x x x x x x π=+=++， 则由222262k x k πππππ−+≤+≤+，Z k ∈得：36k x k ππππ−+≤≤+，Z k ∈，()f x \的单调递增区间为(),36k k k Z ππππ−++∈，C 正确； 对于D ，()22tan tan 21tan xf x x x ==−，tan 2y x ∴=的最小正周期为2π，D 正确.故选：ACD.10. 如图所示，该几何体由一个直三棱柱111ABC A B C -和一个四棱锥11D ACC A −组成，12AB BC AC AA ====，则下列说法正确的是（ ）A. 若AD AC ⊥，则1AD A C ⊥B. 若平面11A C D 与平面ACD 的交线为l ，则AC //lC. 三棱柱111ABC A B C -的外接球的表面积为143πD. 当该几何体有外接球时，点D 到平面11ACC A【答案】BD 【解析】【分析】根据空间线面关系，结合题中空间几何体，逐项分析判断即可得解. 【详解】对于选项A ，若AD AC ⊥，又因为1AA ⊥平面ABC ， 但是D 不一定在平面ABC 上，所以A 不正确；对于选项B ，因为11//A C AC ，所以//AC 平面11A C D ， 平面11AC D ∩平面ACD l =，所以//AC l ，所以B 正确； 对于选项C ，取ABC ∆的中心O ，111A B C ∆的中心1O ，1OO中点为该三棱柱外接球的球心，所以外接球的半径R ， 所以外接球的表面积为22843R ππ=，所以C 不正确； 对于选项D ，该几何体的外接球即为三棱柱111ABC A B C -的外接球，1OO 的中点为该外接球的球心，该球心到平面11ACC A的点D 到平面11ACC A 的最大距离为R ，所以D 正确. 故选：BD11. 同学们，你们是否注意到，自然下垂的铁链；空旷的田野上，两根电线杆之间的电线；峡谷的上空，横跨深洞的观光索道的钢索.这些现象中都有相似的曲线形态.事实上，这些曲线在数学上常常被称为悬链线.悬链线的相关理论在工程、航海、光学等方面有广泛的应用.在恰当的坐标系中，这类函数的表达式可以为()e e x x f x a b −=+（其中a ，b 是非零常数，无理数e 2.71828⋅⋅⋅），对于函数()f x 以下结论正确的是（ ）A. a b =是函数()f x 为偶函数的充分不必要条件；B. 0a b +=是函数()f x 为奇函数的充要条件；C. 如果0ab <，那么()f x 为单调函数；D. 如果0ab >，那么函数()f x 存在极值点. 【答案】BCD 【解析】【分析】根据奇偶函数的定义、充分条件和必要条件的定义即可判断AB ；利用导数，分类讨论函数的单调性，结合极值点的概念即可判断CD.【详解】对于A ，当a b =时，函数()f x 定义域为R 关于原点对称，()()e e =x x f x a b f x −−=+，故函数()f x 为偶函数；当函数()f x 为偶函数时，()()=0f x f x −−，故()()0e e x xa b b a −−+−=， 即()()2e =xa b a b −−，又2e 0x >，故a b =，所以a b =是函数()f x 为偶函数的充要条件，故A 错误； 对于B ，当0a b +=时，函数()f x 定义域为R 关于原点对称，()()=e e ()()=0x x f x f x a b a b −+−+++，故函数()f x 为奇函数，当函数()f x 为奇函数时，()()=e e ()()=0xxf x f x a b a b −+−+++，因为e 0x >，e 0x −>，故0a b +=.所以0a b +=是函数()f x 为奇函数的充要条件，故B 正确；对于C ，()=e e x xa f xb −−′，因为0ab <，若0,0a b ><，则()e e0=xxa xb f −−>′恒成立，则()f x 为单调递增函数，若0,0a b <>则()e e0=xxa xb f −−<′恒成立，则()f x 为单调递减函数，故0ab <，函数()f x 为单调函数，故C 正确；对于D ，()2e e e ==ex xxxa ba b f x −−−′， 令()=0f x ′得1=ln 2bx a，又0ab >， 若0,0a b >>，当1,ln 2b x a∈−∞，()0f x ′<，函数()f x 为单调递减. 当1ln ,2b x a∈+∞，()0f x ¢>，函数()f x 为单调递增.函数()f x 存在唯一的极小值. 若0,0a b <<， 当1ln2b x a∈−∞，，()0f x ¢>，函数()f x 为单调递增. 当1ln ,2b x a∈+∞，()0f x ′<，函数()f x 为单调递减.故函数()f x 存在唯一的极大值. 所以函数存在极值点，故D 正确. 故答案为：BCD.12. 设等比数列{}n a 的公比为q ，其前n 项和为n S ，前n 项积为n T ，且满足条件11a >，202220231a a >⋅，()()20222023110a a −⋅−<，则下列选项正确的是（ ）A. {}n a 为递减数列B. 202220231S S +<C. 2022T 是数列{}Tn 中的最大项D. 40451T >【答案】AC 【解析】【分析】根据题意先判断出数列{}n a 的前2022项大于1，而从第2023项开始都小于1.再对四个选项一一验证：对于A ：利用公比的定义直接判断；对于B ：由20231a <及前n 项和的定义即可判断；对于C ：前n 项积为n T 的定义即可判断；对于D ：先求出4045T 40452023a =，由20231a <即可判断.【详解】由()()20222023110a a −⋅−<可得：20221a −和20231a −异号，即202220231010a a −> −< 或202220231010a a −<−> . 而11a >，202220231a a >⋅，可得2022a 和2023a 同号，且一个大于1，一个小于1.因为11a >，所有20221a >，20231a <，即数列{}n a 的前2022项大于1，而从第2023项开始都小于1. 对于A ：公比202320221a q a =<，因为11a >，所以11n n a a q −=为减函数，所以{}n a 为递减数列.故A 正确； 对于B ：因为20231a <，所以2023202320221a S S =−<，所以202220231S S +>.故B 错误；对于C ：等比数列{}n a 的前n 项积为n T ，且数列{}n a 的前2022项大于1，而从第2023项开始都小于1，所以2022T 是数列{}Tn 中的最大项.故C 正确； 对于D ：40451234045T a a a a = ()()()240441111a a q a q a q = 404512340441a q +++= 4045202240451a q ×= ()404520221a q =40452023a =因为20231a <，所以404520231a <，即40451T <.故D 错误.故选：AC第Ⅱ卷三、填空题：本题共4小题，每小题5分，共20分.13. 已知(2,),(3,1)a b λ=−=，若()a b b +⊥ ，则a = ______ .【答案】【解析】【分析】根据题意求得(1,1)a b λ+=+ ，结合向量的数量积的运算公式求得λ的值，得到a的坐标，利用向量模的公式，即可求解．【详解】因为(2,),(3,1)a b λ=−=，可得(1,1)a bλ+=+ ， 又因为()a b b +⊥，可得()(1,1)(3,1)310b ba λλ=+⋅=++=⋅+ ，解得4λ=−， 所以(2,4)a =−−，所以a =故答案为：14. 已知函数51,2()24,2xx f x x x −≤ =−>，则函数()()g x f x =零点个数为______. 【答案】3 【解析】【分析】令()0g x =得()f x =，根据分段函数性质可在同一直角坐标系中作出()f x，y =的大致图象，由图象可知，函数()y f x =与y =的图象有3个交点，即可得出答案．【详解】令()0g x =得()f x =可知函数()g x 的零点个数即为函数()f x与y =的交点个数，在同一直角坐标系中作出()f x，y =的大致图象如下：由图象可知，函数()y f x =与y =的图象有3个交点，即函数()g x 有3个零点， 故答案为：3.15. 已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则平面α截此正方体所得截面面积的最大值为______.【解析】【分析】利用正方体的结构特征，判断平面α所在的位置，然后求得截面面积的最大值即可.的【详解】根据相互平行的直线与平面所成的角是相等的，可知在正方体1111ABCD A B C D −中，平面11AB D 与直线1AA ，11A B ，11A D 所成的角是相等的，所以平面11AB D 与平面α平行，由正方体的对称性：要求截面面积最大，则截面的位置为过棱的中点的正六边形（过正方体的中心），边，所以其面积为26S .16. 如图1所示，古筝有多根弦，每根弦下有一个雁柱，雁柱用于调整音高和音质.图2是根据图1绘制的古筝弦及其雁柱的简易平面图.在图2中，每根弦都垂直于x 轴，相邻两根弦间的距离为1，雁柱所在曲线的方程为 1.1x y =，第n 根弦（n ∈N ，从左数首根弦在y 轴上，称为第0根弦）分别与雁柱曲线和直线l ：1y x =+交于点(),n n n A x y 和(),n n n B x y ′′，则20n n n y y =′=∑______.（参考数据：取221.18.14=.）【答案】914 【解析】【分析】根据题意可得1, 1.1n n n y n y ′=+=，进而利用错位相减法运算求解.【详解】由题意可知：1, 1.1n n n y n y ′=+=，则()20201192000011.111.121.1201.1211.1n n n n n y y n =′=+=×+×++×+×∑∑L ， 可得2012202101.111.121.1201.1211.1nn n yy =′×=×+×++×+×∑L ，两式相减可得：2120120212101 1.10.1 1.1 1.1 1.1211.1211.11 1.1n n n y y =−′−×=+++−×=−×−∑L 2121221 1.10.1211.11 1.118.1491.40.10.10.1−+××++====−−−−， 所以20914nn n yy =′=∑.故答案为：914.四、解答题：本题共6小题，共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.17. 如图，在直三棱柱111ABC A B C -中，2CACB ==，AB =13AA =，M 为AB 中点.（1）证明：1//AC 平面1B CM ； （2）求点A 到平面1B CM 的距离. 【答案】（1）证明见解析 （2【解析】【分析】(1)利用线面平行的判定定理证明； (2)利用等体积法求解.的【小问1详解】连接1BC 交1B C 于点N ，连接MN ， 则有N 为1BC 的中点，M 为AB 的中点， 所以1//AC MN ，且1AC ⊄平面1B CM ，MN ⊂平面1B CM ， 所以1//AC 平面1B CM . 【小问2详解】连接1AB ,因为2CACB ==，所以CM AB ⊥,又因为1AA ⊥平面ABC ，CM ⊂平面ABC ，所以1AA CM ⊥，1AB AA A ∩=,所以CM ⊥平面11ABB A , 又因为1MB ⊂平面11ABB A ,所以1CM MB ⊥,又222CA CB AB +=，所以ABC 是等腰直角三角形，112CM AB MB ====,所以1112CMB S CM MB =⋅=△1111222ACM ACB S S CA CB ==×⋅=△△, 设点A 到平面1B CM 的距离为d ， 因为11A B CM B ACM V V −−=,所以111133B CM ACM S d S AA ××=×× ,所以11ACM B CMS AA dS ×= .18. 记锐角ABC 的内角,,A B C 的对边分别为,,a b c �已知sin()sin()cos cos A B A C B C−−=．（1）求证：B C =； （2）若sin 1a C =，求2211a b+的最大值． 【答案】（1）见解析； （2）2516. 【解析】【分析】（1）运用两角和与差正弦进行化简即可；（2）根据（1）中结论运用正弦定理得sin 2sin sin 12ba C R Ab A R === ，然后等量代换出2211a b +，再运用降次公式化简，结合内角取值范围即可求解. 【小问1详解】 证明：由题知sin()sin()cos cos A B A C B C−−=，所以sin()cos sin()cos A B C A C B −=−， 所以sin cos cos cos sin cos sin cos cos cos sin cos A B C A B C A C B A C B −=−, 所以cos sin cos cos sin cos A B C A C B = 因为A 为锐角，即cos 0A ≠ ， 所以sin cos sin cos B C C B =， 所以tan tan =B C ， 所以B C =. 【小问2详解】 由（1）知：B C =， 所以sin sin B C =， 因为sin 1a C =， 所以1sin C a=， 因为由正弦定理得：2sin ,sin 2b aR A B R=， 所以sin 2sin sin 12b a C R A b A R=== ,所以1sin A b =， 因为2A B C C ππ=−−=− ，所以1sin sin 2A C b==， 所以222211sin sin 2a bC C++ 221cos 2(1cos 2)213cos 2cos 222CC C C −+−=−−+因为ABC 是锐角三角形，且B C =， 所以42C ππ<<，所以22C ππ<<，所以1cos 20C −<<， 当1cos 24C =−时，2211a b +取最大值为2516， 所以2211a b +最大值为：2516. 19. 甲、乙足球爱好者为了提高球技，两人轮流进行点球训练（每人各踢一次为一轮），在相同的条件下，每轮甲、乙两人在同一位置，一人踢球另一人扑球，甲先踢，每人踢一次球，两人有1人进球另一人不进球，进球者得1分，不进球者得1−分；两人都进球或都不进球，两人均得0分，设甲、乙每次踢球命中的概率均为12，甲扑到乙踢出球的概率为12，乙扑到甲踢出球的概率13，且各次踢球互不影响． （1）经过1轮踢球，记甲的得分为X ，求X 的分布列及数学期望； （2）求经过3轮踢球累计得分后，甲得分高于乙得分的概率． 【答案】（1）分布列见解析；期望为112（2）79192【解析】【分析】（1）先分别求甲、乙进球的概率，进而求甲得分的分布列和期望；（2）根据题意得出甲得分高于乙得分的所有可能情况，结合（1）中的数据分析运算. 【小问1详解】记一轮踢球，甲进球为事件A ，乙进球为事件B ，A ，B 相互独立， 由题意得：()1111233P A =×−= ，()1111224P B =×−= ， 甲的得分X 的可能取值为1,0,1−，()()()()11111346P X P AB P A P B =−===−×= ，()()()()()()()11117011343412P X P AB P AB P A P B P A P B ==+=+=×+−×−=()()()()11111344P X P AB P A P B ====×−= ，所以X 的分布列为：()1711101612412E X =−×+×+×=.【小问2详解】经过三轮踢球，甲累计得分高于乙有四种情况：甲3轮各得1分；甲3轮中有2轮各得1分，1轮得0分；甲3轮中有2轮各得1分，1轮得1−分；甲3轮中有1轮得1分，2轮各得0分，甲3轮各得1分的概率为3111464P ==， 甲3轮中有2轮各得1分，1轮得0分的概率为2223177C 41264P =×=， 甲3轮中有2轮各得1分，1轮得1−分的概率为2233111C 4632P =×= ， 甲3轮中有1轮得1分，2轮各得0分的概率为21431749C 412192P =××=， 所以经过三轮踢球，甲累计得分高于乙的概率1714979646432192192P =+++=.20. 已知数列{}n a 中，10a =，()12n n a a n n N∗+=+∈.（1）令11n n n b a a +=−+，求证：数列{}n b 是等比数列； （2）令3nn n a c =，当n c 取得最大值时，求n 的值． 【答案】（1）证明见解析；（2）3n =. 【解析】 【分析】（1）求得21a =，12b =，利用递推公式计算得出12n n b b +=，由此可证得结论成立；（2）由（1）可知112nn n a a +−+=，利用累加法可求出数列{}n a 的通项公式，可得出213n n nn c −−=，利用定义法判断数列{}n c 的单调性，进而可得出结论.【详解】（1）在数列{}n a 中，10a =，12n n a a n +=+，则21211a a =+=， 11n n n b a a +=−+ ，则12112b a a −+，则()()()111112211212n n n n n n n n b a a a n a n a a b ++−−=−+=+−+−+=−+=，所以，数列{}n b 为等比数列，且首项为2，所以，1222n n n b −=×=；（2）由（1）可知，2n n b =即121nn n a a +−=−，可得2123211212121n n n a a a a a a −−−=− −=−−=− ， 累加得()()()()1211212222112112n n n n a a n n n −−−−=+++−−=−−=−−− ，21n n a n ∴=−−.213n n n n c −−∴=，()111112112233n n n n n n n c +++++−+−−−==， 11112221212333n n nn n n n n n n n c c ++++−−−−+−∴−=−=， 令()212nf n n =+−，则()11232n f n n ++=+−，所以，()()122nf n f n +−=−.()()()()1234f f f f ∴=>>> ，()()1210f f ==> ，()310f =−<，所以，当3n ≥时，()0f n <.所以，123c c c <<，345c c c >>> . 所以，数列{}n c 中，3c 最大，故3n =.【点睛】方法点睛：求数列通项公式常用的七种方法：（1）公式法：根据等差数列或等比数列的通项公式()11n a a n d +−=或11n n a a q −=进行求解；（2）前n 项和法：根据11,1,2n nn S n a S S n −= = −≥ 进行求解；（3）n S 与n a 的关系式法：由n S 与n a 的关系式，类比出1n S −与1n a −的关系式，然后两式作差，最后检验出1a 是否满足用上面的方法求出的通项；（4）累加法：当数列{}n a 中有()1n n a a f n −−=，即第n 项与第n 1−项的差是个有规律的数列，就可以利用这种方法；（5）累乘法：当数列{}n a 中有()1nn a f n a −=，即第n 项与第n 1−项的商是个有规律的数列，就可以利用这种方法；（6）构造法：�一次函数法：在数列{}n a 中，1n n a ka b −=+（k 、b 均为常数，且1k ≠，0k ≠）. 一般化方法：设()1n n a m k a m −+=+，得到()1b k m =−，1b m k =−，可得出数列1n b a k+ −是以k的等比数列，可求出n a ；�取倒数法：这种方法适用于()112,n n n ka a n n N ma p∗−−=≥∈+（k 、m 、p 为常数，0m ≠），两边取倒数后，得到一个新的特殊（等差或等比）数列或类似于1n n a ka b −=+的式子； �1nn n a ba c +=+（b 、c 为常数且不为零，n N ∗∈）型的数列求通项n a ，方法是在等式的两边同时除以1n c +，得到一个1n n a ka b +=+型的数列，再利用�中的方法求解即可. 21. 已知双曲线2222:1(0,0)x y E a b a b−=>>的焦距为10，且经过点M ．A ，B 为双曲线E 的左、右顶点，P 为直线2x =上的动点，连接P A ，PB 交双曲线E 于点C ，D （不同于A ，B ）． （1）求双曲线E 的标准方程．（2）直线CD 是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由． 【答案】（1）221169x y −= （2）直线CD 过定点，定点坐标为(8,0)． 【解析】【分析】（1）方法一：将M 代入方程，结合222+=a b c 求得,a b 得双曲线方程；方法二：根据双曲线定义求得a 得双曲线方程.（2）方法一：设CD 的方程为x my t =+，与双曲线联立，由A 点与C 点写出AC 方程，求出p y ，由B 点与D 点写出BD 方程，求出p y ，利用两个p y 相等建立关系式，代入韦达定理可求得t 为定值.方法二：设CD 的方程为,(2,)x my t P n =+，与双曲线联立，由P 点与A 点写出AC 方程，由P 点与B 点写出BD 方程，将()()1122,,,C x y D x y 代入以上两方程，两式相比消去n 建立关系式，代入韦达定理可求得t 为定值. 【小问1详解】法一．由222225,64271,a b ab += −=解得2216,9a b ==，�双曲线E 的标准方程为221169x y −=． 法二．左右焦点为()()125,0,5,0F F −，125,28c a MF MF ∴==−=，22294,a b c a ∴===−，�双曲线E 的标准方程为221169x y −=．【小问2详解】直线CD 不可能水平，故设CD 的方程为()()1122,,,,x my t C x y D x y =+， 联立221169x my t x y =+−= 消去x 得()()2222916189144=0,9160m y mty t m −++−−≠， 12218916mt y y m −∴+=−，21229144916t y y m −=−，12y y −±，AC 的方程为11(4)4y yx x ++，令2x =，得1164p y y x =+， BD 的方程为22(4)4y yx x −−，令2x =，得2224p y y x −=−，1221112212623124044y y x y y x y y x x −∴=⇔−++=+− ()()21112231240my t y y my t y y ⇔+−+++=()()1212431240my y t y t y ⇔+−++= ()()()()12121242480my y t y y t y y ⇔+−++−−=()22249144(24)180916916m t t mt m m −−⇔−±=−−3(8)(0m t t ⇔−±−=(8)30t m ⇔−= ，解得8t =3m =±，即8t =或4t =（舍去）或4t =−（舍去）， �CD 的方程为8x my =+，�直线CD 过定点，定点坐标为(8,0)． 方法二．直线CD 不可能水平，设CD 的方程为()()1122,,,,,(2,)x my t C x y D x y P n =+， 联立22,1,169x my t x y =+ −= ，消去x 得()2229161891440m y mty t −++−=， 2121222189144,916916mt t y y y y m m −−∴+==−−， AC 的方程为(4)6nyx =+，BD 的方程为(4)2ny x −−， ,C D 分别在AC 和BD 上，()()11224,462n ny x y x ∴=+=−−， 两式相除消去n 得()211211223462444x y y y x x x y −−−=⇔+=+−， 又22111169x y −=，()()211194416x x y ∴+−=．将()2112344x y x y −−+=代入上式，得()()1212274416x x y y −−−=⇔()()1212274416my t my t y y −+−+−=()()221212271627(4)27(4)0m y y t m y y t ⇔++−++−=⇔()22222914418271627(4)27(4)0916916t mtm t m t m m −−++−+−=−−．整理得212320t t +=−，解得8t =或4t =（舍去）． �CD 的方程为8x my =+，�直线CD 过定点，定点坐标为(8,0)． 【点睛】圆锥曲线中直线过定点问题通法，先设出直线方程y kx m =+，通过韦达定理和已知条件若能求出m 为定值可得直线恒过定点，若得到k 和m 的一次函数关系式，代入直线方程即可得到直线恒过定点.22. 设函数()()2cos 102x f x x x =−+≥.（1）求()f x 的最值；（2）令()sin g x x =，()g x 的图象上有一点列()*11,1,2,...,,22i ii A g i n n =∈N ，若直线1i i A A +的斜率为()1,2,...,1i k i n =−，证明：1217 (6)n k k k n −+++>−. 【答案】（1）()f x 在[)0,∞+上的最小值为()00f =，()f x 在[)0,∞+上无最大值. （2）见解析 【解析】【分析】（1）求出原函数的二阶导数后可判断二阶导数非负，故可判断导数非负，据此可求原函数的最值.（2）根据（1）可得3sin (0)6x x x x ≥−≥，结合二倍角的正弦可证：2271162i i k +>−×，结合等比数列的求和公式可证题设中的不等式. 【小问1详解】()sin f x x x ′=−+，设()sin s x x x =−+，则()cos 10s x x ′=−+≥（不恒为零），故()s x 在()0,∞+上为增函数，故()()00s x s >=，所以()0f x ¢>，故()f x 在[)0,∞+上为增函数， 故()f x 在[)0,∞+上的最小值为()00f =，()f x 在[)0,∞+上无最大值. 【小问2详解】先证明一个不等式：3sin (0)6x x x x ≥−≥，证明：设()3sin ,06x u x x x x =−+≥，则()2cos 1()02x u x x f x ′=−+=≥（不恒为零），故()u x 在[)0,∞+上为增函数， 故()()00u x u ≥=即3sin (0)6x x x x ≥−≥恒成立. 当*N i ∈时，11111111222sin sin 112222i i i i i i i ig g k ++++ − ==− − 11111111111122sin cos sin 2sin 2cos 122222i i i i i i i +++++++=−=×−由（1）可得()2cos 102x x x ≥−>，故12311cos 1022i i ++≥−>， 故111112311112sin2cos 12sin 2112222i i i i i i ++++++ ×−≥×−−1112213322111112sin121222622i i i i i i i +++++++  ×−≥−−  × 2222224422117111711111622626262i i i i i +++++ =−−=−×+×>−×  × , 故1214627111...16222n nk k k n −+++>−−+++41111771112411166123414n n n n −− =−−×=−−×−× −771797172184726n n n n =−−+×>−>−. 【点睛】思路点睛：导数背景下数列不等式的证明，需根据题设中函数的特征构成对应的函数不等式，从而得到相应的数列不等式，再结合不等式的性质结合数列的求和公式、求和方法等去证明目标不等式.。

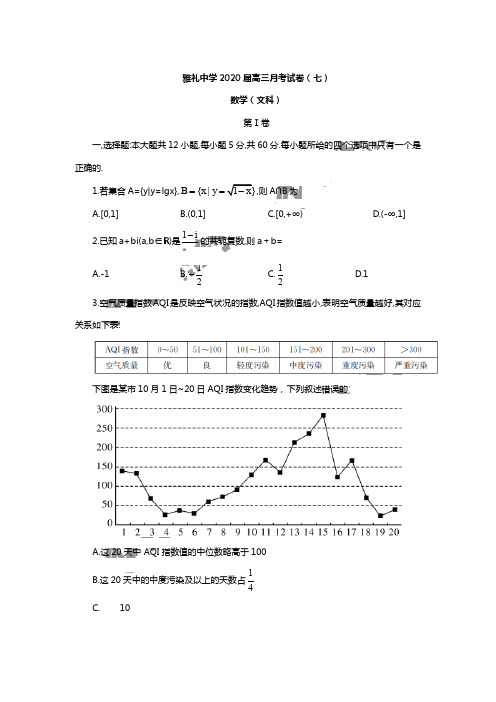
雅礼中学高三月考试卷(一)数学一、单项选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项符合题目要求。

1.已知集合A =-2,0 ,B =x x 2-2x =0 ，则以下结论正确的是()A.A =BB.A ∩B =0C.A ∪B =AD.A ⊆B2.已知等比数列a n 满足a 1=1,a 3⋅a 5=4a 4-1 ，则a 7的值为()A.2B.4C.92D.63.已知复数z =a +1 -ai a ∈R ，则a =-1是z =1的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知向量a =cos θ,sin θ ，b =2,-1 ，若a ⊥b ，则cos 2θ+12sin2θ的值为()A.13B.35C.45D.235.如图，在棱长为2的正方体ABCD -A 1B 1C 1D 1中，E ，F 分别是棱AA 1，CC 1的中点，过BE 的平面α与直线A 1F 平行，则平面α截该正方体所得截面的面积为()A.5B.25C.4D.56.某工厂有A ,B 两个生产车间，所生产的同一批产品合格率分别是99%和98%，已知某批产品的60%和40%分别是A ,B 两个车间生产，质量跟踪小组从中随机抽取一件，发现不合格，则该产品是由A 车间生产的概率为()A.34B.47C.12D.377.已知椭圆C ：x 2a2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2，P 为椭圆上一点，且∠F 1PF 2=π3，若F 1关于∠F 1PF 2平分线的对称点在椭圆C 上，则该椭圆的离心率为()A.22B.33C.12D.138.△ABC 中，角A ,B ,C 所对的三边分别为a ,b ,c ,c =2b ，若△ABC 的面积为1，则BC 的最小值是()A.2B.3C.3D.33二、多项选择题：本大题共4个小题，每小题5分，共20分。

2020届湖南省长沙市雅礼中学高三上学期第一次月考数学（文）试题一、单选题1．已知集合2}{0|A x x x =-<（），{|11}B x x =-<<，则A B =（）A ．{|12}x x -<<B ．{|1x x <-或2x >}C ．{|01}x x <<D ．{|0x x <或}【答案】C【解析】求出A 中不等式的解集，找出两集合的交集即可 【详解】由题意可得{|02}A x x =<<，{|11}B x x =-<<，所以{|01}A B x x =<<.故选C. 【点睛】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键． 2．已知复数2a ii+-是纯虚数（i 是虚数单位），则,实数a 等于 A.-2 B.2C.12D.-1【答案】C 【解析】2a i i +-21255a a i -+=+是纯虚数,所以21210,0552a a a -+=≠∴=，选C. 3．“26m <<”是“方程22126x y m m+=--为椭圆”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B【解析】试题分析：若方程22126x ym m+=--表示椭圆，则20{6026m m m m->->-≠-，解得26m <<且4m ≠，所以26m <<是方程22126x y m m+=--表示椭圆的必要不充分条件，故选B ．【考点】椭圆的标准方程；必要不充分条件的判定．4．如果()()221f x ax a x =--+在区间1,2⎛⎤-∞ ⎥⎝⎦上为减函数，则a 的取值（ ）A.(]0,1B.[)0,1C.[] 0,1D.()0,1【答案】C【解析】根据题意，利用一元二次函数的性质，对a 进行讨论，即可推得答案。

注意事项：1．答题前，先将自己的姓名、考号填写在试卷和答题卡上，并将考号条形码粘贴在答 题卡上的指定位置。

2．请在答题卡上各题号对应的答题区域内答题，写在试卷、草稿纸和答题卡上的非答 题区域均无效。

3．选择题用 2B 铅笔把所选答案的标号涂黑，非选择题用黑色签字笔作答。

一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合=+<∈=P x x x N Q |log (1)1,,1,3,56}{}{，M ＝P ∪Q ，则集合M 中的元素共有（ ） A ．4个B ．6个C ．8个D ．无数个2．设函数f x mx mx =−−2()1，命题“x ∃∈1,3][，f x m ≤−+()2是假命题”，则实数m 的取值范围是（ ）A ．,37−∞⎛⎝⎤⎦⎥ B ．−∞,3]( C ．37,+∞⎛⎝ ⎫⎭⎪ D ．3,+∞)(3．《九章算术》是我国古代数学成就的杰出代表，其中《方田》章有弧田面积计算问题， 计算术曰：以弦乘矢，矢又自乘，并之，二而一.其大意是，弧田面积的计算公式为：弧田面积=21（弦×矢+矢×矢）.弧田是由圆弧（简称为弧田弧）和以圆弧的端点为端点的线段（简称为弧田弦）围成的平面图形，公式中“弦”指的是弧田弦的长，“矢”等于弧田弧所在圆的半径与圆心到弧田弦的距离之差.现有一弧田，其弦长AB 等于6m ，其弧所在圆为圆O ，若用上述弧田面积计算公式算得该弧田的面积为2m 72，则∠=AOB cos （ ）A ．251 B ．−257C ．51D ．257 4．已知⎝⎭ ⎪+=⎛⎫απ32sin 1，则⎝⎭ ⎪+⎛⎫απ6sin 2的值为（ ）A ．21B ．−21CD5．如图，在棱长为2的正方体−ABCD A B C D 1111中，E ，F 分别是棱AA 1，CC 1的中点，过BE 的平面α与直线A F 1平行，则平面α截该正方体所得截面的面积为（ ） AB．C ．4D ．56．已知函数f (x )＝x 3＋ax 2－x 的图象在点A (1，f (1))处的切线方程为y ＝4x －3，则函数y ＝f (x)湖南省雅礼中学高三年级第一次月考 数学试卷的极大值为（ ） A ．1B ．527−C ．−2527D ．－17. 20222022202232022322022212022020202222C C C C C +−+−的值为A ．0B ．1C ．－1D ．202228．已知函数()f x 是定义在R 上的奇函数，对任意的x ∈R ，均有(2)()f x f x +=且(1)0f =，当[0,1)x ∈时，()21x f x =−，则方程()1||0f x g x −=的实根个数为（ ） A ．6B ．8C ．10D ．12二､多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．已知由样本数据点集合{}(,)123,i i x y i n =，，，，求得的回归直线方程为 1.50.5y x =+，且3x =，现发现两个数据点12,2(2)..和4.8,(7)8.误差较大，去除后重新求得的回归直线l 的斜率为1.2，则（ ）A ．变量x 与y 具有正相关关系B ．去除后y 的估计值增加速度变快C ．去除后与去除前均值x ，y 不变D ．去除后的回归方程为 1.2 1.4y x =+10．如图所示，是一个3×3九宫格，现从这9个数字中随机挑出3个不同的数字，记事件A 1：恰好挑出的是1、2、3；记事件A 2：恰好挑出的是1、4、7；记事件A 3：挑出的数字里含有数字1.下列说法正确的是（ ）12 B ．事件A 1，A 2是独立事件 C ．P (A 1|A 3)＝P (A 2|A 3)D ．P (A 3)＝P (A 1)＋P (A 2)11．在正四面体ABCD 中，若AB = ） A ．该四面体外接球的表面积为3πB ．直线与平面BCDC ．如果点M 在CD 上，则AM BM +D ．过线段一个三等分点且与 12．若存在实常数k 和b ，使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足：()F x kx b ≥+和()G x kx b ≤+恒成立，则称此直线y kx b =+为()F x 和()G x 的“隔离直线”，已知函数()2f x x =（R x ∈），()1g x x=（0x <），()2eln h x x =（e 为自然对数的底数），则（ ）A ．()()()m x f x g x =−在x ⎛⎫∈ ⎪⎝⎭内单调递增B ．()f x 和()g x 间存在“隔离直线”，且k 的取值范围是[]4,1−C ．()f x 和()g x 之间存在“隔离直线”，且b 的最小值为1−三､填空题：本题共4小题，每小题5分，共20分.13．已知随机变量X 服从正态分布()28,X N σ~，(10)P x m ≥=，(68)P x n ≤≤=，则182m n+的最小值为____________．14．某中学元旦晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在节目乙的前面,节目丙不能排在最后一位,则该晚会节目演出顺序的编排方案共有_________． 15．=−−20cos 6420cos 120sin 3222_________． 16．已知函数()eln 2x f x x =，()22x g x x m=−，若函数()()()h x g f x m =+有3个不同的零点x 1，x 2，x 3(x 1＜x 2＜x 3)，则()()()1232f x f x f x ++的取值范围是_________．四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.17．已知.2,4,53)4sin(,4,0,553cos sin ⎪⎭⎫⎝⎛∈=−⎪⎭⎫ ⎝⎛∈=+ππβπβπααα （1）求α2sin 和α2tan 的值； （2）求()βα2cos +的值.18．已知2mx⎛⎝的展开式中，第4项的系数与倒数第4项的系数之比为.（1）求m 的值；（2）求展开式中所有项的系数和与二项式系数和； （3）将展开式中所有项重新排列，求有理项不相邻的概率.19．已知函数2()(,)f x x bx c b c R =++∈，且()0f x ≤的解集为[1,2]−. （1）求函数()f x 的解析式；（2）解关于x 的不等式mf(x)>2(x −m −1)；（3）设g(x)=2f(x)+3x−1，若对于任意的x 1,x 2∈[−2,1]都有()()12g x g x M −≤，求M 的最小值.20．某学校共有2000名学生，其中女生1200人，为了解该校学生在学校的月消费情况，采取分层抽样随机抽取了200名学生进行调查，月消费金额分布在550～1050元之间．根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示，将月消费金额不低于850元的学生称为“高消费群”．(1)求a 的值，并估计该校学生月消费金额的平均数；（同一组中的数据用该组区间的中点值作代表）(2)若样本中属于“高消费群”的男生有10人，完成下列2×2列联表，并判断是否有99.9%以上的把握认为该校学生属于“高消费群”与“性别”有关．（()()()()()2n ad bc K a b c d a c b d −=++++，其中n ＝a ＋b ＋c ＋d ）21．在多面体ABCDE 中，平面ACDE ⊥平面ABC ，四边形ACDE 为直角梯形，CD ∥AE ，AC ⊥AE ，AB ⊥BC ，CD =1，AE =AC =2，F 为DE 的中点，且点E 满足4EB EG =．（1）证明：GF ∥平面ABC ；（2）当多面体ABCDE 的体积最大时，求二面角A -BE -D 的余弦值．22．已知函数()e cos x f x x x =+．(1)判断函数()f x 在[0,)+∞上的单调性，并说明理由；(2)对任意的0x ≥，e sin cos 2x x x x ax ++≥+，求实数a 的取值范围．湖南省雅礼中学高三年级第一次月考数学试卷参考答案一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．B 2．B 3．D 4．B 5．B 6．A 7．B 8．D二､多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．ACD 10．AC 11．ACD 12．AD三､填空题：本题共4小题，每小题5分，共20分.13．25 14．300种 15．-32 16．()11002⎛⎫−⋃ ⎪⎝⎭，，四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.17．18．（1）展开式的通项为()152222122rrm m rrr r r mm T C x x C x −−−+⎛⎫=⋅⋅=⋅⋅ ⎪⎝⎭， ∴展开式中第4项的系数为332m C ⋅，倒数第4项的系数为332m m m C −−⋅，33332122m m m m C C −−⋅∴=⋅，即611,722m m −=∴=. （2）令1x =可得展开式中所有项的系数和为732187=，展开式中所有项的二项式系数和为72128=.（3）展开式共有8项，由（1）可得当522rm −为整数，即0,2,4,6r =时为有理项，共4项， ∴由插空法可得有理项不相邻的概率为484485 114A A A =. 19．（1）因为()0f x ≤的解集为[1,2]−，所以20x bx c ++=的根为1−，2， 所以1b −=，2c =−，即1b =−，2c =−；所以2()2f x x x =−−；（2）mf(x)>2(x −m −1)，化简有()222(1)m x x x m −−>−−，整理得(2)(1)0mx x −−>，所以当0m =时，不等式的解集为(,1)−∞，当02m <<时，不等式的解集为2(,1),⎛⎫−∞+∞ ⎪⎝⎭m ，当2m =时，不等式的解集为(,1)(1,)−∞+∞， 当2m >时，不等式的解集为()2(,)1,−∞+∞m，（3）因为[2,1]x ∈−时2()3123f x x x x +−=+−，根据二次函数的图像性质，有2()3123[4,0]f x x x x +−=+−∈−， 则有2()3123()22f x x xx g x +−+−==，所以，1(),116⎡⎤∈⎢⎥⎣⎦g x ，因为对于任意的x 1,x 2∈[−2,1]都有()()12g x g x M −≤， 即求()()12max g x g x M −≤，转化为()()−≤max min g x g x M ， 而()(1)1==max g x g ， 1()(1)16min g x g =−=， 所以，此时可得1516M ≥， 所以M 的最小值为1516. 20．（1）由频率分布直方图中所有小矩形的面积之和为1得到方程，解得a ，再根据频率分布直方图中平均数计算公式计算可得；（2）按照分层抽样求出样本中男生、女生的人数，再由频率分布直方图求出“高消费群”的人数，即可完善列联表，计算出卡方，即可判断； （1）解：由频率分布直方图可得()1000.00150.00350.00150.0011a ⨯++++=，解得0.0025a =， 所以样本的平均数为()6000.00157000.00358000.00259000.001510000.001100770⨯+⨯+⨯+⨯+⨯⨯=（元）（2）解：依题意知，样本中男生20001200200802000−⨯=人，女生12002001202000⨯=人，属于“高消费群”的有()0.00150.00110020050+⨯⨯=人，列出下列22⨯列联表：所以22001080407011.1110.828 5015080120K⨯−⨯=≈>⨯⨯⨯，所以有99.9%以上的把握认为该校学生属于“高消费群”与“性别”有关．21．（1）取AB，EB中点M，N，连接CM，MN，ND．在梯形ACDE中，DC∥EA且DC=12EA，且M，N分别为BA，BE中点，∴MN//EA，MN=12EA，∴MN//CD，MN=CD，即四边形CDNM是平行四边形，∴CM//DN，又14EG EB=，N为EB中点，∴G为EN中点，又F为ED中点，∴GF//DN，即GF//CM，又CM⊂平面ABC，GF⊄平面ABC，∴GF∥平面ABC．（2）在平面ABC内，过B作BH⊥AC交AC于H．∴平面ACDE⊥平面ABC，平面ACDE平面ABC=AC，BH⊂平面ABC，BH⊥AC，∴BH⊥平面ACDE，则BH为四棱锥B-ACDE的高，又底面ACDE 面积确定，要使多面体ABCDE 体积最大，即BH 最大，此时AB =BC过点H 作HP ∥AE ，易知HB ，HC ，HP 两两垂直，以{HB ,HC ,HP }为正交基底建立如图所示的平面直角坐标系H -xyz ，∴A (0,−1,0)，B (1,0,0)，E (0,−1,2)，D (0,1,1)，则AB =(1,1,0)，BE =(−1,−1,2)，DE =(0,−2,1)．设n 1⃗⃗⃗⃗ =(x 1,y 1,x 1)为平面ABE 的一个法向量，则1100n AB n BE ⎧⋅=⎪⎨⋅=⎪⎩，即11111020x y x y z +=⎧⎨−−+=⎩，取n 1⃗⃗⃗⃗ =(1,−1,0)，设n 2⃗⃗⃗⃗ =(x 2,y 2,z 2)为平面DBE 的一个法向量，则220n DE n BE ⎧⋅=⎪⎨⋅=⎪⎩，即222222020y z x y z −+=⎧⎨−−+=⎩，取n 2⃗⃗⃗⃗ =(3,1,2)， ∴1212127cos ,7n n n n n n ⋅<>==⋅，由图知：二面角A −BE −D 为钝二面角，∴二面角A −BE −D 的余弦值为. 22．(1)解：函数()f x 在[0,)+∞上是单调增函数，理由如下： 因为()e cos x f x x x =+，所以()e cos (sin )x f x x x x =+−'+． 记()e 1x g x x =−−，则()e 1x g x '=−，令()0g x '=，得0x =． 当0x >时，()0,()'>g x g x 为单调增函数； 当0x <时，()0,()g x g x '<为单调减涵数，所以min ()(0)0g x g ==，所以()e 10x g x x =−−≥，即e 1x x ≥+． 又sin 1,cos 1x x ≤≥−，所以()1cos (sin )(1sin )(1cos )0f x x x x x x x x ≥+++−=−++≥'， 所以函数()f x 在[0,)+∞上是单调增函数． (2)解：记()e sin cos 2(0)x p x x x ax x =++−−≥，是()e cos x p x x x a =+−'． 由（1）知，()e cos x p x x x a =+−'为[0,)+∞上的单调增函数．1°当10a −≥时，(0)10p a =−≥'，所以()(0)0p x p ''≥≥，所以()p x 为[0,)+∞上的单调增函数，所以()(0)0p x p ≥=，即e sin cos 2x x x x ax ++≥+．所以1a ≤符合题意． 2°当10a −<时，(0)10p a =−<'，又()e cos e 2a a p a a a a a =−≥'+−． 记()e 2(1)x q x x x =−>，则()e 2e 20x q x =−>−>'，所以()q x 为(1,)+∞上的单调增函数，所以()(1)e 20q x q >=−>， 所以e 20(1)x x x −>>，所以()e 20a p a a ≥−>'．又()p x 在[0,)+∞上的图象不间断，且()p x 为[0,)+∞上的单调增函数， 根据零点存在性定理知，存在唯一的零点0(0,)x ∈+∞，使得()00p x =． 所以当00x x ≤≤时，()0p x '≤，()p x 单调递减，所以()0(0)0p x p <=， 这与任意的0x ≥，e sin cos 2x x x x ax ++≥+矛盾， 所以1a >不符合题意 综上可得1a ≤．。

2024-2025学年湖南省长沙市雅礼中学高三（上）月考数学试卷（一）一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知集合A ={x |log 2x >1}，B ={x |0<x <4}，则A ∩B =( )A. {x |2<x <4}B. {x |2⩽x <4}C. {x |0<x⩽2}D. {x |x⩽2}2.已知复数z 满足(1―i )z =2i ，且z +ai (a ∈R )为实数，则a =( )A. 1B. 2C. ―1D. ―23.设向量a =(1,0)，b =(12,12)，则下列结论中正确的是( )A. |a |=|b | B. a ⋅b = 22 C. a ―b 与b 垂直 D. a //b4.已知a 是函数f (x )=2x ―log 12x 的零点，若0<x 0<a ，则f (x 0)的值满足( )A. f (x 0)=0B. f (x 0)>0C. f (x 0)<0D. f (x 0)的符号不确定5.若sinx +cosx =13，x ∈(0,π)，则sinx ―cosx 的值为( )A. ± 173 B. ― 173 C. 13 D. 1736.用数字1，2，3，4，5组成的无重复数字的四位偶数的个数为( )A. 8B. 24C. 48D. 1207.函数y =f (x )的图象如图①所示，则如图②所示的函数图象所对应的函数解析式可能为( )A. y =f (1―12x )B. y =―f (1―12x )C. y =f (4―2x )D. y =―f (4―2x )8.刍曹是我国传统建筑造型之一，蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓，展现造型之美.如图，某屋顶可视为五面体ABCDEF ，四边形ABFE 和CDEF 是全等的等腰梯形，△ADE 和△BCF 是全等的等腰三角形.若AB =25m ，BC =AD =10m ，且等腰梯形所在的面、等腰三角形所在的面与底面夹角的正切值均为145.为这个模型的轮廓安装灯带(不计损耗)，则所需灯带的长度为( )A. 102mB. 112mC. 117mD. 125m二、多选题：本题共3小题，共18分。

绝密★启用前 炎德•英才大联考湖南省长沙市雅礼中学2020届高三毕业班高考适应性月考卷(一)数学(文)试题(解析版)本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.时量120分钟.满分150分.第Ⅰ卷一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.1.已知集合2}{0|A x x x =-<（），{|11}B x x =-<<，则A B =（） A. {|12}x x -<<B. {|1x x <-或2x >}C. {|01}x x <<D. {|0x x <或}【答案】C【解析】【分析】 求出A 中不等式的解集，找出两集合的交集即可【详解】由题意可得{|02}A x x =<<,{|11}B x x =-<<,所以{|01}A B x x =<<.故选C.【点睛】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键．2.已知复数2a i i +-是纯虚数（i 是虚数单位）,则实数a 等于 A. -2B. 2C. 12D. -1【答案】C【解析】2a i i +-21255a a i -+=+是纯虚数,所以21210,0552a a a -+=≠∴=,选C.3.“26m <<”是“方程22126x y m m+=--为椭圆”的（ ） A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B【解析】 试题分析：若方程22126x y m m +=--表示椭圆,则20{6026m m m m ->->-≠-,解得26m <<且4m ≠,所以26m <<是方程22126x y m m+=--表示椭圆的必要不充分条件,故选B ． 考点：椭圆的标准方程；必要不充分条件的判定．4.如果()()221f x ax a x =--+在区间1,2⎛⎤-∞ ⎥⎝⎦上为减函数,则a 的取值（ ） A. (]0,1B. [)0,1C. [] 0,1D. ()0,1【答案】C【解析】【分析】 根据题意,利用一元二次函数的性质,对a 进行讨论,即可推得答案．【详解】由题意,当0a =时,可得()21f x x =-+,在R 上是单调递减,满足题意,当0a <时,显然不成立；当0a >时,要使()f x 在1,2⎛⎤-∞ ⎥⎝⎦上为减函数,则2122a a -≥,解得：1,01a a ≤∴<≤.综上：可得01a ≤≤故选C .【点睛】本题主要考查根据一元二次函数的性质求参数．5.已知函数()sin()(0)2f x x πωφωϕ=+><，图象相邻两条对称轴之间的距离为2π,将函数()y f x =的图象向左平移3π个单位后,得到的图象关于y 轴对称,那么函数。

雅礼中学2020届高三月考试卷（六）数 学（文科）注意事项：1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上.2. 回答第Ⅰ卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.写在本试卷上无效.3. 回答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效.4. 考试结束后，将本试卷和答题卡一并交回.第Ⅰ卷一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.1.集合{}13A x x =<<，集合{}2,B y y x x A ==-∈，则集合A B =（ ）A. {}13x x << B. {}13x x -<<C. {}11x x -<<D. ∅【答案】D 【解析】 【分析】求出集合B ，利用交集的定义可求得集合AB .【详解】因为{}13A x x =<<，{}{}2,11B y y x x A y y ==-∈=-<<，所以A B =∅，故选：D.【点睛】本题考查交集的计算，考查计算能力，属于基础题. 2.复数12z i =-的虚部为( ) A. 2i B. 2i -C. 2D. -2【答案】D 【解析】 【分析】根据复数的概念可知复数12z i =-的虚部.【详解】形如(,)a bi a R b R +∈∈的数叫做复数，a 和b 分别叫它的实部和虚部,所以复数12z i =-的虚部为-2. 故选：D.【点睛】考查复数的概念，知识点较为基础.3.已知()f x 是定义在R 上的偶函数,且在(],0-∞上是减函数,设()20.3a f =,()2log 5b f =,()0.32c f =,则,,a b c 的大小关系是()A. b c a <<B. a b c <<C. c b a <<D. a c b <<【答案】D 【解析】 【分析】根据偶函数的对称性可知()f x 在[)0,+∞上为增函数；通过临界值比较出自变量的大小关系，根据单调性可得结果. 【详解】()f x 是R 上的偶函数，且在(],0-∞上为减函数 ()f x ∴在[)0,+∞上为增函数0.30222log 5log 422210.30>=>>=>>()()()0.322log 520.3f f f ∴>>，即a c b <<本题正确选项：D【点睛】本题考查根据函数单调性比较函数值大小的问题，关键是能够利用奇偶性的性质得到函数在自变量所在区间内的单调性，通过自变量大小关系的比较得到函数值的大小关系. 4.若实数x ，y 满足x +y ＞0，则“x ＞0”是“x 2＞y 2”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件【答案】B 【解析】 【分析】根据充分条件、必要条件的判定方法，结合不等式的性质，即可求解，得到答案． 【详解】由题意，实数x ，y 满足x +y ＞0，若x ＞0，则未必有x 2＞y 2， 例如x ＝1，y ＝2时，有x 2＜y 2；反之，若x 2＞y 2，则x 2﹣y 2＞0，即（x +y ）（x ﹣y ）＞0；由于x +y ＞0，故x ﹣y ＞0，∴x ＞y 且x ＞﹣y ，∴x ＞0成立；所以当x +y ＞0时，“x ＞0”推不出“x 2＞y 2”，“x 2＞y 2”⇒“x ＞0”； ∴“x ＞0”是“x 2＞y 2”的必要不充分条件． 答案：B ．【点睛】本题主要考查了不等式的性质，以及充分条件、必要条件的判定，其中解答中熟记充分条件、必要条件的判定方法，结合不等式的性质求解是解答的关键，着重考查了推理与论证能力，属于基础题．5.在长方形ABCD 中，2AB =，1AD =，点E 为BC 的中点，点F 为CD 的中点，则AE BF ⋅=（ ）A. 1-B. 32-C. 2-D. 52-【答案】B 【解析】 【分析】根据题意，得到12=+=+AE AB BE AB AD ，12BF BC CF AD AB =+=-，再由向量数量积的运算法则，直接计算，即可得出结果.【详解】因为在长方形ABCD 中，2AB =，1AD =，点E 为BC 的中点，点F 为CD 的中点，所以12=+=+AE AB BE AB AD ，12BF BC CF AD AB =+=- 1122⎛⎫∴⋅=+⋅⎛⎫ ⎪⎝-+ ⎪⎝⎭⎭AE BF A D A B A AB D 2211313222422AB AD AB AD =-++⋅=-+=-.故选：B【点睛】本题主要考查向量的数量积运算，熟记运算法则即可，属于常考题型.6.一只小虫在边长为2的正方形内部爬行，到各顶点的距离不小于1时为安全区域，则小虫在安全区域内爬行的概率是（ ） A. 14π-B.4πC. 16π-D.6π【解析】 【分析】作出正方形，并作出安全区域，将安全区域的面积与正方形的面积相除可得出所求事件的概率.【详解】如下图所示，由于小虫到每个顶点的距离不小于1为安全区域，则安全区域为以正方形每个顶点为圆心半径为1的扇形弧以及扇形以外的部分，为图中阴影部分，其面积22214S ππ=⨯-⨯=-，故概率4144P ππ-==-. 故选：A.【点睛】本题为平面区域型几何概率问题，确定事件所围成的区域是解题的关键，考查数形结合思想与计算能力，属于中等题.7.已知函数()2sin()(0,0)f x x ωϕωϕπ=+><<的最小正周期为π，若将()f x 的图象向左平移3π个单位后得到函数()g x 的图象关于y 轴对称，则函数()f x 的图象（ ） A. 关于直线2x π=对称 B. 关于直线3x π=对称 C. 关于点(,0)2π对称 D. 关于点(,0)3π对称【答案】B 【解析】 【详解】由条件知22,w wππ=⇒= 2()2sin(2)()2sin(2())2sin(2)33f x xg x x x ππϕϕϕ=+⇒=++=++ 关于y 轴对称，可得(0)2g =±，可得2,6k k z πϕπ=-+∈ ，0ϕπ<<，所以56πϕ=，故得5()2sin(2)6f x x π=+，当,() 2.3x f x π==- 对称中心为：5,0212k k z ππ⎛⎫-∈⎪⎝⎭C ，D ，均不正确.点睛：此题考查的是函数图像的平移和对称，周期性，先根据周期的公式得到2w =， 再根据平移公式得到()g x ，根据轴对称性得到56πϕ=，故得5()2sin(2)6f x x π=+，可以根据选项代入表达式，比如B 选项，可以带入函数判断函数值是否为最值；8.已知实数x ，y 满足521802030x y x y x y +-≤⎧⎪-≥⎨⎪+-≥⎩，若直线10kx y -+=经过该可行域，则实数k 的最大值是（ ） A. 1 B.32C. 2D. 3【答案】B 【解析】 【分析】先根据约束条件画出可行域，再利用直线20kx y -+=过定点()0,1，再利用k 的几何意义，只需求出直线10kx y -+=过点()2,4B 时，k 值即可． 【详解】直线20kx y -+=过定点()0,1， 作可行域如图所示，，由5218020x y x y +-=⎧⎨-=⎩，得()2,4B ．当定点()0,1和B 点连接时，斜率最大，此时413202k -==-，则k 的最大值为：32故选：B ．【点睛】本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题． 9.两个等差数列{}n a 和{}n b ，其前n 项和分别为n S ，n T ，且723n n S n T n +=+，则220715a ab b +=+（ ） A.49B.378C.7914D.14924【答案】D 【解析】 【分析】根据等差数列的性质前n 项和的性质进行求解即可.【详解】因为等差数列{}n a 和{}n b ,所以2201111715111122a a a a b b b b +==+,又211121S a =,211121T b =,故令21n =有2121721214921324S T ⨯+==+,即1111211492124a b =,所以111114924a b = 故选D.【点睛】本题主要考查等差数列的等和性质：若{}n a 是等差数列,且(,,,*)m n p q m n p q N +=+∈,则m n p q a a a a +=+ 与等差数列{}n a 前n 项和n S 的性质*21(21),()n n S n a n N -=-∈10.已知三个实数2、b 、8成等比数列，则双曲线22219y x b-=的渐近线方程为（ ）A. 340±=x yB. 430x y ±=20y ±=D.9160x y ±=【答案】A 【解析】 【分析】根据等比中项的定义求得2b 的值，可得出双曲线的标准方程，进而可求得双曲线的渐近线方程.【详解】由题意，三个实数2、b 、8成等比数列，可得216b =，即双曲线221916y x -=的渐近线方程为340±=x y ，故选：A.【点睛】本题考查双曲线渐近线方程的求解，解答的关键就是求出双曲线的标准方程，考查计算能力，属于基础题.11.定义在R 上的偶函数()f x 在[)0,∞+单调递增，且()f 21-=，则()f x 21-≤的x 的取值范围是（ ） A. []0,4 B. (][),22,∞∞--⋃+ C. (][),04,∞∞-⋃+ D. []2,2-【答案】A 【解析】 【分析】先得()21f =，再根据偶函数化简()21f x -≤，即为()()22fx f -≤，由单调性可得22x -≤，运用绝对值不等式的解法可得x 的取值范围.【详解】定义在R 上的偶函数()f x 在[)0,+∞单调递增， 且()21f -=，可得()()221f f =-=，()21f x -≤，即为()()22f x f -≤，可得22x -≤， 即222x -≤-≤， 解得04x ≤≤，即x 的取值范围是[]0,4，故选A.【点睛】首先根据函数的性质把不等式转化为(())(())f g x f h x >的形式，然后根据函数的单调性去掉“f ”，转化为具体的不等式(组)，此时要注意()g x 与()h x 的取值应在外层函数的定义域内.12.已知函数(),()ln 1xf x e eg x x =-=+，若对于1x ∀∈R ，()20x ∃∈+，∞，使得()()12f x g x ＝，则12x x -的最大值为（ ）A. eB. 1-eC. 1D. 11e-【答案】D 【解析】 【分析】不妨设f(1x )=g(2x )＝a ，从而可得12x x -的表达式，求导确定函数的单调性，再求最小值即可．【详解】不妨设f(1x )=g(2x )＝a ， ∴1x e e -＝21lnx +=a ， ∴1x ＝ln(a+e)，2x ＝1a e -， 故12x x -＝ln(a+e)-1a e -，（a ＞-e ） 令h （a ）＝ln(a+e)-1a e -，h ′（a ）11a e a e-=-+， 易知h ′（a ）在（-e ，+∞）上是减函数， 且h ′（0）＝0，故h （a ）在a 0=处有最大值， 即12x x -的最大值为11e-； 故选D ．【点睛】本题考查了函数的性质应用及导数的综合应用，考查了指对互化的运算，属于中档题．第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分.13.若1sin()43πα-=，则cos()4πα+=__________．【答案】13;【解析】由题意得，1()cos()sin()424443πππππαααα+=--⇒+=-=.14.已知向量a ，b 的夹角为34π，()3,4,10a a b =-⋅=-，则b 的模长是______．【答案】22 【解析】 【分析】由平面向量模的运算及数量积的运算得：由向量，的夹角为，=（-3，4），=-10，得=||||cos =-10，即||==2，得解．【详解】由向量，的夹角为，=（-3，4），=-10，得=||||cos=-10，即||==2，故答案为2．【点睛】本题考查了平面向量模的运算及数量积的运算，属中档题．15.直角ABC 的三个顶点都在球O 的球面上，2AB AC ==，若球O 的表面积为12π，则球心O 到平面ABC 的距离等于__________． 【答案】1 【解析】直角ABC 的斜边CB 为ABC 所在截面小圆的直径，则该截面小圆的半径为2r =的表面积为12π可得球的半径3R ，球心O 到平面ABC 的距离221d R r =-=.16.设(),()f x g x 是定义在R 上两个周期函数，()f x 的周期为4，()g x 的周期为2，且()f x 是奇函数.当2(]0,x ∈时，2()1(1)f x x =--，(2),01()1,122k x x g x x +<≤⎧⎪=⎨-<≤⎪⎩，其中0k >.若在区间(0]9，上，关于x 的方程()()f x g x =有8个不同的实数根，则k 的取值范围是_____.【答案】12,34⎡⎫⎪⎢⎪⎣⎭.【解析】【分析】分别考查函数()f x和函数()g x图像的性质，考查临界条件确定k的取值范围即可.【详解】当(]0,2x∈时，()2()11,f x x=--即()2211,0.x y y-+=≥又()f x为奇函数，其图象关于原点对称，其周期为4，如图，函数()f x与()g x的图象，要使()()f xg x=在(]0,9上有8个实根，只需二者图象有8个交点即可.当1g()2x=-时，函数()f x与()g x的图象有2个交点；当g()(2)x k x=+时，()g x 的图象为恒过点()2,0-的直线，只需函数()f x与()g x的图象有6个交点.当()f x与()g x图象相切时，圆心()1,0到直线20kx y k-+=的距离为1，即2211k kk+=+，得24k=，函数()f x与()g x的图象有3个交点；当g()(2)x k x=+过点1,1（）时，函数()f x与()g x的图象有6个交点，此时13k=，得13k=.综上可知，满足()()f xg x=在(]0,9上有8个实根的k的取值范围为1234⎡⎢⎣⎭，.【点睛】本题考点为参数的取值范围，侧重函数方程的多个实根，难度较大.不能正确画出函数图象的交点而致误，根据函数的周期性平移图象，找出两个函数图象相切或相交的临界交点个数，从而确定参数的取值范围.三、解答题：本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答. （一）必考题：共60分.17.在ABC ∆中，,,a b c 分别为角,,A B C 的对边，且满足274cos cos 2()22A B C -+= （Ⅰ）求角A 的大小；（Ⅱ）若3b c +=，求a 的最小值． 【答案】（Ⅰ）60o A ∴= （Ⅱ）32【解析】 （Ⅰ）A B C π++=，2274cos cos 2()2(1cos )cos 22cos 2cos 322A B C A A A A ∴-+=+-=-++=， 212cos 2cos 02A A ∴-+=．1cos 2A ∴=，0A π<<，60o A ∴=．（Ⅱ）由余弦定理222cos 2b c a A bc+-=，得222bc b c a =+-．2229()39393()24b c a b c bc bc +∴=+-=-≥-=， 32a ∴≥．所以a 的最小值为32， 当且仅当32b c ==时取等号．18.2019年2月13日《烟台市全民阅读促进条例》全文发布，旨在保障全民阅读权利，培养全民阅读习惯，提高全民阅读能力，推动文明城市和文化强市建设．某高校为了解条例发布以来全校学生的阅读情况，随机调查了200名学生每周阅读时间X （单位：小时）并绘制如图所示的频率分布直方图．（1）求这200名学生每周阅读时间的样本平均数x 和中位数a （a 的值精确到0.01）； （2）为查找影响学生阅读时间的因素，学校团委决定从每周阅读时间为[6.5,7.5)，[7.5,8.5)的学生中抽取9名参加座谈会． （i ）你认9个名额应该怎么分配？并说明理由；（ii ）座谈中发现9名学生中理工类专业的较多．请根据200名学生的调研数据，填写下面的列联表，并判断是否有95%的把握认为学生阅读时间不足（每周阅读时间不足8.5小时）与“是否理工类专业”有关？阅读时间不足8.5小时 阅读时间超过8.5小时 理工类专业 40 60 非理工类专业附：22()()()()()n ad bc K a b c d a c b d -=++++（n a b c d =+++）.临界值表：20()P K k ≥ 0.150.10 0.05 0.025 0.010 0.005 0.0010k2.072 2.7063.841 5.024 6.635 7.879 10.828【答案】（1）平均数9，中位数8.99；（2）（i ）按照1:2进行名额分配；理由见详解； （ii ）有.【解析】 【分析】（1）根据平均数，中位数的定义进行求解即可（2）完成列联表，计算2K 的观测值，结合独立性检验的性质进行判断即可. 【详解】（1）该组数据的平均数60.0370.180.290.35100.19x =⨯+⨯+⨯+⨯+⨯110.09120.049+⨯+⨯=，因为0.030.10.20.350.680.5+++=>，所以中位数[8.5,9.5)a ∈， 由0.030.10.2(8.5)0.350.5a +++-⨯=，解得0.50.338.58.990.35a -=+≈；（2）（i ）每周阅读时间为[6.5,7.5)的学生中抽取3名，每周阅读时间为[7.5,8.5)的学生中抽取6名．理由：每周阅读时间为[6.5,7.5)与每周阅读时间为[7.5,8.5)是差异明显的两层，为保持样本结构与总体结构的一致性，提高样本的代表性，宜采用分层抽样的方法抽取样本；因为两者频率分别为0.1，0.2，所以按照1:2进行名额分配．（ii ）由频率分布直方图可知，阅读时间不足8.5小时的学生共有200(0.030.10.2)66⨯++=人，超过8.5小时的共有20066134-=人．于是列联表为：2K 的观测值2200(40742660)4.432 3.84166134100100k ⨯⨯-⨯=≈>⨯⨯⨯， 所以有95%的把握认为学生阅读时间不足与“是否理工类专业”有关．【点睛】本题主要考查独立性检验的应用，根据数据计算出K 2的观测值是解决本题的关键．考查学生的计算能力．19.如图1，等腰梯形ABCD 中，AD BC ∥，2AB AE BE CD ====，4BC ED ==，O 为BE 中点，F 为BC 中点.将ABE △沿BE 折起到A BE '的位置，如图2.（1）证明：CD ⊥平面AOF '；（2）若平面A BE '⊥平面BCDE ，求点F 到平面A EC '的距离. 【答案】（1）证明见解析；（2）32. 【解析】 【分析】（1）先证CD EC ⊥，接着证CD OF ⊥，根据已知条件得AO CD '⊥，即可得结论；（2）点F 到平面A EC '的距离转化为点B 到平面A EC '的距离的一半，取A E '的中点记为H ，证明BH ⊥平面A EC '，求出BH ，即可得结论.【详解】（1）23EC =，∴222BE EC BC +=，即BE EC ⊥， ∵CDBE ，∴CD EC ⊥O 为BE 中点，F 为BC 中点.∴OF EC ∥，∴CD OF ⊥∵A B A E ''=，O 为BE 中点，∴AO BE '⊥，∴AO CD '⊥ 而AO OF O '⋂=，∴CD ⊥平面AOF'.（2）OF EC ∥∴点F 到平面AEC 的距离即为点O 到平面A EC '的距离， 即点B 到平面A EC '的距离的一半.取A E '的中点记为H ，连结BH ，则BH A E '⊥∵平面A BE '⊥平面BCDE ，且交线为BE ， 由（1）知EC BE ⊥，∴EC ⊥平面A BE '，∴EC BH ⊥， 又EC A E E '⋂=∴BH ⊥平面A EC '，BH =， ∴B 到平面A EC '∴点F 到平面A EC '【点睛】本题考查了平面立体转化的问题，运用好折叠之前，之后的图像，考查线面垂直以及点的面的距离，解题的关键是对空间直线与平面的位置关系定理要熟练，属于中档题.20.已知椭圆()2222:10x y C a b a b +=>>过点()2,1，且离心率e =(1)求椭圆C 的方程； (2)已知斜率为12的直线l 与椭圆C 交于两个不同点,A B ，点P 的坐标为()2,1，设直线PA 与PB 的傾斜角分别为,αβ，证明:αβπ+=.【答案】（1）22:182x y C +=（2）证明见解析【解析】 【分析】（1）根据题意，由椭圆的几何性质可得，解可得a 、b 的值，将a 、b 的值代入椭圆的方程即可得答案；22411a b e ⎧+=⎪⎪⎨⎪==⎪⎩（2）证明αβπ+=即证明直线PA 与PB 的斜率120k k +=，根据题意，设直线1:2l y x m =+，联立直线与椭圆的方程，将韦达定理代入1211221122y x k k y x +--+=--变形即可证明．【详解】()1由题意得22411a b e ⎧+=⎪⎪⎨⎪==⎪⎩228,2a b ==，所以椭圆的方程为：22:182x y C +=()2设直线1:2l y x m =+，由2212182y x m x y ⎧=+⎪⎪⎨⎪+=⎪⎩，消去y 得，222240x mx m ++-=，2248160m m =-+>解得22m -<<，当0m =时，12y x =（舍） 设()()1122,,,A x y B x y ，则212122,24x x m x x m +=-=- 由题意，易知PA 与PB 的斜率存在，所以,2παβ≠，设直线PA 与PB 的斜率分别为12,k k则1tan k α=，2tan k β=，要证αβπ+=，即证()tan tan tan απββ=-=-，只需证120k k +=12121211,,22y y k k x x --==-- 故()()()()()()1221121122121212112222y x y x y y x x x x k k --+----+=-=---+又111,2y x m =+2212y x m =+ 所以()()()()12211212y x y x --+--=()()122111121222x m x x m x ⎛⎫⎛⎫+--++--⎪ ⎪⎝⎭⎝⎭， ()()()1212241x x m x x m =+-+--()()()2122422410x x m m m m =-+----=120,k k ∴+=αβπ+=【点睛】本题考查椭圆的方程，考查直线与椭圆的位置关系。