图形旋转练习题

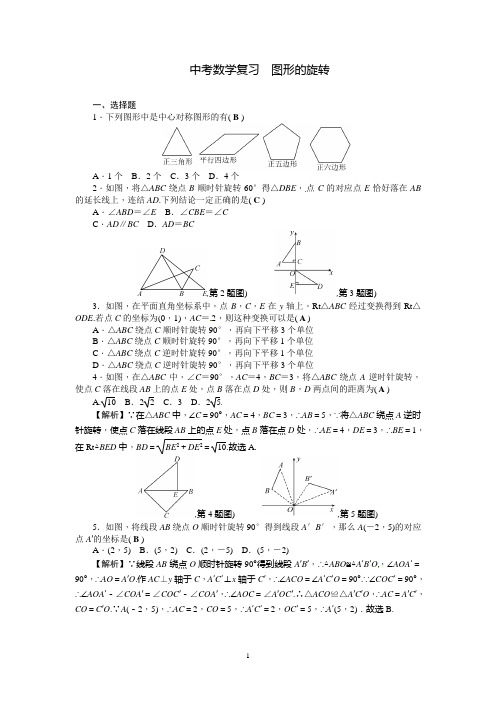
中考数学复习图形的旋转一、选择题1．下列图形中是中心对称图形的有( B )A．1个B．2个C．3个D．4个2．如图，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB 的延长线上，连结AD.下列结论一定正确的是( C )A．∠ABD＝∠E B．∠CBE＝∠CC．AD∥BC D．AD＝BC,第2题图),第3题图) 3．如图，在平面直角坐标系中，点B，C，E在y轴上，Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0，1)，AC＝2，则这种变换可以是( A )A．△ABC绕点C顺时针旋转90°，再向下平移3个单位B．△ABC绕点C顺时针旋转90°，再向下平移1个单位C．△ABC绕点C逆时针旋转90°，再向下平移1个单位D．△ABC绕点C逆时针旋转90°，再向下平移3个单位4．如图，在△ABC中，∠C＝90°，AC＝4，BC＝3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B，D两点间的距离为( A )A.10 B．2 2 C．3 D．25【解析】∵在△ABC中，∠C＝90°，AC＝4，BC＝3，∴AB＝5，∵将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，∴AE＝4，DE＝3，∴BE＝1，在Rt△BED中，BD＝BE2＋DE2＝10.故选A.,第4题图),第5题图) 5．如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A(－2，5)的对应点A′的坐标是( B )A．(2，5) B．(5，2) C．(2，－5) D．(5，－2)【解析】∵线段AB绕点O顺时针旋转90°得到线段A′B′，∴△ABO≌△A′B′O，∠AOA′＝90°，∴AO＝A′O.作AC⊥y轴于C，A′C′⊥x轴于C′，∴∠ACO＝∠A′C′O＝90°.∵∠COC′＝90°，∴∠AOA′－∠COA′＝∠COC′－∠COA′，∴∠AOC＝∠A′OC′.∴△ACO≌△A′C′O，∴AC＝A′C′，CO＝C′O.∵A(－2，5)，∴AC＝2，CO＝5，∴A′C′＝2，OC′＝5，∴A′(5，2)．故选B.6．如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连结AD，BD.则下列结论：①AC＝AD；②BD⊥AC；③四边形ACED是菱形．其中正确的个数是( D ) A．0个B．1个C．2个D．3个【解析】∵将等边△ABC绕点C顺时针旋转120°得到△EDC，∴∠ACE＝120°，∠DCE ＝∠BCA＝60°，A C＝CD＝DE＝CE，∴∠ACD＝120°－60°＝60°，∴△ACD是等边三角形，∴AC＝AD，AC＝AD＝DE＝CE，∴四边形ACED是菱形，∵将等边△ABC绕点C顺时针旋转120°得到△EDC，AC＝AD，∴AB＝BC＝CD＝AD，∴四边形ABCD是菱形，∴BD⊥AC，∴①②③都正确，故选D.二、填空题7．如图，将△AOB绕点O按逆时针方向旋转45°后得到△COD，若∠AOB＝15°，则∠AOD的度数是__60°__．,第7题图),第8题图) 8．如图，在平面直角坐标系xOy中，△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的，写出一种由△OCD得到△AOB的过程：__将△COD绕点C顺时针旋转90°，再向左平移2个单位长度得到△AOB(答案不唯一)．__．9．如图，在△ABC中，∠A＝70°，AC＝BC，以点B为旋转中心把△ABC按顺时针旋转α度，得到△A′BC′，点A恰好落在AC上的点A′处，连结CC′，则∠ACC′＝__110°__．【解析】∵∠A＝70°，AC＝BC，∴∠BCA＝40°，根据旋转的性质，AB＝BA′，BC＝BC′，∴∠α＝180°－2×70°＝40°，∵∠CBC′＝∠α＝40°，∴∠BCC′＝70°，∴∠ACC′＝∠ACB＋∠BCC′＝110°.10．如图，在正方形ABCD中，AD＝23，把边BC绕点B逆时针旋转30°得到线段BP，连结AP并延长交CD于点E，连结PC，则△PCE的面积为__9－53__．【解析】∵四边形ABCD是正方形，∴∠ABC＝90°，∵把边BC绕点B逆时针旋转30°得到线段BP，∴PB＝BC＝AB，∠PBC＝30°，∴∠ABP＝60°，∴△ABP是等边三角形，∴∠BAP ＝60°，AP＝AB＝23，∵AD＝23，∴AE＝4，DE＝2，∴CE＝23－2，PE＝4－23，过P作PF ⊥CD 于F ，∴PF ＝32PE ＝23－3，∴△PCE 的面积为12CE ·PF ＝12×(23－2)×(23－3)＝9－5 3.故答案为9－5 3.,第10题图) ,第11题图)11．如图，正方形ABCD 和正方形CEFG 边长分别为a 和b ，正方形CEFG 绕点C 旋转，则DE 2＋BG 2＝__2a 2＋2b 2__．【解析】连结BD ，EG ，如图所示，∴DO 2＋BO 2＝BD 2＝BC 2＋CD 2＝2a 2，EO 2＋OG 2＝EG 2＝CG 2＋CE 2＝2b 2，则BG 2＋DE 2＝DO 2＋BO 2＋EO 2＋OG 2＝2a 2＋2b 2.三、解答题12. 如图，在边长为1的正方形组成的网格中，△ABC 的顶点均在格点上，点A ，B ，C 的坐标分别是A (－2，3)，B (－1，2)，C (－3，1)，△ABC 绕点O 顺时针旋转90°后得到△A 1B 1C 1.(1)在正方形网格中作出△A 1B 1C 1；(2)在旋转过程中，点A 经过的路径AA 1︵的长度为__132π__；(3)在y 轴上找一点D ，使DB ＋DB 1的值最小，并求出D 点的坐标．,题图),答图)解：(1)如图所示： (2)在旋转过程中，点A 经过的路径AA 1︵的长度为90×π×13180＝132π (3)∵点B ，B 1在y 轴两旁，连结BB 1交y 轴于点D ，设D′为y 轴上异于D 的点，显然D′B ＋D′B 1>DB ＋DB 1，∴当点D 是BB 1与y 轴交点时，DB ＋DB 1最小．设直线BB 1的解析式为y ＝kx ＋b ，依据题意得⎩⎨⎧－k ＋b ＝2，2k ＋b ＝1，解得⎩⎨⎧k ＝－13，b ＝53，∴y ＝－13x ＋53，∴D (0，53) 13．如图，已知正方形ABCD 的边长为3，E ，F 分别是AB ，BC 边上的点，且∠EDF ＝45°，将△DAE 绕点D 逆时针旋转90°，得到△DCM .(1)求证：△DEF ≌△DMF ；(2)若AE ＝1，求FM 的长．解：(1)∵△DAE 逆时针旋转90°得到△DCM ，∴∠FCM ＝∠FCD ＋∠DCM ＝180°，∴F ，C ，M 三点共线，∴DE ＝DM ，∠EDM ＝90°，∴∠EDF ＋∠MDF ＝90°，∵∠EDF＝45°，∴∠MDF ＝∠EDF ＝45°，在△DEF 和△DMF 中，∵⎩⎨⎧DE ＝DM ，∠EDF ＝∠MDF ，DF ＝DF ，∴△DEF ≌△DMF (SAS ) (2)由(1)得EF ＝MF ，设EF ＝MF ＝x ，∵AE ＝CM ＝1，且BC ＝3，∴BM ＝BC ＋CM ＝3＋1＝4，∴BF ＝BM －MF ＝BM －EF ＝4－x ，∵EB ＝AB －AE ＝3－1＝2，在Rt △EBF 中，由勾股定理得EB 2＋BF 2＝EF 2，即22＋(4－x )2＝x 2，解得x ＝52，∴FM ＝5214．如图①，将一个边长为2的正方形ABCD 和一个长为2，宽为1的长方形CEFD 拼在一起，构成一个大的长方形ABEF .现将小长方形CEFD 绕点C 顺时针旋转至CE ′F ′D ′，旋转角为α.(1)当点D ′恰好落在EF 边上时，求旋转角α的值；(2)如图②，G 为BC 中点，且0°＜α＜90°，求证：GD ′＝E ′D ；(3)小长方形CEFD 绕点C 顺时针旋转一周的过程中，△DCD ′与△CBD ′能否全等？若能，直接写出旋转角α的值；若不能，请说明理由．解：(1)∵DC ∥EF ，∴∠DCD ′＝∠CD′E ＝α，∵sin α＝CE CD′＝CE CD ＝12，∴α＝30° (2)∵G 为BC 中点，∴GC ＝CE′＝CE ＝1.∵∠D′CG ＝∠DCG ＋∠DCD′＝90°＋α，∠DCE ′＝∠D′CE′＋∠DCD′＝90°＋α，∴∠D ′CG ＝∠DCE′.又∵CD′＝CD ，∴△GCD ′≌△E ′CD (SAS )，∴GD ′＝E′D (3)能．α＝135°或α＝315°。

小学三年级数学（下）《图形的旋转》练习题一、选择题。

1、如图，2绕中心逆时针旋转90°到（）所在的位置。

A、1B、3C、42、下面的运动属于旋转的是（）。

A、推拉抽屉B、荡秋千C、乘电梯上楼3、是图形经过（）得到的。

A、平移B、旋转C、既平稳又旋转D、无法确定4、下面（）是顺时针旋转一周后的图形。

5、开着的电风扇是属于（）现象。

A、平移B、旋转C、对称6、将下面的图形绕各自的中心点旋转12021，不能与原来图形重合的是（）二、判断题。

1、钟表上的分针运动是平移现象。

（）2、拉抽屉是旋转现象。

（）3、在推导三角形的面积公式时用到平移和旋转方法。

（）4、旋转就是绕一个点或一条轴做圆周运动。

（）5、收费站的转杆打开，旋转了180°（）三、填空题。

1、小明推开教室门，门的运动是（）现象。

2、把一个圆形绕某个点旋转，会得到一个新图形，新图形与原图形（）和（）完全相同。

3、正方形绕中心点旋转（）度与原来的图形重合，旋转一周可以重合（）次。

4、旋转是由（）和（）决定的。

5、图形旋转有三个关键要素，一是旋转的（），二是旋转的（），三是旋转、的（）6、一个长方形绕着它的长边旋转一周可以成为一个（）体。

7、看图填空。

（1）指针从A开始，（）时针旋转90°到B。

（2）指针从C开始，逆时针旋转（）到B。

（3）指针从D开始，逆时针旋转90°到（）。

四、解答题。

1、左边的图形在平面上旋转后，会和右边的哪个图形形状相同？给它涂上颜色。

2、按规律画一画。

附参考答案一、选择。

B，B，B，A，B，C二、判断。

×，×，√，√，×，三、填空。

1、旋转，2、形状和大小，3、90，4，4、旋转中心点，旋转方向，5、中心点，方向，角度，6、圆柱体，7、（1）顺时针，（2）90°，（3）C四、解答。

1、左起第一个。

2。

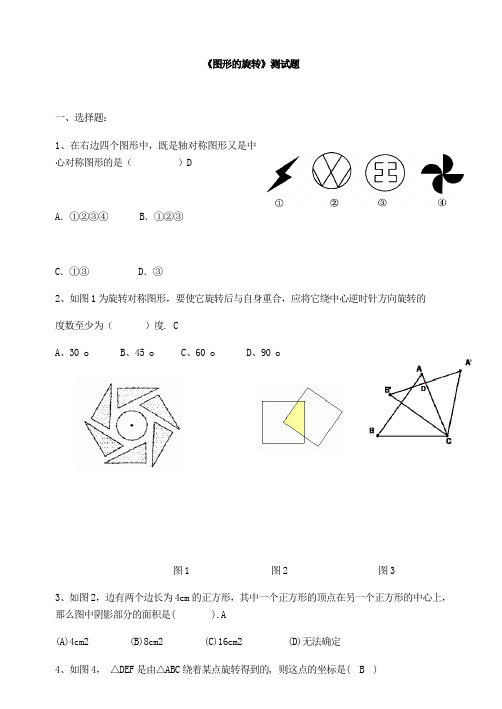
《图形的旋转》测试题一、选择题：1、在右边四个图形中，既是轴对称图形又是中心对称图形的是（）DA．①②③④ B．①②③C．①③ D．③2、如图1为旋转对称图形，要使它旋转后与自身重合，应将它绕中心逆时针方向旋转的度数至少为（）度. CA、30 oB、45 oC、60 oD、90 o图1 图2 图33、如图2，边有两个边长为4cm的正方形，其中一个正方形的顶点在另一个正方形的中心上，那么图中阴影部分的面积是( ).A(A)4cm2 (B)8cm2 (C)16cm2 (D)无法确定4、如图4，△DEF是由△ABC绕着某点旋转得到的, 则这点的坐标是( B )图5 图4 A. (1,1) B. (0,1) C. (−1,1) D. (2,0)二、填空题5、点a 4（，）与3b （，）关于原点对称，则a b += .-76、如图3，把三角形△ABC 绕着点C 顺时针旋转350，得到△A ＇B ＇C ，A ＇B ＇交AC 于点D ，若∠A ＇DC=900，则∠A 的度数是__________。

5507、如图5， △ABC 中, (ACB = 90(, (B = 30(, BC = 6, 三角板绕C 逆时针旋转, 当点A的对应点A' 落在AB 边上时即停止转动, 则BM 的长为 3 .8、如图6，△ABC 中, 已知∠C=90°, ∠B=50°, 点D 在边BC 上, BD=2CD. 把△ABC 绕着点D逆时针旋转m （0(<m<180(）度后, 如果点B 恰好落在初始Rt △ABC 的边上, 那么m = _______.80(或120(.三、解答题9、作图题（1）如图7，画出△ABC 绕点O 顺时针旋转60°所得到的图形．图6 BA CO图7 图8（2）如图8,在直角坐标系中,点P 的坐标为(3,4),将OP 绕原点O 逆时针旋转90°得到线段OP ′,(1)在图中画出线段OP ′;(2)P ′的坐标为 ______. (-4,3)1、如图，在△ABC 中，∠B=900，∠C=300，AB=1，将△ABC 绕顶点A 旋转1800，点C 落在C1处，则C C1的长为（ ）A ．24B ．4C ．32D ．522、如图，△ABC 中，∠ACB=1200，将它绕着点C 旋转300 后得到△DCE ，则∠ACE=∠A+∠E=3、如图，在Rt △ABC 中，∠ACB=90°，∠A=35°，以直角顶点C•为旋转中心，将△ABC 旋转到△A ′B ′C 的位置，其中A ′、B ′分别是A 、B 的对应点，且点B 在斜边A ′B ′上，直角边CA ′交AB 于D ，求∠BDC 的度数．4，如图，正方形ABCD 中，E 在BC 上，F 在AB 上且∠FDE=45°，•△DEC 按顺时针方向转动一个角度后成为△DGA ．（1）图中哪一个点是旋转中心？（2）旋转了多少度？（3）指出图中的对应点，对应线段和对应角；（4）求∠GDF 的度数．5、已知如图，正方形ABCD 中，E 为CD 边上一点，F 为BC 边上一点，CE=CF:(1)EBC FDC ∠∠与相等吗？（2）△DCF 能与△BCE 重合吗？（3）试判断BE 与DF 的位置关系并说明理由,6．如图所示，四边形ABCD 中，∠BAD=∠C=90°，AB=AD ，AE ⊥BC 于E ，△BEA 旋转后能与△DFA 重合．（1）旋转中心是哪一点？（2）旋转了多少度？（3）若AE=5cm ，求四边形ABCD 的面积．7，如图，K是正方形ABCD内一点，以AK为一边作正方形AKLM，使L，M，D在AK的同旁，连结BK和DM，试用旋转的思想说明线段BK与DM的关系．,8，.如图所示，等边△ABC中，D是AB边上的动点(不与A、B重合)，以CD为一边，向上作等边△EDC。

图形的旋转练习题一、选择题1. 一个图形绕某点旋转90度后，其形状和大小：A. 发生变化B. 不发生变化C. 无法确定D. 形状不变，大小变小2. 如果一个图形绕其对称中心旋转180度，其位置：A. 不变B. 改变C. 无法确定D. 形状改变3. 一个正方形绕其中心点旋转45度后，其：A. 形状和位置都不变B. 形状不变，位置改变C. 形状改变，位置不变D. 形状和位置都改变4. 一个等边三角形绕其一个顶点旋转120度后，其：A. 形状和位置都不变B. 形状不变，位置改变C. 形状改变，位置不变D. 形状和位置都改变5. 一个圆绕其圆心旋转任意角度后，其：A. 形状和位置都不变B. 形状不变，位置改变C. 形状改变，位置不变D. 形状和位置都改变二、填空题6. 一个图形绕某点旋转______度后，其形状和位置都不变。

7. 如果一个图形绕其对称中心旋转______度，其位置不变。

8. 一个图形绕某点旋转180度后，其形状______，位置______。

9. 一个图形绕某点旋转90度后，其形状______，位置______。

10. 一个图形绕其对称中心旋转任意角度后，其形状______，位置______。

三、简答题11. 描述一个正方形绕其中心点顺时针旋转90度后，其四个顶点的新位置。

12. 解释为什么一个圆在绕其圆心旋转任意角度后，其形状和位置都不变。

13. 如果一个正六边形绕其中心点旋转60度，描述其顶点的新位置。

14. 一个矩形绕其对角线中点旋转180度后，其四个顶点的新位置是什么？15. 解释为什么一个图形绕其对称中心旋转180度后，其位置不变。

四、应用题16. 一个时钟的时针在12小时内绕钟面中心点旋转了多少度？17. 如果一个图形被设计为可以围绕其对称中心旋转，那么在旋转过程中，它的对称性如何保持？18. 一个图形绕其一个顶点旋转，如果旋转角度是360度的整数倍，图形的最终位置是什么？19. 在一个平面直角坐标系中，一个点绕原点旋转θ度后，其新的坐标如何计算？20. 如果一个图形绕其对称中心旋转了θ度，那么它的对称轴会如何变化？五、综合题21. 给出一个图形的旋转矩阵，并说明如何使用它来计算图形绕某点旋转后的新位置。

小学旋转的练习题一、选择题1. 一个图形绕某一点旋转了90度，这个点被称为图形的：A. 旋转中心B. 旋转轴C. 旋转半径D. 旋转角度2. 一个正方形顺时针旋转90度后，它的四个顶点的位置：A. 保持不变B. 位置互换C. 位置不变但方向改变D. 位置和方向都改变3. 如果一个图形绕某点旋转180度，那么这个图形将：A. 回到原来的位置B. 位置不变，方向改变C. 位置改变，方向不变D. 位置和方向都不变4. 一个图形绕其一边的中点旋转180度，这个图形：A. 保持不变B. 位置互换C. 位置不变，方向改变D. 位置和方向都改变5. 一个图形绕其一个顶点旋转90度，这个图形：A. 保持不变B. 位置互换C. 位置不变，方向改变D. 位置改变，方向不变二、填空题6. 一个图形绕某点旋转____度，这个点被称为图形的旋转中心。

7. 当一个图形绕其一边的中点旋转180度时，这个图形的位置____。

8. 如果一个图形绕其一个顶点旋转90度，这个图形的位置____。

9. 一个图形顺时针旋转90度后，它的四个顶点的位置____。

10. 一个图形绕某点旋转180度，那么这个图形将____。

三、判断题11. 一个图形旋转后，它的形状和大小都不会改变。

（）12. 一个图形绕其一边的中点旋转180度后，图形的每个部分都回到原来的位置。

（）13. 一个正方形顺时针旋转90度后，它的面积不变。

（）14. 一个图形绕某点旋转90度后，图形的每个部分都回到原来的位置。

（）15. 一个图形绕其一个顶点旋转90度后，图形的面积会改变。

（）四、简答题16. 描述一个图形绕其一边的中点旋转180度后，图形的哪些部分发生了变化？17. 解释为什么一个图形旋转后，它的形状和大小不会改变。

18. 如果一个图形绕其一个顶点旋转90度，图形的哪些部分保持不变？19. 为什么一个正方形顺时针旋转90度后，它的面积不会改变？20. 描述一个图形绕某点旋转90度后，图形的哪些部分发生了变化，并解释原因。

五年级图形旋转【1】练习题1.如右图，绕它的中心至少旋转（）才能与原图形重合。

A．30° B．60° C．90° D．180°·2.把图形绕着O点顺时针旋转90°后，得到的图形是（）。

A． B． C． D．3.利用旋转画一朵小花：4．图形（1）是以点（）为中心旋转的；图形（2）是以点（）为中心旋转的；图形（3）是以点（）为中心旋转的。

5．如图，指针从A开始，顺时针旋转了90°到（）点，逆时针旋转了90°到（）点；要从A旋转到C，可以按（）时针方向旋转（）°，也可以按（）时针方向旋转（）°。

6．观察图形，填写空格。

①号图形是绕A点按（）时针方向旋转了（）°；②号图形是绕（）点按顺时针方向旋转了（）°；③号图形是绕（）点按（）时针方向旋转了90°；④号图形是绕（）点按（）时针方向旋转了（）。

7．观察图形并填空。

（1）图1绕点“O”逆时针旋转90°到达图（）的位置；（2）图1绕点“O”逆时针旋转180°到达图（）的位置；（3）图1绕点“O”顺时针旋转（）°到达图4的位置；（4）图2绕点“O”顺时针旋转（）°到达图4的位置；（5）图2绕点“O”顺时针旋转90°到达图（）的位置；（6）图4绕点“O”逆时针旋转90°到达图（）的位置。

8．将下面的图案绕点“O”按顺时针方向旋转90°，得到的图案是( ）。

9.如右图，绕它的中心至少旋转（）才能与原图形重合。

·A．30° B．60° C．90° D．180°10．将下列图形绕着各自的中心点旋转120°后，不能与原来的图形重合的是（）。

11．由图形（1）不能变为图形（2）的方法是( ）。

A.图形（1）绕“O”点逆时针方向旋转90°得到图形（2）B.图形（1）绕“O”点顺时针方向旋转90°得到图形（2）C.图形（1）绕“O”点逆时针方向旋转270°得到图形（2）D.以线段OP所在的直线为对称轴画图形（1）的轴对称图形得到图形（2）12．观察下图，是怎样从图形A得到图形B的（）。

旋转练习题集锦（含答案）一、作图题1、如图，在每个小正方形的边长均为1个单位长度的方格纸中，有一个和一点O，的顶点和点O均与小正方形的顶点重合．（1）在方格纸中，将△ABC向下平移5个单位长度得到，请画出；（2）在方格纸中，将△ABC绕点O旋转180°得到，请画出。

二、简答题2、如图，已知的三个顶点的坐标分别为、、．（1）请直接写出点关于轴对称的点的坐标；（2）将绕坐标原点逆时针旋转90°．画出图形，直接写出点的对应点的坐标；（3）请直接写出：以为顶点的平行四边形的第四个顶点的坐标．三、选择题3、如图所示，在平面直角坐标系中，点A、B的坐标分别为（2，0）和（2，0）.月牙①绕点B顺时针旋转900得到月牙②，则点A的对应点A’的坐标为【】（A）（2，2）（B）（2，4）(C)（4，2） (D)（1，2）4、将图按顺时针方向旋转90°后得到的是( )5、在方格纸（每个小方格都是边长为1个单位长度的正方形）中，我们把每个小正方形的顶点称为格点，以格点为顶点的图形称为格点图形．如上图中的△ABC称为格点△ABC．现将图中△ABC绕点A顺时针旋转，并将其边长扩大为原来的2倍，则变形后点B的对应点所在的位置是（）A．甲 B．乙C．丙 D．丁6、下图是一个旋转对称图形，以O为旋转中心，以下列哪一个角为旋转角旋转，能使旋转后的图形与原图形重合（）A．60° B．90° C．120°D．180°7、在下图右侧的四个三角形中，不能由△ABC经过旋转或平移得到的是 ( )8、下面四个图案中，是旋转对称图形的是（）Ａ．Ｂ．Ｃ．Ｄ．9、下列运动是属于旋转的是( )A．电梯的上下运动 B．火车的运动C．钟表中分针的运动 D．升国旗时，国旗的徐徐运动10、如图所示，将其中的图甲变成图乙，可经过的变换是( )A．旋转、平移 B．平移、对称 C．旋转、对称 D．不能确定11、如图，该图形围绕自己的旋转中心，按下列角度旋转后，不能与其自身重合的是（）A．72° B．108° C．144° D．216°12、如图，D是等腰Rt△ABC内一点，BC是斜边，如果将△ABD绕点A逆时针方向旋转到△ACD’的位置，则∠ADD’的度数是( )A．25° B．30° C．35°D．45°13、如图可以看作是一个等腰直角三角形旋转若干次而成的，则每次旋转的度数最小是( )A．90° B．60° C．45°D．30°14、如图，经过平移或旋转不可能将图甲变为图乙的是（）15、下列图形中，既是中心对称图形，又是轴对称图形的是（）A．菱形B．等边三角形 C．等腰三角形D．平行四边形16、如图所示，可由一个“基本图案”旋转l80°而形成的是（）A B CD17、已知，将点A1（6，1）向左平移4个单位到达点A2的位置，再向上平移3个单位到达点A3的位置，△A1A2A3绕点A2逆时针方向旋转900，则旋转湖A3的坐标为（）A．（－2，1） B．（1，1） C．（－1，1） D．（5，1）18、下图是一张边被裁直的白纸，把一边折叠后，BC、BD为折痕，、、B在同一直线上，则∠CBD的度数（）A．不能确定B．大于C．小于 D．等于四、计算题19、将一张透明的平行四边形胶片沿对角线剪开，得到图①中的两张三角形胶片和．将这两张三角形胶片的顶点与顶点重合，把绕点顺时针方向旋转，这时与相交于点．（1）当旋转至如图②位置，点，在同一直线上时，与的数量关系是．（2）当继续旋转至如图③位置时，（1）中的结论还成立吗？请说明理由．（3）在图③中，连接，探索与之间有怎样的位置关系，并证明．20、如图所示，左边方格纸中每个正方形的边长均为a，右边方格纸中每个正方形的边长均为b，将左边方格纸中的图形顺时针旋转90°，并按b:a的比例画在右边方格纸中．21、点B．C．E在同一直线上，点A．D在直线CE的同侧，AB＝AC，EC＝ED，∠BAC＝∠CED，直线AE、BD交于点F。

图形旋转练习题1. 如图1，P是正三角形ABC内的一点，且PA=6，PB=8，PC=10，求∠APB的度数。

2. 如图P是正方形ABCD内一点，点P到正方形的三个顶点A、B、C的距离分别为PA=1，PB=2，PC=3。

求此正方形ABCD面积。

3.设点E、F分别在正方形ABCD的边BC、CD上滑动且保持∠EAF=450，AP⊥EF于点P（1）求证：AP=AB，（2）若AB=5，求ΔECF的周长。

4.如图17，正方形ABCD，E、F分别为BC、CD边上一点．（1）若∠EAF=45º．求证：EF=BE+DF．（2）若⊿AEF绕A点旋转，保持∠EAF=45º，问⊿CEF的周长是否随⊿AEF位置的变化而变化？（3）已知正方形ABCD的边长为1，如果⊿CEF的周长为2．求∠EAF的度数．5．如图，等腰直角△ABC中，∠ABC=90°，点D在AC上，将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE.⑴求∠DCE的度数；⑵当AB=4，AD∶DC=1∶3时，求DE的长.6. (1)如图①所示，P是等边△ABC内的一点，连结PA、PB、PC，将△BAP绕B点顺时针旋转60°得△BCQ,连结PQ．若PA2+PB2=PC2，证明∠PQC=90°．(2) 如图②所示，P是等腰直角△ABC（∠ABC=90°）内的一点，连结PA、PB、PC，将△BAP绕B点顺时针旋转90°得△BCQ,连结PQ．当PA、PB、PC满足什么条件时，∠PQC=90°？请说明理由.7.阅读下面材料，并解决问题：(1)如图，等边△ABC内有一点P若点P到顶点A，B，C的距离分别为3，4，5则∠APB=__________，由于PA，PB不在一个三角形中，为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌__________这样，就可以利用全等三角形知识，将三条线段的长度转化到一个三角形中从而求出∠APB的度数．(2)请你利用第(1)题的解答思想方法，解答下面问题：已知如图(11)，△ABC中，∠CAB=90°，AB=AC，E、F为BC上的点且∠EAF=45°，求证：EF2=BE2+FC2 ．QCPAB第6题AB CPQ第6题图②BD AF EGC8. （1）如图1，△ABC 中，∠BAC=90°，AB=AC ，D 、E 在BC 上，∠DAE=45°，为了探究BD 、DE 、CE 之间的等量关系，现将△AEC 绕A 顺时针旋转90°后成△AFB ，连接DF ，经探究，你所得到的BD 、DE 、CE 之间的等量关系式是 ．（2）如图2，在△ABC 中，∠BAC=120°，AB=AC ，D 、E 在BC 上，∠DAE=60°、∠ADE=45°，试仿照（1）的方法，利用图形的旋转变换，探究BD 、DE 、CE 之间的等量关系，并证明你的结论．9.操作：在△ABC 中，AC ＝BC ＝2，∠C ＝90°，将一块等腰三角板的直角顶点放在斜边AB 的中点P 处，将三角板绕点P 旋转，三角板的两直角边分别交射线AC 、CB 于D 、E 两点．如图①、②、③是旋转三角板得到的图形中的3种情况，研究：（1）三角板绕点P 旋转，观察线段PD 与PE 之间有什么数量关系？并结合图②说明理由． （2）三角板绕点P 旋转，△PBE 是否能成为等腰三角形？若能，指出所有情况（即写出△PBE 为等腰三角形时CE 的长）；若不能，请说明理由．10.把两个三角形按如图1放置，其中，，，且，．把△DCE 绕点C 顺时针旋转15°得到△D1CE1，如图2，这时AB 与CD1相交于点，与D1E1相交于点F ． （1）求的度数；（2）求线段AD1的长； （3）若把△D1CE1绕点顺时针再旋转30°得到△D2CE2，这时点B 在△D2CE2的内部、外部、还是边上？请说明理由．11．如图，在等腰Rt △ABC 与等腰Rt △DBE 中, ∠BDE=∠ACB=90°,且BE 在AB 边上,取 AE 的中点F,CD 的中点G,连结GF.（1）FG 与DC 的位置关系是 ,FG 与DC 的数量关系是 ； （2）若将△BDE 绕B 点逆时针旋转180°，其它条件不变,请完成下图，并判断（1）中的结论是否仍然成立? 请证明你的结论.B图2AE 1CD 1OF BAC12.如图①，△ABC是正三角形，△BDC是顶角∠BDC＝120°的等腰三角形，以D为顶点作一个60°角，角的两边分别交AB、AC边于M、N两点，连接MN．（1）探究：线段BM、MN、NC之间的关系，并加以证明．（2）若点M、N分别是射线AB、CA上的点，其它条件不变，再探线段BM、MN、NC之间的关系，在图②中画出图形，并说明理由．。

小学四年级旋转练习题在旋转练习题中，我们将通过一系列形状和图形的旋转操作，来提高小学四年级学生的几何认知和思维能力。

下面是一些旋转练习题，帮助学生更好地理解旋转的概念和应用。

旋转练习题一：旋转形状1. 将一个正方形顺时针旋转90°，得到的形状是什么？2. 将一个长方形逆时针旋转180°，得到的形状是什么？3. 将一个圆形逆时针旋转270°，得到的形状是什么？4. 将一个三角形顺时针旋转360°，得到的形状和原来相同吗？旋转练习题二：旋转图形请你观察下面的图形，按要求进行旋转操作。

1. 图形A按顺时针旋转90°。

2. 图形B按逆时针旋转180°。

3. 图形C按逆时针旋转270°。

(在这里插入图形A、B、C的图片，图片可以自行设计或者找现成的图片)旋转练习题三：图形图案现在，我们来尝试用旋转进行绘图。

请你根据以下步骤完成绘图过程。

步骤一：在一张纸上画一个等边三角形。

步骤二：将该三角形按顺时针旋转90°，并画出旋转后的形状。

步骤三：再将该三角形按顺时针旋转90°，并画出旋转后的形状。

步骤四：最后，将该三角形再次按顺时针旋转90°，并画出旋转后的形状。

(在这里插入每个步骤的图形，可以用简笔画或者其他图示方式)通过以上的练习题，小学四年级的学生可以更好地理解旋转的概念和应用。

旋转不仅是一种几何变换，也是我们生活中常见的物体运动方式。

对于学生来说，通过练习旋转，不仅可以加深对几何形状的认识，还能培养他们的观察能力和创造力。

在日常生活中，他们可以注意观察物体的旋转运动，并将所学到的知识应用到实际中去。

希望以上的旋转练习题能够帮助小学四年级的学生更好地学习和掌握旋转的概念。

通过不断的练习和实践，他们将能够在几何学习中取得更好的成绩，并且培养出对数学的兴趣和创造力。

祝愿他们在几何学习中取得更大的进步！。

五年级旋转图形练习题旋转图形是五年级数学课程中的重要内容之一，通过练习旋转图形题目，可以提高学生的空间想象力和几何图形的认知能力。

下面将为你提供一些旋转图形练习题。

练习题一：1. 将一个正方形沿着中心旋转90度，得到的图形是什么？2. 将一个长方形沿着中心旋转180度，得到的图形是什么？3. 将一个三角形沿着顶点旋转270度，得到的图形是什么？4. 将一个菱形沿着对角线旋转360度，得到的图形是什么？练习题二：1. 图形A是一个正方形，边长为4厘米。

请绘制图形A在顺时针旋转90度后的图形，并标注每个顶点的坐标。

2. 图形B是一个长方形，长为6厘米，宽为3厘米。

请绘制图形B 在逆时针旋转180度后的图形，并标注每个顶点的坐标。

3. 图形C是一个等边三角形，边长为5厘米。

请绘制图形C在顺时针旋转270度后的图形，并标注每个顶点的坐标。

4. 图形D是一个梯形，上底长为8厘米，下底长为12厘米，高为4厘米。

请绘制图形D在逆时针旋转360度后的图形，并标注每个顶点的坐标。

练习题三：1. 图形E是一个正方形，边长为6厘米。

请计算图形E在顺时针旋转90度后周长和面积的变化情况。

2. 图形F是一个长方形，长为7厘米，宽为4厘米。

请计算图形F 在逆时针旋转180度后周长和面积的变化情况。

3. 图形G是一个等边三角形，边长为8厘米。

请计算图形G在顺时针旋转270度后周长和面积的变化情况。

4. 图形H是一个梯形，上底长为10厘米，下底长为15厘米，高为6厘米。

请计算图形H在逆时针旋转360度后周长和面积的变化情况。

通过以上练习题，学生们可以巩固对旋转图形的理解和应用能力，同时提高对坐标系的认知和计算能力。

在解答题目时，可以使用纸和铅笔进行绘制和计算，或者使用计算器进行更准确的数值计算。

希望以上练习题对你的学习有所帮助！。