【最新】高考数学一轮复习 第九章 第4讲 直线与圆的位置关系课件 理 苏教版
- 格式:ppt
- 大小:1.50 MB
- 文档页数:41

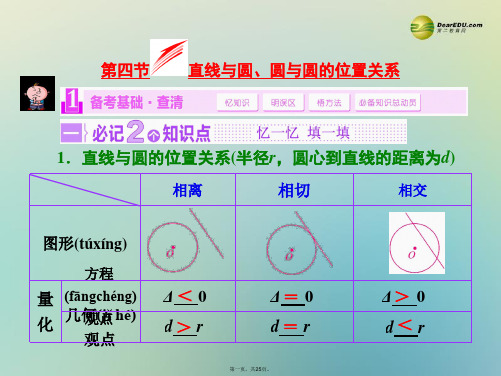
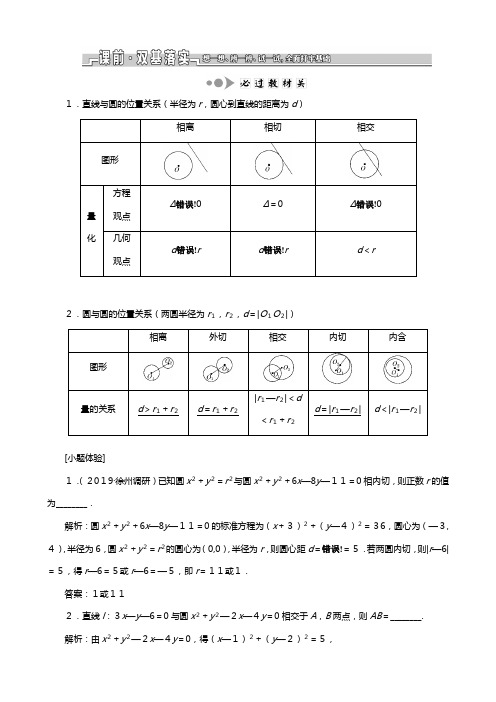
1.直线与圆的位置关系(半径为r,圆心到直线的距离为d)相离相切相交图形量化方程观点Δ错误!0Δ=0Δ错误!0几何观点d错误!r d错误!r d<r2.圆与圆的位置关系(两圆半径为r1,r2,d=|O1O2|)相离外切相交内切内含图形量的关系d>r1+r2d=r1+r2|r1—r2|<d<r1+r2d=|r1—r2|d<|r1—r2|[小题体验]1.(2019·徐州调研)已知圆x2+y2=r2与圆x2+y2+6x—8y—11=0相内切,则正数r的值为________.解析:圆x2+y2+6x—8y—11=0的标准方程为(x+3)2+(y—4)2=36,圆心为(—3,4),半径为6,圆x2+y2=r2的圆心为(0,0),半径为r,则圆心距d=错误!=5.若两圆内切,则|r—6|=5,得r—6=5或r—6=—5,即r=11或1.答案:1或112.直线l:3x—y—6=0与圆x2+y2—2x—4y=0相交于A,B两点,则AB=________.解析:由x2+y2—2x—4y=0,得(x—1)2+(y—2)2=5,所以该圆的圆心坐标为(1,2),半径r=错误!,又圆心(1,2)到直线3x—y—6=0的距离为d=错误!=错误!,由错误!2=r2—d2,得AB2=4错误!=10,即AB=错误!.答案:错误!3.若直线x—y+1=0与圆(x—a)2+y2=2有公共点,则实数a的取值范围为________.解析:由题意可得,圆的圆心为(a,0),半径为错误!,所以错误!≤错误!,即|a+1|≤2,解得—3≤a≤1.答案:[—3,1]4.若圆x2+y2=4与圆x2+y2—2mx+m2—1=0相外切,则实数m=________.解析:将圆x2+y2—2mx+m2—1=0化成标准方程,得(x—m)2+y2=1,圆心为(m,0),半径r1=1,圆x2+y2=4的圆心为(0,0),半径r2=2.由两圆相外切,得|m|=r1+r2=3,解得m=±3.答案:±31.对于圆的切线问题,尤其是圆外一点引圆的切线,易忽视切线斜率k不存在的情形.2.两圆相切问题易忽视分两圆内切与外切两种情形.[小题纠偏]1.过点(2,3)与圆(x—1)2+y2=1相切的直线的方程为________.解析:1若切线的斜率存在时,设圆的切线方程为y=k(x—2)+3,由圆心(1,0)到切线的距离为半径1,得k=错误!,所以切线方程为4x—3y+1=0,2若切线的斜率不存在,则切线方程为x=2,也是圆的切线,所以直线方程为4x—3y+1=0或x=2.答案:x=2或4x—3y+1=02.若圆x2+y2=1与圆(x+4)2+(y—a)2=25相切,则常数a=________.答案:±2错误!或0错误!错误![题组练透]1.(易错题)(2018·苏北四市调研)直线(a+1)x+(a—1)y+2a=0(a∈R)与圆x2+y 2—2x+2y—7=0的位置关系是________.解析:法一:x2+y2—2x+2y—7=0化为圆的标准方程为(x—1)2+(y+1)2=9,故圆心坐标为(1,—1),半径r=3,圆心到直线的距离d=错误!=错误!.再根据r2—d2=9—错误!=错误!,而7a2—4a+7=0的判别式Δ=16—196=—180<0,故有r2>d2,即d<r,故直线与圆相交.法二:由(a+1)x+(a—1)y+2a=0(a∈R)整理得x—y+a(x+y+2)=0,则由错误!解得x=—1,y=—1,即直线(a+1)x+(a—1)y+2a=0(a∈R)过定点(—1,—1),又(—1)2+(—1)2—2×(—1)+2×(—1)—7=—5<0,则点(—1,—1)在圆x2+y2—2x+2y—7=0的内部,故直线(a+1)x+(a—1)y+2a=0(a∈R)与圆x2+y2—2x+2y—7=0相交.答案:相交2.(2019·南京学情调研)在平面直角坐标系xOy中,若直线ax+y—2=0与圆心为C的圆(x—1)2+(y—a)2=16相交于A,B两点,且△ABC为直角三角形,则实数a的值是________.解析:因为△ABC为直角三角形,所以BC=AC=r=4,所以圆心C到直线AB的距离为2错误!,从而有错误!=2错误!,解得a=—1.答案:—13.(2018·苏州高三暑假测试)已知点A(1,0)和点B(0,1),若圆x2+y2—4x—2y+t=0上仅有两个不同的点P,使得△PAB的面积为错误!,则实数t的取值范围是________.解析:由题可得AB=错误!,若△PAB的面积为错误!,则点P到直线AB的距离为错误!,圆x2+y2—4x—2y+t=0的标准方程为(x—2)2+(y—1)2=5—t,圆心到直线AB的距离为错误!,所以错误!—错误!<错误!<错误!+错误!,解得错误!<t<错误!.答案:错误![谨记通法]判断直线与圆的位置关系的两种方法(1)几何法:圆心到直线的距离与圆半径比较大小,即可判断直线与圆的位置关系.这种方法的特点是计算量较小.(2)代数法:将直线方程与圆方程联立方程组,再将二次方程组转化为一元二次方程,该方程解的情况即对应直线与圆的位置关系.这种方法具有一般性,适合于判断直线与圆锥曲线的位置关系,但是计算量较大,能用几何法,尽量不用代数法.错误!错误![锁定考向]与圆有关的切线及弦长问题,是近年来高考的一个热点,常见的命题角度有:(1)求圆的切线方程(切线长);(2)求弦长;(3)由弦长或切线问题求参数.[题点全练]角度一:求圆的切线方程(切线长)1.已知圆的方程为x2+y2=1,则在y轴上截距为错误!的切线方程为________________.解析:在y轴上截距为错误!且斜率不存在的直线显然不是切线,故设切线方程为y=kx+错误!,则错误!=1,所以k=±1,故所求切线方程为y=x+错误!或y=—x+错误!.答案:y=x+错误!或y=—x+错误!角度二:求弦长2.若a2+b2=2c2(c≠0),则直线ax+by+c=0被圆x2+y2=1所截得的弦长为________.解析:因为圆心(0,0)到直线ax+by+c=0的距离d=错误!=错误!=错误!,因此根据直角三角形的关系,弦长的一半就等于错误!=错误!,所以弦长为错误!.答案:错误!角度三:由弦长或切线问题求参数3.(2018·苏州期末)在平面直角坐标系xOy中,已知过点M(1,1)的直线l与圆(x+1)2+(y—2)2=5相切,且与直线ax+y—1=0垂直,则实数a=________.解析:因为点M在圆上,所以切线方程为(1+1)(x+1)+(1—2)(y—2)=5,即2x—y—1=0,所以2a—1=0,即a=错误!.答案:错误!4.已知圆C:(x—1)2+(y—2)2=2截y轴所得线段与截直线y=2x+b所得线段的长度相等,则b=________.解析:记圆C与y轴的两个交点分别是A,B,由圆心C到y轴的距离为1,CA=CB=错误!可知,圆心C(1,2)到直线2x—y+b=0的距离也等于1才符合题意,于是错误!=1,解得b=±错误!.答案:±错误![通法在握]1.圆的切线方程的2种求法(1)代数法:设切线方程为y—y0=k(x—x0),与圆的方程组成方程组,消元后得到一个一元二次方程,然后令判别式Δ=0进而求得k.(2)几何法:设切线方程为y—y0=k(x—x0),利用点到直线的距离公式表示出圆心到切线的距离d,然后令d=r,进而求出k.[提醒] 若点M(x0,y0)在圆x2+y2=r2上,则过M点的圆的切线方程为x0x+y0y=r2.2.弦长的2种求法(1)代数法:将直线和圆的方程联立方程组,消元后得到一个一元二次方程.在判别式Δ>0的前提下,利用根与系数的关系,根据弦长公式求弦长.(2)几何法:若弦心距为d,圆的半径长为r,则弦长l=2错误!.[演练冲关]1.(2019·启东检测)已知点P是直线y=x上一个动点,过点P作圆(x+2)2+(y—2)2=1的切线,切点为T,则线段PT长度的最小值为________.解析:圆心C(—2,2),半径r=1,则切线长PT=错误!.要使PT最小,只需PC最小即可,此时CP垂直于直线y=x,则C到直线x—y=0的距离d=错误!=错误!=2错误!,此时PT=错误!=错误!,故线段PT长度的最小值为错误!.答案:错误!2.过原点且与直线错误!x—错误!y+1=0平行的直线l被圆x2+(y—错误!)2=7所截得的弦长为________.解析:由题意可得l的方程为错误!x—y=0,因为圆心(0,错误!)到l的距离d=错误!=1,所以所求弦长l=2错误!=2错误!=2错误!.答案:2错误!3.已知点A(1,a),圆x2+y2=4.(1)若过点A的圆的切线只有一条,求a的值及切线方程;(2)若过点A且在两坐标轴上截距相等的直线与圆相切,求a的值及切线方程.解:(1)由于过点A的圆的切线只有一条,则点A在圆上,故12+a2=4,得a=±错误!.当a=错误!,即A(1,错误!)时,切线的斜率为—错误!,故切线方程为y—错误!=—错误!(x—1),即x+错误!y—4=0,当a=—错误!,即A(1,—错误!)时,切线的斜率为错误!,故切线的方程为y+错误!=错误!(x—1),即x—错误!y—4=0.所以a=错误!时,切线方程为x+错误!y—4=0,a=—错误!时,切线方程为x—错误!y—4=0.(2)设直线方程为x+y=b,由于直线过点A,所以1+a=b,所以直线方程为x+y=1+a,即x+y—a—1=0.又直线与圆相切,所以d=错误!=2,所以a=±2错误!—1.所以切线方程为x+y+2错误!=0或x+y—2错误!=0.错误!错误![典例引领]1.(2019·常州调研)若圆O:x2+y2=10与圆M:(x—a)2+y2=90(a>0)相交于A,B 两点,且两圆在点A处的切线互相垂直,则线段AB的长度是________.解析:由题意得,O(0,0),r1=错误!,M(a,0),r2=3错误!,∴2错误!<|a|<4错误!.∵OA⊥MA,∴在Rt△AOM中,根据勾股定理,得OM2=OA2+MA2,即a2=(错误!)2+(3错误!)2=100,∴a=10或a=—10(不合题意,舍去),则线段AB的长度为错误!=错误!=6.答案:62.(2018·南京、盐城、连云港、徐州二模)已知圆O:x2+y2=1,动圆M:(x—a)2+(y—a +4)2=1.若圆M上存在点P,过点P作圆O的两条切线,切点为A,B,使得∠APB=60°,则实数a的取值范围为________.解析:由题意得圆心M(a,a—4)在直线x—y—4=0上运动,所以动圆M是圆心在直线x—y—4=0上,半径为1的圆.又因为圆M上存在点P,过点P作圆O的两条切线,切点为A,B,使∠APB=60°,所以OP=2,即点P也在x2+y2=4上,于是2—1≤错误!≤2+1,即1≤错误!≤3,解得2—错误!≤a≤2+错误!,故实数a的取值范围是错误!.答案:错误![由题悟法]圆与圆位置关系问题的解题策略(1)处理两圆位置关系多用圆心距与半径和或差的关系判断,一般不采用代数法.(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差得到.[即时应用]1.已知圆x2+y2=9与圆x2+y2—4x+2y—3=0相交于A,B两点,则线段AB的长为________.解析:由题意,两圆的公共弦为2x—y—3=0,∵圆x2+y2=9的圆心坐标为(0,0),半径为3,∴圆心到直线的距离d=错误!,∴线段AB的长为2错误!=错误!.答案:错误!2.(2019·镇江模拟)若圆C1:x2+y2=1与圆C2:x2+y2—6x—8y+m=0外切,则m=________.解析:圆C1的圆心为C1(0,0),半径r1=1,因为圆C2的方程可化为(x—3)2+(y—4)2=25—m,所以圆C2的圆心为C2(3,4),半径r2=错误!(m<25).从而C1C2=错误!=5.由两圆外切,得C1C2=r1+r2,即1+错误!=5,解得m=9.答案:9一抓基础,多练小题做到眼疾手快1.(2018·扬州期末)已知直线l:x+错误!y—2=0与圆C:x2+y2=4交于A,B两点,则弦AB的长为________.解析:圆心C(0,0)到直线l的距离d=错误!=1,所以AB=2错误!=2错误!,故弦AB的长为2错误!.答案:2错误!2.(2019·南京调研)在平面直角坐标系xOy中,直线x+2y=0与圆(x—3)2+(y—1)2=25相交于A,B两点,则线段AB的长为________.解析:圆(x—3)2+(y—1)2=25的圆心坐标为(3,1),半径为5.∵圆心(3,1)到直线x+2y=0的距离d=错误!=错误!,∴线段AB的长为2错误!=2错误!=4错误!.答案:4错误!3.设圆(x—3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x—3y—2=0的距离等于2,则圆半径r的取值范围为________.解析:∵圆(x—3)2+(y+5)2=r2(r>0)的圆心坐标为(3,—5),半径为r,∴圆心(3,—5)到直线4x—3y—2=0的距离d=错误!=5,∵圆(x—3)2+(y+5)2=r2(r>0)上有且仅有两个点到直线4x—3y—2=0的距离等于2,∴|r—5|<2,解得3<r<7.答案:(3,7)4.(2018·苏锡常镇调研)若直线3x+4y—m=0与圆x2+y2+2x—4y+4=0始终有公共点,则实数m的取值范围是________.解析:圆的标准方程为(x+1)2+(y—2)2=1,故圆心到直线的距离d=错误!≤1.即|m—5|≤5,解得0≤m≤10.答案:[0,10]5.在平面直角坐标系xOy中,已知圆C:x2+y2—6x+5=0的圆心为C,点A,B在圆C上,且AB=2错误!,则S△ABC=________.解析:圆C:x2+y2—6x+5=0化为标准方程得(x—3)2+y2=4,圆心为(3,0),半径为2.∵点A,B在圆C上,且AB=2错误!,∴圆心(3,0)到直线AB的距离为错误!=1,∴S△ABC=错误!×2错误!×1=错误!.答案:错误!6.若圆x2+y2+mx—错误!=0与直线y=—1相切,其圆心在y轴的左侧,则m=________.解析:圆的标准方程为错误!2+y2=错误!2,圆心到直线y=—1的距离错误!=|0—(—1)|,解得m=±错误!,因为圆心在y轴的左侧,所以m=错误!.答案:错误!二保高考,全练题型做到高考达标1.(2019·苏北四市调研)在平面直角坐标系xOy中,若点A到原点的距离为2,到直线错误!x +y—2=0的距离为1,则满足条件的点A的个数为________.解析:如图,作出直线错误!x+y—2=0,作出以原点为圆心,以2为半径的圆,∵原点O到直线错误!x+y—2=0的距离为1,∴在直线错误!x+y—2=0的右上方有一点满足到原点的距离为2,到直线错误!x+y—2=0的距离为1,过原点作直线错误!x+y—2=0的平行线,交圆于两点,则两交点满足到原点的距离为2,到直线错误!x+y—2=0的距离为1.故满足条件的点A共3个.答案:32.(2018·苏州调研)两圆交于点A(1,3)和B(m,1),两圆的圆心都在直线x—y+错误!=0上,则m+c=________.解析:由题意可知线段AB的中点错误!在直线x—y+错误!=0上,代入得m+c=3.答案:33.(2018·南通、扬州、淮安、宿迁、泰州二调)在平面直角坐标系xOy中,过点P(—2,0)的直线与圆x2+y2=1相切于点T,与圆(x—a)2+(y—错误!)2=3相交于点R,S,且PT=RS,则正数a的值为________.解析:因为PT与圆x2+y2=1相切于点T,所以在Rt△OPT中,OT=1,OP=2,∠OTP=错误!,从而∠OPT=错误!,PT=错误!,故直线PT的方程为x±错误!y+2=0,因为直线PT截圆(x—a)2+(y—错误!)2=3得弦长RS=错误!,设圆心到直线的距离为d,则d=错误!,又错误!=2错误!,即d=错误!,即|a±3+2|=3,解得a=—8或a=—2或a=4,因为a>0,所以a=4.答案:44.(2018·无锡模拟)已知圆C:(x—2)2+y2=4,线段EF在直线l:y=x+1上运动,点P 为线段EF上任意一点,若圆C上存在两点A,B,使得错误!·错误!≤0,则线段EF长度的最大值是________.解析:由错误!·错误!≤0得∠APB≥90°,从直线上的点向圆上的点连线成角,当且仅当两条线均为切线时,∠APB才是最大的角,不妨设切线为PM,PN,当∠APB≥90°时,∠MPN≥90°,sin∠MPC=错误!≥sin 45°=错误!,所以PC≤2错误!.另当过点P,C的直线与直线l:y=x+1垂直时,PC min =错误!,以C为圆心,CP=2错误!为半径作圆交直线l于E,F两点,这时的线段长即为线段EF长度的最大值,所以EF max=2错误!=错误!.答案:错误!5.(2019·镇江调研)若圆O:x2+y2=5与圆O1:(x—m)2+y2=20(m∈R)相交于A,B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是________.解析:如图,因为圆O1与圆O在A处的切线互相垂直,则两切线分别过另一圆的圆心,所以O1A⊥OA. 又因为OA=错误!,O1A=2错误!,所以OO1=5.又A,B关于OO1对称,所以AB为Rt△OAO1斜边上高的2倍.由错误!·OA·O1A=错误!OO1·AC,得AC=2.所以AB=4.答案:46.(2018·淮阴期末)圆C1:x2+y2+2ax+a2—4=0和圆C2:x2+y2—2by+b2—1=0相内切,若a,b∈R,且ab≠0,则错误!+错误!的最小值为________.解析:由题意,两圆的标准方程分别为(x+a)2+y2=4,x2+(y—b)2=1,∴圆心分别为(—a,0),(0,b),半径分别为2和1.∵两圆相内切,∴错误!=1,∴a2+b2=1,∴错误!+错误!=错误!(a2+b2)=5+错误!+错误!≥5+4=9,当且仅当错误!=错误!,即a2=错误!,b2=错误!时等号成立.故错误!+错误!的最小值为9.答案:97.(2018·苏北四市期末)已知A,B是圆C1:x2+y2=1上的动点,AB=错误!,P是圆C2:(x—3)2+(y—4)2=1上的动点,则|错误!+错误!|的取值范围为________.解析:如图,因为A,B是圆C1:x2+y2=1上的动点,AB=错误!,所以线段AB的中点H在圆O:x2+y2=错误!上,且|错误!+错误!|=2|错误!|.因为点P是圆C2:(x—3)2+(y—4)2=1上的动点,所以5—错误!≤|错误!|≤5+错误!,即错误!≤|错误!|≤错误!,所以7≤2|错误!|≤13,从而|错误!+错误!|的取值范围为[7,13].答案:[7,13]8.(2019·淮安模拟)已知圆O:x2+y2=1.若直线y=错误!x+2上总存在点P,使得过点P 的圆O的两条切线互相垂直,则实数k的最小值为________.解析:圆O的圆心为O(0,0),半径r=1.设两个切点分别为A,B,则由题意可得四边形PAOB 为正方形,故有PO=错误!r=错误!,∴圆心O到直线y=错误!x+2的距离小于或等于PO=错误!,即错误!≤错误!,即1+k≥2,解得k≥1,∴实数k的最小值为1.答案:19.已知圆C经过点A(2,—1),和直线x+y=1相切,且圆心在直线y=—2x上.(1)求圆C的方程;(2)已知直线l经过原点,并且被圆C截得的弦长为2,求直线l的方程.解:(1)设圆心的坐标为C(a,—2a),则错误!=错误!.化简,得a2—2a+1=0,解得a=1.所以C(1,—2),半径r=|AC|=错误!=错误!.所以圆C的方程为(x—1)2+(y+2)2=2.(2)1当直线l的斜率不存在时,直线l的方程为x=0,此时直线l被圆C截得的弦长为2,满足条件.2当直线l的斜率存在时,设直线l的方程为y=kx,由题意得错误!=1,解得k=—错误!,所以直线l的方程为y=—错误!x.综上所述,直线l的方程为x=0或3x+4y=0.10.如图,在平面直角坐标系xOy中,已知圆C:x2+y2—4x=0及点A(—1,0),B(1,2).(1)若直线l∥AB,与圆C相交于M,N两点,MN=AB,求直线l的方程;(2)在圆C上是否存在点P,使得PA2+PB2=12?若存在,求点P的个数;若不存在,请说明理由.解:(1)圆C的标准方程为(x—2)2+y2=4,所以圆心C(2,0),半径为2.因为l∥AB,A(—1,0),B(1,2),所以直线l的斜率为错误!=1,设直线l的方程为x—y+m=0,则圆心C到直线l的距离为d=错误!.因为MN=AB=错误!=2错误!,而CM2=d2+错误!2,所以4=错误!+2,解得m=0或m=—4,故直线l的方程为x—y=0或x—y—4=0.(2)假设圆C上存在点P,设P(x,y),则(x—2)2+y2=4,PA2+PB2=(x+1)2+(y—0)2+(x—1)2+(y—2)2=12,即x2+y2—2y—3=0,即x2+(y—1)2=4.因为|2—2|<错误!<2+2,所以圆(x—2)2+y2=4与圆x2+(y—1)2=4相交,所以点P的个数为2.三上台阶,自主选做志在冲刺名校1.(2019·苏州调研)过曲线y=2|x—a|+x—a上的点P向圆O:x2+y2=1作两条切线PA,PB,切点为A,B,且∠APB=60°,若这样的点P有且只有两个,则实数a的取值范围是________.解析:根据题意,若经过点P作圆O:x2+y2=1的两条切线,切点为A,B,且∠APB=60°,则∠OPA=30°,所以PO=2AO=2,故点P的轨迹方程为x2+y2=4.y=2|x—a|+x—a=错误!当x≤a时,曲线为x+y—a=0,当x≥a时,曲线为3x—y—3a=0.故当a<0时,若这样的点P有且只有两个,必有错误!<2,即—错误!<2,解得a>—错误!,即—错误!<a<0;当a=0时,曲线为y=2|x|+x=错误!符合题意;当a>0时,若这样的点P有且只有两个,必有错误!<2,解得a<2错误!,即0<a<2错误!,综上,实数a的取值范围是错误!.答案:错误!2.(2018·苏锡常镇调研)在平面直角坐标系xOy中,过点M(1,0)的直线l与圆x2+y2=5交于A,B两点,其中点A在第一象限,且错误!=2错误!,则直线l的方程为__________.解析:法一:易知直线l的斜率存在,设l:y=k(x—1).由错误!=2错误!,可设BM=2t,MA=t,如图,过原点O作OH⊥l于点H,则BH=错误!.设OH=d,在Rt△OBH中,d2+错误!2=r2=5,在Rt△OMH中,d2+错误!2=OM2=1,解得d2=错误!.所以d2=错误!=错误!,解得k=1或k=—1,因为点A在第一象限,错误!=2错误!,由图知k=1,所以直线l的方程为y=x—1,即x—y—1=0.法二:设A(x1,y1),B(x2,y2),所以错误!=(x1—1,y1),错误!=(1—x2,—y2).因为错误!=2错误!,所以错误!即错误!又x错误!+y错误!=5,所以(2x1—3)2+4y错误!=5,联立错误!解得x1=2,代入可得y1=±1,又点A在第一象限,故A(2,1),所以直线l的方程为y=x—1,即x—y—1=0.答案:x—y—1=03.已知圆C1:(x+1)2+y2=1和圆C2:(x—4)2+y2=4.(1)过点C1作圆C2的切线,求该切线方程;(2)过圆心C1作倾斜角为θ的直线l交圆C2于A,B两点,且A为C1B的中点,求sin θ;(3)过点P(m,1)引圆C2的两条割线l1和l2.直线l1和l2被圆C2截得的弦的中点分别为M,N,试问过点P,M,N,C2的圆是否过定点(异于点C2)?若过定点,求出该定点;若不过定点,说明理由.解:(1)显然切线的斜率存在,设切线方程为y=k(x+1),由题意得错误!=2,解得k=±错误!,所以所求直线方程为y=±错误!(x+1),即2x±错误!y+2=0.(2)设直线l的方程为y=k(x+1),则圆心C2到直线l的距离d=错误!,设AB的中点为R,则AR=错误!=错误!AB=错误!C1R=错误!错误!,解得d2=错误!.在Rt△C1RC2中,sin θ=错误!=错误!=错误!.(3)依题意,过点P,M,N,C2的圆即为以PC2为直径的圆,所以(x—4)(x—m)+(y—1)(y—0)=0,即x2—(m+4)x+4m+y2—y=0,整理成关于实数m的等式(4—x)m+x2—4x+y2—y=0恒成立,则错误!所以错误!或错误!(舍去).即存在定点(4,1).命题点一直线与方程、两条直线的位置关系1.(2017·北京高考)已知x≥0,y≥0,且x+y=1,则x2+y2的取值范围是________.解析:依题意,x2+y2可视为原点到线段x+y—1=0(x≥0,y≥0)上的点的距离的平方,如图所示,故(x2+y2)min=错误!2=错误!,(x2+y2)max=|OA|2=|OB|2=1,故x2+y2∈错误!.答案:错误!2.(2015·山东高考改编)一条光线从点(—2,—3)射出,经y轴反射后与圆(x+3)2+(y—2)2=1相切,则反射光线所在直线的斜率为________.解析:由已知,得点(—2,—3)关于y轴的对称点为(2,—3),由入射光线与反射光线的对称性,知反射光线一定过点(2,—3).设反射光线所在直线的斜率为k,则反射光线所在直线的方程为y+3=k(x—2),即kx—y—2k—3=0.由反射光线与圆相切,则有d=错误!=1,解得k=—错误!或k=—错误!.答案:—错误!或—错误!3.(2016·上海高考)已知平行直线l1:2x+y—1=0,l2:2x+y+1=0,则l1与l2的距离是________.解析:由两平行线间的距离公式得d=错误!=错误!.答案:错误!命题点二圆的方程、直线与圆的位置关系1.(2017·江苏高考)在平面直角坐标系xOy中,A(—12,0),B(0,6),点P在圆O:x2+y2=50上.若错误!·错误!≤20,则点P的横坐标的取值范围是________.解析:设P(x,y),则错误!·错误!=(—12—x,—y)·(—x,6—y)=x(x+12)+y(y—6)≤20.又x2+y2=50,所以2x—y+5≤0,所以点P在直线2x—y+5=0的上方(包括直线上).又点P在圆x2+y2=50上,由错误!解得x=—5或x=1,结合图象,可得—5错误!≤x≤1,故点P的横坐标的取值范围是[—5错误!,1].答案:[—5错误!,1]2.(2018·全国卷Ⅲ改编)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x—2)2+y2=2上,则△ABP面积的取值范围是________.解析:设圆(x—2)2+y2=2的圆心为C,半径为r,点P到直线x+y+2=0的距离为d,则圆心C(2,0),r=错误!,所以圆心C到直线x+y+2=0的距离为错误!=2错误!,可得d max=2错误!+r=3错误!,d min=2错误!—r=错误!.由已知条件可得|AB|=2错误!,所以△ABP面积的最大值为错误!×|AB|×d max=6,△ABP面积的最小值为错误!×|AB|×d min=2.综上,△ABP面积的取值范围是[2,6].答案:[2,6]3.(2018·北京高考改编)在平面直角坐标系中,记d为点P(cos θ,sin θ)到直线x—my—2=0的距离,当θ,m变化时,d的最大值为________.解析:由题知点P(cos θ,sin θ)是单位圆x2+y2=1上的动点,所以点P到直线x—my—2=0的距离可转化为单位圆上的点到直线的距离.又直线x—my—2=0恒过点(2,0),所以当m变化时,圆心(0,0)到直线x—my—2=0的距离错误!的最大值为2,所以点P到直线x—my—2=0的距离的最大值为3,即d的最大值为3.答案:34.(2018·全国卷Ⅰ)直线y=x+1与圆x2+y2+2y—3=0交于A,B两点,则|AB|=________.解析:由x2+y2+2y—3=0,得x2+(y+1)2=4.∴圆心C(0,—1),半径r=2.圆心C(0,—1)到直线x—y+1=0的距离d=错误!=错误!,∴|AB|=2错误!=2错误!=2错误!.答案:2错误!5.(2017·全国卷Ⅲ)在直角坐标系xOy中,曲线y=x2+mx—2与x轴交于A,B两点,点C 的坐标为(0,1),当m变化时,解答下列问题:(1)能否出现AC⊥BC的情况?说明理由;(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.解:(1)不能出现AC⊥BC的情况,理由如下:设A(x1,0),B(x2,0),则x1,x2满足x2+mx—2=0,所以x1x2=—2.又C的坐标为(0,1),故AC的斜率与BC的斜率之积为错误!·错误!=—错误!,所以不能出现AC⊥BC的情况.(2)证明:由(1)知BC的中点坐标为错误!,可得BC的中垂线方程为y—错误!=x2错误!.由(1)可得x1+x2=—m,所以AB的中垂线方程为x=—错误!.联立错误!可得错误!所以过A,B,C三点的圆的圆心坐标为错误!,半径r=错误!.故圆在y轴上截得的弦长为2错误!=3,即过A,B,C三点的圆在y轴上截得的弦长为定值.6.(2016·江苏高考)如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2—12x—14y+60=0及其上一点A(2,4).(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;(2)设平行于OA的直线l与圆M相交于B,C两点,且BC=OA,求直线l的方程;(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得错误!+错误!=错误!,求实数t的取值范围.解:圆M的标准方程为(x—6)2+(y—7)2=25,所以圆心M(6,7),半径为5.(1)由圆心N在直线x=6上,可设N(6,y0).因为圆N与x轴相切,与圆M外切,所以0<y0<7,圆N的半径为y0,从而7—y0=5+y0,解得y0=1.因此,圆N的标准方程为(x—6)2+(y—1)2=1.(2)因为直线l∥OA,所以直线l的斜率为错误!=2.设直线l的方程为y=2x+m,即2x—y+m=0,则圆心M到直线l的距离d=错误!=错误!.因为BC=OA=错误!=2错误!,而MC2=d2+错误!2,所以25=错误!+5,解得m=5或m=—15.故直线l的方程为2x—y+5=0或2x—y—15=0.(3)设P(x1,y1),Q(x2,y2).因为A(2,4),T(t,0),错误!+错误!=错误!,所以错误!1因为点Q在圆M上,所以(x2—6)2+(y2—7)2=25.2将1代入2,得(x1—t—4)2+(y1—3)2=25.于是点P(x1,y1)既在圆M上,又在圆[x—(t+4)]2+(y—3)2=25上,从而圆(x—6)2+(y—7)2=25与圆[x—(t+4)]2+(y—3)2=25有公共点,所以5—5≤错误!≤5+5,解得2—2错误!≤t≤2+2错误!.因此,实数t的取值范围是[2—2错误!,2+2错误!].。


高考数学大一轮复习 9.4直线、圆的位置关系学案理苏教版1、能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系、2、能用直线和圆的方程解决一些简单的问题、3、在学习过程中,体会用代数方法处理几何问题的思想、自主梳理1、直线与圆的位置关系位置关系有三种:________、________、________、判断直线与圆的位置关系常见的有两种方法:①代数法:利用判别式Δ,即直线方程与圆的方程联立方程组消去x或y整理成一元二次方程后,计算判别式Δ=b2-4ac②几何法:利用圆心到直线的距离d和圆半径r的大小关系:d<r⇔________,d=r⇔________,d>r⇔________、2、圆的切线方程若圆的方程为x2+y2=r2,点P(x0,y0)在圆上,则过P点且与圆x2+y2=r2相切的切线方程为______________________、注:点P必须在圆x2+y2=r2上、经过圆(x-a)2+(y-b)2=r2上点P(x0,y0)的切线方程为________________________、3、计算直线被圆截得的弦长的常用方法(1)几何方法运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算、(2)代数方法运用韦达定理及弦长公式AB=|xA-xB|=、说明:圆的弦长、弦心距的计算常用几何方法、4、圆与圆的位置关系(1)圆与圆的位置关系可分为五种:________、________、________、________、________、判断圆与圆的位置关系常用方法:(几何法)设两圆圆心分别为O1、O2,半径为r1、r2 (r1≠r2),则O1O2>r1+r2________;O1O2=r1+r2________;|r1-r2|<O1O2<r1+r2________;O1O2=|r1-r2|________;0≤|O1O2|<|r1-r2|________、(2)已知两圆x2+y2+D1x+E1y+F1=0和x2+y2+D2x+E2y+F2=0相交,则与两圆共交点的圆系方程为_________________________________________________________ ___,其中λ为λ≠-1的任意常数,因此圆系不包括第二个圆、当λ=-1时,为两圆公共弦所在的直线,方程为(D1-D2)x +(E1-E2)y+(F1-F2)=0、自我检测1、(xx江西)直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若MN≥2,则k的取值范围是________、2、圆x2+y2-4x=0在点P(1,)处的切线方程为______________、3、圆C1:x2+y2+2x+2y-2=0与圆C2:x2+y2-4x-2y+1=0的公切线有________条、4、过点(0,1)的直线与x2+y2=4相交于A、B两点,则AB的最小值为________、5、若P(2,-1)为圆C:(x-1)2+y2=25的弦AB的中点,则直线AB的方程是______________、探究点一直线与圆的位置关系例1 已知圆C:x2+y2+2x-4y+3=0、(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有PM=PO,求使得PM取得最小值时点P的坐标、变式迁移1 从圆C:(x-1)2+(y-1)2=1外一点P(2,3)向该圆引切线,求切线的方程及过两切点的直线方程、探究点二圆的弦长、中点弦问题例2 已知点P(0,5)及圆C:x2+y2+4x-12y+24=0、(1)若直线l过点P且被圆C截得的线段长为4,求l的方程;(2)求过P点的圆C的弦的中点的轨迹方程、变式迁移2 已知圆C:x2+y2-6x-8y+21=0和直线kx-y-4k+3=0、(1)证明:不论k取何值,直线和圆总有两个不同交点;(2)求当k取什么值时,直线被圆截得的弦最短,并求这条最短弦的长、探究点三圆与圆的位置关系例3 已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,m为何值时,(1)圆C1与圆C2相外切;(2)圆C1与圆C2内含、变式迁移3 已知⊙A:x2+y2+2x+2y-2=0,⊙B:x2+y2-2ax-2by+a2-1=0、当a,b变化时,若⊙B始终平分⊙A的周长,求:(1)⊙B的圆心B的轨迹方程;(2)⊙B的半径最小时圆的方程、探究点四综合应用例4 已知圆C:x2+y2-2x+4y -4=0、问在圆C上是否存在两点A、B关于直线y=kx-1对称,且以AB为直径的圆经过原点?若存在,写出直线AB的方程;若不存在,说明理由、变式迁移4 已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y -3)2=1相交于M、N两点、(1)求实数k的取值范围;(2)若O为坐标原点,且=12,求k的值、1、求切线方程时,若知道切点,可直接利用公式;若过圆外一点求切线,一般运用圆心到直线的距离等于半径来求,但注意有两条、2、解决与弦长有关的问题时,注意运用由半径、弦心距、弦长的一半构成的直角三角形,也可以运用弦长公式、这就是通常所说的“几何法”和“代数法”、3、判断两圆的位置关系,从圆心距和两圆半径的关系入手、(满分:90分)一、填空题(每小题6分,共48分)1、直线l:y-1=k(x-1)和圆x2+y2-2y=0的位置关系是________、2、直线x-y+m=0与圆x2+y2-2x-2=0相切,则实数m=______________、3、过原点且倾斜角为60的直线被圆x2+y2-4y=0所截得的弦长为________、4、若圆(x-3)2+(y+5)2=r2上有且仅有两个点到直线4x-3y-2=0的距离为1,则半径r的取值范围是______________、5、若圆x2+y2=4与圆x2+y2+2ay-6=0(a>0)的公共弦的长为2,则a=________、6、已知点A是圆C:x2+y2+ax+4y-5=0上任意一点,A点关于直线x+2y-1=0的对称点也在圆C上,则实数a=________、7、设直线3x+4y-5=0与圆C1:x2+y2=4交于A,B两点,若圆C2的圆心在线段AB上,且圆C2与圆C1相切,切点在圆C1的劣弧上,则圆C2的半径的最大值是________、8、(xx全国Ⅰ改编)已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么的最小值为____________、二、解答题(共42分)9、(14分)圆x2+y2=8内一点P(-1,2),过点P的直线l 的倾斜角为α,直线l交圆于A、B两点、(1)当α=时,求AB的长;(2)当弦AB被点P平分时,求直线l的方程、10、(14分)自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线l所在直线的方程、11、(14分)已知两圆x2+y2-2x-6y-1=0和x2+y2-10x -12y+m=0、求:(1)m取何值时两圆外切?(2)m取何值时两圆内切?(3)m=45时两圆的公共弦所在直线的方程和公共弦的长、学案48 直线、圆的位置关系答案自主梳理1、相切相交相离①相交相切相离②相交相切相离2、x0x+y0y=r2 (x0-a)(x-a)+(y0-b)(y-b)=r24、(1)外离外切相交内切内含外离外切相交内切内含(2)(x2+y2+D1x+E1y+F1)+λ(x2+y2+D2x+E2y+F2)=0自我检测1、2、x-y+2=03、24、25、x-y-3=0课堂活动区例1 解题导引(1)过点P作圆的切线有三种类型:当P在圆外时,有2条切线;当P在圆上时,有1条切线;当P在圆内时,不存在、(2)利用待定系数法设圆的切线方程时,一定要注意直线方程的存在性,有时要进行恰当分类、(3)切线长的求法:过圆C外一点P作圆C的切线,切点为M,半径为R,则PM=、解(1)将圆C配方得(x+1)2+(y-2)2=2、①当直线在两坐标轴上的截距为零时,设直线方程为y=kx,由=,解得k=2,得y=(2)x、②当直线在两坐标轴上的截距不为零时,设直线方程为x+y-a=0,由=,得|a-1|=2,即a=-1,或a=3、∴直线方程为x+y+1=0,或x+y-3=0、综上,圆的切线方程为y=(2+)x,或y=(2-)x,或x+y+1=0,或x+y -3=0、(2)由PO=PM,得x+y=(x1+1)2+(y1-2)2-2,整理得2x1-4y1+3=0、即点P在直线l:2x-4y+3=0上、当PM取最小值时,即OP取得最小值,直线OP⊥l,∴直线OP的方程为2x+y=0、解方程组得点P的坐标为、变式迁移1 解设圆切线方程为y-3=k(x-2),即kx-y+3-2k=0,∴1=,∴k=,另一条斜率不存在,方程为x=2、∴切线方程为x=2和3x-4y+6=0、圆心C为(1,1),∴kPC==2,∴过两切点的直线斜率为-,又x=2与圆交于(2,1),∴过切点的直线为x+2y-4=0、例2 解题导引(1)有关圆的弦长的求法:已知直线的斜率为k,直线与圆C相交于A(x1,y1),B(x2,y2)两点,点C到l的距离为d,圆的半径为r、方法一代数法:弦长AB=|x2-x1|=;方法二几何法:弦长AB=2、(2)有关弦的中点问题:圆心与弦的中点连线和已知直线垂直,利用这条性质可确定某些等量关系、解(1)如图所示,AB =4,取AB的中点D,连结CD,则CD⊥AB,连结AC、BC,则AD=2,AC=4,在Rt△ACD中,可得CD=2、当直线l的斜率存在时,设所求直线的斜率为k,则直线的方程为y-5=kx,即kx-y+5=0、由点C到直线AB的距离公式,得=2,解得k=、当k=时,直线l的方程为3x-4y+20=0、又直线l的斜率不存在时,也满足题意,此时方程为x=0、∴所求直线的方程为3x-4y+20=0或x=0、(2)设过P点的圆C的弦的中点为D(x,y),则CD⊥PD,即=0,(x+2,y-6)(x,y-5)=0,化简得所求轨迹方程为x2+y2+2x-11y+30=0、变式迁移2 (1)证明由kx-y-4k+3=0,得(x-4)k-y+3=0、∴直线kx-y-4k+3=0过定点P(4,3)、由x2+y2-6x-8y+21=0,即(x-3)2+(y-4)2=4,又(4-3)2+(3-4)2=2<4、∴直线和圆总有两个不同的交点、(2)解kPC==-1、可以证明与PC垂直的直线被圆所截得的弦AB最短,因此过P点斜率为1的直线即为所求,其方程为y-3=x-4,即x-y -1=0、PC==,∴AB=2=2、例3 解题导引圆和圆的位置关系,从交点个数也就是方程组解的个数来判断,有时得不到确切的结论,通常还是从圆心距d与两圆半径和、差的关系入手、解对于圆C1与圆C2的方程,经配方后C1:(x-m)2+(y+2)2=9;C2:(x+1)2+(y-m)2=4、(1)如果C1与C2外切,则有=3+2、(m+1)2+(m+2)2=25、m2+3m-10=0,解得m=-5或m=2、(2)如果C1与C2内含,则有<3-2、(m+1)2+(m+2)2<1,m2+3m+2<0,得-2<m<-1,∴当m=-5或m=2时,圆C1与圆C2外切;当-2<m<-1时,圆C1与圆C2内含、变式迁移3 解(1)两圆方程相减得公共弦方程2(a+1)x+2(b+1)y-a2-1=0、①依题意,公共弦应为⊙A的直径,将(-1,-1)代入①得a2+2a+2b+5=0、②设圆B的圆心为(x,y),∵,∴其轨迹方程为x2+2x+2y+5=0、(2)⊙B方程可化为(x-a)2+(y-b)2=1+b2、由②得b=-[(a+1)2+4]≤-2,∴b2≥4,b2+1≥5、当a=-1,b=-2时,⊙B半径最小,∴⊙B方程为(x+1)2+(y+2)2=5、例4 解题导引这是一道探索存在性问题,应先假设存在圆上两点关于直线对称,由垂径定理可知圆心应在直线上,以AB为直径的圆经过原点O,应联想直径所对的圆周角为直角利用斜率或向量来解决、因此能否将问题合理地转换是解题的关键、解圆C的方程可化为(x-1)2+(y+2)2=9,圆心为C(1,-2)、假设在圆C上存在两点A、B,则圆心C(1,-2)在直线y=kx-1上,即k=-1、于是可知,kAB=1、设lAB:y=x+b,代入圆C的方程,整理得2x2+2(b+1)x+b2+4b-4=0,Δ=4(b+1)2-8(b2+4b-4)>0,b2+6b-9<0,解得-3-3<b<-3+3、设A(x1,y1),B(x2,y2),则x1+x2=-b-1,x1x2=b2+2b-2、由O A⊥OB,知x1x2+y1y2=0,也就是x1x2+(x1+b)(x2+b)=0,∴2x1x2+b(x1+x2)+b2=0,∴b2+4b-4-b2-b+b2=0,化简得b2+3b-4=0,解得b=-4或b=1,均满足Δ>0、即直线AB的方程为x-y-4=0,或x-y+1=0、变式迁移4 解(1)∵直线l过点A(0,1)且斜率为k,∴直线l的方程为y=kx+1、将其代入圆C:(x-2)2+(y-3)2=1,得(1+k2)x2-4(1+k)x+7=0、①由题意:Δ=[-4(1+k)]2-4(1+k2)7>0,得<k<、(2)设M(x1,y1),N(x2,y2),则由①得,∴=x1x2+y1y2=(1+k2)x1x2+k(x1+x2)+1=+8=12⇒k=1(经检验符合题意),∴k=1、课后练习区1、相交2、-3或3、2解析如图所示,x2+y2-4y=0⇔x2+(y-2)2=4,∴A(0,2),OA=2,A到直线l:y=x的距离是AN=1,∴ON=,∴弦长OJ=2、4、(4,6)5、16、-107、1解析圆C1的圆心C1(0,0)到直线3x+4y-5=0的距离为=1,圆C1的半径为2,弧上的点到直线3x+4y-5=0距离最大为2-1=1,因此圆C2的半径最大为1、8、-3+2解析设∠APB=2θ,则∠APO=∠BPO=θ,=()2cos2θ=cos2θ=(1-2sin2θ)=+2sin2θ-3≥2-3,当且仅当=2sin2θ,即sin2θ=时取等号、9、解(1)当α=时,kAB=-1,直线AB的方程为y-2=-(x+1),即x+y-1=0、(3分)故圆心(0,0)到AB的距离d==,从而弦长AB=2 =、(7分)(2)设A(x1,y1),B(x2,y2),则x1+x2=-2,y1+y2=4、由两式相减得(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0,即-2(x1-x2)+4(y1-y2)=0,∴kAB==、(12分)∴直线l 的方程为y-2=(x+1),即x-2y+5=0、(14分)10、解已知圆C:x2+y2-4x-4y+7=0关于x轴对称的圆为C1:(x-2)2+(y+2)2=1,其圆心C1的坐标为(2,-2),半径为1,由光的反射定律知,入射光线所在直线方程与圆C1相切、(4分)设l的方程为y-3=k(x+3),则=1,(10分)即12k2+25k+12=0、∴k1=-,k2=-、则l的方程为4x+3y+3=0或3x+4y-3=0、(14分)11、解两圆的标准方程分别为(x-1)2+(y-3)2=11,(x -5)2+(y-6)2=61-m,圆心分别为M(1,3),N(5,6),半径分别为和、(1)当两圆外切时,=+、解得m=25+10、(4分)(2)当两圆内切时,因定圆的半径小于两圆圆心间距离,故只有-=5、解得m=25-10、(8分)(3)两圆的公共弦所在直线的方程为(x2+y2-2x-6y-1)-(x2+y2-10x-12y+45)=0,即4x+3y-23=0、(12分)由圆的半径、弦长、弦心距间的关系,不难求得公共弦的长为2 =2、(14分)第 1 页共 1 页。

(江苏专用)2018版高考数学大一轮复习第九章平面解析几何9.4 直线与圆、圆与圆的位置关系教师用书理苏教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((江苏专用)2018版高考数学大一轮复习第九章平面解析几何9.4 直线与圆、圆与圆的位置关系教师用书理苏教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(江苏专用)2018版高考数学大一轮复习第九章平面解析几何9.4 直线与圆、圆与圆的位置关系教师用书理苏教版的全部内容。
第九章平面解析几何 9.4 直线与圆、圆与圆的位置关系教师用书理苏教版1.判断直线与圆的位置关系常用的两种方法(1)几何法:利用圆心到直线的距离d和圆半径r的大小关系。
d<r⇔相交;d=r⇔相切;d〉r⇔相离.(2)代数法:错误!错误!2。
圆与圆的位置关系设圆O1:(x-a1)2+(y-b1)2=r错误!(r1>0),圆O2:(x-a2)2+(y-b2)2=r错误!(r2〉0).方法位置关系几何法:圆心距d与r1,r2的关系代数法:联立两圆方程组成方程组的解的情况外离d>r1+r2无解外切d=r1+r2一组实数解相交|r1-r2|〈d<r1+r2两组不同的实数解内切d=|r1-r2|(r1≠r2)一组实数解内含0≤d<|r1-r2|(r1≠r2)无解【知识拓展】1。
圆的切线方程常用结论(1)过圆x2+y2=r2上一点P(x0,y0)的圆的切线方程为x0x+y0y=r2.(2)过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的圆的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2。