spss参数与非参数检验实验报告

SPSS应⽤之⾮参数检验统计学的假设检验可以分为参数检验和⾮参数检验，参数检验是根据⼀些假设条件推算⽽来，当这些假设条件⽆法满⾜的时候，参数检验的效能会⼤打折扣，甚⾄出现错误的结果，⽽⾮参数检验通常是没有假设条件的，因此应⽤范围⽐参数检验要⼴。

⾮参数检验在不做任何假设的情况下，最⼤限度的使⽤样本信息，利⽤统计学、数学的⽅法和技巧构造统计量并加以检验，在某些情况下，⾮参数检验⽐参数检验拥有更⾼的效能，尽管如此，我们也不能⼀味的使⽤⾮参数检验，毕竟参数检验更加严谨，通常都是在数据不符合参数检验的条件是，才使⽤⾮参数检验，因此，对于数据的前期观察是⾮常重要的。

⾮参数检验⽅法⾮常多，但是绝⼤部分⾮参数检验⽅法都是基于秩和结来构造统计量的，中⾮参数检验是⼀个独⽴的过程，也保留了旧对话框，新对话框按照样本情况分类，根据样本情况来选择⽅法，并且更倾向于⾃动化分析，旧对话框的分类则不是很明确，分我们按照新对话框来进⾏介绍分析—⾮参数检验—单样本⼀、单样本1.⼆项式检验⼆项式检验也称为⼆项分布检验，⽤来检验样本是否来⾃⼆项分布，也就是检查样本的观测值的频数与某⼀特定⼆项分布下的期望频数是否⼀致。

不仅可以针对于⼆分类变量，对于连续变量也可以当做⼆分类变量来处理，例如成绩的及格与否，产品的合格与否等。

本例中是想检验三门学科的及格率是否都在95%以上2.卡⽅检验卡⽅检验是最常⽤的多分类⾮参数检验，卡⽅统计量也⼴泛被其他检验所引⽤，卡⽅检验依据卡⽅分布，主要包括适应性检验和独⽴性检验，适应性检验⽤于检验实际观察频数与期望频数是否⼀致，独⽴性检验⽤于检验两组或多组计数资料是否相互独⽴。

3.K-S检验全称为Kolmogorov-Smirnow检验，在探索性中，也曾出现过⽤它来检验是否服从正态分布。

该检验属于⾮参数检验，⽤来检验某⼀单样本是否服从某⼀理论分布。

4.Wilcoxon符号秩检验该检验将符号和秩相结合，效能⽐单纯的符号检验和秩和检验都⾼，因此⽐较常⽤5.游程检验我们知道样本的随机性很重要，⽽游程检验就是⽤来检验样本数据是否是随机抽取的。

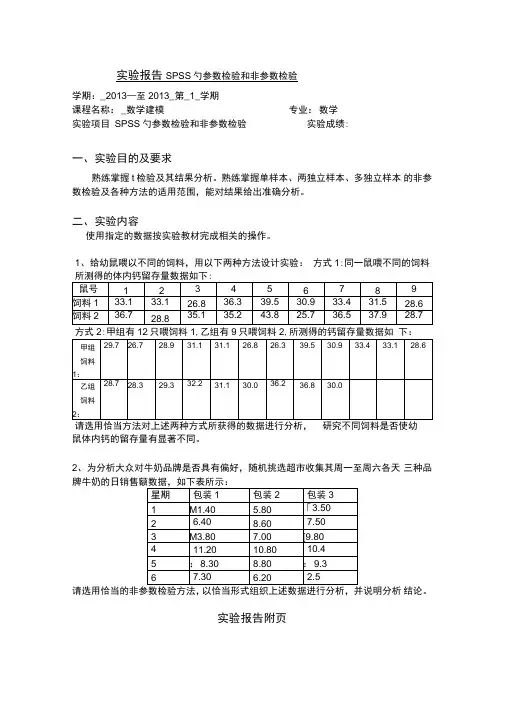
实验报告SPSS 勺参数检验和非参数检验学期：_2013—至2013_第_1_学期 课程名称：_数学建模专业：数学实验项目 SPSS 勺参数检验和非参数检验实验成绩:一、 实验目的及要求熟练掌握t 检验及其结果分析。

熟练掌握单样本、两独立样本、多独立样本 的非参数检验及各种方法的适用范围，能对结果给出准确分析。

二、 实验内容使用指定的数据按实验教材完成相关的操作。

1、给幼鼠喂以不同的饲料，用以下两种方法设计实验： 方式1:同一鼠喂不同的饲料所测得的体内钙留存量数据如下:方式2:甲组有12只喂饲料1,乙组有9只喂饲料2,所测得的钙留存量数据如 下：请选用恰当方法对上述两种方式所获得的数据进行分析，研究不同饲料是否使幼鼠体内钙的留存量有显著不同。

2、为分析大众对牛奶品牌是否具有偏好，随机挑选超市收集其周一至周六各天 三种品牌牛奶的日销售额数据，如下表所示：请选用恰当的非参数检验方法，以恰当形式组织上述数据进行分析， 并说明分析 结论。

实验报告附页三、实验步骤（一）方式1:1、打开SPSS软件，根据所给表格录入数据，建立数据文件；2、选择菜单Analyze —Compare means- Paired-Samples T Test ，出现窗口；3、把检验变量饲料1,饲料2选择到Paired Variables 框，单击OK 方式2:1、打开SPSS软件，根据所给表格录入数据，建立数据文件；2、选择菜单Analyze —Compare mean—Independent-Samples T Test，出现窗口3、选择检验变量饲料到Test Variable（s）框中。

4、选择总体标志变量组号到Group ing Variables 框中5、单击Define Groups按钮定义两总体的标志值1、2，单击OK（二）1、打开SPSS软件，根据所给表格录入数据，建立数据文件；2、选择菜单Analyze->Nonparametric->k Independent sample3、选择待检验的若干变量入包装1,包装2,包装3到Test Variable（s）框中;4、选择推广的平均秩检验（Friedman检验），单击OK四、实验结果分析与评价（一）:方式1:Paired Samples Correlations由上表知：两配对变量饲料1和饲料2对应的概率p值为0.108>0.05通过了检验，可以认为两配对变量饲料1和饲料2无相关关系。

实验报告——（非参数检验）实验目的：1、学会使用SPSS软件进行非参数检验。

2、熟悉非参数检验的概念及适用范围，掌握常见的秩和检验计算方法。

实验内容：1、某公司准备推出一个新产品，但产品名称还没有正式确定，决定进行抽样调查，在受访200人中，52人喜欢A名称，61人喜欢B名称，87人喜欢C 名称，请问ABC三种名称受欢迎的程度有无差别？(数据表自建)SPSS计算结果如下：此题为总体分布的卡方检验。

零假设：样本来自总体分布形态和期望分布没有显著差异。

即ABC三种名称受欢迎的程度无差别,分布形态为1：1：1，呈均匀分布。

观察结果，上表为200个观察数据对A、B、C三个名称（分别对应1，2，3）的喜爱的期望频数以及实际观察频数和期望频数的差。

从下表中可以看出相伴概率值为0.007小于显著性水平0.05，因此拒绝零假设，认为样本来自的总体分布与制定的期望分布有显著差异，即A、B、C三种名称受欢迎的程度有差异。

2、某村庄发生了一起集体食物中毒事件，经过调查，发现当地居民是直接饮用河水，研究者怀疑是河水污染所致，县按照可疑污染源的大致范围调查了沿河居民的中毒情况，河边33户有成员中毒（+）和均未中毒（-）的家庭分布如下：（案例数据run.sav）-+++*++++-+++-+++++----++----+----毒源问：中毒与饮水是否有关？SPSS计算结果如下：此题为单样本变量值随机检验零假设：总体某变量的变量值是随机出现的。

即中毒的家庭沿河分布的情况随机分布，与饮水无关。

相伴概率为0.036，小于显著性水平0.05，拒绝零假设，因此中毒与饮水有关。

3、某试验室用小白鼠观察某种抗癌新药的疗效，两组各10只小白鼠，以生存日数作为观察指标，试验结果如下，案例数据集为：npara1.sav，问两组小白鼠生存日数有无差别。

试验组：24 26 27 30 32 34 36 40 60 天以上对照组：4 6 7 9 10 10 12 13 16 16SPSS计算结果如下：此题为两独立样本非参数检验。

SPSS的参数检验和非参数检验SPSS是一种非常常用的统计分析软件，可以用于参数检验和非参数检验。

参数检验是假设检验的一种方法，用于判断统计样本是否代表总体。

而非参数检验则是用于检验数据是否满足一些分布假设，或判断两个或多个群体是否具有差异。

参数检验主要有t检验、方差分析和回归分析等。

其中，t检验用于比较两个样本均值是否有显著差异，包括独立样本t检验和相关样本t检验。

方差分析用于比较三个或更多样本均值是否有显著差异，可以进行单因素方差分析或多因素方差分析。

回归分析用于建立预测模型，可以通过线性回归或多项式回归进行。

非参数检验通常适用于数据不满足正态分布或方差齐性的情况，如Wilcoxon符号秩检验、Kruskal-Wallis H检验、Mann-Whitney U检验等。

Wilcoxon符号秩检验用于比较两个配对样本的差异是否有显著差异，Kruskal-Wallis H检验用于比较三个或更多独立样本的差异是否有显著差异，Mann-Whitney U检验用于比较两个独立样本的差异是否有显著差异。

在SPSS中进行参数检验和非参数检验一般需要进行以下步骤：1.导入数据：将数据导入SPSS软件，可以通过选择文件-导入功能进行操作。

2.设定分析变量：定义需要进行分析的变量，并将其添加到分析列表中。

3.选择统计方法：根据实验设计和数据分布情况，选择合适的参数检验或非参数检验方法。

4.执行分析：点击运行按钮进行分析，在分析结果中可以查看得到显著性水平、均数、方差等指标。

5.结果解释：根据分析结果进行假设检验，判断是否存在显著差异，并解释其结果。

无论是参数检验还是非参数检验，在进行分析前需要注意数据的合理性、样本的选择和实验设计的合理性等，以保证分析结果的可靠性。

同时，还应根据不同的研究目的和数据特点选择适当的方法，并合理解释分析结果。

在SPSS软件中，可以通过图表、表格和描述性统计等形式展示和解释结果，并通过结果进行科学判断和相关推断。

岭南师范学院2014年－2015学年第一学期期末考试（考察）实验报告调查题目：岭南师院学生生活费支出情况的调查科目：统计软件成绩：姓名：陈文超学号： 2011224529 巫军福 2011224539李裕慧 2011224522李立聪 2011224515 专业：数学与应用数学班级： 11金融数学班内容： SPSS软件数据预处理、基本统计分析、参数检验非参数检验、方差分析有关说明：现在大学生的生活费大部分是家里给的，当然也有一部分的学生是通过做各种的兼职，例如：家教、派传单、送餐等，获得一小部分的零花钱。

那么，对于大学生来说，如何能让自己的一定额度的生活费用在合理的方面，这是非常重要的。

这也是一个关于生活费的理财计划，处理得好的话，可以每月都能有一点的剩余或者可以买些自己喜欢的商品。

基于这个原因，我们小组经过讨论后，确定了这个题目，也为了了解当今大学生的生活支出情况，从而可以做出相应的改善。

调查目的：大学生是一个新兴的消费群体，为了调查清楚我校大学生生活费支出状况，我们决定采用简单随机抽样发放问卷以及网上填写问卷的方法对学校的同学进行一次大学生生活费支出的调查，并进行统计分析。

主要弄清楚大学生要花多少钱，花在了什么地方，花的是否合理，如果不合理怎样改进。

我们用数据来倡导大家在校期间生活费的合理使用。

调查范围：岭南师范学院。

调查对象：我校不同学院不同专业的学生群体。

调查研究的方法：采用简单随机不重复抽样的方法发放问卷，网上不重复填写问卷的方法，并进行统计分析。

具体统计分析有:1.根据样本的生活费来源，分布状况的均值，比例等分布的数字特征，推断大学生总体分布的相应参数。

2.根据性别进行男女两个总体生活费均值之差的比较以及比例的比较。

3.根据大一、大二、大三、大四进行四个总体生活费均值之差及比例的比较4.绘制统计图使样本数据直观化并对统计量进行分析。

小组分工安排：巫军福、陈文超、李裕慧、李立聪四个人一起讨论确定选题以及调查的主体、范围、方法，也初步定出调查问卷的初稿。

实验报告非参数检验学院:参赛队员:参赛队员:参赛队员:指导老师:目录一、实验目的 (3)1.了解假设检验的基本容； (3)2.了解卡方检验； (3)3.了解二项分布检验； (3)4.了解两个独立样本检验； (3)5.学会运用spss软件求解问题； (3)6.加深理论与实践相结合的能力。

(3)二、实验环境 (3)三、实验方法 (3)1.卡方检验； (3)2.二项分布检验； (3)3.两个独立样本检验。

(3)四、实验过程 (3)问题一： (3)1.1实验步骤 (4)1.1.1输入数据 (4)1.1.2选择：数据加权个案 (4)1.1.3选择：分析→非参数检验→旧对话框→卡方 (4)1.1.4将变量面值放入检验变量列表 (5)1.1.5观察结果 (5)1.2输出结果 (5)1.3结果分析 (5)问题二： (5)2.1问题叙述 (5)2.2提出假设 (6)2.3实验步骤 (6)2.3.1导入excel文件数据 (6)2.3.2二项分布检验 (7)2.3.3输出结果 (8)2.4结果分析 (8)问题三： (8)3.1实验步骤 (8)3.1.1数据的输入 (8)3.1.2选择 (9)3.1.3检验变量 (9)3.2输出结果 (9)3.3结果分析 (11)五、实验总结 (11)参数检验一、实验目的1.了解假设检验的基本容；2.了解卡方检验；3.了解二项分布检验；4.了解两个独立样本检验；5.学会运用spss软件求解问题；6.加深理论与实践相结合的能力。

二、实验环境Spss、office三、实验方法1.卡方检验；2.二项分布检验；3.两个独立样本检验。

四、实验过程问题一：1.1实验步骤1.1.1输入数据1.1.2选择：数据加权个案1.1.3选择：分析→非参数检验→旧对话框→卡方1.1.4将变量面值放入检验变量列表，期望全距从数据中获取，期望值所有类别相等1.1.5观察结果1.2输出结果1.3结果分析此处，sig值为0.111>0.05，所以接受原假设，认为样本来自的总体分布形态与期望分布不存在显著差异，则认为该骰子均匀问题二：2.1问题叙述2.2提出假设H0:硬币不是均匀的 vs H1:硬币是均匀的2.3实验步骤2.3.1导入excel文件数据先将数据输入进excel表格中，用SPSS打开；在SPSS页面点击文件→打开→数据2.3.2二项分布检验选择：分析→非参数检验→旧对话框→二项式2.3.3输出结果2.4结果分析由输出结果知，精确显著性（双侧）=1.000>0.05，所以接受原假设H0，所以硬币不是均匀的。

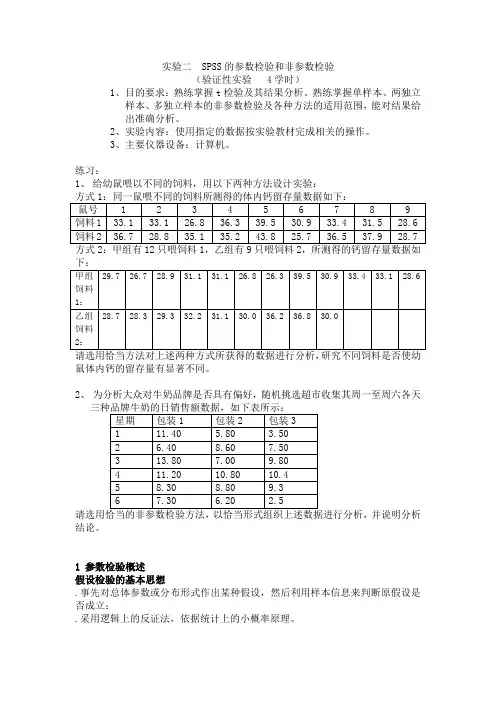
实验二 SPSS的参数检验和非参数检验（验证性实验 4学时）1、目的要求：熟练掌握t检验及其结果分析。

熟练掌握单样本、两独立样本、多独立样本的非参数检验及各种方法的适用范围，能对结果给出准确分析。

2、实验内容：使用指定的数据按实验教材完成相关的操作。

3、主要仪器设备：计算机。

练习：1、给幼鼠喂以不同的饲料，用以下两种方法设计实验：鼠体内钙的留存量有显著不同。

2、为分析大众对牛奶品牌是否具有偏好，随机挑选超市收集其周一至周六各天并说明分析结论。

1 参数检验概述假设检验的基本思想.事先对总体参数或分布形式作出某种假设，然后利用样本信息来判断原假设是否成立；.采用逻辑上的反证法，依据统计上的小概率原理。

2 单样本的T检验2.1检验目的：•检验单个变量的均值是否与给定的常数(总体均值)之间是否存在显著差异。

如：分析学生的IQ平均分是否为100分；大学生考研率是否为5%。

•要求样本来自的总体服从或近似服从正态分布。

2.2 单样本T检验的实现思路•提出原假设：•计算检验统计量和概率P值●给定显著性水平与p值做比较：如果p值小于显著性水平，小概率事件在一次实验中发生，则我们应该拒绝原假设，反之就不能拒绝原假设。

2.3 单样本t检验的基本操作步骤1、选择选项Analyze－Compare means－One-Samples T test，出现窗口：2、在Test Value框中输入检验值。

3、单击Option按钮定义其他选项。

Option选项用来指定缺失值的处理方法。

其中，Exclude cases analysis by analysis表示计算时涉及的变量上有缺失值，则剔除在该变量上为缺失值的个案；Exclude cases listwise表示剔除所有在任意变量上含有缺失值的个案后再进行分析。

可见，较第二种方式，第一种处理方式较充分地利用了样本数据。

在后面的分析方法中，SPSS对缺失值的处理方法与此相同，不再赘述。

SPSS进⾏两配对样本的⾮参数检验（Wilcoxon符号秩检验）-实验⽅法-丁⾹通⼀、概述
⾮参数检验对于总体分布没有要求，因⽽使⽤范围更⼴泛。

对于两配对样本的⾮参数检验，⾸
选Wilcoxon符号秩检验。

它与配对样本t检验相对应。

⼆、问题
为了研究某放松⽅法（如听⾳乐）对于⼊睡时间的影响，选择了10名志愿者，分别记录未进⾏
放松时的⼊睡时间及放松后的⼊睡时间（单位为分钟），数据如下笔。

请问该放松⽅法对⼊睡
时间有⽆影响。

本例可以采⽤配对样本t检验，但由于样本量少，数据可能不符合正太分布，所以考虑⽤⾮参数
检验。

三、统计操作
数据视图
菜单选择
打开如下的对话框。

一、实验名称：实验三二、实验要求：1、所有的文件上传到网络硬盘中。

2、数据文件保存，用文件名“学号+姓名+人员登记”。

3、撰写实验报告。

每个操作要写出实验步骤，及操作结果。

4、要求电子版实验报告，用文件名“学号+姓名+实验一”保存，学期结束上交。

5、练习上课讲过（第6-9章）的例子。

（无需写实验报告）。

三、实验步骤及结果：“CH6CH9CH10证券投资额与依据”的数据是对杭州市股民的调查数据，试进行以下分析。

（需写实验报告）（1）北京市股民的“证券外年收入”为4.8万元，杭州股民的“证券外年收入”和北京股民的相同吗？分析：此题为“单样本T检验”，检查相应总体均值是否为某个值。

1.1实验步骤：1）启动SPSS，调入样本值，2）点击Analyze->Compare Means->One-Sample T Test，弹出小窗口，将“券外收入”添加到Test Variable(s)中，3)在Test Value中输入4.8,如图1.114）点击OK.图1.11 单样本T检验窗口1.2实验结果：如图：1.12，T检验的最后结果p=0.164>0.05,可知杭州股民的“证券外年收入”和北京股民的没有显著差异。

图1.12 有关单样本T检验（2）杭州股民投入股市的资金超过他们的年收入吗？分析：此题为“配对样本的T检验”，即两组样本不可以颠倒顺序，不然将出现错误。

2.1实验步骤：1）点击Analyze->Compare Means->Paired-Samples T Test，2）从左框变量中选出“券外收入”和“投资总额”，用箭头放入右边的Test variables 框中，此时右框中的2个变量已差的形式出现，如图2.11。

3）点击OK。

图2.11 配对T检验窗口2.2实验结果：图2.12中的paired samples test表格中可知T检验的最后结果p=0.00<0.05,两者有显著性差异，从第一张表格中可以得知“投入总资金”>“卷外收入”。

实验报告 SPSS的参数检验和非参数检验学期：_2013__至2013_ 第_1_学期课程名称:_数学建模专业:数学实验项目__SPSS的参数检验和非参数检验实验成绩：＿＿＿＿＿一、实验目的及要求熟练掌握t检验及其结果分析。

熟练掌握单样本、两独立样本、多独立样本的非参数检验及各种方法的适用范围，能对结果给出准确分析。

二、实验内容使用指定的数据按实验教材完成相关的操作。

1、给幼鼠喂以不同的饲料，用以下两种方法设计实验：方式1：同一鼠喂不同的饲料所测得的体内钙留存量数据如下：方式2：甲组有12只喂饲料1，乙组有9只喂饲料2，所测得的钙留存量数据如下：请选用恰当方法对上述两种方式所获得的数据进行分析，研究不同饲料是否使幼鼠体内钙的留存量有显着不同。

2、为分析大众对牛奶品牌是否具有偏好，随机挑选超市收集其周一至周六各天三种品牌牛奶的日销售额数据，如下表所示：请选用恰当的非参数检验方法，以恰当形式组织上述数据进行分析，并说明分析结论。

实验报告附页三、实验步骤（一）方式1：1、打开SPSS软件，根据所给表格录入数据，建立数据文件；2、选择菜单Analyze－Compare means－Paired-Samples T Test，出现窗口；3、把检验变量饲料1，饲料2 选择到Paired Variables框，单击OK。

方式2：1、打开SPSS软件，根据所给表格录入数据，建立数据文件；2、选择菜单Analyze－Compare means－Independent-Samples T Test，出现窗口3、选择检验变量饲料到Test Variable(s)框中。

4、选择总体标志变量组号到Grouping Variables框中。

5、单击Define Groups按钮定义两总体的标志值1、2，单击OK。

（二）1、打开SPSS软件，根据所给表格录入数据，建立数据文件；2、选择菜单Analyze->Nonparametric->k Independent sample3、选择待检验的若干变量入包装1，包装2，包装3到Test Variable(s)框中；4、选择推广的平均秩检验(Friedman检验)，单击OK。

实验项目非参数检验实验时间2017.10.27实验地点S308 成绩三、实验内容1、将一颗骰子连掷120次，各次所出现的点数顺次如“shai.sav” 所示，试检验掷骰子点数是否服从均匀分布？2、从随机数表中抽得20个数据如下：0.55 0.8 0.15 0.12 0.21 0.4 0.46 0.17 0.62 0.770.63 0.71 0.99 0.88 0.30 0.64 0.51 0.68 0.50 0.60要求：（1）利用单个样本的K–S检验法检验这些数据是否服从正态分布；（2）对结果进行分析，并填写新的实验报告。

1、SPSS单样本K-S检验的基本操作步骤如下：（1）选择菜单：【分析（A）】→【非参数检验（N）】→【旧对话框（L）】→【1样本K-S（1）】出现如图1-1所示的窗口。

图1-1 单样本K-S检验窗口（2）选择待检验的变量到【检验变量列表（T）】框中。

（3）在【检验分布】框中指定理论分布，这里选择【相等】，即代表均匀分布。

至此，SPSS将自动计算K-S检验统计量和对应的概率P-值，并将结果输出到查看器窗口中。

分析结果如图1-2所示。

图1-2掷骰子总体分布的K-S检验结果图1-2表明，数据极小值为1.00，极大值为6.00。

最大绝对差值为0.158，正差极值为0.158，负差极值为-0.142。

SPSS自动计算输出了√nD值（1.734）和概率P-值（0.005）。

如果显著性水平α为0.05，由于概率P-值小于显著性水平，因此拒绝原假设，接受备择假设，即掷骰子点数的总体分布为不是均匀分布。

2、SPSS单样本K-S检验的基本操作步骤如下：（1）选择菜单：【分析（A）】→【非参数检验（N）】→【旧对话框（L）】→【1样本K-S（1）】出现如图2-1所示的窗口。

图2-1单样本K-S检验窗口（2）选择待检验的变量到【检验变量列表（T）】框中。

（3）在【检验分布】框中指定理论分布，这里选择【常规】，即代表正态分布。

参数检验与非参数检验一、参数检验与非参数检验的区别（1）参数检验：一般是数据的总体分布已知的情况下，对数据分布的参数是否落在相应范围内进行检验。

是对参数平均值、方差进行的统计检验，是推断统计的重要组成部分。

适用条件：当总体分布已知（如总体为正态分布），根据样本数据对总体分布的统计参数进行推断。

此时，总体的分布形式是给定的或是假定的，只是其中一些参数的取值或范围未知，分析的主要目的是估计参数的取值，或对其进行某种统计检验。

这类问题往往用参数检验来进行统计推断。

它不仅仅能够对总体的特征参数进行推断，还能够实现两个或多个总体的参数进行比较。

（2）非参数检验：一般是在不知道数据总体分布的前提下，检验数据的分布情况。

适用条件：在数据分析过程中，由于种种原因，往往无法对总体分布形态作简单假定，此时参数检验不再适用。

非参数检验正是基于这种考虑，在总体方差未知或知道甚少的情况下，利用样本数据对总体分布形态等进行推断的方法。

二、参数检验方法及适用条件三、非参数检验方法及适用条件四、使用方法当分析某个因素对变量的影响差异时，即检验该因素分类的若干个样本差异：（1）如果因素为两个，使用独立样本T-检验，来分析两个总体平均数相等的显著性；结果判定：先看方差齐性F检验结果，再看均值相等性的t检验结果，即a.如果方差齐性显著性>0.05，则表明方差齐性显著，再看第一行的检验统计值t及显著性p（p<0.05表示差异明显）；b.如果方差齐性显著性<=0.05，则表明方差显著不齐，再看第二行的检验统计值t及显著性p（p<0.05表示差异明显）；（2）如果因素为多个，使用单因素方差检验（即F检验），来分析该因素的影响差异。

结果判定：方差齐性显著则看ANOVA的检验统计值F及其显著性p。

SPSS统计软件实训报告一、引言SPSS（Statistical Product and Service Solutions）统计软件是一种常用的统计分析软件，被广泛应用于数据分析和统计研究领域。

本报告旨在总结并分析在SPSS实训课程中所学到的基本操作和统计分析方法。

二、实训内容在SPSS统计软件实训中，我们学习了以下主要内容： 1. SPSS软件的安装和介绍； 2. 数据输入和修改； 3. 数据清洗和处理； 4. 描述性统计分析； 5. 参数检验和非参数检验； 6. 方差分析； 7. 相关分析； 8. 回归分析等。

三、实训过程1. SPSS软件的安装和介绍我们首先安装了SPSS统计软件，并对其界面和基本功能进行了介绍。

SPSS软件提供了直观的用户界面，可以进行数据输入、数据处理和统计分析等操作。

2. 数据输入和修改为了方便后续的统计分析，我们学习了数据的输入和修改方法。

在SPSS软件中，我们可以手动输入数据，也可以从Excel等其他文件中导入数据。

此外，我们还学习了如何修改数据，包括添加变量、删除变量、重命名变量等操作。

3. 数据清洗和处理在实际应用中，数据往往存在一些错误或缺失。

为了保证统计分析的准确性，我们需要对数据进行清洗和处理。

SPSS软件提供了一系列的数据清洗工具，如删除重复数据、替换缺失值、筛选数据等。

4. 描述性统计分析描述性统计分析是对收集到的数据进行总结和描述的方法。

我们学习了如何计算数据的均值、中位数、众数、标准差等统计量。

通过绘制直方图、箱线图等图表，我们可以对数据的分布进行可视化展示。

5. 参数检验和非参数检验参数检验和非参数检验是统计分析中常用的两种方法，用于判断样本间差异是否显著。

我们学习了t检验、方差分析、卡方检验等方法，并通过SPSS软件进行了实际操作。

6. 方差分析方差分析是用于比较三个或三个以上样本均值是否存在显著差异的方法。

我们学习了单因素方差分析和多因素方差分析，并通过SPSS软件进行了实际分析。