代数体函数与常微分方程(何育赞,萧修治著)思维导图
- 格式:xmin
- 大小:4.30 KB
- 文档页数:1




高中数学最全的思维导图小数老师2015-11-23 11:08很多同学一轮复习已经过半,但还不知道该怎么总结,小数老师给大家提个建议,要想总结,主要还是首先梳理出脉络来,提到某个知识点,那么关于这个知识点相关的所有知识你都要弄明白,这样你就成功了一半!下面是8张思维导图,先研究下看看吧!夷示方法元表、隼合之闾的关系集台「1f映射i I 函数三要妄性质表示定义定义域值域单调性周期性性质対称性基本初等函数分段国数运算:交、弃、补确定性、互异性、无序性解析达列表法使解析式有意义丿对应关采[」换元法求解析式JA连意应用函数的单调在求值域圏象法u函薮破个区圈MlWt减I与曲谒国直是秃亍区减占鱼乂耒冒:2,征阴尊讶*勒査『斷人导披追;儿麗舍弼戴的鱼调性亘塑」是乂填黄于旗点时歌氐L©社有盘文的奇證戳弋r如即)r的奇圈埶詡⑵二呻书⑹=£)最值—C环酩变拱)—f皑拦变彗)—{棒编变箕)亘合函数二次函巍、基本不等式、打崗(耐克)函〕数、三角函数有界性、数形结台、异数.L —次、二次函数、反比例函數一幕函数指数函数对数函数三甬函埶亘台III埶的单调性:同潸异减I哦值法、典型的函数1抽象函数函数与方程函埶的应用图象V性质和应用二分注、图象迭、二次展三次方程根的分布)空间几何体liii台区梭怪梭台L囲台Sfe-正枝{王,长方体、正方体EW.四面体、正四面体一l点在Mh±点与线纬与面一面勻面点在面內点在面外竝面岂強-直线在平窗内厂平行—相乂—f平行关系的]A 转化J i ■■-平厅J垂直曲罕的]线线1相互轉化J垂嵐L相父L平行L三视團•r直观團长对正-喜平齐卞伯隼」一刚面积.表面理体段口高—个公共点没有缺旦漫有有公扛耳------------------ 厂W T 厂直线在平面外-^―---------------- L相交亠线面- "平行「面直垂畳线面甜r-J_ -面面■乎行價耕角的畫化与糾率的变化)位臭关养相立I—C且必:-今血芒:)狂童:战距可正A可员,也可为0. J注at:栽距可正可员,也可訂oj直迭万程茹形式直迭万程茹形式两亶线的交点两亶线的交点圧意若种开式的辕化和运用范圈圧意若种开式的辕化*□运用范围不等式群三即T通项会式等比数列一1(样。

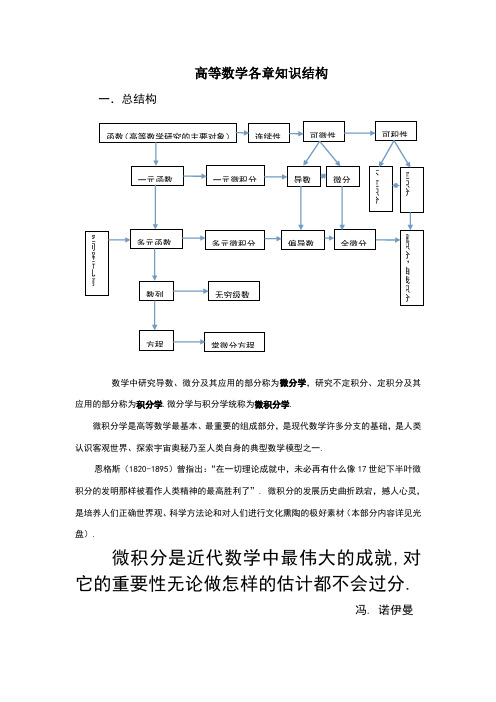
高等数学各章知识结构一.总结构数学中研究导数、微分及其应用的部分称为微分学,研究不定积分、定积分及其应用的部分称为积分学.微分学与积分学统称为微积分学.微积分学是高等数学最基本、最重要的组成部分,是现代数学许多分支的基础,是人类认识客观世界、探索宇宙奥秘乃至人类自身的典型数学模型之一.恩格斯(1820-1895)曾指出:“在一切理论成就中,未必再有什么像17世纪下半叶微积分的发明那样被看作人类精神的最高胜利了”. 微积分的发展历史曲折跌宕,撼人心灵,是培养人们正确世界观、科学方法论和对人们进行文化熏陶的极好素材(本部分内容详见光盘).微积分是近代数学中最伟大的成就,对它的重要性无论做怎样的估计都不会过分.冯. 诺伊曼注:冯. 诺依曼(John von Neumann,1903-1957,匈牙利人),20世纪最杰出的数学家之一,在纯粹数学、应用数学、计算数学等许多分支,从集合论、数学基础到量子理论与算子理论等作多方面,他都作出了重要贡献. 他与经济学家合著的《博弈论与经济行为》奠定了对策论的基础,他发明的“流程图”沟通了数学语言与计算机语言,制造了第一台计算机,被人称为“计算机之父”.微积分中重要的思想和方法:1.“极限”方法,它是贯穿整个《微积分》始终。
导数是一种特殊的函数极限;定积分是一种特殊和式的极限;级数归结为数列的极限;广义积分定义为常义积分的极限;各种重积分、曲线积分、曲面积分都分别是某种和式的极限。
所以,极限理论是整个《微积分》的基础。
尽管上述各种概念都是某种形式的极限,但是它们都有各自独特和十分丰富深刻的内容,这是《微积分》最有魅力的地方之一。
2.“逼近”思想,它在《微积分》处处体现。
在近似计算中,用容易求的割线代替切线,用若干个小矩形面积之和代替所求曲边梯形面积;用折线段的长代替所求曲线的长;用多项式代替连续函数等。
这种逼近思想在理论和实际中大量运用。
3.“求极限、求导数和求积分”是最基本的方法。
第四章常微分方程
常微分方程基本概念
微分方程微分方程的阶
微分方程的解
通解
特解
初始条件积分曲线
一阶微分方程
可分离变量的方程
齐次微分方程一阶线性微分方程
高阶线性微分方程
线性微分方程的解的结构
齐次特解+齐次特解(线性无关)=齐次通解两个线性无关齐次特解+非齐次特解=非齐次通解非齐次特解-非齐次特解=齐次解
非齐次特解1+非齐次特解2=方程(1+2)的特解
k个非齐特解相加=非齐次解⇔k系数之和=1k个非齐特解相加=齐次解⇔k系数之和=0
常系数齐次线性微分方程
两个不等实特征根r1≠r2二重实特征根r1=r2共轭复根r=α±iβ常系数非齐次线性微分方程
f(x)=x^k·Qm(x)·e^λx
f(x)=x^k·e^αx·[Rm ₁(x)·cosβx+Rm ₂(x)·sinβx]
常见题型
微分方程求解
可分离变量线性齐次
x,y对调变量代换
判别类型,选择方法微分方程所有解≥通解
综合题应用题差分方程
差分方程
一阶常系数线性齐次差分方程
yt+1+a·yt=0
通解=C·(-a)^t 一阶常系数线性非齐次差分方程
yt+1+a·yt=f(t)
f(t)=Pm(t)a≠-1;a=1f(t)=d^t·Pm(t)
a+d≠0;a+d=0。
数学高一下知识点思维导图数学是一门理科学科,是一门需要逻辑思维的学科。
在高一下学期,学生会接触到更深入的数学知识,并需要掌握更多的数学技巧。
下面是高一下学期数学知识点的思维导图,帮助学生整理和梳理学习内容。
1. 代数- 线性方程组- 高斯消元法- 初等变换- 二次函数- 顶点坐标- 对称轴- 判别式- 不等式- 解不等式- 图像表示2. 几何- 平面几何- 平行线与垂直线 - 四边形性质- 三角形面积- 空间几何- 空间直线和平面 - 空间向量- 空间几何关系 - 三角函数- 正弦定理- 余弦定理- 向量叉乘3. 概率与统计- 随机事件- 概率的定义- 加法规则和乘法规则 - 统计分布- 频数分布- 直方图- 折线图- 抽样调查- 抽样方法- 数据分析- 推论统计4. 数列与数学归纳法- 等差数列- 公差和通项公式- 前n项和- 等比数列- 公比和通项公式- 前n项和- 数学归纳法- 原理与应用- 数学归纳证明5. 导数与微分- 导数的定义- 函数导数的定义与性质 - 高阶导数- 函数的求导法则- 乘积法则- 商法则- 链式法则- 函数的应用- 切线与法线- 最值问题- 凹凸性与拐点以上就是高一下学期数学知识点的思维导图。
通过这样的整理,学生可以更加清晰地了解数学知识点之间的联系和重点内容。
同时,思维导图也能够帮助学生在复习时更加高效地回顾相关知识。
希望这个思维导图能对学生的学习有所帮助!。