中小学数学几何画板题目
- 格式:doc
- 大小:372.52 KB
- 文档页数:19
![中学数学[全套]课件制作实例[几何画板]](https://uimg.taocdn.com/05fe639cf705cc1755270997.webp)
中学数学全套课件制作实例(几何画板)1、《几何画板》:绘制三角形内接矩形的面积函数图像2、《几何画板》:求过两点的直线方程3、《几何画板》:验证两点间距离公式4、《几何画板》:绘制分段函数的图像5、《几何画板》:绘制某区间内的函数图像6、《几何画板》:运用椭圆工具制作圆柱7、《几何画板》:绘制四棱台8、《几何画板》:绘制三棱柱9、《几何画板》:绘制正方体10、《几何画板》:绘制三角形的内切圆11、《几何画板》:通过不在一条直线上的3点绘制圆12、《几何画板》:给定半径和圆心绘制圆13、《几何画板》:绘制棱形14、《几何画板》:绘制平行四边形15、《几何画板》:绘制等腰直角三角形16、《几何画板》:旋转体教学17、《几何画板》:画角度的箭头18、《几何画板》:“派生”关系进行轨迹教学板19、《几何画板》:制作“椭圆”工具20、《几何画板》:显示圆和直线的位置关系21、《几何画板》:研究圆切线的性质22、《几何画板》:“垂径定理”的教学23、《几何画板》:证明三角形的中线交于一点24、《几何画板》:验证分割高线长定理25、《几何画板》:证明三角形外心和重心的距离等于垂心与重心的距离的一半26、《几何画板》:证明三角形内角和等于180度27、《几何画板》:验证三角形面积公式28、《几何画板》:验证勾股定理29、《几何画板》:验证正弦定理30、《几何画板》:验证圆弧的三项比值相等31、《几何画板》:巧用Excel制作函数图像32、《几何画板》:绘制极坐标系中的曲线函数图像33、《几何画板》:绘制带参数的幂函数图像34、《几何画板》:绘制带参数的正弦函数图像35、《几何画板》:绘制带参数的抛物线函数图像36、《几何画板》:绘制带参数的圆函数图像37、《几何画板》绘制带参数直线函数图像《几何画板》:绘制三角形内接矩形的面积函数图像第1步,启动几何画板,依次单击“图表”→“定义坐标系”菜单命令,在操作区建立直角坐标系。

中学数学全套课件制作实例(几何画板)1、《几何画板》:绘制三角形内接矩形的面积函数图像2、《几何画板》:求过两点的直线方程3、《几何画板》:验证两点间距离公式4、《几何画板》:绘制分段函数的图像5、《几何画板》:绘制某区间内的函数图像6、《几何画板》:运用椭圆工具制作圆柱7、《几何画板》:绘制四棱台8、《几何画板》:绘制三棱柱9、《几何画板》:绘制正方体10、《几何画板》:绘制三角形的内切圆11、《几何画板》:通过不在一条直线上的3点绘制圆12、《几何画板》:给定半径和圆心绘制圆13、《几何画板》:绘制棱形14、《几何画板》:绘制平行四边形15、《几何画板》:绘制等腰直角三角形16、《几何画板》:旋转体教学17、《几何画板》:画角度的箭头18、《几何画板》:“派生”关系进行轨迹教学板19、《几何画板》:制作“椭圆”工具20、《几何画板》:显示圆和直线的位置关系21、《几何画板》:研究圆切线的性质22、《几何画板》:“垂径定理”的教学23、《几何画板》:证明三角形的中线交于一点24、《几何画板》:验证分割高线长定理25、《几何画板》:证明三角形外心和重心的距离等于垂心与重心的距离的一半26、《几何画板》:证明三角形内角和等于180度27、《几何画板》:验证三角形面积公式28、《几何画板》:验证勾股定理29、《几何画板》:验证正弦定理30、《几何画板》:验证圆弧的三项比值相等31、《几何画板》:巧用Excel制作函数图像32、《几何画板》:绘制极坐标系中的曲线函数图像33、《几何画板》:绘制带参数的幂函数图像34、《几何画板》:绘制带参数的正弦函数图像35、《几何画板》:绘制带参数的抛物线函数图像36、《几何画板》:绘制带参数的圆函数图像37、《几何画板》绘制带参数直线函数图像《几何画板》:绘制三角形内接矩形的面积函数图像第1步,启动几何画板,依次单击“图表”→“定义坐标系”菜单命令,在操作区建立直角坐标系。

中学数学全套课件制作实例(几何画板)1、《几何画板》:绘制三角形内接矩形的面积函数图像2、《几何画板》:求过两点的直线方程3、《几何画板》:验证两点间距离公式4、《几何画板》:绘制分段函数的图像5、《几何画板》:绘制某区间内的函数图像6、《几何画板》:运用椭圆工具制作圆柱7、《几何画板》:绘制四棱台8、《几何画板》:绘制三棱柱9、《几何画板》:绘制正方体10、《几何画板》:绘制三角形的内切圆11、《几何画板》:通过不在一条直线上的3点绘制圆12、《几何画板》:给定半径和圆心绘制圆13、《几何画板》:绘制棱形14、《几何画板》:绘制平行四边形15、《几何画板》:绘制等腰直角三角形16、《几何画板》:旋转体教学17、《几何画板》:画角度的箭头18、《几何画板》:“派生”关系进行轨迹教学板19、《几何画板》:制作“椭圆”工具20、《几何画板》:显示圆和直线的位置关系21、《几何画板》:研究圆切线的性质22、《几何画板》:“垂径定理”的教学23、《几何画板》:证明三角形的中线交于一点24、《几何画板》:验证分割高线长定理25、《几何画板》:证明三角形外心和重心的距离等于垂心与重心的距离的一半26、《几何画板》:证明三角形内角和等于180度27、《几何画板》:验证三角形面积公式28、《几何画板》:验证勾股定理29、《几何画板》:验证正弦定理30、《几何画板》:验证圆弧的三项比值相等31、《几何画板》:巧用Excel制作函数图像32、《几何画板》:绘制极坐标系中的曲线函数图像33、《几何画板》:绘制带参数的幂函数图像34、《几何画板》:绘制带参数的正弦函数图像35、《几何画板》:绘制带参数的抛物线函数图像36、《几何画板》:绘制带参数的圆函数图像37、《几何画板》绘制带参数直线函数图像《几何画板》:绘制三角形内接矩形的面积函数图像第1步,启动几何画板,依次单击“图表”→“定义坐标系”菜单命令,在操作区建立直角坐标系。

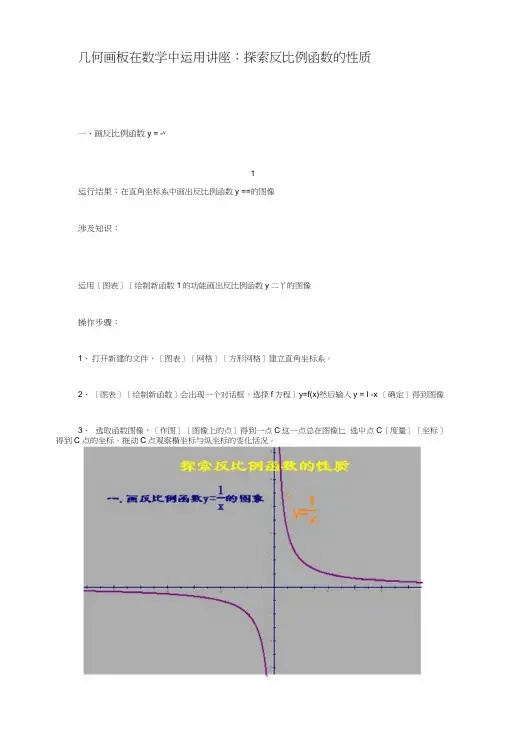
几何画板在数学中运用讲座:探索反比例函数的性质一、画反比例函数y = -v1运行结果:在直角坐标系中画出反比例函数y ==的图像涉及知识:运用[图表][绘制新函数1的功能画出反比例函数y二丫的图像操作步骤:1、打开新建的文件,[图表][网格][方形网格]建立直角坐标系。
2、[图表][绘制新函数]会出现一个对话框。
选择f方程]y=f(x)然后输入y = I -x [确定]得到图像3、选取函数图像,[作图][图像上的点]得到一点C这一点总在图像匕选屮点C[度量][坐标]得到C 点的坐标。
拖动C点观察横坐标与纵坐标的变化恬况。
二、探索反比例函数图象的对称性运行结果:移动函数上的点C,发现它关于y = X与y = - X对称的点都在反比例函数上1涉及知识:运用[图表][绘制新函数]的功能画出反比例函数y = 乂的图像,运用[变换][反射]得到C 点关于y = x和y =・x的对称点操作步骤:2、打开新建的文件,[图表][网格][方形网格]建立宜角世标系。
2、[图萄〔绘制新函数]会出现一个对话框。
选择[方程]y司x)然后输入y = 1 -x [确定]得到图像3、选取函数图像,[作图][图像上的点]得到一点C这一点总在图像上。
选屮点C[度議][坐标]得到C 点的坐标。
4、画直线y = x和y二-x,双击[变换][反射],得到C点关于y = x与y = - x的对称点,选中这两点[度量1[朋标],拖动C点,观察C点及两个对称点的横朋标与纵朋标的变化情况。
设置变化过程屮保留痕迹,探索kA ;图像的关系。
涉及知识:运用[图表][绘制新函数]的功能画出反比例函数y 二入的图像,学会运用[新建参数功能] [动画]按钮的制作操作步骤:1、 打开新建的文件,[图表][网格][方形网格]建立直角坐标系。
2、 [图表][绘制新函数],在对话框中选取方程y=f(x)[数值][新建参数],得到一个对话框将对话框屮的 II 选中输入k,然后输入kmx [确定],得到函数图像。




运用几何画板辅助初中数学教学的实践及案例几何画板是一种教学辅助工具,可以帮助初中学生更好地理解和掌握几何知识。
在数学教学中,几何画板的运用可以提高学生的学习兴趣,增强他们的几何思维能力和空间想象力。
下面将介绍几个几何画板在初中数学教学中的实践案例。
案例一:平面图形的绘制在初中数学中,学生需要学习各种平面图形的性质和判断方法。
通过几何画板,可以让学生直观地绘制各种平面图形,并观察它们的性质。
例如,在学习三角形的内角和定理时,可以让学生使用几何画板绘制不同形状的三角形,并测量它们的内角和,验证定理的正确性。
案例二:立体图形的展示在初中数学中,学生需要学习各种立体图形的性质和计算方法。
通过几何画板,可以让学生观察和展示各种立体图形的特点。
例如,在学习正方体的表面积和体积时,可以让学生使用几何画板绘制一个正方体,并计算它的表面积和体积。
通过实践操作,学生可以更好地理解和记忆相关的公式和计算方法。
案例三:图形的变换在初中数学中,学生需要学习各种图形的平移、旋转和翻转等变换方法。
通过几何画板,可以方便地进行图形的变换操作,并观察变换后图形的特点。
例如,在学习平移变换时,可以让学生使用几何画板上的移动工具,将一个图形平移到指定位置,并观察变换前后图形的位置关系和性质变化。
案例四:图形的相似和全等在初中数学中,学生需要学习图形的相似和全等的判定方法和性质。
通过几何画板,可以让学生进行图形的相似和全等判定,并观察它们的性质。
例如,在学习全等三角形的判定方法时,可以让学生使用几何画板绘制两个三角形,并进行边长和角度的测量,以判断它们是否全等。
总结起来,几何画板在初中数学教学中的实践可以通过平面图形的绘制、立体图形的展示、图形的变换以及图形的相似和全等等方面进行。
通过几何画板的运用,可以提高学生对几何知识的理解和掌握能力,增强他们的几何思维和空间想象能力。
教师可以结合具体的教学内容和学生的实际情况,设计相应的实践案例,让学生在实际操作中探索和学习几何知识。

中学数学全套课件制作实例(几何画板)1、《几何画板》:绘制三角形内接矩形的面积函数图像2、《几何画板》:求过两点的直线方程3、《几何画板》:验证两点间距离公式4、《几何画板》:绘制分段函数的图像5、《几何画板》:绘制某区间内的函数图像6、《几何画板》:运用椭圆工具制作圆柱7、《几何画板》:绘制四棱台8、《几何画板》:绘制三棱柱9、《几何画板》:绘制正方体10、《几何画板》:绘制三角形的内切圆11、《几何画板》:通过不在一条直线上的3点绘制圆12、《几何画板》:给定半径和圆心绘制圆13、《几何画板》:绘制棱形14、《几何画板》:绘制平行四边形15、《几何画板》:绘制等腰直角三角形16、《几何画板》:旋转体教学17、《几何画板》:画角度的箭头18、《几何画板》:“派生”关系进行轨迹教学板19、《几何画板》:制作“椭圆”工具20、《几何画板》:显示圆和直线的位置关系21、《几何画板》:研究圆切线的性质22、《几何画板》:“垂径定理”的教学23、《几何画板》:证明三角形的中线交于一点24、《几何画板》:验证分割高线长定理25、《几何画板》:证明三角形外心和重心的距离等于垂心与重心的距离的一半26、《几何画板》:证明三角形内角和等于180度27、《几何画板》:验证三角形面积公式28、《几何画板》:验证勾股定理29、《几何画板》:验证正弦定理30、《几何画板》:验证圆弧的三项比值相等31、《几何画板》:巧用Excel制作函数图像32、《几何画板》:绘制极坐标系中的曲线函数图像33、《几何画板》:绘制带参数的幂函数图像34、《几何画板》:绘制带参数的正弦函数图像35、《几何画板》:绘制带参数的抛物线函数图像36、《几何画板》:绘制带参数的圆函数图像37、《几何画板》绘制带参数直线函数图像《几何画板》:绘制三角形内接矩形的面积函数图像第1步,启动几何画板,依次单击“图表”→“定义坐标系”菜单命令,在操作区建立直角坐标系。

中学数学全套课件制作实例(几何画板)1、《几何画板》:绘制三角形内接矩形的面积函数图像2、《几何画板》:求过两点的直线方程3、《几何画板》:验证两点间距离公式4、《几何画板》:绘制分段函数的图像5、《几何画板》:绘制某区间内的函数图像6、《几何画板》:运用椭圆工具制作圆柱7、《几何画板》:绘制四棱台8、《几何画板》:绘制三棱柱9、《几何画板》:绘制正方体10、《几何画板》:绘制三角形的内切圆11、《几何画板》:通过不在一条直线上的3点绘制圆12、《几何画板》:给定半径和圆心绘制圆13、《几何画板》:绘制棱形14、《几何画板》:绘制平行四边形15、《几何画板》:绘制等腰直角三角形16、《几何画板》:旋转体教学17、《几何画板》:画角度的箭头18、《几何画板》:“派生”关系进行轨迹教学板19、《几何画板》:制作“椭圆”工具20、《几何画板》:显示圆和直线的位置关系21、《几何画板》:研究圆切线的性质22、《几何画板》:“垂径定理”的教学23、《几何画板》:证明三角形的中线交于一点24、《几何画板》:验证分割高线长定理25、《几何画板》:证明三角形外心和重心的距离等于垂心与重心的距离的一半26、《几何画板》:证明三角形内角和等于180度27、《几何画板》:验证三角形面积公式28、《几何画板》:验证勾股定理29、《几何画板》:验证正弦定理30、《几何画板》:验证圆弧的三项比值相等31、《几何画板》:巧用Excel制作函数图像32、《几何画板》:绘制极坐标系中的曲线函数图像33、《几何画板》:绘制带参数的幂函数图像34、《几何画板》:绘制带参数的正弦函数图像35、《几何画板》:绘制带参数的抛物线函数图像36、《几何画板》:绘制带参数的圆函数图像37、《几何画板》绘制带参数直线函数图像《几何画板》:绘制三角形内接矩形的面积函数图像第1步,启动几何画板,依次单击“图表”→“定义坐标系”菜单命令,在操作区建立直角坐标系。
几何画板完全教程pdf一、教学内容本节课的教学内容选自人教版小学数学四年级下册第五单元《几何画板的使用》。
本节课主要介绍如何使用几何画板进行基本的绘图操作,包括绘制线段、射线、直线,以及圆和正方形等基本几何图形。
二、教学目标1. 学生能够熟练掌握几何画板的基本操作,绘制出各种基本几何图形。
2. 学生能够通过几何画板加深对数学几何图形概念的理解。
3. 学生能够运用几何画板进行简单的几何问题探究。
三、教学难点与重点重点:掌握几何画板的基本操作,绘制基本几何图形。
难点:理解并运用几何画板进行几何问题的探究。
四、教具与学具准备教具:多媒体教学设备、几何画板软件。
学具:每人一台计算机,安装有几何画板软件。
五、教学过程1. 实践情景引入:教师通过多媒体展示一些常见的几何图形,如线段、射线、直线、圆和正方形等,引导学生思考如何用工具绘制这些图形。
2. 基本操作学习:教师演示如何使用几何画板进行基本操作,如绘制线段、射线、直线,以及圆和正方形等。
学生在教师的引导下,跟随操作,体会几何画板的使用方法。
3. 随堂练习:教师给出一些简单的几何图形绘制任务,如绘制一条线段,一个圆,一个正方形等,学生独立完成,加深对几何画板操作的理解。
4. 例题讲解:教师通过几何画板演示一些基本的几何问题,如线段的和差,圆的周长和面积等,引导学生理解并掌握这些几何问题的解决方法。
5. 课堂互动:学生分组,使用几何画板解决一些简单几何问题,如相互绘制三角形,计算三角形的面积等,教师巡回指导,解答学生疑问。
6. 作业布置:学生利用几何画板绘制一个自己设计的图形,并计算其面积或周长,下节课分享。
六、板书设计板书内容主要包括本节课的主要内容和操作步骤,如线段的绘制方法,圆的面积计算公式等。
七、作业设计作业题目:利用几何画板绘制一个你喜欢的图形,并计算其面积或周长。
答案:学生根据自己的喜好绘制图形,并利用几何画板计算出面积或周长。
八、课后反思及拓展延伸课后反思:教师对本节课的教学进行反思,看是否达到了教学目标,学生是否掌握了几何画板的基本操作。
《几何画板》在使用中常见问题及对策《几何画板》是当前中学数学教师作图、课件制作的常用软件之一。
具有学习容易、操作简单、交互性强、资源节省及其强大的图形、图象功能、动画功能等特点,又能够广泛的应用在平面几何、平面解析几何、立体几何、函数、三角等数学课程的教学中。
是一个很适合用于几何教学和学习的工具软件平台。
不过,我通过实际的使用,发现一些地方也不尽人意,甚至给作图带来麻烦,也想出了一些应对方法,供大家参考,使之更好的为教学服务。
一、线段的长短画法在《几何画板》中,所画线段的长度是能够改变的。
对于有一定长度要求的线段,我们能够改变其长度以达到要求。
具体做法是:先画出任意一条线段,单击菜单栏中“度量”—→“长度”,这时,该线段的长度值就显现出来。
观察其长度数值,若与要求不一致则可选中任意一个端点,用鼠标拖曳或用方向键改变线段的长度(改变长度时,长度数值也会随之改变),从而达到所要求的长度(方向键的用法:水平运动用“←”键或“→”键,垂直运动用“↑”键或“↓”键;若同时使用“←”和“↑”键,则端点向左上45°方向运动;若同时使用“→”和“↑”键,则端点向右上45°方向运动。
其它类同。
)。
二、直线、射线的“有限长度”画法《几何画板》中,所画直线、射线是向两端或一端无限延伸的,是“名副其实”的直线、射线。
复制到文档中的直线、射线要占用很大空间、带有箭头且不能修改,给实际作图和教学演示带来麻烦(实际教学中的直线和射线都是不带箭头的,这与教材要求相统一)。
如何解决这个问题呢?这时能够画出一条适当长度的线段,选中端点单击右键,“隐藏点”即可。
这样,线段就变成有限长度的直线、射线,给学生带来与课本相统一的视觉效果。
三、删除与隐藏的合理使用在《几何画板》的作图过程中,一般情况下,不宜使用删除键。
因为,若用删除键删除图形中的某一局部时,有可能会把与之有联系的整个图形删除。
如:把一条线段变成射线,若用删除方法删除一个端点,则会将整条线段删除;再如,要画一个没有圆心的圆,删除已画好的圆的圆心,就会把整个圆删除。
小学数学实验4221几何画板如何改变角的度数4221几何画板是一种小学数学实验仪器,主要用于展示和探讨几何相关知识。
在4221几何画板上,通过改变角的度数,可以观察到不同的角度对应的图形变化。
下面将通过1200字以上的篇幅,详细介绍4221几何画板如何改变角的度数。
4221几何画板是由一个固定的直角三角形和一个可以旋转的直角三角形组成的。
固定的直角三角形上有一个角π/4,可以代表45度角;可旋转的直角三角形上也有一个角π/4,可以通过旋转改变这个角的度数。
为了更好地理解4221几何画板如何改变角的度数,我们可以先了解一下角度的基本知识。
在数学中,角是由两条射线共享一个公共端点而形成的图形。
常用的度量角度的单位是度。
一个圆周被分为360度,每度又可以细分为60分,每分又可以细分为60秒。
除了度外,还有弧度作为角度的单位。
360度等于2π弧度,1度约等于π/180弧度。
在小学数学中,通常使用度来度量角度。
4221几何画板中的旋转直角三角形可以通过旋转来改变角的度数。
具体来说,可以通过以下步骤来改变角的度数:1.将旋转直角三角形上的角锁定在其中一度数上,可以用一个锁定钉固定角度。
2.将旋转直角三角形沿着右边直角边的旋转轴旋转,旋转的度数即为角的度数。
3.可以旋转的度数通常以刻度盘的形式显示在绘图板上,如从0度到180度。
4.旋转角度时,可以观察到图形相应地发生变化。
通过连续旋转,角的度数也可以连续改变。
由于4221几何画板是通过旋转来改变角的度数,因此可以通过逐渐增加或减小旋转的角度来实现角的度数的逐渐增大或减小。
通过改变角的度数,我们可以观察到不同角度所对应的图形变化。
例如,当角的度数为0度时,旋转直角三角形不发生任何变化,保持与固定直角三角形相重合;当角的度数为90度时,旋转直角三角形与固定直角三角形的斜边重合,形成一个直角三角形;当角的度数为180度时,旋转直角三角形与固定直角三角形完全相反,形成一个与固定直角三角形相似但方向相反的三角形。
几何画板作品100例小学数学第一章小学数学1.1数与代数实例1整数加法口算出题器实例25 以内数的分成实例3分数意义的动态演示实例4求最大公约数和最小公倍数实例5直线上的追及问题1.2 空间与图形实例6三角形分类演示实例7三角形三边的关系实例8三角形内角和的动态演示实例9三角形面积公式的推导实例10长方形周长的动态演示实例11长方体的初步认识实例12长方体的体积 .1.3 统计与概率实例13数据的收集与整理实例14折线统计图第二章中学数学2.1平面几何实例15中点四边形实例16三角形的高线实例17三角形全等实例18三角形拼接成平行四边形实例19三线八角实例20变式习题实例21轴对称图形 .实例22三角形相似实例23正n边形实例24平行四边形的面积实例25环形跑道实例26圆幂定理实例27车轮的滚动实例28动画彩轮2.2代数实例29一次函数实例30二次函数图像的动态演示实例31二次函数在闭区间上的值域实侧32. 两数的报合工具|实例33圆周上的追及问题实例34二分法求方程的根实例35函数y=a x的图像与y=log a x的图像的关系实例36用函数的观点研究等差数列前n项和的最值实例37等比数列的图像 (一)实例38等比数列的图像 (二)实例39函数 y= Asin(wx+中)的图像实例40轨迹- -边红、一边篮实例41正弦函数线实例42定积分意义的动态演示实例43打造个性化的课件2.3立体几何实例44异面直线所成的角实例45旋转二面角实例46切割三棱柱实例47截锥得台实例48棱柱、棱锥、棱台的辨证统一实例49圆的直观图实例50圆柱2.4解析几何实例51直线的斜率实例52两直线重直实例53网页探究型课件实例54览相圆大双曲线)的第二定义印实例55椭圆长、短轴变化(一)实例56椭圆长、短轴变化(二)实例57椭圆工具(已知项点和任意-一点) 实例58发掘课本习题的作用实例59半椭圆实例60双曲线的第一定义实例61双曲线的切线实例62抛物线的切线实例63抛物线的焦点弦实例64圆锥曲线的统一形式实例65与定线段成定张角的点的轨迹实例65与定线段成定张角的点的轨迹实例65与定线段成定张角的点的轨迹实例66到定点的距离与定直线的距离的比值等于定值的点的轨迹实例67与两定点的距离的比值等于定值的点的轨迹实例68与两定点连线的斜率之积等于定值的点的轨迹实例69与两定直线的距离之积等于定值的点的轨迹实例70心形曲线的构造第三章中学物理3.1力学实例71运动的合成与分解实例72圆周运动与向心力实例73匀变速运动 s-t图像研究实例74匀加速运动物体追赶匀速运动物体问题研究实例75动态演示力的分解实例76波的形成实例77调幅波与调频波实例78波的传播与质点振动实例79单摆实例80运动的合成与分解一纯滚动实例81弹簧摆的李萨如图实例82地球突然失去重力以后实例83简谐运动的图像实例84纵波的形成与传播实例85光斑的移动实例86水星的进动实例87行星的椭圆轨道3.2光学实例88光的三原色实例89水的折射成像研究实例90彩虹的成因实例91抛物线的光学特性3.3电磁学实例92电容器内部的场强与正对面积的关系实例93回旋加速器的工作原理实例94交流电的产生3.4热学实例95扩散现象实例96浸润现象与不浸润现象实例97分子间力3.3 自定义物理工具实例98力的分析工具实例99自定义弹簧工具实例100自定义箭头工具。
圆的函数表达式几何画板在数学中,我们常常需要学习与使用圆的函数表达式来解决相关问题。
而另一个非常有用的工具是几何画板,可以帮助我们直观地理解与解决问题。
在本文中,我们将介绍如何使用几何画板来帮助我们理解和绘制圆的函数表达式。
以下是详细的步骤:步骤一:打开几何画板软件首先,我们需要打开几何画板软件,这里我们推荐使用GeoGebra 软件。
打开软件后,我们可以看到一个坐标系界面。
步骤二:绘制圆的基本图形在坐标系界面上,我们可以使用“圆”的绘图工具来绘制圆的基本图形。
首先我们需要拖动光标来取得圆心,并拖动鼠标绘制出圆的形状。
要想得到一个完整的圆,需要在绘图工具的选项中设定半径。
此时,我们可以看到圆的尺寸与位置可以进行调整。
步骤三:编写圆的函数表达式接下来,我们需要编写圆的函数表达式。
一个标准的圆的方程形式是(x - a)² + (y - b)² = r²,其中(a,b)是圆心的坐标,r为半径的长度。
在我们的绘图板上,a、b可以通过更改圆心的位置轻松地调整。
而半径r也可以通过设定半径来轻松改变。
这时候,我们可以在工具栏上找到“输入”选项,然后在其中输入对应的函数表达式,就可以绘制对应的图像了。
步骤四:调整圆的参数在绘制完成后,我们可以调整圆的参数来观察圆的长相与性质。
尝试改变圆心位置、半径长度等参数,并观察圆的图像的变化。
我们可以看到随着参数的不同,圆的形态也会发生变化,这有助于我们更好地理解与应用圆的函数表达式。
总结:以上是使用几何画板绘制圆的函数表达式的步骤。
几何画板是一个非常有用的工具,它可以帮助我们直观地理解数学问题,并进行可视化的解答。
在学习圆的函数表达式时,结合几何画板可以让我们更深入地理解圆的性质与应用。
最后,我们要提醒大家,学习数学不是一蹴而就的,需要不断地实践和探索,相信您能够在数学学习中取得更好的成绩。
小学数学数与代数一、5以内数的分成(例2)原理:计算并判断点与点之间的距离。
二、分数意义的动态演示(例3)表示把单位“1”平均分成4份,表示这样的1份的数。
41三、求最大公约数和最大公倍数(例4)\samples\custom tools\fraction.gsp 为最简分数,最大公约为t2/最简分数的分母;最小公倍数为t2*t1/最大公约数。
用几何画板表现最大公约数与最小公倍数鼠标选中“甲数”或“乙数”双击,在弹出的对话框中输入任意的正整数最小公倍数 = 392最大公约数 = 2乙数 = 8甲数 = 98四、追及问题(例5)注意:“初始”按钮一定要设置为高速,才能消踪迹。
五、数据的收集与整理(例13)数据收集与整理不合格人数合格人数优秀人数16个六、折线统计图的动态绘制七、整数加法口算出题器利用几何画板的“带参数的迭代”功能,将图形与参数“结合”起来,然后利用“动画”功能控制数的变化,构造出“随机数”。
(本题要用到截尾函数Trunc ())整数加法口算出题器8+7=15D'C空间与图形一、三角形分类(例6)三角形的分类是小学数学中很重要的一个内容,教材中依照三角形的类别将三角形划分为锐角三角形、钝角三角形和直角三角形。
本例采用动态变换的形式演示了按最大角进行分类的情况。
直角三角形角C = 51.53︒角B = 38.47︒角A = 90.00︒C二、三角形三边关系(例7) 注意:设置移动时要选“快速”线段c = 5.00 厘米线段b = 4.00 厘米线段a = 3.00 厘米三、三角形内角和(例8)三角形内角和演示三个内角的和角A = 42.06︒角C = 42.06︒角B = 95.88︒B拖我四、三角形面积(例9)三角形面积计算公式推导演五、长方形周长(例10)长方形的周长演示六、长方形的动态模型(例11) 直接用-三维坐标系工具-坐标系在操作中,观察长方体,思考:长方体的大小维旋下翻转水平翻转七.长方形的体积(例12)直接用-三维坐标系工具-坐标系长方体体积计算公式的探索调整小正方体的大小上下旋转长方体中学数学【课件效果】揭示四边形ABCD 可以演变成斜平行四边形、矩形、菱形和正方形的情况 【要点:】用“工具箱”中的工具进行构图;用“构造“菜单”的命令进行构图;“分离/合并”命令的运用;“度量”菜单的运用【课件效果】当三角形ABC 是锐角三角形时,它的三条高线都在三角形的内部且交于一点P; 当三角形ABC 是钝角三角形时,它的两条高线到发三角形的外部,交于一点P;利用”分离/合并”功能,把三角形变成直角三角形.【要点:】线型的选择;角度的度量和制表。
直角画法:角工具-加直角标记∠D【课件效果】单击“三角形全等”按钮,会从三角形ABC 中显示另一三角形时,它运动到三角形A ’B ’C ’并隐藏;单击“边角边”按钮,可实现BC=B ’C ’,∠ABC=∠A ’B ’C ’及AB=A ’B ’的动态演示 【要点:】用“变换/平移”命令构造全等三角形;借助另一三角形,另外的线段、角来实现动态效果;充分利用“编辑/操作类按钮”命令演示由边角边得到三角形全等的过程。
XYMN【课件效果】单击“旋转”按钮,可将三角形拼接成平行四边行;单击“还原”按钮,可实现可还原成三角形。
【要点:】标记角度的方法;及其旋转的方法。
【课件效果】用几何画板来进行习题的变式训练,界面简捷,操作简单。
【要点:】用“构造”菜单的命令进行构图;用按钮控制点的移动;“系列”按钮的制作。
下面分别是三个变式:例21:轴对称图形【课件效果】单击“转动”按钮,在三角形ABC的位置会有一个三角形沿着直线MN折叠,与三角形A’B’C’重合。
【要点:】用“变换”-“标记镜面”命令构造反射图形;用“构造”-“轨迹”命令构造椭圆;用“标记比”进行点的缩放;制作点的移动按钮来控制图形的折叠。
【课件效果】单击“验证”按钮,在三角形A ’B ’C ’的位置会移出一个小三角形,经过相似变换与三角形ABC 重合;单击“复原”按钮,小三角形按刚才的相似变换加到原来的位置。
【要点:】用“变换”-“缩放”命令构造相似三角形;用“平移”命令构造验证三角形相似动画。
【课件效果】单击“增加边数”按钮,可增加正n 边形的边数,单击“减少边数”按钮,可减少正n 边形的边数, 【要点:】用“迭代”命令构造正n 边形;参数类型动画按钮的制作。
360t 1()⋅1︒ = 45.00︒t 1 = 8【课件效果】单击“切割”按钮,可将四边形演变成长方形,单击“还原”按钮,可将图形还原成平行四边形。
【要点:】“标记向量”的设置方法;利用“移动”命令,构造切割动画的方法。
【课件效果】中学数学有关行程问题的应用题是一个重点,也是一个难点,尤其是环行跑道的行程问题。
如图环形跑道,单击“运行”按钮,小球会在环行跑道上畅通无阻且匀速前进 【要点:】用符号函数sgn()构造分段函数的区间;构造分段的参数方程;点在轨道上的匀速运动;区间参数的构造。
【步骤:】1。
构造矩形,求一组对边的中点坐标系y O = 2.00x O = 10.01y N = 2.00x N = 0.002、定义分段参数方程的区间,此式值为1,表示x 在[a,b]区间,此式为0表示x 不在[a,b]区间)则本题四段为k4x () =sgn x-2⋅x O -π⋅y N ()⋅2⋅x O +2⋅π⋅y N ()-x ()()+12k3x () =sgn x-x O -π⋅y O ()⋅2⋅x O +π⋅y O ()-x ()()+12k2x () =sgn x-x O ()⋅x O +π⋅y O ()-x ()()+12k1x () =sgn x ⋅x O -x ()()+123.定义分段参数方程:(x 为长度,X ,Y 为坐标) 第一段:)0(00x x Y xX <<⎩⎨⎧==)0(90180sin 90180cos 0n o n o n n o n o y x x y x x y y Y y x x y x X ⋅<-<⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛︒-︒⋅⋅-+=⎪⎪⎭⎫⎝⎛︒-︒⋅⋅-+=πππ第三段:)2(2)(0n n o nn o o y x x y x y Y y x x x X ⋅+<<⋅+⎩⎨⎧=⋅---=πππh 1x () =sgn x-a ()⋅b-x ()()+12第二段:)222(901802sin 901802cos 0n o n o n n o n n n o n o y x x y x y y x x y y Y y y x x y x X ⋅+<<⋅+⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛︒+︒⋅⋅⋅--+=⎪⎪⎭⎫⎝⎛︒+︒⋅⋅⋅--+=ππππππx1x () = x x4x () = x N +y N ⋅cosx-2⋅x O -π⋅y Nπ⋅y N()⋅180︒+90︒()x3x () = x O -x-x O -π⋅y N x2x () = x O +y N ⋅cosx-x O π⋅y N()⋅180︒-90︒()y4x () = y N +y N ⋅sinx-2⋅x O -π⋅y Nπ⋅y N()⋅180︒+90︒()y3x () = 2⋅y N y2x () = y O +y N ⋅sin x-x O π⋅y N()⋅180︒-90︒()y1x () = 04.将分段的参数方程并为一体)(4)(4)(3)(3)(2)(2)(1)(1)()(4)(4)(3)(3)(2)(2)(1)(1)(x y x k x y x k x y x k x y x k x y x x x k x x x k x x x k x x x k x x ⋅+⋅+⋅+⋅=⋅+⋅+⋅+⋅=5.求出tt x () =FHFG⋅2⋅x O +2⋅π⋅y O ()6.绘制H 的被动点(1)计算x(t),y(t)的值,绘制点I 。
(2)同时选中I 和H ,“构造”-“轨迹” 7.制作动画(1)在点I 在画小圆 (2)选H ,“编辑/操作类按钮/动画”FGH第四段:【课件效果】分别演示”割线””相交弦””切割线”状态下圆幂定理. 【要点:】利用点的移动控制图形交换;利用”度量”功能度量线段长度;利用”度量/计算”命令计算线段的长度.【课件效果】单击”圆的滚动”按钮,圆P 滚动,圆P 上一点E 的运动踪迹显现。
【要点:】轨迹的构造方法;重合对象的任一选取。
【课件效果】单击”运动点”按钮彩轮的颜色不断变化。
【要点:】两点间距离的度量;用参数值控制对象颜色的变化;“构造|轨迹”命令的运用;制作点的动画按钮。
PG = 8.92 厘米PH = 7.72 厘米PM = 9.82 厘米代数一、园周上的追及问题(例33)说明 V 2 > V 1= 0.00追及所需时间 = 56.89第几次追到 = 1= 56.89V 2 = 7.00V 1 = 6.00二、二分法求方程x e x f x +=)(的根(例34)2)sgn(1)(x x s -=⎥⎦⎤⎢⎣⎡+*⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡++∙⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+=22)(2)(0'b a b a f b f s a b a f a f s a b b a f b f s b a b a f a f s b *⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡+∙⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+=2)(22)(0'三、函数x a y =的图像与x y a log =的图像的关系注意:最后构造轨迹时一定要同时选择x 上的点和圆内部的部分,才能做轨迹。
五、定积分意义的动态演示(例42)选择t按键盘上+与-号解析几何一.定长线段|AB|,M是线段上一点,并按定比λ分线段。
点A,B分别在任意两相交轴上滑动,画出M点的轨迹。
二.双曲线第一定义(例60)三、抛物线的切线(例62)。