北京市一零一中学2019-2020学年高一第二学期期末数学试题(含答案)

北京市海淀区北京一零一中学2020学年高一数学下学期期末考试试题（含解析）一、选择题:在每小题列出的四个选项中，选出符合题目要求的一项。

1.不等式1 xx->0的解集是（）A. （－∞，0）U（1，+∞）B. （－∞，0）C. （1，+∞）D. （0，1）【答案】A【解析】【分析】由题意可得，()1010xx xx->⇔->，求解即可.【详解】()1010xx xx->⇔->，解得1x>或0x<，故解集为（－∞，0）U（1，+∞），故选A.【点睛】本题考查了分式不等式的解法，考查了计算能力，属于基础题.2.如图，长方体1111ABCD A B C D-的体积为1V，E为棱1CC上的点,且113CE CC=，三棱锥E－BCD的体积为2V，则21VV=（）A.13B.16C.19D.118【答案】D【解析】【分析】分别求出长方体1111ABCD A B C D -和三棱锥E －BCD 的体积，即可求出答案. 【详解】由题意，11ABCD V S CC =⋅，21111113321318BCD ABCD ABCD V S CE S CC S CC ⎛⎫⎛⎫=⋅==⋅ ⎪⎪⎝⎭⎝⎭V ，则21118V V =. 故选D.【点睛】本题考查了长方体与三棱锥的体积的计算，考查了学生的计算能力，属于基础题.3.如图，在平行六面体1111ABCD A B C D -中，M ，N 分别是所在棱的中点，则MN 与平面1BB D 的位置关系是（ ）A. MN ⊂平面1BB DB. MN 与平面1BB D 相交C. MN //平面1BB DD. 无法确定MN 与平面1BB D 的位置关系 【答案】C 【解析】 【分析】取CD 的中点E ，连结,ME EN ，可证明平面//EMN 平面1BB D ，由于MN ⊂平面EMN ，可知//MN 平面1BB D .【详解】取CD 的中点E ，连结,ME EN ，显然11//,////EM BD EN CC BB ， 因为EM ⊄平面1BB D ，EN ⊄平面1BB D ， 所以//EM 平面1BB D ，//EN 平面1BB D ， 又EM EN E =I ，故平面//EMN 平面1BB D ，又因为MN ⊂平面EMN ，所以//MN 平面1BB D . 故选C.【点睛】本题考查了直线与平面的位置关系，考查了线面平行、面面平行的证明，属于基础题.4.已知x ，y ∈R ，且x >y >0，则（ ） A. 11x y x y->- B. cos cos 0x y -<C.110x y-> D. ln x +ln y >0【答案】A 【解析】 【分析】结合选项逐个分析，可选出答案.【详解】结合x ，y ∈R ，且x >y >0，对选项逐个分析：对于选项A ，0x y ->，110y xx y xy--=<，故A 正确； 对于选项B ，取2πx =，3π2y =，则3cos cos cos 2cos 1002x y -=π-π=->，故B 不正确； 对于选项C ，110y x x y xy--=<，故C 错误； 对于选项D ，ln ln ln x y xy +=，当1xy <时，ln 0xy <，故D 不正确. 故选A.【点睛】本题考查了不等式的性质，属于基础题.5.等比数列{a n }中，T n 表示前n 项的积，若T 5＝1，则( ) A. a 1＝1 B. a 3＝1 C. a 4＝1 D. a 5＝1【答案】B 【解析】分析：由题意知25511T a q （）==，由此可知211a q =，所以一定有31a =． 详解2342551111111T a a q a q a q a q a q =⋅⋅⋅⋅==：（），211a q ∴= ，31a ∴= ．故选：B ．点睛：本题考查数列的性质和应用，解题时要认真审题，仔细解答．6.设α，β为两个平面，则能断定α∥β的条件是（ ） A. α内有无数条直线与β平行 B. α，β平行于同一条直线 C. α，β垂直于同一条直线 D. α，β垂直于同一平面【答案】C 【解析】 【分析】对四个选项逐个分析，可得出答案.【详解】对于选项A ，当α，β相交于直线l 时，α内有无数条直线与β平行，即A 错误； 对于选项B ，当α，β相交于直线l 时，存在直线满足：既与l 平行又不在两平面内，该直线平行于α，β，故B 错误；对于选项C ，设直线AB 垂直于α，β平面，垂足分别A,B ，假设α与β不平行，设其中一个交点为C ，则三角形ABC 中，90ABC BAC ︒∠=∠=，显然不可能成立，即假设不成立，故α与β平行，故C 正确；对于选项D ，α，β垂直于同一平面，α与β可能平行也可能相交，故D 错误. 【点睛】本题考查了面面平行的判断，考查了学生的空间想象能力，属于中档题.7.如图，A ，B 是半径为1的圆周上的定点，P 为圆周上的动点，∠APB 是锐角，大小为β.图中△PAB 的面积的最大值为（ ）A.1sin 2β+sin2β B. sin β+12sin2β C. β+sin β D. β+cos β【答案】B 【解析】 【分析】 由正弦定理可得，22sin ABR APB==∠，则2sin AB β=，12ABC S AB h =⋅V ，当点P 在AB的中垂线上时，h 取得最大值，此时ABP △的面积最大，求解即可. 【详解】在ABP △中，由正弦定理可得，22sin ABR APB==∠，则2sin AB β=.12ABC S AB h =⋅V ，当点P 在AB 的中垂线上时，h 取得最大值，此时ABP △的面积最大. 取AB 的中点C ，过点C 作AB 的垂线，交圆于点D ，取圆心为O ，则2221sin cos OC OB BC ββ=-=-=（β为锐角），1cos CD DO OC β=+=+.所以ABP △的面积最大为()()1112sin 1cos sin sin cos sin sin 2222S AB DC βββββββ=⋅=⋅+=+=+. 故选B.【点睛】本题考查了三角形的面积的计算、正弦定理的应用，考查了三角函数的化简，考查了计算能力，属于基础题.8.已知三棱锥P －ABC 的四个顶点在球O 的球面上，PA=PB=PC ，△ABC 2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°.则球O 的体积为（ ） A. 86π B. 43π6πD.3π2【答案】D 【解析】 【分析】计算可知三棱锥P －ABC 的三条侧棱互相垂直，可得球O 是以PA 为棱的正方体的外接球，球的直径23d PA =O 的体积.【详解】在△PAC 中，设PAC θ∠=，2PA PB PC x ===，,0EC y x =>，0y >， 因为点E ，F 分别是PA ，AB 的中点，所以1,2EF PB x AE x ===， 在△PAC 中，22cos 222x θ=⨯⨯，在△EAC 中，22cos 22x θ=⨯⨯整理得221x y -=-，因为△ABC是边长为2的正三角形，所以6 CF=，又因为∠CEF=90°，所以2232x y+=，所以12x=，所以21PA PB PC x====.又因为△ABC是边长为2的正三角形，所以PA,PB,PC两两垂直，则球O是以PA为棱的正方体的外接球，则球的直径233d PA==，所以外接球O的体积为33443πππ3322dV r⎛⎫==⨯=⎪⎝⎭.故选D.【点睛】本题考查了三棱锥的外接球，考查了学生的空间想象能力，属于中档题.二、填空题。

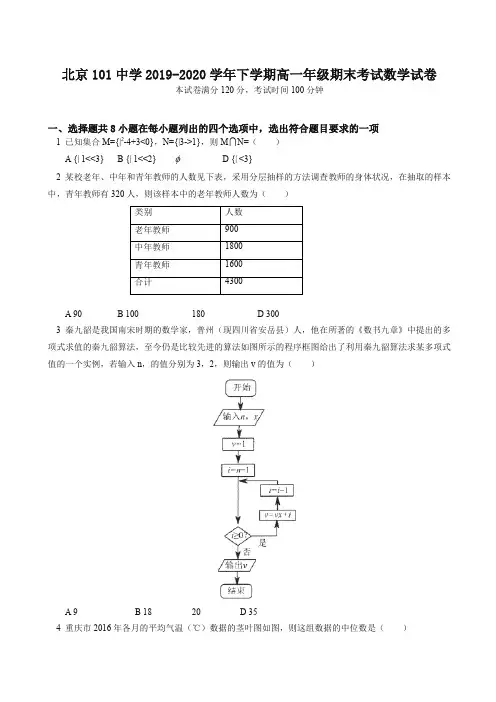
北京101中学2019-2020学年下学期高一年级期末考试数学试卷本试卷满分120分，考试时间100分钟一、选择题共8小题在每小题列出的四个选项中，选出符合题目要求的一项1 已知集合M={|2-4+3<0}，N={|3->1}，则M N=（）A {| 1<<3}B {| 1<<2} D {| <3}2 某校老年、中年和青年教师的人数见下表，采用分层抽样的方法调查教师的身体状况，在抽取的样本中，青年教师有320人，则该样本中的老年教师人数为（）A 90B 100 180 D 3003 秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n，的值分别为3，2，则输出v的值为（）A 9B 18 20 D 354 重庆市2016年各月的平均气温（℃）数据的茎叶图如图，则这组数据的中位数是（）A 19B 20215D 235 在区间[0，2]上随机取一个实数，若事件“3-<0”发生的概率为61，则实数的值为（ ） A l B2131D61 6 已知实数，y 满足⎪⎩⎪⎨⎧≤≥-+≥--,3,03,01y y x y x 则2+y 的最小值为（ ）A 11B 54D 27 已知实数，y 满足a<a y （0<a<1），则下列关系式恒成立的是（ ） A111122+>+y x B ln （2+1）>ln （y 2+1） sin>sinyD 3>y 38 如图，正方体ABD-A 1B 11D 1的棱长为1，线段B 1D 1上有两个动点E ，F ，且EF=21，有下列结论：①A ⊥BE ；②EF ∥平面ABD ；③平面A 1A 1⊥平面BEF ；④△AEF 的面积与△BEF 的面积相等正确的个数为（ ）A 1B 23D 4二、填空题共6小题9 已知函数f （）=+x8-3（>0），则f （）的最小值是__________10 抽样统计甲、乙两位射击运动员的5次训练成绩（单位：环），结果如下：则成绩较为稳定（方差较小）的那位运动员成绩的方差为_______11 把红、黄、蓝、白4张纸牌随机地分发给甲、乙、丙、丁4个人，事件“甲分得红牌”与“乙分得红牌”是_______（填序号）①对立事件；②不可能事件；③互斥但不对立事件；④对立不互斥事件12 从1，2，3，4这四个数中一次随机取两个数，则其中一个数是另一个的两倍的概率为_______ 13 已知直线l ⊥平面α，直线⊂平面β，给出下列命题，其中正确命题的序号是_______ ①α∥β⇒l ⊥；②α⊥β⇒l ∥；③l ∥⇒α⊥β；④l ⊥⇒α∥β14 在平面上，过点P 作直线l 的垂线所得的垂足称为点P 在直线l 上的投影由区域⎪⎩⎪⎨⎧≥+-≥+≤-043,0,02y x y x x 中的点在直线+y-2=0上的投影构成的线段记为AB ，则|AB|=_________三、解答题共5小题解答应写出文字说明、演算步骤或证明过程15 某儿童乐园在“六一儿童节推出了一项趣味活动参加活动的儿童需转动如图所示的转盘两次，每次转动后，待转盘停止转动时，记录指针所指区域中的数设两次记录的数分别为，y 奖励规则如下：①若y ≤3，则奖励玩具一个; ②若y ≥8，则奖励水杯一个； ③其余情况奖励饮料一瓶假设转盘质地均匀，四个区域划分均匀小亮准备参加此项活动 （1）求小亮获得玩具的概率；（2）请比较小亮获得水杯与获得饮料的概率的大小，并说明理由16 如图，在三棱锥V-AB 中，平面V AB ⊥平面AB ，△V AB 为等边三角形，A ⊥B 且A=B ，O ，M 分别为AB ，V A 的中点求证：（1）VB∥平面MO；（2）O⊥平面V AB17 我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨），一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费，为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，05），[05，1），…，[4，45]分成9组制成了如图所示的频率分布直方图（1）求直方图中a的值；（2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；（3）若该市政府希望使85％的居民每月的用水量不超过标准（吨），估计的值，并说明理由18 如图所示，在正方体ABD-A1B11D1中，M，N，E分别是AA1，A，AB的中点，求证：（1）平面MEN∥平面A1B；（2）A 1⊥1D ；（3）平面A 1E ⊥平面A 1D19 已知a ∈R ，函数f （）=lg 2（x1+a ） （1）当a=5时，解不等式f （）>0；（2）若关于的方程f （）-lg 2[（a-4）+2a-5]=0的解集中恰有一个元素，求a 的取值范围； （3）设a>0，若对任意t ∈[21，1]，函数f （）在区间[t ，t+1]上的最大值和最小值的差不超过1，求a 的取值范围参考答案1 B23 B4 B5 A6 B7 D89 42-3 10 2 11 ③ 123113 ①③ 14 32 15 （1）用数对（，y ）表示儿童参加活动先后记录的数，则基本事件空间Ω与点集S={（，y ）| ∈N ，y ∈N ，1≤≤4，l ≤y ≤4}一一对应因为S 中元素的个数是4×4=16，所以基本事件总数为n=16 记“y ≤3”为事件A ，则事件A 包含的基本事件共有5个， 即（1，1），（1，2），（1，3），（2，1），（3，1）， 所以P （A ）=165，即小亮获得玩具的概率为165（2）记“y ≥8”为事件B ，“3<y<8”为事件 事件B 包含的基本事件共有6个，即（2，4），（3，3），（3，4），（4，2），（4，3），（4，4），所以P （B ）=166=83事件包含的基本事件共有5个，即（1，4），（2，2），（2，3），（3，2），（4，1），所以P （）=165 因为83>165， 所以小亮获得水杯的概率大于获得饮料的概率 16 （1）因为O ，M 分别为AB ，V A 的中点， 所以OM ∥VB又因为OM ⊂平面MO ，VB ⊄平面MO ， 所以VB ∥平面MO（2）因为A=B ，O 为AB 的中点， 所以O ⊥AB又因为平面VAB ⊥平面AB ，且O ⊂平面AB ，平面AB 平面V AB=AB ，所以O ⊥平面VAB 17 （1）由频率分布直方图知，月均用水量在[0，05）中的频率为008×05=004，同理，在[05，1），[15，2），[2，25），[3，35），[35，4），[4，45）中的频率分别为008，020，026，006，004，002由004+008+05×a+020+026+05×a+006+004+002=l ， 解得a=030（2）由（1）100位居民每人月均用水量不低于3吨的频率为006+004+002=012由以上样本的频率分布，可以估计全市30万居民中月均用水量不低于3吨的人数为300000×012=36000（3）因为前6组的频率之和为004+008+015+020+026+015=088>085， 而前5组的频率之和为004+008+015+020+026=073<085， 所以25≤<3，由03×（-25）=085-073， 解得=29，所以估计月用水量标准为29吨时，85％的居民每月的用水量不超过标准 18 （1）因为M ，N ，E 分别是AA 1，A ，AB 的中点， 所以MN ∥A 1，ME ∥A 1B 又因为MN ME=M ， 所以平面MEN ∥平面A 1B（2）因为B ⊥平面DD 11，1D ⊂平面DD 1l ， 所以B ⊥1D又在平面DD ll 中，1D ⊥D 1，B D 1=， 所以1D ⊥平面BD 1A l ， 又因为A 1⊂平面BD l A l ， 所以A 1⊥1D（3）连结A 1D ，取A 1D 中点F ，取A 1中点O ，连结AF ，OF ，OE ，则AF ⊥A 1D因为1D ⊥平面A A DD l ，AF ⊂平面A A DD l ， 所以AF ⊥D ， 又1D A 1D=D ， 所以AF ⊥平面A 1D ， 因为OF21D ，EA 21D ， 所以OF EA ，所以四边形OFAE 为平行四边形， 所以EO ∥AF ， 所以EO ⊥平面A 1D ， 又EO ⊂平面A 1E ， 所以平面A 1E ⊥平面A 1D 19 （1）lg 2（x 1+5）>0⇔x 1+5>1⇔xx 14+>0⇔（4+1）>0， 所以不等式的解为{| >0或<-41} （2）依题意，lg 2（x1+a ）=lg 2[（a-4）+2a-5]， 所以x1+a=（a-4）+2a-5，① 可得（a-4）2+（a-5）-1=0， 即（+1）[（a-4）-1]=0， ②当a=4时，方程②的解为=-1，代入①式，成立 当a=3时，方程②的解为=-1，代入①式，成立 当a ≠3且a ≠4时，方程②的解为=-l 或=41-a 若=-1为方程①的解，则x1+a=a-1>0，即a>1 若=41-a 为方程①的解，则x1+a=2a-4>0，即a>2 要使得方程①有且仅有一个解，则1<a ≤2综上，若原方程的解集有且只有一个元素，则a 的取值范围为1<a ≤2或a=3或a=4 （3）在f （）在区间[t ，t+1]上单调递减 依题意，f （t ）-f （t+1）≤1， 即lg 2（t 1+a ）-lg 2（11+t +a ）≤1， 所以t 1+a ≤2（11+t +a ），即a ≥t 1-12+t =)1(1+-t t t设1-t=r ，则r ∈[0，21]， )1(1+-t t t =)2)(1(r r r --=232+-r r r当r=0时，232+-r r r=0 当0<r ≤21时，232+-r r r =321-+rr 因为函数y=+x2在（0，2）递减， 所以r+r 2≥21+4=29， 所以321-+r r ≤3291-=32， 所以a 的取值范围为a ≥32。

北京101中学2019-2019学年下学期高一年级期末考试数学试卷本试卷满分120分，考试时间100分钟一、选择题共10小题。

在每小题列出的四个选项中，选出符合题目要求的一项。

1. 不等式21-+x x ≤0的解集是（ ） A. {x|-1≤X ≤2}B. {x|-1≤X<2}C. {x|x>2或x ≤-1}D. {x|x<2} 2. 设等差数列{a n }的前n 项和S n ，若a 4+a 10=4，则S 13=（ ）A. 13B. 14C. 26D. 523. 在△ABC 中，若sin 2A+sin 2B<sin 2C ，则△ABC 的形状是（ ）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定 4. 已知直线l 1的方程为3x+4y-7=0，直线l 2的方程为3x+4y+1=0，则直线l 1和l 2的距离为（ ） A. 58 B. 59 C. 54 D. 109 5. 设某直线的斜率为k ，且k ∈（-3，33），则该直线的倾斜角α的取值范围是（ ） A. （3π，65π） B. （6π，32π） C. [0，3π） （65π，π） D. [0，6π） （32π，π） 6. 对于直线m ，n 和平面α，β，能得出α⊥β的一个条件是（ ）A. m ⊥n ，m ∥α，n ∥βB. m ⊥n ，α β=m ，n ⊂αC. m ∥n ，n ⊥β，m ⊂αD. m ∥n ，m ⊥α，n ⊥β 7. 如图是正方体的平面展开图，在这个正方体中，有以下四个命题：①BM ⊥平面ADNE ；②CN ∥平面ABFE ；③平面BDM ∥平面AFN ；④平面BDE ⊥平面NCF 。

其中正确命题的序号是（ ）A. ②③B. ①②③C. ②③④D. ①②③④ 8. 某几何体的三视图如图所示，则该几何体的体积是（ ） A. 38 B. 34C. 2D. 4 9. 《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马。

2019-2020学年北京市101中学高一（下）期末数学试卷一、选择题（本大题共5小题，共15.0分）1. 设向量a ⃗ ，b ⃗ 满足|a ⃗ |=2，|b ⃗ |=1，<a ⃗ ，b ⃗ >=60°，则|a ⃗ +2b ⃗ |=( ) A. 2 √2 B. 2 √3 C. √10 D. 122. 下列函数中，周期为1的奇函数是( )A. y =1−2sin 2πxB. y =sin (2πx +π3) C. y =tg π2xD. y =sinπxcosπx3. 要想得到函数y =sin(2x −π3)的图象，只需将函数y =sinx 的图象上所有的点( )A. 先向右平移π3个单位长度，再将横坐标伸长为原来的2倍，纵坐标不变 B. 先向右平移π6个单位长度，横坐标缩短为原来的12倍，纵坐标不变 C. 横坐标缩短为原来的12倍，纵坐标不变，再向右平移π6个单位长度 D. 横坐标变伸长原来的2倍，纵坐标不变，再向右平移π3个单位长度4. 在△ABC 中，c−a2c =sin 2B2(a 、b 、c 分别为角A 、B 、C 的对边)，则△ABC 的形状为( )A. 直角三角形B. 等边三角形C. 等腰三角形或直角三角形D. 等腰直角三角形5. 在正方体AC 1中，E 是棱CC 1的中点，F 是侧面BCC 1B 1内的动点，且A 1F 与平面D 1AE 的垂线垂直，如图所示，下列说法不正确的是( )A. 点F 的轨迹是一条线段B. A 1F 与BE 是异面直线C. A 1F 与D 1E 不可能平行D. 三棱锥F −ABD 1的体积为定值二、填空题（本大题共10小题，共30.0分）6. 已知角α的终边经过点P(−3,4)，则sinα=______．7. 已知f(x)=cos 2x −sin 2x ，则f(x)的最小正周期是______．8. 已知A(1,2)，B(2,3)，C(−2,5)，则AB ⃗⃗⃗⃗⃗ ⋅AC⃗⃗⃗⃗⃗ =______； 9. 在△ABC 中，a =2，b =2√3，A =30°，则角B =______．10. 设α，β是两个不同的平面，1是直线且1⊂α，则“1⊥β”是“α⊥β”的______条件(参考选项：充分不必要，必要不充分，充分必要，既不充分也不必要)．11. 如图，长方体ABCD −A 1B 1C 1D 1的体积为60，E 为CC 1的中点，则三棱锥E −BCD 的体积是______．12. 若在△ABC 中，角A ，B ，C 对应边为a ，b ，c ，若A =60°，b =1，S △ABC =√3，则a+b+csinA+sinB+sinC =______．13. 已知三棱柱ABC −A 1B 1C 1的6个顶点都在球O 的球面上，若AB =3cm ，AC =4cm ，AB ⊥AC ，AA 1=12cm ，则球O 的表面积为______cm 2． 14. 如图，在矩形ABCD 中，AB =√2，BC =2，点E 为BC 的中点，点F 在边CD 上，若AB ⃗⃗⃗⃗⃗ ⋅AF ⃗⃗⃗⃗⃗ =√2，则AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ 的值是______．15. 如图，以正方形的各边为底可向外作四个腰长为1的等腰三角形，则阴影部分面积的最大值是______．三、解答题（本大题共5小题，共60.0分） 16. 已知函数f(x)=2sin(2x −π6).(1)求函数f(x)的对称轴；(2)当x ∈[0,π2]时，求函数f(x)的最大值与最小值．17. 在△ABC 中，a ，b ，c 分别是角A.B ，C 的对边，且c =√2,A =105°,C =30°(1)求b 的值(2)△ABC的面积．18.如图，三棱柱ABC−A1B1C1中，D，E，F分别为棱AB，BC，C1B1中点．(1)求证：AC1//平面B1DE；(2)求证：AF//平面B1DE．c=b．19.已知△ABC的角A，B，C所对的边分别为a，b，c，且acosC+12(1)求角A的大小；(2)若a=1，求△ABC周长l的最大值．20.如左图，在△ABC中，D，E分别为AB，AC的中点，O为DE的中点，AB=AC=2√5，BC=4.将△ADE沿DE折起到△A1DE的位置，使得平面A1DE⊥平面BCED，F为A1C的中点，如右图．(Ⅰ)求证：EF//平面A1BD；(Ⅱ)求证：平面A1OB⊥平面A1OC；(Ⅲ)线段OC上是否存在点G，使得OC⊥平面EFG？说明理由．答案和解析1.【答案】B【解析】解：向量a⃗，b⃗ 满足|a⃗|=2，|b⃗ |=1，<a⃗，b⃗ >=60°，则|a⃗+2b⃗ |2=a⃗2+4a⃗⋅b⃗ +4b⃗ 2=4+4×2×12×1+4=12，则|a⃗+2b⃗ |=2√3．故选：B．直接利用向量的模以及数量积的运算法则求解即可．本题考查向量的数量积的应用，向量的模的求法，考查计算能力．2.【答案】D【解析】解：∵y=1−2sin2πx=cos2πx，为偶函数，排除A．∵对于函数y=sin (2πx+π3)，f(−x)=sin(−2πx+π3)≠−sin(2πx+π3)，不是奇函数，排除B．对于y=tgπ2x，T=ππ2=2≠1，排除C．对于y=sinπxcosπx=12sin2πx，为奇函数，且T=2π2π=1，满足条件．故选D．对A先根据二倍角公式化简为y=cos2πx为偶函数，排除；对于B验证不是奇函数可排除；对于C求周期不等于1排除；故可得答案．本题主要考查三角函数的奇偶性和最小正周期的求法，一般先将函数化简为y=Asin(wx+ρ)的形式，再由最小正周期的求法T=2πw、奇偶性的性质、单调性的判断解题．3.【答案】C【解析】解：将函数y=sinx的图象上所有的点横坐标缩短为原来的12倍，可得y=sin2x，纵坐标不变，再向右平移π6个单位长度，可得y=sin2(x−π6)=sin(2x−π3).故选：C．根据函数y=Asin(ωx+φ)的图象变换规律，可得结论．本题主要考查了函数y=Asin(ωx+φ)的图象变换规律，属于基础题．4.【答案】A【解析】解：∵c−a2c =sin2B2，∴1−cosB2=c−a2c，∵cosB=ac ，又由余弦定理可得cosB=a2+c2−b22ac，∴可得：a2+b2=c2，∴三角形为以∠C为直角的直角三角形．故选：A．由倍角公式化简已知可得1−cosB 2=c−a 2c，结合余弦定理可得ac=a 2+c 2−b 22ac，可得：a 2+b 2=c 2，即可判定得解．本题主要考查倍角公式及余弦定理的应用，考查三角型的形状判断，属于基础题． 5.【答案】C【解析】解：对于A.设平面AD 1E 与直线BC 交于点G ，连接AG 、EG ，则G 为BC 的中点分别取B 1B 、B 1C 1的中点M 、N ，连接AM 、MN 、AN ，则∵A 1M//D 1E ，A 1M ⊄平面D 1AE ，D 1E ⊂平面D 1AE ， ∴A 1M//平面D 1AE.同理可得MN//平面D 1AE ， ∵A 1M 、MN 是平面A 1MN 内的相交直线∴平面A 1MN//平面D 1AE ，由此结合A 1F//平面D 1AE ，可得直线A 1F ⊂平面A 1MN ，即点F 是线段MN 上上的动点．∴A 正确．对于B.∵平面A 1MN//平面D 1AE ，BE 和平面D 1AE 相交， ∴A 1F 与BE 是异面直线，∴B 正确．对于C ，由A 知，平面A 1MN//平面D 1AE ， ∴A 1F 与D 1E 不可能平行，∴C 错误．对于D ，因为MN//EG ，则F 到平面AD 1E 的距离是定值，三棱锥F −AD 1E 的体积为定值，所以D 正确； 故选：C ．分别根据线面平行的性质定理以及异面直线的定义，以及体积公式分别进行判断． 本题考查了正方形的性质、空间位置关系、空间角、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．6.【答案】45【解析】解：∵知角a 的终边经过点P(−3,4)， ∴sinα=4√(−3)2+42=45．故答案为：45．由三角函数的定义可直接求得sinα．本题考查任意角的三角函数的定义，属于基础题． 7.【答案】π【解析】解：函数f(x)=cos 2x −sin 2x =cos2x ，函数的周期为：2π2=π．故答案为：π．利用二倍角的余弦函数以及函数的周期求解即可． 本题考查两角和与差的三角函数，三角函数的周期的求法，考查计算能力，属于基础题． 8.【答案】0【解析】解：AB⃗⃗⃗⃗⃗ =(1,1)，AC ⃗⃗⃗⃗⃗ =(−3,3)， AB ⃗⃗⃗⃗⃗ ⋅AC⃗⃗⃗⃗⃗ =1×(−3)+1×3=0． 故答案为：0．首先求出AB ⃗⃗⃗⃗⃗ 、AC ⃗⃗⃗⃗⃗ 的坐标，而后可求AB ⃗⃗⃗⃗⃗ ⋅AC⃗⃗⃗⃗⃗ =0． 本题考查了向量数量积的坐标运算，属于基础题． 9.【答案】60°或120°【解析】解：∵a =2,b =2√3，A =30°， ∴由正弦定理asinA =bsinB ，可得：sinB =b⋅sinA a=2√3×122=√32， ∵b >a ，可得：B ∈(30°,180°)， ∴B =60°或120°．故答案为：60°或120°．由已知及正弦定理可求sin B 的值，结合范围B ∈(30°,180°)，可求B 的值． 本题主要考查了正弦定理在解三角形中的应用，属于基础题．10.【答案】充分不必要【解析】解：面面平行的判定定理：一个平面过另一个平面的垂线，则这两个平面垂直． 因为直线l ⊂α，且l ⊥β 所以由判断定理得α⊥β．所以直线l ⊂α，且l ⊥β⇒α⊥β若α⊥β，直线l ⊂α则直线l ⊥β，或直线l//β，或直线l 与平面β相交，或直线l 在平面β内．所以“l ⊥β”是“α⊥β”成立的充分不必要条件． 故答案为：充分不必要．面面平行的判定定理：一个平面过另一个平面的垂线，则这两个平面垂直．根据题意由判断定理得l ⊥β⇒α⊥β.若α⊥β，直线l ⊂α则直线l ⊥β，或直线l//β，或直线l 与平面β相交，或直线l 在平面β内．由α⊥β，直线l ⊂α得不到l ⊥β，故可得出结论．． 解决此类问题的关键是判断充要条件可以先判断命题的真假，最好用⇒来表示，再转换为是什么样的命题，最后转化是什么样的条件． 11.【答案】5【解析】解：在长方体ABCD −A 1B 1C 1D 1中，设AB =a ，AD =b ，AA 1=c ， 由题意可得，abc =60， ∵E 为CC 1的中点， ∴V E−BCD =13⋅12a ⋅b ⋅12c =112abc =5．故答案为：5．设AB =a ，AD =b ，AA 1=c ，由题意可得abc =60，再由棱锥体积公式求得三棱锥E −BCD 的体积．本题考查棱柱与棱锥体积的求法，是基础的计算题．12.【答案】2√393【解析】【分析】利用三角形面积公式求出c 的值，再利用余弦定理求出a 的值，最后根据正弦定理及比例性质即可得到所求式子的比值．此题考查了正弦定理，余弦定理，三角形的面积公式，特殊角的三角函数值以及比例的性质，属于中档题． 【解答】解：由A =60°，得到sinA =√32，cosA =12，又b =1，S △ABC =√3， ∴12bcsinA =12×1×c ×√32=√3，解得c =4，根据余弦定理得：a 2=b 2+c 2−2bccosA =1+16−4=13， 解得a =√13，根据正弦定理asinA =bsinB =csinC =√13√32=2√393，则a+b+c sinA+sinB+sinC=2√393．故答案为：2√39313.【答案】169π【解析】解：由题意，三棱柱ABC −A 1B 1C 1为直三棱柱ABC −A 1B 1C 1，底面ABC 为直角三角形，把直三棱柱ABC −A 1B 1C 1补成四棱柱，则四棱柱的体对角线是其外接球的直径， 所以外接球半径为12√32+42+122=13，则三棱柱ABC −A 1B 1C 1外接球的表面积是4πR 2=169πcm 2．故答案为：169π．由于直三棱柱ABC −A 1B 1C 1的底面ABC 为直角三角形，我们可以把直三棱柱ABC −A 1B 1C 1补成四棱柱，则四棱柱的体对角线是其外接球的直径，求出外接球的直径后，代入外接球的表面积公式，即可求出该三棱柱的外接球的表面积．本题考查球的体积和表面积，球的内接体问题，考查学生空间想象能力，是基础题． 14.【答案】√2【解析】解：∵AF⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ ， AB⃗⃗⃗⃗⃗ ⋅AF ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ ⋅(AD ⃗⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ )=AB ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ ⋅DF ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ ⋅DF ⃗⃗⃗⃗⃗ =√2|DF ⃗⃗⃗⃗⃗ |=√2， ∴|DF ⃗⃗⃗⃗⃗ |=1，|CF ⃗⃗⃗⃗⃗ |=√2−1， ∴AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ =(AB ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ )(BC ⃗⃗⃗⃗⃗ +CF ⃗⃗⃗⃗⃗ )=AB ⃗⃗⃗⃗⃗ ⋅CF ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =−√2(√2−1)+1×2=−2+√2+2=√2，故答案为：√2根据所给的图形，把已知向量用矩形的边所在的向量来表示，做出要用的向量的模长，表示出要求得向量的数量积，注意应用垂直的向量数量积等于0，得到结果． 本题考查平面向量的数量积的运算．本题解题的关键是把要用的向量表示成已知向量的和的形式，本题是一个中档题目． 15.【答案】2+2√2【解析】解：设等腰三角形的底角为θ，则θ∈(0,π4)， 则等腰三角形的底边为2cosθ，高为sinθ，则S 阴=(2cosθ)2+4×12×2sinθcosθ=2sin2θ+2cos2θ+2=2√2sin(2θ+π4)+2，又2θ+π4∈(π4,3π4)，当2θ+π4=π2，即θ=π8时，S阴取最大值2+2√2，故答案为：2+2√2．由三角函数的定义设等腰三角形的底角为θ，则θ∈(0,π4)，则等腰三角形的底边为2cosθ，高为sinθ，由二倍角公式及辅助角公式S阴=(2cosθ)2+4×12×2sinθcosθ=2sin2θ+2cos2θ+2=2√2sin(2θ+π4)+2，再求函数的最大值即可本题考查了三角函数的定义、二倍角公式及辅助角公式，属中档题．16.【答案】解：(1)函数f(x)=2sin(2x−π6).令2x−π6=kπ+π2(k∈Z)，解得x=kπ2+π3(k∈Z)，所以函数f(x)的对称轴方程为：x=kπ2+π3(k∈Z)．(2)由于x∈[0,π2]，所以2x−π6∈[−π6,5π6]，故sin(2x−π6)∈[−12,1]．则：−1≤f(x)≤2．故：当x=0时，函数的最小值为−1．当x=π3时，函数的最大值为2．【解析】(1)直接利用正弦型函数的性质的应用求出函数的对称轴方程．(2)利用函数的定义域的应用求出函数的值域，进一步求出函数的最大和最小值．本题考查的知识要点：正弦型函数的性质的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型．17.【答案】解：(1)∵A=105°，C=30°，∴B=45°，又c=√2，sinC=12，∴由正弦定理bsinB =csinC得：b=csinBsinC=√2×√2212=2；(2)∵b=2，c=√2，sinA=sin105°=sin(60°+45°)=sin60°cos45°+ cos60°sin45°=√6+14，∴S△ABC=12bcsinA=12×2×√2×√6+14=1+√34．【解析】(1)由A与C度数求出B的度数，再由c及C的度数，利用正弦定理求出b的值即可；(2)由b，c及sin A的值，利用三角形面积公式即可求出三角形ABC的面积．此题考查了正弦定理，三角形的面积公式，以及两角和与差的正弦函数公式，熟练掌握正弦定理是解本题的关键．18.【答案】证明：(1)在△ABC中，D，E分别为棱AB，BC中点．所以DE//AC，因为DE⊂平面B1DE，AC⊄平面B1DE，所以AC//平面B1DE．(2)在三棱柱ABC−A1B1C1中，BC−//B1C1，因为E，F分别为BC，C1B1中点，所以CE−//B1F，所以B1ECF是平行四边形，所以FC//B1E，因为FC⊄平面B1ED，B1E⊂平面B1ED，所以FC//平面B1DE，又因为AC//平面B1DE，AC∩CF=C，所以平面ACF//平面B1DE，所以AF//平面B1DE．【解析】(1)由已知利用三角形的中位线的性质可证DE//AC，进而利用线面平行的判定定理即可证明AC//平面B1DE．(2)由已知可证B1ECF是平行四边形，进而证明FC//B1E，利用线面平行的判定证明FC//平面B1DE，根据面面平行的判定证明平面ACF//平面B1DE，根据面面平行的性质即可可证AF//平面B1DE．本题主要考查了三角形的中位线的性质，线面平行的判定，面面平行的判定以及面面平行的性质，考查了空间想象能力和推理论证能力，属于中档题．19.【答案】解：(1)△ABC中，∵ab cosC+c2b=1，∴由正弦定理可得sinAcosC+12sinC=sinB=sin(A+C)=sinAcosC+cosAsinC，∴12sinC=cosAsinC，∴cosA=12．结合A∈(0,π)，可得A=π3．(2)由正弦定理得b=asinBsinA =2√3sinB, c=2√3sinC，∴周长l=a+b+c=1+√3(sinB+sinC)=1+√3[sinB+sin(A+B)]=1+2(√32sinB+12cosB)=1+2sin(B+π6)．∵A=π3，∴B∈(0, 2π3), B+π6∈(π6, 5π6)，∴sin(B+π6)∈(12, 1]，故△A BC的周长l的最大值为3．【解析】(1)由题意利用正弦定理，两角和差的三角公式，求得cos A的值，可得A的值．(2)利用正弦定理求得b、c的解析式，可得周长l的解析式，再利用正弦函数的定义域和值域，求得△A BC的周长l的最大值．本题主要考查正弦定理，两角和差的三角公式的应用，正弦函数的定义域和值域，属于中档题．20.【答案】(Ⅰ)证明：如图，取线段A1B的中点H，连接HD，HF．因为在△ABC中，D，E分别为AB，AC的中点，BC．所以DE//BC，DE =12因为H，F分别为A1B，A1C的中点，BC，所以HF//BC，HF=12所以HF//DE，HF=DE，所以四边形DEFH为平行四边形，所以EF//HD．又因为EF⊄平面A1BD，HD⊂平面A1BD，所以EF//平面A1BD．(Ⅱ)证明：因为在△ABC中，D，E分别为AB，AC的中点，AB=AC，所以AD=AE，所以A1D=A1E.又O为DE的中点，所以A1O⊥DE．因为平面A1DE⊥平面BCED，且A1O⊂平面A1DE，平面A1DE∩平面BCED=DE，所以A1O⊥平面BCED，因为CO⊂平面BCED，所以CO⊥A1O.)2+AO2=√4+(5−1)=2√2，在△OBC中，BC=4，OB=OC=√(BC2所以根据勾股定理逆定理可得CO⊥BO，又因为A1O∩BO=O，A1O、BO⊂平面A1OB，所以CO⊥平面A1OB，又CO⊂平面A1OC，所以平面A1OB⊥平面A1OC．(Ⅲ)解：线段OC上不存在点G，使得OC⊥平面EFG.理由如下：假设线段OC上存在点G，使得OC⊥平面EFG，连接GE，GF，则必有OC⊥GF，且OC⊥GE．在Rt△A1OC中，由F为A1C的中点，OC⊥GF，得G为OC的中点．在△EOC中，因为OC⊥GE，所以EO=EC，这与EO=1，EC=√5矛盾．所以线段OC上不存在点G，使得OC⊥平面EFG．【解析】本题考查线面平行、面面垂直的证明，考查满足线面垂直的点是否存在的判断与求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档偏难题．(Ⅰ)取线段A1B的中点H，连接HD，HF，推导出四边形DEFH为平行四边形，从而EF//HD.由此能证明EF//平面A1BD．(Ⅱ)推导出A1O⊥DE，CO⊥A1O，CO⊥BO，从而CO⊥平面A1OB，由此能证明平面A1OB⊥平面A1OC．(Ⅲ)假设线段OC上存在点G，使得OC⊥平面EFG，连接GE，GF，则必有OC⊥GF，且OC⊥GE.推导出EO=EC，这与EO=1，EC=√5矛盾，从而线段OC上不存在点G，使得OC⊥平面EFG．。

北京一零一中2019-2020学年度第二学期期末考试高二数学（本试卷满分120分，考试时间100分钟）一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1. 已知集合{}220A x x x =-->，则A =R（ ）A. {}12-<<x xB. {}12x x -≤≤C. {}{}12x x x x <-⋃> D. {}{}12x x x x ≤-⋃≥【答案】B 【解析】 【分析】解一元二次不等式得到A 的解集，结合数轴表示A 的解集，进而可知A R【详解】由220x x -->有(2)(1)0x x -+>，则2x >或1x <- ∴{|2A x x =>或1}x <-，数轴上表示如下∴A =R{}12x x -≤≤故选：B【点睛】本题主要考查了集合的补集运算，应用了一元二次不等式的解法，结合数轴求解集的补集2. 若0.76a =，60.7b =，0.7log 6c =，则（ ） A. b c a <<B. b a c <<C. c a b <<D.c b a <<【答案】D 【解析】 【分析】由指数函数和对数函数的图像可以判断,,a b c 和0, 1的大小，从而可以判断出答案. 【详解】由指数函数的单调性有：0.70661a =>=，600.70.71b =<=.由对数函数的单调性有：0.70.7log 6log 10c =<= 所以a b c >>. 故选：D【点睛】本题考查利用插值法比较大小，考查指数函数、对数函数的图像和性质，属于基础题.3. 设x ∈R ，则“05x <<”是“11x -<”的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件D. 既不充分也不必要条件 【答案】B 【解析】 【分析】求出11x -<的解集，根据两解集的包含关系确定.【详解】11x -<等价于02x <<，故05x <<推不出11x -<； 由11x -<能推出05x <<．故“05x <<”是“|1|1x -<”的必要不充分条件． 故选B ．【点睛】充要条件的三种判断方法： (1)定义法：根据p ⇒q ，q ⇒p 进行判断；(2)集合法：根据由p ，q 成立的对象构成的集合之间的包含关系进行判断；(3)等价转化法：根据一个命题与其逆否命题的等价性，把要判断的命题转化为其逆否命题进行判断．这个方法特别适合以否定形式给出的问题．4. 某班由24名男生和16名女生组成，现按分层抽样的方法选取10名同学参加志愿者服务，某男同学必须参加，则志愿者人员组成的不同方法种数为（ ） A. 642416C C B. 462416C CC. 542316C CD. 632415C C【答案】C 【解析】 【分析】结合分层抽样的性质可得抽取的男女生人数，再由组合的知识即可得解. 【详解】由题意，抽取的10名同学中，男生有241062416⨯=+人，女生有161042416⨯=+人，又某男同学必须参加，所以志愿者人员组成的不同方法种数为542316C C . 故选：C.【点睛】本题考查了分层抽样及组合的应用，考查了运算求解能力，属于基础题.5. 若对于任意的实数x ，有3230123(2)(2)(2)x a a x a x a x =+-+-+-，则2a 的值为（ ）A. 3B. 6C. 9D. 12【答案】B 【解析】试题分析：因为33230123[2(2)](2)(2)(2)x x a a x a x a x =+-=+-+-+-，所以212326a C ==，故选择B.考点：二项式定理.6. 下列函数()f x 图象中，满足1(3)(2)4f f f ⎛⎫>>⎪⎝⎭的只可能是（ ） A. B.C. D.【答案】D【分析】由题意结合函数图象的特征逐项判断即可得解.【详解】对于A ，函数在()0,∞+上单调递增，所以不满足1(3)(2)4f f f ⎛⎫>> ⎪⎝⎭，故A 错误；对于B ，函数在R 上单调递增，所以不满足1(3)(2)4f f f ⎛⎫>>⎪⎝⎭，故B 错误； 对于C ，函数图象开口朝上，且对称轴为1x =，所以17(3)44f f f ⎛⎫⎛⎫=<⎪ ⎪⎝⎭⎝⎭，故C 错误； 对于D ，函数在()0,1上单调递减，在()1,+∞上单调递增，故可能满足1(3)(2)4f f f ⎛⎫>> ⎪⎝⎭，故D 正确. 故选：D.7. 如图所示，1，2，3表示三个开关，若在某段时间内它们每个正常工作的概率都是0.9，那么此系统的可靠性是（ ）A. 0.999B. 0.981C. 0.980D. 0.729【答案】B 【解析】 【分析】求出开关1、2均正常工作的概率及开关3正常工作的概率，由相互独立事件概率公式、对立事件的概率公式即可得解.【详解】由题意，开关1、2在某段时间内均正常工作的概率10.90.90.81P =⨯=， 开关3正常工作的概率20.9P =，故该系统正常工作的概率()()()()12111110.8110.90.981P P P =---=--⨯-=, 所以该系统的可靠性为0.981.8. 设函数()()f x x ∈R 为奇函数，1(1)2f -=-，(2)()(2)f x f x f +=+，则()5f =（ ） A. 0 B. 1C. 52D. 5【答案】C 【解析】 【分析】由奇函数的性质可得1(1)2f =，令1x =-代入可得(2)1f =，再逐步计算即可得解. 【详解】因为函数()()f x x ∈R 为奇函数，1(1)2f -=-，所以1(1)2f =，又(2)()(2)f x f x f +=+，令1x =-，则(1)(1)(2)f f f =-+，所以(2)(1)(1)1f f f =--=， 所以3(3)(1)(2)2f f f =+=，5(3)(25)2()f f f =+=. 故选：C.9. 已知函数()2()xf x x a e =+有最小值，则函数()y f x '=的零点个数为（ ）A. 0B. 1C. 2D. 不确定【答案】C 【解析】 【分析】对函数求导，转化条件为()0f x '<有解，再结合二次函数的性质即可得解. 【详解】由题意，()2()2xf x x a e x +'=+， 因为函数()f x 有最小值，且0x e >，所以函数存在单调递减区间，即()0f x '<有解， 所以220x x a ++=有两个不等实根， 所以函数()y f x '=的零点个数为2. 故选：C.【点睛】本题考查了利用导数研究函数的最值，考查了运算求解能力，属于基础题.10. 设直线l 1，l 2分别是函数f(x)= ln ,01,{ln ,1,x x x x -<<>图象上点P 1，P-2处的切线，l 1与l 2垂直相交于点P ，且l 1，l 2分别与y 轴相交于点A ，B ，则△PAB 的面积的取值范围是 A. (0,1) B. (0,2)C. (0,+∞)D. (1,+∞)【答案】A 【解析】试题分析：设()()111222,ln ,,ln P x x P x x -（不妨设121,01x x ><<），则由导数的几何意义易得切线12,l l 的斜率分别为121211,.k k x x ==-由已知得12122111,1,.k k x x x x =-∴=∴=∴切线1l 的方程分别为()1111ln y x x x x -=-，切线2l 的方程为()2221ln y x x x x +=--，即1111ln y x x x x ⎛⎫-=-- ⎪⎝⎭．分别令0x =得()()110,1ln ,0,1ln .A xB x -++又1l 与2l 的交点为221111112222111121211,ln .1,1,0111211PAB A B P PAB x x x x P x x S y y x S x x x x ∆∆⎛⎫-++>∴=-⋅=<=∴<< ⎪++++⎝⎭，故选A ．考点：1.导数的几何意义；2.两直线垂直关系；3.直线方程的应用；4.三角形面积取值范围.二、填空题共5小题，每小题5分，共25分.11.函数()f x =__________. 【答案】(,1)[1,)-∞-+∞【解析】 【分析】使函数式有意义即可．【详解】由题意101x x -≥+，(1)(1)010x x x -+≥⎧⎨+≠⎩，解得1x <-或1≥x ．故答案为：(,1)[1,)-∞-+∞．【点睛】本题考查求函数的定义域，一般使函数式有意义的自变量的取值范围即为函数的定义域，掌握基本初等函数的定义是解题关键．当然实际问题中自变量还有实际意义的限制． 12. 函数()ln 2f x x x =++的零点个数是__________. 【答案】1 【解析】 【分析】由函数的单调性结合3()0f e -<、(1)0f >，由零点存在性定理即可得解.【详解】由题意，函数()ln 2f x x x =++在()0,∞+上单调递增，又3333()ln 2320f e e e e ----=++=-++<，(1)ln112120f =++=+>， 所以函数()ln 2f x x x =++在区间()3,1e -内有1个零点， 所以函数()ln 2f x x x =++的零点个数是1. 故答案为：1.13. 已知55log log 2x y +=，则4x y +的最小值为__________. 【答案】20 【解析】 【分析】由对数运算的性质可得25xy =且0x >，0y >，再由基本不等式即可得解. 【详解】因为555log log log 2x y xy +==，所以25xy =且0x >，0y >， 所以42420x y xy +≥=，当且仅当4x y =即10x =，52y =时，等号成立， 所以4x y +的最小值为20. 故答案为：20.【点睛】本题考查了对数运算性质及基本不等式的应用，考查了运算求解能力，属于基础题. 14. 设函数()|2|f x x x =-，则()f x 的极小值是__________. 【答案】0【解析】 【分析】按绝对值定义去掉绝对值符号后结合二次函数的单调性可得．【详解】由题意222,2()2,2x x x f x x x x ⎧-≥=⎨-+<⎩，∴()f x 在(,1)-∞上递增，在(1,2)上递减，在(2,)+∞上递增， ∴2x =时，()f x 极小值＝(2)0f =． 故答案为：0．【点睛】本题考查求函数的极值，掌握极值的定义是解题关键，解题时可先确定函数的单调性，由单调性得极值．15. 定义在R 上的函数()f x 满足2log (1),0()1(1),02x x f x f x f x x -≤⎧⎪=⎨⎛⎫---> ⎪⎪⎝⎭⎩，则()2020f 的值是________. 【答案】22log 3【解析】 【分析】转化条件可得当0x >时，()f x 的周期为3，进而可得()()20201f f =，运算即可得解. 【详解】因为当0x >时，()1(1)2f x f x f x ⎛⎫=--- ⎪⎝⎭， 所以()1111(1)(1)2222f x f x f x f x f x f x f x ⎛⎫⎛⎫⎛⎫⎛⎫+=--=-----=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，所以()32f x f x ⎛⎫+=- ⎪⎝⎭，()()332f x fx f x ⎛⎫+=-+= ⎪⎝⎭，所以当0x >时，()f x 的周期为3，所以()()()()()21120202020673310log 1022f f f f f f ⎛⎫⎛⎫=-⨯==-=--⎪ ⎪⎝⎭⎝⎭()221102212log 1log 23f f f ⎛⎫⎛⎫==--=- ⎪ ⎪⎛⎫+= ⎪⎝⎭⎝⎭⎝⎭.故答案为：22log 3. 【点睛】本题考查了函数周期性的判断与应用，考查了对数的运算，合理转化条件是解题关键，属于中档题.三、解答题共5小题，共55分.解答应写出文字说明、演算步骤或证明过程.16. 设{}2log A x Ry x =∈=∣，{}1221x xB x R -=∈->∣，则求A B .【答案】{}1x Rx ∈>∣ 【解析】 【分析】由对数函数、指数函数的性质可得{}0A x Rx =∈>∣，{}1B x R x =∈>∣，再由交集的定义即可得解.【详解】由题意，{}{}2log 0A x R y x x R x =∈==∈>∣∣， {}(){}{21221222021x xxx x B x R x R x R -=∈->=∈-->=∈<-∣∣∣或}22x >{}1x R x =∈>∣，所以{}1x B x R A=∈>∣.【点睛】本题考查了对数函数、指数函数的性质及集合的交集运算，考查了运算求解能力，属于基础题. 17. 已知关于x的一元二次不等式()22600kx x k k -+<≠.（1）若不等式的解集是{|3x x <-或}2x >-，求k 的值； （2）若不等式的解集是R ，求k 的取值范围.【答案】（1）25-；（2）⎛-∞ ⎝⎭，. 【解析】 【分析】（1）由不等式的解集为{}32x x x <->-或知k 0<,且3-，2-是方程2260kx x k -+=的两根，代入可解.（2）不等式的解集为R ，知二次函数图像恒在x 轴下方，则利用k 0<且24240k ∆=-<可解【详解】（1）∵不等式的解集为{}32x x x <->-或 ∴3-，2-是方程2260kx x k -+=的两根，且k 0< ∴25k =-（2）∵不等式的解集为R ∴k 0<且24240k ∆=-<∴6k <-∴k的取值范围是(-∞， 【点睛】解含参数的一元二次不等式时分类讨论的依据(1)二次项中若含有参数应讨论是等于0，小于0，还是大于0，然后将不等式转化为一次不等式或二次项系数为正的形式．(2)当不等式对应方程的实根的个数不确定时，讨论判别式∆与0的关系．(3)确定无实根时可直接写出解集，确定方程有两个实根时，要讨论两实根的大小关系，从而确定解集形式．18. 已知函数2()af x x x=+（0x ≠，常数a ∈R ）. （1）讨论函数()f x 奇偶性，并说明理由；（2）若函数()f x 在[2,)+∞上为增函数，求a 的取值范围.【答案】（1）0a =时，()f x 为偶函数，0a ≠时，()f x 既不是奇函数也不是偶函数； （2）16a ≤． 【解析】 【分析】（1）根据奇偶性的定义判断；（2）求出导函数()'f x ，由()0f x '≥在[2,)+∞上恒成立求得a 的范围．【详解】（1）函数定义域是{|0}x x ≠，关于原点对称，0a =时，2()f x x =，则22()()()f x x x f x -=-==，()f x 为偶函数，0a ≠时，2()a f x x x -=-，2()()2f x f x x -+=不恒为0，2()()0a f x f x x --=≠，()f x 既不是奇函数也不是偶函数；（2）2()2a f x x x '=-，由题意3222()20a x a f x x x x-'=-=≥在[2,)+∞上恒成立， ∴[2,)x ∈+∞时，320x a -≥，即32a x ≤，此时32x 的最小值为16，∴16a ≤．【点睛】本题考查函数的奇偶性，考查用导数研究函数的单调性，掌握单调性与导数的关系是解题关键．19. 某中学号召学生在今年春节期间至少参加一次社会公益活动（以下简称活动）．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．（I ）求合唱团学生参加活动的人均次数；（II ）从合唱团中任意选两名学生，求他们参加活动次数恰好相等的概率．（III ）从合唱团中任选两名学生，用ξ表示这两人参加活动次数之差的绝对值，求随机变量ξ的分布列及数学期望E ξ．【答案】（I ）合唱团学生参加活动的人均次数为2.3；（II ）04199P =；（III ）23E ξ=． 【解析】【详解】解：由图可知，参加活动1次、2次和3次的学生人数分别为10、50和40． （I ）该合唱团学生参加活动的人均次数为110250340230 2.3100100⨯+⨯+⨯==． （II ）从合唱团中任选两名学生，他们参加活动次数恰好相等的概率为222105040021004199C C C P C ++==． （III ）从合唱团中任选两名学生，记“这两人中一人参加1次活动，另一人参加2次活动”为事件A ，“这两人中一人参加2次活动，另一人参加3次活动”为事件B ，“这两人中一人参加1次活动，另一人参加3次活动”为事件C ．易知(1)()()P P A P B ξ==+111110505040241001005099C C C C C C =+=； (2)()P P C ξ==1110402100899C C C ==；41(0)99P ξ==. ξ的分布列：ξ的数学期望：20129999993E ξ=⨯+⨯+⨯=． 20. 对于函数y ＝H (x )，若在其定义域内存在x 0，使得x 0·H (x 0)＝1成立，则称x 0为函数H (x )的“倒数点”．已知函数f (x )＝ln x ，g (x )＝12(x ＋1)2－1. (1)求证：函数f (x )有“倒数点”，并讨论函数f (x )的“倒数点”的个数；(2)若当x ≥1时，不等式xf (x )≤m [g (x )－x ]恒成立，试求实数m 的取值范围．【答案】（1）见解析；（2）[1，＋∞).【解析】【分析】（1）构造函数()1h x ln x x＝－ (x >0)，转化为研究该函数的零点问题即可； （2）对不等式进行转化得2x ·ln x ≤m (x 2－1)，当x ≥1时恒成立，构造函数()12?d x ln x m x x ⎛⎫- ⎪⎝⎭＝－，x ≥1，通过求导分析函数的单调性最值求参数范围即可.【详解】(1)证明设h(x)＝ln x－(x>0)，则h′(x)＝＋>0(x>0)，所以h(x)在(0，＋∞)为单调递增函数．而h(1)<0，h(e)>0，所以函数h(x)有零点且只有一个零点．所以函数f(x)有“倒数点”且只有一个“倒数点”．(2)xf(x)≤m[g(x)－x]等价于2x·ln x≤m(x2－1)，设d(x)＝2ln x－m，x≥1.'d x＝，x≥1，则()易知－mx2＋2x－m＝0的判别式为Δ＝4－4m2.①当m≥1时，d′(x)≤0，d(x)在[1，＋∞)上单调递减，d(x)≤d(1)＝0，符合题意；②当0<m<1时，方程－mx2＋2x－m＝0有两个正根且0<x1<1<x2，则函数d(x)在(1，x2)上单调递增，此时d(x)>d(1)＝0，不合题意；③当m＝0时，d′(x)>0，d(x)在(1，＋∞)上单调递增，此时d(x)>d(1)＝0，不合题意；④当－1<m<0时，方程－mx2＋2x－m＝0有两个负根，d(x)在(1，＋∞)上单调递增，此时d(x)>d(1)＝0，不合题意；⑤当m≤－1时，d′(x)≥0，d(x)在(1，＋∞)上单调递增，此时d(x)>d(1)＝0，不合题意．综上，实数m的取值范围是[1，＋∞)．【点睛】本题考查了运用导数求含有参量的函数单调区间及不等式恒成立问题，在求单调区间时需要注意分类讨论，做到不漏情况，属于中档题.。

北京市海淀区北京一零一中学2018-2019学年高一数学下学期期末考试试题（含解析）一、选择题:在每小题列出的四个选项中，选出符合题目要求的一项。

1.不等式1 xx->0的解集是（）A. （－∞，0）U（1，+∞）B. （－∞，0）C. （1，+∞）D. （0，1）【答案】A【解析】【分析】由题意可得，()1010xx xx->⇔->，求解即可.【详解】()1010xx xx->⇔->，解得1x>或0x<，故解集为（－∞，0）U（1，+∞），故选A.【点睛】本题考查了分式不等式的解法，考查了计算能力，属于基础题.2.如图，长方体1111ABCD A B C D-的体积为1V，E为棱1CC上的点,且113CE CC=，三棱锥E－BCD的体积为2V，则21VV=（）A.13B.16C.19D.118【答案】D【解析】【分析】分别求出长方体1111ABCD A B C D -和三棱锥E －BCD 的体积，即可求出答案. 【详解】由题意，11ABCD V S CC =⋅，21111113321318BCD ABCD ABCD V S CE S CC S CC ⎛⎫⎛⎫=⋅==⋅ ⎪⎪⎝⎭⎝⎭V ，则21118V V =. 故选D.【点睛】本题考查了长方体与三棱锥的体积的计算，考查了学生的计算能力，属于基础题.3.如图，在平行六面体1111ABCD A B C D -中，M ，N 分别是所在棱的中点，则MN 与平面1BB D 的位置关系是（ ）A. MN ⊂平面1BB DB. MN 与平面1BB D 相交C. MN //平面1BB DD. 无法确定MN 与平面1BB D 的位置关系 【答案】C 【解析】 【分析】取CD 的中点E ，连结,ME EN ，可证明平面//EMN 平面1BB D ，由于MN ⊂平面EMN ，可知//MN 平面1BB D .【详解】取CD 的中点E ，连结,ME EN ，显然11//,////EM BD EN CC BB ， 因为EM ⊄平面1BB D ，EN ⊄平面1BB D ， 所以//EM 平面1BB D ，//EN 平面1BB D ， 又EM EN E =I ，故平面//EMN 平面1BB D ，又因为MN ⊂平面EMN ，所以//MN 平面1BB D . 故选C.【点睛】本题考查了直线与平面的位置关系，考查了线面平行、面面平行的证明，属于基础题.4.已知x ，y ∈R ，且x >y >0，则（ ） A. 11x y x y->- B. cos cos 0x y -<C.110x y-> D. ln x +ln y >0【答案】A 【解析】 【分析】结合选项逐个分析，可选出答案.【详解】结合x ，y ∈R ，且x >y >0，对选项逐个分析：对于选项A ，0x y ->，110y xx y xy--=<，故A 正确； 对于选项B ，取2πx =，3π2y =，则3cos cos cos 2cos 1002x y -=π-π=->，故B 不正确； 对于选项C ，110y x x y xy--=<，故C 错误； 对于选项D ，ln ln ln x y xy +=，当1xy <时，ln 0xy <，故D 不正确. 故选A.【点睛】本题考查了不等式的性质，属于基础题.5.等比数列{a n }中，T n 表示前n 项的积，若T 5＝1，则( ) A. a 1＝1 B. a 3＝1 C. a 4＝1 D. a 5＝1【答案】B 【解析】分析：由题意知25511T a q （）==，由此可知211a q =，所以一定有31a =． 详解2342551111111T a a q a q a q a q a q =⋅⋅⋅⋅==：（），211a q ∴= ，31a ∴= ．故选：B ．点睛：本题考查数列的性质和应用，解题时要认真审题，仔细解答．6.设α，β为两个平面，则能断定α∥β的条件是（ ） A. α内有无数条直线与β平行 B. α，β平行于同一条直线 C. α，β垂直于同一条直线 D. α，β垂直于同一平面【答案】C 【解析】 【分析】对四个选项逐个分析，可得出答案.【详解】对于选项A ，当α，β相交于直线l 时，α内有无数条直线与β平行，即A 错误； 对于选项B ，当α，β相交于直线l 时，存在直线满足：既与l 平行又不在两平面内，该直线平行于α，β，故B 错误；对于选项C ，设直线AB 垂直于α，β平面，垂足分别A,B ，假设α与β不平行，设其中一个交点为C ，则三角形ABC 中，90ABC BAC ︒∠=∠=，显然不可能成立，即假设不成立，故α与β平行，故C 正确；对于选项D ，α，β垂直于同一平面，α与β可能平行也可能相交，故D 错误. 【点睛】本题考查了面面平行的判断，考查了学生的空间想象能力，属于中档题.7.如图，A ，B 是半径为1的圆周上的定点，P 为圆周上的动点，∠APB 是锐角，大小为β.图中△PAB 的面积的最大值为（ ）A.1sin 2β+sin2β B. sin β+12sin2β C. β+sin β D. β+cos β【答案】B 【解析】 【分析】 由正弦定理可得，22sin ABR APB==∠，则2sin AB β=，12ABC S AB h =⋅V ，当点P 在AB的中垂线上时，h 取得最大值，此时ABP △的面积最大，求解即可. 【详解】在ABP △中，由正弦定理可得，22sin ABR APB==∠，则2sin AB β=.12ABC S AB h =⋅V ，当点P 在AB 的中垂线上时，h 取得最大值，此时ABP △的面积最大. 取AB 的中点C ，过点C 作AB 的垂线，交圆于点D ，取圆心为O ，则2221sin cos OC OB BC ββ=-=-=（β为锐角），1cos CD DO OC β=+=+.所以ABP △的面积最大为()()1112sin 1cos sin sin cos sin sin 2222S AB DC βββββββ=⋅=⋅+=+=+. 故选B.【点睛】本题考查了三角形的面积的计算、正弦定理的应用，考查了三角函数的化简，考查了计算能力，属于基础题.8.已知三棱锥P －ABC 的四个顶点在球O 的球面上，PA=PB=PC ，△ABC 2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°.则球O 的体积为（ ） A. 86π B. 43π6πD.3π2【答案】D 【解析】 【分析】计算可知三棱锥P －ABC 的三条侧棱互相垂直，可得球O 是以PA 为棱的正方体的外接球，球的直径23d PA =O 的体积.【详解】在△PAC 中，设PAC θ∠=，2PA PB PC x ===，,0EC y x =>，0y >， 因为点E ，F 分别是PA ，AB 的中点，所以1,2EF PB x AE x ===， 在△PAC 中，22cos 222x θ=⨯⨯，在△EAC 中，22cos 22x θ=⨯⨯整理得221x y -=-，因为△ABC 是边长为2的正三角形，所以6CF =， 又因为∠CEF =90°，所以2232x y +=， 所以12x =， 所以21PA PB PC x ====.又因为△ABC 是边长为2的正三角形， 所以PA,PB,PC 两两垂直，则球O 是以PA 为棱的正方体的外接球， 则球的直径233d PA ==，所以外接球O 的体积为33443πππ3322d V r ⎛⎫==⨯= ⎪⎝⎭.故选D.【点睛】本题考查了三棱锥的外接球，考查了学生的空间想象能力，属于中档题.二、填空题。

绝密★启用前2019-2020学年北京市高一下学期期末阶段测试数学试题注意事项：1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上一、选择题共10小题，每小题4分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）在复平面内，复数i(1+i)对应的点位于A 第一象限B 第二象限C 第三象限D 第四象限 答案：B2．向量(,)a m n =，向量(1,2)b =，(1,1)c =，若向量()a c b +∥，且a c ⊥，则a 的值为（）．A ．13B C ．29D ．19答案：B∵(1,1)a c m n +=++且()a c b +∥， ∴2(1)1m n +=+①， ∵a c ⊥， ∴0m n +=②，由①②得13m =-，13n =，∴11,33a ⎛⎫=- ⎪⎝⎭，∴1||3a ⎛⎫=-= ⎪3．某正方体的外接球体积36π，则此正方体的棱长为（）．A ．6B ．3CD ．答案：D∵外接球体积为36π，设半径为R ， 则24π36π3R =，3R =， 又∵正方体的外接球直径为其体对角线，∴设正方体的棱长为a 26R ==，即a =．4．在ABC △中，若2a =，b =30A =︒，则B 为（ ）．A ．60︒B ．60︒或120︒C ．30︒D ．30︒或150︒【考点】HP ：正弦定理．【分析】利用正弦定理和题设中两边和一个角的值求得B ．【解答】解：由正弦定理可知sin sin a bA B=，∴1sin 2sin 2b A B a ===， ∵(0,180)B ∈︒，∴60B ∠=︒或120︒． 故选B ．5．在下列函数中，最小值是2的是（ ）．A ．22x y x=+B ．0)y x => C ．1sin sin y x x =+，π0,2x ⎛⎫∈ ⎪⎝⎭D ．77x x y -=+【考点】7F ：基本不等式．【分析】由基本不等式成立的条件，逐个选项验证可得．【解答】解：选项A ，x 正负不定，不能满足最小值是2，故错误；选项B ，2y ，，即0x=时取等号，但0x>，故错误；选项C，∵π0,2x⎛⎫∈ ⎪⎝⎭，∴sin(0,1)x∈，∴1sin2siny xx=+≥，当且仅当1sinsinxx=，即sin1x=时取等号，但sin(0,1)x∈，取不到1，故错误；选项D，177727x x xxy-=+=+≥，当且仅当177xx=即0x=时取等号，故正确．故选：D．6．在ABC△中，内角A，B，C所对的边分别是a，b，c．已知85b c=，2C B=，则cos C=（）．A．725B．725-C．725±D．2425【考点】HQ：正弦定理的应用；GL：三角函数中的恒等变换应用．【分析】直接利用正弦定理以及二倍角公式，求出sin B，cos B，然后利用平方关系式求出cos C的值即可．【解答】解：因为在ABC△中，内角A，B，C所对的边分别是a，b，c．已知85b c=，2C B=，所以8sin5sin5sin210sin cosB C B B B===，所以4cos5B=，B为三角形内角，所以π0,4B⎛⎫∈ ⎪⎝⎭．π2C<．所以3sin5B=．所以4324sin sin225525C B==⨯⨯=，7cos25C==．故选：A．7．如图所示，C、D、A三点在同一水平线上，AB是塔的中轴线，在C、D两处测得塔顶部B处的仰角分别是α和β，如果C 、D 间的距离是a ，测角仪高为b ，则塔高为（ ）．C 1A.b a a a +-)sin(sin sin ββB ．cos cos cos()a αββα-C ．cos cos cos()a b αββα+-D ．sin sin sin()a αββα-【考点】HP ：正弦定理；HR ：余弦定理．【分析】分别在BCD △、ABD △这两个三角形中运用正弦定理，即可求解． 【解答】解：在BCD △中，sin sin CD BDCBD C=∠∠，∴sin()sin BDαβαα=-，即sin sin()a BD αβα=-，在ABD △中，sin sin AB BDADB A=∠∠，∴sin sin90AB BDβ=︒， 即sin sin sin sin()a AB BD αββαβ==-⋅，则塔高为b a a a +-)sin(sin sin ββ，故选：A ．8．设a ，b 是两个非零向量，且+=-a b a b ，则a 与b 夹角的大小为（）A 120︒B 90︒C 60︒D 30︒答案：B9．在△ABC 中，若sin sin a A b B =，则△ABC 的形状一定是（）A 等边三角形B 等腰三角形C 直角三角形D 钝角三角形答案：B10.如图,正方体1111ABCD A B C D -的棱长为2，点O 为底面ABCD 的中心，点P 在侧面11BB C C 的边界及其内部运动.若1D O OP ⊥，则△11D C P 面积的最大值为 （A ）25（B ）45（C ）5 （D ）25答案C二、填空题共5小题，每小题5分，共25分。

北京一零一中学2019-2020学年高三数学理下学期期末试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 某三棱柱侧棱和底面垂直，底面边长均为a，侧棱长为2a，其体积为，若它的三视图中的俯视图如图所示，侧视图是一个矩形，则这个矩形的面积是 ( )A. 4B.C. 8D.参考答案：B2. 如图，在三棱锥中，面，，，，，则（）A．B．C．D．参考答案：D根据题意可得，设，则，，在中，，，由余弦定理得，即：，整理得：，解得或（舍），所以．故选D．3. 若关于的不等式对任意恒成立，则的取值范围为（）A．B．C．D．参考答案：B4. 设复数满足，则（）A．B．C．D．参考答案：A5. 已知向量，若，则实数（）A. 2B. －2C.D.参考答案：D【分析】根据平面向量的坐标运算与共线定理，列方程求出λ的值．【详解】向量（2，﹣1），（1，λ），则（4，﹣1+2λ），（3，﹣2﹣λ），又（）∥（），所以4（﹣2﹣λ）﹣3（﹣1+2λ）＝0，解得λ．故选：D．【点睛】本题考查了平面向量的坐标表示与共线定理的应用问题，是基础题．6. 设x∈R，若函数f（x）为单调递增函数，且对任意实数x，都有f[f（x）﹣e x]=e+1（e 是自然对数的底数），则f（ln2）的值等于（）A．1 B．e+l C．3 D．e+3参考答案：C【考点】3F：函数单调性的性质．【分析】利用换元法将函数转化为f（t）=e+1，根据函数的对应关系求出t的值，即可求出函数f（x）的表达式，即可得到结论．【解答】解：设t=f（x）﹣e x，则f（x）=e x+t，则条件等价为f（t）=e+1，令x=t，则f（t）=e t+t=e+1，∵函数f（x）为单调递增函数，∴函数为一对一函数，解得t=1，∴f（x）=e x+1，即f（ln2）=e ln2+1=2+1=3，故选：C．7. 若展开式各项系数和为256，设为虚数单位，复数的运算结果为（）A．4 B．-4 C．2 D．-2参考答案：B8. 已知，，若，那么与在同一坐标系内的图像可能是（）参考答案：C略9. 过椭圆+=1（0<b<a）中心的直线与椭圆交于A、B两点，右焦点为F2(c,0)，则△ABF2的最大面积是（）A．ab B．ac C．bc D．b2参考答案：C略10. 已知则A．B．C．D．参考答案：C略二、填空题:本大题共7小题,每小题4分,共28分11. 函数的单调减区间为 .参考答案：（-1,11）12. 已知数列{a n}的前n项和为S n，且满足，则______参考答案：【分析】对题目所给等式进行赋值，由此求得的表达式，判断出数列是等比数列，由此求得的值.【详解】解：，可得时，，时，，又，两式相减可得，即，上式对也成立，可得数列是首项为1，公比为的等比数列，可得．【点睛】本小题主要考查已知求，考查等比数列前项和公式，属于中档题.13. 定义在R上的偶函数y＝f(x)，当x≥0时，y＝f(x)是单调递增的，f(1)·f(2)<0.则函数y＝f(x)的图象与x轴的交点个数是________．参考答案：2略14. 某班主任在其工作手册中，对该班每个学生用十二项能力特征加以描述．每名学生的第（）项能力特征用表示，若学生的十二项能力特征分别记为，，则两名学生的不同能力特征项数为（用表示）．如果两个同学不同能力特征项数不少于，那么就说这两个同学的综合能力差异较大．若该班有名学生两两综合能力差异较大，则这名学生两两不同能力特征项数总和的最小值为．参考答案：22设第三个学生为则不同能力特征项数总和恰为22 ，所以最小值为22 ．15. 下面有六个命题：①函数在第一象限是增函数.②终边在坐标轴上的角的集合是③在同一坐标系中，函数y=sinx的图象和函数y=x的图象只有一个公共点.④函数⑤的图象中一条对称轴是⑥函数的最小正周期是。

2019-2020学年北京某校高一（下）期末数学试卷一、选择题共8小题，每小题4分，共32分．在每小题列出的四个选项中，选出符合题目要求的一项．1. 若sin α>0，且tan α<0，则角α的终边位于（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限2. 函数y ＝sin 4x ，x ∈R 的最小正周期为（ ） A.2π B.πC.π2D.π43. 要得到函数y =sin (2x +π3)的图象，只要将函数y =sin 2x 的图象( )A.向左平移π3个单位长度 B.向右平移π3个单位长度 C.向左平移π6个单位长度 D.向右平移π6个单位长度4. 在空间中，给出下列四个命题：①平行于同一个平面的两条直线互相平行；②垂直于同一个平面的两个平面互相平行； ③平行于同一条直线的两条直线互相平行；④垂直于同一个平面的两条直线互相平行． 其中正确命题的序号是（ ） A.①② B.①③ C.②④ D.③④5. 已知向量a →，b →满足|a →|=2，|b →|=1，a →⋅b →=√2，则向量a →，b →的夹角为（ ） A.3π4B.2π3C.π4D.−π46. 在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，已知B ＝30∘，c ＝15，b ＝5√3，那么这个三角形是（ ） A.等边三角形 B.等腰三角形C.直角三角形D.等腰三角形或直角三角形7. 如图，在长方体ABCD −A 1B 1C 1D 1中，若E ，F ，G ，H 分别是棱A 1B 1，BB 1，CC 1，C 1D 1的中点，则必有( )A.BD 1 // GHB.BD // EFC.平面EFGH // 平面ABCDD.平面EFGH // 平面A 1BCD 18. 函数f(x)＝A sin x(A >0)的图象如图所示，P ，Q 分别为图象的最高点和最低点，O 为坐标原点，若OP ⊥OQ ，则A ＝（ ）A.3B.√3π2C.√3π3D.1二、填空题共10小题，每小题4分，共40分．若角α的终边经过点P(1, 2)，则sin α等于________．设向量a →、b →的长度分别为4和3，夹角为60∘，则|a →+b →|＝________．函数f(x)＝3sin x 的最大值为________．设α是第一象限角，sin α=35，则tan α＝________．cos 2α＝________．设向量a →=(0, 2)，b →=(√3, 1)，则a →⋅b →=________；向量a →，b →的夹角等于________．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若a ＝2，B ＝60∘，A ＝45∘，则b ＝________，△ABC 的面积是________．在△ABC 中，三个内角A ，B ，C 的对边分别是a ，b ，c ，若a =2，b =3，c =4，则cos A =________．已知函数f(x)＝cos 2x +√3sin x cos x 在区间[0, m]上单调递增，则实数m 的最大值是________π6 ．已知点A(0, 4)，B(2, 0)，如果AB →=2BC →，那么点C 的坐标为________；设点P(3, t)，且∠APB 是钝角，则t 的取值范围是________．已知a ，b 是异面直线．给出下列结论：①一定存在平面α，使直线b ⊥平面α，直线a // 平面α； ②一定存在平面α，使直线b // 平面α，直线a // 平面α；③一定存在无数个平面α，使直线b 与平面α交于一个定点，且直线a // 平面α； ④一定存在平面α，使直线a ⊥平面α，直线b ⊥平面α． 则所有正确结论的序号为________．三、解答题共6小题，每小题13分，共78分．解答应写出文字说明、演算步骤或证明过程．.已知函数f(x)＝sin (2x −π3)． (Ⅰ)求f(π3)的值；(Ⅱ)求f(x)的最小正周期；(Ⅲ)求函数f(x)的单调递增区间．已知函数f(x)＝2√3sin x cos x +2cos 2x −1． (Ⅰ)求f(x)的最小正周期； (Ⅱ)求f(x)的对称中心的坐标；(Ⅲ)求函数f(x)在的区间[−π6, π4]上的最大值和最小值．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且a ＝2，cos C =−14． (Ⅰ)求sin C 的值；(Ⅱ)如果b ＝3，求c 的值； (Ⅲ)如果c ＝2√6，求sin B 的值．如图，四棱锥P −ABCD 的底面是正方形，侧棱PA ⊥底面ABCD ，E 是PA 的中点． (Ⅰ)求证：CD // 平面PAB ； (Ⅱ)求证：PC // 平面BDE ； (Ⅲ)证明：BD ⊥CE ．如图，在多面体ABCDEF 中，底面ABCD 为矩形，侧面ADEF 为梯形，AF // DE ，DE ⊥AD ，DC ＝DE ． (Ⅰ)求证：AD ⊥CE ；(Ⅱ)求证：BF // 平面CDE ；(Ⅲ)判断线段BE 上是否存在点Q ，使得平面ADQ ⊥平面BCE ？并说明理由．已知向量a →=(sin x, cos x)，b →=(cos x, −cos x)，设函数f(x)=a →⋅(a →+b →)． （1）求f(x)的最小正周期；（2）求f(x)的单调增区间；（3）若函数g(x)＝f(x)−k ，x ∈[0,π2]，其中k ∈R ，试讨论函数g(x)的零点个数．参考答案与试题解析2019-2020学年北京某校高一（下）期末数学试卷一、选择题共8小题，每小题4分，共32分．在每小题列出的四个选项中，选出符合题目要求的一项．1.【答案】B【考点】象限角、轴线角【解析】由sinα>0，则角α的终边位于一二象限，由tanα<0，则角α的终边位于二四象限，两者结合即可解决问题．【解答】解：∵sinα>0，则角α的终边位于一二象限，∵由tanα<0，∴角α的终边位于二四象限，∴角α的终边位于第二象限．故选B.【点评】本题考查三角函数值的符号规律，属于基础题，合理地将条件化简，从而将问题转化为已知三角函数值的符号问题．2.【答案】C【考点】三角函数的周期性【解析】直接利用三角函数的周期公式求解即可．【解答】函数y＝sin4x，x∈R的最小正周期为：2π4=π2．【点评】本题考查三角函数的周期的求法，是基本知识的考查．3.【答案】C【考点】函数y=Asin（ωx+φ）的图象变换【解析】利用函数y=A sin(ωx+φ)的图象变换规律，可得结论．【解答】解：将函数y=sin2x，向左平移π6个单位长度，可得y=sin2(x+π6)，即sin2(x+π6)=sin(2x+π3)．故选C. 【点评】本题主要考查函数y=A sin(ωx+φ)的图象变换规律，属于基础题．4.【答案】D【考点】命题的真假判断与应用【解析】利用直线与直线的平行直线与平面的垂直关系判断选项的正误即可．【解答】①平行于同一个平面的两条直线互相平行也可以相交也可能异面直线；所以①不正确；②垂直于同一个平面的两个平面互相平行也可能相交；所以②不正确；③平行于同一条直线的两条直线互相平行；正确；④垂直于同一个平面的两条直线互相平行．满足直线与平面垂直的性质定理，正确．【点评】本题考查直线与平面，直线与直线的位置关系的综合应用，是基本知识的考查．5.【答案】C【考点】数量积表示两个向量的夹角【解析】根据平面向量的夹角公式计算即可．【解答】解：设向量a→，b→的夹角为θ，则θ∈[0, π]，由|a→|=2，|b→|=1，a→⋅b→=√2，所以cosθ=a→⋅b→|a→|×|b→|=√22×1=√22，所以向量a→，b→的夹角为θ=π4．故选C.【点评】本题考查了平面向量的数量积与夹角计算问题，是基础题．6.【答案】D【考点】三角形的形状判断【解析】由正弦定理求出sin C的值，可得C＝60∘或120∘．再根据三角形的内角和公式求出A的值，由此即可这个三角形的形状．【解答】∵△ABC中，已知B＝30∘，c＝15，b＝5√3，由正弦定理bsin B =csin C，可得：5√312=15sin C，∴解得：sin C=√32，可得：C＝60∘或120∘．当C＝60∘，∵B＝30∘，∴A＝90∘，△ABC是直角三角形．当C＝120∘，∵B＝30∘，∴A＝30∘，△ABC是等腰三角形．故△ABC是直角三角形或等腰三角形，【点评】本题主要考查正弦定理的应用，三角形的内角和公式，判断三角形的形状的方法，体现了分类讨论的数学思想，属于中档题．7.【答案】D【考点】空间中平面与平面之间的位置关系空间中直线与平面之间的位置关系空间中直线与直线之间的位置关系【解析】根据题意，结合图形，分别判断选项中的命题是否正确即可．【解答】解：对于A，由图形知BD1与GH是异面直线，∴A错误；对于B，由题意知BD与EF也是异面直线，∴B错误；对于C，平面EFGH与平面ABCD是相交的，∴C错误；对于D，平面EFGH // 平面A1BCD1，理由是：由E，F，G，H分别是棱A1B1，BB1，CC1，C1D1的中点，得出EF // A1B，EH // A1D1，∴EF // 平面A1BCD1，EH // 平面A1BCD1.∵EF∩EH=E，∴平面EFGH // 平面A1BCD1.故选D.【点评】本题考查了空间中的直线与平面之间的位置关系应用问题，是基础题．8.【答案】B【考点】正弦函数的图象【解析】由题意，△OPQ是直角三角形，过P，Q作x轴的垂线，利用勾股定理求解QP，OP，OQ，建立关系可得A的值．【解答】函数f(x)＝A sin x(A>0)，周期T＝2π，可得：P(π2, A)，Q(3π2,−A)．连接PQ，过P，Q作x轴的垂线，可得：QP2＝4[A2+(π2)2]，OP2＝A2+(π2)2]，OQ2＝A2+(3π2)2]，由题意，△OPQ是直角三角形，∴QP2＝OP2+OQ2，即2A2+π2=52π2，解得：A=√3π2【点评】本题考查了正弦型三角函数的图象和性质，着重考查了勾股定理、由y＝A sin(ωx+φ)的部分图象建立关系．二、填空题共10小题，每小题4分，共40分．【答案】2√55【考点】任意角的三角函数【解析】由题意利用任意角的三角函数的定义，求得sinα的值．【解答】∵角α的终边经过点P(1, 2)，则sinα=√12+22=2√55，【点评】本题主要考查任意角的三角函数的定义，属于基础题．【答案】√31【考点】数量积表示两个向量的夹角向量的概念与向量的模【解析】首先对要求的向量的模平方，变为已知向量的平方和数量积之和，代入模长和夹角，求出结果，注意最后要对求得的结果开方．【解答】∵a→、b→的长度分别为4和3，夹角为60∘，∴a→2+a→⋅b→+b→2=16+4×3×cos60∘+9＝31∵|a→+b→|=√(a→+b→)2=√a→2+2a→⋅b→+b→2=√31，【点评】从最近几年命题来看，向量为每年必考考点，都是以选择题呈现，从2006到现在几乎各省都对向量的运算进行了考查，主要考查向量的数量积的运算． 【答案】 3【考点】三角函数的最值 【解析】直接利用正弦型函数性质的应用求出结果． 【解答】当x ＝2kπ+π2(k ∈Z)时，函数的最大值为3．【点评】本题考查的知识要点：正弦型函数的性质的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型． 【答案】34,725【考点】二倍角的三角函数同角三角函数间的基本关系【解析】由已知利用同角三角函数基本关系式可求cos α，进而可求tan α的值，根据二倍角的余弦函数公式即可求解cos 2α的值． 【解答】∵ α是第一象限角，sin α=35， ∴ cos α=√1−sin 2α=45， ∴ tan α=sin αcos α=3545=34．∴ cos 2α＝1−2sin 2α＝1−2×(35)2=725．【点评】本题主要考查了同角三角函数基本关系式，二倍角的余弦函数公式在三角函数化简求值中的应用，考查了计算能力和转化思想，属于基础题． 【答案】 2,π3【考点】平面向量数量积的性质及其运算 【解析】直接根据数量积的定义以及夹角的计算公式即可求解结论． 【解答】因为向量a →=(0, 2)，b →=(√3, 1)，故|a →|＝2；|b →|=√(√3)2+12=2； 故a →⋅b →=0×√3+2×1＝2； 向量a →，b →的夹角θ满足cos θ=a →⋅b→|a →|⋅|b →|=22×2=12；因为θ∈[0, π]⇒θ=π3，故向量a →，b →的夹角等于π3．【点评】本题考查向量数量积公式及其应用，属于基础题． 【答案】 √6,3+√32【考点】 正弦定理 【解析】由已知利用正弦定理可求b 的值，根据三角形内角和定理可求C 的值，进而根据三角形的面积公式即可求解． 【解答】若a ＝2，B ＝60∘，A ＝45∘， 则由正弦定理asin A =bsin B ，可得：b =a⋅sin B sin A=2×√32√22=√6，可求C ＝180∘−A −B ＝75∘，可得△ABC 的面积S △ABC =12ab sin C =12×2×√6×sin 75∘=√6sin (45∘+30∘)=√6(√22×√32+√22×12)=3+√32．【点评】本题主要考查了正弦定理，三角形内角和定理，三角形的面积公式在解三角形中的应用，考查了计算能力和转化思想，属于基础题． 【答案】78【考点】 余弦定理 【解析】由余弦定理代入三角形的边长，可得出答案． 【解答】解：在△ABC 中， cos A =b 2+c 2−a 22bc =9+16−42×3×4=78.故答案为：78.【点评】本题考查解三角形，牢记余弦定理公式是关键． 【答案】π6【考点】两角和与差的三角函数 正弦函数的单调性【解析】利用辅助角公式进行化简，结合函数的单调性进行求解即可． 【解答】 f(x)=1+cos 2x2+√32sin 2x ＝sin (2x +π6)+12，当0≤x ≤m 时，π6≤x ≤2m +π6， ∵ f(x)在区间[0, m]上单调递增， ∴ 2m +π6≤π2，得m ≤π6，即m 的最大值为π6，【点评】本题主要考查三角函数单调性的应用，利用辅助角公式进行转化，结合三角函数的单调性是解决本题的关键．难度中等． 【答案】 (3, −2),(1, 3) 【考点】平面向量数量积的性质及其运算 【解析】第一空：根据题意，设C 的坐标为(x, y)，求出向量AB →与BC →的坐标，由共线向量的坐标表示方法可得(2, −4)＝2(x −2, y)，计算可得x 、y 的值，即可得答案；第二空：由P 的坐标计算可得PA →、PB →的坐标，由向量数量积的计算公式可得PA →⋅PB →=(−3)×(−1)+(4−t)×(−t)<0，且(−3)×(−t)≠(−1)×(4−t)，解可得t 的取值范围，即可得答案． 【解答】根据题意，设C 的坐标为(x, y)，又由点A(0, 4)，B(2, 0)，则AB →=(2, −4)，BC →=(x −2, y)， 若AB →=2BC →，则有(2, −4)＝2(x −2, y)， 则有2＝2(x −2)，−4＝2y ， 解可得x ＝3，y ＝−2， 则C 的坐标为(3, −2)，又由P(3, t)，则PA →=(−3, 4−t)，PB →=(−1, −t)，若∠APB 是钝角，则PA →⋅PB →=(−3)×(−1)+(4−t)×(−t)<0，且(−3)×(−t)≠(−1)×(4−t)， 解可得1<t <3，即t 的取值范围为(1, 3)； 【点评】本题考查向量数量积的坐标计算公式，涉及向量平行的坐标表示方法，关键是掌握向量坐标计算的公式． 【答案】 ②③ 【考点】命题的真假判断与应用 【解析】假设①④结论正确，推出矛盾结论判断①④错误，根据线面位置的性质关系判断②③． 【解答】（2）设异面直线a ，b 的公垂线为m ，平面α⊥m ，且a ，b 均不在α内， 则a ，b 均与平面α平行，故②正确（1）（3）在直线b 上取点A ，显然过点A 有无数个平面均与直线a 平行，故③正确（2）（4）假设④正确，则由a ⊥α，b ⊥α可得a // b ，显然这与a ，b 是异面直线矛盾，故④错误． 故答案为：②③． 【点评】本题考查了空间直线与直线、直线与平面的位置关系，属于基础题．三、解答题共6小题，每小题13分，共78分．解答应写出文字说明、演算步骤或证明过程．. 【答案】（1）由于函数f(x)＝sin (2x −π3)，可得f(π3)＝sin (2×π3−π3)＝sin π3=√32； （2）f(x)的最小正周期T =2π2=π；(Ⅲ)令−π2+2kπ≤2x −π3≤π2+2kπ，k ∈Z ，可得：kπ−π12≤x ≤kπ+5π12，k ∈Z ，可得函数f(x)的单调递增区间为：[kπ−π12, kπ+5π12]，k ∈Z ．【考点】正弦函数的单调性 三角函数的周期性 【解析】(Ⅰ)由已知可求f(π3)＝sin π3=√32即可得解； (Ⅱ)利用正弦函数的周期公式即可求解； (Ⅲ)利用正弦函数的单调性即可求解． 【解答】（1）由于函数f(x)＝sin (2x −π3)，可得f(π3)＝sin (2×π3−π3)＝sin π3=√32； （2）f(x)的最小正周期T =2π2=π；(Ⅲ)令−π2+2kπ≤2x −π3≤π2+2kπ，k ∈Z ，可得：kπ−π12≤x ≤kπ+5π12，k ∈Z ，可得函数f(x)的单调递增区间为：[kπ−π12, kπ+5π12]，k ∈Z ．【点评】本题主要考查了正弦函数的单调性和周期性的应用，考查了函数思想的应用，属于基础题．【答案】（1）f(x)=√3sin2x+cos2x＝2sin(2x+π6)，则f(x)的最小正周期T=2π2=π，（2）由2x+π6=kπ，k∈Z，得x=12kπ−π12，k∈Z，即f(x)的对称中心的坐标为(12kπ−π12, 0)，k∈Z．(Ⅲ)当−π6≤x≤π4时，−π6≤2x+π6≤2π3，则当2x+π6=π2时，函数取得最大值，最大值为2sinπ2=2，当2x+π6=−π6时，函数取得最小值，最小值为2sin(−π6)＝2×(−12)＝−1．【考点】两角和与差的三角函数三角函数的周期性三角函数的最值【解析】(Ⅰ)利用辅助角公式进行化简，结合周期公式进行计算即可(Ⅱ)根据三角函数的对称性进行求解(Ⅲ)求出角的范围，结合三角函数的有界性以及最值性质进行求解即可．【解答】（1）f(x)=√3sin2x+cos2x＝2sin(2x+π6)，则f(x)的最小正周期T=2π2=π，（2）由2x+π6=kπ，k∈Z，得x=12kπ−π12，k∈Z，即f(x)的对称中心的坐标为(12kπ−π12, 0)，k∈Z．(Ⅲ)当−π6≤x≤π4时，−π6≤2x+π6≤2π3，则当2x+π6=π2时，函数取得最大值，最大值为2sinπ2=2，当2x+π6=−π6时，函数取得最小值，最小值为2sin(−π6)＝2×(−12)＝−1．【点评】本题主要考查三角函数的图象和性质，利用辅助角公式进行转化，结合三角函数的周期性，对称性以及最值的性质是解决本题的关键．难度不大．【答案】（1）在△ABC中，cos C=−14，且sin2C+cos2C＝1，则sin C＝±√154，又sin C>0，故sin C=√154．（2）∵a＝2，b＝3，∴cos C=−14=a2+b2−c22ab=4+9−c212，解得c2＝16，故c＝4．(Ⅲ)∵asin A=csin C，∴2sin A=√6√154，解得sin A=√108，又c>a，则cos A=3√68，sin B＝sin(A+C)＝sin A cos C+sin C cos A=√108×(−14)+√154×3√68=√104．【考点】余弦定理正弦定理【解析】(Ⅰ)由同角三角函数公式以及C为三角形的内角，可得出sin C的值；(Ⅱ)由余弦定理可得c；(Ⅲ)由正弦定理求出sin A，进而求出cos A，根据大边对大角确定cos A的符号，再根据三角形内角和为π，以及两角和与差的正弦公式得出答案．【解答】（1）在△ABC中，cos C=−14，且sin2C+cos2C＝1，则sin C＝±√154，又sin C>0，故sin C=√154．（2）∵a＝2，b＝3，∴cos C=−14=a2+b2−c22ab=4+9−c212，解得c2＝16，故c＝4．(Ⅲ)∵asin A=csin C，∴2sin A=√6√154，解得sin A=√108，又c>a，则cos A=3√68，sin B＝sin(A+C)＝sin A cos C+sin C cos A=√108×(−14)+√154×3√68=√104．【点评】本题考查解三角形的应用，熟记正余弦定理公式和两角和与差公式是解题的关键．【答案】证明：(Ⅰ)∵四棱锥P−ABCD的底面是正方形，∴CD // AB，∵CD⊄平面PAB，AB⊂平面PAB，∴CD // 平面PAB．（2）连结AC，BD，交于点O，连结OE，∵四棱锥P−ABCD的底面是正方形，∴O是AC中点，∵E是PA的中点．∴OE // PC，∵PC⊄平面BDE，OE⊂平面BDE，∴PC // 平面BDE．(Ⅲ)∵四棱锥P−ABCD的底面是正方形，侧棱PA⊥底面ABCD，∴BD⊥AC，BD⊥PA，∵AC∩PA＝A，∴BD⊥平面ACE，∵CE⊂平面ACE，∴BD⊥CE．【考点】直线与平面平行直线与平面垂直【解析】(Ⅰ)推导出CD // AB，由此能证明CD // 平面PAB．(Ⅱ)连结AC，BD，交于点O，连结OE，推导出OE // PC，由此能证明PC // 平面BDE．(Ⅲ)推导出BD⊥AC，BD⊥PA，从而BD⊥平面ACE，由此能证明BD⊥CE．【解答】证明：(Ⅰ)∵四棱锥P−ABCD的底面是正方形，∴CD // AB，∵CD⊄平面PAB，AB⊂平面PAB，∴CD // 平面PAB．（2）连结AC，BD，交于点O，连结OE，∵四棱锥P−ABCD的底面是正方形，∴O是AC中点，∵E是PA的中点．∴OE // PC，∵PC⊄平面BDE，OE⊂平面BDE，∴PC // 平面BDE．(Ⅲ)∵四棱锥P−ABCD的底面是正方形，侧棱PA⊥底面ABCD，∴BD⊥AC，BD⊥PA，∵AC∩PA＝A，∴BD⊥平面ACE，∵CE⊂平面ACE，∴BD⊥CE．【点评】本题考查线面平行、线线垂直的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．【答案】（1）由底面ABCD为矩形，知AD⊥CD．……………又因为DE⊥AD，DE∩CD＝D，……………所以AD⊥平面CDE．……………又因为CE⊂平面CDE，所以AD⊥CE．……………（2）由底面ABCD为矩形，知AB // CD，又因为AB⊄平面CDE，CD⊂平面CDE，所以AB // 平面CDE．……………同理AF // 平面CDE，又因为AB∩AF＝A，所以平面ABF // 平面CDE．……………又因为BF⊂平面ABF，所以BF // 平面CDE．……………(Ⅲ)结论：线段BE上存在点Q（即BE的中点），使得平面ADQ⊥平面BCE．证明如下：取CE的中点P，BE的中点Q，连接AQ，DP，PQ，则PQ // BC．由AD // BC，得PQ // AD．所以A，D，P，Q四点共面．……………由(Ⅰ)，知AD⊥平面CDE，所以AD⊥DP，故BC⊥DP．在△CDE中，由DC＝DE，可得DP⊥CE．又因为BC∩CE＝C，所以DP⊥平面BCE．……………又因为DP⊂平面ADPQ所以平面ADPQ⊥平面BCE（即平面ADQ⊥平面BCE）．即线段BE上存在点Q（即BE中点），使得平面ADQ⊥平面BCE．……【考点】直线与平面平行直线与平面垂直平面与平面垂直【解析】（I）由AD⊥DE，AD⊥CD可得AD⊥平面CDE，故而AD⊥CE；(II)证明平面ABF // 平面CDE，故而BF // 平面CDE；(III)取CE的中点P，BE的中点Q，证明CE⊥平面ADPQ即可得出平面ADQ⊥平面BCE．【解答】（1）由底面ABCD为矩形，知AD⊥CD．……………又因为DE⊥AD，DE∩CD＝D，……………所以AD⊥平面CDE．……………又因为CE⊂平面CDE，所以AD⊥CE．……………（2）由底面ABCD为矩形，知AB // CD，又因为AB⊄平面CDE，CD⊂平面CDE，所以AB // 平面CDE．……………同理AF // 平面CDE，又因为AB∩AF＝A，所以平面ABF // 平面CDE．……………又因为BF⊂平面ABF，所以BF // 平面CDE．……………(Ⅲ)结论：线段BE上存在点Q（即BE的中点），使得平面ADQ⊥平面BCE．证明如下：取CE的中点P，BE的中点Q，连接AQ，DP，PQ，则PQ // BC．由AD // BC，得PQ // AD．所以A，D，P，Q四点共面．……………由(Ⅰ)，知AD⊥平面CDE，所以AD⊥DP，故BC⊥DP．在△CDE中，由DC＝DE，可得DP⊥CE．又因为BC∩CE＝C，所以DP⊥平面BCE．……………又因为DP⊂平面ADPQ所以平面ADPQ⊥平面BCE（即平面ADQ⊥平面BCE）．即线段BE上存在点Q（即BE中点），使得平面ADQ⊥平面BCE．……【点评】本题考查了线面垂直，线面平行的判定，属于中档题．【答案】函数f(x)=a→⋅(a→+b→)＝(sin x, cos x)⋅(sin x+cos x, 0)＝sin2x+sin x cos x=1−cos2x2+12sin2x=√22sin(2x−π4)+12．所以函数的最小正周期为：π．因为函数y=√22sin(2x−π4)+12，由2kπ−π2≤2x−π4≤π2+2kπk∈Z，即kπ−π8≤x≤3π8+kπk∈Z，所以函数的单调增区间为：[−π8+kπ,3π8+kπ](k∈Z)．y=√22sin(2x−π4)+12，x∈[0,π2]，所以2x−π4∈[−π4,3π4]，y=√22sin(2x−π4)+12∈[0,√2+12]，函数g(x)＝f(x)−k=√22sin(2x−π4)+12−k，x∈[0,π2]，其中k∈R，当k<0或k>√2+12时，零点为0个；当k∈[1,√2+12)时函数有两个零点，当k=1+√22或0≤k<1时，函数有一个零点；【考点】函数的零点正弦函数的单调性三角函数的周期性【解析】（1）通过向量的数量积求出函数的表达式，利用二倍角公式以及两角和的正弦函数化为一个角的一个三角函数的形式，即可求出函数的最小正周期．（2）利用正弦函数的单调增区间，直接求出函数的单调增区间即可．（3）求出函数在x∈[0,π2]时函数的取值范围，即可根据函数的零点的判断方法推出函数零点的个数．【解答】函数f(x)=a →⋅(a →+b →)＝(sin x, cos x)⋅(sin x +cos x, 0) ＝sin 2x +sin x cos x =1−cos 2x2+12sin 2x =√22sin (2x −π4)+12．所以函数的最小正周期为：π． 因为函数 y =√22sin (2x −π4)+12，由 2kπ−π2≤2x −π4≤π2+2kπk ∈Z ，即 kπ−π8≤x ≤3π8+kπk ∈Z ，所以函数的单调增区间为：[−π8+kπ,3π8+kπ](k ∈Z)．y =√22sin (2x −π4)+12，x ∈[0,π2]，所以2x −π4∈[−π4,3π4]，y =√22sin (2x −π4)+12∈[0,√2+12]， 函数g(x)＝f(x)−k =√22sin (2x −π4)+12−k ，x ∈[0,π2]，其中k ∈R ，当k <0或k >√2+12时，零点为0个； 当k ∈[1,√2+12)时函数有两个零点， 当k =1+√22或0≤k <1时，函数有一个零点；【点评】本题是中档题，考查向量的数量积的应用，三角函数的化简求值，函数的单调增区间的求法，函数零点的判断方法，考查计算能力．。