中考数学专项训练：二次根式

中考数学总复习《二次根式》练习题附带答案一、单选题1．√123÷√213×√125值为（）A．1B．3C．√33D．√7 2．若√(a−b)2=b﹣a，则（）A．a＞b B．a＜b C．a≥b D．a≤b 3．与√a3b不是同类次根式的是（）A．1√abB．√baC．√ab2D．√ba34．下列运算正确的是（）A．√3+3=3√3B．4√2−√2=4C．√2+√3=√5D．3√3−√3=2√35．若代数式1x−1+√x有意义，则实数x的取值范围是（）A．x≠1B．x≥0C．x≠0D．x≥0且x≠1 6．a、b在数轴上的位置如图所示，那么化简√(b−a)2的结果是（）A．a-b B．a+b C．b-a D．-a-b7．设实数a，b在数轴上对应的位置如图所示，化简√a2+|a+b|的结果是（）A．-2a+b B．2a+b C．-b D．b8．若√3−m为二次根式，则m的取值为（）A．m≤3B．m＜3C．m≥3D．m＞39．下列运算正确的是（）A．(x−y)2=x2−y2B．|√3−2|=2−√3C．√8−√3=√5D．﹣（﹣a+1）=a+110．已知2<a<4，则化简√1−2a+a2+√a2−8a+16的结果是() A．2a﹣5B．5﹣2a C．﹣3D．311．下列运算中正确的是（）A．√2+√3=√5B．(−√5)2=5C．3√2−2√2=1D．√16=±4 12．下列计算正确的是（）A．(m−n)2=m2−n2B．(2ab3)2=2a2b6C．√8a3=2a√a D．2xy+3xy=5xy 二、填空题13．计算：√45﹣√25× √50=．14．若√12x是一个整数，则x可取的最小正整数是3．（判断对错）15．计算：√24−√12√3=．16．如果x2﹣3x+1=0，则√x2+1x2−2的值是．17．化简：√75=.18．已知实数a，b，c在数轴上的位置如图所示，化简代数式√a2−|a+c|+√(b−c)2−|−b|三、综合题19．完成下列问题：（1）若n（n≠0）是关于x的方程x2+mx+2n=0的根，求m+n的值；（2）已知x，y为实数，且y= √2x−5+√5−2x﹣3，求2xy的值．20．阅读材料，解答问题：（1）计算下列各式：①√4×9=，√4×√9=；②√16×25=，√16×√25=．通过计算，我们可以发现√a×b=（a>0，b>0）从上面的结果可以得到：√8=√2×√4=2√2，√12=√3×√4=2√3（2）根据上面的运算，完成下列问题①化简：√24②计算：√27+√48③化简：√a2b（a>0，b>0）21．在数学课外学习活动中，小明和他的同学遇到一道题：已知a=12+√3，求2a2−8a+1的值.他是这样解答的：∵a=2+√3=√3(2+√3)(2−√3)=2−√3，∴a−2=−√3∴(a−2)2=3，a2−4a+4=3∴a2−4a=−1∴2a2−8a+1=2(a2−4a)+1=2×(−1)+1=−1.请你根据小明的解析过程，解决如下问题：（1）1√3+√2=；（2）化简 √2+1+√3+√2√4+√3⋯+√256+√255 ； （3）若 a =√10−3，求 a 4−6a 3+a 2−12a +3 的值. 22．已知 x =√3+12 ， y =√3−12与 m =xy 和 n =x 2−y 2 . （1）求m ，n 的值；（2）若 √a −√b =m +72， √ab =n 2 求 √a +√b 的值. 23．计算： （1）√135•2 √3 •（﹣ 12 √10 ）； （2）√3a 2b •（ √b a ÷2 √1b）． 24．计算下列各题 （1）计算：（ 12 ）﹣2﹣6sin30°﹣（ √7−√5）0+ √2 +| √2 ﹣ √3 | （2）化简：（ x+2x 2−2x ﹣ x−1x 2−4x+4 ）÷ x−4x ，然后请自选一个你喜欢的x 值，再求原式的值．参考答案1．【答案】A2．【答案】D3．【答案】C4．【答案】D5．【答案】D6．【答案】A7．【答案】D8．【答案】A9．【答案】B10．【答案】D11．【答案】B12．【答案】D13．【答案】√514．【答案】对15．【答案】2√2−216．【答案】√517．【答案】5√318．【答案】019．【答案】（1）将x=n 代入方程x 2+mx+2n=0得n 2+mn+2n=0,则n(n+m+2)=0 因为n≠0,所以n+m+2=0即m+n=-2.（2）因为y=√2x −5+√5−2x -3有意义，则{2x −5≥05−2x ⩾0解得{x ⩾52x ≤52则x=52 所以y=0+0-3=-3即2xy=2×52×（-3）=-15. 20．【答案】（1）6；6；20；20；√a ×√b（2）解：①√24=√4×6=√4×√6=2√6；②√27+√48=√3×9+√3×16=√3×√9+√3×√16=3√3+4√3=7√3 ；③√a 2b =√a 2⋅√b =a √b （a >0，b >0）．21．【答案】（1）√3−√2（2）解：原式 =√2−1+√3−√2+√4−√3+⋯+√256−√255=−1+√2−√2+√3−√3+√4−⋯−√255+√256=√256−1=16−1=15 ；（3）解： ∵ a =√10−3 =√10+3 ∴a −3=√10∴(a −3)2=10即 a 2−6a +9=10 .∴a 2−6a =1 .∴a 4−6a 3=a 2∴a 4−6a 3+a 2−12a +3=2a 2−12a +3=2(a 2−6a)+3=2+3=5 .22．【答案】（1）解：由题意得， m =xy =√3+12×√3−12=12 n =(x +y)(x −y)=(√3+12+√3−12)(√3+12−√3−12)=√3 （2）解：由（1）得， √a −√b =4 √ab =3 ∴(√a +√b)2=(√a −√b)2+4√ab =42+4×3=28∵√a +√b >0∴√a +√b =2√723．【答案】（1）解： √135 •2 √3 •（﹣ 12 √10 ） =2×（﹣ 12 ） √135×3×10 =﹣ √16×3=﹣4 √3（2）解： √3a 2b •（ √b a ÷2 √1b）= √3a2b × √ba× 12× √b= √3424．【答案】（1）解：原式=4﹣6× 12﹣1+ √2+ √3﹣√2 = √3；（2）解：原式=[x+2x(x−2)﹣x−1(x−2)2]•xx−4= (x+2)(x−2)−x(x−1)x(x−2)2•xx−4=x−4x(x−2)2•xx−4=1 (x−2)2当x=10时，原式= 1 64．。

最简二次根式课堂用卷
定义：
它要求满足以下两条：
⑴被开方数中的因数是整数，因式是整式.
⑵被开方数中不含能开得尽方的因式或因数.
我们把符合这两个条件的二次根式，叫做最简二次根式.
1．判断下列各式是否为最简二次根式？
⑴；⑵；⑶；⑷；
⑸；⑹；⑺
2．把下列各式化成最简二次根式：
3．把下列各式化成最简二次根式：
⑴⑵
4．把下列各式化成最简二次根式：
⑴⑵⑶⑷
5．判断下列各等式是否成立，若不成立请说出正确的解法和答案.
⑴；⑵；
⑶；⑷
6．化简：
⑴；⑵
⑶；⑷
7．把下列二次根式化为最简二次根式
⑴⑵
8．把下列二次根式化为最简二次根式
⑴⑵
9．在式子中，为最简二次根式的是.
10．当时，把中的移进根号内，.
11．下列根式，为最简根式的是（）
A． B． C． D．12．化简的结果是（）
A． B． C． D．。

中考数学复习重点知识专项训练6---数的开方和二次根式一、选择题5．（2020•衢州x 的值可以为（ ）A ．0B ．1C ．2D ．46.(2020·宁波)x 的取值范围是A ．x >2B ．x ≠2C ．x ≥2D ．x ≤24．（2020台州）无理数√10在（ ）A ．2和3之间B ．3和4之间C ．4和5之间D ．5和6之间5．(2020·绥化)下列等式成立的是( )A4 B2 C ．－a8 6．（2020·聊城）计算45÷33×53的结果正确的是（ ） A ．1 B ．35 C ．5 D ．9 2．（2020·南京）3的平方根是( )A ．9 B． CD ．5．（2020·a 的取值范围是（ ）A ．a ≥1B ．a ≤1C ．a ≥0D ．a ≤－1（2020·济宁）3.下列各式是最简二次根式的是（ ）A.13 B.12 C.2a D.353．（2020·南通） 下列计算正确的是AB ．3＋C＝3D＝3．（2020·泰州）下列等式成立的是（ ）A．3+= B．=C=D3=4．（2020·常州）8的立方根是( )A ．2 2B ．±2 2C ．2D ．±26．（2020·天津）估计的值在（ ）A. 3和4之间B. 4和5之间C. 5和6之间D. 6和7之间（2020·包头）1）A ．5 BC．D．45．（2020·广东）若式子x 的取值范围是（ ） A ．2x B ．2x C ．2x D ．2x3．（2020·宜昌）对于无理数3，添加关联的数或者运算符号组成新的式子，其运算结果能成为有理数的是（ ）.A ．23-32B ．33+C ．()33 D ．30⨯6．（2020·凉山州）下列等式成立的是（ ） A±B22= C ．11()2--＝－D ．(tan45°－1)0＝1 7．（2020·临沂）设2a =，则（ ）A.2 3a <<B.34a <<C.45a <<D.56a <<2．（2020·武汉）式子2-x 在实数范围内有意义，则x 的取值范围是（ ）A ．x ≥0B ．x ≤2C ．x ≥－2D ．x ≥211．（2020·武汉）计算()23-的结果是_________．6. （2020·攀枝花） 下列说法中正确的是（ ）A. 0.09的平方根是0.3B. 4=±C. 0的立方根是0D. 1的立方根是1±二、填空题14．（2020·铜仁）函数y ＝中，自变量x 的取值范围是 ．13．（2020·遵义）计算_________．11．（2020·=______． 14．（2020·哈尔滨）计算61624+的结果是 . 9．（2020·江苏徐州）7的平方根是 .11．（2020x 的取值范围是 .11.（2020在实数范围内有意义的x 的取值范围是_____. 14．(2020自贡)与√14−2最接近的自然数是 ．10．（2020·南京）______.11．（2020·北京）.9．（2020·青岛）计算：)3412(-{（2020·德州）13.= .2．（2020·镇江）使 √x −2 有意义的 x 的取值范围是．13．（2020·南通）已知m ＜m ＋1，m 为整数，则m 的值为 ▲ ．（2020·山西）11．计算: （＋）2－＝_________．11. (2020·湘潭)=_______________．13.（2020·株洲）计算3⨯结果是________．14．（2020·天津）计算1)+的结果等于_______．（2020·包头）15、计算：2=．13．（2020·广东）若10b ，则2020ab . 17．（2020·河北）已知:222218b a =-=-，则ab =__________．11．（2020·黄冈）若20x -=，则12xy -＝________．13．（2020·x 的取值范围为________．12.（2020·广州）计算：= .13．（2020·淄博）计算：√−83+√16= 2 ．15．（2020·邵阳）在如图的方格中，若要使横，竖，斜对角的3个实数相乘都得到同样的结的果，则2个空格的实数之积为 .14．（2020·广西北部湾经济区）计算：√12−√3= ．3.（2020·云南）要使有意义，则x的取值范围是 ．三、解答题20．（2020·通辽）用※定义一种新运算：对于任意实数m 和n ，规定m ※n ＝m 2n ﹣mn ﹣3n ，如：1※2＝12×2﹣1×2﹣3×2＝﹣6．（1）求（﹣2（2）若3※m ≥﹣6，求m 的取值范围，并在所给的数轴上表示出解集．。

备战中考之二次根式习题一、单选题（共15题；）1.对于任意的正数m 、n 定义运算※为：m ※n={√m −√n (m ≥n )√m +√n (m <n )),计算（3※2）×（8※12）的结果为（ ）A. 2﹣4√6B. 2C. 2√5D. 20 2.要使二次根式√3−2x 有意义，则x 的取值范围是（ ）A. x ⩾32 B. x ⩽32 C. x ⩾23 D. x ⩽23 3.下列各实数中最大的一个是（ ） A. 5× √0.039 B.3.141πC.√14+√7D. √0.3 + √0.24.已知x 为实数，化简√−x 3−x√−1x的结果为（ ）A. (x −1)√−xB. (−1−x )√−xC. (1−x )√−xD. (1+x )√−x 5.若√x −1+√x +y =0 ，则x 2005+y 2005 的值为： （ ）A. 0B. 1C. -1D. 26.等式√xx−3=√x√x−3成立的条件是（ ） A. x≠3 B. x≥0 C. x≥0且x≠3 D. x>3 7.下列二次根式中，最简二次根式是( ).A. B.C.D.8.已知是正整数，则实数n 的最大值为（ ）A. 12B. 11C. 8D. 39.如果最简根式 √3a −8 与√17−2a 是同类二次根式,那么使√4a −2x 有意义的x 的取值范围是（ ） A. x≤10 B. x≥10 C. x ＜10 D. x ＞10 10.已知 y =√4−x +√x −4+3 ，则 yx 的值为（ ）A. 43 B. −43 C. 34 D. −34 11.若x +y ＝3+2 √2 ，x ﹣y ＝3﹣2 √2 ，则 √x 2−y 2 的值为（ ） A. 4 √2 B. 1 C. 6 D. 3﹣2 √2 12.函数 y =1x+1−√2−3x 中，自变量 x 的取值范围是（ ）A. x ≤23 B. x ≥23 C. x <23 且 x ≠−1 D. x ≤23 且 x ≠−113.利用计算器计算时，依次按键下： ，则计算器显示的结果与下列各数中最接近的一个是（ ）A. 2.5B. 2.6C. 2.8D. 2.914.把代数式(a－1) √11−a的a－1移到根号内，那么这个代数式等于（）A. －√1−aB. √a−1C. √1−aD. －√a−115.一个三角形的三边长分别为1，k，4，化简|2k－5|－√k2−12k+36的结果是( )A. 3k－11B. k＋1C. 1D. 11－3k二、填空题（共15题；）16.若|1001−a|+√a−1002=a，则a−10012=________．17.观察下列运算过程：1+√2=√2+1=√2(√2+1)(√2−1)=√2(√2)2−12=√2−1√2+√3=√3+√2=√3√2(√3+√2)(√3−√2)=√3√2(√3)2−(√2)2=√3−√2……请运用上面的运算方法计算：1+√3+√3+√5√5+√7⋯+√2015+√2017√2017+√2019=________．18.如图，数轴上点A表示的数为a，化简：a+√a2−4a+4=________19.√12与最简二次根式5 √a+1是同类二次根式，则a=________．20.读取表格中的信息，解决问题．满足n n n√3+√2≥2014×(√3−√2+1)的n可以取得的最小整数是________．21.已知|6﹣3m|+（n﹣5）2=3m﹣6﹣√(m−3)n2，则m﹣n=________22.若m=√2012−1，则m5﹣2m4﹣2011m3的值是________．23.若√20n是整数，则正整数n的最小值为________．24.已知√a（a﹣√3）＜0，若b=2﹣a，则b的取值范围是________．25.如果（x﹣√x2−2008）（y﹣√y2−2008）=2008，求3x2﹣2y2+3x﹣3y﹣2007=________．26.已知a、b为有理数，m、n分别表示5−√7的整数部分和小数部分，且amn+bn2=1，则2a+b=________.27.若实数x，y，m满足等式√3x+5y−3−m+(2x+3y−m)2=√x+y−2−√2−x−y，则m+4的算术平方根为________．28.若x、y都为实数，且y=2008√x−5+2007√5−x+1，则x2+y=________。

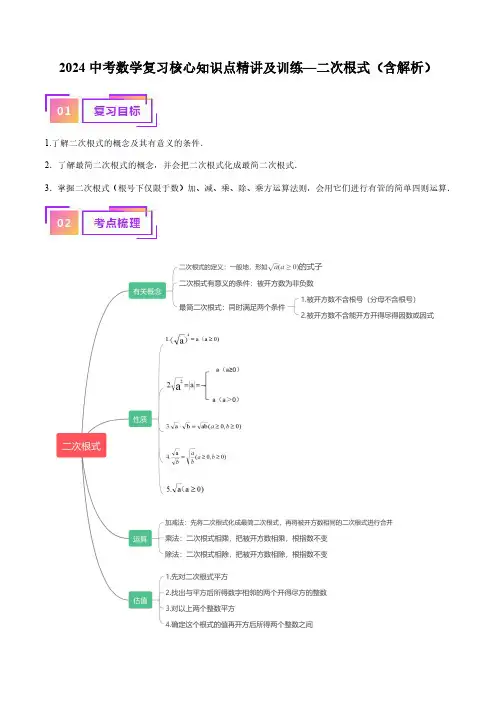
二次根式复习一、知识归纳 （一）二次根式定义1注意：（12，（2）被开方数是非负数2、二次根式在实数范围内有意义的条件是 a ≥0 。

（二）二次根式的性质1、二次根式的双重非负性≥0，a ≥0a ≥0）表示非负数a 的算术平方根，≥0，2、）2=a (a ≥0)(0)0(0)(0)a a a a a a ⎧⎪===⎨⎪-⎩＞＜（三）、最简二次根式和同类二次根式 1、最简二次根式的两个条件：（1）被开方数不含 ；（2）被开方数不含 的因数或因式。

满足：（1）根号内不含有分母，有分母的先通分，再将分母开出来 （2）根号内每个因式或因数的指数都小于根指数2，如果根号内含有因式或因数的指数大于根指数2，就利用，将每个因式或因数的指数都小于根指数2（3）分母内不含有根式，如果分母内含有根号，则利用分母有理化，将根号划去。

（1）判断一个二次根式是否是最简二次根式，要紧扣最简二次根式的特点： ①被开方数不含分母；②被开方数不能含开得尽方的因数或因式.即把每一个因数或因式都写成底数较小、乘方的形式后，因数或因式的指数小于2.③若被开方数是和（或差）的形式，则先把被开放方数写成积的形式，再作判定，若无法写成积（或一个数）的形式，则为最简二次根式.=简二次根式.=，且因式2和22()x y +的指数都是1，是最简二次根式.22a b +无法变成一个数（或因式）式.（2）化简二次根式一般例如为两步：一如果被开方数是分数或分式，利用分母有理化化简；二化去被开方数中的分母之后，再将被开方数分解成几个数相乘的形式或分解因式，然后利用积的算术平方根的性质把能开得尽方的因数或因式开出来.若被开方数中不含分母，则只需第二步.同类二次根式：几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式叫做同类二次根式.同类二次根式与同类项类似. 对同类二次根式的理解应注意以下几点：（1）判断几个二次根式是否是同类二次根式时，首先将二次根式化为最简二次根式，其次看被开方数是否相同.（2）几个二次根式是否是同类二次根式，只与被开方数和根指数有关，与根号外的系数无关. 将同类二次根式的系数相加减，根指数与被开方数保持不变.（1）二次根式的系数就是这个二次根式根号外的因式（或因数），它包含前面的符号.（2）当二次根式的系数为带分数时，必须将其化为假分数.（3）不是同类二次根式，千万不要合并.（四）二次根式的运算0)=≥，≥0a b=≥，＞00)a b≥，≥0a b0)=≥，＞00)a b二次根式的加减实质上就是合并同类二次根式.4、二次根式加减的步骤：（1）先将二次根式化成。

2024中考数学复习核心知识点精讲及训练—二次根式（含解析）1.了解二次根式的概念及其有意义的条件．2．了解最简二次根式的概念，并会把二次根式化成最简二次根式．3．掌握二次根式（根号下仅限于数）加、减、乘、除、乘方运算法则，会用它们进行有管的简单四则运算．【题型1：二次根式有意义的条件】【典例1】（2023•济宁）若代数式有意义，则实数x的取值范围是（）A．x≠2B．x≥0C．x≥2D．x≥0且x≠2【答案】D【解答】解：由题意得x≥0且x﹣2≠0，解得x≥0且x≠2，故选：D．1．（2023•金华）要使有意义，则x的值可以是（）A．0B．﹣1C．﹣2D．2【答案】D【解答】解：由题意得：x﹣2≥0，解得：x≥2，则x的值可以是2，故选：D．2．（2023•通辽）二次根式在实数范围内有意义，则实数x的取值范围在数轴上表示为（）A．B．C．D．【答案】C【解答】解：二次根式在实数范围内有意义，则1﹣x≥0，解得：x≤1，则实数x的取值范围在数轴上表示为：．故选：C．3．（2023•湘西州）若二次根式在实数范围内有意义，则x的取值范围是x≥5．【答案】x≥5．【解答】解：由二次根式在实数范围内有意义可得：2x﹣10≥0，解得：x≥5；故答案为：x≥5．【题型2：二次根式的性质】【典例2】（2023•泰州）计算等于（）A．±2B．2C．4D．【答案】B【解答】解：＝2．故选：B．1．（2021•苏州）计算（）2的结果是（）A．B．3C．2D．9【答案】B【解答】解：（）2＝3．故选：B．2.（2023•青岛）下列计算正确的是（）A．B．C．D．【答案】C【解答】解：与无法合并，则A不符合题意；2﹣＝，则B不符合题意；×＝＝，则C符合题意；÷3＝＝，则D不符合题意；故选：C．3．（2021•娄底）2、5、m是某三角形三边的长，则+等于（）A．2m﹣10B．10﹣2m C．10D．4【答案】D【解答】解：∵2、5、m是某三角形三边的长，∴5﹣2＜m＜5+2，故3＜m＜7，∴+＝m﹣3+7﹣m＝4．故选：D．4．（2022•遂宁）实数a、b在数轴上的位置如图所示，化简|a+1|﹣+＝2．【答案】2．【解答】解：由数轴可得，﹣1＜a＜0，1＜b＜2，∴a+1＞0，b﹣1＞0，a﹣b＜0，∴|a+1|﹣+＝a+1﹣（b﹣1）+（b﹣a）＝a+1﹣b+1+b﹣a＝2，故答案为：2．【题型3：二次根式的运算】【典例3】（2023•金昌）计算：÷×2﹣6．【答案】6．【解答】解：原式＝3××2﹣6＝12﹣6＝6．1．（2023•聊城）计算：（﹣3）÷＝3．【答案】3．【解答】解：原式＝（4﹣3×）÷＝（4﹣）÷＝3÷＝3．故答案为：3．2．（2023•山西）计算：的结果为﹣1．【答案】﹣1．【解答】解：原式＝（）2﹣（）2＝2﹣3＝﹣1．故答案为：﹣1．3．（2023•兰州）计算：．【答案】．【解答】解：原式＝3﹣2＝．4．（2023•陕西）计算：．【答案】2﹣2．【解答】解：原式＝﹣3++1＝2﹣3+1＝2﹣2．1．（2023秋•福鼎市期中）下列各数不能与合并的是（）A．B．C．D．【答案】B【解答】解：A、∵＝＝，∴能与合并，故A不符合题意；B、∵＝2，∴不能与合并，故B符合题意；C、∵＝3，∴能与合并，故C不符合题意；D、∵＝4，∴能与合并，故D不符合题意；故选：B．2．（2023秋•云岩区校级期中）下列式子中，属于最简二次根式的是（）A．B．C．D．【答案】D【解答】解：A、＝＝，被开方数含分母，不是最简二次根式，不符合题意；B、＝＝4，被开方数中含能开得尽方的因数，不是最简二次根式，不符合题意；C、＝，被开方数含分母，不是最简二次根式，不符合题意；D、是最简二次根式，符合题意；故选：D．3．（2022秋•泉州期末）若二次根式有意义，则x的取值范围是（）A．x＜3B．x≠3C．x≤3D．x≥3【答案】C【解答】解：∵二次根式有意义，∴3﹣x≥0，解得：x≤3．故选：C．4．（2023秋•龙泉驿区期中）下列运算中，正确的是（）A．B．C．D．【答案】D【解答】解：A、±＝±3，故A不符合题意；B、与﹣不能合并，故B不符合题意；C、2﹣＝，故C不符合题意；D、÷＝，故D符合题意；故选：D．5．（2023秋•锦江区校级期中）若a＞b＞0，则的结果是（）A．a B．2b﹣a C．a﹣2b D．﹣a 【答案】A【解答】解：∵a＞b＞0，∴+＝|b|+|b﹣a|＝b+a﹣b＝a，故选：A．6．（2023春•河东区期中）把x根号外的因数移到根号内，结果是（）A．B．C．﹣D．﹣【答案】C【解答】解：由x可知x＜0，所以x＝﹣＝﹣，故选：C．7．（2023春•铁岭县期末）计算：的结果是（）A．2B．0C．﹣2D．﹣【答案】B【解答】解：＝﹣＝2﹣2＝0，故选：B．8．（2023春•抚顺月考）二次根式的计算结果是（）A．B．C．±D．【答案】B【解答】解：＝＝×＝3，故选：B．9．（2023春•西丰县期中）已知a＝+2，b＝﹣2，则a﹣b的值是（）A．2B．4C．2+4D．2﹣4【答案】B【解答】解：∵a＝+2，b＝﹣2，∴a﹣b＝+2﹣（﹣2）＝+2﹣+2＝4，故选：B．10．（2023春•工业园区期末）下列各组二次根式中，是同类二次根式的是（）A．与B．与C．与D．与【答案】D【解答】解：A、∵＝2，∴与不是同类二次根式，故A不符合题意；B、∵＝2，∴与不是同类二次根式，故B不符合题意；C、与不是同类二次根式，故C不符合题意；D、∵＝2，∴与是同类二次根式，故D符合题意；故选：D．11．（2023春•武昌区校级期中）若是整数，则满足条件的最小正整数n的值为6．【答案】见试题解答内容【解答】解：＝2，∵是整数，∴满足条件的最小正整数n＝6．故答案为：6．12．（2023春•固镇县月考）计算＝﹣．【答案】﹣．【解答】解：＝2﹣3＝﹣，故答案为：﹣．13．（2023春•高安市期中）化简计算：＝2．【答案】2．【解答】解：＝（）2﹣12＝3﹣1＝2，故答案为：2．14．（2023秋•高新区校级期中）计算：（1）×；（2）．【答案】（1）﹣11；（2）5﹣4．【解答】解：（1）×＝﹣4×3＝﹣12＝﹣11；（2）＝4﹣5+4﹣4+2＝5﹣4．15．（2023秋•秦都区校级期中）计算：﹣×．【答案】4﹣+2．【解答】解：﹣×＝3﹣+2＝﹣+2＝4﹣+2．1．（2022秋•鼓楼区校级期末）实数a在数轴上的位置如图所示，则化简结果为（）A．7B．﹣7C．2a﹣15D．无法确定【答案】A【解答】解：∵由图可知：4＜a＜10，∴a﹣4＞0，a﹣11＜0，∴原式＝+＝a﹣4+11﹣a＝7．故选：A．2．（2023春•新郑市校级期末）若＝在实数范围内成立，则x的取值范围是（）A．x≥1B．x≥4C．1≤x≤4D．x＞4【答案】D【解答】解：∵＝在实数范围内成立，∴x﹣1≥0，x﹣4＞0，∴x＞4．故选：D．3．（2023秋•西安校级月考）若x，y都是实数，且，则xy的值是（）A．0B．4C．2D．不能确定【答案】B【解答】解：根据题意得，x﹣1≥0且1﹣x≥0，解得x≥1且x≤1，∴x＝1，∴y＝4，∴xy＝1×4＝4．故选：B．4．（2023•商水县一模）我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为a，b，c，记，则其面积，这个公式也被称为海伦一秦九韶公式．若p＝5，c＝2，则此三角形面积的最大值为（）A ．B ．C ．D ．5【答案】C【解答】解：∵p ＝，p ＝5，c ＝2，∴5＝，∴a +b ＝8，∴a ＝8﹣b ，∴S ＝＝＝＝＝＝＝当b ＝4时，S 有最大值为．故选：C ．5．（2023秋•闵行区期中）计算：＝．【答案】．【解答】解：，＝＝＝＝＝，故答案为：．6．（2023春•科左中旗校级期末）观察下列等式：第1个等式：a1＝＝﹣1，第2个等式：a2＝＝，第3个等式：a3＝＝2﹣，第4个等式：a4＝＝﹣2，…按上述规律，计算a1+a2+a3+…+a n＝﹣1．【答案】见试题解答内容【解答】解：第1个等式：a1＝＝﹣1，第2个等式：a2＝＝，第3个等式：a3＝＝2﹣，第4个等式：a4＝＝﹣2，…a1+a2+a3+…+a n＝﹣1+﹣+…+﹣＝﹣1故答案为：﹣1．7．（2023春•中江县月考）已知的值是7．【答案】7．【解答】解：∵m＝+1，n＝＝﹣1，∴m+n＝2，mn＝1，∴m2+mn+n2＝（m+n）2﹣mn＝（2）2﹣1＝7．故答案为：7．8．（2023春•禹州市期中）如图，在数学课上，老师用5个完全相同的小长方形在无重叠的情况下拼成了一个大长方形，已知小长方形的长为，宽为，则这个大长方形的周长为22．【答案】22．【解答】解：∵大长方形的宽＝3+2＝5，大长方形的长＝3×2＝6，∴大长方形的周长＝（5+6）×2＝22，故答案为：22．9．（2023春•宿豫区期末）计算的结果为3．【答案】3．【解答】解：原式＝+＝+＝2+＝3．故答案为：3．10．（2023秋•双流区校级期中）已知a＝3+，b＝3﹣，分别求下列代数式的值：（1）a2﹣b2；（2）a2﹣3ab+b2．【答案】（1）12；（2）1．【解答】解：（1）∵a＝3+，b＝3﹣，∴a+b＝3++3﹣＝6，a﹣b＝3+﹣3+＝2，ab＝（3）（3）＝7，则a2﹣b2＝（a+b）（a﹣b）＝6×＝12；（2）由（1）知a﹣b＝2，ab＝（3）（3）＝7，∴a2﹣3ab+b2＝（a﹣b）2﹣ab，＝＝8﹣7＝1．11．（2023春•双柏县期中）阅读下面问题：＝＝﹣1；＝＝﹣；＝＝﹣2．（1）求的值；（2）计算：+++…++．【答案】见试题解答内容【解答】解：（1）原式＝＝﹣；（2）原式＝﹣1+﹣+…+﹣+﹣＝10﹣1＝9．12．（2023秋•二七区校级月考）阅读材料：我们来看看完全平方公式在无理数化简中的作用．问题提出：该如何化简？建立模型：形如的化简，只要我们找到两个数a，b，使a+b＝m，ab＝n，这样（）2+（）2＝m，•＝．那么便有：（a＞b），问题解决：化简：，解：首先把化为，这里m＝7，n＝12，由于4+3＝7，4×3＝12，即，．∴，模型应用1：利用上述解决问题的方法化简下列各式：（1）；（2）．模型应用2：（3）在Rt△ABC中，∠C＝90°，AB＝4﹣，AC＝，那么BC边的长为多少？（直接写出结果，结果化成最简）．【答案】（1）1+；（2）2﹣；（3）2﹣2．【解答】解：（1）m＝6，n＝5．∵1+5＝6，1×5＝5，∴（）2+（）2＝6，×＝，∴＝＝1+．（2）∵＝．∴m＝13，n＝40，∵5+8＝13，5×8＝40，∴（）2+（）2＝13，×＝，∴＝＝＝2．（3）BC＝＝．∵＝，∴m＝16，n＝48，∵4+12＝16，4×12＝48，∴（）2+（）2＝16，×＝，∴BC＝＝＝＝2﹣2．1．（2022•桂林）化简的结果是（）A．2B．3C．2D．2【答案】A【解答】解：＝2，故选：A．2．（2022•内蒙古）实数a在数轴上的对应位置如图所示，则+1+|a﹣1|的化简结果是（）A．1B．2C．2a D．1﹣2a【答案】B【解答】解：根据数轴得：0＜a＜1，∴a＞0，a﹣1＜0，∴原式＝|a|+1+1﹣a＝a+1+1﹣a＝2．故选：B．3．（2022•河北）下列正确的是（）A．＝2+3B．＝2×3C．＝32D．＝0.7【答案】B【解答】解：A、原式＝，故该选项不符合题意；B、原式＝×＝2×3，故该选项符合题意；C、原式＝＝92，故该选项不符合题意；D、0.72＝0.49，故该选项不符合题意；故选：B．4．（2022•湖北）下列各式计算正确的是（）A．B．C．D．【答案】D【解答】解：A、与不属于同类二次根式，不能运算，故A不符合题意；B、，故B不符合题意；C、，故C不符合题意；D、，故D符合题意；故选：D．5．（2022•青岛）计算（﹣）×的结果是（）A．B．1C．D．3【答案】B【解答】解：（﹣）×＝﹣＝﹣＝3﹣2＝1，故选：B．6．（2022•安顺）估计（+）×的值应在（）A．4和5之间B．5和6之间C．6和7之间D．7和8之间【答案】B【解答】解：原式＝2+，∵3＜＜4，∴5＜2+＜6，故选：B．7．（2023•绵阳）若式子在实数范围内有意义，则x的最小值为．【答案】．【解答】解：由题意可得2x﹣1≥0，解得：x≥，则x的最小值为，故答案为：．8．（2023•丹东）若代数式在实数范围内有意义，则实数x的取值范围是x≥﹣2，且x≠1．【答案】x≥﹣2，且x≠1．【解答】解：由题可知，x+2≥0，即x≥﹣2，又知分母不能等于0，即x﹣1≠0，则x≠1．故答案为：x≥﹣2，且x≠1．9.（2022•武汉）计算的结果是2．【答案】2．【解答】解：法一、＝|﹣2|＝2；法二、＝＝2．故答案为：2．10．（2023•内蒙古）实数m在数轴上对应点的位置如图所示，化简：＝2﹣m．【答案】2﹣m．【解答】解：由数轴可知：1＜m＜2，∴m﹣2＜0，∴＝|m﹣2|＝2﹣m．故答案为：2﹣m．11．（2022•荆州）若3﹣的整数部分为a，小数部分为b，则代数式（2+a）•b的值是2．【答案】2．【解答】解：∵1＜＜2，∴1＜3﹣＜2，∵若3﹣的整数部分为a，小数部分为b，∴a＝1，b＝3﹣﹣1＝2﹣，∴（2+a）•b＝（2+）（2﹣）＝2，故答案为：2．12．（2022•泰安）计算：•﹣3＝2．【答案】2．【解答】解：原式＝﹣3×＝4﹣2＝2，故答案为：2．13．（2022•济宁）已知a＝2+，b＝2﹣，求代数式a2b+ab2的值．【答案】﹣4．【解答】解：∵a＝2+，b＝2﹣，∴a2b+ab2＝ab（a+b）＝（2+）（2﹣）（2++2﹣）＝（4﹣5）×4＝﹣1×4＝﹣4．。

一、选择题1．下列运算结果正确的是（ ）A 9=-B 3=C ．(22= D 5=-2．有意义，则x 的取值范围是（ ） A ．x≠2 B ．x >-2 C ．x <-2 D ．x≠-23．下列各式是二次根式的是（ ）A B C D 4．下列运算中，正确的是( )A =B 1=C =D =5．下列运算中，正确的是( )A =3B ．=-1C D ．36．下列式子一定是二次根式的是 ( )A B C D7．若2019202120192020a =⨯-⨯，b =，c a ，b ，c 的大小关系是（ ） A ．a b c <<B ．a c b <<C ．b a c <<D ．b c a <<8．实数a ，b ，c ，满足|a |+a =0，|ab |=ab ，|c |-c =0，a +b |+|a -c |-（ ）A ．2c -bB ．2c -2aC ．-bD ．b9．下列各式成立的是（ ）A 2B 5=-C xD 6=-10．下列各式中，一定是二次根式的是（ ）A B C D 二、填空题11．设4 a,小数部分为 b.则1a b- = __________________________. 12．设12211112S =++，22211123S =++，32211134S =++，设12...n S S S S =+++，则S=________________ (用含有n 的代数式表示，其中n 为正整数)．13．为了简洁、明确的表示一个正数的算术平方根，许多数学家进行了探索，期间经历了400余年，直至1637年法国数学家笛卡儿在他的《几何学》中开始使用“”表示算数平方根．我国使用根号是由李善兰（1811-1882年）译西方数学书时引用的，她在《代数备旨》中把图1所示题目翻译为： 22164?a x a x +=则图2所示题目（字母代表正数）翻译为_____________，计算结果为_______________.14．120654010144152118+++235a b c +的形式(,,a b c 为正整数)，则abc =______.15．下面是一个按某种规律排列的数阵：11第行325 62第行7223 10 11 233第行 13154 1732 19254第行根据数阵排列的规律，第 5 行从左向右数第 3 个数是 ，第 n （n 3≥ 且 n 是整数）行从左向右数第 n 2- 个数是 （用含 n 的代数式表示）． 16．若2x ﹣3x 2﹣x=_____．17．对于任意实数a ，b ，定义一种运算“◇”如下：a ◇b ＝a(a －b)＋b(a ＋b)，如：3◇2＝3×(3－2)＋2×(3＋2)＝1332＝_____. 18．化简：3222＝_____．19．观察分析下列数据：0，36，-3，231532的规律得到第10个数据应是__________．20．下列各式：③4是最简二次根式的是:_____（填序号）三、解答题21．若x ，y 为实数，且y12．求x y y x ++2－xy y x +-2的值．【分析】根据二次根式的性质，被开方数大于等于0可知：1﹣4x ≥0且4x ﹣1≥0，解得x =14，此时y =12．即可代入求解． 【详解】解：要使y 有意义，必须140410x x -≥⎧⎨-≤⎩，即1414x x ⎧≤⎪⎪⎨⎪≥⎪⎩∴ x ＝14．当x ＝14时，y ＝12． 又∵x y y x ++2－x yy x +-2＝－| ∵x ＝14，y ＝12，∴ x y ＜y x．∴+当x ＝14，y ＝12时，原式＝．【点睛】（a ≥0）叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．22．我国南宋时期有个著名的数学家秦九韶提出了一个利用三角形的三边求三角形的面积的公式，若三角形三边为a b c 、、，则此三角形的面积为：1S = 同样古希腊有个几何学家海伦也提出了一个三角形面积公式：2S =2a b cp ++=（1）在ABC 中，若4AB =，5BC =，6AC =，用其中一个公式求ABC 的面积．（2）请证明：12S S【答案】（1）4；（2） 证明见解析 【分析】（1）将4AB =，5BC =，6AC =代入1S = （2）对1S 和2S 分别平方，再进行整理化简得出2212S S =，即可得出12S S ．【详解】解：（1）将4AB =，5BC =，6AC =代入1S =得：4S == （2）222222211[()]24a b a S c b +-=-=222222)1(22(4)a b c a b c ab ab +-+--+ =2222()2(21)4c a c a b b +⋅---⋅ =()(1()()16)c a b c a b a b c a b c +-++-++- 22()()()S p p a p b p c =---∵2a b cp ++=， ∴22()(2)(222)S a a b c a b c a b c a b cb c +++++++-+=-- =2222a b c b c a a c b a b c+++-+-+-⋅⋅⋅ =1()()()()16a b c b c a a c b a b c +++-+-+-∴2212S S =∵10S >，20S >， ∴12S S ．【点睛】本题考查了二次根式的运算，解题的关键是理解题中给出的公式，灵活运用二次根式的运算性质进行运算．23．先观察下列等式，再回答下列问题：111111112=+-=+；111112216=+-=+1111133112=+-=+(1) (2)请你按照上面各等式反映的规律，用含n 的等式表示（n 为正整数）．【答案】(1)1120(2)()111n n ++（n 为正整数） 【解析】试题分析：（1）从三个式子中可以发现，第一个加数都是1，第二个加数是个分数，设分母为n ，第三个分数的分母就是n+1，结果是一个带分数，整数部分是1，分数部分的分子也是1，分母是前项分数的分母的积．所以由此可计算给的式子；（2）根据（1）找的规律写出表示这个规律的式子．试题解析：(1)=1+14−141+=1120，1120(2)1 n −1 n 1+=1+()1n n 1+ (n 为正整数).a =，也考查了二次根式的运算.此题是一道阅读题目，通过阅读找出题目隐含的条件.总结：找规律的题目，都要通过仔细观察找出和数之间的关系，并用关系式表示出来.24．先化简，再求值：(()69x x x x --+，其中1x =.【答案】化简得6x+6，代入得【分析】根据整式的运算公式进行化简即可求解.【详解】(()69x x x x+--+=22369x x x--++=6x+6把1x=代入原式=61）【点睛】此题主要考查实数的运算，解题的关键熟知整式的运算法则.25．计算②)21-【答案】①【分析】①根据二次根式的加减法则计算；②利用平方差、完全平方公式进行计算．【详解】解：①原式＝②原式＝(5-2-＝【点睛】本题考查二次根式的运算，熟练掌握完全平方公式、平方差公式是关键．26．计算：（1）0 1 2⎛⎫ ⎪⎝⎭（2）(4【答案】（1）-5;（2）9【分析】（1）第一项利用算术平方根的定义计算，后一项利用零指数幂法则计算，即可得到结果；（2）利用平方差公式计算即可．【详解】（1）012⎛⎫ ⎪⎝⎭41=--， 5=-；（2）(4167=-9=．【点睛】本题考查了二次根式的混合运算以及零指数幂，熟练掌握平方差公式是解题的关键．27．先化简再求值：（a ﹣22ab b a -）÷22a b a-，其中，b=1．【答案】原式=a ba b-=+【分析】括号内先通分进行分式的加减运算，然后再进行分式的乘除法运算，最后将数个代入进行计算即可. 【详解】原式=()()222a ab b aa ab a b -+⨯+-=()()()2·a b a aa b a b -+- =a b a b-+，当，b=1时，原式【点睛】本题考查了分式的化简求值，熟练掌握分式混合运算的运算顺序以及运算法则是解题的关键.28．先化简，再求值：24224x x x x x x ⎛⎫÷- ⎪---⎝⎭，其中2x =．【答案】22x x +-，1 【分析】先把分式化简，然后将x 、y 的值代入化简后的式子求值即可．原式(2)(2)22(2)2x x x xx x x x+-+=⋅=---，当2x=时，原式1==.【点睛】本题考查了分式的化简求值这一知识点，把分式化到最简是解题的关键．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据二次根式的性质及除法法则逐一判断即可得答案．【详解】9=，故该选项计算错误，不符合题意，=C.(22=，故该选项计算正确，符合题意，5=，故该选项计算错误，不符合题意，故选：C．【点睛】本题考查二次根式的性质及运算，理解二次根式的性质并熟练掌握二次根式除法法则是解题关键．2．B解析：B【分析】根据二次根式的被开方数是非负数，且分母不能为零，可得答案．【详解】有意义，得：20x+>，解得：2x>-．【点睛】本题考查了二次根式有意义的条件，利用被开方数是非负数，分母不能为零得出不等式是解题关键．3．A解析：A【分析】根据二次根式定义和有意义的条件：被开方数是非负数，即可判断．【详解】解：A、符合二次根式有意义条件，符合题意；B、-1＜0B选项不符合题意；C、是三次根式，所以C选项不符合题意；D、π-4＜0D选项不符合题意．故选：A．【点睛】a≥0．4．C解析：C【分析】根据二次根式的加、减、乘、除运算法则对各项进行计算即可得到结果．【详解】不是同类二次根式，不能合并，故此选项错误；不是同类二次根式，不能合并，故此选项错误；=D=，故此选项错误；故选：C．【点睛】此题主要考查了二次根式的混合运算，熟练掌握二次根式的运算法则是解答此题的关键．5．D解析：D【分析】根据二次根式的加减乘除法则逐项判断即可得．【详解】=+=，此项错误A314==-，此项错误B、23===⨯=，此项错误C2428=，此项正确D、3故选：D．【点睛】本题考查了二次根式的加减乘除运算，熟记二次根式的运算法则是解题关键．6．A解析：A【分析】根据二次根式的定义，直接判断得结论．【详解】A A正确；a<B错误；B、0C是三次根式，故C错误；a<D错误；D、0故选：A．【点睛】a≥)是二次根式，注意二次根式的被开方数是非负数．7．A解析：A【分析】利用平方差公式计算a，利用完全平方公式和二次根式的化简求出b，利用二次根式大小的比较办法，比较b、c得结论．【详解】解：a=2019×2021-2019×2020=（2020-1）（2020+1）-（2020-1）×2020=20202-1-20202+2020=2019；∵20222-4×2021=（2021+1）2-4×2021=20212+2×2021+1-4×2021=20212-2×2021+1=（2021-1）2=20202，∴b=2020；>∴c＞b＞a．故选：A．【点睛】本题考查了完全平方公式、平方差公式、二次根式的化简、二次根式大小的比较等知识点．变形2019×2021-2019×2020解决本题的关键．8．D解析：D【解析】解：∵|a|+a=0，∴|a|=﹣a，∴﹣a≥0，∴a≤0，∵|ab|=ab，∴ab≥0，∴b≤0，∵|c|﹣c=0，∴| c|=c，∴c≥0，∴原式=﹣b+（a+b）﹣（a﹣c）﹣（c﹣b）=b．故选D．9．A解析：A【分析】直接利用二次根式的性质化简求出即可．【详解】解：，正确，故选项A符合题意；=，原选项计算错误，故选项B不符合题意；=，原选项计算错误，故选项C不符合题意；||xD. =，原选项计算错误，故选项D不符合题意．故选：A．【点睛】此题主要考查了二次根式的性质与化简，正确掌握二次根式的性质是解答此题的关键．10．D解析：D【分析】根据二次根式的意义,如果一定是二次根式,则不论字母取何值,被开方数一定是非负数,逐一判断即可得．【详解】解:A,不是二次根式；B x ＜0时无意义,不一定是二次根式；C 在-2＜a ＜2时,无意义,不一定是二次根式；D a 2≥0,一定是二次根式；故选：D ．【点睛】本题主要考查二次根式的定义,一般地,a≥0）的式子叫做二次根式．二、填空题11．【分析】根据实数的估算求出a,b ，再代入即可求解.【详解】∵1＜＜2，∴-2＜-＜-1，∴2＜＜3∴整数部分a=2,小数部分为-2=2-，∴==故填：.【点睛】此题主要考查无理解析：1 【分析】根据实数的估算求出a,b ，再代入1a b -即可求解. 【详解】∵1＜2，∴-2＜＜-1，∴2＜43∴整数部分a=2,小数部分为4，∴1ab -=2222=-=12-故填：1. 【点睛】此题主要考查无理数的估算，分母有理化等，解题的关键熟知实数的性质.12．【分析】先根据题目中提供的三个式子，分别计算的值，用含n 的式子表示其规律，再计算S 的值即可．【详解】解：∵，∴；∵，∴；∵，∴；……∵，∴；∴．故答案为：【点睛】本题 解析：221n n n ++ 【分析】n 的式子表示其规律，再计算S 的值即可．【详解】 解：∵1221191=124S =++311122===+-； ∵222114912336S =++=7111116623===+=+-； ∵32211169134144S =++=1311111121234===+=+-； …… ∵()()()222222111111n n n S n n n n ++=++=++，()()2111111111n n n n n n n n ++===+=+-+++；∴...S =1111111112231n n =+-++-++-+…+ 111n n =+-+． 221n n n +=+ 故答案为：221n n n ++ 【点睛】本题为规律探究问题，难度较大，根据提供的式子发现规律，并表示规律是解题的关键，同时要注意对于式子()11111n n n n =-++的理解． 13．a+3【分析】根据题意可知图中的甲代表a,据此可写出图2中表示的式子.再根据二次根式的性质进行化简.【详解】解：根据题意可知图中的甲代表a,∴图2所示题目（字母代表正数）翻【分析】根据题意可知图中的甲代表a,据此可写出图2中表示的式子.再根据二次根式的性质进行化简.【详解】解：根据题意可知图中的甲代表a,∴图2∵a ＞0+3.a =a+3. 【点睛】本题考查阅读理解的能力，正确理解题意是关键. 14．【解析】【分析】根据题意，可得到=，利用平方关系把根号去掉，根据、、的系数相等的关系得到关于a ，b ，c 的三元方程组，解方程组即可.∵=∴，即．解得．【点睛】本题考查了解析：【解析】【分析】a ，b ，c 的三元方程组，解方程组即可.【详解】∴(22118=，即2222118235a b c =+++++． 2222352118,2120,2540,2144,a b c ab ac bc ⎧++=⎪=⎪∴⎨=⎪⎪=⎩ 解得15,4,18.a b c =⎧⎪=⎨⎪=⎩154181080abc ∴=⨯⨯=．【点睛】本题考查了二次根式的加减，解本题的关键是将等式平方去根号，利用等量关系中等式左、.15．；．【分析】根据被开方数是连续的自然数写出即可；根据每一行的最后一个数的被开方数是所在的行数乘比行数大1的数写出第（n-1）行的最后一个数，然后被开方数加上（n-2）即可求解．观察表【分析】根据被开方数是连续的自然数写出即可；根据每一行的最后一个数的被开方数是所在的行数乘比行数大1的数写出第（n-1）行的最后一个数，然后被开方数加上（n-2）即可求解．【详解】观察表格中的数据可得，第5行从左向右数第3=∵第（n-1，∴第n（n≥3且n是整数）行从左向右数第n-2个数是．．【点睛】本题是对数字变化规律的考查，观察出被开方数是连续自然数并且每一行的最后一个数的被开方数是所在的行数乘比行数大1的数是解题的关键．16．【解析】【分析】根据完全平方公式以及整体的思想即可求出答案．【详解】解：∵2x﹣1= ，∴（2x﹣1）2=3∴4x2﹣4x+1=3∴4（x2﹣x）=2∴x2﹣x=故答案为【点解析：1 2【解析】【分析】根据完全平方公式以及整体的思想即可求出答案．【详解】解：∵2x﹣，∴（2x﹣1）2=3∴4x 2﹣4x+1=3∴4（x 2﹣x ）=2∴x 2﹣x=12故答案为12【点睛】 本题考查二次根式的运算，解题的关键是熟练运用完全平方公式，本题属于基础题型． 17．5【解析】◇==5.故本题应填5.点睛：理解新定义运算的运算规则，其实就是一个对应关系，a 对应，b 对应，即将a=，b=，代入到代数式a(a －b)＋b(a ＋b)中，再根据二次根式的混合运算法则解析：5【解析】32==5. 故本题应填5.点睛：理解新定义运算的运算规则，其实就是一个对应关系，a ，b ，即将，代入到代数式a(a －b)＋b(a ＋b)中，再根据二次根式的混合运算法则进行计算，注意最终的结果一定要化为最简二次根式.18．【分析】直接合并同类二次根式即可．【详解】解：．故答案为【点睛】合并同类二次根式实际是把同类二次根式的系数相加，而根指数与被开方数都不变． 解析：【分析】直接合并同类二次根式即可．【详解】解：=．故答案为合并同类二次根式实际是把同类二次根式的系数相加，而根指数与被开方数都不变． 19．6【分析】通过观察可知，根号外的符号以及根号下的被开方数依次是：，，…，可以得到第13个的答案．【详解】解：由题意知道：题目中的数据可以整理为：，，…，∴第13个答案为：．故答案为6．解析：6【分析】 通过观察可知，根号外的符号以及根号下的被开方数依次是：11(1)30，21(1)31，31(1)32…1(1)3(1)n n ，可以得到第13个的答案．【详解】 解：由题意知道：题目中的数据可以整理为：11(1)30，21(1)31，31(1)32…1(1)3(1)n n ，∴第13个答案为：131(1)3(131)6．故答案为6．【点睛】此题主要考查了二次根式的运算以及学生的分析、总结、归纳的能力，规律型的习题一般是从所给的数据和运算方法进行分析，从特殊值的规律上总结出一般性的规律． 20．②③【分析】根据最简二次根式的被开方数不含分母；被开方数不含能开得尽方的因数或因式，可得答案．【详解】② ③ 是最简二次根式，故答案为②③．【点睛】本题考查最简二次根式的定义，解析：②③【分析】根据最简二次根式的被开方数不含分母；被开方数不含能开得尽方的因数或因式，可得答案．是最简二次根式，故答案为②③．【点睛】本题考查最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．三、解答题21．无22．无23．无24．无25．无26．无27．无28．无。

2020中考数学 二次根式专项练习（含答案）一、单选题（共有9道小题） 1.在下列实数中，无理数是（ ） A.31 B.π C.16 D.7222.94的值等于( ) A ．32 B ．32- C ．32± D ．81163.下列计算正确的是（ ） A ．233363⨯= B ．235+=C ．552233-=D ．6233÷=4.化简22)(-的结果是( )A ．－2B ．±2C ．2D ．45.要使代数式23x -有意义，则x 的（ ）A.最大值是23B.最小值是23C. 最大值是32D.最小值是326.下列各二次根式是最简二次根式的是( ) A. 4a B.21x -C.13aD.2x y7.36的平方根是（ ）A.6B.±6C.6D.6± 8.下列四个式子中，x 的取值范围为2x ≥的是（ ）A ．22x x -- B ．12x - C ．2x - D ．2x -9.设4r ≥，111a rr =-+，111b r r =-+，()11c rr r =++，则下列各式一定成立的是______．A ．a b c >>B ．b c a >>C ．c a b >>D ．c b a >>二、填空题（共有7道小题） 10.计算：34--=11.计算()()107107+-= 12.计算()463222-÷=13.化简：3227=14.()232-=15.在下列说法中，正确的有 ．（只填序号） ①0.09是0.81的平方根 ②－9的平方根是±3 ③的算术平方根是－5； ④是一个负数 ⑤0的相反数和倒数都是0 ⑥；⑦已知是实数，则2(5)-2-42=±a 2||a a =⑧全体实数和数轴上的点一一对应．16.关于m 的一元二次方程22720nm n m --=的一个根为2，则22n n -+=三、计算题（共有6道小题） 17.计算：()02020272cos602-++-o18.计算：()1123tan 452 1.413-⎛⎫--++- ⎪⎝⎭19.计算：()()22112323++-20.化简下列各式：2221244112x x a a x x ++-+--+（112a ≤≤）21. 化简：64332181236+++++22. 化简：1014152110141521+--+++四、解答题（共有4道小题） 23. 比较大小： 26+与35+24. 已知数14的小数部分是b ，求4321237620b b b b +++-25.已知在等式ax b s cx d+=+中，a b c d ，，，为有理数，x 是无理数。

2021年九年级数学中考一轮复习突破训练：二次根式的化简计算（附答案）1．已知：a+b＝﹣5，ab＝1，则+的值为（）A．5B．﹣5C．25D．5或﹣52．若x2+y2＝1，则的值为（）A．0B．1C．2D．3 3．设，，，……，，其中n为正整数，则的值是（）A．B．C．D．4．若x2+y2＝1，则++的值为（）A．0B．1C．2D．35．已知x＝﹣2，x4+8x3+16x2的值为（）A．B．C．3D．96．若a＝2﹣，则代数式2a2﹣8a﹣1的值等（）A．1B．﹣1C．4+4D．﹣27．已知a+b＝﹣7，ab＝4，则+＝（）A．B．﹣C．D．﹣8．设等式在实数范围内成立，其中a、x、y是三个不同的实数，则的值是（）A．3B．C．2D．9．的值是（）A．B．C．1D．10．设x＝，y＝，则x5+x4y+xy4+y5的值为（）A．47B．135C．141D．15311．已知x＝+1，y＝﹣1，则x2﹣y2的值为．12．若m2＝100，||＝1，则m+＝．13．若＝2.5，则的值为．14．已知a＝，b＝，则a2﹣b2的值是．15．如果+＝0，则+＝16．已知：m+n＝10，mn＝9，则＝．17．已知x＝2﹣，则代数式（7+4）x2的值是．18．已知x＝2﹣，则代数式x2﹣2x﹣1的值为．19．若a＝3﹣，则a2﹣6a+9的值为．20．小明在解决问题：已知a＝，求2a2﹣8a+1的值，他是这样分析与解答的：∵a＝．∴a﹣2＝﹣．∴（a﹣2）2＝3，即a2﹣4a+4＝3．∴a2﹣4a＝﹣1，∴2a2﹣8a+1＝2（a2﹣4a）+1＝2×（﹣1）+1＝﹣1．请你根据小明的分析过程，解决如下问题：（1）计算：＝；（2）计算：+…+；（3）若a＝，求2a2﹣8a+1的值．21．已知x＝，y＝，求的值．22．在解决问题“已知a＝，求3a2﹣6a﹣1的值”时，小明是这样分析与解答的：∵a＝＝＝+1，∴a﹣1＝，∴（a﹣1）2＝2，a2﹣2a+1＝2，∴a2﹣2a＝1，∴3a2﹣6a＝3，3a2﹣6a﹣1＝2．请你根据小明的分析过程，解决如下问题：（1）化简：．（2）若a＝，求2a2﹣12a+1的值．23．若x＝，y＝（1）求x+y的值；（2）求x2﹣xy+y2的值．24．先化简，再求值：[+]÷，其中x＝1，y ＝2．25．当a＝时，求﹣﹣的值．26．求代数式a+的值，其中a＝﹣2020．如图是小亮和小芳的解答过程．（1）的解法是错误的；（2）错误的原因在于未能正确地运用二次根式的性质：；（3）求代数式a+2的值，其中a＝﹣2019．27．（1）解方程：（x﹣1）2﹣9＝0；（2）已知x＝+1，求x2﹣2x+5的值．参考答案1．解：∵a+b＝﹣5，ab＝1，∴a＜0，b＜0，+＝﹣﹣＝﹣，又∵a+b＝﹣5，ab＝1，∴原式＝﹣＝5；故选：A．2．解：因为x2+y2＝1，所以﹣1≤x≤1，﹣1≤y≤1，因为＝，其中y﹣2＜0，所以x+1≤0，又因为﹣1≤x≤1，所以x+1＝0，x＝﹣1，所以y＝0，所以原式＝+＝2+0＝2．故选：C．3．解：∵n为正整数，∴＝＝＝＝＝＝1+，∴＝（1+）+（1+）+（1+）+…+（1+）＝2020+1﹣+＝2020+1﹣＝2020．故选：B．4．解：∵x2+y2＝1，∴﹣1≤x≤1，﹣1≤y≤1，∵＝＝，x+1≥0，y﹣2＜0，（x+1）（y﹣2）≥0，∴x+1＝0，∴x＝﹣1，∴y＝0，∴++＝2+1+0＝3．故选：D．5．解：∵x＝﹣2，∴x2＝（﹣2）2＝（）2﹣2××2+22＝7﹣4+4＝11﹣4，则原式＝x2（x2+8x+16）＝x2（x+4）2＝（11﹣4）（﹣2+4）2＝（11﹣4）（2+）2＝（11﹣4）（11+4）＝112﹣（4）2＝121﹣112＝9，故选：D．6．解：∵a＝2﹣，∴2a2﹣8a﹣1＝2（a﹣2）2﹣9＝2（2﹣﹣2）2﹣9＝2×5﹣9＝1．故选：A．7．解：∵a+b＝＜0，ab＞0，∴a＜0，b＜0原式＝（﹣）+（﹣）＝﹣，∵a+b＝﹣7，ab＝4，∴原式＝﹣＝．故选：A．8．解：由于根号下的数要是非负数，∴a（x﹣a）≥0，a（y﹣a）≥0，x﹣a≥0，a﹣y≥0，a（x﹣a）≥0和x﹣a≥0可以得到a≥0，a（y﹣a）≥0和a﹣y≥0可以得到a≤0，∴a只能等于0，将a＝0代入等式得﹣＝0，∴x＝﹣y，即：y＝﹣x，由于x，y，a是三个不同的实数，∴x＞0，y＜0．将x＝﹣y代入原式得：原式＝＝．故选：B．9．解：由题意可知第k项是∴原式＝（++＝1﹣＝1﹣＝．故选：B．10．解：∵x＝，y＝，∴x+y＝3，xy＝1∴x2+y2＝（x+y）2﹣2xy＝7，∴x5+x4y+xy4+y5＝（x5+x4y）+（xy4+y5）＝x4（x+y）+y4（x+y）＝（x4+y4）（x+y）＝[（x2+y2）2﹣2x2y2]（x+y）＝（49﹣2）×3＝141．故选C．11．解：∵x＝+1，y＝﹣1，∴x+y＝2，x﹣y＝2，∴x2﹣y2＝（x+y）（x﹣y）＝2×2＝4；故答案为4．12．解：∵m2＝100，||＝1，∴m＝±10，n＝±3，∴n2＝9，∴m+＝±10+3，即m+＝13或m+＝﹣7，故答案为：13或﹣7．13解：∵（）（），＝（24﹣t2）﹣（8﹣t2），＝24﹣t2﹣8+t2，＝16，∵＝2.5，则＝＝，故答案为：．14．解：∵a＝＝＝﹣，b＝＝＝+，∴a2﹣b2＝（a+b）（a﹣b）＝（﹣++）（﹣﹣﹣）＝2×（﹣2）＝﹣4，故答案为：﹣4．15．解：∵+＝0，∴a﹣2＝0、3﹣b＝0，则a＝2、b＝3，所以原式＝+＝+＝2．16．解：∵m+n＝10，mn＝9，∴（）2＝＝＝＝，∴＝±．故答案是：．17．解：原式＝[（2+）x]2，当x＝2﹣时，原式＝[（2+）（2﹣）]2＝1，故答案为1．18．解：原式＝x2﹣2x+1﹣2＝（x﹣1）2﹣2＝（2﹣﹣1）2﹣2＝（1﹣）2﹣2＝1+2﹣2﹣2＝1﹣2．故答案为：1﹣2．19．解：当a＝3﹣时，a2﹣6a+9＝（a﹣3）2＝（3﹣﹣3）2＝（﹣）2＝7，故答案为：7．20．解：（1）＝＝﹣1，故答案为：；（2）原式＝﹣1+﹣+﹣+…+﹣＝﹣1＝；（3）∵a＝+2，∴a2＝（+2）2＝9+4，∴2a2﹣8a+1＝2（9+4）﹣8（+2）+1＝18+8﹣8﹣16+1＝3．答：2a2﹣8a+1的值为3．21．解：当x＝＝5﹣2，y＝＝5+2时，原式＝+＝+＝+＝245﹣100﹣98+240+245+100+98+240＝970．22．解：（1）＝＝＝3+；（2）∵a＝＝＝＝3﹣2，∴a﹣3＝﹣2，∴（a﹣3）2＝8，即a2﹣6a+9＝8，∴a2﹣6a＝﹣1，∴2a2﹣12a＝﹣2，则2a2﹣12a+1＝﹣2+1＝﹣1．23．解：x＝＝，y＝＝（1）x+y＝＝2；（2）x2﹣xy+y2＝（x﹣y）2+xy＝（）2+（）（）＝4+1＝5．24．解：[+]÷＝[﹣]÷＝×＝×＝，当x＝1，y＝2时，原式＝＝．25．解：∵a＝＝﹣1，∴＝﹣a﹣1﹣﹣＝a+1+﹣＝a+1＝﹣．26．解：（1）∵a＝﹣2020，∴1﹣a＝1﹣（﹣2020）＝2021，故小芳开方时，出现错误，故答案为：小芳；（2）错误的原因在于未能正确地运用二次根式的性质：＝|a|，故答案为：＝|a|；（3）a+2＝a+2，∵a＝﹣2019，∴a﹣3＜0，∴原式＝a+2（3﹣a）＝a+6﹣2a＝6﹣a＝6﹣（﹣2019）＝6+2019＝2025，即代数式a+2的值是2025．27.1．解：（1）∵（x﹣1）2﹣9＝0，∴（x﹣1）2＝9，∴x﹣1＝±3，∴x＝±3+1，∴x1＝4，x2＝﹣2；（2）∵x＝+1，∴x﹣1＝，∴x2﹣2x+5＝（x﹣1）2+4＝（）2+4＝2+4＝6。

一、选择题1．5﹣x ，则x 的取值范围是（ ） A ．为任意实数 B ．0≤x≤5 C ．x≥5 D ．x≤5 2．下列式子中，是二次根式的是( )A B CD ．x3．下列各式计算正确的是（ ）A ．6232126()b a b a b a---⋅=B ．（3xy ）2÷（xy ）=3xyC =D ．2x •3x 5=6x 64．有意义，则x 的取值范围是（ ） A ．x≠2B ．x >-2C ．x <-2D ．x≠-25．已知226a b ab +=，且a>b>0，则a ba b+-的值为( )A B C ．2D ．±26． ）A ．30 B ．C ．30D ．7．化简二次根式 ）A B C D 8．若化简1682+-x x -1x -的结果为5-2x ，则x 的取值范围是（ ） A ．为任意实数 B ．1≤x≤4C ．x≥1D ．x≤49．下列各式计算正确的是（ ）A B ．C ．D10．230x -=成立的x 的值为（ ）A ．-2B ．3C ．-2或3D ．以上都不对二、填空题11．使函数212y x x=+有意义的自变量x 的取值范围为_____________12．已知112a b +=，求535a ab b a ab b++=-+_____．13．化简并计算：...+=________．（结果中分母不含根式）14．2==________．15．甲容器中装有浓度为a ，乙容器中装有浓度为b ，两个容器都倒出m kg ，把甲容器倒出的果汁混入乙容器，把乙容器倒出的果汁混入甲容器，混合后，两容器内的果汁浓度相同，则m 的值为_________．16．已知函数1x f xx，那么1f _____．17．10=，则222516x y +=______.18．若实数x ，y ，m 满足等式()223x y m +-=m+4的算术平方根为________． 19．若实数a =，则代数式244a a -+的值为___.20． (a ≥0)的结果是_________.三、解答题21．先阅读材料，再回答问题：因为)111=1=；因为1=，所以=1== （1= ，= ； （2⋅⋅⋅+的值．【答案】（12）9 【分析】（1）仿照例子，由1+=的值；由1+=的值；（2）根据（1）中的规律可将每个二次根式分母有理化，可转化为实数的加减法运算，再寻求规律可得答案．【详解】 解：（1）因为1-=；因为1=1（2⋅⋅⋅+1=+⋅⋅⋅1=1019=-=．【点睛】本题考查了分母有理化，分子分母都乘以分母这两个数的差进行分母有理化是解题关键．22．阅读材料，回答问题：两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，我们就说这两个代数式a =，)111=11互为有理化因式．（1）1的有理化因式是 ；（2）这样，化简一个分母含有二次根式的式子时，采用分子、分母同乘以分母的有理化因式的方法就可以了，例如：==25384532++====-进行分母有理化． （3）利用所需知识判断：若a =，2b =a b，的关系是 ． （4）直接写结果：)1=．【答案】（1）1；（2）7-；（3）互为相反数；（4）2019 【分析】（1）根据互为有理化因式的定义利用平方差公式即可得出；（2）原式分子分母同时乘以分母的有理化因式(2，化简即可；（3）将a=（4）化简第一个括号内的式子，里面的每一项进行分母有理化，然后利用平方差公式计算即可．【详解】解：（1）∵()()1111=，∴1的有理化因式是1；（22243743--==--（3）∵2a===，2b=-，∴a和b互为相反数；（4）)1 ++⨯=)11⨯=)11=20201-=2019，故原式的值为2019.【点睛】本题考查了互为有理化因式的定义及分母有理化的方法，并考查了利用分母有理化进行计算及探究相关式子的规律，本题属于中档题．23．已知m，n满足m4n=3+.【答案】12015【解析】【分析】由43m n+=2﹣2）﹣3＝0，将，代入计算即可．【详解】解：∵4m n+＝3，)22﹣2）﹣3＝0，）2﹣23＝0，+13）＝0，＝﹣13，∴原式＝3-23+2012＝12015．【点睛】本题主要考查二次根式的混合运算，解题的关键是熟练掌握完全平方公式的运用及二次根式性质．24．小明在解决问题：已知2a2﹣8a+1的值，他是这样分析与解的：∵=2∴a﹣2=∴（a﹣2）2=3，a2﹣4a+4=3∴a2﹣4a=﹣1∴2a2﹣8a+1=2（a2﹣4a）+1=2×（﹣1）+1=﹣1请你根据小明的分析过程，解决如下问题：（1（2）若，求4a2﹣8a+1的值．【答案】（1）9；（2）5．【解析】试题分析：（1）此式必须在把分母有理化后才能实现化简，即各分式分子分母同乘以一个因式，使得1===.(2)先对a1，若就接着代入求解，计算量偏大．模仿小明做法，可先计算2(1)a-的值，就能较为简单地算出结果；也可对这个二次三项式进行配方，再代入求值．后两种方法都比直接代入计算量小很多.解：（1）原式=1)+++⋯（2）∵1a===，解法一：∵22(1)11)2a -=-= ， ∴2212a a -+= ，即221a a -=∴原式=24(2)14115a a -+=⨯+= 解法二∴ 原式=24(211)1a a -+-+24(1)3a =--211)3=--4235=⨯-=点睛：（1得22=-=-a b ，去掉根号，实现分母有理化.（2）当已知量为根式时，求这类二次三项式的值，直接代入求值，计算量偏大，若能巧妙利用完全平方公式或者配方法，计算要简便得多.25．先化简，再求值：a ，其中【答案】2a-1，【分析】先根据二次根式的性质进行化简，再代入求值即可． 【详解】解：1a =-∴原式=1a a --=21a -当1a =-∴原式=(211-=1-【点睛】此题主要考查化简求值，正确理解二次根式的性质是解题关键．26．先化简，再求值：2443(1)11m m m m m -+÷----，其中2m =.【答案】22mm-+ 1． 【解析】分析：先根据分式的混合运算顺序和运算法则化简原式，再将m 的值代入计算可得．详解：原式=221m m --（）÷（31m -﹣211m m --）=221m m --（）÷241m m --=221m m --（）•122m m m --+-（）（） =﹣22m m -+=22m m-+当m ﹣2时，原式===﹣1+=1．点睛：本题主要考查分式的化简求值，解题的关键是掌握分式的混合运算顺序和运算法则．27．先化简，再求值：221()a ba b a b b a-÷-+-，其中a =2b =- 【答案】1a b -+，12-． 【分析】先把分式进行化简，得到最简分式，然后把a 、b 的值代入计算，即可得到答案． 【详解】 解：原式1()()a b a b aa b a b b a b b--=⨯-⨯+-+()()a b a b a b b a b -=--++()b bb a =-+1a b=-+，当a =2b =原式12==-．【点睛】本题考查了二次根式的混合运算，分式的化简求值，分式的混合运算，解题的关键是熟练掌握运算法则进行解题．28．计算：（1）-（2）【答案】（1）21【分析】（1）先把二次根式化为最简二次根式，然后合并即可；（2）先利用二次根式的乘除法则运算，再合并即可．【详解】解：（1）原式==（2）原式3+21==．【点睛】本题考查二次根式的混合运算：在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】根据二次根式的性质得出5-x≥0，求出即可．【详解】==-=-，|5|5x x∴5-x≥0，解得：x≤5，故选D．【点睛】本题考查了二次根式的性质的应用，注意：当a≥0，当a≤0．2．A解析：A【分析】a≥0）的式子叫做二次根式，据此可得结论．【详解】解：A 是二次根式，符合题意； B是三次根式，不合题意；C 、当x ＜0D 、x 属于整式，不合题意； 故选：A ． 【点睛】此题考查二次根式的定义，关键是根据二次根式的定义理解被开方数是非负数．3．D解析：D 【分析】依据单项式乘以单项式、单项式除以单项式以及二次根式的加法法则对各项分别计算出结果，再进行判断即可得到结果． 【详解】A. 2321526()b a b a b a---⋅=，故选项A 错误；B. （3xy ）2÷（xy ）=9xy ，故选项B 错误；C 错误； D. 2x •3x 5=6x 6，正确． 故选：D ． 【点睛】此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．4．B解析：B 【分析】根据二次根式的被开方数是非负数，且分母不能为零，可得答案． 【详解】有意义，得： 20x +>，解得：2x >-． 故选：B ． 【点睛】本题考查了二次根式有意义的条件，利用被开方数是非负数，分母不能为零得出不等式是解题关键．5．A解析：A【解析】【分析】已知a 2+b 2=6ab ，变形可得（a+b ）2=8ab ，（a-b ）2=4ab ，可以得出（a+b ）和（a-b ）的值，即可得出答案． 【详解】∵a 2+b 2=6ab ， ∴（a+b ）2=8ab ，（a-b ）2=4ab ， ∵a ＞b ＞0，∴∴a b a b +-= 故选A.【点睛】本题考查了分式的化简求值问题，观察式子可以得出应该运用完全平方式来求解，要注意a 、b 的大小关系以及本身的正负关系．6．C解析：C 【解析】故选C ．点睛：此题主要考查了二次根式的化简，解题关键是利用分数的通分求和，然后把其分母有理化即可求解，比较简单，但是易出错，是常考题.7．B解析：B 【分析】首先根据二次根式有意义的条件求得a 、b 的取值范围，然后再利用二次根式的性质进行化简即可 【详解】2202a a aa a +-∴+<∴<-a a ∴==•=-故选B【点睛】本题考查了二次根式的性质及化简，解题的关键是根据二次根式有意义的条件判断字母的取值范围．本题需要重点注意字母和式子的符号．8．B解析：B【解析】【分析】先把多项式化简为|x-4|-|1-x|，然后根据x的取值范围分别讨论，求出符合题意的x的值即可．【详解】-=|x-4|-|1-x|，解：原式1x当x≤1时，此时1-x≥0，x-4＜0，∴（4-x）-（1-x）=3，不符合题意，当1≤x≤4时，此时1-x≤0，x-4≤0，∴（4-x）-（x-1）=5-2x，符合题意，当x≥4时，此时x-4≥0，1-x＜0，∴（x-4）-（x-1）=-3，不符合题意，∴x的取值范围为：1≤x≤4故选B．【点睛】本题主要考查绝对值及二次根式的化简，要注意正负号的变化，分类讨论．9．D解析：D【解析】不是同类二次根式，因此不能计算，故不正确.根据同类二次根式，可知，故不正确；根据二次根式的性质，可知，故不正确；==，故正确.3故选D.10．B解析：B【分析】根据二次根式有意义的条件以及二次根式的乘法进行分析即可得答案.【详解】-=，x30=，=0∴x=-2或x=3，又∵2030x x +≥⎧⎨-≥⎩， ∴x=3，故选B.【点睛】本题考查了二次根式的乘法以及二次根式有意义的条件，熟练掌握相关知识是解题的关键.二、填空题11．【分析】利用二次根式有意义的条件和分式中分母不为零，即可完成.【详解】根据题意，解得：①当时，解得：即：①当时，解得：即：故自变量x 的取值范围为【点睛】 解析：11,022x x -≤≤≠ 【分析】利用二次根式有意义的条件和分式中分母不为零，即可完成.【详解】根据题意，220x x +≠解得：0,2x x ≠≠-12||0x -≥①当0x >时，120x -≥ 解得：12x ≤ 即：102x <≤①当0x <时，120x +≥解得：21x ≥-即：102x -≤< 故自变量x 的取值范围为11,022x x -≤≤≠ 【点睛】 本题考查二次根式以及分式有意义的条件，熟练掌握分类讨论和解不等式组是解题关键. 12．13【解析】【分析】由得a+b=2ab ，然后再变形，最后代入求解即可.【详解】解：∵∴a+b=2ab∴故答案为13.【点睛】本题考查了已知等式求代数式的值，解答的关键是通过变形找解析：13【解析】【分析】 由112a b +=得a+b=2ab ，然后再变形535a ab b a ab b++-+，最后代入求解即可. 【详解】 解：∵112a b+= ∴a+b=2ab ∴()5353510ab 3===132ab a b ab a ab b ab a ab b a b ab ab+++++-++-- 故答案为13.【点睛】 本题考查了已知等式求代数式的值，解答的关键是通过变形找到等式和代数式的联系. 13．【分析】根据=，将原式进行拆分，然后合并可得出答案．【详解】解：原式==．故答案为．【点睛】此题考查了二次根式的混合运算，解答本题的关键是将原式进行拆分，有一定的技巧性，注意仔细观【分析】-，将原式进行拆分，然后合并可得出答案．【详解】解：原式===【点睛】此题考查了二次根式的混合运算，解答本题的关键是将原式进行拆分，有一定的技巧性，注意仔细观察．14．【解析】【分析】用换元法代替两个带根号的式子，得出m、n的关系式，解方程组求m、n的值即可．【详解】设m＝，n＝，那么m−n＝2①，m2＋n2＝()2＋()2＝34②．由①得，m＝2解析：13【解析】【分析】用换元法代替两个带根号的式子，得出m、n的关系式，解方程组求m、n的值即可．【详解】设m n那么m−n ＝2①，m 2＋n 2＝2＋2＝34②．由①得，m ＝2＋n ③，将③代入②得：n 2＋2n−15＝0，解得：n ＝−5（舍去）或n ＝3，因此可得出，m ＝5，n ＝3（m≥0，n≥0）．n ＋2m ＝13．【点睛】此题考查二次根式的减法，本题通过观察，根号里面未知数的系数为相反数，可通过换元法求解．15．【分析】分别求出甲，乙容器中原溶液中纯果汁的含量，再求出mkg 溶液中纯果汁的含量，最后利用混合后果汁的浓度相等列出关系式，求出m 即可．【详解】解：根据题意，甲容器中纯果汁含量为akg ，乙容器【分析】分别求出甲，乙容器中原溶液中纯果汁的含量，再求出mkg 溶液中纯果汁的含量，最后利=，求出m 即可．【详解】， 甲容器倒出mkg 果汁中含有纯果汁makg ，乙容器倒出mkg 果汁中含有纯果汁mbkg ，，=，整理得，-6b =5ma -5mb ，∴（a -b ）=5m （a -b ），∴m =5．故答案为：5【点睛】本题考查二次根式的应用，能够正确理解题意，化简二次根式是解题的关键．16．【分析】根据题意可知，代入原函数即可解答.【详解】因为函数，所以当时，．【点睛】本题主要考查了代数式求值问题，熟练掌握相关知识点以及二次根式的运算是解题关键.解析：2+【分析】根据题意可知1x=，代入原函数即可解答.【详解】因为函数1xf xx，所以当1x=时，211()2221f x．【点睛】本题主要考查了代数式求值问题，熟练掌握相关知识点以及二次根式的运算是解题关键. 17．【解析】【分析】把带根号的一项移项后平方，整理后再平方，然后整理即可得解.【详解】移项得，两边平方得，整理得，两边平方得，所以，两边除以400得，1.故答案为1.【点睛】解析：【解析】把带根号的一项移项后平方，整理后再平方，然后整理即可得解.【详解】10=-两边平方得，()()22223=1003x y x y ++--+整理得，253x =- 两边平方得，22225150225256251509x x y x x -++=-+ 所以，221625400x y +=两边除以400得，222516x y +=1. 故答案为1.【点睛】本题考查了非负数的性质，此类题目难点在于把两个算术平方根通过移项分到等式左右两边.18．3【解析】【分析】先根据二次根式有意义的条件得出x+y 的值，再根据非负数的性质列出关于x ，y ，m 的方程组，求出m 的值，进而可得出结论．【详解】依题意得：，解得：x=1，y=1，m ＝5，∴3解析：3【解析】【分析】先根据二次根式有意义的条件得出x +y 的值，再根据非负数的性质列出关于x ，y ，m 的方程组，求出m 的值，进而可得出结论．【详解】依题意得：35302302x y m x y m x y +--=⎧⎪+-=⎨⎪+=⎩，解得：x =1，y =1，m ＝5，∴==3．故答案为3．【点睛】 本题考查了二次根式有意义得条件及非负数的性质，熟知二次根式具有非负性是解答此题的关键．19．3∵ =，∴=（a-2）2==3，故答案为3.解析：3【解析】∵a =∴244a a -+=（a-2）2=()222+=3， 故答案为3.20．4a【解析】【分析】根据二次根式乘法法则进行计算即可得.【详解】===4a ，故答案为4a.【点睛】本题考查了二次根式的乘法，熟练掌握二次根式乘法法则是解题的关键.解析：4a【解析】【分析】根据二次根式乘法法则进行计算即可得.)0a ≥===4a ，故答案为4a.【点睛】本题考查了二次根式的乘法，熟练掌握二次根式乘法法则是解题的关键.三、解答题21．无22．无23．无24．无25．无26．无27．无28．无。

二次根式专题测试题一、单选题1．（2023·湖南·统考中考真题）若代数式1x -在实数范围内有意义，则x 的取值范围是( ) A ．x <1B ．x ≤1C ．x >1D ．x ≥12．（2023·内蒙古通辽·统考中考真题）二次根式1x -在实数范围内有意义，则实数x 的取值范围在数轴上表示为（ ） A ． B ． C ．D ．3．（2023·辽宁大连·统考中考真题）下列计算正确的是（ ） A ．()22= B ．233356+= C ．842= D ．()3232623-=-4．（2023·山东·统考中考真题）若代数式2xx -有意义，则实数x 的取值范围是（ ）A ．2x ≠B ．0x ≥C ．2x ≥D ．0x ≥且2x ≠5．（2023·湖北荆州·统考中考真题）已知()()25353k =+⋅-，则与k 最接近的整数为（ ） A ．2B ．3C ．4D ．56．（2023·河北·统考中考真题）若27a b ==，，则2214a b=（ ） A ．2B ．4C ．7D ．27．（2023·天津·统考中考真题）2sin 452︒+的值等于（ ）A ．1B ．2C ．3D ．2二、填空题三、解答题二次根式专题测试题解析一、单选题1．（2023·湖南·统考中考真题）若代数式1x-在实数范围内有意义，则x的取值范围是()A．x<1 B．x≤1C．x>1 D．x≥1【答案】D【分析】根据二次根式有意义的条件列出关于x的不等式，求出x的取值范围即可．【详解】解：由题意得，x－1≥0，解得x≥1．故选：D．【点睛】本题主要考查二次根式有意义的条件，解题的关键是掌握要使二次根式有意义，其被开方数应为非负数．2．（2023·内蒙古通辽·统考中考真题）二次根式1x-在实数范围内有意义，则实数x的取值范围在数轴上表示为（）A．B．C．D．【答案】C【分析】根据被开方数大于等于0列不等式计算即可得到x的取值范围，然后在数轴上表示即可得解．【详解】解：根据题意得10x -≥， 解得1x ≤，在数轴上表示如下：故选：C ．【点睛】本题考查了二次根式有意义的条件，不等式的解法，以及在数轴上表示不等式的解集，理解二次根式有意义的条件是解题关键． 3．（2023·辽宁大连·统考中考真题）下列计算正确的是（ ） A ．()22= B ．233356+= C ．842= D ．()3232623-=-【答案】D【分析】根据零指数幂，二次根式的加法以及二次根式的性质，二次根式的混合运算进行计算即可求解． 【详解】解：A. ()021=，故该选项不正确，不符合题意；B. 233353+=，故该选项不正确，不符合题意；C. 822=，故该选项不正确，不符合题意；D.()3232623-=-，故该选项正确，符合题意；故选：D ．【点睛】本题考查了零指数幂，二次根式的加法以及二次根式的性质，二次根式的混合运算，熟练掌握二次根式的运算法则是解题的关键． 4．（2023·山东·统考中考真题）若代数式2xx -有意义，则实数x 的取值范围是（ ）A ．2x ≠B ．0x ≥C ．2x ≥D ．0x ≥且2x ≠【答案】D二、填空题x为正整数，∴可取x故答案为：【点睛】本题考查了二次根式有意义的条件，熟知根号下的式子小于零时，二次三、解答题。

第3讲分式及二次根式 2023年中考数学一轮复习专题训练（浙江专用）一、单选题1．（2022·江北模拟）无论x取什么数，总有意义的代数式是（）A．√x2B．4xx3+1C．1(x−2)2D．√x+32．（2022·浦江模拟）若分式1x−1有意义，则x的取值范围是（）A．x>1B．x>2C．x≠0D．x≠13．（2022·平阳模拟）若分式x−2x−3的值为0，则x的值为（）A．-3B．-2C．0D．2 4．（2022·慈溪模拟）若二次根式√1−x在实数范围内有意义，则下列各数中，x 可取的值是()A．4B．πC．√2D．1 5．（2022·北仑模拟）若二次根式√3−x在实数范围内有意义，则x的取值范围是（）A．x≠3B．x≥3C．x≤3D．x<3 6．（2022·慈溪模拟）下列计算正确的是()A．22+23=25B．23−22=2C．23⋅22=25D．2−1=−27．（2022·定海模拟）对于以下四个命题：①若直角三角形的两条边长与3与4，则第三边的长是5；②(√a)2=a；③若点P(a，b)在第三象限，则点Q(−a，−b)在第一象限；④两边及其第三边上的中线对应相等的两个三角形全等，正确的说法是（）A．只有①错误，其他正确B．①②错误，③④正确C．①④错误，②③正确D．只有④错误，其他正确8．（2022·宁波模拟）二次根式√x−3中字母x的取值范围是（）A．x＞3B．x≠3C．x≥3D．x≤39．（2022·洞头模拟）计算2aa+2−a−22+a的结果为（）A．a+2B．a−2C．1D．a−2a+210．（2021·北仑模拟）要使代数式√x−1有意义，x的取值应满足() A．x≥1B．x>1C．x≠1D．x≠0二、填空题11．（2022·台州）如图的解题过程中，第①步出现错误，但最后所求的值是正确的，则图中被污染的x的值是．先化简，再求值：3−xx−4+1，其中x=解：原式=3−xx−4⋅(x−4)+(x−4)…①=3−x+x−4=−112．（2022·丽水）如图，标号为①，②，③，④的矩形不重叠地围成矩形PQMN.已知①和②能够重合，③和④能够重合，这四个矩形的面积都是5，AE=a，DE=b，且a>b.（1）若a，b是整数，则PQ的长是；（2）若代数式a2﹣2ab﹣b2的值为零，则S四边形ABCDS矩形PQMN的值是．13．（2022·宁波模拟）若二次根式√3+x在实数范围内有意义，则x的取值范围是.14．（2022·衢江模拟）二次根式√x−4中字母x的取值范围是.15．（2022·温州）计算：x 2+xyxy+xy−x2xy=．16．（2022·金华）若分式2x−3的值为2，则x的值是.17．（2022·永康模拟）若分式1x−3有意义，则x的取值范围为．18．（2022·湖州）当a=1时，分式 a+1a 的值是 . 19．（2022·萧山模拟）计算：√3×√2= .20．（2022·宁波模拟）分式 2x−6x+1有意义的条件是 .三、计算题21．（2022·北仑模拟）先化简，直求值：(2a −1)⋅aa 2−4，共中a ＝√2−2.22．（2022·温州模拟）（1）计算：6÷(−3)+√4−8×2−2.（2）化简：2x x 2−4−1x−2.23．（2022·衢州模拟）计算：（1）−12+20180−(12)−1+√83； （2）a 2−b 2a−b ÷a+b 2a−2b.24．（2022·龙湾模拟）（1）计算： 2−1−(√5−1)0+|−32|−√273 ． （2）化简： a 2+3a 2−a +3a−a2 ．25．（2022·瓯海模拟）（1）计算：（﹣2）2×32+|﹣5|﹣√9．（2）化简：a 2a 2−2a +42a−a 2． 四、解答题26．（2022·衢州模拟）先化简，再求值：（1x−1−1x+1）÷x+2x 2−1，然后从﹣1，1，3中选择适当的数代入求值.27．（2022·台州模拟）先化简，再求值：（1﹣1a ）÷a 2−1a，其中a ＝2020.28．（2022·衢州模拟）先化简4m 2−4−1m−2，从-2，-1，0，2四个数中选取一个合适的数代入求值.29．（2022·余杭模拟）化简： 3x−1+x−31−x 2小明的解答如下： 原式= 3x−1−x−3x 2−1=（x2-1）3x−1-（x 2-1）x−3x2−1=3（x+1）-（x-3）=2x+6小明的解答正确吗？如果不正确，请写出正确的解答过程．30．（2022·江干模拟）化简：xx−1−1x+1−1.小马的解答如下，小马的解答正确吗？如果不正确，写出正确的解答.解：xx−1−1x+1−1=x(x+1)−(x−1)−1=x2+x−x+1−1=x2答案解析部分1．【答案】A【解析】【解答】解：A 、无论x 取任何数，√x 2有意义，A 选项符合题意； B 、x≠-1时，4xx 3+1有意义，B 选项不符合题意；C 、x≠2时，1（x−2）2有意义，C 选项不符合题意； D 、x≥-3时，√x +3有意义，D 选项不符合题意. 故答案为：A.【分析】根据二次根式有意义的条件，即被开方数为非负数，及分式有意义的条件，即分母不为零，逐项进行判断即可.2．【答案】D【解析】【解答】解：∵分式1x−1有意义，∴x −1≠0，解得x ≠1， 故答案为：D.【分析】分式有意义的条件：分母不为0，据此解答即可.3．【答案】D【解析】【解答】解：∵分式x−2x−3的值为0∴x ﹣2＝0，x ﹣3≠0， ∴x ＝2. 故答案为：D.【分析】根据分式值为0的条件可得x-2＝0，x-3≠0，求解即可.4．【答案】D【解析】【解答】解：由题意得1-x≥0 解之：x≤1. ∴x 可以为1. 故答案为：D.【分析】利用二次根式有意义的条件：被开方数是非负数，可求出x 的取值范围，即可求解.5．【答案】C【解析】【解答】解：要使二次根式√3−x在实数范围内有意义，必须3−x≥0，解得：x≤3.故答案为：C.【分析】根据二次根式有意义的条件是被开方数不为负数，据此可得3−x≥0，求解即可.6．【答案】C【解析】【解答】解：22+23≠25，故A不符合题意；B、23-22≠2，故B不符合题意；C、22·23=25，故C符合题意；D、2−1=12，故D不符合题意；故答案为：C.【分析】同底数幂相加减，要先算乘方，再算加法或减法，可对A，B作出判断；利用同底数幂相乘，底数不变，指数相加，可对C作出判断；利用负整数指数幂的性质，可对D作出判断.7．【答案】A【解析】【解答】解：①错误，应强调为直角三角形的两条直角边长为3与4，则第三边的长是5；②正确，隐含条件a≥0，根据二次根式的意义，等式成立；③正确，若点P（a，b）在第三象限，则a＜0，b＜0；则-a＞0，-b＞0，点Q（-a，-b）在第一象限；④正确，已知：如图，AB=A'B'，AC=A'C'，AD=A'D'，BD=CD，B'D'=C'D'，求证：△ABC≌△A'B'C'；证明：过点C作CE∥AB交AD的延长线于E，∵∠BAD=∠E，∠ABD=∠ECD，∵BD=CD，∴△ABD≌△ECD（AAS），∴AB=CE，AD=DE，过点C'作C'E'∥A'B'交A'D'的延长线于E'，同理：A'B'=C'E'，A'D'=D'E'，∵AD=A'D'，AB=A'B'，∴AE=A'E'，CE=C'E'，∵AC=A'C'，∴△ACE≌△A'C'E'（SSS），∴∠CAE=∠C'A'E'，∠E=∠E'=∠BAD=∠B'A'D'，∴∠BAC=∠B'A'C'，∴△ABC≌△A'B'C'（SAS），即：两边及第三边上的中线对应相等的两个三角形全等，正确.故答案为：A.【分析】根据勾股定理可判断①；根据二次根式有意义的条件可得a≥0，据此判断②；根据点的坐标与象限的关系可判断③；画出示意图，已知AB=A'B'，AC=A'C'，AD=A'D'，BD=CD，B'D'=C'D'，过点C作CE∥AB交AD的延长线于E，证明△ABD ≌△ECD，得到AB=CE，AD=DE，过点C'作C'E'∥A'B'交A'D'的延长线于E'，证明△ACE≌△A'C'E'（SSS），得到∠CAE=∠C'A'E'，∠E=∠E'=∠BAD=∠B'A'D'，推出∠BAC=∠B'A'C'，据此判断④.8．【答案】C【解析】【解答】解：∵√x −3，∴x-3≥0， ∴x≥3. 故答案为：C.【分析】根据二次根式被开方数为非负数，即x-3≥0，求解不等式即可得x 的取值范围.9．【答案】C【解析】【解答】解：原式=2a−a+2a+2=a+2a+2 =1.故答案为：C.【分析】直接根据同分母分式减法法则进行计算即可.10．【答案】B【解析】【解答】解：由题意得：{x −1≥0x −1≠0，解得x ＞1.故答案为：B.【分析】依据被开方数大于等于0及分母不为零，列出不等式组，求解即可.11．【答案】5【解析】【解答】解：原式=3−x x−4+x−4x−4=−1x−4∵最后所求的值是正确的∴−1x−4=-1 解之：x=5经检验：x=5是方程的解. 故答案为：5.【分析】先通分计算，再由题意可得到−1x−4=-1；然后解方程求出x 的值. 12．【答案】（1）a-b（2）3+2√2【解析】【解答】解：(1)∵①和②能够重合，③和④能够重合，AE=a ，DE=b ，∴PQ=AE+DE-2ED=a+b-2b=b ，故答案为：a-b ； (2)∵a 2- 2ab- b 2=0， ∴a 2-b 2=2ab ， 则(a-b)2=2b 2，∴a=(√2+1)b 或(1-√2)b(舍去)，∵四个矩形的面积都是5，AE=a ，DE=b ， ∴EP=5a ，EN=5b，∴S四边形ABCD S矩形PQMN=(a+b )(5a +5b )(a−b )(5b −5a)=a 2+2ab+b2a 2−2ab+b 2=a 2b2=(√2+1)2b2b2=3+2√2.故答案为：3+2√2.【分析】(1)直接根据线段和差关系，结合两组全等矩形的边相等，列式计算可得结论；(2)解关于a 的二元一次方程：a 2-2ab-b 2=0， 得到a=(√2+1)b ，根据四个矩形的面积都是5分别表示小矩形的宽，再利用含a 、b 的代数式表示S四边形ABCDS 矩形PQMN，化简后，再代入a=(√2+1)b ，即可解答.13．【答案】x≥-3【解析】【解答】解：由题意得： 3+x ≥0，解得： x ≥−3， 故答案为： x ≥−3.【分析】根据二次根式的被开方数不能为负数可得3+x≥0，求解即可.14．【答案】x≥4【解析】【解答】解：由题意，得x-4≥0， 解得：x≥4. 故答案为：x≥4.【分析】根据二次根式有意义的条件是被开方数不能为负数，可得x-4≥0，求解即可.15．【答案】2【解析】【解答】解：原式=x 2+xy+xy−x 2xy=2..故答案为：2.【分析】利用同分母分式相加，分母不变，把分子相加，然后化简即可.16．【答案】4【解析】【解答】解：∵分式2x−3的值为2，∴2x−3=2， ∴2=2x-6， ∴x=4. 故答案为：4.【分析】由分式2x−3的值为2，得2x−3=2，再解分式方程即可求出x 的值.17．【答案】x≠3【解析】【解答】解：由题意得x-3≠0 解之：x≠3. 故答案为：x≠3.【分析】利用分式有意义的条件：分母不等于0，可得到关于x 的不等式，然后求出不等式的解集.18．【答案】2【解析】【解答】解：把a=1代入分式中， ∴a+1a =1+11=2.故答案为：2.【分析】把a=1代入分式中，化简求值即可求解.19．【答案】√6【解析】【解答】解：√3×√2，=√3×2， =√6； 故答案为：√6.【分析】直接根据二次根式的乘法法则进行计算.20．【答案】x≠-1【解析】【解答】解：要使分式有意义，则x+1≠0，∴x≠-1.故答案为：x≠-1.【分析】分式有意义的条件是分母不等于零，依此列式求解，即可解答.21．【答案】解：(2a −1)⋅a a 2−4=2−a a ⋅a (a+2)(a−2)=−1a+2 当a =√2−2时，原式=1√2−2+2=1√2=−√22 【解析】【分析】对括号中的式子进行通分，对括号外分式的分母进行分解，然后约分即可对原式进行化简，接下来将a 的值代入计算即可.22．【答案】（1）解：6÷(−3)+√4−8×2−2=−2+2−8×14=−2+2−2=−2（2）解：2x x 2−4−1x−2 =2x −(x +2)(x +2)(x −2)=x −2(x +2)(x −2)=1x +2 【解析】【分析】（1）根据算术平方根的概念、负整数指数幂的运算性质及有理数的除法法则分别计算，然后计算乘法，再计算加减法即可；（2）对第一个分式的分母进行分解，然后通分，再约分即可.23．【答案】（1）解：−12+20180−(12)−1+√83 =﹣1+1﹣2+2=0；（2）解：a 2−b 2a−b ÷a+b 2a−2b=(a+b)(a−b)a−b ÷a+b 2(a−b) =(a+b)(a−b)a−b×2(a−b)a+b =2(a −b)=2a ﹣2b.【解析】【分析】（1）根据乘方、开方、零指数幂及负整数幂的性质分别h 进行计算，然后根据有理数的加减法法则算出答案即可；（2）先将分子、分母进行因式分解，再将除法转化为乘法，然后约分即可.24．【答案】（1）解：原式=12-1+32-3=-2. （2）解：原式=a 2+3a 2−a −3a 2−a=a 2a (a−1)=a a−1. 【解析】【分析】（1）根据负整数指数幂的性质、零指数幂的性质、立方根的定义进行化简，再计算加减法，即可得出答案；（2）先通分，再计算分式的减法，即可得出答案.25．【答案】（1）解：（﹣2）2×32+|﹣5|﹣√9 =4×32+5﹣3 =6+5-3=8（2）解：a 2a 2−2a +42a−a 2=a 2a(a−2)+4a(2−a)=a 2a(a −2)−4a(a −2)=a 2−4a(a −2)=(a +2)(a −2)a(a −2)=a+2a ．【解析】【分析】（1）根据有理数的乘方法则、绝对值的性质以及算术平方根的概念可得原式=4×32+5-3，然后计算乘法，再计算加减法即可； （2）对两个分式的分母进行分解，然后结合同分母分式减法法则进行计算.26．【答案】解：(1x−1−1x+1)÷x+2x 2−1=x+1−x+1(x−1)(x+1)÷x+2(x−1)(x+1)=2(x−1)(x+1)×(x−1)(x+1)x+2 =2x+2； ∵x −1≠0，x +1≠0，x +2≠0，∴x ≠±1，x ≠−2，当x =3时，2x+2=23+2=25【解析】【分析】对括号中的式子进行通分，对括号外分式的分母进行分解，然后将除法化为乘法，再约分即可对原式进行化简，接下来选择一个使分式有意义的x 的值代入计算即可.27．【答案】解：原式=a−1a ·a (a+1)(a−1)=1a+1当a=2020时，原式=12021【解析】【分析】对括号中的式子进行通分，将第二个分式的分子分解因式，同时除法化为乘法，再进行约分即可对原式进行化简，接下来将a 的值代入计算即可.28．【答案】解：原式=4(m+2)(m−2)−1m−2=4−(m +2)(m +2)(m −2)=2−m (m +2)(m −2)=−1m +2要使分式有意义，则m 2−4≠0且m −2≠0解得m≠±2，∴只能选择-1或0当m=-1时，原式=−1当m=0时，原式=−1 2【解析】【分析】对第一个分式的分母进行分解，再通分后按同分母分式的加减法进行计算，并进行约分即可对原式进行化简，然后选取一个使分式有意义的m的值代入进行计算.29．【答案】解：不正确原式＝－＝－＝＝【解析】【分析】根据分式加法法则，先通分，化为同分母的分式相加减，再进行计算，即可得出答案.30．【答案】解：不正确，正确解答如下：xx−1−1x+1−1=x(x+1)x2−1−x−1x2−1−x2−1x2−1=x2+x−x+1−x2+1x2−1=2x2−1.【解析】【分析】首先第一项的分子、分母都乘以（x+1），第二项的分子、分母都乘以（x-1），第三项的分析分母都乘以（x+1）（x-1）进行通分，然后根据同分母分式减法法则进行计算。

中考数学专题复习第六讲：二次根式【基础知识回顾】 一、二次根式式子a （ ）叫做二次根式【赵老师提醒：①次根式a 必须注意a___o 这一条件，其结果也是一个非数即：a ___o②二次根式a （a ≥o ）中，a 可以表示数，也可以是一切符合条件的代数式】二、二次根式的性质：①（a ）2= （a ≥0）= （a ≥0 ,b ≥0）(a ≥0, b ≥0)【赵老师提醒：二次根式的性质注意其逆用：如比较23和的大小，可逆用（a ）2=a(a ≥0)将根号外的整数移到根号内再比较被开方数的大小】 三、最简二次根式：最简二次根式必须同时满足条件：1、被开方数的因数是 ，因式是整式2、被开方数不含 的因数或因式 四、二次根式的运算：1、二次根式的加减：先将二次根式化简，再将 的二次根式进行合并，合并的方法同合并同类项法则相同2、二次根式的乘除：= （a ≥0 ,b ≥0）（a ≥0，b ＞0） 3、二次根式的混合运算顺序：先算 再算 最后算【赵老师提醒：1、二次根式除法运算过程一般情况下是用将分母中的根号化= = 2、二次根式混合运算过程要特别注意两个乘法公式的运用 3、二次根式运算的结果一定要化成 】 【重点考点例析】考点一：二次根式有意义的条件（a ≥o ）（a ＜o ）例1 （2012•潍坊）如果代数式43x -有意义，则x 的取值范围是（ ） A ．x ≠3 B ．x ＜3 C ．x ＞3 D ．x ≥3思路分析：根据二次根式的意义得出x-3≥0，根据分式得出x-3≠0，即可得出x-3＞0，求出即可． 解：要使代数式43x -有意义， 必须x-3＞0， 解得：x ＞3． 故选C ．点评：本题考查了二次根式有意义的条件，分式有意义的条件的应用，注意：分式B A中A ≠0，二次根式a 中a ≥0． 对应训练1．（2012•德阳）使代数式21xx -有意义的x 的取值范围是（ ） A ．x≥0 B ．x≠12 C ．x≥0且x≠12D ．一切实数 1．C1．解：由题意得：2x-1≠0，x≥0， 解得：x≥0，且x≠12， 故选：C ．考点二：二次根式的性质例2 （2012•张家界）实数a 、b 在轴上的位置如图所示，且|a|＞|b|，则化简2||a a b -+的结果为（ ）A ．2a+bB ．-2a+bC ．bD ．2a-b思路分析：现根据数轴可知a ＜0，b ＞0，而|a|＞|b|，那么可知a+b ＜0，再结合二次根式的性质、绝对值的计算进行化简计算即可． 解：根据数轴可知，a ＜0，b ＞0，原式=-a-[-（a+b ）]=-a+a+b=b ． 故选C ．点评：本题考查了二次根式的化简和性质、实数与数轴，解题的关键是注意开方结果是非负数、以及绝对值结果的非负性． 对应训练为 ． 1．-b2．解：∵由数轴可知：b ＜0＜a ，|b|＞|a|，=|a+b|+a =-a-b+a =-b ，故答案为：-b ．考点三：二次根式的混合运算思路分析：利用二次根式的分母有理化以及分数指数幂的性质和负整数指数幂的性质，分别化简，进而利用有理数的混合运算法则计算即可．=3． 点评：此题主要考查了二次根式的混合运算以及负整数指数幂的性质，熟练利用这些性质将各式进行化简是解题关键． 对应训练4=+考点四：与二次根式有关的求值问题222)(1)(x x x ++-思路分析：先根据分式混合运算的法则把原式进行化简，再把x 的值代入进行计算即可．2(1)1)4x x x+0，(1)1)4x x x +=本题考查的是二次根式及分式的化简求值，解答此题的关键是当1，此题难度不大．对应训练A ．0B ．25C ．50D ．804．D分析：根据平方差公式求出1142-642=（114+64）×（114-64）=178×50，再提出50得出50×（178-50）=50×128，分解后开出即可．=80， 故选D ．点评：本题考查了平方差公式，因式分解，二次根式的运算等知识点的应用，解此题的关键是能选择适当的方法进行计算，本题主要考查学生的思维能力和应变能力，题目比较好，是一道具有代表性的题目．【聚焦山东中考】1．（2012•泰安）下列运算正确的是（ ）A 5=-B ．21()164--=C ．x 6÷x 3=x 2 D ．（x 3）2=x 5 1．B ．2.（2012•临沂）计算：= ． 2．03．7【备考真题过关】一、选择题A ．x ＞0B ．x≥-2C ．x≥2D ．x≤2 1．DA B ．5 C ．2 D ．22．AA ．3BC ．D ．3．C ．A ．5＜m ＜6B ．4＜m ＜5C ．-5＜m ＜-4D ．-6＜m ＜-5 4．A即5＜m ＜6， 故选A ．5．（2012•南充）下列计算正确的是（ ）A ．x 3+x 3=x 6B ．m 2•m 3=m 6C ．3=D = 5．D6．（2012•黔东南州）下列等式一定成立的是（ ）A ．945-=B ．5315⨯=C ．93=±D ．2(9)9--=6．B7．（2012•广西）使式子有意义的x 的取值范围是（ ）A ． x ≥﹣1B ． ﹣1≤x ≤2C ． x ≤2D ．﹣1＜x ＜2 考点： 二次根式有意义的条件。

专题05二次根式1．（2023·湖南·统考中考真题）若代数式1x 在实数范围内有意义，则x 的取值范围是()A ．x <1B ．x ≤1C ．x >1D ．x ≥12．（2023·内蒙古通辽·统考中考真题）二次根式1x 在实数范围内有意义，则实数x 的取值范围在数轴上表示为（）A ．B ．C ．D ．3．（2023·辽宁大连·统考中考真题）下列计算正确的是（）A ．22 B ．233356 C ．842D ．32326234．（2023·山东·统考中考真题）若代数式2xx 有意义，则实数x 的取值范围是（）A ．2x B ．0x C ．2x D ．0x 且2x 5．（2023·湖北荆州·统考中考真题）已知25353k，则与k 最接近的整数为（）A ．2B ．3C ．4D ．56．（2023·河北·统考中考真题）若27a b ，，则2214a b（）A ．2B ．4C ．7D ．27．（2023·天津·统考中考真题）2sin 452的值等于（）A ．1B ．2C ．3D ．28．（2023·山东临沂·统考中考真题）设15455m ，则实数m 所在的范围是（）A ．5m B ．54m C ．43m D ．3m 9．（2023·湖南·统考中考真题）对于二次根式的乘法运算，一般地，有a b ab ．该运算法则成立的条件是（）A ．0,0a b B ．0,0a b C ．0,0a b D ．0,0a b 10．（2023·山东烟台·统考中考真题）下列二次根式中，与2是同类二次根式的是（）三、解答题。

2023年中考数学一轮复习专题练习八下 第12章 二次根式一、 选择题1. 9的平方根是A ．±3B ．3C ．±4．5D ．4．5 2. 使代数式12-x x 有意义的x 的取值范围是（ ） A ．x≥0 B ．x≠21 C ．x≥0且x≠21 D ．一切实数 3. 下列计算正确的是（ ）A ．a 6÷a 2＝a 3B ．（a 3）2＝a 2C ．25＝±5D ．38-＝－24. 若5＝a ，17＝b ，则85.0的值用a. b 可表示为（ ） A ．10b a + B ．10a b - C ．10ab D ．ab 5. 能使等式22-=-x x x x 成立的x 的取值范围是 （ ） A ．x≠2 B ．x≥0 C ．x ＞2 D ．x≥2 6. 下列计算正确的是（ ）A ．0(2)0-=B ．239-=-C 3=D =7. 已知实数x ，y 满足8|4|-+-y x ＝0，则以x ，y 的值为两边长的等腰三角形的周长是（ ）A ．20或16B ．20C ．16D ．以上答案均不对8. 如果ab>0，a+b<0，给出下列各式：①b a b a =，②1=•a b b a ，③b b a ab -=÷，那么其中正确的是（ ）A ．①②B ．②③C ．①③D ．①②③二、填空题9. x 应满足的条件是 ＿＿＿＿＿＿＿ 。

10. 若y ＝22-+-x x ＋4，则xy 的平方根为＿＿＿＿＿＿＿。

11. 当x 满足＿＿＿＿＿＿时，0)3(11--++x x x 有意义。

12. 式子2x x -有意义的x 取值范围是________。

13. 若｜x ＋y ＋4｜＋2)2(-x ＝0，则3x ＋2y ＝＿＿＿＿＿。

14. 若y ＝x x x 21)1(122-+-+-，则（x ＋y ）2008＝＿＿＿＿＿。

15. 实数a. b 在数轴上的位置如图所示，则化简a b a ++2)(的结果为＿＿＿＿。

中考数学常考考点专题之二次根式测试卷一．选择题（共12小题）1．下列根式中与√2是同类二次根式的是（）A．√5B．√6C．√7D．√8 2．若二次根式√7−x有意义，则下列各数符合要求的是（）A．8B．9C．10D．4 3．若3√2□√2=3，则运算符号“□”表示（）A．+B．﹣C．×D．÷4．使式子√x−1有意义，x的取值范围是（）A．x＞1B．x＝1C．x≥1D．x≤15．若√x+2有意义，则实数x的取值范围为（）A．x≥﹣2B．x＞﹣2C．x≠﹣2D．x＞2 6．下列运算正确的是（）A．√(−2)2=−2B．(13)−1=−13C．（a2）3＝a6D．a8÷a4＝a2（a≠0）7．下列计算正确的是（）A．√2+√3=√5B．2√3−√3=2C．√2×√3=√6D．√12÷3=2 8．不等式x﹣1＜√5的正整数解的个数有（）A．3个B．4个C．5个D．6个9．下列运算正确的是（）A．√3+2√3=2√6B．（﹣a2）3＝a6C．12a +1a=23aD．13ab÷b3a=1b210．在函数y=√x+12x−1中，自变量x的取值范围是（）A．x≥﹣1B．x＞﹣1且x≠12C．x≥﹣1且x≠12D．x≤﹣1且x≠1211．下列运算正确的是（）A．（√3）2＝3B．3√2−√2=3C．2﹣1＝﹣2D．|√2−2|=√2−2 12．下列二次根式中，与√2是同类二次根式的是（）A．√4B．√6C．√8D．√12二．填空题（共8小题）13．若二次根式√2x −1有意义，则x 的取值范围是 ．14．计算：√27−3√13= ．15．化简√18= ．16．若式子√−x +1在实数范围内有意义，则实数x 的取值范围是 ．17．若√a +√3=3√3，则a ＝ ．18．计算：√20×√5= ．19．实数m 在数轴上对应点的位置如图所示，化简：√(m −2)2= ．20．计算(√7+2)(√7−2)的结果等于 ．三．解答题（共5小题）21．（1）计算：√12+|√3−√8|−2sin45°−(√33)−1；（2）解不等式组：{2x ≤6−x x−12−x−36＞1． 22．计算：√3×(√3+2)−2tan60°+(−1)2023．23．观察下列各式：①√1+13=2√13，②√2+14=3√14；③√3+15=4√15，… （1）请观察规律，并写出第④个等式： ；（2）请用含n （n ≥1）的式子写出你猜想的规律： ；（3）请证明（2）中的结论．24．（1）计算：−14+√12×√33−(−12)−3． （2）下面是小彬同学练习整式运算的过程，请认真阅读并完成相应任务．化简：[（2x +y ）（2x ﹣y ）﹣（2x ﹣3y ）2]（﹣2y ）解：原式＝[（4x 2﹣y 2）﹣（4x 2﹣12xy +9y 2）]（﹣2y ）…第一步＝[4x 2﹣y 2﹣4x 2﹣12xy +9y 2]（﹣2y ）…第二步＝（﹣12xy +8y 2）（﹣2y ）…第三步＝6x ﹣4y …第四步任务：①以上求解步骤中，第一步运算用到的数学公式是，；②以上求解步骤中，第步开始出现错误，具体的错误是；③化简的正确结果为．25．化简：√3−√(√3−2)2，以下是小曹同学的解答过程．思考并完成以下任务．解：原式=√3−(√3−2)①；=√3−√3+2②；＝2③；任务：（1）小曹的解答过程是从第几步开始出错的，请指出错误的原因；（2）请尝试写出正确的化简过程．。

九年级数学中考总复习 二次根式及运算 专题训练题1． 计算35－25的结果是( ) A. 5 B ．2 5 C ．3 5 D ．62. 下列计算正确的是( ) A.5－3＝ 2 B ．35×23＝615C ．(22)2＝16 D.33＝13. 使二次根式x －1有意义的x 的取值范围是( )A ．x ≠1B ．x ＞1C ．x ≤1D ．x ≥14．估计7＋1的值( )A ．在1和2之间B ．在2和3之间C ．在3和4之间D ．在4和5之间 5．下列根式中，不是最简二次根式的是( ) A.10 B.8 C. 6 D. 26．当1＜a ＜2时，代数式（a －2）2＋|1－a|的值是( )A ．－1B ．1C ．2a －3D ．3－2a 7．已知y ＝2x －5＋5－2x －3，则2xy 的值为( )A ．－15B ．15C ．－152 D.1528．对于任意的正数m ，n 定义运算※为：m ※n ＝⎩⎪⎨⎪⎧m －n （m ≥n ），m ＋n （m<n ），计算(3※2)×(8※12)的结果为( )A ．2－4 6B ．2C ．2 5D ．209. 下列计算正确的是( ) A.3＋2＝ 5 B.12÷3＝2 C ．(5)－1＝ 5 D ．(3－1)2＝210. 下列四个式子中，x 的取值范围x≥2的是( ) A.x －2x －2 B.1x －2 C.x －2 D.2－x 11. 若代数式x －1x有意义，则x 的取值范围是__ __． 12．计算：27·83÷12＝__12__． 13．若两个连续整数x ，y 满足x ＜5＋1＜y ，则x ＋y 的值是__7__．14．计算(5＋3)(5－3)的结果等于__2__．15．已知x ＝5－12，则x 2＋x ＋1＝__2__． 16. 计算：(1212－13＋48)÷23＝____． 17. 计算： |22－3|－8＋18；18. 计算： (3－7)(3＋7)＋2(2－2)19. 先化简，再求值：(x 2－y x －x －1)÷x 2－y 2x 2－2xy ＋y 2，其中x ＝2，y ＝ 6.20. 已知x＝3＋1，y＝3－1，求代数式x2－y2的值．21. 观察下面的变形规律：12＋1＝2－1，13＋2＝3－2，14＋3＝4－3，15＋4＝5－4，…解答下面的问题：(1)若n为正整数，请你猜想1n＋1＋n＝____；(2)计算：(12＋1＋13＋2＋14＋3＋…＋12016＋2015)×(2016＋1)参考答案：1---10 ABDCB BABBC11. x ≥112. 1213. 714. 215. 216. 7317. 解：原式＝3－ 218. 解：原式＝2 219. 解：(x 2－y x －x －1)÷x 2－y 2x 2－2xy ＋y 2＝(x 2－y x －x 2x －x x )×（x －y ）2（x ＋y ）（x －y ）＝－y －x x ×x －y x ＋y ＝－x －y x ，把x ＝2，y ＝6代入得：原式＝－2－62＝－1＋ 3 20. 解：原式＝(x ＋y)(x －y)，∵x ＝3＋1，y ＝3－1，∴原式＝(3＋1＋3－1)(3＋1－3＋1)＝23×2＝4 321. (1) n ＋1－n(2)原式＝[(2－1)＋(3－2)＋(4－3)＋…＋(2016－2015)](2016＋1)＝(2016－1)(2016＋1)＝(2016)2－12＝2015。

专题06二次根式（24题）一、单选题1．（2024·湖南·27）A ．7B ．72C ．14D 14【答案】D【分析】此题主要考查了二次根式的乘法，正确计算是解题关键．直接利用二次根式的乘法运算法则计算得出答案．【详解】解：2714⨯=，故选：D2．（2024·内蒙古包头·2296-所得结果是（）A ．3B 6C ．35D ．35±【答案】C【分析】本题考查化简二次根式，根据二次根式的性质，化简即可．【详解】解：229681364535-=-==；故选C ．3．（2024·云南·x x 的取值范围是（）A ．0x >B ．0x ≥C ．0x <D ．0x ≤【答案】B【分析】本题主要考查了二次根式有意义的条件．根据二次根式有意义的条件，即可求解．【详解】解：∵式子x 在实数范围内有意义，∴x 的取值范围是0x ≥．故选：B4．（2024·黑龙江绥化·23m -有意义，则m 的取值范围是（）A ．23m ≤B ．32m ≥-C ．32m ≥D ．23m ≤-【答案】C【分析】本题考查了二次根式有意义的条件，根据题意可得230m -≥，即可求解．5．（2024·四川乐山·中考真题）已知12x <<2x +-的结果为（）A ．1-B ．1C ．23x -D ．32x-6．（2024·重庆·中考真题）已知m =m 的范围是（）A ．23m <<B ．34m <<C ．45m <<D ．56m <<7．（2024·江苏盐城·，设其面积为2cm S ，则S 在哪两个连续整数之间（）A ．1和2B ．2和3C ．3和4D ．4和5【答案】C【分析】本题主要考查无理数的估算，二次根式的乘法，先计算出矩形的面积S ，再利用放缩法估算无理数大小即可．【详解】解：2510S =⨯=，91016<<，∴91016<<，∴3104<<，即S 在3和4之间，故选：C ．8．（2024·安徽·中考真题）下列计算正确的是（）A ．356a a a +=B ．632a a a ÷=C ．()22a a -=D 2a a=【答案】C【分析】题目主要考查合并同类项、同底数幂的除法、积的乘方运算、二次根式的化简，根据相应运算法则依次判断即可【详解】解：A 、3a 与5a 不是同类项，不能合并，选项错误，不符合题意；B 、633a a a ÷=，选项错误，不符合题意；C 、()22a a -=，选项正确，符合题意；D 、当0a ≥时，2a a =，当0a <时，2a a =-，选项错误，不符合题意；故选：C9．（2024·重庆·1223的值应在（）A ．8和9之间B ．9和10之间C ．10和11之间D ．11和12之间【答案】C【分析】本题考查的是二次根式的乘法运算，无理数的估算，先计算二次根式的乘法运算，再估算即可．【详解】解：∵()1223266+=+，而424265<=<，∴1026611<+<，故答案为：C10．（2024·四川德阳·，按以下方式进行排列：则第八行左起第1个数是（）A ．B ．CD ．二、填空题11．（2024·江苏连云港·x 的取值范围是．12．（2024·江苏扬州·有意义，则x 的取值范围是．13．（2024·贵州·23的结果是．【答案】6【分析】利用二次根式的乘法运算法则进行计算．【详解】解：原式=23⨯=6，故答案为：6．【点睛】本题考查二次根式的乘法运算，掌握二次根式乘法的运算法则a b ab ⋅=（a ≥0，b ＞0）是解题关键．14．（2024·北京·9x -x 的取值范围是．【答案】9x ≥【分析】根据二次根式有意义的条件，即可求解．【详解】解：根据题意得90x -≥，解得：9x ≥．故答案为：9x ≥【点睛】本题主要考查了二次根式有意义的条件，熟练掌握二次根式的被开方数为非负数是解题的关键．15．（2024·天津·中考真题）计算()111111-+的结果为．【答案】10【分析】利用平方差公式计算后再加减即可．【详解】解：原式11110=-=．故答案为：10．【点睛】本题考查了二次根式的混合运算，掌握二次根式的混合运算法则及平方差公式是解题的关键．16．（2024·四川德阳·()23-＝．【答案】3【分析】根据二次根式的性质“2a a =”进行计算即可得．【详解】解：()2333-=-=，故答案为：3．【点睛】本题考查了化简二次根式，解题的关键是掌握二次根式的性质．17．（2024·黑龙江大兴安岭地·中考真题）在函数32y x =+中，自变量x 的取值范围是．【答案】3x ≥/3x≤【分析】本题主要考查函数自变量取值范围，分别根据二次根式有意义的条件和分式有意义的条件列出不等式求解即可．【详解】解：根据题意得，30x -≥，且20x +≠，解得，3x ≥，故答案为：3x ≥．18．（2024·山东烟台·x 的取值范围为．【答案】1x >/1x<【分析】本题考查代数式有意义，根据分式的分母不为0，二次根式的被开方数为非负数，进行求解即可．【详解】解：由题意，得：10x ->，解得：1x >；故答案为：1x >．19．（2024·山东威海·=．20．（2024·黑龙江齐齐哈尔·中考真题）在函数2y x =+中，自变量x 的取值范围是．【答案】3x >-且2x ≠-【分析】本题考查了求自变量的取值范围，根据二次根式有意义的条件和分式有意义的条件列出不等式组解答即可求解，掌握二次根式有意义的条件和分式有意义的条件是解题的关键．【详解】解：由题意可得，3020x x +>⎧⎨+≠⎩，解得3x >-且2x ≠-，故答案为：3x >-且2x ≠-．三、解答题21．（2024·内蒙古包头·中考真题）（1）先化简，再求值：()()2121x x +-+，其中22x =（2）解方程：2244x xx x --=．【答案】（1）21x -，7；（2）3x =【分析】本题考查了整式的运算，二次根式的运算，解分式方程等知识，解题的关键是：（1）先利用完全平方公式、去括号法则化简，然后把x 的值代入计算即可；（2）先去分母，去括号，移项，合并同类项，系数化1，检验，解分式方程即可．【详解】解：（1）()()2121x x +-+22122x x x =++--21x =-，当22x =时，原式()22217=-=；（2）2244x x x x --=--去分母，得()224x x x ---=，解得3x =，把3x =代入43410x -=-=-≠，∴3x =是原方程的解．22．（2024·上海·中考真题）计算：1021|13|24(13)23-++--+．【答案】26【分析】本题考查了绝对值，二次根式，零指数幂等，掌握化简法则是解题的关键．先化简绝对值，二次根式，零指数幂，再根据实数的运算法则进行计算．【详解】解：121|13|24(13)23-++--+2331261(23)(23)-=-++-+-3126231=-++--26=．23．（2024·甘肃·318122【答案】0【分析】根据二次根式的混合运算法则计算即可．24．（2024·河南·中考真题）（1(01；（2）化简：231124a a a +⎛⎫+÷ ⎪．。