高中数学复习不等式人教版

人教版高一必修一数学不等式解法步骤高中数学不等式是数学学科的一个重要部分，不等式在实际生活和科学技术领域中都有着广泛的应用。

在高中必修一数学课程中，学生需要学习不等式的解法步骤，掌握不等式的基本概念和解题方法，提高解决实际问题的能力。

人教版高一必修一数学不等式解法步骤主要包括以下内容：1.不等式的基本概念和性质：首先，学生需要了解不等式的基本概念和性质。

不等式是指两个数或者两个代数式之间的大小关系，包括大于、小于、大于等于、小于等于等不等式关系。

在学习不等式的过程中，学生还需要掌握不等式的可加性、可乘性等基本性质，这些性质是解不等式问题的关键。

2.不等式的解法方法：解不等式是数学学科中的一个重要问题，不等式的解法方法有很多种，包括直接法、间接法、分情况讨论法、参数法等。

学生需要掌握这些解法方法，根据不同的不等式问题选择合适的解法，并且要熟练运用这些解法方法解决实际问题。

3.一元一次不等式的解法：在学习不等式的过程中，学生首先需要掌握一元一次不等式的解法。

一元一次不等式是指不等式中只含有一个未知数，并且未知数的最高次数为一次的不等式。

解一元一次不等式的关键是通过变形和等价变换将不等式化为标准形式，然后通过对不等式进行加减乘除等操作来求解未知数的取值范围。

4.一元二次不等式的解法：学生在学习一元一次不等式之后，需要进一步学习一元二次不等式的解法。

一元二次不等式是指不等式中含有一个未知数，并且未知数的最高次数为二次的不等式。

解一元二次不等式一般需要借助图像或者特殊的代数方法来求解，学生需要掌握各种解法方法，并熟练应用到实际问题中去。

5.不等式组的解法：在学习一元不等式之后，学生还需要学习不等式组的解法。

不等式组是由多个不等式组成的一种复合不等式，解不等式组的关键是找出其解的交集或者并集，并求出满足所有不等式的未知数的取值范围。

学生需要通过练习不等式组的解题方法，提高解决实际问题的能力。

6.不等式问题的应用：在学习不等式的过程中，学生还需要了解不等式在实际问题中的应用。

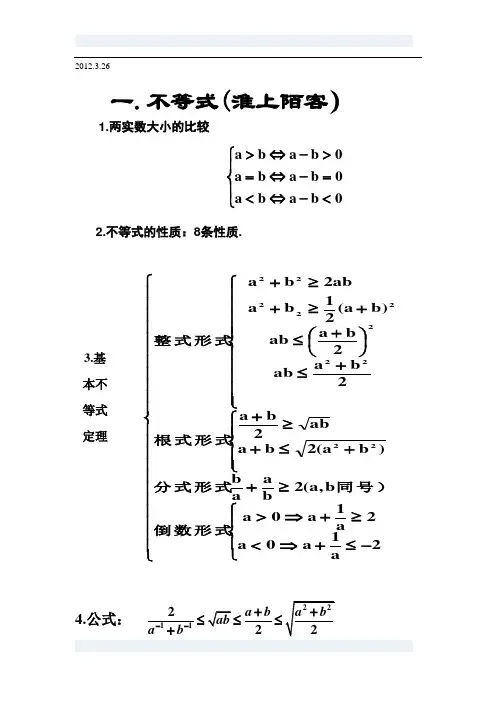
2012.3.264.公式： 1.两实数大小的比较⎪⎩⎪⎨⎧<-⇔<=-⇔=>-⇔>0b a b a 0b a b a 0b a b a 一.不等式(淮上陌客）3.基 本不等式定理⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧-≤+⇒<≥+⇒>≥+⎪⎪⎩⎪⎪⎨⎧+≤+≥+⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+≤⎪⎭⎫ ⎝⎛+≤+≥+≥+2a 1a 0a 2a 1a 0ab ,a (2b aa b )b a (2b a ab 2b a 2b a ab 2b a ab )b a (21b a ab 2b a 2222222222倒数形式同号）分式形式根式形式整式形式2211222a b a b ab a b --++≤≤≤+2.不等式的性质：8条性质.3.解不等式(1)一元一次不等式(2)一元二次不等式：判别式△=b2- 4ac△>0 △=0△<0y=ax2+bx+c的图象(a>0)ax2+bx+c=0 (a>0)的根有两相异实根x1, x2 (x1<x2)有两相等实根x1=x2=没有实根ax2+bx+c>0(y>0)的解集{x|x<x1,或x>x2} {x|x≠}Rax2+bx+c<0 (y<0)的解集{x|x1< x <x2}ΦΦx1x2xyOyxO x1yxO⎪⎩⎪⎨⎧<<>>≠>)0a(abx)0a(abx)0a(baxab2-ab2-一元二次不等式的求 解流程：一化：化二次项前的系数为正数. 二判：判断对应方程的根. 三求：求对应方程的根. 四画：画出对应函数的图象.五解集：根据图象写出不等式的解集. (3)解分式不等式：高次不等式：(4)解含参数的不等式：（1）(x – 2)(ax – 2)>0（2）x 2 – (a +a 2)x +a 3>0；（3）2x 2 +ax +2 > 0；注:解形如ax 2+bx+c>0的不等式时分类讨 论的标准有：1、讨论a 与0的大小；2、讨论⊿与0的大小；3、讨论两根的大小；二、运用的数学思想：1、分类讨论的思想；2、数形结合的思想；3、等与不等的化归思想(4)含参不等式恒成立的问题：⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧≠≤⋅⇔≤>⋅⇔>0)x (g 0)x (g )x (f 0)x (g )x (f 0)x (g )x (f 0)x (g )x (f 0)())((21>---n a x a x a x⎪⎩⎪⎨⎧用图象分离参数后用最值函数、、、321例1．已知关于x 的不等式在(–2，0)上恒成立，求实数a 的取值范围． 例2．关于x 的不等式对所有实数x ∈R 都成立，求a 的取值范围.(5)一元二次方程根的分布问题：方法：依据二次函数的图像特征从：开口方向、判别式、对称轴、 函数值三个角度列出不等式组，总之都是转化为一元二次20,31xx a x x >≤++恒成立，例3.若对任意则 的取值范围.a22(3)210x a x a +-+-<)1(log 22++-=ax ax y不等式组求解. 二次方程根的分布问题的讨论：y()020f k b k a >⎧⎪⎪-<⎨⎪∆>⎪⎩1．x 1< x 2< kxOkx 1x 2xyO x 2x 1 k ()020f k b k a >⎧⎪⎪->⎨⎪∆>⎪⎩2．k < x 1< x xyO xx 1 k()0f k <3．x 1< k < x 24． k 1 < x 1 < x 2 < k 2 5． x 1 < k 1 < k 2 < x 2 1212()0()002f k f k b k k a >⎧⎪>⎪⎪⎨∆>⎪⎪<-<⎪⎩12()0()0f k f k >⎧⎨>⎩6． k 1 <x 1 < k 2 < x 2< k 3122()0()0()0f k f k f k >⎧⎪<⎨⎪>⎩ 4解线性规划问题的一般步骤：第一步：在平面直角坐标系中作出可行域； 第二步：在可行域内找到最优解所对应的点；第三步：解方程的最优解，从而求出目标函数的最大值或最小值。

目录不等关系与不等式 (2)考点1 ：不等关系与不等式 (2)考点2 :等式性质与不等式性质 (7)考点1:不等关系与不等式知识点一基本事实两个实数a，b,其大小关系有三种可能，即a=b. a<b.思考 F+1与2%两式都随x的变化而变化，其大小关系并不显而易见.你能想个办法，比较W+1与2%的大小吗？答案作差：x2+l-2x=（x-l）2^0,所以x2+1^2x.知识点二重要不等式bWR,有R+夕仝2db,当且仅当a=b时，等号成立.型1 ：用不等式（组）表示不等关系例1《铁路旅行常识》规左：一、随同成人旅行，身高在1.2〜L5米的儿童享受半价客票（以下称儿童票），超过1.5米的应买全价票，每一爼成人旅客可免费带一名身高不足1.2米的儿童，超过一名时，超过的人数应买儿童票.十、旅客免费携带物品的体枳和重量是每件物品的外部长、宽、高尺寸之和不得超过160 厘米，杆状物品不得超过200厘米.重量不得超过20千克……设身高为加米），物品外部长、宽、高尺寸之和为P（厘米），请用不等式表示下表中的不等关系.解由题意可获取以下主要信息：（1）身高用力（米）表示•物体长、宽、高尺寸之和为P（厘米）;(2)题中要求用不等式表示不等关系•解答本题应先理解题中所提供的不等关系，再用不等式表示.身高在1.2〜1.5米可表示为1.20W1.5,身高超过1.5米可表示为Q1.5,身高不足1.2米可表示为*1.2,物依长、宽、高尺寸之和不得超过160厘米可表示为PW160.如下表所示：变式某套试卷原以每本2.5元的价格销售，可以售出8万本.据市场调查，若单价每提髙0.1元，销售量就可能相应减少2 000本.若把提价后试卷的立价设为X元，怎样用不等式表示销售的总收入仍不低于20万元呢？解提价后销售的总收入为(8—讦尹X0.2》万元，那么不等关系'‘销售的总收入仍不低于20万元”可以表示为不等式(8—违尹X0.2》220(2.5Wx<6.5).题型2 :作差法比较大小例2已知e b均为正实数.试利用作差法比较”+沪与Hb+a，的大小.解•/，+，一(a2b+abr)=(a3—crb)+&—air)=a2(a—b)+b2(b—a)=(a—b)(a2—b2)=(a—b)2(a + b)・当a=b 时，a-b=Q. a3+b3=a2b+a^;当a^b时，(a-b)2>09 a+bX), a3-^b3>a2b+ab2.综上所述.变式已知;r<l,试比较W—1与R-h的大小.解 V(X3-1)-(2A2-2X)=X3-2X2+2X-1=(x3—X2)—(A2—2x+l)=x2(x—1)—(x—I)2= (x_ l)(x2-x+ l) = (x- 1｛卜-齐+ ||又V （x-|）2+|>0, x-KO,考点1 ：练习题1. 下列说法正确的是（）A. 某人月收入x 元不高于2 OOO 元可表示为“*2 000”B. 小明的身高为x,小华的身髙为），，则小明比小华矮可表示为“心，”C. 变量x 不小于a 可表示为“xMa”D. 变量y 不超过a 可表示为 答案C解析 对于A, x 应满足xW2 000,故A 错误；对于B, x, y 应满足xvy,故B 错误；C 正 确；对于D, y 与“的关系可表示为“yWa”，故D 错误.2. 在开山工程爆破时，已知导火索燃烧的速度是每秒0.5 cm,人跑开的速度为每秒4 m, 为了使点燃导火索的人能够在爆破时跑到100 m 以外的安全区，导火索的长度x （cm ）应满足 的不等式为（） A ・ 4X^2100 B ・ 4X 吉W10° ° 4X 吉>100 答案cD ・4X 着100解析导火索燃烧的时间*秒，人在此时间内跑的路程为4Xyr m .由题意可得4X 点 >100.3・设M=x2, N=-x-l,则M 与N 的大小关系是（） A. M>NB ・ M=N C. M<N答案AD.与x 有关解析 TM —"=工+乂+1=卜+少+弓>0,:.M>N,4.若>*i=2x 2—2x+L V2=x 2—4x —h 则yi 与尹2的大小关系是（ ）A. yi>y^2 B ・ yi =1^2.•・仗_1林_期+詐0,：.x 3-l<2x 2-2x.D ・随x 值变化而变化5・如图，在一个而积为200 m 2的矩形地基上建造一个仓库，四周是绿地，仓库的长a 大于 宽b 的4倍，则表示上述的不等关系正确的是()答案C解析由题意知a>4b,根据面积公式可以得到@+4)0+4)=200,故选C.6. 某次数学智力测验，共有20道题，答对一题得5分，答错一题得一2分，不答得零分.某 同学有一道题未答，设这个学生至少答对x 题，成绩才能不低于80分，列岀英中的不等关 系： _______ •(不用化简) 答案 5x-2(19-x)^80, xWPT解析 这个学生至少答对X 题，成绩才能不低于80分.即5x-2(19-x)^80, xGN 4.7. 某商品包装上标有重疑500±1克，若用x 表示商品的重量，则可用含绝对值的不等式表 示该商品的重量的不等式为 _________ . 答案 |x-500|Wl解析：•某商品包装上标有重量500±1克，若用X 表示商品的重量， 则一 1WX —500W1, "一 50001.8. ____________________________________ 若MR,则占与扌的大小关系为• • X 1 二厲一1一工_一&一1)2 • 1+W 2(1+F) — 2(1+F)、U9.已知a, bWR, b, y=a 2b~a.试比较x 与y 的大小.解因为 x —y =a i—b —a 1b^a =a 2(a — b)'¥a—b — (a —b)(g 2^V).所以当a>b 时，：r —y>0,所以x 刁；C ・ yi<y 2A. a>4b a>4b 9 C.\[(“+4)9+4)=200 2-2 m-仓 库-2 m-绿地2ma>4b,D|4"=200解析B ・(a+4)(b+4)=200 答案当a=b时，x—y=O,所以x=y；当a<b时，x—3<0,所以10.已知甲、乙、丙三种食物的维生素A, B含捲及成本如下表:若用甲.乙、丙三种食物各xkg.ykg’kg配成100kg的混合食物，并使混合食物内至少含有56 000单位维生素A和63 000单位维生素B.试用x,表示混合食物成本c元，并写出x, y所满足的不等关系.解依题意得c=llx+刘+4z,又x+y+z=100, •••C=400+7X+5N600x+70Qy+4（XhM56 000,由］, 及z=100—x—800.Y+400V+500z^63 000•*Q+3&160,得｛L3x-y^l30.去+3舞160,3x-v^l30.•••x, y所满足的不等关系为（,亠0<y^Q.11・已知0勺01,0勺2<1,记N=ai+d2—1，则A/与N的大小关系是（）A. M<NB. M>NC. M=N D・无法确定答案B解析 TOva产 1、0勺2<1, •: —1<^1 —1<0, —1<^2 —1<0, /.Af—N=ag2—（心+。

人教版高二数学上向量的三角形不等式归纳高二数学向量的三角形不等式1、∣∣a∣-∣b∣∣∣a+b∣∣a∣+∣b∣;① 当且仅当a、b反向时，左边取等号;② 当且仅当a、b同向时，右边取等号。

2、∣∣a∣-∣b∣∣∣a-b∣∣a∣+∣b∣。

① 当且仅当a、b同向时，左边取等号;② 当且仅当a、b反向时，右边取等号。

高中数学学习方法(1)记数学笔记，特别是对概念理解的不同侧面和数学规律，教师在课堂中拓展的课外知识。

记录下来本章你觉得最有价值的思想方法或例题，以及你还存在的未解决的问题，以便今后将其补上。

(2)建立数学纠错本。

把平时容易出现错误的知识或推理记载下来，以防再犯。

争取做到：找错、析错、改错、防错。

达到：能从反面入手深入理解正确东西;能由果朔因把错误原因弄个水落石出、以便对症下药;解答问题完整、推理严密。

(3)熟记一些数学规律和数学小结论，使自己平时的运算技能达到了自动化或半自动化的熟练程度。

(4)经常对知识结构进行梳理，形成板块结构，实行整体集装，如表格化，使知识结构一目了然;经常对习题进行类化，由一例到一类，由一类到多类，由多类到统一;使几类问题归纳于同一知识方法。

(5)阅读数学课外书籍与报刊，参加数学学科课外活动与讲座，多做数学课外题，加大自学力度，拓展自己的知识面。

(6)及时复习，强化对基本概念知识体系的理解与记忆，进行适当的反复巩固，消灭前学后忘。

(7)学会从多角度、多层次地进行总结归类。

如：①从数学思想分类②从解题方法归类③从知识应用上分类等，使所学的知识系统化、条理化、专题化、网络化。

(8)经常在做题后进行一定的反思，思考一下本题所用的基础知识，数学思想方法是什么，为什么要这样想，是否还有别的想法和解法，本题的分析方法与解法，在解其它问题时，是否也用到过。

(9)无论是作业还是测验，都应把准确性放在第一位，通法放在第一位，而不是一味地去追求速度或技巧，这是学好数学的重要问题。

目录不等关系与不等式 (2)考点1：不等关系与不等式 (2)考点2：等式性质与不等式性质 (7)考点1：不等关系与不等式知识点一基本事实两个实数a，b，其大小关系有三种可能，即a>b，a＝b，a<b.思考x2＋1与2x两式都随x的变化而变化，其大小关系并不显而易见．你能想个办法，比较x2＋1与2x的大小吗？答案作差：x2＋1－2x＝(x－1)2≥0，所以x2＋1≥2x.知识点二重要不等式∀a，b∈R，有a2＋b2≥2ab，当且仅当a＝b时，等号成立．题型1：用不等式(组)表示不等关系例1《铁路旅行常识》规定：一、随同成人旅行，身高在1.2～1.5米的儿童享受半价客票(以下称儿童票)，超过1.5米的应买全价票，每一名成人旅客可免费带一名身高不足1.2米的儿童，超过一名时，超过的人数应买儿童票．……十、旅客免费携带物品的体积和重量是每件物品的外部长、宽、高尺寸之和不得超过160厘米，杆状物品不得超过200厘米，重量不得超过20千克……设身高为h(米)，物品外部长、宽、高尺寸之和为P(厘米)，请用不等式表示下表中的不等关系.解由题意可获取以下主要信息：(1)身高用h(米)表示，物体长、宽、高尺寸之和为P(厘米)；(2)题中要求用不等式表示不等关系．解答本题应先理解题中所提供的不等关系，再用不等式表示．身高在1.2～1.5米可表示为1.2≤h ≤1.5， 身高超过1.5米可表示为h >1.5， 身高不足1.2米可表示为h <1.2，物体长、宽、高尺寸之和不得超过160厘米可表示为P ≤160.如下表所示：变式 某套试卷原以每本2.5元的价格销售，可以售出8万本．据市场调查，若单价每提高0.1元，销售量就可能相应减少2 000本．若把提价后试卷的定价设为x 元，怎样用不等式表示销售的总收入仍不低于20万元呢？解 提价后销售的总收入为⎝⎛⎭⎫8－x －2.50.1×0.2x 万元，那么不等关系“销售的总收入仍不低于20万元”可以表示为不等式⎝⎛⎭⎫8－x －2.50.1×0.2x ≥20(2.5≤x <6.5)．题型2：作差法比较大小例2 已知a ，b 均为正实数．试利用作差法比较a 3＋b 3与a 2b ＋ab 2的大小． 解 ∵a 3＋b 3－(a 2b ＋ab 2)＝(a 3－a 2b )＋(b 3－ab 2) ＝a 2(a －b )＋b 2(b －a )＝(a －b )(a 2－b 2)＝(a －b )2(a ＋b )． 当a ＝b 时，a －b ＝0，a 3＋b 3＝a 2b ＋ab 2； 当a ≠b 时，(a －b )2>0，a ＋b >0，a 3＋b 3>a 2b ＋ab 2. 综上所述，a 3＋b 3≥a 2b ＋ab 2.变式 已知x <1，试比较x 3－1与2x 2－2x 的大小． 解 ∵(x 3－1)－(2x 2－2x )＝x 3－2x 2＋2x －1 ＝(x 3－x 2)－(x 2－2x ＋1)＝x 2(x －1)－(x －1)2 ＝(x －1)(x 2－x ＋1)＝(x －1)⎣⎡⎦⎤⎝⎛⎭⎫x －122＋34，又∵⎝⎛⎭⎫x －122＋34>0，x －1<0， ∴(x －1)⎣⎡⎦⎤⎝⎛⎭⎫x －122＋34<0，∴x 3－1<2x 2－2x .考点1：练习题1．下列说法正确的是( )A ．某人月收入x 元不高于2 000元可表示为“x <2 000”B ．小明的身高为x ，小华的身高为y ，则小明比小华矮可表示为“x >y ”C ．变量x 不小于a 可表示为“x ≥a ”D ．变量y 不超过a 可表示为“y ≥a ” 答案 C解析 对于A ，x 应满足x ≤2 000，故A 错误；对于B ，x ，y 应满足x <y ，故B 错误；C 正确；对于D ，y 与a 的关系可表示为“y ≤a ”，故D 错误．2．在开山工程爆破时，已知导火索燃烧的速度是每秒0.5 cm ，人跑开的速度为每秒4 m ，为了使点燃导火索的人能够在爆破时跑到100 m 以外的安全区，导火索的长度x (cm)应满足的不等式为( ) A ．4×x0.5≥100B ．4×x0.5≤100 C ．4×x0.5>100D ．4×x0.5<100答案 C解析 导火索燃烧的时间x 0.5秒，人在此时间内跑的路程为4×x0.5m ．由题意可得4×x0.5>100. 3．设M ＝x 2，N ＝－x －1，则M 与N 的大小关系是( ) A ．M >N B ．M ＝N C ．M <N D ．与x 有关答案 A解析 ∵M －N ＝x 2＋x ＋1＝⎝⎛⎭⎫x ＋122＋34>0， ∴M >N .4．若y 1＝2x 2－2x ＋1，y 2＝x 2－4x －1，则y 1与y 2的大小关系是( ) A ．y 1>y 2B ．y 1＝y 2C ．y 1<y 2D ．随x 值变化而变化答案 A5．如图，在一个面积为200 m 2的矩形地基上建造一个仓库，四周是绿地，仓库的长a 大于宽b 的4倍，则表示上述的不等关系正确的是( )A ．a >4bB ．(a ＋4)(b ＋4)＝200C.⎩⎪⎨⎪⎧a >4b ，(a ＋4)(b ＋4)＝200 D.⎩⎪⎨⎪⎧a >4b ，4ab ＝200 答案 C解析 由题意知a >4b ，根据面积公式可以得到(a ＋4)(b ＋4)＝200，故选C.6．某次数学智力测验，共有20道题，答对一题得5分，答错一题得－2分，不答得零分．某同学有一道题未答，设这个学生至少答对x 题，成绩才能不低于80分，列出其中的不等关系：________.(不用化简) 答案 5x －2(19－x )≥80，x ∈N *解析 这个学生至少答对x 题，成绩才能不低于80分，即5x －2(19－x )≥80，x ∈N *. 7．某商品包装上标有重量500±1克，若用x 表示商品的重量，则可用含绝对值的不等式表示该商品的重量的不等式为________． 答案 |x －500|≤1解析 ∵某商品包装上标有重量500±1克， 若用x 表示商品的重量， 则－1≤x －500≤1， ∴|x －500|≤1.8．若x ∈R ，则x 1＋x 2与12的大小关系为________．答案x 1＋x 2≤12解析 ∵x 1＋x 2－12＝2x －1－x 22(1＋x 2)＝－(x －1)22(1＋x 2)≤0.∴x 1＋x 2≤12. 9．已知a ，b ∈R ，x ＝a 3－b ，y ＝a 2b －a ，试比较x 与y 的大小． 解 因为x －y ＝a 3－b －a 2b ＋a ＝a 2(a －b )＋a －b ＝(a －b )(a 2＋1)，所以当a >b 时，x －y >0，所以x >y ； 当a ＝b 时，x －y ＝0，所以x ＝y ； 当a <b 时，x －y <0，所以x <y .10．已知甲、乙、丙三种食物的维生素A ，B 含量及成本如下表：若用甲、乙、丙三种食物各x kg 、y kg 、z kg 配成100 kg 的混合食物，并使混合食物内至少含有56 000单位维生素A 和63 000单位维生素B.试用x ，y 表示混合食物成本c 元，并写出x ，y 所满足的不等关系． 解 依题意得c ＝11x ＋9y ＋4z ， 又x ＋y ＋z ＝100，∴c ＝400＋7x ＋5y ，由⎩⎪⎨⎪⎧600x ＋700y ＋400z ≥56 000，800x ＋400y ＋500z ≥63 000及z ＝100－x －y ， 得⎩⎪⎨⎪⎧2x ＋3y ≥160，3x －y ≥130. ∴x ，y 所满足的不等关系为⎩⎪⎨⎪⎧2x ＋3y ≥160，3x －y ≥130，x ≥0，y ≥0.11．已知0<a 1<1,0<a 2<1，记M ＝a 1a 2，N ＝a 1＋a 2－1，则M 与N 的大小关系是( ) A ．M <N B ．M >N C ．M ＝N D ．无法确定答案 B解析 ∵0<a 1<1,0<a 2<1，∴－1<a 1－1<0，－1<a 2－1<0，∴M －N ＝a 1a 2－(a 1＋a 2－1)＝a 1a 2－a 1－a 2＋1＝a 1(a 2－1)－(a 2－1)＝(a 1－1)(a 2－1)>0， ∴M >N ，故选B.12．若0<a 1<a 2，0<b 1<b 2，且a 1＋a 2＝b 1＋b 2＝1，则下列代数式中值最大的是( ) A ．a 1b 1＋a 2b 2 B ．a 1a 2＋b 1b 2 C ．a 1b 2＋a 2b 1 D.12答案 A解析 令a 1＝0.1，a 2＝0.9；b 1＝0.2，b 2＝0.8.则A 项a 1b 1＋a 2b 2＝0.74；B 项，a 1a 2＋b 1b 2＝0.25；C 项，a 1b 2＋a 2b 1＝0.26，故最大值为A.13．一个盒子中红、白、黑三种球分别为x 个、y 个、z 个，黑球个数至少是白球个数的一半，至多是红球个数的13，白球与黑球的个数之和至少为55，则用不等式(组)将题中的不等关系表示为________．答案 ⎩⎪⎨⎪⎧y 2≤z ≤x 3，y ＋z ≥55(x ，y ，z ∈N *)解析 由题意可得⎩⎪⎨⎪⎧y 2≤z ≤x 3，y ＋z ≥55(x ，y ，z ∈N *)．14．若a 1<a 2，b 1<b 2，则a 1b 1＋a 2b 2________a 1b 2＋a 2b 1.(填“>”“<”“＝”) 答案 >解析 a 1b 1＋a 2b 2－(a 1b 2＋a 2b 1) ＝a 1(b 1－b 2)＋a 2(b 2－b 1) ＝(b 1－b 2)(a 1－a 2)， ∵a 1<a 2，b 1<b 2， ∴b 1－b 2<0，a 1－a 2<0， 即(b 1－b 2)(a 1－a 2)>0， ∴a 1b 1＋a 2b 2>a 1b 2＋a 2b 1.考点2：等式性质与不等式性质知识点一 等式的基本性质 (1)如果a ＝b ，那么b ＝a . (2)如果a ＝b ，b ＝c ，那么a ＝c . (3)如果a ＝b ，那么a ±c ＝b ±c . (4)如果a ＝b ，那么ac ＝bc . (5)如果a ＝b ，c ≠0，那么a c ＝bc .知识点二 不等式的性质题型1：利用不等式的性质判断或证明例1 (1)给出下列命题： ①若ab >0，a >b ，则1a <1b ；②若a >b ，c >d ，则a －c >b －d ；③对于正数a ，b ，m ，若a <b ，则a b <a ＋mb ＋m .其中真命题的序号是________．答案 ①③解析 对于①，若ab >0，则1ab>0， 又a >b ，所以a ab >b ab ，所以1a <1b ，所以①正确；对于②，若a ＝7，b ＝6，c ＝0，d ＝－10， 则7－0<6－(－10)，②错误； 对于③，对于正数a ，b ，m ， 若a <b ，则am <bm ， 所以am ＋ab <bm ＋ab ， 所以0<a (b ＋m )<b (a ＋m )， 又1b (b ＋m )>0，所以a b <a ＋m b ＋m ，③正确．综上，真命题的序号是①③.(2)已知a >b >0，c <d <0.求证：3a d<3b c. 证明 因为c <d <0，所以－c >－d >0. 所以0<－1c <－1d.又因为a >b >0，所以－a d >－bc>0.所以3－ad>3－bc，即－3a d>－3b c， 两边同乘－1，得3a d<3b c.变式 若1a <1b <0，有下面四个不等式：①|a |>|b |，②a <b ，③a ＋b <ab ，④a 3>b 3. 则不正确的不等式的个数是( ) A ．0 B ．1 C ．2 D ．3 答案 C解析 由1a <1b <0可得b <a <0，从而|a |<|b |，①②均不正确；a ＋b <0，ab >0，则a ＋b <ab 成立，③正确；a 3>b 3，④正确． 故不正确的不等式的个数为2.题型2：利用性质比较大小例2 若P ＝a ＋6＋a ＋7，Q ＝a ＋5＋a ＋8(a >－5)，则P ，Q 的大小关系为( ) A ．P <Q B ．P ＝Q C ．P >Q D ．不能确定答案 C解析 P 2＝2a ＋13＋2(a ＋6)(a ＋7)， Q 2＝2a ＋13＋2(a ＋5)(a ＋8)，因为(a ＋6)(a ＋7)－(a ＋5)(a ＋8)＝a 2＋13a ＋42－(a 2＋13a ＋40)＝2>0， 所以(a ＋6)(a ＋7)>(a ＋5)(a ＋8)，所以P 2>Q 2，所以P >Q .变式 下列命题中一定正确的是( ) A ．若a >b ，且1a >1b ，则a >0，b <0B ．若a >b ，b ≠0，则ab >1C ．若a >b ，且a ＋c >b ＋d ，则c >dD ．若a >b ，且ac >bd ，则c >d 答案 A解析 对于A ，∵1a >1b ，∴b －a ab >0，又a >b ，∴b －a <0，∴ab <0， ∴a >0，b <0，故A 正确；对于B ，当a >0，b <0时，有ab<1，故B 错；对于C ，当a ＝10，b ＝2时，有10＋1>2＋3，但1<3， 故C 错；对于D ，当a ＝－1，b ＝－2时，有(－1)×(－1)>(－2)×3，但－1<3，故D 错．题型3：利用性质比较大小例3 已知12<a <60,15<b <36.求a －b 和ab 的取值范围．解 ∵15<b <36，∴－36<－b <－15， ∴12－36<a －b <60－15，即－24<a －b <45. 又136<1b <115，∴1236<a b <6015，即13<a b <4. 故－24<a －b <45，13<a b <4.变式 已知0<a ＋b <2，－1<b －a <1，则2a －b 的取值范围是____________． 答案 －32<2a －b <52解析 因为0<a ＋b <2，－1<－a ＋b <1，且2a －b ＝12(a ＋b )－32(－a ＋b )，结合不等式的性质可得，－32<2a －b <52.考点2：练习题1．如果a <0，b >0，那么下列不等式中正确的是( )A.1a <1bB.－a <bC ．a 2<b 2D ．|a |>|b |答案 A解析 ∵a <0，b >0，∴1a <0，1b >0，∴1a <1b ，故选A.2．若a ，b ，c ∈R ，且a >b ，则下列不等式一定成立的是() A ．a ＋c ≥b －c B ．ac >bcC.c 2a －b >0 D ．(a －b )c 2≥0答案 D解析 ∵a >b ，∴a －b >0，∴(a －b )c 2≥0，故选D.3．已知a >b >c ，则1b －c ＋1c －a 的值是( )A ．正数B ．负数C ．非正数D ．非负数答案 A解析 1b －c ＋1c －a ＝c －a ＋b －c (b －c )(c －a )＝b －a (b －c )(c －a )， ∵a >b >c ，∴b －c >0，c －a <0，b －a <0，∴1b －c ＋1c －a>0，故选A. 4．若x >1>y ，下列不等式不一定成立的是( )A ．x －y >1－yB ．x －1>y －1C ．x －1>1－yD ．1－x >y －x 答案 C解析 利用性质可得A ，B ，D 均正确，故选C.5．已知a <0，b <－1，则下列不等式成立的是( )A ．a >a b >a b 2 B.a b 2>a b >a C.a b >a >a b 2 D.a b >a b 2>a 答案 D解析 ∵a <0，b <－1，∴a b>0，b 2>1， ∴0<1b 2<1，∴0>a b 2>a 1， ∴a b >a b 2>a . 6．不等式a >b 和1a >1b同时成立的条件是________． 答案 a >0>b解析 若a ，b 同号，则a >b ⇒1a <1b. 7．给出下列命题：①a >b ⇒ac 2>bc 2；②a >|b |⇒a 2>b 2；③a >b ⇒a 3>b 3；④|a |>b ⇒a 2>b 2.其中正确命题的序号是________．答案 ②③解析 ①当c 2＝0时不成立；②一定成立；③当a >b 时，a 3－b 3＝(a －b )(a 2＋ab ＋b 2)＝(a －b )·⎣⎡⎦⎤⎝⎛⎭⎫a ＋b 22＋34b 2>0成立； ④当b <0时，不一定成立．如：|2|>－3，但22<(－3)2.8．设a >b >c >0，x ＝a 2＋(b ＋c )2，y ＝b 2＋(c ＋a )2，z ＝c 2＋(a ＋b )2，则x ，y ，z 的大小顺序是________．答案 z >y >x解析 ∵a >b >c >0，y 2－x 2＝b 2＋(c ＋a )2－a 2－(b ＋c )2＝2ac －2bc＝2c (a －b )>0，∴y 2>x 2，即y >x .同理可得z >y ，故z >y >x .9．判断下列各命题的真假，并说明理由．(1)若a <b ，c <0，则c a <c b； (2)a c 3<b c 3，则a >b ； (3)若a >b ，且k ∈N *，则a k >b k ；(4)若a >b ，b >c ，则a －b >b －c .解 (1)假命题．∵a <b ，不一定有ab >0，∴1a >1b不一定成立， ∴推不出c a <c b，∴是假命题． (2)假命题．当c >0时，c －3>0，则a <b ，∴是假命题．(3)假命题．当a ＝1，b ＝－2，k ＝2时，显然命题不成立，∴是假命题．(4)假命题．当a ＝2，b ＝0，c ＝－3时，满足a >b ，b >c 这两个条件，但是a －b ＝2<b －c ＝3，∴是假命题．10．若－1<a ＋b <3,2<a －b <4，求2a ＋3b 的取值范围．解 设2a ＋3b ＝x (a ＋b )＋y (a －b )，则⎩⎪⎨⎪⎧ x ＋y ＝2，x －y ＝3，解得⎩⎨⎧ x ＝52，y ＝－12.因为－52<52(a ＋b )<152，－2<－12(a －b )<－1， 所以－92<52(a ＋b )－12(a －b )<132， 所以－92<2a ＋3b <132. 11．下列命题正确的是( )A ．若ac >bc ，则a >bB ．若a 2>b 2，则a >bC ．若1a >1b，则a <b D ．若a <b ，则a <b答案 D 解析 对于A ，若c <0，其不成立；对于B ，若a ，b 均小于0或a <0，其不成立；对于C ，若a >0，b <0，其不成立；对于D ，其中a ≥0，b >0，平方后显然有a <b .12．已知x >y >z ，x ＋y ＋z ＝0，则下列不等式中一定成立的是( )A ．xy >yzB ．xz >yzC ．xy >xzD ．x |y |>z |y | 答案 C解析 因为x >y >z ，x ＋y ＋z ＝0，所以3x >x ＋y ＋z ＝0,3z <x ＋y ＋z ＝0，所以x >0，z <0.所以由⎩⎪⎨⎪⎧x >0，y >z ，可得xy >xz . 13．若a ，b ，c ∈R ，a >b ，则下列不等式成立的是( )A.1a <1bB ．a 2>b 2 C.a c 2＋1>b c 2＋1D ．a |c |>b |c |答案 C解析 对于A ，若a >0>b ，则1a >0，1b<0， 此时1a >1b，∴A 不成立； 对于B ，若a ＝1，b ＝－2，则a 2<b 2，∴B 不成立；对于C ，∵c 2＋1≥1，且a >b ，∴a c 2＋1>b c 2＋1恒成立，∴C 成立； 对于D ，当c ＝0时，a |c |＝b |c |，∴D 不成立．14．有外表一样，重量不同的四个小球，它们的重量分别是a ，b ，c ，d ，已知a ＋b ＝c ＋d ，a ＋d >b ＋c ，a ＋c <b ，则这四个小球由重到轻的排列顺序是( )A ．d >b >a >cB ．b >c >d >aC ．d >b >c >aD ．c >a >d >b答案 A解析 ∵a ＋b ＝c ＋d ，a ＋d >b ＋c ，∴a ＋d ＋(a ＋b )>b ＋c ＋(c ＋d )，即a >c .∴b <d .又a＋c<b，∴a<b.综上可得，d>b>a>c.。

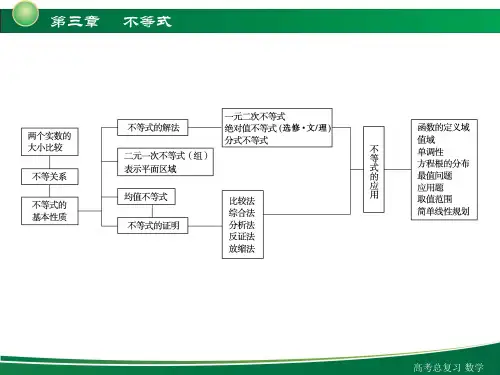
高中数学《不等式》复习不 等 式 不等式的概念 不等关系 不等关系文字语言与符号语言的转换：大于、小于、不等于，不超过等 与不等式比较实数的大小 依据、比较方法 不等式不等式的性质：解证不等式问题的依据一元二次不等式：含有一个未知数，未知数的最高次数是2的不等式 一元二次 不等式及 其解法三个“二次”的关系：方程，函数，不等式 一元二次不等式的解法 三个二次之间的关系、含参数 求不等式的解集一元二次不等式问题 分式不等式及高次不等式的解法：转化法，穿根法二元一次 不等式 组 与简单的线性规划问题二元一次不等式 二元一次不等式 组 ：解集，几何意义 组 与平面区域平面区域：以线定界，以点定域简单的线性 相关概念：约束条件，目标函数，可行解，可行域，最优解规划问题解法 图解法 应用种类：效益最大，利润最大，耗材最少基本不等式及其应用基本不等式：常见的变形，重要不等式链 应用：最值问题，比较实数的大小，不等式的证明专题一 ⇨不等关系与不等式的性质 (1)不等式的性质是比较数的大小，求代数式的取值范围，证明不等式等的主要依据．尤 其注意“同向不等式”才可加，运用可乘性(乘除、乘方)时一定要注意符号． (2)比较数的大小是主要题型之一，常见方法有作差法、作商法、介值法(a>b，b>c⇒ a>c)， 注意解题过程中，配方、乘方、因式分解、配凑、放缩等技巧的运用． (3)证明不等式是常见题型，对于简单不等式的证明可直接由已知条件，利用不等式的 性质，通过对不等式变形得证． 对于不等式两边都比较复杂的式子，直接利用不等式的性质不易得证，可考虑将不等式 的两边作差，然后进行变形，根据条件确定每一个因式(式子)的符号，利用符号法则判断最 终的符号，完成证明． (4)求代数式的取值范围也是常见题型．解题时可借助性质、基本不等式、函数值域等 知识综合考虑，特别注意限制条件．例题 1 已知 a、b 为正实数，试比较 a ＋ b 与 a＋ b的大小． ba[分析] 利用作商法或作差法进行比较．[解析]ab 解法一：( ＋ )－(a＋b)baa ＝( －b)＋( b －a)＝a－b＋b－ababa＝ a－ba－ b ＝ aba＋ ba－ b 2ab∵a、b 为正实数，∴ a＋ b>0， ab>0，( a－ b)2≥0，∴ a＋ ba－b2≥0，当且仅当 a＝b 时，等号成立，abab ∴＋≥a＋b．baab＋bab 3＋ a 3解法二：＝a＋ b ab a＋ ba＋ b a＋b－ ab ＝ab a＋ b＝a＋b－ab ＝aba－ b 2＋ ab ＝1＋aba－ b 2 ≥1．ab当且仅当 a＝b 时，等号成立．ab 又∵ ＋ >0，a＋b>0，∴ a ＋ b ≥a＋b．baba『规律总结』 作差法是比较两式大小最常用的方法，作商法是必要的补充，无论是作差还是作商，都要进行合理地变形，以利于比较．专题二 ⇨一元二次不等式的应用(1)直接求解一元二次不等式常与集合运算相结合．(2)抓住三个二次之间的关系是解决一元二次不等式问题的关键．(3)含参数的一元二次不等与恒成立问题是常见题型，关键是等价转化与合理分类．构造函数法与判别式、根与系数的关系是常见思考方向．(4)高次不等式、分式不等式要等价转化． 例题 2 已知函数 y＝lg[(a2－1)x2＋(a＋1)x＋1]的定义域是 R，求实数 a 的取值范围．[分析] 本题考查一元二次不等式与二次函数的关系，以及对数函数的性质．解题的关 键是由题意得出(a2－1)x2＋(a＋1)x＋1>0 的解集是 R，从而转化为解决一元二次不等式问题．[解析] 由对数函数定义及题设条件，知(a2－1)x2＋(a＋1)x＋1>0 的解集是 R． 当 a2－1＝0 时，a＝±1． 若 a＝1，则不等式(a2－1)x2＋(a＋1)x＋1>0 可化简为 2x＋1>0，解得 x>－12，与已知矛 盾． 若 a＝－1，则不等式(a2－1)x2＋(a＋1)x＋1>0 可化简为 1>0，此式恒成立，符合题意． 当 a2－1≠0 时，根据题意，有a2－1>0 Δ＝ a＋12－4a2－1<0，即a32a－2－1>20a－5>0a>1或a<－1 ，解得a>53或a<－1，即 a<－1，或 a>53．综上，a5 的取值范围是(－∞，－1]∪(3，＋∞)．『规律总结』 对有关复合函数的问题，我们往往采用“化复合函数为基本函数”的办法，使之一步步转化为我们熟知的题型．此题就是把一个复合函数求范围的问题转化为不等式恒成立的问题．专题三 ⇨简单的线性规划问题(1)求平面区域的面积通过“直线定界，特殊点定域”准确确定平面区域形状及分界点是解题关键，割补计算是主要方法．(2)线性规划问题求解方法是图解法．关键环节是：图形尽量准确，注意目标函数对应直线与图形边界线斜率大小关系，弄清所求最值与“目标函数”直线纵截距关系．(3)非线性目标函数最值，关键搞清“目标函数”表达式的几何意义．(4)整点问题，特别注意最优解不是边界点的找法．(5)含参数的问题．若约束条件中含有参数：此时可行域是可变的，应分情况作出可行域，结合条件求出不同情况下的参数值．若目标函数中含有参数：此时目标函数对应的直线是可变的，如果斜率一定，则对直线作平移变换；如果斜率可变，则要利用斜率与倾斜角间的大小关系分情况确定最优解的位置，从而求出参数的值．(6)实际应用问题，解答时关键是读懂题意，准确设出变量，抓住体现不等关系的词语列出不等式组与目标函数．确定最优解时，注意实际意义． x＋y≤4 例题 3 ：若变量 x、y 满足约束条件x－y≤23x－y≥0，则 3x＋y 的最大值是__10__．[解析] 首先根据题意所给的约束条件画出其表示的平面区域如下图所示，然后根据图 象可得：目标函数 z＝3x＋y 过点 B(3,1)时 z 取得最大值，即 zmax＝3×3＋1＝10，故应填 10．『规律总结』 求目标函数的最值一般采用图解法：①求二元一次函数 z＝ax＋by(ab≠0)的最值，将函数 z＝ax＋by 转化为直线的斜截式：y＝－abx＋zb，通过求直线的截距zb的最值间接求出z的最值．一般地，当b>0时，截距z b取最大值时，z 取最大值；截距zb取最小值时，z 也取最小值；当 b<0 时，截距zb取最大值时，z取最小值；截距zb取最小值时，z 取最大值.②目标函数 z＝ax＋by＋c 的最值的求解，可先求 ax＋by 的最值，再求 z＝ax＋by＋c的最值．专题四 ⇨基本不等式基本不等式的常见应用有：求最值、证明不等式、比较数的大小，解题关键是注意“一正、二定、三相等”的条件和合理变形、配凑、等价转化．例题 4 已知 x、y 都是正实数，且 x＋y－3xy＋5＝0，求 xy 的最小值．[分析] 合理变形，但应注意等号成立的条件．[解析] ∵x＋y－3xy＋5＝0∴3xy＝x＋y＋5≥2 xy＋5，∴3xy－2 xy－5≥0，∴( xy＋1)(3 xy－5)≥0，∴ xy≥53，即 xy≥295，等号成立的条件是 x＝y＝53， 故 xy 的最小值是295． 专题五 ⇨不等式与函数、方程的问题 例题 5 设 a∈R，关于 x 的一元二次方程 7x2－(a＋13)x＋a2－a－2＝0 有两个实根 x1、 x2，且 0<x1<1<x2<2，求 a 的取值范围． [分析] 令 f(x)＝7x2－(a＋13)x＋a2－a－2，它的图象是开口向上的抛物线，它在(0,1) 和(1,2)区间内与 x 轴相交，则有 f(0)>0，f(1)<0，f(2)>0，所以只需解关于 a 的不等式组f 0 >0 f 1 <0 f 2 >0，即可求得 a 的取值范围．[解析] 设 f(x)＝7x2－(a＋13)x＋a2－a－2，图象如图．∵x1、x2 是方程 f(x)＝0 的两个实根， 且 0<x1<1,1<x2<2．f 0 >0 ∴f 1 <0f 2 >0 a2－a－2>0 ⇒ 7－ a＋13 ＋a2－a－2<028－2 a＋13 ＋a2－a－2>0 a2－a－2>0 ⇒ a2－2a－8<0a2－3a>0 a<－1，或a>2 ⇒ －2<a<4a<0，或a>3⇒ －2<a<－1，或 3<a<4． ∴a 的取值范围是{a|－2<a<－1，或 3<a<4}． 『规律总结』 设一元二次方程 ax2＋bx＋c＝0(a>0)对应的二次函数为 f(x)＝ax2＋bx ＋c(a>0)．结合图象可得：Δ>0 (1)方程 f(x)＝0 在区间(－∞，k)内有两个不等的实根，则有 －2ba<k f k >0k 为常数，Δ＝b2－4ac，以下同)．(其中Δ>0 (2)方程 f(x)＝0 在区间(k，＋∞)内有两个不等的实根，则有 －2ba>k．f k >0(3)方程 f(x)＝0 有一根大于 k，另一根小于 k，则有 f(k)<0． (4)方程 f(x)＝0 在区间(k1，k2)内有且只有一根(不包括重根)，则有 f(k1)·f(k2)<0(k1、 k2 为常数，以下同)． (5) 方 程 f(x) ＝ 0 在 区 间 (k1 ， k2) 内 有 两 个 不 等 的 实 根 ， 则 有Δ>0k1<－2ba<k2．f k1 >0，且f k2 >0 Δ>0 (6)方程 f(x)＝0 在区间(k1，k2)外有两个不等的实根，则有f k1 <0 ．f k2 <0专题六 ⇨数学思想方法的应用 例题 6 解关于 x 的不等式 x2－ax－2a2<0(a∈R)． [分析] 先将不等式左边分解因式，然后对两根的大小比较，分类求解不等式． [解析] 原不等式转化为(x－2a)(x＋a)<0． 对应的一元二次方程的根为 x1＝2a，x2＝－a． (1)当 a>0 时，x1>x2， 不等式的解集为{x|－a<x<2a}； (2)当 a＝0 时，原不等式化为 x2<0，无解； (3)当 a<0 时，x1<x2， 不等式的解集为{x|2a<x<－a}． 综上所述，当 a>0 时，原不等式的解集为{x|－a<x<2a}， 当 a＝0 时，原不等式的解集为∅， 当 a<0 时，原不等式的解集为{x|2a<x<－a}． 『规律总结』 解含参数不等式需分类的情况：(1)二次项系数为字母且没有给出具体范围时，要分大于 0、等于 0、小于 0 三类讨论． (2)利用单调性解题时，抓住使单调性变化的参数值，进行讨论． (3)对应方程的根无法判断大小时，要分类讨论． (4)若判别式含参数，则在确定解的情况时需分Δ>0、Δ＝0、Δ<0 三种情况进行讨论． 例题 7 若不等式 x2＋ax＋3－a>0 对于满足－2≤x≤2 的一切实数 x 恒成立，求实数 a的取值范围． [分析] 因为(x－1)的符号不确定，所以参变量 a 不能分离，只好研究二次函数 y＝x2＋ax＋3－a． [解析] 设 f(x)＝x2＋ax＋3－a，其函数图象为开口向上的抛物线，要使得对于满足－2≤x≤2 的一切实数 x 恒有 f(x)>0，只需满足： (1)Δ＝a2－4(3－a)<0；Δ＝a2－4 3－af 2 ＝7＋a>0(2)－a2>2≥0Δ＝a2－4 3－a ≥0f －2 ＝7－3a>0，或－a2<－2，解(1)(2)得，当－7<a<2 时，不等式 x2＋ax＋3－a>0 对于满足－2≤x≤2 的一切实数 x恒成立．『规律总结』 一元二次不等式恒成立可以转化为判别式Δ和开口方向应满足不等式组，也可利用函数最值进行转化，即转化为求函数的最值问题．第三章 学业质量标准检测一、选择题(本大题共 12 个小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．设 M＝2a(a－2)＋7，N＝(a－2)(a－3)，则有( A )A．M＞NB．M≥NC．M＜ND．M≤N[解析] M－N＝(2a2－4a＋7)－(a2－5a＋6)＝a2＋a＋1＝(a＋12)2＋34＞0，∴M＞N.故选 A．2．设集合 A＝{x|(x＋1)(x－2)<0}，集合 B＝{x|1<x<3}，则 A∪B＝( A )A．{x|－1<x<3}B．{x|－1<x<1}C．{x|1<x<2}D．{x|2<x<3}[解析] A＝{x|－1<x<2}，B＝{x|1<x<3}，∴A∪B＝{x|－1<x<3}，选 A．3．若 a＞b＞c，则下列不等式成立的是( B )A．a－1 c＞b－1 cB．a－1 c＜b－1 cC．ac＞bcD．ac＜bc[解析] ∵a＞b＞c，∴a－c＞b－c>0，11 ∴a－c＜b－c，故选 B．4．不等式1x<12的解集是( D )A．(－∞，2)B．(2，＋∞)C．(0,2)D．(－∞，0)∪(2，＋∞)[解析] 因1x<12，得1x－12＝22－xx<0，即 x(x－2)>0，解得 x<0 或 x>2，故选 D．5．不等式(x＋5)(3－2x)≥6 的解集是( D )A．x|x≤－1，或x≥92B．x|－1≤x≤29C．x|x≤－92或x≥1D.x|－92≤x≤1[解析] 解法一：取 x＝1 检验，满足排除 A；取 x＝4 检验，不满足排除 B、C；∴选 D．解法二：原不等式化为：2x2＋7x－9≤0，即(x－1)(2x＋9)≤0，∴－92≤x≤1，选 D．6．(2018－2019 学年度吉林省德惠市实验中学高二月考)已知关于 x 的不等式 x2－ax＋2a＞0 在 R 上恒成立，则实数 a 的取值范围是( A )A．(0,8)B．(1,8)C．(0,10) [解析] 由题意得 a2－8a＜0，D．(1,10)∴0＜a＜8，故选 A． 7．若关于 x 的不等式 2x2－8x－4－a≥0 在 1≤x≤4 内有解，则实数 a 的取值范围是(A)A．a≤－4B．a≥－4C．a≥－12D．a≤－12[解析] ∵y＝2x2－8x－4(1≤x≤4)在 x＝4 时，取最大值－4，当 a≤－4 时，2x2－8x－4≥a 存在解．故选 A．8．(2018－2019 学年度江西戈阳一中高二月考)设 f(x)＝ex,0＜a＜b，若 p＝f( ab)，q＝f(a＋2 b)，r＝ f a f b ，则下列关系正确的是( C )A．q＝r＜pB．p＝r＜qC．q＝r＞p [解析] f(x)＝ex 是增函数，D．p＝r＞q∵0＜a＜b，∴ ab＜a＋2 b，∴f( ab)＜f(a＋2 b)∴p＜q又 f(a＋2 b)＝ea＋2 b＝ eab，f a f b ＝ ea·eb＝ ea＋b，∴r＝q，故选 C．9．不等式(x－2a)(x＋1)(x－3)<0 的解集为(－∞，－1)∪(3,4)，则 a 的值为( D )A．－4B．－2C．4D．2[解析] 当 2a＝4 时，用穿针引线法易知不等式的解集满足题意，∴a＝2．10．下列函数中，最小值是 4 的函数是( C )A．y＝x＋4xB．y＝sinx＋si4nx(0<x<π) C．y＝ex＋4e－x(其中 e 为自然对数的底数)D．y＝log3x＋logx81 [解析] 当 x＜0 时，y＝x＋4x≤－4，排除 A；∵0＜x＜π，∴0＜sinx＜1.y＝sinx＋si4nx≥4.但 sinx＝si4nx无解，排除 B；ex＞0，y＝ex＋4e－x≥4.等号在 ex＝e4x即 ex＝2 时成立．∴x＝ln2，D 中，x＞0 且 x≠1，若 0＜x＜1，则 log3x＜0，logx81＜0，∴排除 D．11．(2016·全国卷Ⅰ理，8)若 a>b>1,0<c<1，则( C )A．ac<bcB．abc<bacC．alogbc<blogacD．logac<logbc[解析] 对于选项 A，考虑幂函数 y＝xc，因为 c>0，所以 y＝xc 为增函数，又 a>b>1，所以 ac>bc，A 错．对于选项 B，abc<bac⇔(ba)c<ba，又 y＝(ba)x 是减函数，所以 B 错．对于选项 D，由对数函数的性质可知 D 错，故选 C． 12．(2018－2019 学年度吉林省德惠市实验中学高二月考)函数 y＝xx2－＋12(x＞1)的最小值是( A )A．2 3＋2B．2 3－2C．2 3D．2[解析]y＝xx2－＋12＝x－12＋2 x－1 x－1＋3＝(x－1)＋x－3 1＋2，∵x＞1，∴(x－1)＋x－3 1＋2≥2x－1·3 x－1＋2＝2 3＋2，当且仅当 x－1＝x－3 1，即(x－1)2＝3，x－1＝ 3，x＝ 3＋1 时，等号成立．二、填空题(本大题共 4 个小题，每个小题 5 分，共 20 分，将正确答案填在题中横线上)13．不等式 2x2＋2x－4≤12的解集为__[－3,1]__．[解析] 不等式 2x2＋2x－4≤12化为 2x2＋2x－4≤2－1，∴x2＋2x－4≤－1，∴x2＋2x－3≤0，∴－3≤x≤1，∴原不等式的解集为[－3,1]． 14．函数 y＝a1－x(a>0，a≠1)的图象恒过定点 A，若点 A 在直线 mx＋ny－1＝0(m、n>0)上，则1m＋1n的最小值为__4__．[解析] 由题意知 A(1,1)，∴m＋n＝1，∵m>0，n>0，∴1m＋1n＝(1m＋1n)·1＝(1m＋1n)·(m＋n)＝nm＋mn＋2≥4．等号在nm＝mn时成立，由mnm＋ ＝mnn＝1，得 m＝n＝12．∴1m＋1n的最小值为 4．15．若mm2xx＋－11＜0(m≠0)对一切x≥4恒成立，则实数m1 的取值范围是__(－∞，－2)__．[解析] 依题意，对任意的 x∈[4，＋∞)，有 f(x)＝(mx＋1)(m2x－1)＜0 恒成立，结合图象分析可知⎩⎪⎨⎪⎧m ＜0－1m＜41m 2＜4，由此解得m ＜－12，即实数m 的取值范围是(－∞，－12)．16．某校今年计划招聘女教师a 名，男教师b 名，若a 、b 满足不等式组⎩⎪⎨⎪⎧2a －b ≥5a －b ≤2a <7，设这所学校今年计划招聘教师最多x 名，则x ＝__13__．[解析] 由题意得x ＝a ＋b ，如图所示，画出约束条件所表示的可行域，作直线l ：b ＋a ＝0，平移直线l ，再由a ，b ∈N ，可知当a ＝6，b ＝7时，x 取最大值，∴x ＝a ＋b ＝13．三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤) 17．(本题满分10分)若函数f (x )＝lg(8＋2x －x 2)的定义域为M ，函数g (x )＝1－2x －1的定义域为N ，求集合M 、N 、M ∩N ．[解析] 由8＋2x －x 2>0，即x 2－2x －8<0， ∴(x －4)(x ＋2)<0， ∴－2<x <4． ∴M ＝{x |－2<x <4}． 由1－2x －1≥0，得x －3x －1≥0， ∴x <1或x ≥3． ∴N ＝{x |x <1或x ≥3}．∴M ∩N ＝{x |－2<x <1或3≤x <4}．18．(本题满分12分)不等式(m 2－2m －3)x 2－(m －3)x －1<0对一切x ∈R 恒成立，求实数m 的取值范围．[解析] 由m 2－2m －3＝0，得m ＝－1或m ＝3． 当m ＝3时，原不等式化为－1<0恒成立； 当m ＝－1时，原不等式化为4x －1<0，∴x <14，故m ＝－1不满足题意．当m 2－2m －3≠0时，由题意，得⎩⎪⎨⎪⎧m 2－2m －3<0Δ＝[－m －3]2＋4m 2－2m －3<0，即⎩⎪⎨⎪⎧－1<m <3－15<m <3，∴－15<m <3．综上可知，实数m 的取值范围是－15<m ≤3．19．(本题满分12分)(2018－2019学年度福建莆田一中高二月考)解关于x 的不等式m 2x 2＋2mx －3＜0(m ∈R )．[解析] 当m ＝0时，原不等式化为－3＜0，∴x ∈R ． 当m ≠0时，原不等式化为(mx －1)(mx ＋3)＜0， ∵m 2＞0，∴(x －1m )(x ＋3m)＜0．当m ＞0时，－3m ＜x ＜1m ，当m ＜0时，1m＜x ＜－3m．综上所述，当m ＝0时，原不等式的解集为R ； 当m ＞0时，原不等式的解集为(－3m ，1m )；当m ＜0时，原不等式的解集为(1m，－3m)．20．(本题满分12分)某摩托车生产企业，上年度生产摩托车的投入成本为1万元/辆，出厂价为1.2万元/辆，年销售量为1 000辆．本年度为适应市场需求，计划提高产品档次，适度增加投入成本．若每辆车投入成本增加的比例为x (0<x <1)，则出厂价相应的提高比例为0.75x ，同时预计年销售量增加的比例为0.6x ．已知年利润＝(出厂价－投入成本)×年销售量．(1)写出本年度预计的年利润y 与投入成本增加的比例x 的关系式；(2)为使本年度的年利润比上年度有所增加，问投入成本增加的比例x 应在什么范围内？[解析] (1)依题意得y ＝[1.2×(1＋0.75x )－1×(1＋x )]×1 000×(1＋0.6x )(0<x <1)． 整理，得：y ＝－60x 2＋20x ＋200(0<x <1)． ∴本年度年利润与投入成本增加的比例的关系式为y ＝－60x 2＋20x ＋200(0<x <1)．(2)要保证本年度的年利润比上年度有所增加，当且仅当⎩⎪⎨⎪⎧y － 1.2－1×1 000>00<x <1，即⎩⎪⎨⎪⎧－60x 2＋20x >00<x <1，解得：0<x <13，所以为保证本年度的年利润比上年度有所增加，投入成本增加的比例x 应满足0<x <13．21．(本题满分12分)若a ＜1，解关于x 的不等式axx －2>1 ．[解析] a ＝0时，不等式的解集为∅，ax x －2>1⇔a －1x ＋2x －2＞0 ⇔[(a －1)x ＋2](x －2)＞0． ∵a ＜1，∴a －1＜0． ∴化为(x －21－a)(x －2)＜0， 当0<a <1时，21－a >2，∴不等式的解为2<x <21－a ；当a <0时，1－a >1， ∴21－a<2， ∴不等式解为21－a<x <2，∴当0＜a ＜1时，不等式解集为⎩⎨⎧⎭⎬⎫x |2＜x ＜21－a ；当a ＜0时，不等式解集为⎩⎨⎧⎭⎬⎫x |21－a ＜x ＜2；当a ＝0时，解集为∅． 22．(本题满分12分)已知关于x 的方程(m ＋1)x 2＋2(2m ＋1)x ＋1－3m ＝0的两根为x 1、x 2，若x 1<1<x 2<3，求实数m 的取值范围．[解析] 设f (x )＝(m ＋1)x 2＋2(2m ＋1)x ＋1－3m ，显然m ＋1≠0． (1)当m ＋1>0时，可画简图：则⎩⎪⎨⎪⎧ m ＋1>0f 1<0f 3>0，即⎩⎪⎨⎪⎧ m >－1m <－2m >－89，不等式组无解．(2)当m ＋1<0时，可画简图：则⎩⎪⎨⎪⎧m ＋1<0f 1>0f 3<0，即⎩⎪⎨⎪⎧m <－1m >－2m <－89.得－2<m <－1．由(1)、(2)知m 的取值范围是(－2，－1)．。

第四节 基本不等式【知识清单】1、如果R b a ∈,，那么ab b a 222≥+（当且仅当b a =时，等号成立） 2、基本不等式： 如果0,>b a ，那么ab ba ≥+2（当且仅当b a =时，等号成立） （其中2ba +称为算术平均数，ab 称为几何平均数，因此也称均值不等式） 注：两个正数的算术平均数不小于其几何平均数。

3、利用基本不等式求最值问题 已知,0,0>>y x 则（1）若积xy 是定值,p 则当且仅当y x =时，y x +有最小值是.2p (记：积定和最小)．（2）若和y x +是定值,p ，则当且仅当y x =时，xy 有最大值是.42p (记：和定积最大)． 注①基本不等式主要是利用和积转化求最值。

②利用基本不等式求最值时，要注意其必须满足的三个条件：01一正二定三相等．“一正”就是各项必须为正数；【例】 )0(41>+=x xx y 的最小值是________ 解析：141241=⋅≥+=x x x x y （当且仅当x x 41=即21=x 时，等号成立） 【例】若正数b a ,满足111=+b a ，则11614-+-b a 的最小值________ 解析：111=+b a 变形为ab b a =+；161642)1)(1(64211614=+--=--≥-+-b a ab b a b a 02“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值； 【例】已知45<x ，则函数54124-+-=x x y 的最小值为______ 解析：,2)]54([1)]54([≥--+--x x （当且仅当41=x 时，等号成立）1541242)54(1)54(≤-+-⇒-≤-+-x x x x03“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方．这是只能利用对勾函数结合单调性或导数解决。

第5讲基本不等式1．基本不等式：ab≤a＋b2(1)基本不等式成立的条件：a≥0，b≥0.(2)等号成立的条件：当且仅当时取等号．(3)其中称为正数a，b的算术平均数，称为正数a，b的几何平均数．2．利用基本不等式求最值已知x≥0，y≥0，则(1)如果积xy是定值p，那么当且仅当时，x＋y有最小值是．(简记：积定和最小)(2)如果和x＋y是定值s，那么当且仅当时，xy有最大值是．(简记：和定积最大)常用结论几个重要的不等式(1)a2＋b2≥2ab(a，b∈R)，当且仅当a＝b时取等号．(2)ab(a，b∈R)，当且仅当a＝b时取等号．(3)a2＋b22≥(a，b∈R)，当且仅当a＝b时取等号．(4)b a＋ab≥2(a，b同号)，当且仅当a＝b时取等号．考点1利用基本不等式求最值[典例]1.（2022·河北·高三阶段练习）已知实数a ，b 满足条件33ba b ++=，则22a b +的最小值为（）A ．8B ．6C ．4D ．22．（2022·湖南湖南·二模）函数()122y x x x =+>-+的最小值为（）A ．3B ．2C ．1D ．03．（多选）（2022·河北石家庄·二模）设正实数m ，n 满足2m n +=，则下列说法正确的是（）A ．11m n+上的最小值为2B ．mn 的最大值为1C 的最大值为4D ．22m n +的最小值为544.[2021河南平顶山模拟]若对于任意x >0，不等式xx 2＋3x ＋1≤a 恒成立，则实数a 的取值范围为()A ．15，＋BC ∞D ∞，15[举一反三]1．（2022·山西·怀仁市第一中学校二模（文））函数413313y x x x ⎛⎫⎪⎝=>-⎭+的最小值为（）A ．8B ．7C ．6D ．52．（2022·安徽·高三阶段练习（文））已知0x >，0y >，22x y +=，则12x y+的最小值是（）A ．1B ．2C ．4D ．63．（2022·全国·模拟预测）已知a ，b 为非负数，且满足26a b +=，则()()2214a b ++的最大值为（）A ．40B ．1674C ．42D ．16944．（2022·重庆巴蜀中学高三阶段练习）已知正实数a ，b 满足220ab a +-=，则4a b +的最小值是（）A ．2B ．2C ．2D ．65．（多选）（2022·河北保定·一模）下面描述正确的是（）A ．已知0a >，0b >，且1a b +=，则22log log 2a b +≤-B ．函数()lg f x x =，若0a b <<，且()()f a f b =，则2+a b 的最小值是C ．已知()1210,012x y x x y+=>>++，则3x y +的最小值为2+D ．已知()22200,0x y x y xy x y +---+=>>，则xy 的最小值为7126．（多选）（2022·重庆八中高三阶段练习）设001a b a b >>+=，，，则下列不等式中一定成立的是（）A ．114a b+≥B ．2212a b +≥CD ．10b +<7．（2022·天津市西青区杨柳青第一中学高三阶段练习）已知a ，b 为正实数，且2a b +=，则2221a b a b +++的最小值为____________，此时=a ____________．8．（2022·浙江·镇海中学模拟预测）已知1x y >>，则()41x y x y xy y-+++-的最小值为___________.9．（2022·天津·大港一中高三阶段练习）设0m n >>，那么()41m m n n+-的最小值是___________.10．（2022·天津河北·一模）已知0a >，0b >，且1a b +=，则11a ba b +++的最大值为__________.11．（2022·全国·高三专题练习）已知0,0,0,233x y z x y z >>>++=，求222111()(2)(3)462x y z y z x+++++的最小值；考点2利用基本不等式证明不等式（2022·全国·高三专题练习）已知,,a b c 都是正数，求证：(1)()()24a b ab cabc ++≥；(2)若1a b c ++=，则11192a b b c c a ++≥+++.[举一反三]1．（2022·云南·昆明一中高三阶段练习（文））已知a ，b ，c 为正数.(1)求24a a +的最小值；(2)求证：bc ac ab a b c a b c++≥++.2．（2022·陕西·西安工业大学附中高三阶段练习（文））已知0,0a b >>.(1)若2a b +=，求1411+++a b的最小值；(2)求证：2222(1)++≥++a b a b ab a b .3．（2022·河南开封·二模（文））已知,,R a b c +∈，且abc =1.(1)求证：222111a b c a b c++++≥；(2)若a =b +c ，求a 的最小值.4．（2022·全国·高三专题练习）已知正数a ，b ，c 满足3a b c ++=．(1)求abc 的最大值；(2)证明：3333a b b c c a abc ++≥．考点3基本不等式中的恒成立问题典例1．（2022·全国·高三专题练习）若对任意220,1xx a x x >≥++恒成立，则实数a 的取值范围是（）A ．[1,)-+∞B ．[3,)+∞C ．2,3⎡⎫+∞⎪⎢⎣⎭D ．(,1]-∞2．（2022·全国·高三专题练习）设,a b c >>，n N ∈，且2110na b b c a c+≥---恒成立，则n 的最大值是（）A ．2B ．3C ．4D ．5[举一反三]1．（2021·重庆梁平·高三阶段练习）已知正实数a ，b 满足191a b+=，若不等式2418a b x x m +≥-++-对任意的实数x 恒成立，则实数m 的取值范围是（）A ．[)3,+∞B ．(],3-∞C ．(],6-∞D ．[)6,+∞2．（2021·浙江·模拟预测）对任意正实数,a b不等式2(1)2a b ab a bλλ+-+≥+则（）A ．实数λ有最小值1B ．实数λ有最大值1C ．实数λ有最小值12D ．实数λ有最大值123．（多选）（2022·全国·高三专题练习）当0x >，0y >，R m ∈时，2222y xm m k x y+>-++恒成立，则k 的取值可能是（）A ．2-B ．1-C ．1D ．24．（2022·全国·高三专题练习）不等式22221122xy yz a a x y z ++-++≤对任意正数x ，y ，z 恒成立，则a 的最大值是__________．5．（2021·重庆一中高三阶段练习）已知对任意正实数x ，y ，恒有()2222x y a x xy y +-+≤，则实数a 的最小值是___________.6．（2022·全国·高三专题练习）若不等式()x a x y ++对一切正实数,x y 恒成立，则实数a 的最小值为_____．考点4基本不等式与其他专题综合典例1．（2022·安徽安庆·二模（文））若函数()41sin 2cos 33f x x x a x =-+在(),-∞+∞内单调递增，则实数a 的取值范围是___________.2.[2021湖北鄂东南联考]方程(x 2018＋1)(1＋x 2＋x 4＋…＋x 2016)＝2018x 2017的实数解的个数为________．3．（2022·广东·高三阶段练习）在足球比赛中，球员在对方球门前的不同的位置起脚射门对球门的威胁是不同的，出球点对球门的张角越大，射门的命中率就越高.如图为室内5人制足球场示意图，设球场（矩形）长BC 大约为40米，宽AB 大约为20米，球门长PQ 大约为4米.在某场比赛中有一位球员欲在边线BC 上某点M 处射门（假设球贴地直线运行），为使得张角PMQ ∠最大，则BM 大约为（）（精确到1米）A ．8米B ．9米C ．10米D ．11米[举一反三]1．（2022·北京·101中学高三阶段练习）已知某产品的总成本C （单位：元）与年产量Q （单位：件）之间的关系为23300010C Q =+．设该产品年产量为Q 时的平均成本为f （Q ）（单位：元/件），则f （Q ）的最小值是（）A ．30B ．60C ．900D ．18002．（多选）（2022·重庆·模拟预测）已知ABC 为锐角三角形，且sin sin sin A B C =，则下列结论中正确的是（）A ．tan tan tan tanBC B C +=B ．tan tan tan tan tan tan A B C A B C =++C ．41tan 3A <≤D ．tan tan tan A B C 的最小值为43．（2021·全国·高三专题练习）如图，将一矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ，要求点B 在AM 上，点D 在AN 上，且对角线MN 过点C ，已知4AB =，3AD =，那么当BM =_______时，矩形花坛的AMPN 面积最小，最小面积为______.第5讲基本不等式1．基本不等式：ab≤a＋b2(1)基本不等式成立的条件：a≥0，b≥0.(2)等号成立的条件：当且仅当a＝b时取等号．(3)其中a＋b2称为正数a，b的算术平均数，ab称为正数a，b的几何平均数．2．利用基本不等式求最值已知x≥0，y≥0，则(1)如果积xy是定值p，那么当且仅当x＝y时，x＋y有最小值是2p．(简记：积定和最小)(2)如果和x＋y是定值s，那么当且仅当x＝y时，xy有最大值是s24．(简记：和定积最大)常用结论几个重要的不等式(1)a2＋b2≥2ab(a，b∈R)，当且仅当a＝b时取等号．(2)ab(a，b∈R)，当且仅当a＝b时取等号．(3)a2＋b22≥(a，b∈R)，当且仅当a＝b时取等号．(4)b a＋ab≥2(a，b同号)，当且仅当a＝b时取等号．考点1利用基本不等式求最值[典例]1.（2022·河北·高三阶段练习）已知实数a ，b 满足条件33ba b ++=，则22a b +的最小值为（）A ．8B ．6C ．4D ．2【答案】D【解析】因为33ba b ++=≥，当且仅当33a b=，即a b =时取等号，所以643a b a b ++≥⋅，所以24a b +≥，2a b +≥，()222122a b a b +≥+=，当且仅当1a b ==时等号成立，所以22a b +的最小值为2故选：D.2．（2022·湖南湖南·二模）函数()122y x x x =+>-+的最小值为（）A ．3B ．2C ．1D ．0【答案】D【解析】因为2x >-，所以20x +>，102x >+，利用基本不等式可得11222022x x x x +=++-≥=++，当且仅当122x x +=+即1x =-时等号成立.故选：D.3．（多选）（2022·河北石家庄·二模）设正实数m ，n 满足2m n +=，则下列说法正确的是（）A ．11m n+上的最小值为2B ．mn 的最大值为1C的最大值为4D ．22m n +的最小值为54【答案】AB【解析】∵0,0,2m n m n >>+=，∴()1111111222222n m m n m n m n m n ⎛⎫⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，当且仅当n mm n=，即1m n ==时等号成立，故A 正确；2m n +=≥ 1mn ≤，当且仅当1m n ==时，等号成立，故B 正确；22224⎡⎤≤+=⎢⎥⎣⎦，2=，当且仅当1m n ==时等号成立，最大值为2，故C 错误；()22222m n m n++≥=，当且仅当1m n ==时等号成立，故D 错误．故选：AB4.[2021河南平顶山模拟]若对于任意x >0，不等式xx 2＋3x ＋1≤a 恒成立，则实数a 的取值范围为()A ．15，＋BC ∞D ∞，15[答案]A[解析]由x >0，xx 2＋3x ＋1＝1x ＋1x＋3，令t ＝x ＋1x ，则t ≥2x ·1x＝2，当且仅当x ＝1时，t 取得最小值2.x x 2＋3x ＋1取得最大值15，所以对于任意的x >0，不等式x x 2＋3x ＋1≤a 恒成立，则a ≥15.[举一反三]1．（2022·山西·怀仁市第一中学校二模（文））函数413313y x x x ⎛⎫⎪⎝=>-⎭+的最小值为（）A ．8B ．7C ．6D ．5【答案】D【解析】因为13x >，所以3x －1>0，所以()4433112153131y x x x x =+=-++≥=--，当且仅当43131x x -=-，即x =1时等号成立，故函数413313y x x x ⎛⎫⎪⎝=>-⎭+的最小值为5．故选：D ．2．（2022·安徽·高三阶段练习（文））已知0x >，0y >，22x y +=，则12x y+的最小值是（）A ．1B ．2C ．4D ．6【答案】C【解析】解：因为0x >，0y >，22x y +=，所以()1211214122244222y x x y x y x y x y ⎛⎛⎫⎛⎫+=++=+++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝，当且仅当4y x x y =，即12x =，1y =时取等号；故选：C3．（2022·全国·模拟预测）已知a ，b 为非负数，且满足26a b +=，则()()2214a b ++的最大值为（）A ．40B ．1674C ．42D ．1694【答案】D 【解析】()()222222222214444444a b ab a b a b ab ab a b ++=+++=++-++()()()22222362a b ab ab =++-=+-，又2112902()2222a b ab a b +≤=⋅⋅≤=，当且仅当3,32a b ==时取“=”，则22916936(2)36(2)24ab +-≤+-=，所以当3,32a b ==时，()()2214a b ++的最大值为1694.故选：D4．（2022·重庆巴蜀中学高三阶段练习）已知正实数a ，b 满足220ab a +-=，则4a b +的最小值是（）A ．2B ．2C ．2D ．6【答案】B【解析】由220ab a +-=，得22a b =+，所以()a b b b b b +=+=++-=++884222222，当且仅当,a b b b ==+++28222，即a b ==2取等号.故选：B.5．（多选）（2022·河北保定·一模）下面描述正确的是（）A ．已知0a >，0b >，且1a b +=，则22log log 2a b +≤-B ．函数()lg f x x =，若0a b <<，且()()f a f b =，则2+a b的最小值是C ．已知()1210,012x y x x y+=>>++，则3x y +的最小值为2+D ．已知()22200,0x y x y xy x y +---+=>>，则xy 的最小值为712【答案】AC【解析】对于选项A ，∵0a >，0b >，1a b +=，∴1a b =+≥，∴14ab ≤，当且仅当12a b ==时取等号，∴22221log log log log 24a b ab +=≤=-，∴A 正确；对于选项B ：因为1ab =，所以22a b a a+=+，又01a <<，所以由对勾函数的单调性可知函数()2=+h a a a在()0,1上单调递减，所以()()3,h a ∈+∞，即23+>a b ，故B 不正确；对于选项C ，根据题意，已知()()3121x y x x y +=+++-，则()()()21122123321212x x y x x y x x y x x y +⎛⎫+++++=++≥+⎡⎤ ⎣⎦++++⎝⎭当且仅当()21212++=++x x y x x y ，即1==x y时，等号成立，所以32x y +≥+，故C 正确；对于选项D ，()()2222032x y x y xy x y x y xy +---+=⇒+-+=-，令0x y t +=>，所以214t t -≥-，所以1732412xy xy -≥-⇒≥，此时1,2712x y xy ⎧+=⎪⎪⎨⎪=⎪⎩无解，所以选项D 不正确，故选：AC ．6．（多选）（2022·重庆八中高三阶段练习）设001a b a b >>+=，，，则下列不等式中一定成立的是（）A ．114a b+≥B ．2212a b +≥CD ．10b +<【答案】AB【解析】对于A ：因为001a b a b >>+=，，，所以()11111124b a a b a b a b a b ⎛⎫+=++=+++≥+ ⎪⎝⎭，当且仅当b a a b =，即12a b ==时取等号，所以114a b+≥成立.故A 正确；对于B ：因为001a b a b >>+=，，，所以2124a b ab +⎛⎫≤= ⎪⎝⎭，当且仅当12a b ==时取等号.所以()22212122a b a b ab ab +=+-=-≥成立.故B 正确；对于C ：因为001a b a b >>+=，，，所以()()113a b +++=，所以()()311a b =+++≥.记u =，则0u >，所以211336u a b =++++≤+=，所以u <≤≤故C 错误；对于D ：因为0,b >所以10+>b .故D 错误.故选：AB7．（2022·天津市西青区杨柳青第一中学高三阶段练习）已知a ，b 为正实数，且2a b +=，则2221a b a b +++的最小值为____________，此时=a____________．【答案】6-63+【解析】 a ,b 为正实数,且2a b +=,222221111a b b a a b a b +-+∴+=+++2111a b a b =++-++2111a b =+++()()1211131a b a b ⎛⎫=++++ ⎪+⎝⎭()2111331b a a b ⎛⎫+=+++ ⎪+⎝⎭(1133≥++当且仅当()2112b aa b a b ⎧+=⎪⎨+⎪+=⎩即6a =-4b =时取“=”故答案为:6-63+8．（2022·浙江·镇海中学模拟预测）已知1x y >>，则()41x y x y xy y-+++-的最小值为___________.【答案】9【解析】()()()()41414411911x y x y x y x y x y xy y x y x y -+⎡⎤-+⎛⎫⎡⎤⎣⎦++=++=-++++⎪⎢⎥---⎣⎦⎝⎭≥，当且仅当32x y =⎧⎨=⎩时等号成立，取等条件满足1x y >>，所以()41x y x y xy y -+++-的最小值为9.故答案为：99．（2022·天津·大港一中高三阶段练习）设0m n >>，那么()41m m n n+-的最小值是___________.【答案】8【解析】解：0m n >>Q ，所以()()2224m n n m m n n ⎡⎤-+-≤=⎢⎥⎣⎦，当且仅当m n n -=，即2m n =时取等号；所以214()m n n m ≥-，所以()()42422448114m m m m n nm m +≥+-⨯≥+==，当且仅当2244m m =，即1m =时取等号，所以()481m m n n +≥-，当且仅当1m =、12n =时取等号；故答案为：810．（2022·天津河北·一模）已知0a >，0b >，且1a b +=，则11a b a b +++的最大值为__________.【答案】23【解析】1111111111211111111a b a b a b a b a b a b +-+-⎛⎫+=+=-+-=-+ ⎪++++++++⎝⎭.因为0a >，0b >，且1a b +=，所以()1111111111311a b a b a b ⎛⎫⎛⎫+⋅=++++ ⎪ ⎪++++⎝⎭⎝⎭()1111142222311333b a a b ⎛++⎛⎫=++≥+=+= ⎪ ++⎝⎭⎝，当且仅当11111b a a b a b ++⎧=⎪++⎨⎪+=⎩即12a b ==时取等.所以114222111133a b a b a b ⎛⎫+=-≤-= ⎪++++⎝⎭.，即11a b a b +++的最大值为23.故答案为：23.11．（2022·全国·高三专题练习）已知0,0,0,233x y z x y z >>>++=，求222111()(2)(3)462x y z y z x+++++的最小值；【答案】274【解析】由222111[()(2)(3)]462x y z y z x+++++222(111)++2111[()1(2)1(3)1]462x y z y z x ≥+⨯++⨯++⨯2111[(23)()]462x y z y z x=+++++21232323[3()]623x y z x y z x y z x y z++++++=+++212332[3(3)]62323y x z x z y x y x z y z =+++++++2381(324≥+=.所以222111()(2)(3)462x y z y z x +++++≥274，当且仅当231x y z ===时等号成立，综上，222111()(2)(3)462x y z y z x +++++的最小值为274. 考点2利用基本不等式证明不等式（2022·全国·高三专题练习）已知,,a b c 都是正数，求证：(1)()()24a b ab cabc ++≥；(2)若1a b c ++=，则11192a b b c c a ++≥+++.【解】(1)()()2222244a b ab c abc a b acab bc abc++-=+++-()()()()22222222b a ac c a b bc c b a c a b c =-++-+=-+-，∵,,a b c 都是正数，∴()()220b a c a b c -+-≥，当且仅当“a b c ==”时等号成立，∴()()24a b ab c abc ++≥.(2)()()()11111112a b b c c a a b b c c a a b b c c a ⎛⎫++=+++++++⎡⎤ ⎪⎣⎦++++++⎝⎭132a b b c b c c a c a a b b c a b c a b c a b c a ⎡++++++⎤⎛⎫⎛⎫⎛⎫=++++++ ⎪ ⎪⎢⎥++++++⎝⎭⎝⎭⎝⎭⎣⎦132⎛≥+ ⎝()19322222=+++=，当且仅当“13a b c ===”时等号成立，∴11192a b b c c a ++≥+++.[举一反三]1．（2022·云南·昆明一中高三阶段练习（文））已知a ，b ，c 为正数.(1)求24a a +的最小值；(2)求证：bc ac ab a b c a b c++≥++.【解】(1)因为24a a+24=322a a a ++≥=，当且仅当“2a =”时等号成立，所以当2a =时，24a a+的最小值为3.(2)因为2bc ac c a b +≥=，同理2ac ab a b c +≥，2bc ab b a c +≥，所以三式相加得22()bc ac ab a b c a bc ⎛⎫++≥++ ⎪⎝⎭，所以bc ac aba b c a b c++≥++，当且仅当“a b c ==”时等号成立2．（2022·陕西·西安工业大学附中高三阶段练习（文））已知0,0a b >>.(1)若2a b +=，求1411+++a b的最小值；(2)求证：2222(1)++≥++a b a b ab a b .【解】(1)因为0,0a b >>，所以10,10a b +>+>，又2a b +=，所以1++14a b +=，所以14114114(1)19()[(1)(1)][5](54)1141141144b a a b a b a b a b +++=++++=++≥+=++++++当且仅当14(1)112b a a b a b ++⎧=⎪++⎨⎪+=⎩，即1353a b ⎧=⎪⎪⎨⎪=⎪⎩时取等号，所以1411+++a b 的最小值为94.(2)因为22222a b a a b +≥①，222a b ab +≥②，22222a b b ab +≥③，所以，由①②③，同向不等式相加可得：222222222222a b a b a b ab ab ++≥++，当且仅当ab a b ==，即1a b ==时取等号.即2222(1)++≥++a b a b ab a b 成立.3．（2022·河南开封·二模（文））已知,,R a b c +∈，且abc =1.(1)求证：222111a b c a b c++++≥；(2)若a =b +c ，求a 的最小值.【解】(1)111abc abc abc bc ac ab a b c a b c++=++=++222222222222b c a c a b a b c +++≤++=++，当且仅当1a b c ===时等号成立.(2)依题意,,R a b c +∈，11,abc bc a==，所以a b c =+≥=，当且仅当b c =时等号成立.所以23322,2a a ≥≥，所以a 的最小值为232，此时23222a b c ===.4．（2022·全国·高三专题练习）已知正数a ，b ，c 满足3a b c ++=．(1)求abc 的最大值；(2)证明：3333a b b c c a abc ++≥．【解】(1)由a b c ++≥，当且仅当a b c ==时，取得等号．又3a b c ++=，所以3313abc ⎛⎫≤= ⎪⎝⎭．故当且仅当1a b c ===时，abc 取得最大值1．(2)证明：要证3333a b b c c a abc ++≥，需证2223a b c c a b++≥．因为()222222a b c a b c a b c c a b c a bc a b ⎛⎫⎛⎫⎛⎫+++++=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()26a b c ≥=++=，即2223a b c c a b++≥，当且仅当1a b c ===时取得等号．故3333a b b c c a abc ++≥． 考点3基本不等式中的恒成立问题1．（2022·全国·高三专题练习）若对任意220,1xx a x x >≥++恒成立，则实数a 的取值范围是（）A ．[1,)-+∞B ．[3,)+∞C ．2,3⎡⎫+∞⎪⎢⎣⎭D ．(,1]-∞【答案】C【解析】解：因为0x >，所以22221131x x x x x =≤=++++，当且仅当1x x =即1x =时取等号，因为221x a x x ≥++恒成立，所以23a ≥，即2,3a ⎡⎫∈+∞⎪⎢⎣⎭；故选：C2．（2022·全国·高三专题练习）设,a b c >>，n N ∈，且2110na b b c a c+≥---恒成立，则n 的最大值是（）A ．2B ．3C ．4D ．5【答案】C【解析】解：2110n a b b c a c+≥---等价于2110()a c n a b b c ⎛⎫+-≥ ⎪--⎝⎭，()110110()a c a b b c a b b c a b b c ⎛⎫⎛⎫+-=-+- ⎪ ⎪----⎝⎭⎝⎭10()111111b c a ba b b c --=++≥+=+--故得到211,n n N +≥∈则n 的最大值是4.故选：C.[举一反三]1．（2021·重庆梁平·高三阶段练习）已知正实数a ，b 满足191a b+=，若不等式2418a b x x m +≥-++-对任意的实数x 恒成立，则实数m 的取值范围是（）A ．[)3,+∞B ．(],3-∞C ．(],6-∞D ．[)6,+∞【答案】D【解析】因为0a >，0b >，191a b+=，所以()199101016a a b a b a b a b b ⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当9b a a b =，即4a =，12b =时取等号．由题意，得241186x x m ≥-++-，即242x x m --≥-对任意的实数x 恒成立，又()2242266x x x --=--≥-，所以6m -≥-，即6m ≥．故选：D ．2．（2021·浙江·模拟预测）对任意正实数,a b不等式2(1)2a b ab a bλλ+-+≥+则（）A ．实数λ有最小值1B ．实数λ有最大值1C ．实数λ有最小值12D ．实数λ有最大值12【答案】C【解析】2(1)2a b ab a b λλ+-++故222a b ab ab a b a b λ+⎛⎫-≥ ⎪++⎝⎭，()()22022a b a b ab a b a b -+-=≥++，当a b =时，不等式恒成立；当a b¹时，222aba ba b aba bλ+≥+-+12，a b=时等号成立，a b¹12<，故12λ≥.故选：C.3．（多选）（2022·全国·高三专题练习）当0x>，0y>，Rm∈时，2222y x m m kx y+>-++恒成立，则k的取值可能是（）A．2-B．1-C．1D．2【答案】AB【解析】因为0x>，0y>，所以222y xx y+≥=，当且仅当2x y=时，等号成立．因为()222111m m k m k k-++=--++≤+．若2222y x m m kx y+>-++恒成立，则12k+<，解得1k<．故选：AB.4．（2022·全国·高三专题练习）不等式22221122xy yz a ax y z++-++≤对任意正数x，y，z恒成立，则a的最大值是__________．【答案】1【解析】因为222222212222xy yz xy yz xy yzx y z x y y z xy yz+++==++++++≤，当x y z==时取等号，所以2222xy yzx y z+++的最大值是12，即211122a a+-≥，解得112a-≤≤，所以a的最大值是1．故答案为：15．（2021·重庆一中高三阶段练习）已知对任意正实数x，y，恒有()2222x y a x xy y+-+≤，则实数a的最小值是___________.【答案】2【解析】解：因为0,0x y>>，则()2220x xy y x y xy-+=-+>，则()2222x y a x xy y +-+≤，即2222x y a x xy y +-+≤，又22222211x y xy x xy y x y +=-+-+，因为222x y xy +≥，所以22112xy x y -≥+，所以22121xy x y≤-+，即22222x y x xy y +≤-+，当且仅当x y =时，取等号，所以2222max2x y x xy y ⎛⎫+= ⎪-+⎝⎭，所以2a ≥，即实数a 的最小值是2.故答案为：2.6．（2022·全国·高三专题练习）若不等式()x a x y ++对一切正实数,x y 恒成立，则实数a 的最小值为_____．【答案】2【解析】()()22=22x a x y x x x y x y ++∴++++ ，当且仅当=2x y 时取等号，0,0x y >> 0x y ∴+>()x a x y ++maxa ∴≥⎝⎭222x yx y +≤=+max=2a ∴≥⎝⎭，a ∴的最小值为2故答案为：2考点4基本不等式与其他专题综合[典例]1．（2022·安徽安庆·二模（文））若函数()41sin 2cos 33f x x x a x =-+在(),-∞+∞内单调递增，则实数a 的取值范围是___________.【答案】[]33-【解析】因函数()f x 在(),-∞+∞内单调递增，则R x ∀∈，42()cos 2sin 033f x x a x '=--≥，即42sin cos 233a x x ≤-，整理得242sin 33a x x ≤+，当sin 0x =时，则203≤成立，R a ∈，当sin 0x >时，42sin 33sin a x x ≤+，而4221sin (2sin )33sin 3sin x x x x +=+≥当且仅当12sin sin x x =，即sin 2x =时取“=”，则有3a ≤，当sin 0x <时，42sin 33sin a x x ≥+，而4221sin [(2sin )]33sin 3sin x x x x +=--+≤--当且仅当12sin sin x x -=-，即sin x =时取“=”，则有a ≥综上得，33a -≤≤所以实数a 的取值范围是[]33-.故答案为：,33⎡-⎢⎣⎦2.[2021湖北鄂东南联考]方程(x 2018＋1)(1＋x 2＋x 4＋…＋x 2016)＝2018x 2017的实数解的个数为________．[答案]1[解析]由题意知x >0，∴(x 2018＋1)(1＋x 2＋x 4＋…＋x 2016)≥2x 2018·1×12(21·x 2016＋2x 2·x 2014＋…＋2x 2016·1)＝2018x 2017，当且仅当x ＝1时等号成立，因此实数解的个数为1.3．（2022·广东·高三阶段练习）在足球比赛中，球员在对方球门前的不同的位置起脚射门对球门的威胁是不同的，出球点对球门的张角越大，射门的命中率就越高.如图为室内5人制足球场示意图，设球场（矩形）长BC 大约为40米，宽AB 大约为20米，球门长PQ 大约为4米.在某场比赛中有一位球员欲在边线BC 上某点M 处射门（假设球贴地直线运行），为使得张角PMQ ∠最大，则BM 大约为（）（精确到1米）A ．8米B ．9米C ．10米D ．11米【答案】C【解析】由题意知，8,12PB QB ==，设,,PMB QMB BM x ∠=∠==αβ，则812tan ,tan x x==αβ，所以()212844tan tan 1289696962612x x x PMQ x x x x x x x -∠=-===≤=++⋅+⋅βα，当且仅当96x x =，即96x =9610≈，所以BM 大约为10米.故选：C.[举一反三]1．（2022·北京·101中学高三阶段练习）已知某产品的总成本C （单位：元）与年产量Q （单位：件）之间的关系为23300010C Q =+．设该产品年产量为Q 时的平均成本为f （Q ）（单位：元/件），则f （Q ）的最小值是（）A ．30B ．60C ．900D ．1800【答案】B【解析】23300010()Q C f Q Q Q +==3300010Q Q =+3300022306010Q Q≥⋅⨯=，当且仅当3300010Q Q=，即当100Q =时等号成立.所以f （Q ）的最小值是60.故选：B.2．（多选）（2022·重庆·模拟预测）已知ABC 为锐角三角形，且sin sin sin A B C =，则下列结论中正确的是（）A ．tan tan tan tanBC B C +=B ．tan tan tan tan tan tan A B C A B C =++C ．41tan 3A <≤D ．tan tan tan A B C 的最小值为4【答案】ABC【解析】解：因为()sin sin sin cos sin cos sin sin A B C B C C B B C =+=+=，两边同除cos cos B C 得tan tan tan tan B C B C +=，故A 正确；由均值不等式tan tan tan tan B C B C +=≥tan tan 4B C ≥当且仅当tan tan 2B C ==时取等号，()tan tan tan tan 1tan tan B CA B C B C+=-+=--，所以tan tan tan tan tan tan A B C A B C ++=，故B 正确；tan tan 1tan 1tan tan 1tan tan 1B C A B C B C ==+--，由tan tan 4B C ≥，所以110tan tan 13B C <≤-，所以得31tan 1ta 1n tan 14A B C =+≤-<，故C 正确；22tan tan 1tan tan 12tan tan t 1ta t n t 1a n t n a n an a A B C B C B C B B C C ==-++--，由tan tan 13B C -≥且1y x x =+在[)3,+∞上单调递增，所以tan tan tan A B C 的最小值为163，故D 错误．故选：ABC3．（2021·全国·高三专题练习）如图，将一矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ，要求点B 在AM 上，点D 在AN 上，且对角线MN 过点C ，已知4AB =，3AD =，那么当BM =_______时，矩形花坛的AMPN 面积最小，最小面积为______.【答案】448【解析】解：设BM x =，则34x x AN =+，则123AN x=+，则()1248433242448AMPN S x x x x ⎛⎫=++=+++= ⎪⎝⎭，当且仅当483xx=，即4x=时等号成立，故矩形花坛的AMPN面积最小值为48．即当4BM=时，矩形花坛的AMPN面积最小，最小面积为48.故答案为：4；48.。