当前位置：文档之家 › 图解伺服电机选型实例

图解伺服电机选型实例

  • 格式：doc
  • 大小：371.00 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

伺服电机计算选择应用实例

伺服电机计算选择应用实例

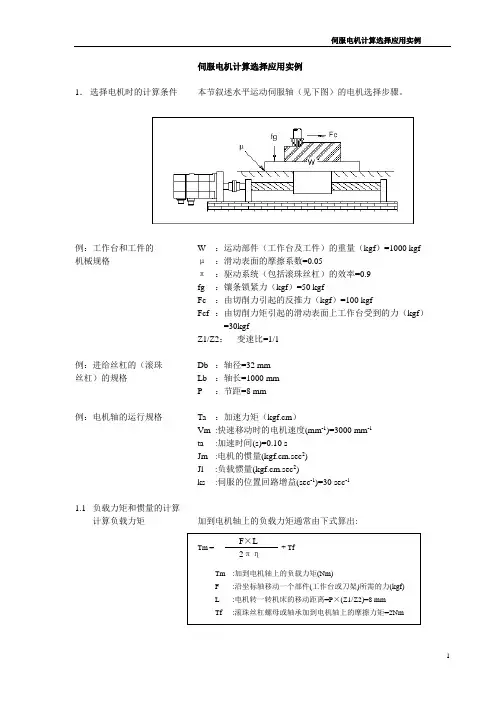
伺服电机计算选择应用实例1． 选择电机时的计算条件 本节叙述水平运动伺服轴（见下图）的电机选择步骤。

例：工作台和工件的 W ：运动部件（工作台及工件）的重量（kgf ）=1000 kgf 机械规格 μ ：滑动表面的摩擦系数=0.05π ：驱动系统（包括滚珠丝杠）的效率=0.9 fg ：镶条锁紧力（kgf ）=50 kgfFc ：由切削力引起的反推力（kgf ）=100 kgfFcf ：由切削力矩引起的滑动表面上工作台受到的力（kgf ）=30kgfZ1/Z2： 变速比=1/1 例：进给丝杠的（滚珠 Db ：轴径=32 mm 丝杠）的规格 Lb ：轴长=1000 mm P ：节距=8 mm例：电机轴的运行规格 Ta ：加速力矩（kgf.cm ）Vm :快速移动时的电机速度(mm -1)=3000 mm -1 ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2) Jl :负载惯量(kgf.cm.sec 2)ks :伺服的位置回路增益(sec -1)=30 sec -1 1.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + TfTm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L :电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2Nm无论是否在切削，是垂直轴还是水平轴，F 值取决于工作台的重量，摩擦系数。

若坐标轴是垂直轴，F 值还与平衡锤有关。

对于水平工作台，F 值可按下列公式计算： 不切削时： F = μ（W+fg ） 例如： F=0.05×(1000+50)=52.5 (kgf) Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf) 例如: F=100+0.05×(1000+50+30)=154(kgf) Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1，应根据数据单选择电机，其负载力矩在不切削时应大于0.9（Nm ），最高转速应高于3000（min -1）。

伺服电机计算选择应用实例全解

伺服电机计算选择应用实例全解

伺服电机计算选择应用实例1． 选择电机时的计算条件 本节叙述水平运动伺服轴（见下图）的电机选择步骤。

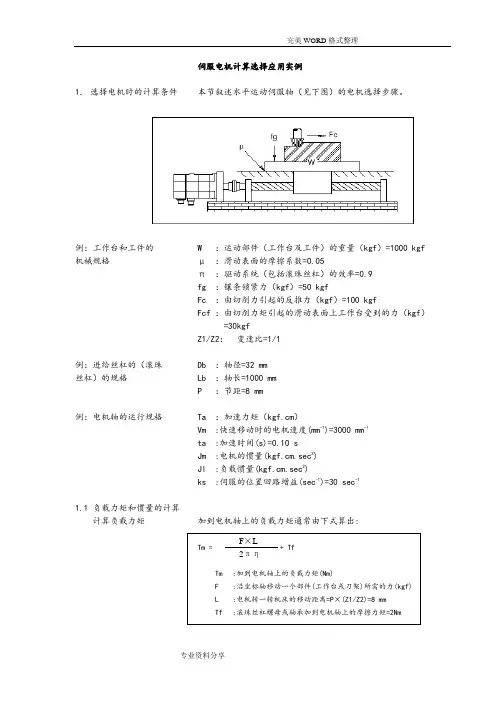
例：工作台和工件的W ：运动部件（工作台及工件）的重量（kgf ）=1000 kgf 机械规格 μ ：滑动表面的摩擦系数=0.05π ：驱动系统（包括滚珠丝杠）的效率=0.9 fg ：镶条锁紧力（kgf ）=50 kgfFc ：由切削力引起的反推力（kgf ）=100 kgfFcf：由切削力矩引起的滑动表面上工作台受到的力（kgf ） =30kgfZ1/Z2： 变速比=1/1例：进给丝杠的（滚珠 Db ：轴径=32 mm 丝杠）的规格 Lb ：轴长=1000 mm P ：节距=8 mm例：电机轴的运行规格 Ta ：加速力矩（kgf.cm ）Vm :快速移动时的电机速度(mm -1)=3000 mm -1 ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2) Jl :负载惯量(kgf.cm.sec 2)ks :伺服的位置回路增益(sec -1)=30 sec -11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L :电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF ×L2πη无论是否在切削，是垂直轴还是水平轴，F值取决于工作台的重量，摩擦系数。

若坐标轴是垂直轴，F值还与平衡锤有关。

对于水平工作台，F值可按下列公式计算：不切削时：F = μ（W+fg）例如：F=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1，应根据数据单选择电机，其负载力矩在不切削时应大于0.9（Nm），最高转速应高于3000（min-1）。

伺服电机选型计算实例

伺服电机选型计算实例

伺服电机选型计算实例伺服电机是一种控制器控制的电机，具有高精度和高速度的特点，广泛应用于机械设备中。

在选型伺服电机时，需要考虑多个参数来满足具体的应用要求。

下面以一个选型计算实例来详细介绍伺服电机的选型过程。

假设我们需要选型一台伺服电机用于驱动一个线传动机构，具体要求如下：1.最大负载力为2000N，工作速度范围为0-10m/s。

2. 线传动机构的负载惯量为500kg·m²。

3. 需要保证驱动精度在±0.2mm范围内。

4.工作环境温度范围为0-40℃。

首先，我们需要计算所需的转矩。

根据公式：转矩=负载力×工作半径，其中工作半径等于线传动机构的负载惯量÷2、由于我们没有具体的线传动机构参数，假设负载惯量为500kg·m²，即工作半径为0.25m。

则最大转矩=2000N×0.25m=500N·m。

考虑到一般情况下，峰值转矩为最大转矩的2倍，即1000N·m。

接下来，我们需要计算伺服电机的速度要求。

根据给定的工作速度范围0-10m/s，我们可以选择合适的额定转速。

假设我们选择的额定转速为2000rpm，则转速范围为0-2000rpm。

考虑到加速度和减速度的要求，一般额定转速的选择会略高于平均线速度，假设为2200rpm。

接下来，我们需要选择合适的伺服电机型号。

在选型之前，我们还需要考虑工作环境的温度范围。

根据给定的工作环境温度范围为0-40℃，我们需要选择具备合适温度范围的伺服电机。

一般伺服电机的温度范围为0-50℃，因此我们可以选择标准型号的伺服电机。

在选择伺服电机型号时，我们需要参考厂家提供的电机性能参数。

主要包括额定转矩、额定转速、额定电压、额定电流、额定功率等。

根据我们的要求，我们可以对比不同型号的伺服电机并选择合适的型号。

最后，我们需要根据具体应用需求考虑伺服电机的控制方式、接口类型以及其他附件等。

《伺服电机的选型》课件

《伺服电机的选型》课件
考虑环境因素
考虑工作环境的温度、湿度、尘埃等条件，选择能够 在恶劣环境下稳定运行的伺服电机。
规格匹配
电机尺寸
根据安装空间和实际需求，选择合适的电机 尺寸。
电机重量
对于需要轻量化的应用，应考虑电机的重量 。
接口兼容性
确保所选伺服电机与控制系统和驱动器之间 的接口兼容。
技术评估
技术规格比较
对比不同品牌和型号伺服电机的技术规格，评 估其性能优劣。
可能是由于散热不良、负载过大或润 滑不足，应加强散热、减轻负载或增 加润滑。
运行噪音
可能是轴承损坏、螺丝松动或电气问 题，应更换轴承、紧固螺丝或检查电 气线路。
振动过大
可能是机械不平衡、安装不正确或负 载不均，应重新平衡机械、纠正安装 或调整负载分布。
无法启动
可能是电源故障、控制信号问题或机 械卡阻，应检查电源、控制信号或消 除机械障碍。
产品测试报告
查看第三方测试报告或制造商提供的产品测试 数据，了解电机的实际性能表现。
客户评价
参考其他客户的评价和使用经验，了解电机的可靠性和售后服务。
价格比较
成本效益分析
综合考虑电机的性能、品牌、技术支持等因素，评估其性价比。
报价与谈判
向供应商询价，了解价格优惠和谈判空间，争取获得更好的采购条 件。
THANKS FOR WATCHING
感谢您的观看
防护等级与环境适应性：分析各品牌伺服 电机的防水、防尘等防护等级，以及在各 种恶劣环境下的稳定运行能力。
应用案例分享
案例1
数控机床：介绍品牌A的伺服电机 在数控机床中的应用案例，突出 其在高精度加工和高效生产方面 的优势。
案例2
包装机械：分享品牌B的伺服电机 在包装机械中的成功应用案例， 强调其在提高包装效率和降低成 本方面的作用。

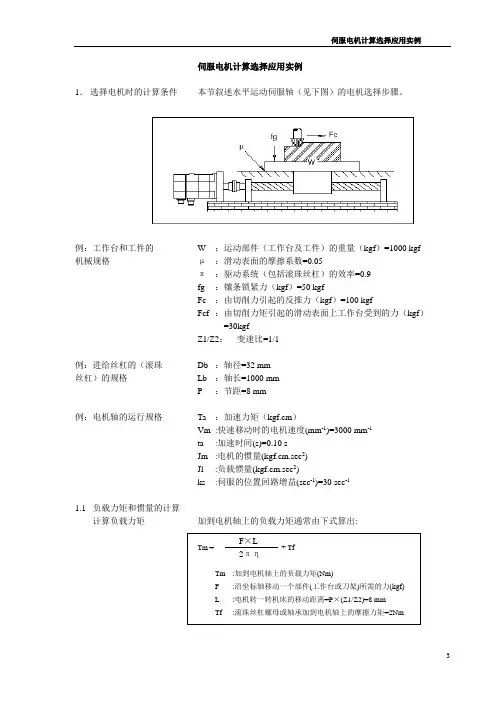
伺服电机计算选择应用实例

伺服电机计算选择应用实例

伺服电机计算选择应用实例1． 选择电机时的计算条件 本节叙述水平运动伺服轴（见下图）的电机选择步骤。

例：工作台和工件的 W ：运动部件（工作台及工件）的重量（kgf ）=1000 kgf 机械规格 μ ：滑动表面的摩擦系数=0.05π ：驱动系统（包括滚珠丝杠）的效率=0.9 fg ：镶条锁紧力（kgf ）=50 kgfFc ：由切削力引起的反推力（kgf ）=100 kgfFcf ：由切削力矩引起的滑动表面上工作台受到的力（kgf ）=30kgfZ1/Z2： 变速比=1/1例：进给丝杠的（滚珠 Db ：轴径=32 mm 丝杠）的规格 Lb ：轴长=1000 mm P ：节距=8 mm例：电机轴的运行规格 Ta ：加速力矩（kgf.cm ）Vm :快速移动时的电机速度(mm -1)=3000 mm -1ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2)Jl :负载惯量(kgf.cm.sec 2)ks:伺服的位置回路增益(sec -1)=30 sec-11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L:电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf :滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF ×L 2πη无论是否在切削，是垂直轴还是水平轴，F值取决于工作台的重量，摩擦系数。

若坐标轴是垂直轴，F值还与平衡锤有关。

对于水平工作台，F值可按下列公式计算：不切削时：F = μ（W+fg）例如：F=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1，应根据数据单选择电机，其负载力矩在不切削时应大于0.9（Nm），最高转速应高于3000（min-1）。

伺服电机计算选择应用实例

伺服电机计算选择应用实例

伺服电机计算选择应用实例1．选择电机时的计算条件本节叙述水平运动伺服轴（见下图）的电机选择步骤。

例：工作台和工件的W ：运动部件（工作台及工件）的重量（kgf）=1000 kgf 机械规格μ：滑动表面的摩擦系数=0.05π：驱动系统（包括滚珠丝杠）的效率=0.9fg ：镶条锁紧力（kgf）=50 kgfFc ：由切削力引起的反推力（kgf）=100 kgfFcf ：由切削力矩引起的滑动表面上工作台受到的力（kgf）=30kgfZ1/Z2：变速比=1/1例：进给丝杠的（滚珠Db ：轴径=32 mm丝杠）的规格Lb ：轴长=1000 mmP ：节距=8 mm例：电机轴的运行规格Ta ：加速力矩（kgf.cm）Vm :快速移动时的电机速度(mm-1)=3000 mm-1ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec2)Jl :负载惯量(kgf.cm.sec2)ks :伺服的位置回路增益(sec-1)=30 sec-11.1 负载力矩和惯量的计算计算负载力矩加到电机轴上的负载力矩通常由下式算出:Tm = + TfTm :加到电机轴上的负载力矩(Nm)F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf)L :电机转一转机床的移动距离=P×(Z1/Z2)=8 mmTf :滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF×L2πη无论是否在切削，是垂直轴还是水平轴，F值取决于工作台的重量，摩擦系数。

若坐标轴是垂直轴，F值还与平衡锤有关。

对于水平工作台，F值可按下列公式计算：不切削时：F = μ（W+fg）例如：F=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1，应根据数据单选择电机，其负载力矩在不切削时应大于0.9（Nm），最高转速应高于3000（min-1）。

伺服电机选型计算最简单方式

伺服电机选型计算最简单方式

伺服电机选型计算最简单方式伺服电机的工作原理下图所示是一种采用功率运算放大器LM675制成的伺服电动机控制电路，电动机采用直流伺服电动机。

从图可见，功率运算放大器LM675由15V供电，15V电压经RP1加到运算放大器LM675的同相输入端，LM675的输出电压加到伺服电动机的输入端。

电动机上装有测速信号产生器，用于实时检测电动机的转速。

实际上测速信号产生器是一种发电机，它输出的电压与转速成正比。

测速信号产生器G输出的电压经分压电路后作为速度误差信号反馈到运算放大器的反相输入端。

速度指令电位器RP1设定的电压值经R1.R2分压后加到运算放大器的同相输入端，相当于基准电压。

伺服电动机的控制原理图伺服电动机用字母M表示伺服电动机，是驱动系统的动力之源。

运算放大器：用电路名称表示，即LM675，是伺服控制电路中的放大器件，为伺服电动机提供驱动电流。

速度指令电位器RP1：在电路中设定运算放大器的基准电压，即速度设定。

放大器增益调整电位器RP2：在电路中分别用于微调放大器的增益和速度反馈信号的大小。

当电动机的负载发生变动时，反馈到运算放大器反相输入端的电压也会发生变化，即电动机负载加重时，速度会降低，测速信号产生器的输出电压也会降低，使运算放大器反相输入端的电压降低，该电压与基准电压之差增加，运算放大器的输出电压增加。

反之，当负载变小、电动机速度增加时，测速信号产生器的输出电压上升，加到运算放大器反相输入端的反馈电压增加，该电压与基准电压之差减小，运算放大器的输出电压下降，会使电动机的速度随之下降，从而使转速能自动稳定在设定值。

伺服电机优点1、精度：实现了位置，速度和力矩的闭环控制；克服了步进电机失步的问题；2、转速：高速性能好，一般额定转速能达到2000～3000转；3、适应性：抗过载能力强，能承受三倍于额定转矩的负载，对有瞬间负载波动和要求快速起动的场合特别适用；4、稳定：低速运行平稳，低速运行时不会产生类似于步进电机的步进运行现象。

伺服电机的选型计算及应用案例介绍

伺服电机的选型计算及应用案例介绍

1.滚珠丝杆的质量： Bw=ρxV=7.9*103*π(0.02/2)2*0.5
=1.24kg
2.负载部分的惯量：
JL=JC+JB=JC+BW*BD2/8+WA*BP2/4π2 =0.00001+(1.24*0.022)/8+10*0.022/4π2 =1.73*10-4kg.m2
3.预选电机
若选200W,则JM= 0.14*10-4kg.m2
六.实例应用讲解
案例1
已知：负载重量WA=10kg，螺杆螺距BP=20mm，螺杆直径 BD=20mm，螺杆长BL=0.5m，机械效率η=0.9，摩擦系数 μ=0.1，负载移动距离0.3m，加减速时间ta=td=0.1s，匀速 时间tb=0.8s，静止时间t4=1s。联轴器的惯量Jc= 10x10-6 kg.m2 .请选择满足负载需求的最小功率伺服电机。
2.与转动惯量有关的因素：
1.刚体的总质量 2.质量分布 3.转轴的位置
3.转动惯量的计算： （1）单个质点的转动惯量: J=mr2
（2）质量离散分布刚体的转动惯量:
J m jrj2 m1r12 m2r22 j
r2 m2
（3）质量连续分布刚体的转动惯量:
r1
m1
r3 m3
转轴
J r2dm dm:质量元
4.电机转速和扭矩（转矩）公式
扭矩公式：T=9550P/n
T是扭矩，单位N·m； P是输出功率，单位KW； n是电机转速，单位r/min
扭矩公式：T=973P/n
T是扭矩，单位kg·m； P是输出功率，单位KW； n是电机转速，单位r/min
5.扭矩计算
电机转矩T （N.m）
滑轮半径r （m）

伺服电机选型计算实例

伺服电机选型计算实例

1
·注
伺服电机计算选择应用实例
无论是否在切削，是垂直轴还是水平轴，F 值取决于工作台的重量， 摩擦系数。若坐标轴是垂直轴，F 值还与平衡锤有关。对于水平工 作台，F 值可按下列公式计算：
不切削时： F = μ（W+fg） 例如： F=0.05×(1000+50)=52.5 (kgf) Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm) = 0.9(Nm)
Ta =
Vm × 2π× 1
60
ta
×Jm×（1-e-ks。ta）+
+ Vm × 2π× 1
60
ta
×JL×（1-e-ks。ta）÷η
1 Vr = Vm×{1- Ta·ks
(1- e-ks。ta )}
Ta :加速力矩(kgf·cm) Vm :电机快速移动速度(min-1) ta :加速时间(sec) Jm :电机的惯量(kgf.cm.s2) JL :负载的惯量(kgf.cm.s2) Vr :加速力矩开始下降的速度(与 Vm 不同) (min-1) Ks :位置回路的增益(sec-1) η :机床的效率
切削时: F = Fc+μ(W+fg+Fcf) 例如: F=100+0.05×(1000+50+30)=154(kgf) Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm) =2.1(Nm)
为了满足条件 1，应根据数据单选择电机，其负载力矩在不切削时 应大于 0.9（Nm），最高转速应高于 3000（min-1）。考虑到加/减速， 可选择α2/3000（其静止时的额定转矩为 2.0 Nm）。

伺服电机选型案例

伺服电机选型案例

伺服电机选型案例伺服电机功率计算选型例子伺服电机功率计算选型例子（新手必看，经典案例分析）伺服电机选型也有相应的规律和公式可循的。

最常见的机械传动结构有同步带，齿轮齿条，丝杆等。

以同步带为例，需要计算的参数有电机转速，电机力矩，转动惯量。

第一，电机额定转速N=（v/2πr）*i，启动瞬间需要的拉力F=（M+m1-m2）a+δ（M+m1-m2）g(水平)，F=（M+m1-m2）a+δ（M+m1-m2）g+（M+m1-m2）g(垂直)，T扭矩=F*R。

T电机=T扭矩/机械减速比n，电机功率=N*T 电机/10，启动惯量J=1/2mR2，电机惯量J电机=J/减速比的平方n2/惯量比i。

第二，同步带轮直径D=100mm、提升机载货台总重M=30kg、货物总重m1=10kg，配重m2=25kg，提升滚动摩擦系数取δ=0.03、加速度a=2m/S2、提升速度v=3m/s。

减速机减速比i=5，电机额定转速n=（v/2πr）*i=3/(2*3.14*0.05)*5*60=2866r/min，启动瞬间需要的拉力F=（M+m1-m2）a+&delta，（M+m1-m2）g+（M+m1-m2）g=（30+10-25）*2+0.03（30+10-25）*10+（30+10-25）*10=184.5N。

T扭矩=F*R=184.5*0.05=9.225Nm，折算电机需要扭矩T1=9.225Nm/5=1.85Nm，折算电机功率P1=2866*1.85/10=0.5KW。

启动惯量J=1/2mR2=0.5*（10+30+25）*0.0025=0.08125kgm2，折算电机需要惯量J1=0.08125/25=0.00325kgm2，根据经验值取惯量比=10，则实际J电=J1/10=0.000325kgm2。

经计算电机至少满足以下条件下面看下1.2千瓦3000RPM，4牛米的电机的惯量是2.98*10-4kgm2。

所以可以选择80ST-M04030的电机。

伺服电机选型计算实例

伺服电机选型计算实例

伺服电机选型计算实例在进行伺服电机选型时，需要考虑到多个因素，包括载荷特性、运动要求、控制要求以及环境要求等。

下面我们将通过一个实际案例来详细介绍伺服电机选型的计算方法。

案例描述：公司需要选购一台适合于自动化生产线上使用的伺服电机，用于驱动一台输送带，具体要求如下：1.输送带长度为2米，宽度为0.5米，预计最大负载为100千克。

2.需要实现起动、停止、加速和减速、定位等功能。

3.运动速度为1米/秒。

4.工作温度范围为-10℃~40℃。

根据以上要求，我们可以按照以下步骤进行伺服电机选型计算：步骤1：计算所需输出功率首先，我们需要计算伺服电机的输出功率。

根据输送带的长度、宽度和预计最大负载，可以计算得到输送带的质量：质量=长度×宽度×质量体积，质量体积可以通过相应材料的密度来获得。

假设输送带材料的密度为1克/立方厘米，则质量=2×0.5×1=1千克。

根据牛顿第二定律，质量乘以加速度等于力，所以我们可以得到加速度=质量/时间^2=100/1=100米/秒^2、再根据功率=力×速度，可以计算得到所需输出功率=力×速度=100×1=100瓦特。

步骤2：根据负载惯性计算电机惯性比为了实现加速和减速的控制要求，需要考虑负载的惯性。

负载的惯性通常用负载惯量来表示，通常使用kg*m^2作为单位。

对于输送带系统，我们假设负载的半径为0.25米（输送带宽度的一半），负载的惯量=负载质量×半径^2=100×0.25^2=6.25kg*m^2、然后，我们需要计算电机的惯性比，电机的惯量通常使用kg*m^2作为单位。

假设选用的伺服电机的惯量为0.01kg*m^2，则电机的惯性比=负载的惯量/电机的惯量=6.25/0.01=625步骤3：根据运动要求计算加速度和最大速度根据运动要求中的加速度和速度，我们可以计算得到实际需要的加速时间和加速距离。

伺服电机选型计算及案例

伺服电机选型计算及案例

伺服电机选型计算及案例
在进行伺服电机选型计算前，首先需要了解以下参数：
1.力矩要求：根据工作负载计算所需的最大输出力矩。

2.转速要求：根据工作过程中所需的最高转速确定。

3.加速度要求：根据工作过程中的速度变化率来计算。

4.环境条件：包括工作温度、工作湿度等环境因素。

下面以一个简单的案例为例，演示如何进行伺服电机选型计算。

案例：自动化生产线运行速度为60米/分钟，工作台上的工件质量为10千克，需要在0.5秒内从静止加速到最终速度并保持匀速运动。

根据这些要求，我们需要选用合适的伺服电机。

步骤1：计算所需的输出力矩。

根据牛顿第二定律，力矩（扭矩）等于质量乘以加速度。

加速度可以通过速度变化与时间的比值来计算。

加速度a = (60 m/min) / (0.5 s) = 120 m/min² = 2 m/s²
力矩T = (质量m) * (加速度a) = 10 kg * 2 m/s² = 20 Nm
所以我们需要选用至少能提供20Nm的输出力矩的伺服电机。

步骤2：计算所需的最高转速。

最高转速通常需要根据具体工作过程来确定。

在这个案例中，我们假设最高转速为3000 rpm（每分钟转数）。

步骤3：计算所需的加速度。

加速度已经在步骤1中计算过，为2m/s²。

步骤4：确定环境条件。

根据实际工作环境，确定伺服电机所需的环境参数，例如工作温度和湿度范围。

通过以上计算，我们得到了选型参数：输出力矩为20 Nm，最高转速为3000 rpm，加速度为2 m/s²。

三个案例告诉你，伺服电机选型计算应该怎么做！

三个案例告诉你，伺服电机选型计算应该怎么做！

三个案例告诉你，伺服电机选型计算应该怎么做！案例一已知：圆盘质量M=50kg，圆盘直径D=500mm，圆盘最高转速60rpm，请选择伺服电机及减速机，构件示意图如下：计算圆盘转动惯量JL= MD2/ 8 = 50 * 2500 / 8 = 15625kg.cm2假设减速机减速比1：R，则折算到伺服电机轴上负载惯量为15625/ R2。

按照负载惯量<3倍电机转子惯量jm的原则,如果选择400w电机，jm= 0.277kg.cm2，则15625="" r2="">3倍电机转子惯量jm的原则,如果选择400w电机，jm=>< 3*0.277，r2="">18803，R>137，输出转速=3000/137=22rpm，不能满足要求。

如果选择500W电机，JM=8.17kg.cm2，则15625 / R2<3*8.17，r2>637，R>25，输出转速=2000/25=80rpm，满足要求。

这种传动方式阻力很小，忽略扭矩计算。

案例二已知：负载重量M=50kg，同步带轮直径D=120mm，减速比R1=10，R2=2，负载与机台摩擦系数µ=0.6，负载最高运动速度30m/min，负载从静止加速到最高速度时间200ms，忽略各传送带轮重量，驱动这样的负载最少需要多大功率电机？构件示意图如下：1.计算折算到电机轴上的负载惯量JL=M * D2 / 4 / R12 =50 * 144 / 4 / 100 =18kg.cm2按照负载惯量<>JM>6kg.cm22.计算电机驱动负载所需要的扭矩克服摩擦力所需转矩Tf=M*g*µ*(D/2)/ R2/R1= 50 * 9.8 * 0.6 * 0.06 / 2 / 10= 0.882N.m加速时所需转矩Ta=M*a*(D/2)/R2/R1=50 * (30 / 60 / 0.2) * 0.06 / 2 / 10=0.375 N.m伺服电机额定转矩>Tf ，最大扭矩>Tf +Ta3.计算电机所需要转速N= v/(πD)*R1= 30 / (3.14 * 0.12) * 10= 796 rpm案例三已知：负载重量M=200kg，螺杆螺距PB=20mm，螺杆直径DB=50mm，螺杆重量MB=40kg，摩擦系数µ=0.2，机械效率η=0.9，负载移动速度V=30m/min，全程移动时间t=1.4s，加减速时间t1=t3=0.2s，静止时间t4=0.3s。

图解伺服电机选型实例

图解伺服电机选型实例

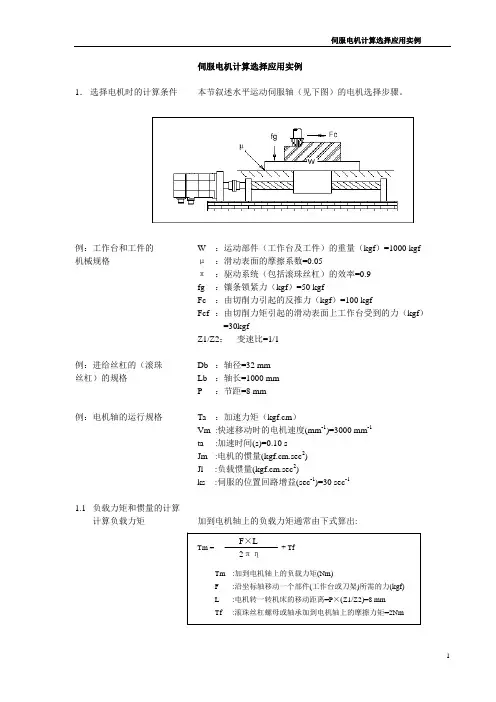
伺服电机计算选择应用实例1． 选择电机时的计算条件 本节叙述水平运动伺服轴（见下图）的电机选择步骤。

例：工作台和工件的 W ：运动部件（工作台及工件）的重量（kgf ）=1000 kgf 机械规格 μ ：滑动表面的摩擦系数=0.05π ：驱动系统（包括滚珠丝杠）的效率=0.9 fg ：镶条锁紧力（kgf ）=50 kgfFc ：由切削力引起的反推力（kgf ）=100 kgfFcf ：由切削力矩引起的滑动表面上工作台受到的力（kgf ）=30kgfZ1/Z2： 变速比=1/1例：进给丝杠的（滚珠 Db ：轴径=32 mm 丝杠）的规格 Lb ：轴长=1000 mmP：节距=8 mm例：电机轴的运行规格 Ta ：加速力矩（kgf.cm ）Vm :快速移动时的电机速度(mm -1)=3000 mm -1 ta :加速时间(s)=0.10 s Jm :电机的惯量(kgf.cm.sec 2)Jl:负载惯量(kgf.cm.sec 2)ks :伺服的位置回路增益(sec -1)=30 sec -11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L :电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2Nm无论是否在切削，是垂直轴还是水平轴，F 值取决于工作台的重量，摩擦系数。

若坐标轴是垂直轴，F 值还与平衡锤有关。

对于水平工作台，F 值可按下列公式计算： 不切削时：F = μ（W+fg ）例如：F ×L 2πηF=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf) 例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1，应根据数据单选择电机，其负载力矩在不切削时应大于0.9（Nm ），最高转速应高于3000（min -1）。

伺服电机选型计算实例

伺服电机选型计算实例

伺服电机计算选择应用实例1． 选择电机时的计算条件 本节叙述水平运动伺服轴（见下图）的电机选择步骤。

例：工作台和工件的W ：运动部件（工作台及工件）的重量（kgf ）=1000 kgf 机械规格 μ ：滑动表面的摩擦系数=0.05π ：驱动系统（包括滚珠丝杠）的效率=0.9 fg ：镶条锁紧力（kgf ）=50 kgfFc ：由切削力引起的反推力（kgf ）=100 kgfFcf：由切削力矩引起的滑动表面上工作台受到的力（kgf ） =30kgfZ1/Z2： 变速比=1/1例：进给丝杠的（滚珠 Db ：轴径=32 mm 丝杠）的规格 Lb ：轴长=1000 mm P ：节距=8 mm例：电机轴的运行规格 Ta ：加速力矩（kgf.cm ）Vm :快速移动时的电机速度(mm -1)=3000 mm -1 ta :加速时间(s)=0.10 sJm :电机的惯量(kgf.cm.sec 2) Jl :负载惯量(kgf.cm.sec 2)ks :伺服的位置回路增益(sec -1)=30 sec -11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L :电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2NmF ×L2πη无论是否在切削，是垂直轴还是水平轴，F值取决于工作台的重量，摩擦系数。

若坐标轴是垂直轴，F值还与平衡锤有关。

对于水平工作台，F值可按下列公式计算：不切削时：F = μ（W+fg）例如：F=0.05×(1000+50)=52.5 (kgf)(52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)=Tm= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf)例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1，应根据数据单选择电机，其负载力矩在不切削时应大于0.9（Nm），最高转速应高于3000（min-1）。

伺服电机功率计算选型例子

伺服电机功率计算选型例子
= 50 * 9.8 * 0.6 * 0.06 / 2 / 10 = 0.882 N.m 加速时所需转矩Ta = M * a * (D / 2) / R2 / R1 = 50 * (30 / 60 / 0.2) * 0.06 / 2 / 10 = 0.375 N.m 伺服电机额定转矩 > Tf ，最大扭矩 > Tf + Ta
微信公众号：ACE萦梦工作室
举例计算3
3. 计算电机驱动负载所需要的扭矩 克服摩擦力所需转矩Tf = M * g * µ * PB / 2π / η
= 200 * 9.8 * 0.2 * 0.02 / 2π / 0.9 = 1.387 N.m 重物加速时所需转矩TA1 = M * a * PB / 2π / η
JL=1/2*M1*r12 + 1/2*M2*r12 + M3*r12
M3 M1 r1
r2 M2
微信公众号：ACE萦梦工作室
伺服选型原则
连续工作扭矩 < 伺服电机额定扭矩
瞬时最大扭矩 < 伺服电机最大扭矩 (加速时)
负载惯量
< 3倍电机转子惯量
连续工作速度 < 电机额定转速
微信公众号：ACE萦梦工作室
按照负载惯量 < 3倍电机转子惯量JM的原则
如果选择400W电机，JM = 0.277kg.cm2，则 15625 / R2 < 3*0.277，R2 > 18803，R > 137 输出转速=3000/137=22 rpm，不能满足要求。
如果选择500W电机，JM = 8.17kg.cm2，则 15625 / R2 < 3*8.17，R2 > 637，R > 25 输出转速=2000/25=80 rpm，满足要求。 这微种信公传众号动：AC方E萦式梦工阻作室力很小，忽略扭矩计算。

伺服电机选型计算及案例(傻瓜式)讲课讲稿

伺服电机选型计算及案例(傻瓜式)讲课讲稿

0.637
(N.m )
×
[适
1.23E-05
用的 惯量
比
=30]
0.5096 N.M
1.528 N.M
3000
r/mi n
条件满足
条件满足 条件满足 条件满足 条件满足
①机械系
统的决定
负载质量M（kg）
5
·滚珠丝杠节距P（mm）
10
·滚珠丝杠直径D（mm）
20
·滚珠丝杠质量MB（kg）
3
·滚珠丝杠摩擦系数μ
0.1
·因无减速器，所以G=1、η=1
1
②动作模 式的决定
单一变化 ·负载移动速度V（mm/s） ·行程L（mm） ·行程时间tS（s） ·加减速时间tA（s） ·定位精度AP（mm）
④负载转 矩的计算
对摩擦力的转矩Tw
换算到电机轴负载转矩TL=Tw
7.80E-03 N.m 7.80E-03 N.m
⑤旋转数 的计算
转数N
⑥电机的 初步选定 [选自 OMNUC U 系列的初 步选定举 例]
N=60V/P.G
1800 r/min
选定电机的转子·惯量为负载的 1/30*以上的电机
JM≥JL/30
速度 (mm/s)
300
0 0.2
300
0 1
300 360 1.4 0.2 0.01
0.2 时间(s)
③换算到 电机轴负 载惯量的 计算
滚珠丝杠的惯量JB=
1.50E-04 kg.m2
负载的惯量JW=
1.63E-04 kg.m2
换算到电机轴负载惯量JL=JW
JL=G2x(JW+J2)+J1
1.63E-04 kg.m2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

伺服电机计算选择应用实例1． 选择电机时的计算条件 本节叙述水平运动伺服轴（见下图）的电机选择步骤。

例：工作台和工件的 W ：运动部件（工作台及工件）的重量（kgf ）=1000 kgf 机械规格 μ ：滑动表面的摩擦系数=0.05π ：驱动系统（包括滚珠丝杠）的效率=0.9 fg ：镶条锁紧力（kgf ）=50 kgfFc ：由切削力引起的反推力（kgf ）=100 kgfFcf ：由切削力矩引起的滑动表面上工作台受到的力（kgf ）=30kgfZ1/Z2： 变速比=1/1例：进给丝杠的（滚珠 Db ：轴径=32 mm 丝杠）的规格 Lb ：轴长=1000 mmP：节距=8 mm例：电机轴的运行规格 Ta ：加速力矩（kgf.cm ）Vm :快速移动时的电机速度(mm -1)=3000 mm -1 ta :加速时间(s)=0.10 s Jm :电机的惯量(kgf.cm.sec 2)Jl:负载惯量(kgf.cm.sec 2)ks :伺服的位置回路增益(sec -1)=30 sec -11.1 负载力矩和惯量的计算 计算负载力矩 加到电机轴上的负载力矩通常由下式算出:Tm = + Tf Tm :加到电机轴上的负载力矩(Nm) F :沿坐标轴移动一个部件(工作台或刀架)所需的力(kgf) L :电机转一转机床的移动距离=P ×(Z1/Z2)=8 mmTf:滚珠丝杠螺母或轴承加到电机轴上的摩擦力矩=2Nm无论是否在切削，是垂直轴还是水平轴，F 值取决于工作台的重量，摩擦系数。

若坐标轴是垂直轴，F 值还与平衡锤有关。

对于水平工作台，F 值可按下列公式计算： 不切削时：F = μ（W+fg ）例如：F ×L 2πηF=0.05×(1000+50)=52.5 (kgf)Tm = (52.5×0.8) / (2×μ×0.9)+2=9.4(kgf.cm)= 0.9(Nm)切削时:F = Fc+μ(W+fg+Fcf) 例如:F=100+0.05×(1000+50+30)=154(kgf)Tmc=(154×0.8) / (2×μ×0.9)+2=21.8(kgf.cm)=2.1(Nm)为了满足条件1，应根据数据单选择电机，其负载力矩在不切削时应大于0.9（Nm ），最高转速应高于3000（min -1）。

考虑到加/减速，可选择α2/3000（其静止时的额定转矩为2.0 Nm ）。

·注计算力矩时，要注意以下几点：。

考虑由镶条锁紧力（fg ）引起的摩擦力矩根据运动部件的重量和摩擦系数计算的力矩通常相当小。

镶条锁紧力和滑动表面的质量对力矩有很大影响。

滚珠丝杠的轴承和螺母的预加负荷，丝杠的预应力及其它一些因素有可能使得滚动接触的Fc 相当大。

小型和轻型机床其摩擦力矩会大大影响电机的承受的力矩。

考虑由切削力引起的滑动表面摩擦力（Fcf ）的增加。

切削力和驱动力通常并不作用在一个公共点上如下图所示。

当切削力很大时，造成的力矩会增加滑动表面的负载。

当计算切削时的力矩时要考虑由负载引起的摩擦力矩。

进给速度会使摩擦力矩变化很大。

欲得到精确的摩擦力矩值，应仔细研究速度变化，工作台支撑结构（滑动接触，滚动接触和静压力等），滑动表面材料，润滑情况和其它因素对摩擦力的影响。

。

机床的装配情况，环境温度，润滑状况对一台机床的摩擦力矩影响也很大。

大量搜集同一型号机床的数据可以较为精确的计算其负载力矩。

调整镶条锁紧力时，要监测其摩擦力矩，注意不要产生过大的力矩。

计算负载惯量与负载力矩不同，负载惯量可以精确地算出。

由电机的转动 驱动的物体的惯量形成电机的负载惯量，无论该物体是转动还是沿直线运动。

对各运动物体分别计算其惯量，然后按一定规则将各物体的惯量加在一起，即可得出总惯量。

总惯量可按下述方法计算：·圆柱体（滚珠丝杠，齿轮， 联轴节等）的惯量计算圆柱体绕其中心轴回转的惯量可按下式计算：J = D b 4L b （kgf.Cm.s 2）πγ32×980J : 惯量(kgf.cm.s 2)γ ：物体的比重（kg/cm 3） D b ：直径（cm ）L b：长度（cm ）若物体的材料是铁（其比重为7.8×10-3kg/cm 3）, 则惯量的近似值为： J=0.78×10-6D b 4L b （kgf.cm.s 2）例如: 滚珠丝杠的D b 为32mm ，L b 为1000mm ，其惯量为J b 为： J = 0.78×10-6×3.24×100 = 0.0082(kg.cm.s 2)·沿直线运动物体(工作台,工件等)的惯量J = × ( )2 (kgf.cm.s 2)W :沿直线运动物体的重量(kg)L:电机一转物体沿直线的移动距离(cm)例如:工作台和工件的W 为1000kg ，L 为8mm ，则其惯量计算得： J W = 1000/980×（0.8/2/π）2= 0.0165(kgf.cm.s 2)·速度高于或低于电机轴速的物体的惯量(惯量的折算)惯量J 0折算到电机轴上后的计算方法如下: J = ( )×J 0 (kgf.cm.s 2)J 0:折算前的惯量(kgf.cm.s 2)·回转中心偏离轴心 的圆柱体的惯量J = J 0＋ R 2 (kgf.cm.s 2)J 0 :围绕圆柱体中心回转的转动惯量(kgf.cm.s 2) M :物体的重量(kg)R:回转半径(cm)上述公式用于计算大齿轮等零件的惯量。

为了减小重量和惯量，这W980L 2π Z 1Z 2M980些零件的结构都是中空的。

上述计算的惯量值的和是电机加速的负载惯量J 。

上述例子计算得到的J B 及J W 的和就是负载惯量J L 。

J L = 0.0082＋0.0165 = 0.0247(kgf.cm.s 2)·对负载惯量的限制负载惯量对电机的控制特性和快速移动的加/减速时间都有 很大影响。

负载惯量增加时，可能出现以下问题：指令变化后，需要较长的时间达到新指令指定的速度。

若机床沿着两个轴高速运动加工圆弧等曲线，会造成较大的加工误差。

负载惯量小于或等于电机的惯量时，不会出现这些问题。

若负载惯量为电机的3倍以上，控制特性就会降低。

实际上这对普通金属加工机床的工作的影响不大，但是如果加工木制品或是高速加工曲线轨迹，建议负载惯量要小于或等于电机的惯量。

如果负载惯量比3倍的电机惯量大的多，则控制特性将大大下降。

此时，电机的特性需要特殊调整。

使用中应避免这样大的惯量。

若机械设计出现这种情况，请与FANUC 联系。

1．2加速力矩的计算按下步骤计算加速力矩：计算加速力矩：步骤1假定电机由NC 控制加/减速，计算其加速度。

将加速度乘 以总的转动惯量（电机的惯量 + 负载惯量），乘积就是加速力矩。

计算式如下。

·直线加/减速Ta = × 2π× ×Jm ×（1-e -ks 。

ta ）++ × 2π× ×J L ×（1-e -ks 。

ta ）÷ηVr = Vm ×{1- (1- e -ks 。

ta )}Ta :加速力矩(kgf ·cm) Vm :电机快速移动速度(min -1) ta :加速时间(sec) Jm :电机的惯量(kgf.cm.s 2)J L :负载的惯量(kgf.cm.s 2)Vr :加速力矩开始下降的速度(与Vm 不同) (min -1) Ks :位置回路的增益(sec -1)η:机床的效率例子:在下列条件下进行直线加/减速：电机为α2/3000。

首先计算电机和负载惯量，然后计算加速转矩。

电机惯量Jm 为0.0061(kgf.cm.s 2)，Vm 为3000(min -1)，ta 为0.1(s),ks 为30(sec -1)，J L =0.0247(kgf.cm.s 2)。

Vm60 1 ta Vm601ta1Ta ·ksTa = 3000/60 ×2π×1/0.1×0.0061×（1-e -30×0.1）++ 3000/60×2π×1/0.1×0.0247×（1-e -30×0.1）÷0.9= 100.1(kgf.cm.) = 9.81(Nm)由α2/3000的速度-转矩特性可以看到，9.81（Nm ）的加速 力矩处于断续工作区的外面（见上面的特性曲线和电机的数据单）。

（α2/3000的力矩是不够的。

）如果轴的运行特性（如，加速时间）不变，就必须选择大电机。

比如，选择α3/3000（Jm 为0.02 kgf.cm.s 2），重新计算加速力矩如下： Ta = 123.7(Kg.cm) = 12.1(Nm)Vr = 2049(min -1)由该式可知，加速时，在转速2049(min -1)时，要求加速力矩为12.1 Nm 。

由上面的速度-力矩特性可以看出，用α3/3000电机可满足加速要求。

由于已将电机换为α3/3000，则法兰盘尺寸已经变为130mm ×130mm 。

若机床不允许用较大电机，就必须修改运行特性，例如，使加速时间延长。

·不控制加/减速时 速度 指令 转矩 Vm Ta时间 公式为： Ta = ×2π× ×（Jm+J L ）Ta =计算加速力矩：步骤2 为了得到电机轴上的力矩T ，应在加速力矩Ta 上增加Tm （摩擦力矩）。

T = Ta+TmT = 12.1(Nm)+0.9(Nm) = 13.0 (Nm)计算加速力矩：步骤3核算上面步骤2计算出的力矩T 应小于或等于放大器已限 定的力矩。

用相应电机的速度-转矩特性和数据单核算由步骤1算得的Vr 时的T 应在断续工作区内。

因为Vr 为2049(min -1)，T 为13.0(Nm)，用指定的时间常数加速是Vm 601ta1 ksta可能的（条件2）。

1．3 计算力矩的均方根值计算快速定位频率绘制快速定位一个周期的速度-时间和转矩-时间图，如下 图。

普通切削时，快速定位的频率不会有问题；但是，对于 有些频繁快速定位的机床必须检查加/减速电流是否会引起 电机过热。

根据力矩-时间图可以得到一个运行周期的加于电机上力矩 的均方根值。

对该值进行核算，确保要小于或等于电机的额 定力矩（条件3）。

Trms =Ta ：加速力矩 Tm ：摩擦力矩To ：停止时的力矩如果Trms 小于或等于电机静止时的额定力矩（Ts ），则选择 的电机可以使用。