自旋 我们生活在一个怎样的世界里

物理学中的电子自旋研究自旋是物理学中一个非常重要的概念，尤其在量子力学和固体物理领域。

自旋可以被看作是物质微观世界的一个内禀性质，类似于它的质量和电荷。

在本文中，我们将探讨电子自旋在物理学研究中的重要性以及一些相关的应用。

自旋是指微观粒子围绕着自身轴线旋转的现象。

虽然根据经典物理学的角度来看，自旋的存在似乎没有很大的实际意义，但事实上，在量子力学中，自旋是一种非常重要的性质。

自旋的出现使得许多现象可以在理论上得到解释，并推动了很多科学技术的发展。

量子力学的自旋理论给出了电子自旋的描述。

根据自旋理论，自旋可以取两个不同的值：上自旋和下自旋，通常用"+1/2"和"-1/2"表示。

对于每个自旋，它都对应着一个角动量，因此自旋可视为与角动量类似的物性。

电子自旋在物理学中的研究以及相关应用非常广泛。

一个经典的例子是磁共振成像技术（Magnetic Resonance Imaging，MRI）。

MRI利用了电子自旋的特性来生成人体的影像。

在MRI过程中，被研究的目标暴露在强大的磁场中，使得电子自旋在该磁场中取向有所改变。

通过改变磁场，研究者可以观察到自旋的变化，进而得到关于目标结构和组织的信息。

此外，电子自旋的研究对于开发新型电子器件和计算技术也起到了重要作用。

例如，磁随机存储器（Magnetic Random Access Memory，MRAM）利用了自旋的性质，使得存储信息的位可以通过电子自旋的状态来表示。

相比传统的电荷存储器，MRAM具有快速读写速度和低功耗的优势，因此在信息技术领域有着广泛的应用前景。

电子自旋的研究也为固体物理学提供了重要的理论基础。

例如，在自旋杂化系统中，自旋和电荷之间的相互作用可能导致新的物理现象和性质。

自旋-轨道耦合（spin-orbit coupling）是一种常见的自旋杂化现象，它可以导致自旋在材料中的演化和传输。

通过对自旋杂化现象的研究，科学家们能够发现新的奇特量子态，如拓扑绝缘体和拓扑超导体，这些都为新型能源和电子器件的发展提供了重要思路。

微观粒子的自旋自旋是描述微观粒子性质的一个重要概念，自旋的存在引发了对量子力学的深入研究和理解。

在本文中，我们将探讨微观粒子的自旋的概念、性质以及其在物理学中的应用。

一、自旋的定义和意义自旋是描述微观粒子的内禀角动量的量子数，与地球上物体的自转并无直接联系。

自旋属性是某些粒子独有的，例如电子、质子和中子等。

自旋量子数可以取整数或半整数，用ℏ表示。

自旋对微观粒子的性质和行为产生了重要影响。

自旋决定了粒子相对于外加磁场的取向，并在磁场中产生磁矩，从而影响粒子在磁场中的运动和相互作用。

此外，自旋还与粒子的统计性质有关，通过自旋，理论物理学家引入了泡利不相容原理等重要概念。

二、自旋的特性1. 自旋量子数：自旋量子数是自旋取值范围的一个常数。

对于半整数自旋的粒子（如电子），其自旋量子数为1/2；而对于整数自旋的粒子（如质子），其自旋量子数为1。

2. 自旋态：自旋态描述了微观粒子的自旋取向。

对于自旋1/2的粒子，其自旋态可用“上”和“下”两个本征态表示；对于自旋1的粒子，其自旋态可用“正”、“负”和“零”三个本征态表示。

3. 自旋测量：自旋的测量会使自旋态塌缩为特定的本征态。

测量自旋时，对于自旋1/2的粒子，结果为上/下两个本征态其中之一；对于自旋1的粒子，结果为正/负/零三个本征态其中之一。

4. 自旋相互作用：自旋相互作用是微观粒子之间的相互作用。

根据自旋的相对取向，自旋可以表现出平行（同向）或反平行（反向）的形式。

自旋的相互作用将影响粒子的物理行为和性质。

三、自旋在物理学中的应用1. 磁性材料：自旋与粒子的磁矩相关联，因此在磁性材料的研究中具有重要地位。

通过调控自旋取向，可以实现磁性材料的控制与调制，如磁存储器件等。

2. 强子物理：自旋在强子物理中起着重要作用。

强子是由夸克组成的复合粒子，夸克自旋的组合决定了强子的自旋状态和统计性质。

通过粒子对撞实验，可以揭示强子的自旋结构和强子物理的基本规律。

3. 量子计算和信息：自旋也在量子计算和信息领域有着重要应用。

自旋的原理自旋是量子力学中的一个重要概念，它描述了微观粒子的一种内禀性质。

在物质微观世界中，所有的粒子都有自旋，包括电子、质子、中子等。

自旋最初是根据物理学家斯特恩和格拉赫（Otto Stern和Walter Gerlach）的实验发现的。

他们在1922年的实验中，通过将银蒸汽通过一个狭缝后，将其传播到一个磁场中，发现银原子的轨迹并不均匀地分成两束。

这一实验结果表明，银原子存在一个围绕某个轴旋转的内禀角动量，这就是我们所称的自旋。

自旋是一个量子性质，与经典物理学中的角动量类似，但又有一些不同之处。

经典物理学中，角动量是轨道运动造成的，而自旋则是粒子固有的、与其自身性质相关的。

自旋可以用一个“角动量矢量”来描述，这个矢量的大小和方向代表了自旋的强度和方向。

自旋有两个可能的取值：上自旋和下自旋，通常用记号↑⟩和↓⟩来表示。

对电子而言，上自旋表示自旋朝向与外磁场相反，下自旋表示自旋朝向与外磁场相同。

自旋也可以视为粒子固有的旋转，但与经典物理学中的旋转不同，自旋并没有具体的轴，它是一种无轴的旋转。

自旋的原理可以从量子力学的观点来解释。

在量子力学中，粒子的状态可以用一个量子态来描述，量子态可以表示为一个数学上的矢量。

自旋态是另一种量子态，描述了粒子的自旋特性。

自旋态可以用一个二维向量空间来表示，这个空间称为自旋空间。

在自旋空间中，有两个正交归一的基态组成的基。

这两个基态分别对应于上自旋和下自旋。

在量子态中，一个自由粒子的自旋态可以看作是上自旋和下自旋的线性叠加。

例如，一个电子的自旋态可以表示为：ψ⟩ = a ↑⟩ + b ↓⟩其中，a和b是复数，且满足归一化条件a ^2 + b ^2 = 1。

这个复数表示了粒子的自旋在上自旋和下自旋之间的分布情况。

自旋态的系数a和b的平方可以解释为发现上自旋或下自旋的概率。

自旋在物理中起着重要的作用。

首先，自旋是粒子的内禀性质，与其它量子数（如电荷、质量等）无关。

因此，自旋在描述粒子的整体特性时是不可或缺的。

生活中的旋转旋转是生活中一个常见的现象，它存在于各个层面和方面。

从日常生活的细节到宇宙的大规模旋转，旋转是一个普遍存在且多样化的概念。

本文将探讨生活中的旋转，从物理学、生物学和文化艺术等方面分析其意义和影响。

1. 物理学中的旋转在物理学中，旋转是一个重要的概念。

从最基本的旋转运动到宏观物体的自转，旋转在物质世界中无处不在。

例如，地球的自转造成了昼夜的交替以及极地地区的极夜和极昼现象。

太阳系中的行星也以自转的方式运动，这种旋转运动对地球的稳定性和生命的存在至关重要。

除了天体运动，微观世界也存在旋转。

例如，原子和分子的旋转运动决定了物质的性质和化学反应的过程。

旋转对电子、自旋态和磁场等物理现象也有重要影响。

因此，研究旋转运动在物理学中具有重要意义，对我们理解宇宙和物质的本质有深远影响。

2. 生物学中的旋转旋转不仅存在于物理世界，也在生物世界中起着重要作用。

生物体的旋转运动广泛存在于生物学中，如旋转的细胞分裂、旋转的水涡和旋转的植物枝干等。

在细胞生物学中，旋转是细胞分裂过程中的一个重要步骤。

细胞通过旋转的方式将染色体均匀分离到新生细胞中，确保细胞遗传物质的稳定传递。

旋转在叶绿体分裂、线粒体分裂和鞭毛的生长等生物过程中也起着关键作用。

在生物体的结构和运动中，旋转同样是重要的组成部分。

例如，许多生物体拥有旋转的器官，如眼球的转动、耳朵的传声骨的旋转和蜗牛壳的螺旋形状等。

这些旋转结构和运动使得生物可以适应不同的环境，并进行感知和运动。

3. 文化艺术中的旋转旋转不仅在自然界中存在，而且在文化艺术中也得到广泛应用。

旋转运动常常被用来表达动态、活力和变化，成为了舞蹈、音乐和视觉艺术的重要元素。

在舞蹈中，旋转动作给人以独特的视觉和音乐上的享受。

旋转动作可以使得舞者在空间中留下美丽的弧线，给人以快乐和轻盈的感觉。

例如，芭蕾舞中的旋转和旋转跳动作展示了舞者的灵活性与技巧。

在音乐中，旋转音符、旋转节奏和旋转旋律常被运用，赋予音乐以律动感和活力。

“旋转”是宇宙物质运动的基本特征和存在形式无论你感觉到或感觉不到，我们都是生活在一个旋转的世界里。

“天旋、地旋、人亦旋”是物质存在的普遍特征。

没有不旋转的物质存在，也没有物质不旋转。

物质的旋转是绝对的，不旋是相对的。

1、旋转是物质存在的最基本形态我们生活在地球上，地球不仅以大约一年的时间围绕太阳公转，而且以大约24小时的时间在自转，所以，地球上的一切，包括人和物都随地球在公转和自转，无一例外。

毛泽东诗词：“坐地日行八万里”也就是说的这个意思。

我们常见或感性认识的旋转是水中以及江河中的涡旋，还有卫星云图上气旋或台风的涡旋云系。

随着现代科技的发展，不仅探测到很多外太空的涡旋星系，而且整个宇宙都是一个大涡旋套小涡旋的众多复杂涡旋结构的系统。

如太阳系行星围绕太阳旋转；太阳系又围绕银河系的中心旋转；银河系又围绕星系团中心旋转；小星系团又围绕大星系团中心旋转，大星系团组成的整个宇宙物质围绕宇宙轴旋转等等。

从微观上讲，从组成物质的原子构成看，电子不仅有自旋而且还围绕原子核公转；原子核也是更小的基本粒子组成，并且这些基本粒子几乎都有自旋。

2、旋转的特征和产生的原因旋转的形态有左旋和右旋两种。

其结构有周期性和非周期性两种。

严格的讲，自然界的旋转多是非周期性或拟周期性的（近似周期性）。

涡旋就是一种常见的非周期性旋转，地球绕太阳公转是拟周期性的。

由于物质结构的非均匀特征，使得内部压力不均匀一致，导致系统产生扭力而表现为涡旋运动。

这种涡旋的产生机制不仅对微观还是宏观都是成立的。

理论上只有均匀的或无形状无大小的质点才会直线运动，但质点是不存在的。

所以在设计过程中，要使运动不岀现旋转或振动，其物体要尽可能的保持对称或均匀。

3、没有旋转就没有空间没有物质就没有空间，物质存在的基本运动形式是旋转。

旋转是物质和能量的高聚集区和集散地。

没有旋转，物质就会消散，就没有空间存在；只有旋转才能产生动态稳定平衡，所以，宇宙空间的大小基本就是宇宙物质旋转的大小。

自旋三重态解释嘿，朋友们！今天咱来聊聊自旋三重态这玩意儿。

你说这自旋三重态啊，就像是一场奇妙的舞蹈。

想象一下，粒子们就像是一群欢快的舞者，它们在微观世界里尽情地跳跃、旋转。

自旋三重态呢，就是其中一种特别带劲的舞蹈风格。

在这个微观的舞台上，粒子们有着自己独特的舞步和节奏。

自旋三重态的粒子就像是那些充满活力、激情四溢的舞者，它们以一种特别的方式展现着自己的魅力。

咱们日常生活里也有类似的情况呀。

比如说，一场热闹的派对，有些人特别活跃，能带动整个气氛，这就有点像自旋三重态的粒子。

它们充满了能量，让周围的一切都变得生动起来。

而且哦，这自旋三重态可不是随随便便就出现的，它得在特定的条件下才会闪亮登场。

这就好像一个优秀的舞者，需要在合适的舞台、合适的音乐下才能发挥出最佳水平。

你知道吗，科学家们为了研究这自旋三重态可没少下功夫！他们就像一群执着的观众，努力去理解这些粒子的“舞蹈语言”。

他们通过各种实验和观察，一点点地揭开自旋三重态的神秘面纱。

想想看，要是没有这些科学家们的努力，我们怎么能知道这么奇妙的微观世界呢？这自旋三重态可真是让我们大开眼界啊！它就像是一个隐藏在微观世界里的宝藏，等待着我们去发现、去探索。

每次想到这里，我就忍不住感叹，这世界可真是太神奇了！我们生活的这个世界，既有宏观的壮丽景象，又有微观的奇妙之处。

而自旋三重态就是微观世界里一颗璀璨的明珠。

它让我们看到了物质的另一种表现形式，让我们对世界的认识更加深入、更加全面。

这难道不令人兴奋吗？所以啊，朋友们，不要小看这小小的自旋三重态，它里面蕴含着大大的学问呢！让我们一起保持对科学的好奇心，继续去探索这个充满神奇的世界吧！总之，自旋三重态就是这么神奇、这么有趣，值得我们好好去研究和了解。

量子力学科普：电子自旋，一种在宏观世界无法理解的特殊运动量子力学科普：电子自旋，一种在宏观世界无法理解的特殊运动相信喜欢量子力学的读者一定听说过这样一个名词：自旋，的确，每一个微观粒子都存在自旋这种现象，但微观粒子的自旋行为又与宏观物体的自旋行为截然不同，在宏观世界又找不到相同的现象作为参考，所以微观粒子的自旋是很难理解的，而在互联网上关于粒子自旋介绍的更是少之又少，往往都是简单介绍一下定义与公式，这篇文章以电子自旋为例，和大家一起聊一聊在微观世界中，自旋究竟是一种什么样的行为。

自旋，量子力学对自旋的定义是：由粒子内禀角动量引起的内禀运动，好吧，我相信大多数人看了这个定义之后还是无法理解自旋是什么，由粒子内禀角动量引起的内禀运动，这个解释实在是太抽象，角动量是什么？我们可以通俗的将角动量理解为一个描述物质旋转的物理量，角动量等于质量×半径平方×角速度，微观粒子的旋转可以分为两种，第一种是自旋角动量，第二种是轨道角动量，如果是质子、中子、原子核这种复合粒子，那么复合粒子的自旋就等于自旋角度量与轨道角动量之和。

下面来讲一讲自旋，从字面上来理解，就是代表这物体沿轴做自我旋转，例如：地球沿着地轴做自转，这里以电子为例，如果将宏观物质的自转概念直接套用到带电子身上，那么电子自旋也就是电子沿着电子中心轴进行自转，可问题来了：电子是一种不可再分的点粒子，点粒子有点类似于物理中质点的概念，点粒子是没有体积的，那么一个不存在体积的电子如何沿着中心轴自转呢？因为不存在体积，就根本不会存在中心轴的概念，所以将宏观物体自转的概念直接套用到电子身上是根本解释不通的。

早在1925年，著名物理学家泡利手下的两个助手就结合实验现象提出了电子存在自旋的行为，结果被泡利大骂了一顿，因为如果将电子的自旋理解成宏观物体的自转，那么电子表面的速度就要超越光速，这显然违背了相对论中光速最快的定论（如果当时泡利没有大骂这两个助手，而是认真的分析、总结，可能泡利就是第一个提出自旋行为的物理学家，那么泡利将会提前20年获得诺贝尔物理学奖）。

我们应该如何来理解粒子的自旋导读：本章摘自独立学者灵遁者量子力学科普书籍《见微知著》。

此文旨在帮助大家认识我们身处的世界。

世界是确定的，但世界的确定性不是我们能把我的。

自旋现象在经典物理学和量子力学中都存在，我们这里着重介绍量子力学中的特点。

在量子力学中，自旋是粒子所具有的内禀性质，其运算规则类似于经典力学的角动量，并因此产生一个磁场。

虽然有时会与经典力学中的自转（例如行星公转时同时进行的自转）相类比，但实际上本质是迥异的。

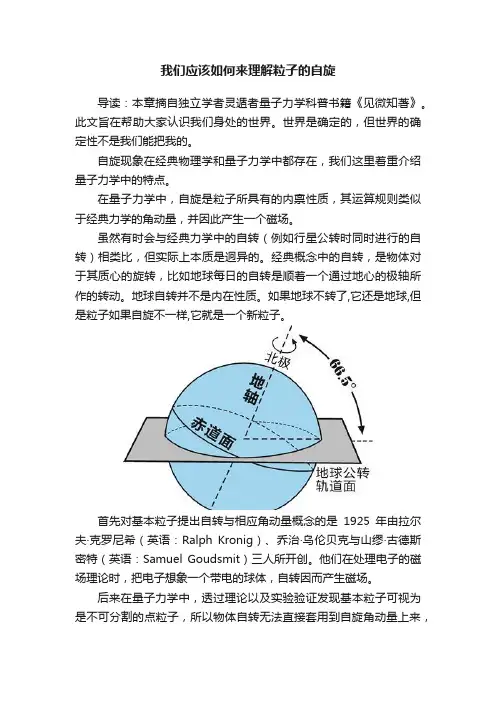
经典概念中的自转，是物体对于其质心的旋转，比如地球每日的自转是顺着一个通过地心的极轴所作的转动。

地球自转并不是内在性质。

如果地球不转了,它还是地球,但是粒子如果自旋不一样,它就是一个新粒子。

首先对基本粒子提出自转与相应角动量概念的是1925年由拉尔夫·克罗尼希（英语：Ralph Kronig）、乔治·乌伦贝克与山缪·古德斯密特（英语：Samuel Goudsmit）三人所开创。

他们在处理电子的磁场理论时，把电子想象一个带电的球体，自转因而产生磁场。

后来在量子力学中，透过理论以及实验验证发现基本粒子可视为是不可分割的点粒子，所以物体自转无法直接套用到自旋角动量上来，因此仅能将自旋视为一种内禀性质，为粒子与生俱来带有的一种角动量，并且其量值是量子化的，无法被改变（但自旋角动量的指向可以透过操作来改变）。

自旋对原子尺度的系统格外重要，诸如单一原子、质子、电子甚至是光子，都带有正半奇数（1/2、3/2等等）或含零正整数（0、1、2）的自旋；半整数自旋的粒子被称为费米子（如电子），整数的则称为玻色子（如光子）。

复合粒子也带有自旋，其由组成粒子（可能是基本粒子）之自旋透过加法所得；例如质子的自旋可以从夸克自旋得到。

灵遁者量子物理科普书籍《见微知著》在灵遁者淘宝有。

自旋角动量是系统的一个可观测量，它在空间中的三个分量和轨道角动量一样满足相同的对易关系。

每个粒子都具有特有的自旋。

物理学中的自旋现象自旋是量子力学中一个重要的现象，指的是粒子固有角动量的一种表现形式。

它在物理学中有着广泛的应用，涉及到许多领域，包括固态物理、量子信息等。

在这篇文章中，我们将深入探讨自旋的性质、应用以及可能带来的未来发展。

一、自旋的特性自旋是粒子的固有属性，类似于电荷和质量。

不同于电荷和质量的是，自旋是一种角动量，同时具有类似于电子磁矩的特性。

自旋根据量子力学的原理，只能取离散的特定值，其中最常见的是1/2。

不仅电子、质子和中子等基本粒子具有自旋，一些原子和分子也能表现出自旋的相关特性。

二、自旋的应用在固态物理领域中，自旋在研究磁性材料时有着重要的作用。

磁性材料的磁矩与自旋有关，因此了解自旋的特性能够帮助我们更加深入地理解磁性材料的物理性质。

同时，自旋的应用在磁存储方面也具有潜在的优势。

目前的磁存储技术以磁场作用为主，而自旋电子学技术则利用了自旋电子的特性，在研究和开发新型的非易失性存储器方面具有良好的前景。

在量子计算和量子通讯方面，自旋也扮演着重要的角色。

量子计算利用量子比特进行计算，而自旋是量子比特的一种实现方式。

自旋比特具有高度的稳定性，因此是理想的实现方式。

另一方面，量子通讯中需要传输的信息是用自旋编码传递的，自旋的相关性质也被用于实现量子密钥分发等技术。

三、自旋技术的未来发展自旋在物理学中的研究已经有了许多重要的进展，但仍存在许多未知的领域。

在研究自旋的过程中，科学家们不仅关注自旋的电子性质，还开始研究自旋和其他基本粒子的相互作用。

在这些相互作用中，自旋的特性可能有着新的展现，带来意料之外的应用。

同时，目前自旋技术的应用还停留在实验室阶段，面临着许多挑战和限制。

例如，在量子计算领域中，自旋比特的实现和控制仍需要进一步提高，才能让自旋技术真正应用于实际计算中。

在量子通讯方面，自旋编码的传输距离和速率也存在一定的限制。

因此，未来自旋技术的发展需要科学家们在实验和理论方面同时努力，不断突破技术和理论的瓶颈，扩展自旋技术的应用范围。

十大惊艳物理现象
1.黑洞：这是一种极端密集的物体，其引力场极强，甚至可以使光无法逃脱。

黑洞的存在证明了爱因斯坦的广义相对论。

2.量子纠缠：两个粒子之间存在着神秘的联系，即使它们之间隔着很远的距离，一个粒子的状态的改变会立即影响到另一个粒子的状态。

3.时间膨胀：根据相对论，当物体的速度越快，时间就会变得越慢。

这被称为时间膨胀。

4.光子隧穿：在经过非常薄的透镜或障碍物时，光子可以“穿透”这些物体，这被称为光子隧穿。

5.量子超越：量子物理学中有一个奇怪的现象，即粒子可以同时处于两个状态。

这种现象被称为量子超越。

6.超导：超导材料可以在极低的温度下导电，这种现象被称为超导。

7.相变：当物质的状态发生改变时，比如从液态到固态或从固态到液态，就发生了相变。

8.自旋：自旋是一种微观物理学现象，它描述的是粒子的自转。

9.多维宇宙：根据一些物理学家的理论，我们生活在一个有三个空间维度和一个时间维度的宇宙中，但还有可能存在其他维度的宇宙。

10.量子涨落：在量子物理学中，粒子的位置和能量是以概率的
形式存在的，这种概率性就是量子涨落。

- 1 -。

空间自旋状态-概述说明以及解释1.引言1.1 概述概述空间自旋状态是量子力学中一个重要的概念，它描述了微观粒子的自旋在三维空间中的定向和旋转。

自旋是一种固有的属性，类似于粒子的旋转角动量，但并不对应于经典意义上的旋转。

相反，自旋是量子力学中特有的现象，只能用数学上的态矢来描述。

空间自旋状态的研究对于理解微观粒子的行为具有重要的意义。

首先，它是描述微观粒子内部量子态的一种有效方式。

自旋可以有多种取值，例如电子的自旋可以是1/2，也就是说它有两个可能的状态。

不同粒子的自旋可以具有不同的取值，这决定了它们的性质和行为。

其次，空间自旋状态对于理解宏观世界中的物理现象也有着重要的作用。

自旋是量子力学的基础，在很多方面决定了微观粒子的相互作用和性质。

例如，自旋可以影响粒子的磁性，决定了材料的磁性质。

在核磁共振成像中，自旋的定向和旋转是实现成像的基础。

本文将系统地介绍空间自旋状态的定义和特性。

首先，我们将阐述空间自旋状态的基本概念和量子力学中的相关原理。

然后，我们将探讨空间自旋状态的特性，如自旋量子数的取值范围、自旋态的叠加和测量等。

最后，我们将总结空间自旋状态的重要性，并展望未来的研究方向。

通过深入研究空间自旋状态，我们可以更好地理解和应用量子力学的基本原理，推动科学技术的发展。

1.2文章结构文章结构部分可以包括以下内容：文章结构部分的目的是介绍本篇长文的整体组织架构，以便读者能够更好地理解文章的内容和结构。

本文分为引言、正文和结论三个部分。

引言部分主要分为三个小节，分别是概述、文章结构和目的。

首先，概述部分将简要介绍空间自旋状态的背景和基本概念。

在这一部分，读者可以了解空间自旋状态的基本含义以及其在物理领域中的重要性。

其次，文章结构部分将详细介绍本篇长文的组织架构。

该部分用于提醒读者文章整体的结构，并给予读者对文章内容的预期。

最后，目的部分将说明本篇长文的写作目的。

通过对写作目的的阐述，读者可以更好地了解为什么选择撰写关于空间自旋状态的文章，以及读者可以从本文中获得哪些有价值的信息或知识。

物理学中的自旋理论与应用自旋理论是物理学中的一个重要概念，它涉及到微观粒子的自旋状态，以及自旋状态对于这些粒子的行为和特性的影响。

自旋理论在研究物理世界中的许多现象和过程时起着重要作用，同时也为现代科技的发展带来了许多重大的应用。

1. 自旋的概念和本质自旋是物理学中一种与粒子本身内部结构有关的性质，正如电荷和质量一样。

自旋本质上是一个量子力学概念，它并不能够被直接观测到，但可以通过一些实验手段来观测其效应。

自旋的本质是粒子内部某种固有角动量的存在，它并非物理空间中的旋转，也不是经典物理中的角动量。

自旋只能取离散值，以自旋量子数的形式表现。

不同性质的粒子具有不同的自旋量子数，例如电子的自旋量子数为1/2，光子的自旋量子数为1。

自旋量子数不同的粒子在物理行为上也会存在明显的差异。

2. 自旋的量子力学表述自旋在量子力学中可以用一个数学符号来表示，称为自旋角动量算符。

自旋角动量算符只能取两个值，分别代表粒子自旋向上和自旋向下两种状态。

自旋算符的平方用于表示自旋量子数，其取值范围为(1/2)^2和(1)^2。

由于自旋角动量算符和空间角动量算符的运算规则存在差异，因此自旋对于量子力学的研究具有独特的意义。

利用自旋角动量算符和其他量子力学理论，可以在物理实验中观测到自旋的效应。

例如，在杨-米尔斯双缝干涉实验中，光子的自旋会在通过磁场后偏转，从而改变其相位，进而影响干涉图案。

3. 自旋理论的应用自旋在物理学中的应用非常广泛，其具有的光电性质和信息携带能力成为了众多现代科技的基石。

自旋磁共振成像技术（MRI）是一种常见的医学成像技术，它利用了自旋与磁场相互作用的性质，可以观测人体内部的结构和组织状态，并对疾病进行诊断和治疗。

自旋电子学则是一种新兴的电子学技术，利用了电子自旋的偏振和操控，可以实现高速、高清晰度的信息存储和传输。

总的来说，自旋理论在物理研究和应用领域发挥了重要作用，其对于人类认识自然和发展现代科技都有着巨大的贡献。

自旋名词解释自旋啊，这可是个超级有趣又神秘的东西。

你可以把它想象成微观粒子的专属小秘密“舞蹈动作”。

就好比每个微观粒子都是一个超级小的舞者，它们的自旋就是独特的舞步。

这些粒子可不像我们人类跳舞，扭扭腰、摆摆手这么简单。

它们的自旋是一种内在的属性，就像天生自带的一种特殊才艺。

你要是把微观粒子想象成一个个小星球的话，自旋就不是那种星球绕着轴转的常规转动哦。

它更像是小星球的一种超能力，这种超能力是与生俱来的，不管外界怎么干扰，它都有自己的自旋状态。

有些粒子的自旋就像是一个永远停不下来的小陀螺，一直在那自顾自地转着。

而且它们自旋的方向也很神奇，不是简单的顺时针或者逆时针，就像这个小陀螺有着自己独特的旋转密码。

自旋还特别调皮呢，它不像宏观世界里的物体旋转那么好理解。

如果说宏观物体的旋转像一辆规规矩矩在马路上行驶的汽车，那微观粒子的自旋就像是一辆可以瞬间消失又瞬间出现，还能做出各种不可思议动作的魔法汽车。

从量子力学的角度看，自旋的取值也是特别怪异。

就好像是老天爷在分配这个特殊才艺的时候，不是按照我们常规的想法来的。

它有一些固定的、离散的值，就像是抽奖的时候只有特定的几个号码能中奖，粒子的自旋取值就是这么任性。

想象一下，一群微观粒子在一个微观的舞池里，每个粒子都用自己独特的自旋舞步在跳动。

有的跳得快，有的跳得慢，有的舞步还特别复杂，就像一场混乱又有序的量子舞会。

要是微观粒子能说话，它们可能会说：“嘿，我们的自旋可是我们最酷的标志，你们宏观世界的家伙可理解不了。

”这种微观世界的自旋现象，就像是一扇通往神秘量子领域的大门，我们人类只能透过门缝去窥视其中的奇妙。

自旋这个概念虽然很难完全理解透彻，但就像探索一个充满宝藏的神秘岛屿一样。

每多了解一点关于自旋的知识，就像是在这个神秘岛屿上发现了一颗闪闪发光的宝石。

它让我们对微观世界的认知更加丰富，也让我们感叹这个世界真是充满了无尽的奇妙之处。

电子自旋微观世界中的旋转粒子早在20世纪20年代，科学家们发现在电子内部存在一种特殊的性质，称之为自旋。

自旋不是真正的旋转，而是一种与电子相关的量子属性。

自此以后，电子的自旋便成为了微观世界中的一个重要领域进行研究的课题。

本文将探讨电子自旋及其在微观世界中的各种现象。

一、自旋的概念和性质在经典物理学中，我们通常将物体的旋转视为物体自身的属性。

然而，在量子力学中，情况却略有不同。

电子的自旋并不是它真正存在的旋转，而是一种纯量。

简单来说，自旋可以被看作是电子的一种内禀的特性，类似于一个内部的“旋钮”，它决定了电子在磁场中的相互作用。

自旋有许多重要的性质。

首先，自旋是量子化的，只能取离散的数值。

其次，电子的自旋可以取两个方向，分别标记为“上旋”和“下旋”，用符号↑和↓表示。

不同自旋状态的电子在相同的能级上具有不同的能量，从而对电子的运动和行为产生影响。

二、自旋的实验观测方法科学家们通过实验观测，揭示了电子自旋的一些特性。

这些观测方法包括：1. 斯特恩-盖拉赫实验：斯特恩-盖拉赫实验是20世纪20年代进行的一项重要实验，证明了电子具有自旋。

实验中，通过将银原子束通过磁场，科学家观察到了束分裂成两个组分的现象，从而得出了电子自旋的结论。

2. 核磁共振：核磁共振是利用原子核的自旋相互作用实现原子核磁共振现象。

这种现象在医学中得到广泛应用，用于核磁共振成像。

通过对物质中的原子核进行共振激发，可以得到关于原子核自旋的信息。

三、自旋在量子计算中的应用自旋不仅对电子本身的性质产生影响，还被广泛应用于量子计算中。

量子计算是一种基于量子力学原理的计算模式，利用量子比特（qubit）的超定位和干涉性质进行信息的存储和处理。

自旋作为一种量子比特的载体，在量子计算中具有重要的地位。

通过控制和操作电子的自旋，可以实现量子比特之间的纠缠和量子门操作，从而实现量子计算中的复杂运算。

电子自旋作为量子计算的基本单元，不仅可以进行信息的储存和传递，还可以通过与其他量子系统的相互作用，实现量子通信和量子网络。

微观粒子自旋现象及其理论解释自旋是微观粒子的一种内禀性质，它是指粒子围绕自身轴心旋转的角动量。

尽管名称与日常生活中的旋转相似，但自旋与经典物体的旋转不同，它是一种量子力学现象。

在本文中，我们将探讨微观粒子自旋的一些基本特性以及目前对其理论解释的认识。

首先，自旋是量子力学中的一种杂化性质。

与经典的内禀自由度，如质量和电荷不同，自旋不能通过经典的运动方程来描述。

实际上，自旋是由量子力学的波函数所描述的。

其次，自旋具有离散的特征。

根据量子力学的理论，自旋可以采取两个离散的数值：正一半（+1/2）和负一半（-1/2），分别代表自旋向上或向下的方向。

这意味着任何微观粒子的自旋必须处于这两个数值之一。

第三，自旋有助于解释一些微观粒子的性质。

例如，自旋是解释化学元素周期表的重要参考。

将所有电子按照自旋方向排列后，我们可以清楚地看到其对于元素的化学性质的影响。

此外，自旋还在其他物理学领域发挥着重要的作用，比如核物理和粒子物理研究中。

关于自旋的理论解释，磁化率实验是最早对自旋现象进行研究的方法之一。

磁化率是指物质在受到外部磁场作用时的磁化程度。

通过测量不同自旋状态下物质对磁场的响应，科学家们可以推断出微观粒子的自旋方向及其可能的状态。

另一个与自旋相关的理论解释是著名的斯特恩-盖拉赫实验。

该实验通过将自由电子束通过磁场，观察到了电子在磁场中被分为两束的现象。

这表明电子具有自旋，而且自旋的方向只能是上或下。

斯特恩-盖拉赫实验奠定了自旋观念的基础，为后来的研究提供了理论基础。

另一种理论解释是使用狄拉克方程对自旋进行描述。

狄拉克方程是描述自旋½粒子的重要方程，它是量子力学的基础之一。

狄拉克方程描述了自旋与粒子的动量和能量之间的关系，提供了自旋性质的更深层次理解。

此外，微观粒子自旋的理论解释还包括自旋动力学理论和自旋-统计定理。

自旋动力学理论研究了自旋如何随时间演化，以及它与其他物理量之间的关系。

而自旋-统计定理则是描述了不同自旋的粒子遵循不同的统计行为，比如费米子和玻色子。

物体的自旋与自旋力矩自旋是物理学中一个引人注目的现象。

自旋是物体内在的旋转运动，类似于地球的自转。

虽然自旋在日常生活中并不常见，但它在微观尺度中对物质结构和性质起着重要作用。

与自旋紧密相关的概念是自旋力矩。

物质的自旋可以用一个量子数来描述，其数值与自旋的特性相关。

量子力学对于自旋的理论解释揭示了其与粒子之间的相互作用和态的演化之间的关系。

自旋的量子性在许多物理现象中都得到了验证，如原子核自旋和电子自旋。

与自旋密切相关的是自旋力矩。

自旋力矩是由于自旋产生的磁矩引起的力矩。

对于一个物体来说，其自旋力矩大小与自旋的大小成正比，方向与自旋的方向垂直。

自旋力矩在磁场中会受到力矩的作用，使物体产生一种稳定的旋转状态。

自旋力矩的作用在许多领域中都得到了应用。

在核磁共振成像（MRI）中，利用自旋力矩的性质可以对人体组织进行成像。

MRI是一种无创的诊断技术，通过测量人体内部的自旋力矩来获取图像信息。

借助于自旋力矩的原理，医生可以检测出人体内部的疾病或异常情况，以便进行诊断和治疗。

除了在医学领域中的应用，自旋力矩也在信息存储领域中发挥着重要的作用。

在硬盘驱动器中，磁性材料的自旋力矩被用来存储和读取信息。

通过改变自旋力矩的方向，可以改变磁性材料的磁性状态，从而实现信息的存储和读取操作。

自旋力矩技术使得硬盘驱动器具备高速读写和大容量存储的能力，成为现代计算机存储领域不可或缺的部分。

同时，自旋力矩的应用也延伸到了量子计算领域。

量子比特（qubit）作为量子计算的基本单位，可以利用自旋力矩来进行存储和操作。

通过调整自旋力矩的强度和方向，可以实现对量子态的控制和操作，从而进行量子计算。

自旋力矩作为量子比特的重要性质，为实现量子计算提供了有力的基础。

自旋和自旋力矩的研究不仅对于理论物理学和量子力学有着重大意义，而且在应用层面也有着广泛的用途。

物体的自旋能够揭示物质内部微观结构和性质，自旋力矩则在医学成像、信息存储和量子计算等领域发挥着重要作用。

自旋统计规律嘿，朋友们！今天咱来聊聊这个神奇的自旋统计规律呀！你说这自旋统计规律，就像是一场微观世界里的奇妙舞蹈。

粒子们在那里跳着属于它们自己的独特舞步呢！咱就打个比方哈，粒子就像是一个个小精灵，它们有着自己的个性和特点。

有的精灵转得快，有的转得慢，这就是它们的自旋啦。

想象一下，在一个小小的微观王国里，这些小精灵们遵循着特定的规则在活动。

它们可不是随便乱转的哟！这自旋统计规律就像是给它们设定的游戏规则。

比如说电子这个小精灵，它就有着特定的自旋。

而且呢，不同的粒子根据这个规律会有不同的表现。

这多有意思呀！你看啊，我们生活的这个宏观世界有各种各样的规律，那微观世界肯定也有呀。

自旋统计规律就是其中很重要的一个呢。

要是没有这个规律，那微观世界还不得乱套呀！粒子们都不知道该怎么转了，那可不行。

这就好比我们走路，总得有个方向，有个规则吧，不能乱走一气呀。

而且呀，这自旋统计规律可不是随便就能被打破的。

它就像是一道坚固的城墙，守护着微观世界的秩序。

科学家们通过不断地研究和探索，才慢慢发现和理解了这个神奇的规律呢。

这也让我们更加感叹大自然的奇妙呀！这么复杂又这么精妙。

咱再换个角度想想，要是没有自旋统计规律，那很多物理现象我们都没法解释啦。

比如说一些材料的磁性呀，导电性呀，可能都会变得不一样。

哎呀，真不敢想象那会是个什么样子！所以说呀，这自旋统计规律可真是太重要啦！它就像是微观世界的定海神针。

让我们好好感谢那些科学家们吧，是他们的努力让我们对这个世界有了更深刻的认识。

总之呢，自旋统计规律就是微观世界中一个非常非常重要的存在，我们可不能小瞧它哟！。