随机过程 第三章 马尔科夫链

第三章 马尔可夫链 一、马尔可夫链的概念马尔可夫过程是一类有重要应用意义的随机过程，它具有如下特征：随机过程‘将来’所处的状态仅与‘现在’所处的状态有关，而与‘过去’曾处于什么状态无关。

马尔可夫过程按其状态和时间参数是离散还是连续的可以分成三类 （1） 时间和状态都是离散的马尔可夫过程，称为马尔可夫链。

（2） 时间连续、状态离散的马尔可夫过程，称为连续时间的马尔可夫链。

（3） 时间和状态都连续的马尔可夫过程。

本章介绍马尔可夫链定义1 设}0,{≥n X n 为随机序列，其状态空间为},,,{210 i i i I =，如果对任意正整数n 及任意n+2个状态I i i i i n ∈+1210,,,, ，有},,,{110011n n n n i X i X i X i X P ====++}{11n n n n i X i X P ===++则称此随机序列}0,{≥n X n 为马尔可夫链。

若将时刻n 称为‘现在’，将时刻n+1称为‘将来’，而把0，1，2，……，n-1称为‘过去’。

定义中的等式便可通俗解释为：在已知}0,{≥n X n ‘现在’所处的状态条件下，‘将来’所要达到的状态与‘过去’所经历的状态无关，这一特性常称为马尔可夫的无后效性。

例1．一个n 级数字传输系统，每一级的输入和输出信号只取0或1两个值，每一级的输出是下一级的输入；并假定当一级输入为0时，其输出为0和为1的概率分别为p 和1-p;当输入为1时，其输出为1和0的概率分别为p 和1-p （见图）令Xn 表示第n 级输出，则{ Xn,n ≥0}便为一个马尔可夫链。

例2．从1，2，……，N 数字中任取一个数，记为X0；再从1，2，……，X0数字中任取一个数，记为X1；再从1，2，……，X1中任取一个数，记为X2；依此类推，在1，2，……，Xn-1中任取一个数，记为Xn 。

可以证明{ Xn,n ≥0}为马尔可夫链。

事实上，{ Xn,n ≥0}的状态空间为I={1，2，……，N}，对任意正整数n ，取n+1个状态I i i i i n ,,,,210 ,由题意可知故{ Xn,n ≥0}为马尔可夫链。

第三章 马尔科夫过程第一节 随机过程的概念1、 随机系数必然事件自然界中出现的事件分为 不可能事件随机事件事物的变化过程 必然过程随机过程（1） 必然过程：有确定的变化形式，可以用精确的数学关系式来描述。

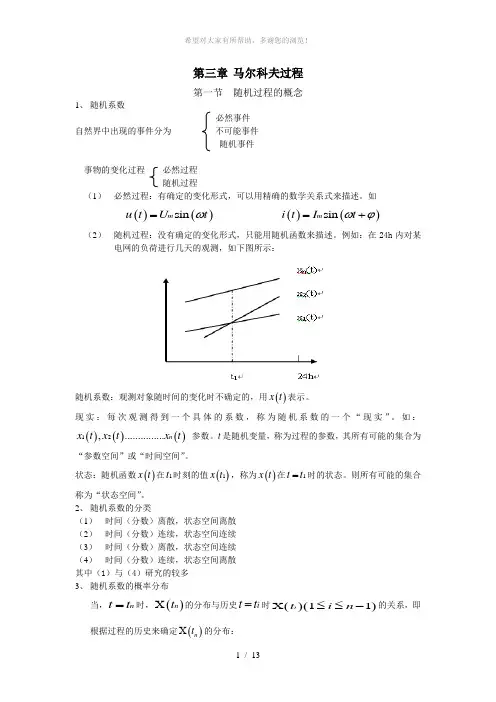
如()()sin m u t U t ω= ()()sin m i t I t ωϕ=+（2） 随机过程：没有确定的变化形式，只能用随机函数来描述。

例如：在24h 内对某电网的负荷进行几天的观测，如下图所示：随机系数：观测对象随时间的变化时不确定的，用()x t 表示。

现实：每次观测得到一个具体的系数，称为随机系数的一个“现实”。

如：()()()12,...............n x t x t x t 参数。

t 是随机变量，称为过程的参数，其所有可能的集合为“参数空间”或“时间空间”。

状态：随机函数()x t 在1t 时刻的值()1x t ，称为()x t 在1t t =时的状态。

则所有可能的集合称为“状态空间”。

2、 随机系数的分类（1） 时间（分数）离散，状态空间离散 （2） 时间（分数）连续，状态空间连续 （3） 时间（分数）离散，状态空间连续 （4） 时间（分数）连续，状态空间离散 其中（1）与（4）研究的较多 3、 随机系数的概率分布当，n t t =时，()n t X 的分布与历史i t t =时()()11i t i n X ≤≤-的关系，即根据过程的历史来确定()n t X 的分布：用条件概率来描述：（()i x t 简化成i x ）()112211/,............n n n n P x x x x --X =X =X =X = （1）若在特定的情况下，n X 的分布与过去的历史无关，则()()112211/,............n n n n n n P x x x x P x --X =X =X =X ==X =称为过程独立（无记忆过程）。

若n X 的分布只与过去的一部分历史有关，如只与最近一次时间的状态有关，而与以前所有时刻的状态都是无关，即()()11221111/,............/n n n n n n n n P x x x x P x x ----X =X =X =X ==X =X =第二节 马尔科夫链1、 概述将参数和状态空间都是系数的马尔科夫过程称为马尔科夫链。

随机过程中的马尔可夫链理论随机过程是概率论中的一个重要分支，研究时间上的变化不确定性。

马尔可夫链是随机过程中的一种特殊形式，它具有马尔可夫性质，即未来状态只依赖于当前状态，与过去状态无关。

在本文中，我们将深入探讨随机过程中的马尔可夫链理论。

一、马尔可夫链的定义马尔可夫链是一种离散随机过程，它由一系列的状态和状态转移概率组成。

设S={S1, S2, ...}为状态空间，P={Pij}为状态转移概率矩阵，其中Pij表示从状态Si到状态Sj的概率。

马尔可夫链满足以下两个条件：1) 转移概率只与当前状态有关；2) 对于任意状态Si，状态转移概率之和等于1。

二、马尔可夫链的性质1. 马尔可夫性质由定义可知，马尔可夫链具有马尔可夫性质，即未来状态只与当前状态有关，与过去状态无关。

这一性质使得马尔可夫链在建模和分析中具有较大的灵活性。

2. 随机游走马尔可夫链可以看作是一种随机游走的过程。

在状态空间S中，根据状态转移概率进行转移，从而实现状态之间的随机变动。

通过研究随机游走的路径和特性，可以揭示马尔可夫链的一些重要特性。

3. 平稳分布对于某些马尔可夫链，存在一个平稳分布使得在长时间模拟中，状态分布趋于稳定。

这一性质在实际应用中广泛使用，例如在排队论、金融风险管理等领域。

三、马尔可夫链的应用1. 自然语言处理马尔可夫链在自然语言处理中得到广泛应用，特别是在文本生成和语音识别方面。

通过学习语料库中的转移概率，可以生成新的语句或者识别语音中的词组。

2. 生物信息学在DNA和蛋白质序列的分析中，马尔可夫链可以用于模拟和预测相关的状态变化。

通过构建转移矩阵，可以研究序列中的概率事件和模式。

3. 市场分析马尔可夫链在市场分析中具有较大的潜力。

通过研究股票价格或者交易策略的状态转移，可以辅助投资决策和风险管理。

四、马尔可夫链的改进为了更好地描述现实世界中复杂的系统和过程，研究者们对传统的马尔可夫链进行了改进。

例如，高阶马尔可夫链能够捕捉更长期的状态依赖性；隐马尔可夫模型则能够处理观测序列的概率计算问题。

随机过程与马尔可夫链随机过程是数学中研究随机事件在时间序列上变化的一种数学模型。

在实际生活中，我们会遇到很多随机变化的现象，比如天气的变化、股票价格的变动等等。

理解和研究这些现象的规律，对于预测未来的发展和做出合理决策具有重要意义。

而马尔可夫链就是随机过程的一种特殊形式，它具有“无记忆”的特性，即未来的状态只与当前状态有关，与过去的状态无关。

这一特性使得马尔可夫链具有简单的数学性质和可计算的特点，使得它成为概率论和统计学中研究的重要工具。

马尔可夫链的基本定义是一个离散状态空间上的随机变量序列，满足马尔可夫性质。

具体来说，给定当前状态，未来状态的概率分布只与当前状态有关，与过去的状态无关。

这一概率分布称为转移概率矩阵，可以用矩阵形式表示。

随机过程中的状态可以是离散的，也可以是连续的。

在马尔可夫链中，我们主要关注的是离散状态的情况。

离散状态的马尔可夫链可以用有向图表示，图中的节点表示状态，边表示状态之间的转移概率。

在实际问题中，我们可以通过观察历史数据来估计状态间的转移概率，并利用得到的转移概率矩阵来进行未来的预测。

这一方法被广泛应用于金融市场的价格预测、自然语言处理中的语言模型、网络流量的分析等领域。

除了基本的马尔可夫链模型，还有一些扩展和变形的模型，如高阶马尔可夫链、隐马尔可夫链等。

这些模型在更复杂的问题中有着重要的应用，比如自然语言处理中的词性标注、语音识别中的模式识别等。

总结一下，随机过程与马尔可夫链是概率论和统计学中重要的概念和工具。

它们可以帮助我们理解和预测随机变化的现象，为决策提供依据。

通过观察历史数据并建立概率模型，我们可以利用马尔可夫链进行未来的预测和分析，为各个领域的应用提供支持。

在未来的研究中，我们还可以探索更多关于马尔可夫链的特性和应用，进一步拓展其在实际问题中的应用。

随机过程是概率论中的一个重要概念，它描述了一组随机变量在时间上的演化规律。

其中，马尔可夫链是一种重要的随机过程，具有许多重要的应用。

本文将对随机过程、马尔可夫链以及其中的常返性进行介绍，并探讨解题技巧。

一、随机过程随机过程是指一组随机变量的集合，它是对一组随机事件进行建模的数学工具。

随机过程在统计学、金融工程、生态学等领域具有广泛的应用。

在随机过程中，我们通常关注的是随机变量在时间上的演化规律，即随机变量随着时间的推移如何变化。

二、马尔可夫链马尔可夫链是一种随机过程，它具有马尔可夫性质，即在已知当前状态的情况下，未来的状态只与当前状态有关，而与过去的状态无关。

马尔可夫链通常用状态空间和转移概率矩阵来描述，其中状态空间表示随机变量可能的取值，转移概率矩阵表示在当前状态下转移到下一状态的概率分布。

在马尔可夫链中，我们通常关注的问题包括平稳分布、收敛性、常返性等。

平稳分布是指当马尔可夫链收敛时，存在一个分布使得随机变量收敛到该分布。

收敛性描述了马尔可夫链的状态在时间推移中是否会趋于稳定。

常返性是衡量马尔可夫链状态转移的一个重要性质，它描述了马尔可夫链是否在有限时间内会回到某个状态。

三、常返性在马尔可夫链中，常返性是一个重要的性质。

常返性描述了马尔可夫链在有限时间内回到某个状态的概率。

如果马尔可夫链从某个状态出发，最终会以概率1回到该状态，则称该状态是常返的。

否则，该状态是暂态的。

对于一个马尔可夫链，如果所有状态都是常返的，则称该链是常返的。

常返性是马尔可夫链收敛性的一个重要条件。

若一个马尔可夫链是常返的，且满足一定的条件，那么该链将会收敛到一个平稳分布。

解题技巧在研究随机过程和马尔可夫链时，我们常常需要解决一些与状态转移、概率分布、收敛性等相关的问题。

以下是一些解题技巧，可以帮助我们更好地理解和应用随机过程和马尔可夫链。

1. 注意状态空间的选择：在解题时，我们需要注意选择合适的状态空间，以便清晰地描述随机变量的取值范围。

概率论中的随机过程与马尔可夫链概率论是数学中重要的一个分支，它研究的是随机事件的发生概率以及它们的统计规律。

而随机过程是概率论中的一个重要概念，它是一组随机变量的集合，它们表示随机现象的演化过程。

而马尔可夫链则是随机过程中的一种特殊形式，它具有无记忆性和马氏性质，被广泛应用于各个领域。

第一部分：随机过程的定义随机过程是由一组随机变量组成的，它们表示一个随机现象的演化过程。

随机过程可以用一个函数来描述，这个函数的输入是时间，输出是随机变量的取值。

随机过程可以分为离散时间的随机过程和连续时间的随机过程两种形式。

离散时间的随机过程，也称为随机序列，表示在离散的时间点，随机变量的取值随机变化的过程。

常见的例子包括掷骰子的过程、赌博中的赢输情况、股票价格的涨跌等。

连续时间的随机过程，是指在时间轴上随机变化的过程，输出的是随机变量的取值。

常见的例子包括股票价格在时间轴上的变化、温度在时间轴上的变化、人类寿命的随机变化等。

第二部分：马尔可夫链的定义马尔可夫链是一种随机过程，它具有无记忆性和马氏性。

无记忆性是指在某一时刻的状态，只与上一时刻的状态相关，而与过去的状态无关。

马氏性则是指在随机过程中，下一个状态只与当前状态相关，而与历史状态无关。

马尔可夫链的特点在于它可以用一个转移矩阵来表示，这个转移矩阵是一个方阵，其中的元素表示从一个状态到另一个状态的概率。

换句话说，马尔可夫链的下一个状态只与当前状态有关，而转移矩阵则描述了状态之间的转移概率。

马尔可夫链的应用非常广泛，从物理学、经济学到生物学等各个领域都有应用。

例如，在自然语言处理中，可以使用马尔可夫模型来预测下一个单词出现的概率，从而实现文本生成和自动翻译等功能。

在股票价格预测中，可以使用马尔可夫模型来分析股价走势，从而帮助投资者制定投资策略。

第三部分：马尔可夫链的应用1.自然语言处理在自然语言处理中，马尔可夫模型被广泛应用于文本生成、自动翻译等功能。

马尔可夫模型通过分析语言中词语之间的关系，预测下一个单词可能出现的概率。

随机过程马尔可夫链随机过程是研究随机事件在时间和空间上的变化规律的数学模型。

而马尔可夫链是随机过程的一种，它的特别之处在于，当前时刻的状态只与前一时刻的状态有关，而与其它时间的状态无关。

现在，让我们来详细了解一下随机过程与马尔可夫链。

一、随机过程随机过程实际上就是由一系列随机变量组成的，这些随机变量的取值是在某些规定的时间或空间上进行的。

它是一个随机事件的序列或集合，因此其本质是一种时间或空间上的随机演化。

二、马尔可夫链马尔可夫链是一种特殊的随机过程，其特征在于它只与其前一状态有关。

其实，马尔可夫链是一种转移概率的数学模型，它描绘了系统从一个状态到另一个状态的转移概率，而这些概率只与前一时刻的状态有关。

马尔可夫链的形式化描述就是一个状态空间和一个转移矩阵。

这里，状态空间可以是任意形式的集合，而转移矩阵则是一个矩阵，其每个元素表示从一个状态到另一个状态的概率。

三、马尔可夫链的性质马尔可夫链具有多种性质：1、马尔可夫性质：当前时刻的状态只与前一时刻的状态有关。

2、无记忆性质：其将来的状态与过去的状态无关。

3、多步转移概率：马尔可夫链具有的多步转移概率与初始状态无关。

4、周期性：若马尔可夫链从一个状态出发始终无法到达其它状态，可以说其为周期性的。

四、应用1、生物统计：马尔科夫链应用到多态遗传研究。

2、分子动力学：马尔可夫链应用到高分子链的构象和动力学研究。

3、自然语言处理：将一个英文句子转化为标签序列可以看做是一个马尔可夫链。

总之，随机过程和马尔可夫链是最基础的统计学习模型。

它们在多个领域都有广泛的应用，如金融、医学、工业等。

深刻了解它们的特性和应用将有助于我们更好地理解大量数据背后的规律。

随机过程的马尔可夫链知识点汇总什么是马尔可夫链？马尔可夫链是一种数学模型，描述了一系列随机事件，其中每个事件的概率只依赖于当前事件发生的状态。

换句话说，未来的状态只与当前状态有关，而与过去的状态无关。

马尔可夫链的性质1. 马尔可夫性质（Markov Property）：在一个马尔可夫链中，给定当前状态，未来的状态与过去的状态无关。

2. 状态空间（State Space）：马尔可夫链的所有可能状态的集合。

3. 转移概率（Transition Probability）：描述了从一个状态转移到另一个状态的概率。

4. 长程行为（Long-term Behavior）：马尔可夫链在长时间的演化中，会逐渐趋向于稳定的概率分布。

马尔可夫链的应用1. 模拟和预测：马尔可夫链可以用于模拟和预测各种随机事件的概率分布，如天气预测、股票市场等。

2. 自然语言处理：马尔可夫链可以用于自然语言处理中的文本生成和自动语音识别等任务。

3. 统计学：马尔可夫链在统计学中有广泛的应用，如随机抽样和蒙特卡洛模拟等。

马尔可夫链的改进1. 高阶马尔可夫链（Higher-order Markov Chains）：考虑当前和前几个状态的组合，以改进模型的准确性。

2. 隐马尔可夫模型（Hidden Markov Model, HMM）：在马尔可夫链的基础上引入隐藏状态，用于处理有观测数据和隐藏状态的问题。

3. 非时齐马尔可夫链（Non-homogeneous Markov Chains）：考虑转移概率随时间变化的情况，用于更复杂的应用。

总结马尔可夫链是一种重要的随机过程模型，具有简单的数学结构和丰富的应用。

通过理解马尔可夫链的基本概念和性质，可以更好地应用于各种问题的建模和解决。

随机过程中的随机游动与马尔科夫链随机过程是一类描述随机现象演化的数学模型，常用于对自然现象、社会现象等随机变化的研究。

其中，随机游动和马尔科夫链是比较常见的两种模型。

一、随机游动随机游动模型最早是在布朗运动中产生的。

当时，生物学家RBrown对于花粉在水面上运动的轨迹进行了观察，发现花粉在水面上的运动轨迹非常类似于随机游动的路径。

根据这个现象，布朗运动被普遍用来描述诸如分子、原子等微观粒子的运动过程。

随机游动是一种没有目的的随机行走，其运动特点如下：1. 行走者在各个时间点上所处的位置是随机的；2. 每个时间点行走者的走步长度和方向也是随机的；3. 无论时间走了多长，行走者最终会返回起点，且越接近初始位置，行走路程越短。

随机游动可以用数学模型来进行描述，其中最基础的模型是一维随机游动。

假设在一维数轴上有一个游走者，每个时间点他只能向左或向右走一步，且走步距离是随机的。

我们用$x_n$表示在第$n$步时游走者所在的位置，则$x_n$的变化可以写成：$$x_n=x_{n-1}+\xi_n$$其中，$\xi_n$是一个随机变量，表示在第$n$步时游走者向左或向右走的距离。

假设$\xi_n$服从均值为0、方差为$\sigma^2$的正态分布，则$\xi_n$的概率密度函数为：$$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^2}{2\sigma^2}}$$一维随机游动的路径分布非常复杂，但是当$n$趋于无穷大时，$x_n$的分布趋于高斯分布。

$$f(x)=\frac{1}{\sqrt{2\pi n}\sigma}e^{-\frac{(x-n\mu)^2}{2n\sigma^2}}$$其中$\mu$是$\xi_n$的期望值。

上述结果被称为随机游动的中心极限定理，它表明了在随机游动下，当时间趋于无穷大时，路程在起点两侧的概率趋于相等。

二、马尔科夫链马尔科夫链是一种随机过程，其运动特点是：1. 未来状态只与当前状态相关，与过去状态无关；2. 具有马尔科夫性质，即状态转移概率矩阵不随时间变化。

随机过程中的马尔可夫链模型马尔可夫链是一种描述随机过程的数学模型，它具有“无记忆性”的特点，即未来状态仅受当前状态的影响，与过去状态无关。

在这篇文章中，我们将探讨随机过程中的马尔可夫链模型及其应用。

一、什么是马尔可夫链模型马尔可夫链是一种随机过程，指的是一系列的随机事件，其中每个事件的发生仅依赖于前一个事件的状态。

这种“无记忆性”使得马尔可夫链具有简洁的数学描述和计算特性。

马尔可夫链由五个基本要素组成：状态空间、状态转移概率、初始概率分布、时间步长和转移矩阵。

1. 状态空间：马尔可夫链的状态空间表示系统可能处于的所有状态的集合。

例如，掷骰子的状态空间是{1, 2, 3, 4, 5, 6}。

2. 状态转移概率：状态转移概率表示从一个状态转移到另一个状态的概率。

通常用转移矩阵表示，其中每个元素表示从一个状态到另一个状态的转移概率。

3. 初始概率分布：初始概率分布表示系统在初始时刻处于各个状态的概率分布。

通常用向量形式表示，其中每个元素表示系统处于对应状态的概率。

4. 时间步长：时间步长表示系统从一个状态转移到下一个状态所经过的时间。

5. 转移矩阵：转移矩阵是一个方阵，其中的每个元素表示从一个状态到另一个状态的转移概率。

转移矩阵的每一行之和为1。

二、马尔可夫链模型的应用马尔可夫链模型在许多领域都有广泛的应用，包括自然语言处理、金融市场分析、生物信息学、网络传播模型等。

1. 自然语言处理：在自然语言处理中，马尔可夫链模型被用于文本生成、机器翻译和语音识别等任务。

通过建立一个马尔可夫链模型，可以根据已知的文本数据生成具有相似特征的新文本。

2. 金融市场分析：马尔可夫链模型被广泛应用于金融市场的分析和预测。

通过分析历史数据，建立一个马尔可夫链模型，可以预测未来的市场变化趋势，帮助投资者做出决策。

3. 生物信息学：在生物信息学中，马尔可夫链模型被用于基因序列分析、蛋白质结构预测等任务。

通过构建一个马尔可夫链模型，可以识别基因序列中的编码区域和非编码区域，进而对基因功能进行推断。

随机过程中的马尔可夫链随机过程是指一种具有随机性质的过程，而马尔可夫链是随机过程中的一种基本模型。

马尔可夫链是一种具有马尔可夫性质的随机过程。

所谓马尔可夫性质，是指在一个随机过程中，当前状态的概率分布仅依赖于当前状态，而不依赖于历史状态。

马尔可夫链广泛应用于各个领域，如物理学、生物学、计算机科学等。

一、马尔可夫链的定义与性质马尔可夫链是一种随机过程，其状态空间可以是一个有限集合或可数集合。

若设Xn表示马尔可夫链在时间n的状态，则马尔可夫链具有以下性质：1.满足马尔可夫性质：在给定现在状态下，未来状态的概率分布与过去状态无关。

2.具有无后效性：状态的转移只受当前状态影响，与之前的状态无关。

3.具有Markov性：任意时刻t，下一状态Xt+1只与当前状态Xt有关，与过去状态无关。

二、转移矩阵转移矩阵是马尔可夫链中的重要概念。

假设状态集合为{1，2，3，...，N}，若Xn=j，则转移矩阵Pij表示从状态j转移到状态i的概率。

即在马尔可夫链的当前状态为j时，下一时刻转移至状态i的概率为Pij。

满足下列条件：1.所有元素的值都是非负数；2.每行元素的和等于1。

3.初始转移概率矩阵为pc，则$t\in N^{*}$时，$i, j\in{1,2,3,...,N}$$ P_{ij} P_{j1}=P_{i1}$$ P_{ij} P_{j2}=P_{i2}$$ P_{ij} P_{jr}=P_{ir}$也就是说，转移矩阵是一个n阶方阵，矩阵中的元素为非负实数并且每行的和为1。

三、平稳分布在马尔可夫链中，若转移矩阵满足一定条件，那么存在一个平稳分布，在链条经过足够多的转移后，状态分布不再增长或减少，变得稳定，称之为稳态或平稳分布。

平稳分布是指当马尔可夫链在经过一定转移后，概率分布已经趋于稳定，不再发生变化的状态分布。

平稳分布的计算是求解方程$P_\infty=P_\infty P$。

其中$P_\infty$为平稳分布，$P$为转移矩阵。