下载文档原格式
信息熵在图像处理中的应用图像处理作为计算机视觉和图像识别领域的重要技术之一，一直是研究和应用的热点。
而信息熵作为一种评估信息量的重要指标，也被广泛应用于图像处理中。
本文将探讨信息熵在图像处理中的应用，并探讨其原理和效果。
信息熵是信息论中的概念，用来描述一组数据中所包含的信息量大小。
在图像处理中，信息熵可以通过计算图像的灰度分布来获得。
通过统计一幅图像中所有像素的灰度级别及其对应的像素数，可以得到一个灰度直方图，进而计算出图像的信息熵。
在图像处理中，信息熵可以用来评估图像的复杂度和信息量大小。
一个高熵的图像意味着图像中包含了大量的信息和细节，而低熵的图像则相反。
通过计算图像的信息熵，可以帮助我们理解一幅图像的特性和内容，从而进行更深入的图像分析和处理。
信息熵在图像处理中有许多应用。
首先，信息熵可以用来评估图像的清晰度。
一幅清晰度高的图像往往包含了丰富的细节和高频信息，因此其信息熵也相对较高。
而模糊或者含有噪声的图像则会导致信息熵的降低。
通过计算图像的信息熵，我们可以客观地评估图像的清晰度，从而进行相应的图像增强或者去噪处理。
其次，信息熵可以用于图像分割和目标检测。
在图像分割中，利用图像的信息熵可以帮助我们找到分割点，对图像进行分割并提取其中的目标区域。
在目标检测和识别中，利用图像的信息熵可以帮助我们提取图像中的关键特征，从而实现对目标的自动检测和识别。
此外，信息熵还可以应用于图像压缩和编码。
在图像压缩中，我们可以利用信息熵来评估图像的冗余程度，从而实现对图像的有损或者无损压缩。
在图像编码中，信息熵可以用来指导编码器的设计，帮助我们更高效地对图像进行编码和解码。
虽然信息熵在图像处理中有着广泛的应用，但是也存在一些限制和挑战。
首先，计算图像的信息熵需要统计图像的灰度分布，这个过程在大规模图像数据处理中可能会面临计算效率的问题。
其次，信息熵只能反映图像中像素级别的信息，而无法捕捉到图像中的结构和上下文信息。
信息论在图像处理中的应用研究近年来，随着图像处理技术的迅猛发展，人们对于如何更好地利用信息论方法来优化图像处理过程与结果产生了浓厚的兴趣。
信息论作为一门独特的数学理论，不仅在通信和计算机科学领域发挥了重要作用，也在图像处理中得到了广泛应用。
本文将重点探讨信息论在图像处理中的应用研究，并讨论其在图像压缩、图像增强和图像恢复等方面的具体应用。
一、图像压缩中的信息论应用图像压缩是图像处理领域中的一个重要研究方向。
通过压缩图像数据，可以在仅占用较小存储空间的基础上，实现高质量的图像传输和存储。
信息论方法为图像压缩提供了强有力的理论基础。
首先，我们可以从信息熵的角度来考虑图像压缩。
信息熵是信息论中用来衡量随机变量（如像素值）不确定度的指标。
对于一幅图像而言，其像素分布在各个像素值上可能存在不均匀性。
信息熵的概念可以帮助我们理解这种不均匀性，并借助于有损压缩算法，将图像中信息较低的部分进行舍弃，从而实现图像的压缩。
常见的图像压缩算法，如JPEG压缩算法，利用了信息熵的概念，通过对图像数据的变换和量化来减小图像的信息熵，从而实现图像的有损压缩。
其次，信息论中的编码原理也广泛应用于图像压缩中。
在图像压缩的过程中，编码用来将原始数据转化为紧凑的码字，以减小数据的冗余度。
香农编码是信息论中最为著名的编码方法之一，利用了数据的统计特性，将频繁出现的符号用较短的编码表示，将不经常出现的符号用较长的编码表示。
在图像压缩中，我们可以根据像素值出现的概率来设计自适应的编码方法，使得图像数据可以以更高的压缩比进行存储和传输。
二、图像增强中的信息论应用图像增强是指通过改变图像的外观以改善视觉感知效果的过程。
信息论方法为图像增强提供了一种基于统计学原理的框架，可以用来增强图像的对比度、细节和清晰度等。
在图像增强中，直方图均衡化是一种常用的方法。
该方法通过变换图像的灰度级分布，使其更加均匀，从而增强图像的对比度。
信息论中的信息熵概念被广泛应用于直方图均衡化。
信息熵在图像处理中的应用摘要：为了寻找快速有效的图像处理方法，信息理论越来越多地渗透到图像处理技术中。
文章介绍了信息熵在图像处理中的应用，总结了一些基于熵的图像处理特别是图像分割技术的方法，及其在这一领域内的应用现状和前景 同时介绍了熵在织物疵点检测中的应用。
Application of Information Entropy on Image AnalysisAbstract ：In order to find fast and efficient methods of image analysis ，information theory is used more and more in image analysis ．The paper introduces the application of information entropy on the image analysis ，and summarizes some methods of image analysis based on information entropy ，especially the image segmentation method ．At the same time ，the methods and application of fabric defect inspection based on information entropy ale introduced ．信息论是人们在长期通信实践活动中，由通信技术与概率论、随机过程、数理统计等学科相结合而逐步发展起来的一门新兴交叉学科。
而熵是信息论中事件出现概率的不确定性的量度，能有效反映事件包含的信息。
随着科学技术，特别是信息技术的迅猛发展，信息理论在通信领域中发挥了越来越重要的作用，由于信息理论解决问题的思路和方法独特、新颖和有效，信息论已渗透到其他科学领域。
随着计算机技术和数学理论的不断发展，人工智能、神经网络、遗传算法、模糊理论的不断完善，信息理论的应用越来越广泛。
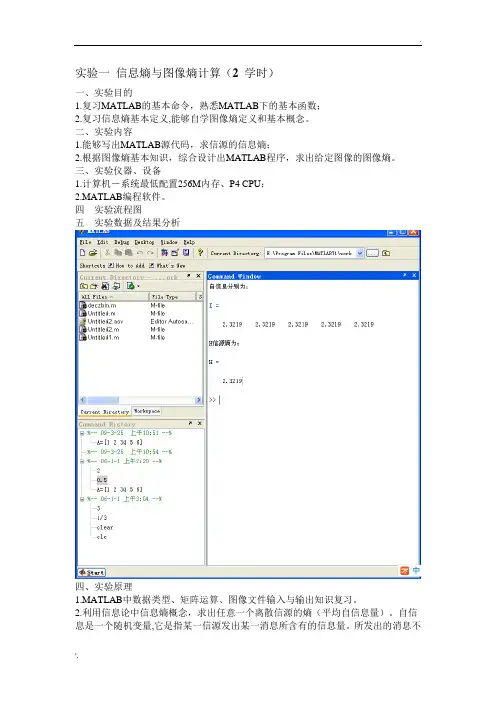
实验一信息熵与图像熵计算（2 学时）一、实验目的1.复习MATLAB的基本命令，熟悉MATLAB下的基本函数；2.复习信息熵基本定义,能够自学图像熵定义和基本概念。
二、实验内容1.能够写出MATLAB源代码，求信源的信息熵；2.根据图像熵基本知识，综合设计出MATLAB程序，求出给定图像的图像熵。
三、实验仪器、设备1.计算机－系统最低配置256M内存、P4 CPU；2.MATLAB编程软件。
四实验流程图五实验数据及结果分析四、实验原理1.MATLAB中数据类型、矩阵运算、图像文件输入与输出知识复习。
2.利用信息论中信息熵概念，求出任意一个离散信源的熵（平均自信息量）。
自信息是一个随机变量,它是指某一信源发出某一消息所含有的信息量。
所发出的消息不同，它们所含有的信息量也就不同。
任何一个消息的自信息量都代表不了信源所包含的平均自信息量。
不能作为整个信源的信息测度，因此定义自信息量的数学期望为信源的平均自信息量：1( ) 1 ( ) [log ] ( ) log ( ) i n i i p a i H E p a p a X 信息熵的意义：信源的信息熵H是从整个信源的统计特性来考虑的。
它是从平均意义上来表征信源的总体特性的。
对于某特定的信源，其信息熵只有一个。
不同的信源因统计特性不同，其熵也不同。
3.学习图像熵基本概念，能够求出图像一维熵和二维熵。
图像熵是一种特征的统计形式，它反映了图像中平均信息量的多少。
图像的一维熵表示图像中灰度分布的聚集特征所包含的信息量，令Pi表示图像中灰度值为i的像素所占的比例，则定义灰度图像的一元灰度熵为：2550 log i i i p p H图像的一维熵可以表示图像灰度分布的聚集特征，却不能反映图像灰度分布的空间特征，为了表征这种空间特征，可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。
选择图像的邻域灰度均值作为灰度2分布的空间特征量，与图像的像素灰度组成特征二元组，记为(i,j)，其中i表示像素的灰度值(0<=i<=255)，j表示邻域灰度(0<=j<=255),2 ( , ) / ij p f i j N上式能反应某像素位置上的灰度值与其周围像素灰度分布的综合特征，其中f(i,j)为特征二元组(i,j)出现的频数，N为图像的尺度，定义离散的图像二维熵为:2550 log ij ij i p p H构造的图像二维熵可以在图像所包含信息量的前提下，突出反映图像中像素位置的灰度信息和像素邻域内灰度分布的综合特征。
本科毕业论文图像分割技术研究Survey on the image segmentation学院名称：电气信息工程学院专业班级：电子信息工程0601班2010年 6 月图像分割技术研究摘要图像分割是图像分析的第一步，是计算机视觉的基础，是图像理解的重要组成部分，也是图像处理、模式识别等多个领域中一个十分重要且又十分困难的问题。
在图像处理过程中，原有的图像分割方法都不可避免的会产生误差，这些误差会影响到图像处理和识别的效果。
遗传算法作为一种求解问题的高效并行的全局搜索方法，以其固有的鲁棒性、并行性和自适应性，使之非常适于大规模搜索空间的寻优，已广泛应用许多学科及工程领域。
在计算机视觉领域中的应用也正日益受到重视，为图像分割问题提供了新而有效的方法。
本文对遗传算法的基本概念和研究进展进行了综述；重点阐述了基于遗传算法的最大类间方差进行图像分割算法的原理、过程，并在MATLAB中进行了仿真实现。
实验结果表明基于遗传算法的最大类间方差方法的分割速度快，轮廓区域分割明显，分割质量高，达到了预期目的。
关键字：图像分割；遗传算法；阈值分割Survey on the image segmentationAbstract I mage segmentation is the first step of image processing and the basic of computer vision. It is an important part of the image, which is a very important and difficult problem in the field of image processing, pattern recognition.In image processing process, the original method of image segmentation can produce inevitable errors and these errors can affect the effect of image processing and identification .This paper discusses the current situation of the genetic algorithms used in the image segmentation and gives some kind of principles and the processes on genetic algorithm of image segmentationIn this paper.It also descripts the basic concepts and research on genetic algorithms .It emphasizes the algorithm based on genetic and ostu and realizes the simulation on Matlab. The experimental results show that this method works well in segmentation speed，the outline of the division and separate areas of high quality and achieve the desired effect.Genetic algorithm (GA) is a sort of efficient，paralled，full search method with its inherent virtues of robustness，parallel and self-adaptive characters. It is suitable for searching the optimization result in the large search space. Now it has been applied widely and perfectly in many study fields and engineering areas. In computer vision field GA is increasingly attached more importance. It provides the image segmentation a new and effective method.Key words image segmentation；genetic algorithm；image threshold segmentation目录第一章绪论 (1)1.1本课题研究的背景、目的与意义 (1)1.2本课题研究的现状与前景 (2)1.3本论文的主要工作及内容安排 (3)第二章图像分割基本理论 (4)2.1图像分割基本概念 (4)2.2图像分割的体系结构 (4)2.3图像分割方法分类 (5)2.3.1阈值分割方法 (5)2.3.2边缘检测方法 (8)2.3.3区域提取方法 (9)2.3.4结合特定理论工具的分割方法 (10)2.4图像分割的质量评价 (11)第三章遗传算法相关理论 (12)3.1遗传算法的应用研究概况 (12)3.2遗传算法的发展 (12)3.3遗传算法的基本概念 (13)3.4遗传算法基本流程 (14)3.5遗传算法的构成 (14)3.5.1编码 (14)3.5.2确定初始群体 (14)3.5.3适应度函数 (15)3.5.4遗传操作 (15)3.5.5控制参数 (17)3.6遗传算法的特点 (18)第四章 MATLAB相关知识 (20)4.1MATLAB简介 (20)4.2MATLAB的主要功能 (20)4.3MATLAB的技术特点 (21)4.4遗传算工法具箱(S HEFFIELD工具箱) (22)第五章基于遗传算法的最大类间方差图像分割算法 (24)5.1最大类间方差法简介 (24)5.2基于遗传算法的最大类间方差图像分割 (25)5.3流程图 (26)5.4实验结果 (27)第六章总结与展望 (29)6.1全文工作总结 (29)6.2展望 (29)致谢 (30)参考文献 (31)附录 (32)第一章绪论1.1本课题研究的背景、目的与意义数字图像处理技术是一个跨学科的领域。
模糊熵的原理和应用实例1. 模糊熵的基本概念模糊熵是信息熵的一个扩展概念，用于评估模糊集合的模糊程度或不确定性。
在模糊集合理论中，熵是一种重要的指标，它可以衡量系统的混乱程度或信息量。
在真实世界中，很多事物的属性往往不是非黑即白的，而是具有模糊性质，因此需要引入模糊熵来描述这种模糊性质。
2. 模糊熵的计算方法模糊熵的计算方法主要有两种，即基于隶属度和基于分割区间。
下面将详细介绍这两种方法。
2.1 基于隶属度的计算方法基于隶属度的计算方法是模糊集合理论中常用的一种方法。
具体步骤如下：1.计算每个元素对于模糊集合的隶属度。
2.根据隶属度计算每个元素的信息量，即使用信息熵的计算公式。
3.对所有元素的信息量进行加权求和，得到模糊集合的模糊熵。
2.2 基于分割区间的计算方法基于分割区间的计算方法是另一种常用的模糊熵计算方法。
具体步骤如下：1.将模糊集合划分为若干个子集。
2.计算每个子集的信息熵。
3.对所有子集的信息熵进行加权求和，得到模糊集合的模糊熵。
3. 模糊熵的应用实例模糊熵在各个领域都有着广泛的应用。
下面列举几个实际应用的例子。
3.1 模糊图像处理模糊图像处理是一种可以消除图像模糊的方法。
通过计算图像的模糊熵，可以评估图像的模糊程度，并根据模糊程度采取相应的处理方法，从而提高图像的清晰度。
3.2 模糊决策在决策问题中，往往存在多个评价指标，而每个指标又具有模糊性质。
通过计算模糊熵，可以衡量各个指标的模糊程度，进而根据模糊程度进行决策，从而提高决策的准确性和可靠性。
3.3 模糊集成模糊集成是一种将多个模糊集合结合起来的方法。
通过计算模糊熵，可以评估各个模糊集合的模糊程度，进而确定各个模糊集合的权重或重要程度，从而在集成过程中更加准确地考虑不确定性因素。
3.4 模糊控制模糊控制是一种能够应对非精确信息和模糊要素的控制方法。
通过计算模糊熵，可以评估控制系统的模糊程度，进而根据模糊程度调整控制规则和参数，从而提高控制系统的鲁棒性和适应性。
实验一信息熵与图像熵计算一、实验目的1．复习MATLAB 的基本命令，熟悉MATLAB 下的基本函数。
2．复习信息熵基本定义, 能够自学图像熵定义和基本概念。
二、实验仪器、设备1．计算机－系统最低配置 256M 内存、P4 CPU。
2．Matlab 仿真软件－ 7.0 / 7.1 / 2006a 等版本Matlab 软件。
三、实验内容与原理（1）内容：1．能够写出MATLAB 源代码，求信源的信息熵。
2．根据图像熵基本知识，综合设计出MATLAB 程序，求出给定图像的图像熵。
（2）原理1． MATLAB 中数据类型、矩阵运算、图像文件输入与输出知识复习。
2．利用信息论中信息熵概念，求出任意一个离散信源的熵（平均自信息量）。
自信息是一个随机变量,它是指某一信源发出某一消息所含有的信息量。
所发出的消息不同，它们所含有的信息量也就不同。
任何一个消息的自信息量都代表不了信源所包含的平均自信息量。
不能作为整个信源的信息测度，因此定义自信息量的数学期望为信源的平均自信息量：信息熵的意义：信源的信息熵H是从整个信源的统计特性来考虑的。
它是从平均意义上来表征信源的总体特性的。
对于某特定的信源，其信息熵只有一个。
不同的信源因统计特性不同，其熵也不同。
3．学习图像熵基本概念，能够求出图像一维熵和二维熵。
图像熵是一种特征的统计形式，它反映了图像中平均信息量的多少。
图像的一维熵表示图像中灰度分布的聚集特征所包含的信息量，令Pi 表示图像中灰度值为i的像素所占的比例，则定义灰度图像的一元灰度熵为：255log i iip p ==∑H图像的一维熵可以表示图像灰度分布的聚集特征，却不能反映图像灰度分布的空间特征，为了表征这种空间特征，可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。
选择图像的邻域灰度均值作为灰度分布的空间特征量，与图像的像素灰度组成特征二元组，记为( i, j )，其中i 表示像素的灰度值(0 <= i <= 255)，j 表示邻域灰度(0 <= j <= 255),2(,)/ijP f i j N =上式能反应某像素位置上的灰度值与其周围像素灰度分布的综合特征，其中f(i, j) 为特征二元组(i, j)出现的频数，N 为图像的尺度，定义离散的图像二维熵为：255logij ijip p ==∑H构造的图像二维熵可以在图像所包含信息量的前提下，突出反映图像中像素位置的灰度信息和像素邻域内灰度分布的综合特征.四、实验步骤1．求解信息熵过程：1) 输入一个离散信源，并检查该信源是否是完备集。
信息熵在图像分割中的应用毕业论文目录摘要 ....................................................... .. (1)ABSTRACT (2)目录 (3)1 引言 (5)1.1信息熵的概念 (5)1.2信息熵的基本性质及证明 (6)1.2.1 单峰性 (6)1.2.2 对称性 (7)1.2.3 渐化性 (7)1.2.4 展开性 (7)1.2.5 确定性 (8)2基于熵的互信息理论 (9)2.1 互信息的概述 (9)2.2 互信息的定义 (9)2.3 熵与互信息的关系 (9)3 信息熵在图像分割中的应用 (11)3.1图像分割的基本概念 (11)3.1.1图像分割的研究现状 (11)3.1.2 图像分割的方法 (11)3.2 基于改进粒子群优化的模糊熵煤尘图像分割 (12)3.2.1 基本粒子群算法 (12)3.2.2 改进粒子群优化算法 (13)3.2.3 Morlet变异 (13)3.2.4改建粒子群优化的图像分割方法 (14)3.2.5 实验结果及分析 (16)3.3 一种新信息熵的定义及其在图像分割中的应用 (19)3.3.1香农熵的概念及性质 (19)3.3.2一种信息熵的定义及证明 (19)3.3.3信息熵计算复杂性分析 (21)3.3.4二维信息熵阈值法 (22)3.3.5二维信息熵阈值法的复杂性分析 (24)3.3.6 结论及分析 (25)4 信息熵在图像配准中的应用 (27)4.1图像配准的基本概述 (27)4.2基于互信息的图像配准 (27)4.3P OWELL算法 (28)4.4变换 (28)4.4.1平移变换 (29)4.4.2旋转变换 (30)4.5基于互信息的图像配准的设计与实现 (31)4.5.1总体设计思路和图像配准实现 (31)4.5.2直方图 (33)4.5.3联合直方图 (33)4.5.4灰度级差值技术 (34)4.4.5优化搜索办法级结论 (35)5结语 (37)致谢 (38)参考文献 (39)1 引言1.1.信息熵的概念1948年，美国科学家发表了一篇著名的论文《通信的数学理论》。
他从研究通信系统传输的实质出发，对信息做了科学的定义，并进行了定性和定量的描述。
他指出，信息是事物运动状态或存在方式的不确定性的描述。
其通信系统的模型如下所示：图1.1 信息的传播信息的基本作用就是消除人们对事物的不确定性。
信息熵是信息论中用于度量信息量的一个概念。
假定X 是随机变量χ的集合，)(x P 表示其概率密度，计算此随机变量的信息熵)(x H 的公式是：∑-=xx p x p X H )(log )()(),(y x P 表示一对随机变量的联合密度函数，他们的联合熵),(y x H 可以表示为：),(log ),(),(Y X p y x p Y X H Yy x ∑∑∈∈-=χ 信息熵描述的是信源的不确定性，是信源中所有目标的平均信息量。
信息量是信息论的中心概念，将熵作为一个随机事件的不确定性或信息量的量度，它奠定了现代信息论的科学理论基础，如果一条信息是由n 个字符连成的字符串组成，并且每个字符有m 种可能，那么这条信息就有n m 种不同的排列情况，那么可以用n m 度量信息量，但这时的信息量随着消息的长度n 按指数增加，为了使信息量的度量值按线性增加，Hartley 给出了取对数的信息量的定义：m n m H n 22log log == (1.1)由上式可以看出，信息量随着消息的可能性组合m 增多而增多，如果消息只有一种可能性时即事件为必然事件时，那么消息中包含的信息量为零01log 2=。
因此可以看出，可能收到的不同消息越多，对收到哪条消息的不确定性就越大;相反，收到只有一种可能性的消息，不确定性为零，Hartley 对消息的度量实际是对不确定性的度量。
Hartley 度量方法的不足之处是他所定义信息量是假定所有符号发生的概率相同，但实际情况各符号并不一定都等概发生，为此，Shannon 用概率加权来衡量消息出现的可能性，对Hartley 的度量方法做出改进。
设某一随机过程中有k 种可能的情况，每种情况发生的概率分别是1P ，2P ，…，k P ，Shannon 给出了熵的如下定义： ∑∑-==i i ii p p p p H 22log 1log干 扰(1.2)当所有可能的事件均以相等的概率发生时，上式就成了Hartley 定 义的熵，并且这时熵取得最大值，即∑∑==-=n n n n n m m mm m H 222log log 11log 1 (1.3)所以，Hartley 熵是,Shannon 熵的特殊情形，而Shannon 更具有一般性。
Shannon 熵包含三种含义：第一种含义是度量信息量，事件发生概率与获得的信息量成反比，即概率越大，信息量越少，又由式(1.3)知，概率越大，信息量越少，熵越小，所以可用熵的大小来度量信息量，熵越大，信息量越大;第二是度量事件概率分布的分散度，概率集中分布时熵值小，分散性越强，熵越大；三含义是度量事件发生的不确定性，概率越大，事件的不确定性越小，熵越小。
利用上面第三个含义，可以用Shannon 熵，来度量图像包含的信息量，图像灰度值的概率分布是每灰度值出现的次数除以图像中所有灰度值出现的总次数，此时图像的信息量可依据这个概率分布来计算，一幅图像中不同的灰度值较少，各灰度值出现的概率较高，则对应的灰度值较低，意味着这幅图像含有的信息量很少。
反之，如果一幅图像中含有很多不同的灰度值，且各灰度值发生的概率又基本一致，则它的熵值会很高，那么这幅图像包含的信息量很大。
1.2信息熵的基本性质及证明1.2.1单峰性信息熵的单峰性可表述为：先考察由1X 、2X 两个事件构成的概率系统，其产生的概率分别为P 和P -1则该系统的信息)).1(log )1(log (22P P P P H --+-=通过求极限 0log lim 20=→x x x 不难证明： (1) 当0=P 时，.0))01(log )01(log 0(22=--+-=H 这是一种1X 产生的概率为0，2X 产生的概率为1 的确定系统。
(2) 当1=P 时.0))11(log )11(1log 1(22=--+-=H 这是一种1X 产生的概率为1，2X 产生的概率为0 的确定系统。
(3) 对函数)).1(log )1(log (22P P P P H --+-=可以通过求导数的方式寻找其极值点。
该函数的一阶导数为.)1(log 2P P dP dH -=令0=dP dH 则有PP )1(log 2-0=，求得21=P 为该函数的驻点。
因为二阶导数,2ln )1(122P P dPH d --= 当10≤≤P 时，22dP H d 恒小于0 ， 所以当21=P 时函数有极大值。
这说明当1X 、2X 两事件产生的概率相同时，H 具有最大值，这是一种不确定性最大的不确定系统。
(4) 若概率系统中有n 个事件，当每一事件产生的概率相同（均为n /1）时，则系统的信息熵H 具有最大值。
该结论可以通过以下的讨论来证明：具有n 个事件的概率系统其信息熵可表示为∑=-=ni i i P P H 12log ，这是在约束条件∑==n i i P11下的极值问题。
应用λ因子法，设：∑∑==-+-=n i ni i i i P P P H 1120).1(log λ将0H 对1X 事件的概率i P 求一阶偏导数，并令00=∂∂i P H 使用约束条件∑==n i i P 11确定λ值，可求得n P i 1=（常数）。
同理有n P P P n 121==== （常数），即当nP P P n 121==== 时，H 有极大值。
1.2.2 对称性信息熵的对称性可表述为：设某一概率系统中n 个事件的概率分布为),,,(21n P P P 当对事件位置的顺序进行任意置换后，得到新的概率分布为),(21n P P P ''' ，并有以下关系成立：).,,(),(2121n n P P P H P P P H '''=它表示概率系统中事件的顺序虽不同，但概率系统的熵H 是不变的，即概率系统的熵与事件的顺序无关。
1.2.3 渐化性信息熵的渐化性可表述为：设概率为)(r q P n +=的事件可分解为概率分别为q 和r 的两个事件，则有：).,()(),,,(),,,(),,(121121121rq r r q q H r q r q P P P H r q P P P P H P P P P H n n n n n ++⋅++=+=--- 1.2.4 展开性信息熵的展开性可表述为：设某一概率系统的概率分布为),,,(21n P P P 则系统的信息熵具有展开性质：).0,,(),(2121n n P P P H P P P H =在此基础上，进一步展开有：=),(21n P P P H ).0,0,,(21 n P P P H根据,0)log (lim 20=-→P P P 上述展开性不难证明。
1.2.5 确定性信息熵的确定性可表述为：设信息系统中，任一事件产生的概率为1，则其他事件产生的概率为0。
这是一种确定的系统，对于这样的系统有：,0)1,0()0,1(==H H .0)1,0,,0()0,0,1,0,,0()0,,0,1(=== H H H根据,0)log (lim 21=-→P P P 很容易证明上述性质。
2 基于熵的互信息理论2.1 互信息的概述互信息（Mutual Information ）来自于信息论，是信息论中的一个基本概念，是两个随机变量统计相关性的测度。
当两幅图像达到最佳配准，它们对应像素的灰度互信息应达到最大。
该测度不需要对不同成像模式下图像灰度间的关系作任何假设，也不需要对图像进行分割或任何预处理，具有自动化程度高的特点。
因此，最近几年将互信息作为图像配准过程的相似性测度，利用最大互信息法进行图像配准成为了图像处理领域的研究热点。
互信息是基于概率统计论提出的，具有统计特性，它被多数研究者公认为是一个很好的图像配准准则，许多图像配准算法的研究均是在互信息的基础上加以改进的。
互信息作为医学图像配准的一个相似性测度，多模态医学图像的配准很实用，其配准原理是两幅基于共同人体解剖结构的图像在配准时具有最大的互信息值。
2.2 互信息定义定义1：随机变量X 和Y 之间的互信息);(Y X I 定义为：)|()();(Y X H X H Y X I -=或定义互信息);(X Y I 为：)|()();(X Y H Y H X Y I -=可以证明二者是相等的，即);(X Y I =);(Y X I 。
