与中点有关的引辅助线方法

数学中构造辅助线的方法
在数学中，构造辅助线是一种常用的解题方法，可以帮助我们更好地理解和解决各种几何问题。

以下是一些常用的构造辅助线的方法：
1.中点、中线段、延长线：如果条件中给出了中点或中线段，可以通过构造延长线来构造辅助线。

例如，过中点作已知线段或直线的平行线，或者过中点作已知线段的垂直平分线等。

2.角平分线、垂直、中线：如果条件中给出了角平分线、垂直或中线，可以通过构造相应的辅助线。

例如，过角平分线上的点作角平分线的垂线，或者过中点作已知直线的垂直平分线等。

3.直角三角形斜边上的中点：如果条件中给出了直角三角形斜边上的中点，可以通过构造辅助线将直角三角形转化为等腰三角形。

例如，过斜边中点作直角边的平行线，或者过斜边中点作斜边的垂线等。

4.等腰三角形底边上的垂直平分线：如果条件中给出了等腰三角形底边上的垂直平分线，可以通过构造辅助线将等腰三角形转化为直角三角形。

例如，过垂直平分线上的点作底边的平行线，或者过垂直平分线上的点作顶角的角平分线等。

5.等边三角形的高、角平分线、中线：如果条件中给出了等边三角形的高、角平分线或中线，可以通过构造辅助线将等边三角形转化为直角三角形。

例如，过高上的点作底的垂直平分线，或者过角平分线上的点作底边的平行线等。

这些方法都是一些常见的构造辅助线的技巧，对于不同的几何问题，需要灵活运用不同的方法来构造辅助线和解决问题。

初中数学三角形中14种辅助线添加方法在三角形中，常用的辅助线有中线、高线、中垂线、角平分线等。

下面是三角形中14种辅助线添加方法：1. 三角形中线的添加方法：在三角形的每个顶点上作一条连接对边中点的线段，则这些线段交于一点，且该点到三角形各顶点的距离相等，即为三角形的重心。

2. 三角形中垂线的添加方法：从三角形的顶点向所对边作垂线，垂足分别为A、B、C，则三个垂足所在直线相交于一点，为三角形的垂心。

3. 三角形高线的添加方法：从三角形的顶点向所对边作垂线，垂线所在直线与所对边的交点称为底部端点，连接三个底部端点，则构成一个矩形，其中两个对角线分别为三角形的两个高。

4. 角平分线的添加方法：从角的顶点向其对边作角平分线，将角平分为两个相等的角，且角平分线上的任意一点到两侧边的距离相等。

5. 外接圆的添加方法：三角形三边的中垂线交于一点，则以该点为圆心，三角形三个顶点分别为圆上的三个点的圆称为三角形的外接圆。

6. 内切圆的添加方法：三角形三条边所在直线的交点为内心，以内心为圆心，作内切圆，该圆与三角形的三边相切。

7. 垂直平分线的添加方法：从线段的中点向垂直于该线段的方向作一条线段，则该线段垂直于原线段且平分其长度。

8. 外角平分线的添加方法：从三角形的一顶点作一条射线，使其不在所在直线内，将相邻两个角的外部划分成两个大小相等的角，则这条射线为该顶点所对的角的外角平分线。

9. 旁切圆的添加方法：以三角形的某一边为半径，在其外侧作一条与该边平行的直线，使其与另外两边所在直线相交，其交点则为旁切圆心。

10. 中位线的添加方法：连接三角形任意两个顶点，则连接这两个顶点的中点的线段称为三角形的中位线，三角形三条中位线交于一点，即为三角形重心。

11. 等腰三角形的中线、高线和垂心重合。

12. 等边三角形的中线、高线、垂心和外心重合。

13. 直角三角形的垂心落在斜边上，且斜边上的高线与斜边垂直。

14. 任意三角形的外心到三个顶点的距离相等。

认真体会， 融会贯通， 灵活运用
练习：
四边形ABCD的对角线AC=BD，M、N 分别是AD、BC的中点，MN与AC、BD 交于F、G，AC、BD交于E，求证：
EF=EG C
D E N
M
F
G
A
P
B
EF= 2 BE
B
AD = BE
E D FC
三、已知中线，常倍长中线
例3. 如图，△ABC中，AD是BC边
上的中线，E是AD上的一点，BE的 A 延长线交AC于F，且AF＝EF。
求证：BE＝AC
F E
AC = BH BE = BH AC = BE
B
C
D
H
四、条件中含有等腰三角形底边上的
中点时，常作出底边的中线，利用三
例1. 已知：如图，△ABC中，
BD和CE是高，M为BC的中点，
P为DE的中点。
求证：PM⊥DE。
E
1 ME=MD= 2 BC
PM⊥DE
B
A
P
D
M
C
二、已知三角形一边的中点，构造三 角形中位线
例2. 已知：如图，△ABC中，AD
A
是高，BE是中线，且∠EBC＝30°。求证：AΒιβλιοθήκη ＝BEEF= 1 AD 21
中点常用的辅助线作法
初中 数学
泰安市岱岳区徂徕一中 梁孝斌
常用方法有四种：
一、已知直角三角形斜边上的中点时，常作斜 边上的中线
二、已知三角形一边的中点，构造三角形中位 线 三、已知中线，常倍长中线
四、条件中含有等腰三角形底边上的中点时， 常作出底边的中线，利用三线合一
一、已知直角三角形斜边上的中点时， 常作斜边上的中线

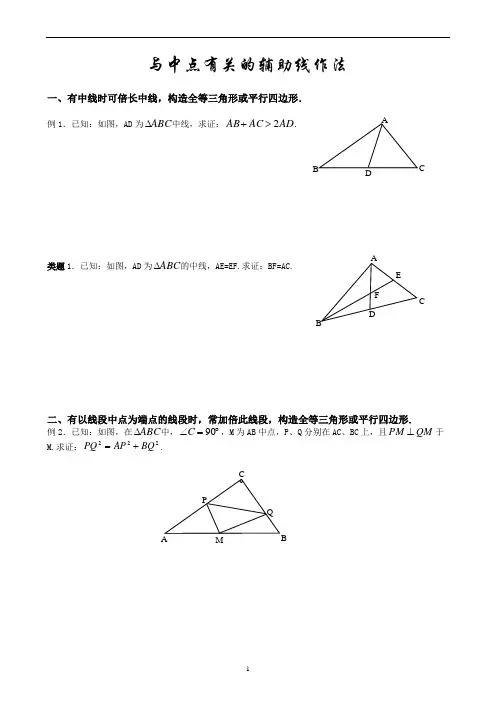
与中点有关的辅助线作法一、有中线时可倍长中线，构造全等三角形或平行四边形．例1．已知：如图，AD 为ABC ∆中线，求证：AD AC AB 2>+.类题1．已知：如图，AD 为ABC ∆的中线，AE=EF.求证：BF=AC.二、有以线段中点为端点的线段时，常加倍此线段，构造全等三角形或平行四边形.例2．已知：如图，在ABC ∆中，︒=∠90C ，M 为AB 中点，P 、Q 分别在AC 、BC 上，且QM PM ⊥于M.求证：222BQ AP PQ +=.CCM类题2．已知：ABC ∆的边BC 的中点为N ，过A 的任一直线BD AD ⊥于D ，AD CE ⊥于E.求证：NE=ND.三、有中点时，可连结中位线．例3．如图，ABC ∆中，D 、E 分别为AB 、AC 上点，且BD=CE ，M 、N 为BE 、CD 中点，连MN 交AB 、AC 于P 、Q ，求证：AP=AQ ．类题3．已知：如图，E 、F 分别为四边形ABCD 的对角线中点，AB>CD.求证：()CD AB EF ->21.A D PB CQ E M N A D F E B C类题4．如图，ABC ∆中，AD 是高，CE 为中线，CE DG ⊥，G 为垂足，DC=BE.求证：（1）G 是CE 的中点；（2）BCE B ∠=∠2.四、有底边中点，连中线，利用等腰三角形“三线合一”性质证题例4．已知：如图，在ABC Rt ∆中，︒=∠90BAC ，AB=AC ，D 为BC 边中点，P 为BC 上一点，AB PF ⊥于F ，AC PE ⊥于E.求证：DF=DE.类题5．已知：如图，矩形ABCD ，E 为CB 延长线上一点，且AC=CE ，F 为AE 中点，求证：FD BF ⊥.六、与梯形中点有关的辅助线：有腰中点时，常见以下三种引辅助线法例5．已知：如图，在直角梯形ABCD 中，AD ∥BC ，BC AB ⊥，M 为CD 的中点.求证：AM=MB.类题6．已知：梯形ABCD 中，AB ∥CD ，E 为BC 中点，AD EF ⊥于F.求证：AD EF S ABCD ⋅=梯形.F （1）B （2）G B（3）【作业】1、 已知△ABC 和△DBE 为等腰直角三角形，∠ABC =∠DBE=90°，A 、B 、D 在同一直线上，M 、N 、P分别是AD 、AC 、DE 边上的中点，试说明MP 与MN 的关系并证明。

十大辅助线口诀在进行几何作图时，辅助线的作用是不可忽视的。

正确使用辅助线可以大大提高作图效率，减少错误率，更加准确地画出所需图形。

为了帮助大家更好地理解和掌握辅助线的使用方法，我们整理出了“十大辅助线口诀”，便于大家记忆和应用。

第一大辅助线口诀：“中点万能定位，利用中垂线交点作图”。

这是一个非常实用的口诀，利用中点和中垂线可以快速定位图形的位置和大小。

例如，在画平行四边形时，只需画出其中一条对角线的中垂线，然后在中垂线上取一点作为原点，再利用对角线的中点和原点连线即可准确画出整个平行四边形。

第二大辅助线口诀：“平移移动平行线，平行四边形任意成”。

这个口诀可以帮助我们在画平行四边形时更加方便灵活。

只要确定两条平行线段，就可以通过平移移动其中一条线段使其与另一条平行线段重合，然后连接相应点即可。

第三大辅助线口诀：“圆周角相等，利用等角、同弦定位”。

在画与圆有关的图形时，这个口诀非常实用。

只需利用圆周角相等的性质，画出等角或同弦即可确定圆上的点位置。

第四大辅助线口诀：“切线垂直半径，直角可随便”。

这个口诀是在画圆和圆内的图形时比较常用的。

利用切线垂直半径的性质，可以确定直角位置，使作图更加准确。

第五大辅助线口诀：“直角三角形，利用勾股定位”。

这个口诀是在画直角三角形时非常实用的。

只要确定两条直角边的长度，就可以利用勾股定理求出第三条边的长度，并画出整个三角形。

第六大辅助线口诀：“四边形内对角线，对半分线交于一点”。

这个口诀是在画四边形时非常实用的，只需将对角线对半分，再连接相应线段的中点即可确定四边形的位置和大小。

第七大辅助线口诀：“平行线分段比，适用比例定位”。

这个口诀是在画平行线间的图形时非常实用的，只需利用线段比例的性质来确定每个点的位置。

第八大辅助线口诀：“正多边形内角和，等于360度”。

这个口诀是在画正多边形时非常实用的，只需根据内角和为360度的性质来确定每个角度，即可画出整个正多边形。

第九大辅助线口诀：“等腰三角形，利用对称轴对称”。

与中点有关的引辅助线方法中点是平面几何中一个重要的概念，它与图形的对称性、平行性、垂直性等性质有着密切的关系。

为了帮助解决与中点有关的问题，我们可以使用引辅助线的方法。

下面我将介绍一些与中点有关的引辅助线方法。

1.引中点辅助线法这是最基本的与中点有关的引辅助线方法。

当我们需要求线段的中点时，可以通过引一条过该线段两端点的直线，然后取该直线上的中点即可。

这样，我们就引出了一个与中点有关的辅助线。

2.引垂直平分线法当我们需要将一个线段平分时，可以通过引一条垂直于该线段的直线，并让该直线与线段的中点相交。

这样，该垂直直线就成为了该线段的垂直平分线。

3.引中垂线法当我们需要求一个线段的中垂线时，可以通过引一条垂直于该线段的直线，并让该直线的中点与该线段的中点相连。

这样，我们就得到了一个与中点有关的辅助线，也就是该线段的中垂线。

4.引平行线法当我们需要构造一个与条直线平行的直线时，可以通过引一条经过该直线上一点的平行线，并让该平行线上的距离与该点到该直线的距离相等。

这样，我们就得到了一个与中点有关的辅助线，也就是与原直线平行的直线。

5.引垂直线法当我们需要构造一个与条直线垂直的直线时，可以通过引一条经过该直线上一点的垂直线，并让该垂直线与原直线相交。

这样，我们就得到了一个与中点有关的辅助线，也就是与原直线垂直的直线。

以上就是与中点有关的几种常用引辅助线方法。

利用这些方法，我们可以更方便地解决与中点有关的问题。

当我们遇到与中点有关的几何问题时，可以根据具体情况选择合适的引辅助线方法，并运用相关的定理和性质进行推导和证明。

通过加深对中点的理解和运用，我们能够更好地掌握几何知识，提高解题的能力。

几何证明例题及常见的添加辅助线方法几何证明是数学中的一个重要分支，通过使用几何定理和性质，以及一些常见的辅助线方法，来证明几何命题的正确性。

下面将提供几个几何证明的例题，并介绍一些常见的添加辅助线方法：1.证明等边三角形的高线与垂直平分线重合。

添加辅助线方法：连接等边三角形的顶点与底边的中点，将三角形分为两个等腰三角形。

然后，通过利用等腰三角形的性质，可以证明三角形的高线与垂直平分线重合。

2.证明等腰梯形的对角线垂直。

添加辅助线方法：在等腰梯形的两个腰上各取一个点，使得这两个点与梯形的底边相连，形成两个等边三角形。

通过证明这两个等边三角形的高线与底边的中线相垂直，可以得出对角线垂直的结论。

3.证明一个四边形是平行四边形的充要条件是其对角线互相垂直。

添加辅助线方法：对四边形的两个对角线进行延长，连接延长线的交点与四边形的两个相邻顶点，形成两个三角形。

通过证明这两个三角形是直角三角形，可以得出对角线互相垂直的结论。

4.证明正方形的对角线互相垂直。

添加辅助线方法：连接正方形的相邻顶点，形成两个等腰三角形。

通过证明这两个等腰三角形的高线与底边的中线相垂直，可以得出对角线互相垂直的结论。

5.证明一个三角形的内心到三边的距离和边长的乘积是相等的。

添加辅助线方法：通过从三角形的顶点向内切圆引垂线，连接垂足与内心，形成三个小三角形。

通过证明这三个小三角形是相似三角形，可以得出内心到三边的距离和边长的乘积相等的结论。

以上是几个常见的几何证明例题及其对应的添加辅助线方法。

在几何证明中，添加辅助线是一种常用的方法，可以将原始图形分解成更简单的图形，以便于应用几何定理和性质进行证明。

但需要注意的是，添加辅助线时应选择合适的位置和方式，以确保辅助线的添加不会引入其他不必要的情况，更好地辅助证明目标命题的正确性。

浅谈怎样添中点问题的辅助线四川省营山县回龙镇初级中学校 梁 涛1、构造全等三角形（1）对于题设中有三角形中线的问题，常将中线延长一倍，构成全等三角形，使问题能在充分的条件下得以解决，如图1，AD 是△ABC 的中线，延长AD 到E ，使DE=AD ，连结EC ，则ΔABD ≅ΔECD 。

（2）对于题设中有一条线段平分另一条线段的题目，可将第一条线段加倍延长，构成全等三角形，如图2，CD 平分AB ，可延长DC 到E ，使CE=CD ，连结BE ，则ΔACD ≅ΔBCE 。

2、构造中位线若三角形一边（或梯形一腰）的中点，往往取另一边（或另一腰）的中点，连结成中位线，然后利用中位线性质进行证明或求解。

3、构造直角三有形斜边上的中线当题设中出现或隐含着直角三角形斜边上的中点的条件，可通过作辅助线构造斜边上的中线，利用直角三角形的性质探求解题方法。

例1 证明：三角形中，如果一个角的平分线是它对边上的中线，那么这个三角形是等腰三角形。

已知：如图3，在ΔABC 中，AD 平分∠BAC ，且BD=DC ，求证：AB=AC 。

思路分析：因为AB 、AC 分别是ΔABD 、ΔACD 的边，根据题设这两个三角形全等的条件不全，由于AD 是ΔABC 的中线，不妨加倍延长中线试一试，容易证明ΔABD ≅ΔECD ，则AB=CE ，要证AB=AC ，再证EC=AC 即可。

证明：延长AD 到E ，使DE=AD ，连接EC在△ABD 和△ECD 中，∴ △ABD ≌△ECD ∴ AB=EC ，∠1=∠E∵ ∠1=∠2， ∴ ∠2=∠E ∴ AC=EC ∴ AB=AC⎪⎩⎪⎨⎧=∠=∠=CD BD 43ED AD题末点评: 对于中线问题，常将中线延长一倍，构成全等三角形，将边、角转移到新的三角形中，从而为证题创造条件。

例2 已知：如图4，在ΔABC 与ΔC B A '''，AB=B A ''，AC=C A ''，AD 、D A ''分别是BC 及C B ''上的中线，且AD=D A ''。

全等三角形六种辅助线方法及例题全等三角形是初中数学中一个非常重要的概念，掌握全等三角形的判定方法和辅助线方法对于解题至关重要。

本文将介绍全等三角形的六种辅助线方法，并结合例题进行详细讲解。

一、辅助线法1.等角分线法：将三角形内角的平分线相互交点构成的点与三角形的另外一个顶点相连，得到一条辅助线。

这条辅助线将三角形分成两个等角的小三角形，从而得到相似或全等三角形。

2.中线法：将三角形任意两边的中点相连，得到三角形的中线。

相等的中线将三角形分成两个面积相等的小三角形，从而得到相似或全等三角形。

3.高线法：将三角形内任意一条边的垂线向另外两边引出，得到三角形的高线。

相等的高线将三角形分成两个面积相等的小三角形，从而得到相似或全等三角形。

4.角平分线法：将三角形内角的平分线相互交点构成的点相连，得到三角形的角平分线。

相等的角平分线将三角形分成两个面积相等的小三角形，从而得到相似或全等三角形。

5.角平分线中垂线法：将三角形内角的平分线的中垂线相互交点构成的点相连，得到三角形的角平分线中垂线。

相等的角平分线中垂线将三角形分成两个面积相等的小三角形，从而得到相似或全等三角形。

6.外心连线法：将三角形外接圆心与三角形三个顶点分别相连，得到三条辅助线。

这三条辅助线相等，将三角形分成三个面积相等的小三角形，从而得到相似或全等三角形。

二、例题解析1.已知△ABC，点D,E分别为BC,AB边上的中点，连接AD，BE相交于点F，求证：△DEF≌△ABC。

解析：由题意可知，△ABC是由两个等腰三角形组成的，因此可使用中线法证明两个三角形的全等。

由于D，E分别是BC,AB边上的中点，因此DE是AC中线，即DE=1/2AC；同理，AE是BC中线，AF=1/2BC。

因此，△ADB和△AEC是等腰三角形，且AD=EC，AB=AB，∠BAC=∠BAC，因此△ADB≌△AEC。

又因为DE是AC中线，BF是AE中线，因此DE=1/2AC，BF=1/2AE。

初中数学】几何题,辅助线的添加方法和典型例题初中数学：几何题型，辅助线的画法和典型例题1.倍长中线法已知在△ABC中，D是BC中点，DE⊥DF，需要判断BE＋CF与EF的大小关系，并证明结论。

思路点拨：利用倍长中线法，倍长过中点的线段DF使DG＝DF，再证明△XXX≌△EDF，△FDC≌△GDB，将BE、CF与EF线段转化到△BEG中，利用两边之和大于第三边证明。

解析：连接BG、EG，因为D是BC中点，所以BD＝CD。

又因为DE⊥DF，在△XXX和△EDF中，ED＝ED，∠XXX∠EDF，DG＝DF，因此△XXX≌△EDF（SAS），所以EG＝EF。

在△XXX与△GDB中，CD＝BD，∠1＝∠2，DF＝DG，因此△FDC≌△GDB（SAS），所以CF＝BG。

因为BG＋BE＞EG，所以BE＋CF＞EF。

结论得证。

总结升华：有中点的时候作辅助线可以考虑倍长中线法（或倍长过中点的线段）。

变式：已知CE、CB分别是△ABC与△ADC的中线，且∠ACB＝∠ABC，需要证明CD＝2CE。

解析：连接BF，延长CE至F使EF＝CE。

因为EC为中线，所以AE＝BE。

在△AEC与△BEF中，AE＝BE，∠AEC ＝∠BEF，CE＝EF，因此△AEC≌△BEF（SAS）。

所以AC ＝BF，∠A＝∠FBE。

又因为∠ACB＝∠ABC，∠XXX∠ACB＋∠A，∠XXX∠ABC＋∠A，所以AC＝AB，∠XXX∠XXX。

因此AB＝BF，BC为△ADC的中线，所以AB＝BD，即BF＝BD。

在△FCB与△DCB中，∠XXX∠DBC，BC＝BC，因此△FCB≌△DCB（SAS），所以CF＝CD。

结论得证。

2.以角平分线为对称轴的翻折变换构造全等三角形已知在△ABC中，∠C＝2∠B，∠1＝∠2，需要证明XXX。

解析：在AB上截取AE＝AC，连接CE，作角ACE的平分线交AB于D，连接CD。

因为∠C＝2∠B，所以∠ACE＝∠XXX∠B，∠XXX∠A＝∠1＝∠2，所以△AED≌△ACD （SAS），因此ED＝CD。

二、 作平行线 。 构造全等三角形 已知 三角形一边 的中点 ， 我们 可以经 过其 中一 个顶 点作对边 的平行线 ， 构造“ 型 图， ” 从而可 以得 到全等三角形 。 Ａ Ｄ 例 ２ 已知 ： 图 ２ Ａ Ｃ 如 ， Ｂ
＝
又 Ｅ 是△Ｂ Ｃ的 中位线 ， Ｍ Ａ Ｅ Ｍ∥Ａ 即 Ｅ Ｃ， ＭＢ＝ Ｃ 。
・ ． ． ‘ ． ‘
Ｍ Ｄ＝ Ｂ Ｄ一 Ｅ Ｄ＝ Ｂ一÷ Ｂ＝ Ｅ Ｅ Ｍ
二
忸 ＝９＊ Ａ ＋ Ｂ ＝ Ｃ ， ０， Ｄ Ｃ Ｄ
Ｃ，
’ ． ．
为佃 的中点 ， 求证 ： Ｄ Ｃ＝ Ｅ
９ 。
仍 ＝ Ｍ ＥＤ ，
证明 ： 长 Ｄ 交 Ｃ 延 Ｅ， Ｂ的延 长线 于点 Ｆ 。
Ｕ
思路方法
３ ７
例 谈 中点 问题 的几 种 辅 助 线 的作 法
■ 娄
在研究几何图形时 ， 若有涉及 中点的问题 ， 我们 常需要添加一些适 当的辅助线来解 答 问题 ， 果能 如 够把这一类问题的一般 方法作 出全面 的归纳 ， 那将 对我们思考问题是很有益处的。 作等腰 三角形底边上的 中线 在等腰三角形中 ， 作它底边上的中线 ， 我们可利 用等腰三角形“ 三线合一” 的性质来解答 问题 。 例 １ 已知 ： 图 １点 Ｄ、 如 ， Ｅ
‘
．
．
的中点问题 ， 了构造 全 等 （ 除 即作 Ｂ Ｍ∥ Ｃ ， Ａ Ｆ交 Ｄ 的延 长线 于点 ） ， 外 也可 以过 中点 Ｄ作平 行线 ， 构
造中位线 。 证明 ： Ｄ 作 Ｇ∥ｃ 交 Ｂ Ｆ， Ｆ于 ｃ，
则 Ａ Ｅ Ｅ： Ｄ＝Ａ 彤 。 Ｆ：
又 ＢＤ＝Ａ ． Ｂ ０，‘ Ｄ：Ａ ． Ｇ。

高中立体几何辅助线技巧简述高中立体几何是数学中的一门重要分支，它主要研究空间中各种几何体的性质和相互关系。

在解决立体几何问题时，辅助线技巧是非常实用的工具。

通过巧妙地引入辅助线，可以简化问题的解决过程，提高解题效率。

本文将简要介绍一些常用的高中立体几何辅助线技巧，帮助读者更好地理解和应用这些方法。

一、平行线辅助线技巧在解决与平行线相关的立体几何问题时，可以尝试通过引入平行线辅助线来简化问题。

具体而言，可以考虑以下两种情况：1. 使用平行线比例关系当需要求解立体几何体的长度比或面积比时，可以尝试通过引入平行线辅助线来构造相应的比例关系。

在求解平行四边形的面积比时，可以通过连接对角线，将平行四边形分割成两个三角形，从而利用三角形面积公式求解面积比。

2. 使用平行线截线关系当需要求解立体几何体内部的长度或角度关系时，可以考虑通过引入平行线截线关系来简化问题。

在求解空间中两条直线的夹角时，可以通过引入一条与之平行的辅助线，从而将问题转化为求解两条平行线与辅助线的夹角，利用平行线夹角定理求解出所需的夹角值。

二、相似三角形辅助线技巧在解决与相似三角形相关的立体几何问题时，可以尝试通过引入相似三角形辅助线来简化问题。

具体而言，可以考虑以下两种情况：1. 使用相似三角形比例关系当需要求解立体几何体的长度比或面积比时，可以尝试通过引入相似三角形辅助线来构造相应的比例关系。

在求解棱锥的体积或表面积比时，可以通过在棱锥中引入一条高线，构造出两个相似三角形，从而利用相似三角形的边比关系求解出所需的比例值。

2. 使用相似三角形角度关系当需要求解立体几何体内部的角度关系时，可以尝试通过引入相似三角形辅助线来简化问题。

在求解棱锥的顶角时，可以通过在棱锥中引入一条高线，构造出一个与之相似的三角形，从而将该问题转化为求解相似三角形的对应角度关系，进而得到所需的顶角值。

三、垂线辅助线技巧在解决与垂线相关的立体几何问题时，可以尝试通过引入垂线辅助线来简化问题。

几何证明题辅助线的技巧和方法
在解决几何证明题时，辅助线是一种常用且有效的工具。

它可以帮助我们发现
隐藏的几何关系，简化证明过程，并提供新的角度来解决问题。

以下是几种常见的辅助线技巧和方法，可用于解决几何证明题。

1. 平行线辅助线法：当题目涉及到平行线时，我们可以通过引入一条平行线作
为辅助线，从而构建出平行线之间的相似三角形或平行四边形。

这样，我们可以得出相应的角度和边的关系，进而证明几何问题。

2. 三角形中线辅助线法：三角形的中线是连接一个顶点与对应中点的线段。

通
过引入三角形中线作为辅助线，我们可以将原问题转化为直角三角形的性质或平行线的性质。

这种方法常常用于证明三角形的等边、等腰等性质。

3. 垂直线辅助线法：当题目涉及到垂直线时，我们可以通过引入一条垂直线作
为辅助线，从而构建出垂直角、直角三角形或平行四边形。

通过利用垂直线的性质，我们可以得到角度、边长等关系，进而解决问题。

4. 内切圆辅助线法：对于一个给定的三角形，可以通过引入其内切圆作为辅助线，来简化证明过程。

内切圆与三角形的的边相切于三个点，这些点可以提供有用的几何关系，如正方形的性质、垂直线的性质等。

5. 类似三角形辅助线法：当计算角度或证明形状相似时，引入类似三角形作为
辅助线可以大大简化证明过程。

通过找到两个或多个类似的三角形，我们可以得到两个三角形的边长比例，并据此解决问题。

总之，辅助线是几何证明中的有效工具，它们可以帮助我们发现关键的几何关系，简化证明过程，并提供新的角度来解决问题。

通过灵活运用各种辅助线技巧和方法，我们可以更加轻松地解决各种几何证明题。

由中点想到的辅助线在三角形中，如果已知一点是三角形某一边上的中点，那么首先应该联想到三角形的中线、中位线、加倍延长中线及其相关性质（直角三角形斜边中线性质、等腰三角形底边中线性质），然后通过探索，找到解决问题的方法。

一、三角形的一条中线把原三角形分成两个面积相等的小三角形即如图1，AD是ΔABC的中线，则SΔABD=SΔACD=SΔABC（因为ΔABD与ΔACD是等底同高的）。

例1．如图2，ΔABC中，AD是中线，延长AD到E，使DE=AD，DF是ΔDCE的中线。

已知ΔABC的面积为2，求：ΔCDF的面积。

解：因为AD是ΔABC的中线，所以SΔACD=SΔABC=×2=1，又因CD是ΔACE的中线，故SΔCDE=SΔACD=1，因DF是ΔCDE的中线，所以SΔCDF=SΔCDE=×1=。

∴ΔCDF的面积为。

二、由中点应想到利用三角形的中位线例2．如图3，在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，BA、CD的延长线分别交EF的延长线G、H。

求证：∠BGE=∠CHE。

证明：连结BD，并取BD的中点为M，连结ME、MF，∵ME是ΔBCD的中位线，∴ME CD，∴∠MEF=∠CHE，∵MF是ΔABD的中位线，∴MF AB，∴∠MFE=∠BGE，∵AB=CD，∴ME=MF，∴∠MEF=∠MFE，从而∠BGE=∠CHE。

三、由中线应想到延长中线，使延长的部分等于中线长例3．如图4，已知ΔABC中，AB=5，AC=3，连BC上的中线AD=2，求BC的长。

解：延长AD到E，使DE=AD，则AE=2AD=2×2=4。

在ΔACD和ΔEBD中，∵AD=ED，∠ADC=∠EDB，CD=BD，∴ΔACD≌ΔEBD，∴AC=BE，从而BE=AC=3。

在ΔABE中，因AE2+BE2=42+32=25=AB2，故∠E=90°，∴BD===，故BC=2BD=2。

例4．如图5，已知ΔABC中，AD是∠BAC的平分线，AD又是BC边上的中线。

【方法归纳】
情形1：倍长中线
如图，在△ABC中，AD是BC边的中线．
辅助线作法一：延长AD至点E，使
DE＝AD，连接BE.
辅助线作法二：过点B作BE∥AC交AD的延长线于点E.
结论：△ACD≌△EBD.
2025版
数学
广西专版
情形2：倍长类中线
如图，在△ABC中，D是边BC的中点，E是边AB上一点，连接DE.
∴AC＝HB，∠CAD＝∠H，
∵AE＝EF，∴∠EAF＝∠AFE＝∠BFH，
∴∠H＝∠BFH，∴BF＝BH，∴AC＝BF.
2025版
数学
广西专版
6．如图，△ABC中，D是BC的中点，DE⊥DF，试判断BE＋CF与EF的大
小关系，并证明你的结论．
2025版
数学
广西专版
解：BE＋CF＞EF.
证明：延长ED至点P，使DP＝DE，连接FP，CP，
2025版
微专题(六)
数学
广西专版
与中点有关的辅助线
(5年2考)
2025版
数学
广西专版
方法一：构造中线
1．如图，在△ABC中，D是BC上一点，AB＝AD，E，F分别是AC，BD
的中点，若EF＝6，则AC的长是 12 .
【解析】连接AF，则∠AFC＝90°.
2025版
数学ቤተ መጻሕፍቲ ባይዱ
广西专版
2．如图，在Rt△ABC中，∠BAC＝90°，BC＝4，E，F分别是BC，AC的
2025版
数学
广西专版
证明：延长AE至点F，使 EF＝EA，连接DF.
∵AE是BD边上的中线，∴BE＝DE.
∴△DEF≌△BEA(SAS)．∴FD＝AB，∠EDF＝∠B.

初中数学添加辅助线的方法汇总作辅助线的基本方法一：中点、中位线，延长线，平行线。

如遇条件中有中点，中线、中位线等，那么过中点，延长中线或中位线作辅助线，使延长的某一段等于中线或中位线；另一种辅助线是过中点作已知边或线段的平行线，以达到应用某个定理或造成全等的目的。

二：垂线、分角线，翻转全等连。

如遇条件中，有垂线或角的平分线，可以把图形按轴对称的方法，并借助其他条件，而旋转180度，得到全等形，，这时辅助线的做法就会应运而生。

其对称轴往往是垂线或角的平分线。

三：边边若相等，旋转做实验。

如遇条件中有多边形的两边相等或两角相等，有时边角互相配合，然后把图形旋转一定的角度，就可以得到全等形，这时辅助线的做法仍会应运而生。

其对称中心，因题而异，有时没有中心。

故可分“有心”和“无心”旋转两种。

四:造角、平、相似，和、差、积、商见。

如遇条件中有多边形的两边相等或两角相等，欲证线段或角的和差积商，往往与相似形有关。

在制造两个三角形相似时，一般地，有两种方法：第一，造一个辅助角等于已知角；第二，是把三角形中的某一线段进行平移。

故作歌诀：“造角、平、相似，和差积商见。

”托列米定理和梅叶劳定理的证明辅助线分别是造角和平移的代表）五：两圆若相交，连心公共弦。

如果条件中出现两圆相交，那么辅助线往往是连心线或公共弦。

六：两圆相切、离，连心，公切线。

如条件中出现两圆相切（外切，内切），或相离（内含、夕卜离），那么，辅助线往往是连心线或内外公切线。

七：切线连直径，直角与半圆。

如果条件中出现圆的切线，那么辅助线是过切点的直径或半径使出现直角；相反，条件中是圆的直径，半径，那么辅助线是过直径（或半径）端点的切线。

即切线与直径互为辅助线。

如果条件中有直角三角形，那么作辅助线往往是斜边为直径作辅助圆，或半圆；相反，条件中有半圆，那么在直径上找圆周角一一直角为辅助线。

即直角与半圆互为辅助线。

八：弧、弦、弦心距；平行、等距、弦。

如遇弧，则弧上的弦是辅助线；如遇弦，则弦心距为辅助线。

初中数学常见辅助线的做法一、中点模型的构造1.已知任意三角形一边上的中点，可以考虑：(1)倍长中线或类中线(与中点有关的线段)构造全等三角形.如图1、图2所示.(2)三角形中位线定理.2.已知直角三角形斜边中点，可以考虑构造斜边中线.3.已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一二4.有些题目的中点不直接给出，此时需要我们挖掘题目中的隐含中点，例如：直角三角形中斜边中点, 等腰三角形底边上的中点，当没有这些条件的时候，可以用辅助线添加.二、角平分线模型的构造与角平分线有关的常用辅助线作法,即角平分线的四大基本模型.已知。

是4MON平分线上一点，(1)若以_L 0M于点4 ,如图1,可以过户点作PB1ON于点&则与二以.可记为“图中有角平分线, 可向两边作垂线”.(2)若点4是射线0M上任意一点，如图2,可以在ON上截取(用=0/1 ,连接/7人构造△()*?三△ /%.可记为“图中有角平分线，可以将图对折看，对称以后关系现二⑶若翼妆舔踹嚼鼠3耳以黠部交0N于点从周造A4 0H基尊健三角形/是底边4加勺中点.可记为“角平分线加垂线，三线合一试试看二(4)若过P点作PQ//0N交0M于点0,如图4,可以构造△P0Q是等腰三角形，可记为“角平分线+平行线，等腰三角形必呈现二三、轴对称模型的构造下面给出几种常见考虑要用或作轴对称的基本图形.(1 )线段或角度存在2倍关系的,可考虑对称.(2)有互余、互补关系的图形，可考虑对称.(3)角度和或差存在特殊角度的，可考虑对称.(4)路径最短问题，基本上运用轴对称，将分散的线段集中到两点之间，从而运用两点之间线段最短，来实现最短路径的求解.所以最短路径问题，需考虑轴对称.几何最值问题的儿种题型及解题作图方法如下表所示.四、圆中辅助线构造在平面几何中，解决与圆有关的问题时，常常需要添加适当的辅助线，架起题设和结论间的桥梁,从而使问题化难为易，顺其自然地得到解决，因此, 灵活掌握作辅助线的一般规律和常见方法，对.提高学生分析问题和解决问题的能力是大有帮助的。