(整理)《振动力学》课程作业.
- 格式:doc
- 大小:2.81 MB
- 文档页数:12

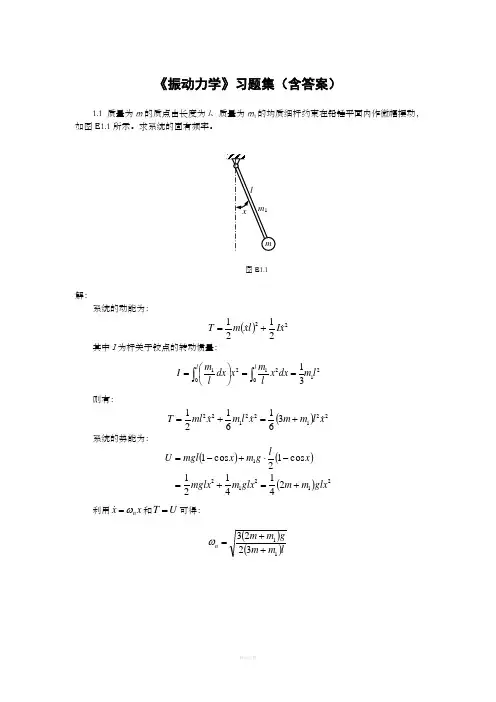
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
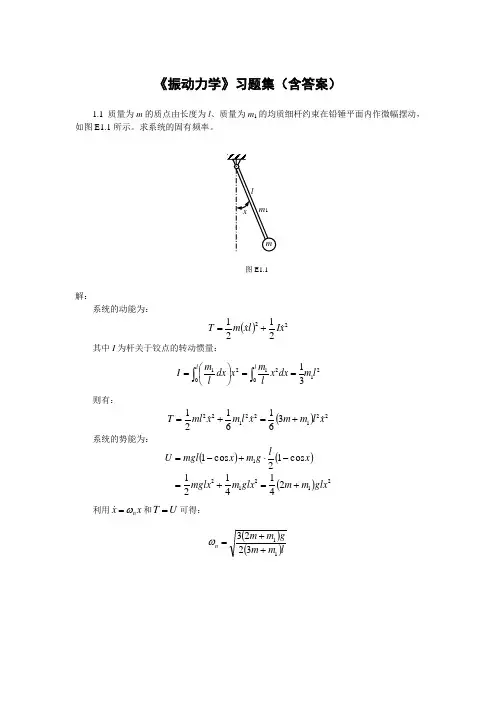
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。

《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得:()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得:()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
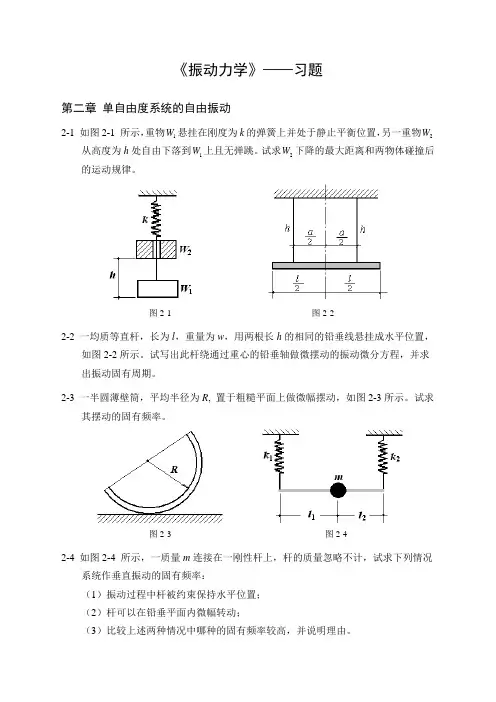
《振动力学》——习题第二章 单自由度系统的自由振动2-1 如图2-1 所示,重物1W 悬挂在刚度为k 的弹簧上并处于静止平衡位置,另一重物2W 从高度为h 处自由下落到1W 上且无弹跳。
试求2W 下降的最大距离和两物体碰撞后的运动规律。
图2-1 图2-2 2-2 一均质等直杆,长为l ,重量为w ,用两根长h 的相同的铅垂线悬挂成水平位置, 如图2-2所示。
试写出此杆绕通过重心的铅垂轴做微摆动的振动微分方程,并求 出振动固有周期。
2-3 一半圆薄壁筒,平均半径为R , 置于粗糙平面上做微幅摆动,如图2-3所示。
试求 其摆动的固有频率。
图2-3 图2-4 2-4 如图2-4 所示,一质量m 连接在一刚性杆上,杆的质量忽略不计,试求下列情况 系统作垂直振动的固有频率:(1)振动过程中杆被约束保持水平位置;(2)杆可以在铅垂平面内微幅转动;(3)比较上述两种情况中哪种的固有频率较高,并说明理由。
2-5 试求图2-5所示系统中均质刚性杆AB在A点的等效质量。
已知杆的质量为m,A 端弹簧的刚度为k。
并问铰链支座C放在何处时使系统的固有频率最高?图2-5 图2-62-6 在图2-6所示的系统中,四个弹簧均未受力。
已知m=50kg,19800N mk=,234900N mk k==,419600N mk=。
试问:(1)若将支撑缓慢撤去,质量块将下落多少距离?(2)若将支撑突然撤去,质量块又将下落多少距离?2-7 图2-7所示系统,质量为m2的均质圆盘在水平面上作无滑动的滚动,鼓轮绕轴的转动惯量为I,忽略绳子的弹性、质量及各轴承间的摩擦力。
试求此系统的固有频率。
图2-72-8 如图2-8所示的系统中,钢杆质量不计,建立系统的运动微分方程,并求临界阻尼系数及阻尼固有频率。
图2-82-9 图2-9所示的系统中,m =1kg ,k =224N/m ,c =48N.s/m ,l 1=l =0.49m ,l 2=l /2,l 3=l /4,不计钢杆质量。

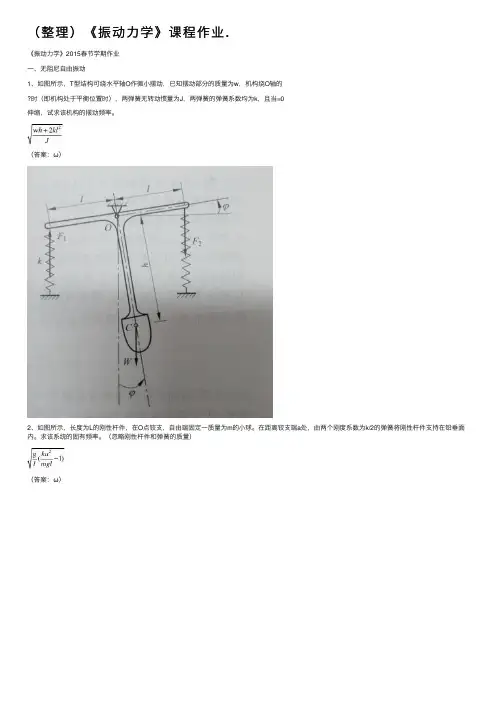
(整理)《振动⼒学》课程作业.《振动⼒学》2015春节学期作业⼀、⽆阻尼⾃由振动1、如图所⽰,T型结构可绕⽔平轴O作微⼩摆动,已知摆动部分的质量为w,机构绕O轴的时(即机构处于平衡位置时),两弹簧⽆转动惯量为J,两弹簧的弹簧系数均为k,且当=0伸缩,试求该机构的摆动频率。
(答案:ω)2、如图所⽰,长度为L的刚性杆件,在O点铰⽀,⾃由端固定⼀质量为m的⼩球。
在距离铰⽀端a处,由两个刚度系数为k/2的弹簧将刚性杆件⽀持在铅垂⾯内。
求该系统的固有频率。
(忽略刚性杆件和弹簧的质量)(答案:ω)3、如图所⽰,悬臂梁长为L ,截⾯抗弯刚度为EI ,梁的⾃由端有质量为m 的质量块,弹簧刚度为k ,求系统的固有频率。
(答案:ω= )4、如图所⽰,半径为R 的均质半圆柱体,在⽔平⾯内只作滚动⽽不滑动的微摆动,求其固有⾓频率。
(答案:ω=)5、如图所⽰,抗弯刚度为623010(N m )EI =?? 的梁AB ,借弹簧⽀撑于A,B 两点处,弹簧系数均为300(/)k N m = 。
忽略梁的质量,试求位于B 点左边3m 处,重量为1000()W N = 的物块⾃由振动的周期。
(答案:T=0.533s )6、⼀个重W 的⽔箱,借助四根端点嵌固的竖置管柱⽀撑着。
每根柱⼦的长为L,抗弯刚度为EI 。
试求该⽔箱顺⽔平⽅向⾃由振动的周期。
(管柱的质量忽略不计)(答案:2T = )7、《结构动⼒学基础》,第2章课后习题,第1题、第2题、第8题⼆、有阻尼⾃由振动1、如图所⽰,库伦曾⽤下述⽅法测定液体的粘性系数'c :在弹簧上悬挂⼀薄板A ,先测出薄板在空⽓中的振动周期1T ,然后测出在待测粘性系数的液体中的振动周期2T 。
设液体对薄板的阻⼒等于2A 'c v ,其中2A 为薄板的表⾯⾯积,v 为薄板的速度。
如薄板重W ,试有测得的数据1T 和2T ,求出粘性系数'c 。
空⽓对薄板的阻⼒不计。
(答案:'c =)2、物体质量为2kg ,挂在弹簧下端。
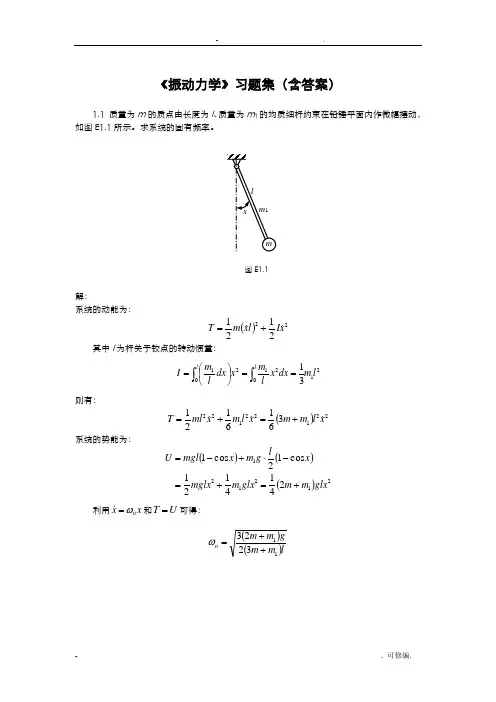
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+= 系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
![《振动力学》习题集[含答案]](https://uimg.taocdn.com/bf1e364afad6195f302ba63b.webp)
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得:()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得:()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
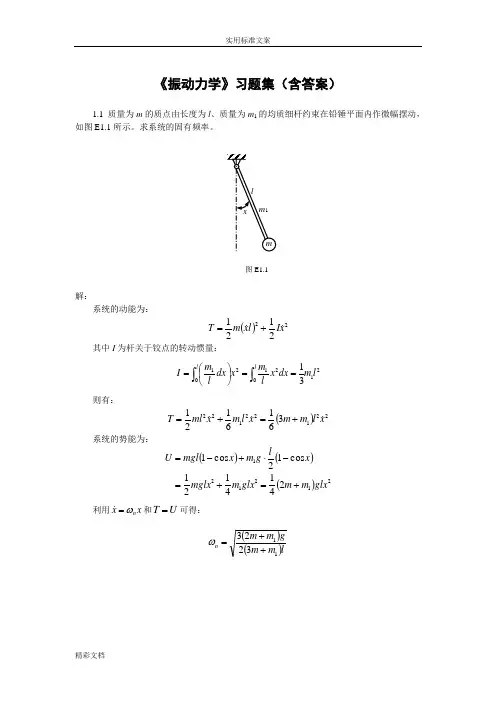
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含答案)质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图所示。
求系统的固有频率。
图解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图所示。
求系统的固有频率。
图解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn = 和U T =可得:()mkR a R mR a R k n 343422+=+=ω转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图所示。
求系统的固有频率。
图解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn = 和U T =可得:()()3232132k k J k k k k k n +++=ω在图所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含答案)质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图所示。
求系统的固有频率。
图解:系统的动能为:()222121x I l x m T &&+=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T &&&+=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω=&和U T =可得: ()()lm m gm m n 113223++=ω质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图所示。
求系统的固有频率。
图解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ&&&mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn =&和U T =可得: ()mkR a R mR a R k n 343422+=+=ω转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图所示。
求系统的固有频率。
图解:系统的动能为:221θ&J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn =&和U T =可得: ()()3232132k k J k k k k k n +++=ω在图所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含答案)————————————————————————————————作者:————————————————————————————————日期:《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T &&+=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T &&&+=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω=&和U T =可得: ()()lm m gm m n 113223++=ωml m 1 x1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ&&&mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn =&和U T =可得: ()mkR a R mR a R k n 343422+=+=ωkk A Ca R θ1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ&J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn =&和U T =可得: ()()3232132k k J k k k k k n +++=ωkk 2 kJ1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》2015春节学期作业一、无阻尼自由振动1、如图所示,T型结构可绕水平轴O作微小摆动,已知摆动部分的质量为w,机构绕O轴的ϕ时(即机构处于平衡位置时),两弹簧无转动惯量为J,两弹簧的弹簧系数均为k,且当=0伸缩,试求该机构的摆动频率。
(答案:ω)2、如图所示,长度为L的刚性杆件,在O点铰支,自由端固定一质量为m的小球。
在距离铰支端a处,由两个刚度系数为k/2的弹簧将刚性杆件支持在铅垂面内。
求该系统的固有频率。
(忽略刚性杆件和弹簧的质量)(答案:ω)3、如图所示,悬臂梁长为L ,截面抗弯刚度为EI ,梁的自由端有质量为m 的质量块,弹簧刚度为k ,求系统的固有频率。
(答案:ω= )4、如图所示,半径为R 的均质半圆柱体,在水平面内只作滚动而不滑动的微摆动,求其固有角频率。
(答案:ω=)5、如图所示,抗弯刚度为623010(N m )EI =⨯⋅ 的梁AB ,借弹簧支撑于A,B 两点处,弹簧系数均为300(/)k N m = 。
忽略梁的质量,试求位于B 点左边3m 处,重量为1000()W N = 的物块自由振动的周期。
(答案:T=0.533s )6、一个重W 的水箱,借助四根端点嵌固的竖置管柱支撑着。
每根柱子的长为L,抗弯刚度为EI 。
试求该水箱顺水平方向自由振动的周期。
(管柱的质量忽略不计)(答案:2T = )7、《结构动力学基础》,第2章课后习题,第1题、第2题、第8题二、有阻尼自由振动1、如图所示,库伦曾用下述方法测定液体的粘性系数'c :在弹簧上悬挂一薄板A ,先测出薄板在空气中的振动周期1T ,然后测出在待测粘性系数的液体中的振动周期2T 。
设液体对薄板的阻力等于2A 'c v ,其中2A 为薄板的表面面积,v 为薄板的速度。
如薄板重W ,试有测得的数据1T 和2T ,求出粘性系数'c 。
空气对薄板的阻力不计。
(答案:'c =)2、物体质量为2kg ,挂在弹簧下端。
弹簧常数k=48.02N/cm,求临界阻尼系数。
(答案:196Ns/m )3、挂在弹簧下端的物体,质量为1.96kg ,弹簧常数k=0.49N/cm,阻尼系数c=0.196Ns/cm 。
设在t=0时刻将物体从平衡位置向下拉5cm ,然后无初速度地释放,求此后的运动。
(答案:55(15t)cm tx e-=+ )4、《结构动力学基础》,第2章课后习题,第12题三、简谐荷载作用下的强迫振动1、如图所示,一无重简支梁,在跨中有重W=20kN 的电机,电机偏心所产生的离心力为(t)10sin F t ω=kN ,若机器每分钟的转数n=500r/min ,梁的截面抗弯刚度为421.00810EI kN m =⨯⋅ 。
在不计阻尼的情况下,试求梁的最大位移和弯矩。
(答案:33max0.00776(m)4848WL FL y EI EI μ=+=;max 58.66(kN m)44WL FLM μ=+=⋅ )2、建立图示系统的动力学平衡方程,并求系统发热稳态响应。
(答案:2222221212122x(t)Asin(t ),k arctan[k k (k k )](k k )(k )A F c m c m ωθωθωωω=+=-=-+++- )3、如图所示,系统的刚性棒质量不计,0(t)F sin f t ω= 。
试建立系统的运动方程,并分别求出○10ωω= ;○20/2ωω= 时,质量块的线位移幅值。
(答案:○1A =;○2A =)四、周期荷载作用下的强迫振动,一般性荷载作用下的强迫振动1、在如图(a )所示的系统中,s x 的变化规律如图(b )所示。
试求系统的稳态响应。
(答案:21,arctan42(n )n n a ka cn x k m ωθπω∞==-=- )2、如图所示,无阻尼单自由度系统受到周期力(t)t F 的作用。
应用傅里叶级数求该系统的稳态响应。
(答案:00222102(cos n 1)sin n t 2(t),,(n )n F x n m T πωπωωπωω∞=-=-=-∑ 为系统自振圆频率)3、如图所示,求无阻尼质量弹簧系统在跃阶力作用下的动态响应。
假设初始条件等于零。
(答案:00200002(1cos t),t T (t)[cos (t T)cos t],t TF m x F m ωωωωω⎧-≤⎪⎪=⎨⎪-->⎪⎩ )4、如图所示,试确定一个自由度系统对图中抛物线施力函数2211(1t /)Q Q t =- 的无阻尼反应。
(答案:○110t t ≤≤时,21222112(1)(1cos t)Q t x m t t ωωω⎡⎤=+--⎢⎥⎣⎦ ;○21t t >时,111221122[cos (t t )cos t]sin (t t )cos t Q x m t t ωωωωωωω⎧⎫=-----⎨⎬⎩⎭)五、逐步积分方法1、如图(a )所示,单自由度钢架,受图(b )所示冲击载荷,取0.12t s ∆= ,试用线性加速度的逐步积分法,计算0<t<0.72s 时段内的线性弹性位移响应。
六、单自由度系统的减振与隔振1、简述减振与隔振的常用方法?结合例子说明隔振的基本原理?七、两自由度系统自由振动1、如图所示,建立系统的运动方程(答案:121220000000M m ml x c c x k k x ml ml mgl θθθ+++⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦)2、如图所示的一个圆板,质量为M ,半径为r ,在板的中心装有一个长度为L 的单摆。
摆端有集中质量m ,摆可以自由旋转,板只能滚动而不滑动。
求系统在平衡位置作微幅振动的固有频率。
(答案:120,ωω==)3、如图所示,当只研究汽车在铅垂平面的振动时,可将车身简化为支撑在两弹簧上的刚性梁。
若汽车质量m=1500kg ,绕质心c 的转动惯量I=22002kg m ⋅,1235/,38/k kN m k kN m ==,121.4, 1.7L m L m ==,以x 和θ为广义坐标,求其自振频率和振型。
(思考:是否可以用弹簧处的铅垂位移1y 和2y 为广义坐标求解?比较两者的异同点)(答案: 12126.82/,9.12/,(10.205),(13.324)T T rad s rad s ωωφφ===-= ;思考比较:列运动微分方程可知后者选取的自由度坐标不仅位移1y 和2y 耦合,而且加速度1y 和2y 之间也有耦合)八&九、多自由度系统自由振动1、《结构动力学基础》 第三章,第3-1题。
2、如图所示,假设(t)0(i 1,2,3)i f == ,建立系统的运动微分方程。
(答案:11122112212222332223323333433343000000000m x c c c x k k k x m x c c c c x k k k k x m x c c c x k k k x +-+-⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+-+-+-+-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-+-+⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦)3、如图所示,三个单摆用弹簧连接,13212,2,m m m m m k k k ===== ,以(i 1,2,3)i φ=为广义坐标。
求系统的自振频率和振型,并画出振型图。
(答案:123ωωω===; 123[111],[101],[111]T T T φφφ==-=- )4、如图,用逆幂法求解系统的第1阶自振频率和振型,要求21ω 的误差3110ε-< 。
(1(11.8022.246)T A ω== )5、如图,已知弹簧质量系统,用综合法求解全部特征对,并画出全部振型图。
(答案:2211222233440.586,(1,2.414,2.414,1);1,(1,2,2,1);2,(1,1,1,1); 3.414,(1,0.414,0..414,1)T T T Tk k A A m mk k A A m mωωωω====--==--==-- )6、如图所示悬臂梁质量不计,梁的弯曲刚度为EI,求系统的固有频率和模态,求作用在梁自由端的静力P 突然移去后系统的自由振动响应。
(答案:121232123112[13.1205],[10.3205],(2.6605cos 0.0062cos )(0.8526cos 0.0193cos )TT Pl x t t EI Pl x t t EI ωωωωωω====-⎧⎫=+⎪⎪⎪⎪⎨⎬⎪⎪=-⎪⎪⎩⎭ϕϕ)十、多自由度系统强迫振动1、如图所示,在第一个质量块个作用有外力sin p t = 。
两质量块的质量122m m == ,弹簧刚度1231k k k === 。
试用振型分解法求系统的稳态响应。
(答案:0sin 1t ⎡⎤⎢⎥⎣⎦)11、动力减振原理与减振器试简述动力减振器的设计步骤?十二&十三、动力学能量原理1、无质量刚性杆可绕杆端的轴自由转动,另一端附有质量m 1,并用弹簧悬挂两质量m 2和m 3,杆中点支以弹簧使杆呈水平,如图所示。
试写出系统动能和势能表达式并依次写出系统的刚度阵和质量阵。
(答案:233222*********x m x m x m T ++=)3232122332232212121)(21)421x x k x x k x k x k k x k k U --++++=(十四、瑞利法1、计算重力坝沿水流方向的自振频率时,可以取沿坝轴线方向单位长度的坝体近似地简化为如图所示的变截面悬臂梁。
试用李兹法求如图所示重力坝的第一阶和第二阶自振频率。
(答案:ρωρωEg h b Eg h b 2221994.4,535.1==)2、取试探振型(1,2 3)T ,用瑞利法求解如图所示三自由度系统的基频。
(答案:mk 465.01=ω)3、《结构动力学基础》第五章,第8题。